Real-World Application of a Quantitative Systems Pharmacology (QSP) Model to Predict Potassium Concentrations from Electronic Health Records: A Pilot Case towards Prescribing Monitoring of Spironolactone
Abstract
1. Introduction
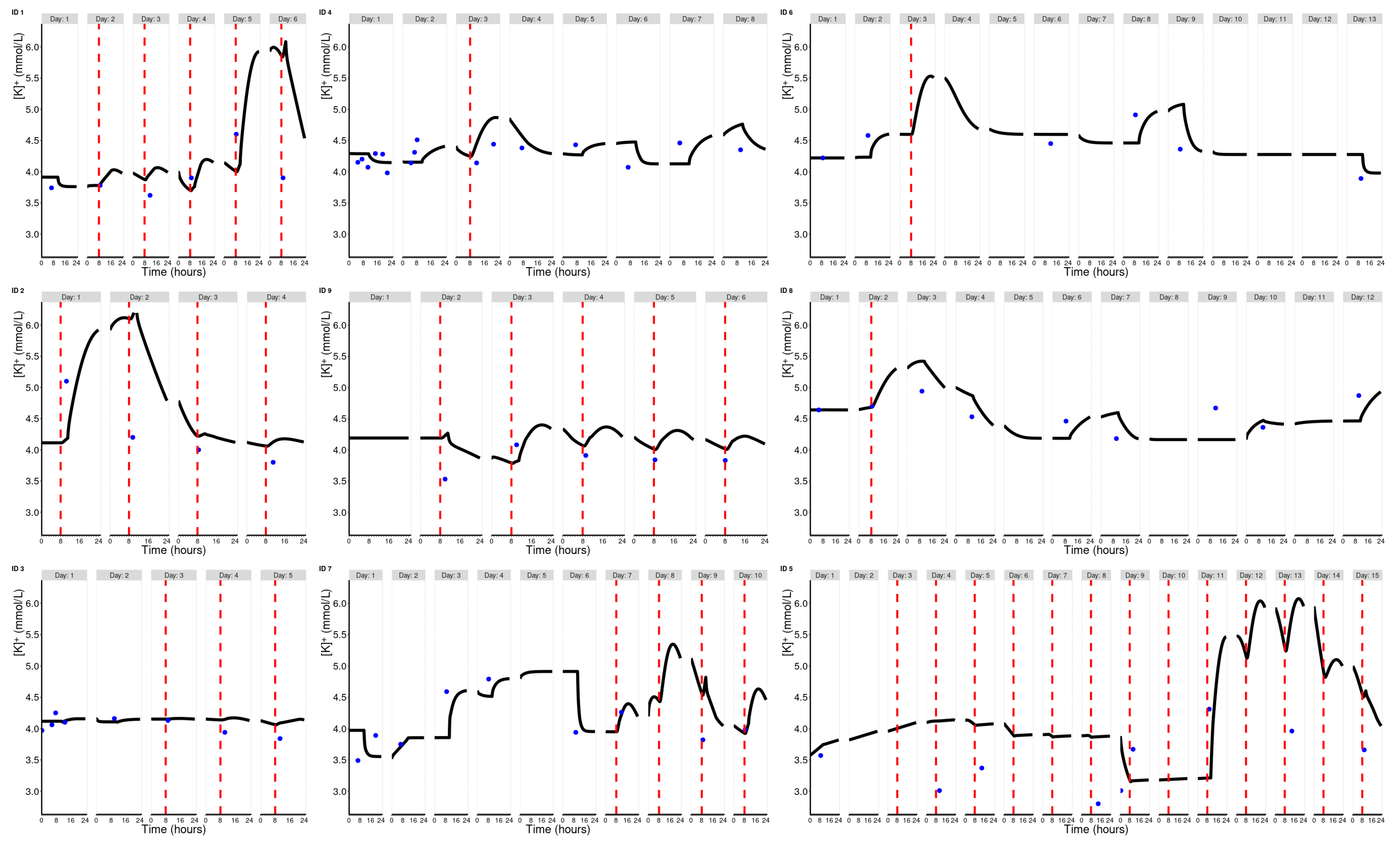
2. Results
3. Discussion
4. Materials and Methods
4.1. EHR Data Management
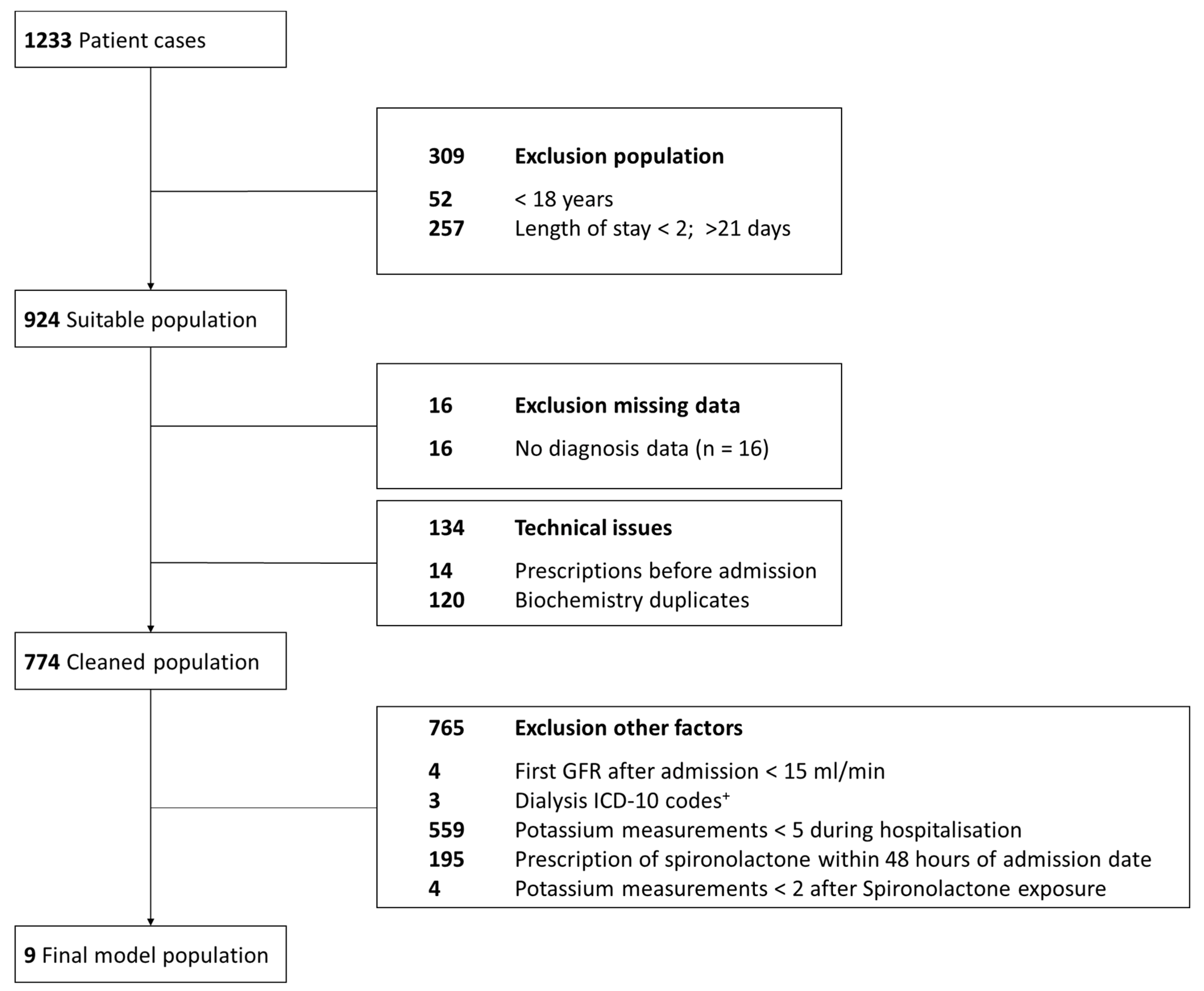
4.1.1. Data Sources and Study Population
4.1.2. Data Preparation of Real-World EHR for Modeling and Simulation
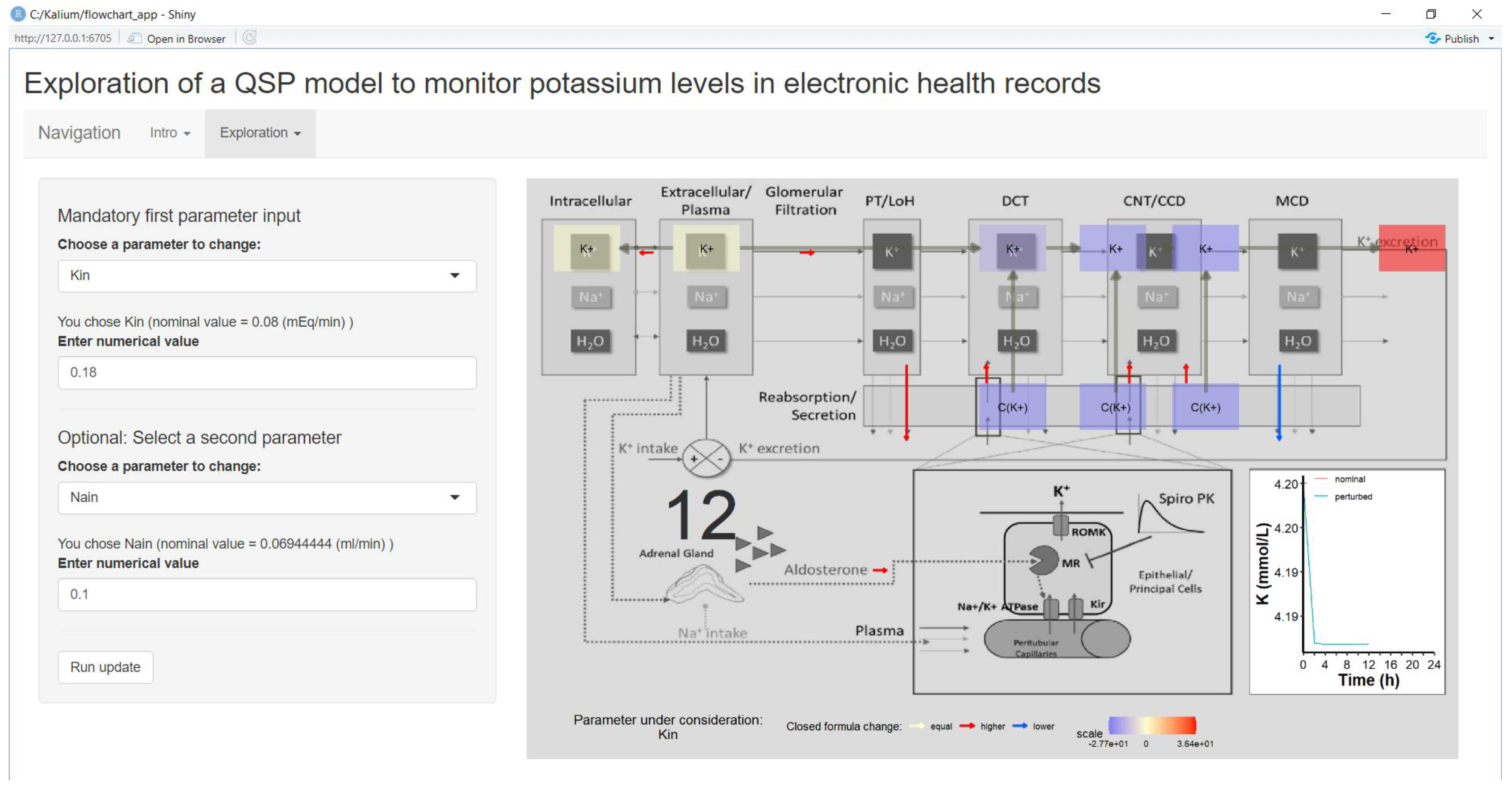
4.2. Parameter Exploration via Shiny App
4.2.1. Fundamental QSP Model
4.2.2. Shiny App
4.3. Parameter Sensitivity Analysis
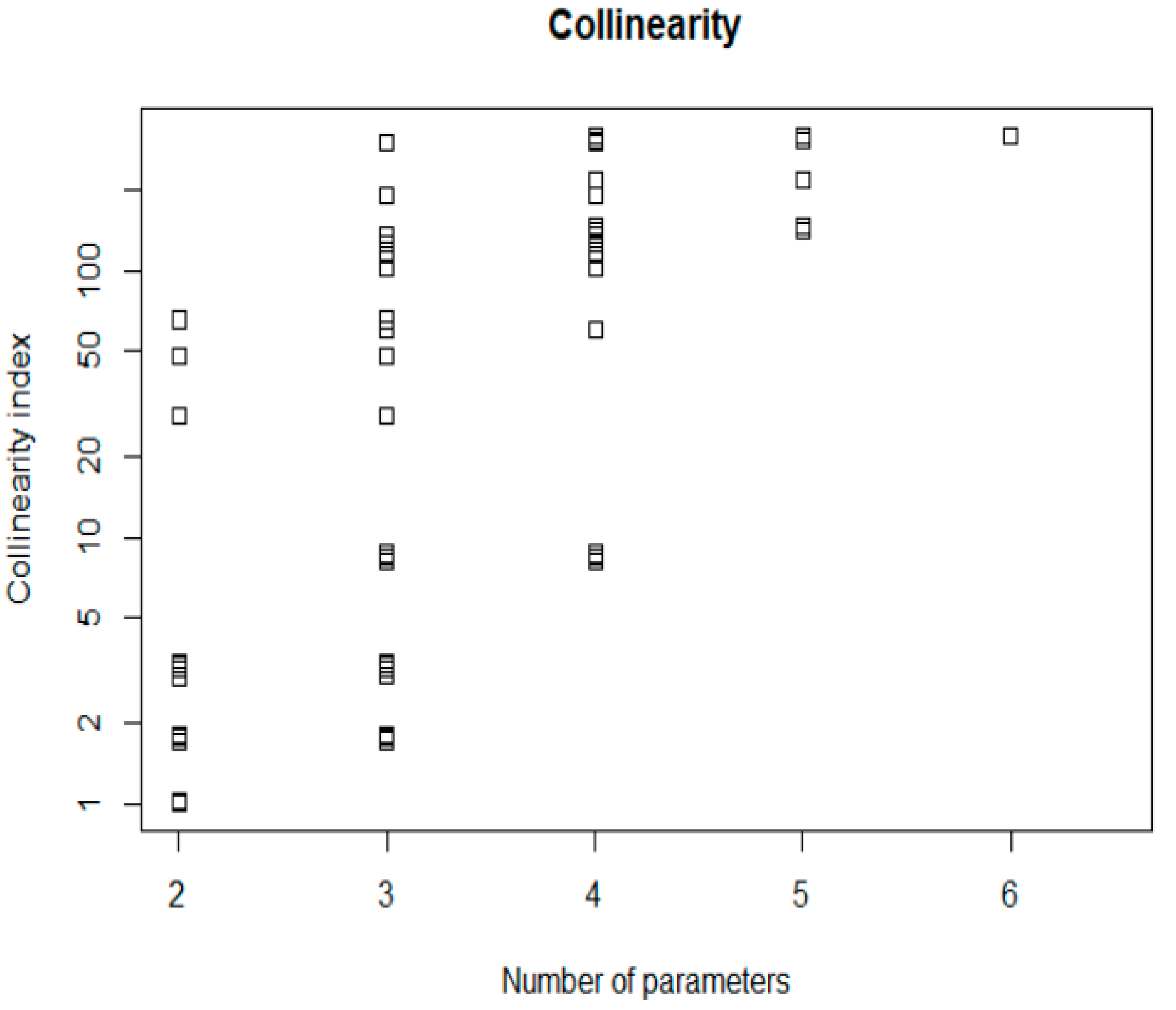
4.3.1. Local Sensitivity Analysis (SA) and Identifiability Analysis (IA)
4.3.2. Global Sensitivity Analysis and Uncertainty Analysis
4.4. Parameter (Variability) Estimation
4.5. Bayesian Parameter Estimation to Predict Potassium Concentrations
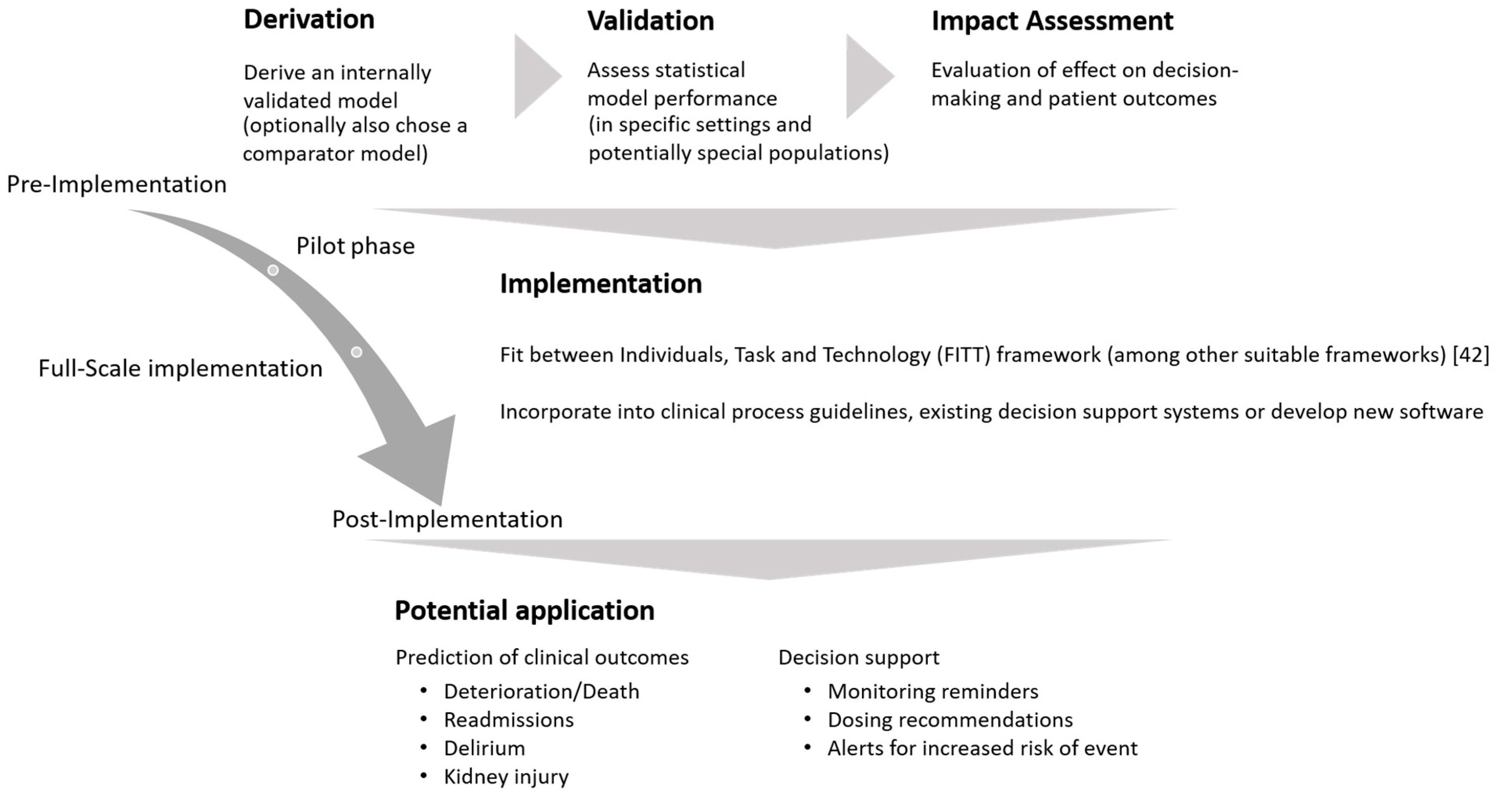
4.5.1. Estimation Setting of a (QSP) Prescribing Monitoring
4.5.2. Performance Assessment
4.6. Software
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Step | Workflow Description | Key Questions to Answer |
|---|---|---|
| 1 | Data preparation of real-world EHR for Modeling and Simulation | How can the formats for laboratory measurements, medical history, and drug administration harmonized to allow model development and model application to predict future potassium trajectories? |
| 2 | Model exploration and parameter assessment | Which parameters are measurable, which are influential and clinically meaningful in EHR data? |
| 3 | Sensitivity:
| Which parameters are influential and estimable that allow flexible predictions when being estimated from real-world EHR data? |
| 4 | Variability in independent data
| (a) Can parameters actually be estimated on a population level in real-world data? (b) How large is the expected IIV and how can this expectation inform the design of the IIV matrix for the Bayesian a posteriori estimation (step 5)? |
| 5 | Bayesian a posteriori estimation [33] to predict future observations
| How are prior information on individual parameters θ and their IIV Ω chosen for (updated) prediction in the longitudinal course of an inpatient stay? |
Appendix B
| Subject Characteristic | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Overall (N = 9) Mean (±SD), Median [Min, Max] or % |
|---|---|---|---|---|---|---|---|---|---|---|
| Age [years] | 74 | 88 | 57 | 70 | 56 | 57 | 59 | 83 | 66 | 68 (±12) |
| Sex (male = 1) | male | female | male | male | female | male | male | male | male | Female: 22% |
| Weight [kg] | 85.0 | 54.0 | 92.0 | 104.0 | 85.0 | 93.0 | 87.0 | 89.0 | 90.0 | 87 (±14) |
| Length of stay [days] | 6.4 | 5.8 | 5.9 | 9.0 | 18.8 | 13.0 | 9.7 | 14.1 | 8.9 | 10.2 (±4.4) |
| Baseline laboratory measurements | ||||||||||
| eGFR (CKD-EPI) [ml/min/1.73 m2] | 69 | 73 | 59 | 33 | 103 | 91 | 101 | 27 | 89 | 72 (±28) |
| Sodium [mmol/L] | 142 | 143 | 135 | 143 | 133 | 142 | 137 | 140 | 138 | 139.22 (±3.67) |
| Potassium [mmol/L] | 4.13 | 4.07 | 4.09 | 4.13 | 3.56 | 4.12 | 3.92 | 4.86 | 4.18 | 4.12 (±0.34) |
| Spironolactone dose | 25 | 25 | 50/100 | 25 | 100 | 25 | 25 | 50 | 25 | 25 [25, 100] |
| Co-medication during spironolactone administration | ||||||||||
| ACE inhibitors 1 [y/n] | no | yes | no | no | no | yes | no | yes | yes | 44% |
| Angiotensin receptor blocker 2 [y/n] | yes | no | no | no | no | no | no | no | no | 11% |
| High ceiling diuretics 3 [y/n] | no | no | yes | no | yes | no | yes | yes | yes | 56% |
| Low ceiling diuretics 4 [y/n] | no | yes | no | no | no | no | no | no | no | 11% |
| Oral potassium additives 5 [y/n] | no | no | no | no | yes | no | yes | yes | yes | 44% |
| Selected comorbidities (Elixhauser [41]) | ||||||||||
| Congestive heart failure [y/n] | yes | no | no | yes | no | yes | yes | yes | yes | 67% |
| Cardiac arrhythmias [y/n] | no | yes | no | yes | yes | yes | yes | no | no | 56% |
| Hypertension, uncomplicated [y/n] | no | no | no | yes | no | no | yes | yes | yes | 44% |
| Diabetes, uncomplicated [y/n] | no | no | no | yes | no | no | no | no | no | 11% |
| Hypothyroidism [y/n] | no | no | yes | no | yes | no | no | no | no | 22% |
| Liver disease [y/n] | no | no | yes | no | yes | no | no | no | no | 22% |
| Coagulopathy [y/n] | no | no | yes | no | no | no | no | no | no | 11% |
| Fluid and electrolyte disorders [y/n] | no | no | no | yes | yes | no | no | no | no | 22% |
| Alcohol abuse [y/n] | no | no | yes | no | yes | no | no | no | no | 22% |
| Elixhauser total score (unweighted) | 1.00 | 1.00 | 4.00 | 5.00 | 6.00 | 2.00 | 3.00 | 2.00 | 2.00 | 2.00 [1.00, 6.00] |




Appendix C




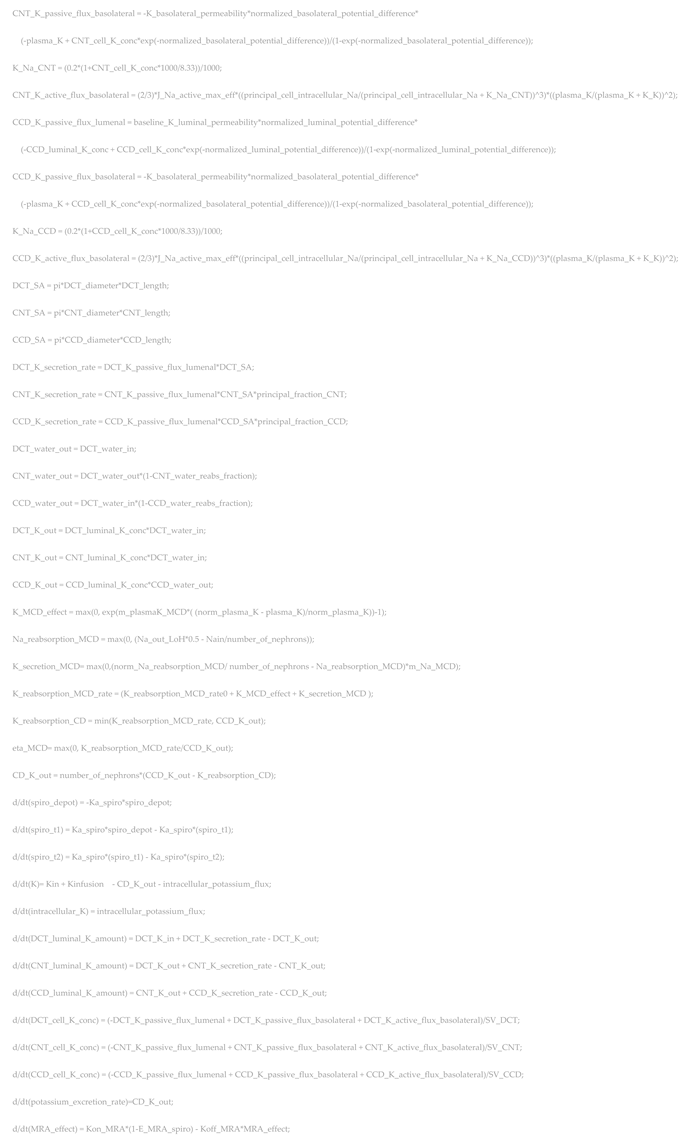

References
- Helmlinger, G.; Sokolov, V.; Peskov, K.; Hallow, K.M.; Kosinsky, Y.; Voronova, V.; Chu, L.; Yakovleva, T.; Azarov, I.; Kaschek, D.; et al. Quantitative Systems Pharmacology: An Exemplar Model-Building Workflow with Applications in Cardiovascular, Metabolic, and Oncology Drug Development. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 380–395. [Google Scholar] [CrossRef]
- Musante, C.J.; Ramanujan, S.; Schmidt, B.J.; Ghobrial, O.G.; Lu, J.; Heatherington, A.C. Quantitative Systems Pharmacology: A Case for Disease Models. Clin. Pharmacol. Ther. 2017, 101, 24–27. [Google Scholar] [CrossRef]
- Visser, S.A.; de Alwis, D.P.; Kerbusch, T.; Stone, J.A.; Allerheiligen, S.R. Implementation of quantitative and systems pharmacology in large pharma. CPT Pharmacomet. Syst. Pharmacol. 2014, 3, e142. [Google Scholar] [CrossRef]
- Cucurull-Sanchez, L. An industry perspective on current QSP trends in drug development. J. Pharmacokinet. Pharmacodyn. 2024, in press. [CrossRef]
- Lasiter, L.; Tymejczyk, O.; Garrett-Mayer, E.; Baxi, S.; Belli, A.J.; Boyd, M.; Christian, J.B.; Cohen, A.B.; Espirito, J.L.; Hansen, E.; et al. Real-world Overall Survival Using Oncology Electronic Health Record Data: Friends of Cancer Research Pilot. Clin. Pharmacol. Ther. 2022, 111, 444–454. [Google Scholar] [CrossRef]
- Purpura, C.A.; Garry, E.M.; Honig, N.; Case, A.; Rassen, J.A. The Role of Real-World Evidence in FDA-Approved New Drug and Biologics License Applications. Clin. Pharmacol. Ther. 2022, 111, 135–144. [Google Scholar] [CrossRef]
- Dagenais, S.; Russo, L.; Madsen, A.; Webster, J.; Becnel, L. Use of Real-World Evidence to Drive Drug Development Strategy and Inform Clinical Trial Design. Clin. Pharmacol. Ther. 2022, 111, 77–89. [Google Scholar] [CrossRef]
- Israni, R.; Betts, K.A.; Mu, F.; Davis, J.; Wang, J.; Anzalone, D.; Uwaifo, G.I.; Szerlip, H.; Fonseca, V.; Wu, E. Determinants of Hyperkalemia Progression Among Patients with Mild Hyperkalemia. Adv. Ther. 2021, 38, 5596–5608. [Google Scholar] [CrossRef]
- Eschmann, E.; Beeler, P.E.; Schneemann, M.; Blaser, J. Developing strategies for predicting hyperkalemia in potassium-increasing drug-drug interactions. J. Am. Med. Inf. Assoc. 2017, 24, 60–66. [Google Scholar] [CrossRef]
- Beeler, P.E.; Eschmann, E.; Schneemann, M.; Blaser, J. Negligible impact of highly patient-specific decision support for potassium-increasing drug-drug interactions—A cluster-randomised controlled trial. Swiss Med. Wkly. 2019, 149, w20035. [Google Scholar] [CrossRef]
- Braakman, S.; Pathmanathan, P.; Moore, H. Evaluation framework for systems models. CPT Pharmacomet. Syst. Pharmacol. 2022, 11, 264–289. [Google Scholar] [CrossRef] [PubMed]
- Cucurull-Sanchez, L.; Chappell, M.J.; Chelliah, V.; Amy Cheung, S.Y.; Derks, G.; Penney, M.; Phipps, A.; Malik-Sheriff, R.S.; Timmis, J.; Tindall, M.J.; et al. Best Practices to Maximize the Use and Reuse of Quantitative and Systems Pharmacology Models: Recommendations from the United Kingdom Quantitative and Systems Pharmacology Network. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 259–272. [Google Scholar] [CrossRef] [PubMed]
- Bittmann, J.A.; Scherkl, C.; Meid, A.D.; Haefeli, W.E.; Seidling, H.M. Event Analysis for Automated Estimation of Absent and Persistent Medication Alerts: Novel Methodology. JMIR Med. Inf. 2024, 12, e54428. [Google Scholar] [CrossRef] [PubMed]
- Maddah, E.; Hallow, K.M. A quantitative systems pharmacology model of plasma potassium regulation by the kidney and aldosterone. J. Pharmacokinet. Pharmacodyn. 2022, 49, 471–486. [Google Scholar] [CrossRef] [PubMed]
- Gardiner, P.; Schrode, K.; Quinlan, D.; Martin, B.K.; Boreham, D.R.; Rogers, M.S.; Stubbs, K.; Smith, M.; Karim, A. Spironolactone metabolism: Steady-state serum levels of the sulfur-containing metabolites. J. Clin. Pharmacol. 1989, 29, 342–347. [Google Scholar] [CrossRef] [PubMed]
- McInnes, G.T.; Perkins, R.M.; Shelton, J.R.; Harrison, I.R. Spironolactone dose-response relationships in healthy subjects. Br. J. Clin. Pharmacol. 1982, 13, 513–518. [Google Scholar] [CrossRef]
- Pérez-Blanco, J.S.; Lanao, J.M. Model-Informed Precision Dosing (MIPD). Pharmaceutics 2022, 14, 2731. [Google Scholar] [CrossRef] [PubMed]
- Darwich, A.S.; Polasek, T.M.; Aronson, J.K.; Ogungbenro, K.; Wright, D.F.B.; Achour, B.; Reny, J.L.; Daali, Y.; Eiermann, B.; Cook, J.; et al. Model-Informed Precision Dosing: Background, Requirements, Validation, Implementation, and Forward Trajectory of Individualizing Drug Therapy. Annu. Rev. Pharmacol. Toxicol. 2021, 61, 225–245. [Google Scholar] [CrossRef] [PubMed]
- Keizer, R.J.; Ter Heine, R.; Frymoyer, A.; Lesko, L.J.; Mangat, R.; Goswami, S. Model-Informed Precision Dosing at the Bedside: Scientific Challenges and Opportunities. CPT Pharmacomet. Syst. Pharmacol. 2018, 7, 785–787. [Google Scholar] [CrossRef]
- Ramos, C.I.; González-Ortiz, A.; Espinosa-Cuevas, A.; Avesani, C.M.; Carrero, J.J.; Cuppari, L. Does dietary potassium intake associate with hyperkalemia in patients with chronic kidney disease? Nephrol. Dial. Transpl. 2021, 36, 2049–2057. [Google Scholar] [CrossRef]
- Connell, J.M.; Davies, E. The new biology of aldosterone. J. Endocrinol. 2005, 186, 1–20. [Google Scholar] [CrossRef] [PubMed]
- He, F.J.; Markandu, N.D.; Sagnella, G.A.; de Wardener, H.E.; MacGregor, G.A. Plasma sodium: Ignored and underestimated. Hypertension 2005, 45, 98–102. [Google Scholar] [CrossRef] [PubMed]
- MacKenzie, S.M.; van Kralingen, J.C.; Davies, E. Regulation of Aldosterone Secretion. Vitam. Horm. 2019, 109, 241–263. [Google Scholar]
- Wang, K.; Parrott, N.; Olivares-Morales, A.; Dudal, S.; Singer, T.; Lavé, T.; Ribba, B. Real-World Data and Physiologically-Based Mechanistic Models for Precision Medicine. Clin. Pharmacol. Ther. 2020, 107, 694–696. [Google Scholar] [CrossRef] [PubMed]
- Brun, R.; Reichert, P. Practical identifiability analysis of large environmental simulation models. Water Resour. Res. 2001, 37, 1015–1030. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Hsieh, N.H.; Reisfeld, B.; Chiu, W.A. pksensi: An R package to apply global sensitivity analysis in physiologically based kinetic modeling. SoftwareX 2020, 12, 100609. [Google Scholar] [CrossRef] [PubMed]
- Faelens, R.; Luyckx, N.; Kuypers, D.; Bouillon, T.; Annaert, P. Predicting model-informed precision dosing: A test-case in tacrolimus dose adaptation for kidney transplant recipients. CPT Pharmacomet. Syst. Pharmacol. 2022, 11, 348–361. [Google Scholar] [CrossRef] [PubMed]
- Krieger, A.; Pistikopoulos, E.N. Model predictive control of anesthesia under uncertainty. Comput. Chem. Eng. 2014, 71, 699–707. [Google Scholar] [CrossRef]
- Saeheng, T.; Na-Bangchang, K.; Karbwang, J. Utility of physiologically based pharmacokinetic (PBPK) modeling in oncology drug development and its accuracy: A systematic review. Eur. J. Clin. Pharmacol. 2018, 74, 1365–1376. [Google Scholar] [CrossRef]
- Wang, W.; Hallow, K.M.; James, D.A. A Tutorial on RxODE: Simulating Differential Equation Pharmacometric Models in R. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving Differential Equations in R: Package deSolve. J. Stat. Softw. 2010, 33, 9. [Google Scholar] [CrossRef]
- Leven, C.; Coste, A.; Mané, C. Free and Open-Source Posologyr Software for Bayesian Dose Individualization: An Extensive Validation on Simulated Data. Pharmaceutics 2022, 14, 442. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, C.M. A model qualification method for mechanistic physiological QSP models to support model-informed drug development. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Gadkar, K.; Kirouac, D.C.; Mager, D.E.; van der Graaf, P.H.; Ramanujan, S. A Six-Stage Workflow for Robust Application of Systems Pharmacology. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 235–249. [Google Scholar] [CrossRef]
- Sher, A.; Niederer, S.A.; Mirams, G.R.; Kirpichnikova, A.; Allen, R.; Pathmanathan, P.; Gavaghan, D.J.; van der Graaf, P.H.; Noble, D. A Quantitative Systems Pharmacology Perspective on the Importance of Parameter Identifiability. Bull. Math. Biol. 2022, 84, 39. [Google Scholar] [CrossRef]
- Soetaert, K.; Petzoldt, T. Inverse Modelling, Sensitivity and Monte Carlo Analysis in R Using Package FME. J. Stat. Softw. 2010, 33, 3. [Google Scholar] [CrossRef]
- Hsieh, N.H.; Reisfeld, B.; Bois, F.Y.; Chiu, W.A. Applying a Global Sensitivity Analysis Workflow to Improve the Computational Efficiencies in Physiologically-Based Pharmacokinetic Modeling. Front. Pharmacol. 2018, 9, 588. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol Sensitivity Analysis: A Tool to Guide the Development and Evaluation of Systems Pharmacology Models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef]
- Omlin, M.; Reichert, P.; Forster, R. Biogeochemical model of Lake Zürich: Model equations and results. Ecol. Model. 2001, 141, 77–103. [Google Scholar] [CrossRef]
- Elixhauser, A.; Steiner, C.; Harris, D.R.; Coffey, R.M. Comorbidity measures for use with administrative data. Med. Care 1998, 36, 8–27. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.C.; Shah, N.U.; Haack, A.; Baxter, S.L. Clinical Implementation of Predictive Models Embedded within Electronic Health Record Systems: A Systematic Review. Informatics 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
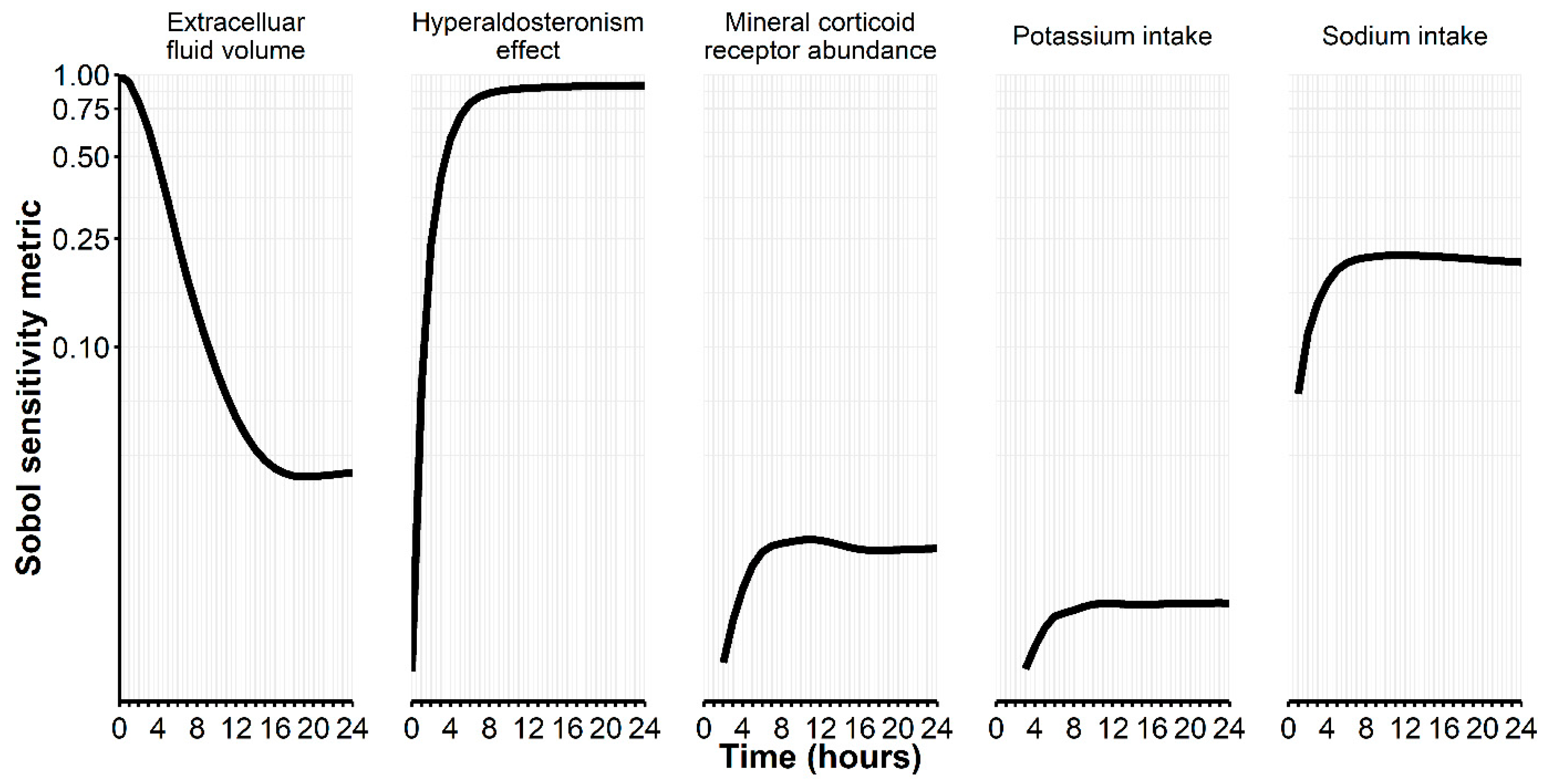
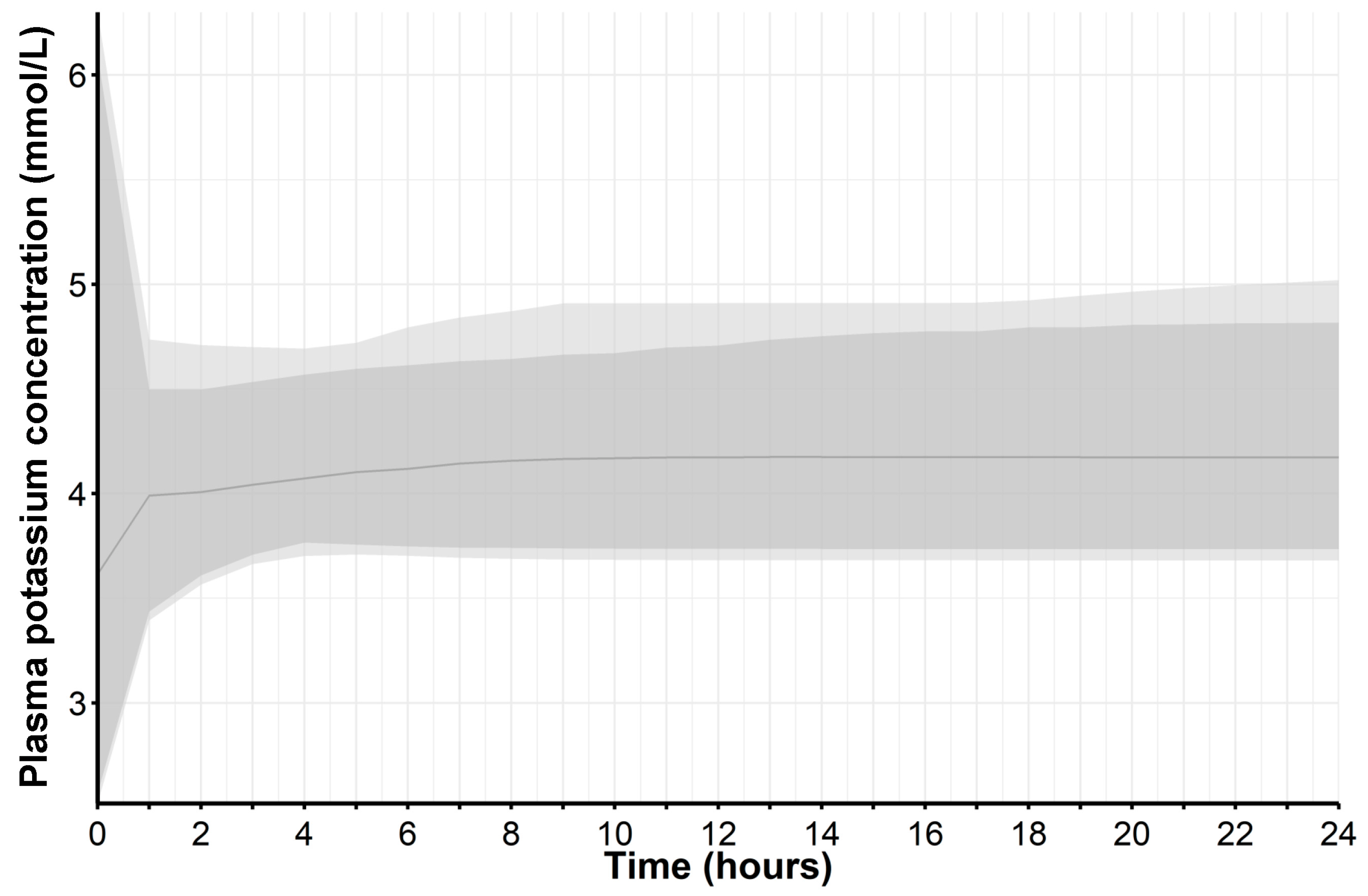
| Sample | Average Fold Error (AFE) | Absolute Average Fold Error (AAFE) | Percent Prediction Error (PPE) 1 |
|---|---|---|---|
| All (n = 9) | 1.06 | 1.19 | 7.3 [5.6; 9] |
| ACE inhibitor use during spironolactone (n = 4) | 1.00 | 1.15 | 6.2 [2.9; 9.5] |
| Without potassium supplementation during spironolactone (n = 5) | 1.07 | 1.19 | 7.1 [4.7; 9.4] |
| With potassium supplementation during spironolactone (n = 4) | 1.04 | 1.20 | 7.7 [5.2; 10] |
| High-ceiling diureticsduring spironolactone(n = 5) | 1.04 | 1.16 | 6.4 [4.4; 8.5] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meid, A.D.; Scherkl, C.; Metzner, M.; Czock, D.; Seidling, H.M. Real-World Application of a Quantitative Systems Pharmacology (QSP) Model to Predict Potassium Concentrations from Electronic Health Records: A Pilot Case towards Prescribing Monitoring of Spironolactone. Pharmaceuticals 2024, 17, 1041. https://doi.org/10.3390/ph17081041
Meid AD, Scherkl C, Metzner M, Czock D, Seidling HM. Real-World Application of a Quantitative Systems Pharmacology (QSP) Model to Predict Potassium Concentrations from Electronic Health Records: A Pilot Case towards Prescribing Monitoring of Spironolactone. Pharmaceuticals. 2024; 17(8):1041. https://doi.org/10.3390/ph17081041
Chicago/Turabian StyleMeid, Andreas D., Camilo Scherkl, Michael Metzner, David Czock, and Hanna M. Seidling. 2024. "Real-World Application of a Quantitative Systems Pharmacology (QSP) Model to Predict Potassium Concentrations from Electronic Health Records: A Pilot Case towards Prescribing Monitoring of Spironolactone" Pharmaceuticals 17, no. 8: 1041. https://doi.org/10.3390/ph17081041
APA StyleMeid, A. D., Scherkl, C., Metzner, M., Czock, D., & Seidling, H. M. (2024). Real-World Application of a Quantitative Systems Pharmacology (QSP) Model to Predict Potassium Concentrations from Electronic Health Records: A Pilot Case towards Prescribing Monitoring of Spironolactone. Pharmaceuticals, 17(8), 1041. https://doi.org/10.3390/ph17081041







