Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage
Abstract
:1. Introduction
2. Energy Storage Model
2.1. Life Model
2.2. Cost Model
2.2.1. Annual Installation Costs
2.2.2. Annual Operation and Maintenance Costs
2.2.3. Energy Storage Capacity Attenuation Costs
2.2.4. Regularization Function for Smoothing the Power Fluctuation of the Grid Connection Point
2.3. Revenue Model
2.3.1. Electricity Revenue
- (1)
- The basic electricity revenue
- (2)
- The kilowatt hour electricity revenue
2.3.2. Reduced Average Annual Transformer Cost
2.3.3. Recovery Value
2.3.4. Demand Response Benefit
2.3.5. Reliability Benefit
2.3.6. Annual Benefit from Government Subsidies
3. Energy Storage Configuration Model
3.1. Objective Function
3.2. Restrictions
3.2.1. State-of-Charge Constraints
3.2.2. Power Limit Constraints
3.2.3. Constraints on the Number of Daily Cycles
3.2.4. Demand Control Constraints and Restrictions on Preventing Power Backwards
3.2.5. Magnification Constraint
3.2.6. Peak Clipping Constraints
3.2.7. Peak and Valley Constraints
4. Energy Storage Scheduling Model
4.1. Pre-Month Optimization Model
4.1.1. Objective Function
4.1.2. Restrictions
4.2. Daily Optimization Model
4.2.1. Objective Function
4.2.2. Restrictions
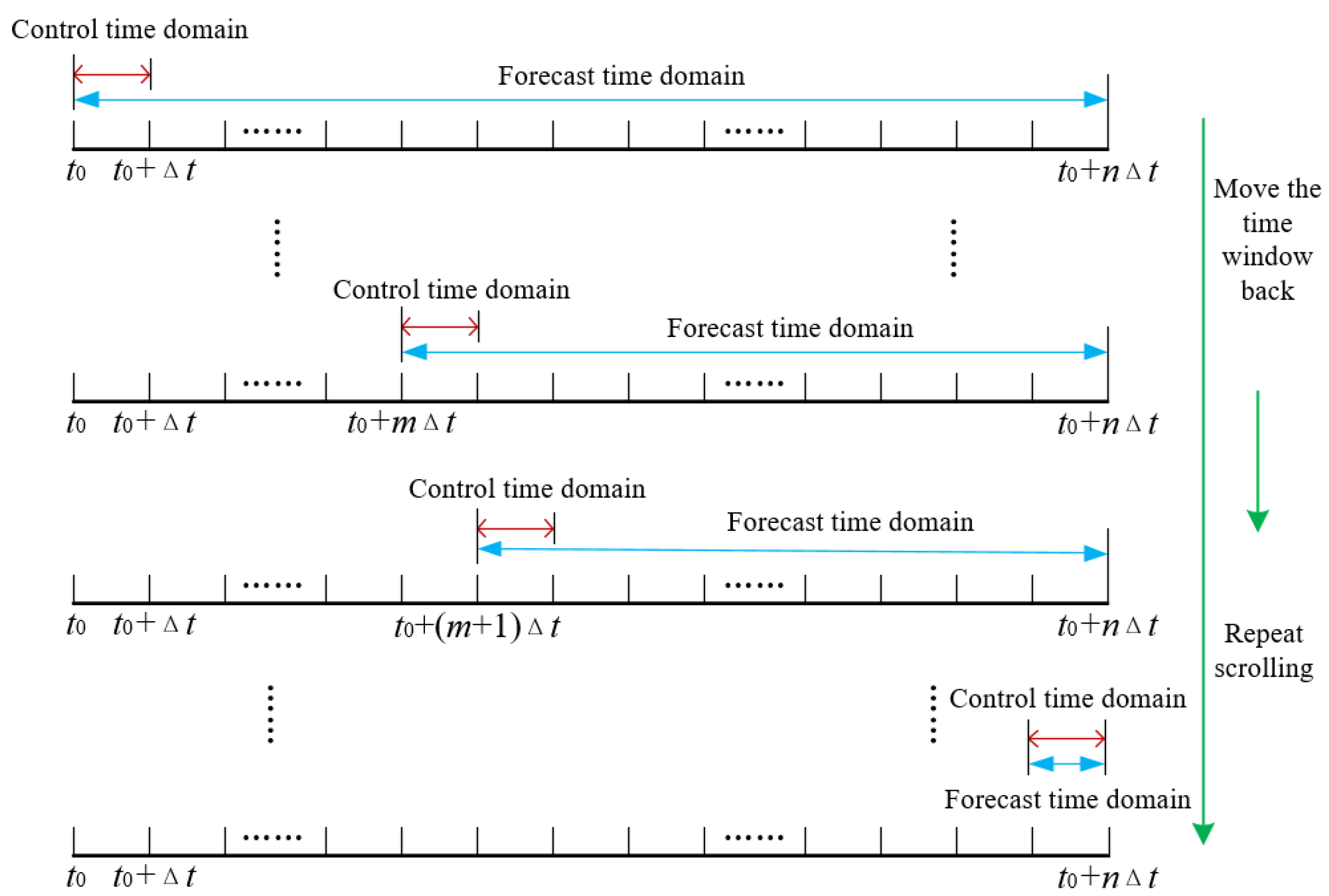
5. Intra-Day Optimal Scheduling Strategy for Energy Storage Based on MPC
6. Model Solving
7. Case Analysis
7.1. Parameter Description
7.2. Energy Storage Optimization Configuration Results
7.3. Energy Storage Optimization Scheduling Results
7.3.1. Monthly Demand Optimization Results
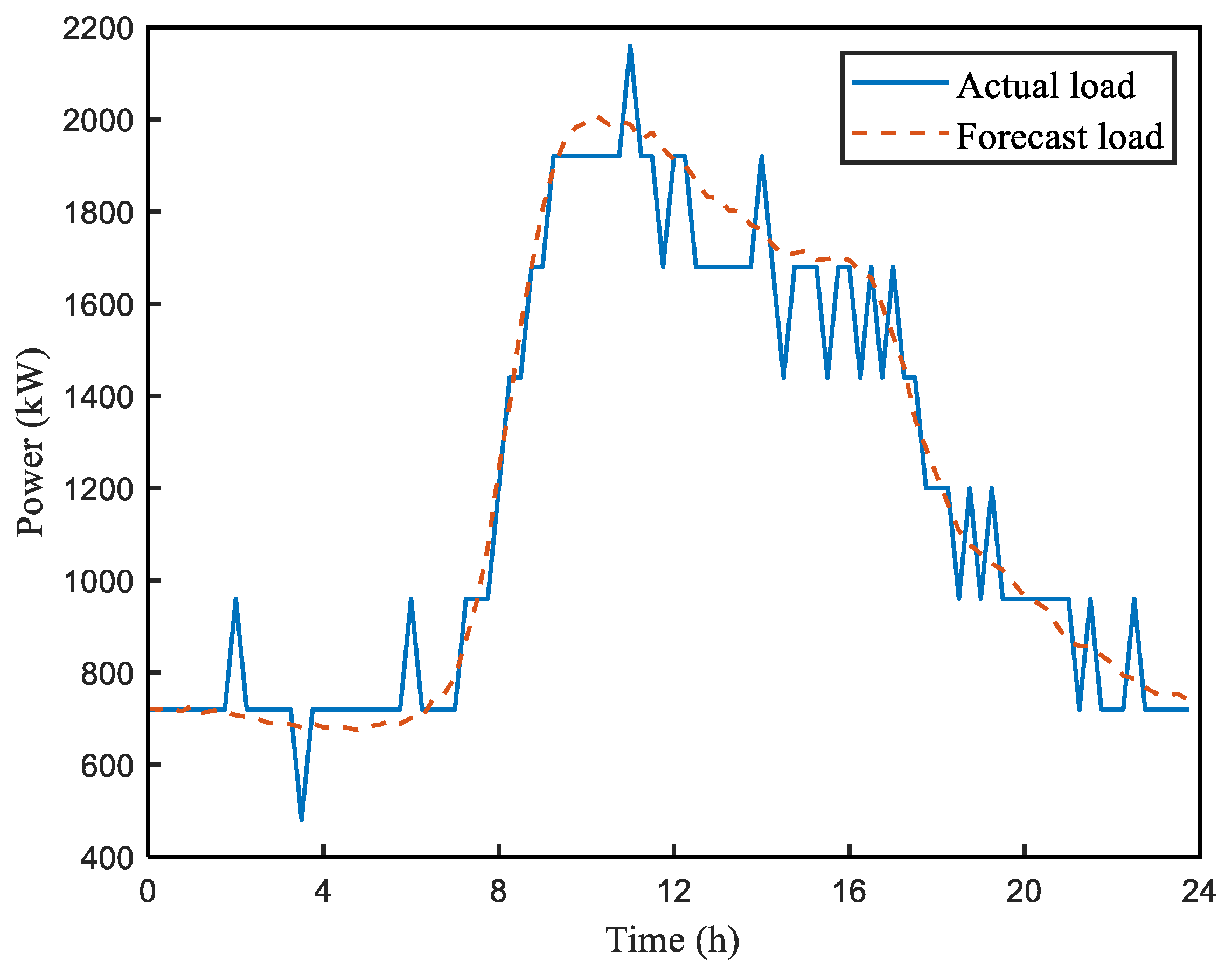
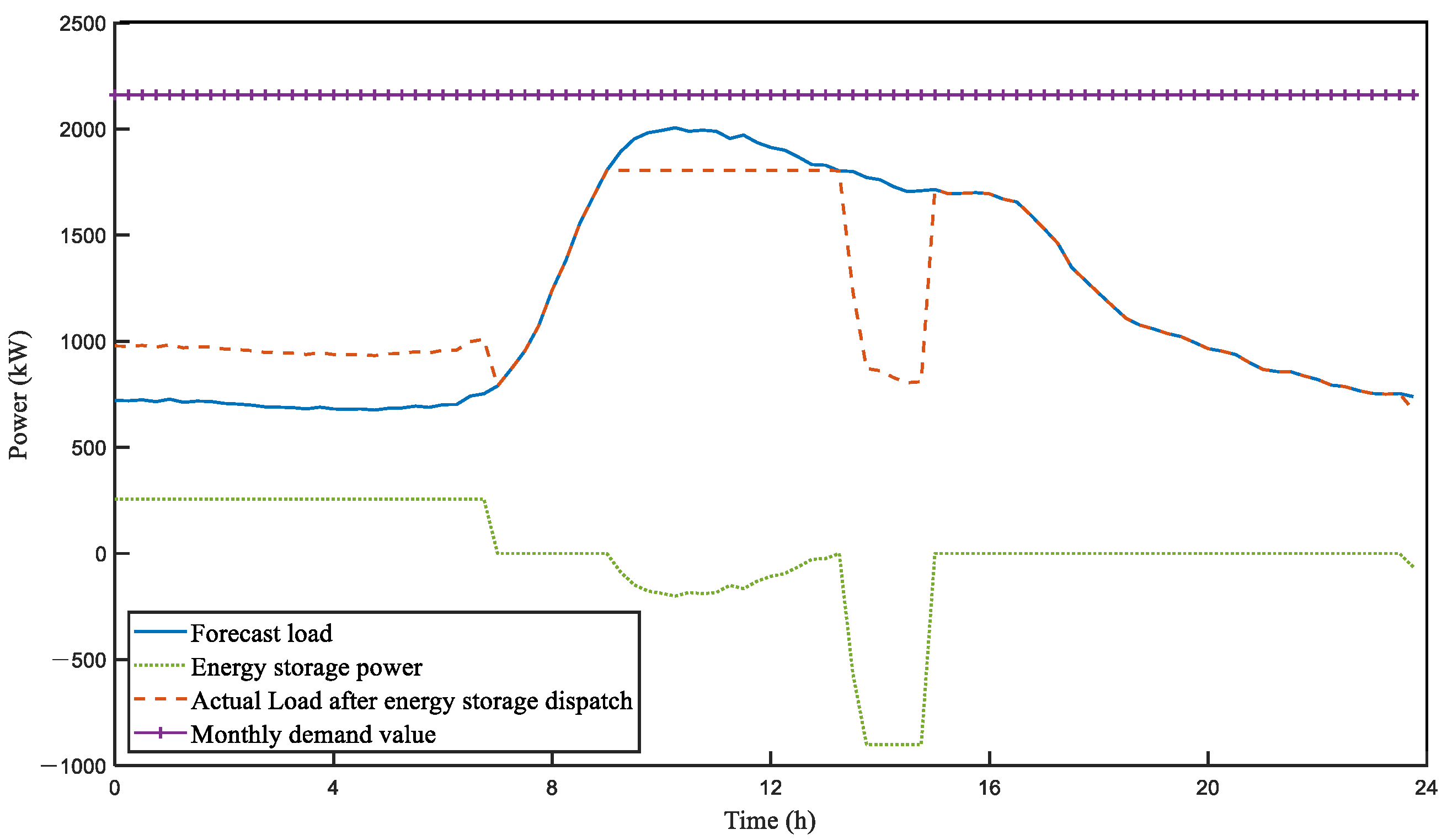
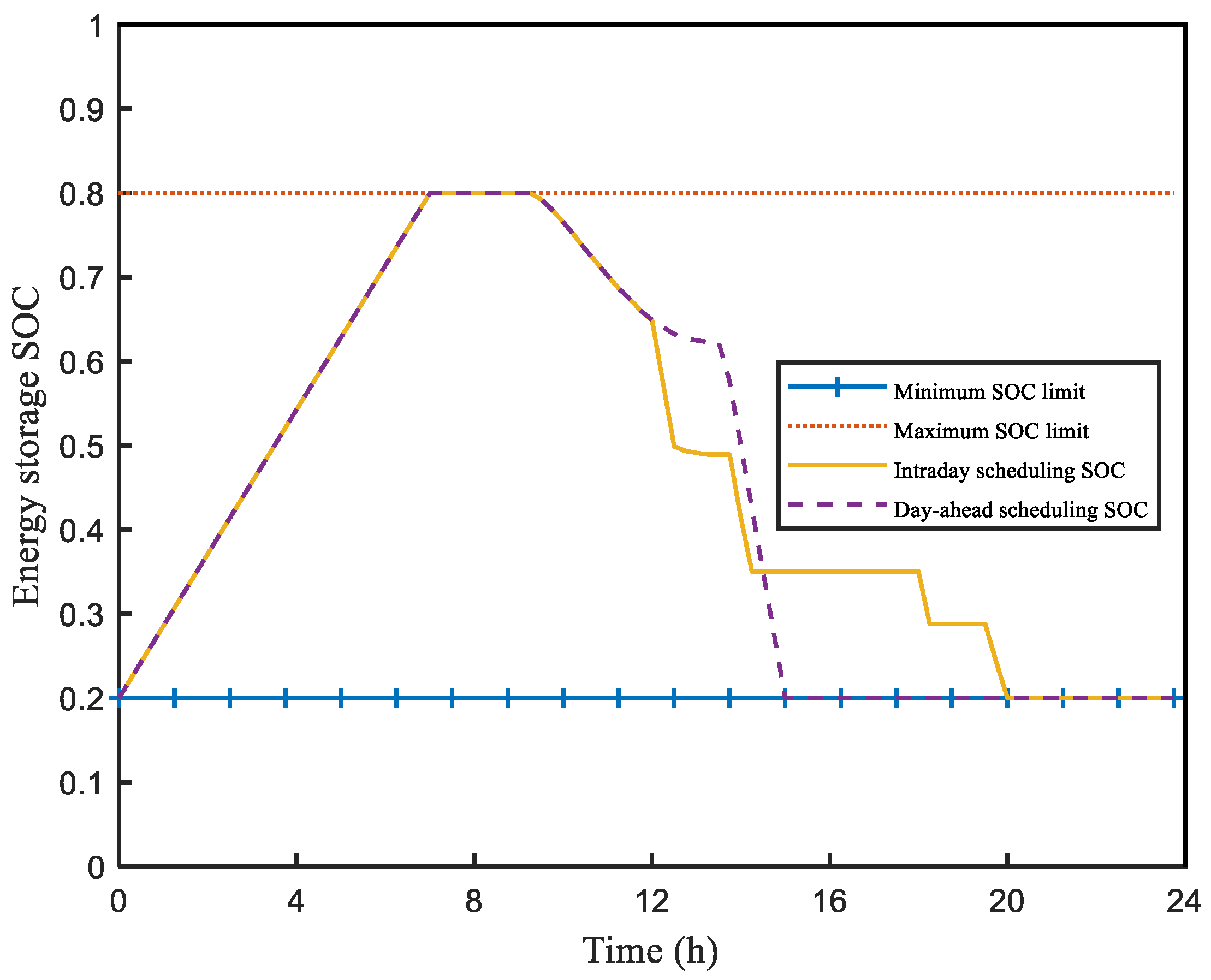
7.3.2. Daily Scheduling Results
8. Conclusions
- (1)
- The established model comprehensively considers the cost models, such as energy storage installation cost, operation and maintenance cost, capacity attenuation cost, regularization function for smoothing the power fluctuation of the grid connection point, and the revenue models, such as electricity tariff revenue, reduced transformer cost due to peak load reduction, recovery value, demand response benefit, reliability benefit due to reduced power outages and government subsidy benefit. The refinement of the model in the planning stage has greatly improved the accuracy of energy storage configuration, which is closer to the actual project.
- (2)
- After the user participates in the power demand response, the energy storage will be discharged in a large amount during the agreed time period, and the charging and discharging activities will be carried out according to the “low storage and high discharge” during the rest of the time period. The configured energy storage achieves peak shaving and valley filling and reduction of load peaks, creating economic benefits for users and ensuring the safe and reliable operation of the power grid.
- (3)
- The proposed optimal scheduling strategy, from full-time offline optimization to partial real-time optimization, not only ensures the economic benefits of users, but also improves the accuracy of energy storage optimization scheduling. It is robust in an uncertain load forecasting environment.
- (4)
- The characteristics of MPC rolling optimization and feedback correction make the model constantly updated, and there may be no optimal solution. In order to make the optimization go forward in a normal and orderly manner, the load forecast data are used at the moment before the scheduling time, and the actual load data are not replaced, which ensures the feasibility of the optimized scheduling model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, W.B.; Xiao, L.Y.; Shi, L.M.; Wang, Z.; Yang, W.H.; Wei, T.Z.; Du, X.J. Research on the principle and structure of a new energy storage technology named vacuum pipeline maglev energy storage. IEEE Access 2020, 8, 89351–89366. [Google Scholar] [CrossRef]
- Xiong, Y.F.; Si, Y.; Zheng, T.W.; Chen, L.J.; Mei, S.W. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game. Trans. China Electrotech. Soc. 2021, 36, 507–516. [Google Scholar]
- Li, Q.; Zhao, S.D.; Pu, Y.C.; Chen, W.R.; Yu, J. Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling. Trans. China Electrotech. Soc. 2021, 36, 486–495. [Google Scholar]
- Zeng, B.; Xu, F.Q.; Liu, Y.X.; Liu, Y.; Gong, D.W. High-dimensional multi-objective optimization for multi-energy coupled system planning with consideration of economic, environmental and social factors. Trans. China Electrotech. Soc. 2021, 36, 1434–1445. [Google Scholar]
- Zheng, H.; Xie, L.R.; Ye, L.; Lu, P.; Wang, K.F. Hybrid energy storage smoothing output fluctuation strategy considering photovoltaic dual evaluation indicators. Trans. China Electrotech. Soc. 2021, 36, 1805–1817. [Google Scholar]
- Li, J.H.; Hou, T.; Mu, G.; Yan, G.G.; Li, C.P. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment. Trans. China Electrotech. Soc. 2021, 36, 1791–1804. [Google Scholar]
- Vatani, B.; Chowdhury, B.; Lin, J. The role of demand response as an alternative transmission expansion solution in a capacity market. IEEE Trans. Ind. Appl. 2018, 54, 1039–1046. [Google Scholar] [CrossRef]
- Xiang, B.; Li, K.P.; Ge, X.X.; Zhen, Z.; Lu, X.X.; Wang, F. Day-ahead probabilistic forecasting of smart households’ demand response capacity under incentive-based demand response program. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019. [Google Scholar]
- Byers, C.; Levin, T.; Botterud, A. Capacity market design and renewable energy: Performance incentives, qualifying capacity, and demand curves. Electron. J. 2018, 31, 65–74. [Google Scholar] [CrossRef]
- Sugimura, M.; Senjyu, T.; Krishna, N.; Mandal, P.; Abdel-Akher, M.; Hemeida, A.M. Sizing and operation optimization for renewable energy facilities with demand response in micro-grid. In Proceedings of the 2019 20th International Conference on Intelligent System Application to Power Systems (ISAP), New Delhi, India, 10–14 December 2019. [Google Scholar]
- Xue, J.H.; Ye, J.L.; Tao, Q.; Wang, D.S.; Sang, B.Y.; Yang, B. Economic feasibility of user-side battery energy storage based on whole-life-cycle cost model. Power Syst. Technol. 2016, 40, 2471–2476. [Google Scholar]
- Jia, X.C.; Li, X.J.; Wang, H.L.; Zhang, Y.H.; Hui, D. Research on consistency assessment method for energy storage battery based on operating data fusion. Distrib. Util. 2017, 34, 29–35. [Google Scholar]
- Yan, P.; Wang, K.; He, K. Study on optimal configuration scheme of user-side battery energy storage system. Electron. Energy Manag. Technol. 2020, 590, 67–71. [Google Scholar]
- Xiong, X.; Ye, L.; Yang, R.G. Optimal allocation and economic benefits analysis of energy storage system on power demand side. Autom. Electron. Power Syst. 2015, 39, 42–48+88. [Google Scholar]
- Xiong, X.; Yang, R.G.; Ye, L.; Li, J.L. Economic evaluation of large-scale energy storage allocation in power demand side. Trans. China Electrotech. Soc. 2013, 28, 224–230. [Google Scholar]
- Ding, Y.X.; Xu, Q.S.; Lv, Y.J.; Li, L. Optimal configuration of user-side energy storage considering power demand management. Power Syst. Technol. 2019, 43, 1179–1186. [Google Scholar]
- Zhao, Y.T.; Wang, H.F.; He, B.T.; Xu, W.N. Optimization strategy of configuration and operation for user-side battery energy storage. Autom. Electron. Power Syst. 2020, 44, 121–128. [Google Scholar]
- Ma, X.F.; Chen, J.; Yu, S.Y.; Li, S.Y.; Lu, W.B. Research on user side energy storage optimization configuration considering capacity market. Trans. China Electrotech. Soc. 2020, 35, 4028–4037. [Google Scholar]
- Zhang, J.Y.; Chen, H.Y.; Wang, W.H. Research on optimal configuration strategy of user-side energy storage considering demand management. Power Demand Side Manag. 2020, 22, 19–24+37. [Google Scholar]
- Chen, L.J.; Wu, T.T.; Liu, H.B.; Huang, G.Y.; Xu, X.H. Demand management based two-stage optimal storage model for large users. Autom. Electron. Power Syst. 2019, 43, 194–200. [Google Scholar]
- Lin, J.H.; Gu, X.W.; Ma, L. Optimal sizing and control of demand-side battery energy storage system. Energy Storage Sci. Technol. 2018, 7, 90–99. [Google Scholar]
- Guo, J.Y.; Liu, Y.; Guo, Y.L.; Xu, L.X. Configuration evaluation and operation optimization model of energy storage in different typical user-side. Power Syst. Technol. 2020, 44, 4245–4254. [Google Scholar]
- Pan, F.R.; Zhang, J.Y.; Zhou, Z.W.; Zhang, X.; Zheng, X.C. Cost-benefit and investment risk analysis of user-side battery energy storage system. Zhejiang Electron. Power 2019, 38, 43–49. [Google Scholar]
- Wang, Z.Y.; Yi, Z.K.; Zhou, J.G.; Duan, R.H.; Zhu, T.; Xia, T.; Xu, Y.L. Wind power integration capability evaluation of large-scale combined heat and power system with additional heat source. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019. [Google Scholar]
- Deng, B.F.; Fang, J.K.; Hui, Q.; Zhang, T.Y.; Chen, Z.; Teng, Y.; Xi, X. Optimal scheduling for combined district heating and power systems using subsidy strategies. CSEE J. Power Energy Syst. 2019, 5, 399–408. [Google Scholar]
- Chen, Z.Y.; Wang, D.; Jia, H.J.; Wang, W.L.; Guo, B.Q.; Qu, B.; Fan, M.H. Research on optimal day-ahead economic dispatching strategy for microgrid considering P2G and multi-source energy storage system. Proc. CSEE 2017, 37, 3067–3077. [Google Scholar]
- Ma, T.F.; Wu, J.Y.; Hao, L.L. Energy flow modeling and optimal operation analysis of micro energy grid based on energy hub. Energy Convers. Manag. 2017, 133, 292–306. [Google Scholar] [CrossRef]
- Moghaddam, I.G.; Saniei, M.; Mashhour, E. A comprehensive model for self-scheduling an energy hub to supply cooling, heating and electrical demands of a building. Energy 2016, 94, 157–170. [Google Scholar] [CrossRef]
- Jin, X.L.; Mu, Y.F.; Jia, H.J.; Yu, X.D.; Chen, N.S.; Ge, X.J.; Yu, J.C. Optimal scheduling method for a combined cooling, heating and power building microgrid considering virtual storage system at demand side. Proc. CSEE 2017, 37, 581–590. [Google Scholar]
- Zhu, X.R.; Xie, W.Y.; Lu, G.W. Day-ahead scheduling of combined heating and power microgrid with the interval multi-objective linear programming. High. Volt. Eng. 2021, 47, 2668–2679. [Google Scholar]
- Qiu, Z.; Wang, B.B.; Ben, S.J.; Hu, N. Bi-level optimal configuration planning model of regional integrated energy system considering uncertainties. Electron. Power Autom. Equip. 2019, 39, 176–185. [Google Scholar]
- Huang, Z.H.; Zhang, Y.C.; Zheng, F.; Lin, J.H.; An, X.L.; Shi, H. Day-ahead and real-time energy management method for active distribution networks based on coordinated optimization of different stakeholders. Power Syst. Technol. 2021, 45, 2299–2308. [Google Scholar]
- Zhu, L.; Li, X.J.; Tang, L.J.; Tian, Z.Q.; Cui, K.S. Distributionally robust optimal operation for microgrid considering phase change storage and building storage. Power Syst. Technol. 2021, 45, 2308–2319. [Google Scholar]
- Sang, B.; Zhang, T.; Liu, Y.J.; Chen, Y.D.; Liu, L.S.; Wang, R. Energy management system research of multi-microgrid: A review. Proc. CSEE 2020, 40, 3077–3093. [Google Scholar]
- Sun, H.J.; Zhang, L.L.; Peng, C.H. Time-domain rolling optimal scheduling of microgrid based on differential demand response model predictive control. Power Syst. Technol. 2021, 45, 3096–3105. [Google Scholar]
- Yang, M.T.; Zhou, B.X.; Dong, S.; Lin, N.; Li, Z.G.; He, F.Y. Design and dispatch optimization of microgrid electricity market supported by blockchain. Electron. Power Autom. Equip. 2019, 39, 155–161. [Google Scholar]
- Jin, X.L.; Mu, Y.F.; Jia, H.J.; Yu, X.D.; Xu, K.; Xu, J. Model predictive control based multiple-time-scheduling method for microgrid system with smart buildings intergrated. Autom. Electron. Power Syst. 2019, 43, 25–33. [Google Scholar]
- Zhou, X.Q.; Ai, Q.; Wang, H. Distributed optimal scheduling of microgrid cluster with function of plug and play. Autom. Electron. Power Syst. 2018, 42, 106–113. [Google Scholar]
- Zhang, F.X.; Jin, X.L.; Mu, Y.F.; Jia, H.J.; Yu, X.D.; Liu, D.T. Model predictive scheduling method for a building microgrid considering virtual storage system. Proc. CSEE 2018, 38, 4420–4428+4642. [Google Scholar]
- Wang, C.S.; Lv, C.X.; Li, P.; Li, S.Q.; Zhao, K.P. Multiple time-scale optimal scheduling of community integrated energy system based on model predictive control. Proc. CSEE 2019, 39, 6791–6803+7093. [Google Scholar]
- Zhang, H.; Zhang, J.; Xiao, Y.Q.; He, Y.; Liu, Y.; Fan, L.Q. Research on intra-day hierarchical dispatching of microgrid based on model prediction. Electron. Power Sci. Eng. 2021, 37, 1–10. [Google Scholar]
- Domanski, P.D.; Lawrynczuk, M. Impact of MPC embedded performance index on control quality. IEEE Access 2021, 9, 24787–24795. [Google Scholar] [CrossRef]
- Soloperto, R.; Kohler, J.; Allgower, F. Augmenting MPC schemes with active learning: Intuitive tuning and guaranteed performance. IEEE Control. Syst. Lett. 2020, 4, 713–718. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Liu, Y.S.; Wen, Y.T.; He, J.; Li, X.; Bi, D.Q. Short-term load forecasting method based on PCC-LSTM model. J. Beijing Univ. Aeronaut. Astronaut. 2021, 30, 1–11. [Google Scholar]






| Parameters | Lithium Iron Phosphate Battery | Lead Carbon Battery | Sodium Sulfur Battery |
|---|---|---|---|
| (USD/(kWh)) | 313.80 | 101.99 | 219.66 |
| (USD/(kW)) | 175.73 | 188.28 | 65.90 |
| (USD/(kW·a)) | 15.22 | 3.92 | 19.46 |
| 0.90 | 0.88 | 0.75 | |
| Depth of discharge, dod | 0.9 | 0.7 | 0.6 |
| State of charge, SOC | [0.2,0.8] | [0.3,0.8] | [0.4,0.8] |
| Daily cycles, n | 1 | 1 | 1 |
| Discount rate, r (%) | 6 | 6 | 6 |
| Parameters | Values |
|---|---|
| Ratio of installation cost to equipment cost, α | 0.30 |
| (USD/(kV·A)) | 78.45 |
| Load factor, K | 0.75 |
| 0.85 |
| Time Period | Time | Electricity Price (USD/(kWh)) |
|---|---|---|
| Valley | 0:00–7:00 | 0.05087 |
| Peak | 10:00–15:00, 18:00–21:00 | 0.14650 |
| Flat | 7:00–10:00, 15:00–18:00, 21:00–24:00 | 0.09800 |
| Parameters | Lithium Iron Phosphate Battery | Lead Carbon Battery | Sodium Sulfur Battery |
|---|---|---|---|
| Equivalent operating life, T (a) | 17 | 10 | 12 |
| Rated capacity, (kWh) | 2694 | 3660 | 3368 |
| (kW) | 900 | 1108 | 1796 |
| (day) | 252 | 252 | 252 |
| 0.1 | 0.1 | 0.1 |
| Project | Lithium Iron Phosphate Battery | Lead Carbon Battery | Sodium Sulfur Battery |
|---|---|---|---|
| Average annual investment cost (USD 10,000) | 15.4876 | 12.8548 | 18.2082 |
| Average annual net benefit (USD 10,000) | 15.5205 | 19.4179 | 14.6262 |
| Average annual total benefit (USD 10,000) | 31.0081 | 32.2728 | 32.8345 |
| Annual average basic electricity bill benefit (USD 10,000) | 5.7331 | 6.3450 | 7.1029 |
| Annual average electricity cost benefit (USD 10,000) | 3.8597 | 4.2520 | 3.1898 |
| Annual average transformer cost benefit reduced by peak load reduction (USD 10,000) | 14.3971 | 14.3971 | 14.3971 |
| Annual average capacity market benefit (USD 10,000) | 5.8885 | 5.8885 | 5.8885 |
| Annual average reliability benefit (USD 10,000) | 1.1297 | 1.3901 | 2.2547 |
| Total investment cost (USD 10,000) | 263.2892 | 128.5482 | 218.4942 |
| Payback period (year) | 8.5 | 4.0 | 6.7 |
| Cost performance index | 2.0 | 2.5 | 1.8 |
| Net benefit in the whole life cycle (USD 10,000) | 263.8415 | 194.1732 | 175.5146 |
| Total benefit in the whole life cycle (USD 10,000) | 527.1369 | 322.7213 | 394.0088 |
| Return on investment (%) | 100 | 151 | 80 |
| Parameters | Values |
|---|---|
| Maximum demand for forecast data (kW) | 2700 |
| Maximum reported demand (kW) | 2161 |
| Electricity bill benefit (USD) | 3844.05 |
| Basic electricity bill benefit (USD) | 4063.71 |
| Monthly net benefit (USD) | 7892.07 |
| Parameters | Day-Ahead Optimization Operation | Intra-Day Optimization Operation |
|---|---|---|
| Daily electricity fee benefit (USD) | 152.26 | 158.71 |
| Input data peak (kW) | 2006 | 2160 |
| Peak load after energy storage scheduling (kW) | 1805 | 1805 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, Q.; Guan, H.; Li, X.; Bi, D.; Guo, Y.; Sun, H. Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage. Electronics 2022, 11, 120. https://doi.org/10.3390/electronics11010120
Liu Y, Liu Q, Guan H, Li X, Bi D, Guo Y, Sun H. Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage. Electronics. 2022; 11(1):120. https://doi.org/10.3390/electronics11010120
Chicago/Turabian StyleLiu, Yushan, Qianqian Liu, Huaimin Guan, Xiao Li, Daqiang Bi, Yingjun Guo, and Hexu Sun. 2022. "Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage" Electronics 11, no. 1: 120. https://doi.org/10.3390/electronics11010120
APA StyleLiu, Y., Liu, Q., Guan, H., Li, X., Bi, D., Guo, Y., & Sun, H. (2022). Optimization Strategy of Configuration and Scheduling for User-Side Energy Storage. Electronics, 11(1), 120. https://doi.org/10.3390/electronics11010120








