An Experimental Evaluation of Resistive Defects and Different Testing Solutions in Low-Power Back-Biased SRAM Cells

Abstract

This paper compares different types of resistive defects that may occur inside low-power SRAM cells, focusing on their impact on device operation. Notwithstanding the continuous evolution of SRAM device integration, manufacturing processes continue to be very sensitive to production faults, giving rise to defects that can be modeled as resistances, especially for devices designed to work in low-power modes. This work analyzes this type of resistive defect that may impair the device functionalities in subtle ways, depending on the defect characteristics and values that may not be directly or easily detectable by traditional test methods. We analyze each defect in terms of the possible effects inside the SRAM cell, its impact on power consumption, and provide guidelines for selecting the best test methods.

1. Introduction

The increasing demand of low-power technologies used for most modern circuits requires more sophisticated systems than ever in terms of power consumption and reliability. The MOS-channels with smaller sizes in modern node technologies involve circuits that are subject to more leakage currents than ever, especially when resistive defects lead to certain malfunction of the system. For this reason, these systems implement specific methods in order to reduce power consumption in logic and memory systems [1] and not only this, particular methods for detecting the defects are implemented as well.

For example, in the context of the Internet of Things, devices may be required to stand in idle mode until other scheduled events or environmental changes arise. Within these periods of time, it is crucial to keep the leakage current to a minimum, especially concerning SRAM cells, which may be part of large arrays and based on smaller technology nodes.

Due to the large area occupied by SRAMs and their high level of integration, memories are critical from the quality point of view as well. For these reasons, manufacturing tests need to be very accurate, to detect any kind of defects inside the system, and these tests have to be as fast as possible in order to contain costs. The situation is worse when the system is affected by defects that become evident under particular conditions, e.g., when the memory changes its status or operation mode as well as when the power supply is reduced to the minimum allowed by the specification of the circuit. Usually, these types of defects occur inside the memory cell during the manufacturing process. They could be associated with parasitic capacitance or resistance between the routing nets and the contacts of the layout. As an example, faulty vias [2,3] may be the cause of misbehavior inside the cell, especially for digital circuits; defects in the silicon die such as imperfections on gate oxide that lead to time-dependent dielectric breakdown [4] are another actual problem, which depends on the manufacturing process node, particularly for circuits subjected to high electrical stress, causing imperfection in the system such as other kinds of manufacturing imperfections that could also cause unwanted resistive connections inside the SRAM cell. Nevertheless, particular attention should be given to power consumption in such low-power SRAMs that need to be made through techniques that allow them to have a lower and lower current consumption.

On the other hand, defects on low-power structures involve misbehavior, which can hardly be detected by usual March tests. Depending on the resistive defect value, the system undergoes different effects. This paper analyzes the impact of such resistive defects on the behavior of low-power 6T-SRAM cells and evaluates the effectiveness of different test methods. This study specifically considers the effects of such defects when the back-bias technique [5] is employed to reduce leakage, also evaluating the impact of current consumption on the memory cell.

In brief, our theoretical and experimental analysis provides overall evidence that some types of effects caused by resistive defects in the memory cell can produce different types of misbehavior inside the system under specific conditions and resistance values. To analyze the impact of the different defects and the effectiveness of the different test solutions, we used an accurate simulation model of a low-power SRAM cell to evaluate and detail the effects of the different resistive defects possibly affecting it. Furthermore, we evaluated the ability of the different test methods proposed in the literature in detecting these defects. To summarize, this article provides an overview of all these defects and how they can be tested, providing useful guidelines to the test engineer in selecting the best test solution(s).

This study is an extension of previous work [6]. Specifically, the current paper further investigates additional resistive defects, including defects in symmetric positions occurring inside low-power SRAM cells, as well as in terms of power consumption and static noise margin (SNM): The effect of each resistive defect injected in the cell is evaluated and then the analysis of the power consumption and SNM is performed for the assessment of non-functional faults inside the system.

This paper is organized as follows: In Section 2, we introduce low-power memories and some background about memory testing, power consumption, and static noise margin analysis; Section 3 describes the impact of the analyzed resistive defects on the cell functionalities, specifically referring to a 160 nm low-power 6T-SRAM, exploiting the back-bias technique and evaluating the behavior of each defect when its size changes (we considered the full range of resistive values for each considered defect inside the cell). Section 4, we introduce the possible tests considered for our analysis, and in Section 5, we report the results obtained from electrical simulations, not only in terms of testing and current consumption, but also in terms of their impact on the SNM. The discussion is presented in Section 6; at last, in Section 7, we draw some conclusions.

2. Background and Motivations

2.1. Memory Testing

Memory testing plays an important role in modern technologies. The design of memory often requires using the maximum storage density in the minimum area. So, the more the technology evolves, the more the data storage and complexity increases, thus making the appearance of manufacturing defects inside the system more likely.

Previous studies considered the different defects that may affect each cell in an SRAM [7]. In particular, special attention is given to resistive defects inside the cell that should be detected by properly set test techniques.

2.2. Low-Power 6T-SRAM Structure

The 6T-SRAM cell considered in this paper is depicted in Figure 1. It is made up of two inverters (composed of transistors M1–M2 and M3–M4, respectively) and two pass-transistors, M5 and M6, that enable the functionalities of the cell. When writing/reading operations are performed, the WL signal is high, allowing the BL and BLB signals to be connected through M5 and M6 to the S and SB nodes, respectively.

If a “0” writing operation is performed in the cell, the bit lines (BL and BLB) must be connected to ground (GND) and the power supply (VDD), respectively. Then, the WL signal activates the pass-transistors M5 and M6 allowing one to move S and SB node to GND and VDD, respectively; moreover, if a “1” writing operation is performed in the cell, BL and BLB are charged to the VDD and GND value, respectively, thus writing a “1” and a “0” in the S and SB node, respectively. If no defects occurred inside the cell, it should stay in the same state as long as a new operation occurs on it.

If a reading operation is performed in the cell, the BL and BLB lines must firstly be pre-charged at a VDD value. Then, the WL signal activates M5 and M6, allowing one to connect the S and SB nodes at the BL and BLB lines, thus creating a voltage difference detected by a sense amplifier.

For the purpose of this paper, we considered low-power SRAM memory using the back-bias technique, a widely used solution that allows the system to reduce the leakage current during the idle periods. This system reduces the rail-to-rail voltage by increasing the voltage of the (virtual) ground node VGND. When the control signal PDM (Power Down Mode) is activated, the cell switches from Normal Mode (NM) to Low-Power Mode (LPM), thus activating the back-bias circuit, during which neither writing nor reading operations can be performed in the cell. The back-bias circuitry is usually inserted in clusters of cells to decrease the current consumption of each cell and thus of the whole arrays. The time that the system requires to switch these operational modes could be measured in milliseconds, that is, the time used to allow the system to switch from normal mode to low-power mode, which is orders of magnitude larger than read/write operations.

2.3. Resistive Defects and Fault Models

The memory cell can be affected by several defects. On a circuit model, some of them can be modeled as Resistive-Bridging [8] and Resistive-Opens defects [9,10,11]:

• Resistive-Bridging defects create an unwanted current path between two nodes in the cell, which are not intended to be connected.
• Resistive-Open defects increase the resistance of existing paths inside the cell.

Both Resistive-Bridging and Resistive-Open defects may force the cell to misbehave when the corresponding resistance holds specific ranges of values. The functional model of a defect is referred to as a fault. A wide body of literature describes the different types of faults that may occur in a SRAM cell [12]. Among them, the following are the most used:

• Stuck-at Fault (SAF), in which the logic value of a cell is always either “0” or “1”.
• Transition Fault (TF), when a cell is unable to change its state (0→1 or 1→0) when a write operation is made.
• Data Retention Fault (DRF) [13] when a memory cell loses its previously stored logic value after a certain period of time during which it has not been accessed.
• Dynamic Data Retention Fault (dDRF) [14], a DRF that occurs when a memory cell loses its previously stored logic value after at least two read or write operations are performed on other cells.
• Dynamic Read Destructive Fault (dRDF) [15], that occurs when a write operation immediately followed by a read operation performed on the cell changes the logic state of this cell and returns an incorrect value on the output.
• Read Destructive Fault (RDF), that occurs when a read operation performed on the cell changes the data in the cell itself and returns an incorrect value on the output.

To detect faults in memory, specific sequences of write and read operations known as March tests are commonly used [16]. Often, the application of such tests exploits embedded built-in self-test (BIST) logic to increase test quality (e.g., with higher frequency operation and taking into account array scrambling) and lower costs.

2.4. Power Consumption

Regarding low-power SRAMs, it is crucial to consider the power consumption of the system. We focused on the pattern of the current of the SRAM cell when the device functionality deviates from the standard operation, especially when the system alternates between different operational modes in the presence of defects inside the cell. In this paper, we will discuss the impact of these resistive defects in terms of power consumption under particular conditions and analyze the range in which we have an effect of the defect. Indeed, the back-bias technique implemented in the cell guarantees a lower power and current consumption of the system: In the case of a defect, e.g., when the resistive defect creates a new unwanted path (resistive-bridge), the system undergoes a larger current consumption that may exceed the device specifications. In addition, a value difference with respect to the nominal current can also be used to detect the fault by means of quiescent current tests. An example is when a resistive path close to the power supply (resistive-open) increases the current on that, thus becoming detectable by tests.

2.5. The Static Noise Margin

The static noise margin [17,18,19,20] measures the stability of the cell and it is defined as the minimum noise voltage present at each of the cell storage nodes (S and SB) necessary to flip the state of the cell. It could be split in three types: Hold noise margin, write noise margin, and read noise margin. For this study, we considered only the hold noise margin, in order to check the reliability of the cell. We analyzed and measured it during each steady-state data simulation. We will consider the impact on SNM not only when the cell does not work because of the defects, but also when the defective cell is working, as well. Indeed, when a defective cell continues working despite the presence of the defect, further analysis could be necessary to better understand if the reliability of the system could be compromised. In Figure 2, we report the typical and symmetrical behavior of the SNM for a fault-free cell. The SNM can be obtained by varying the V1 and V2 voltages that represent the S and SB node voltage values, respectively. The two signals are represented at the same step along the two axes, until the two curves are adjacent. The following flow is implemented to achieve a butterfly-line graph, which is representative of the status of the static noise in the circuit:

• Considering INV-M3,4 we perform a DC analysis on the S node, and we look at the output of the inverter.
• Then, we draw the butterfly graph representing the S node (V1) axe in SB (V2) node axis and vice versa for the SB node, to achieve the correct symmetric picture.

Figure 2. Typical behavior of SNM for a symmetric SRAM cell.

Figure 2. Typical behavior of SNM for a symmetric SRAM cell.

3. Effects of Resistive Defects in the Low-Power SRAM Cell

This study focuses on some resistive defects that may occur in a low-power SRAM cell. These defects may not only influence the functional behavior of the memory, but impact power consumption as well. In this paper, we will focus not only on functional effects, but we will analyze the impact of the main defect we considered inside the cell, evaluating the effect on power and SNM, as well. When one of such defects occurs, the cell may perform differently from the desired behavior, depending on the defect characteristics. In this section, we analyze the impact of each defect.

Figure 3 shows some of the possible resistive defects that may arise in the cell; first, we are going to analyze three different main resistive defects (R1, R2, and R3) inside a single inverter of the low-power 6T-SRAM cell and then we will discuss the other ones, which can be related to the former ones considering the symmetry of the design. Different colors are used in Figure 3 to identify defects playing corresponding roles in the different inverters composing the cell.

3.1. Resistive Path on the Cell Transistor Gate (R1)

The first resistance we consider in this study corresponds to a resistive-bridge defect inside the cell. Concerning the R1 resistance, it creates a resistive path connection between VDD and the gate of M3. This link could produce, under particular conditions, a failure in the reading and writing operations performed in the cell.

Depending on the R1 value, the typical function of the inverter INV-M3,4 may be compromised when the cell is written with a “0”.

We identified three different ranges in which we have different behaviors of the cell with this defect. In the first range of resistance values (0 ÷ RX’), it does not allow the cell to be written since the defect is considered as a short circuit that does not allow any operation. On the other hand, the third range (above RX’’) has no functional effect on the cell, no matter whether we are in the NM or in the LPM.

In the middle range (between RX’ and RX”), the resistive-bridging defect will have no effect on NM, but when the memory switches to LPM, R1 could cause a change in the data stored in the cell when the cell switches again to NM, thus allowing the reading of the stored data. Indeed, during LPM, the VGND node voltage value increases as well as the S and SB node voltage value changing the threshold of the inverters, so when the cell returns to NM, the stored data flip. We define this type of fault as a Low-Power Retention fault (LPRF), as it behaves as a DRF, but it becomes active only when passing through LPM.

To summarize, assuming the cell is written with a “0”, the behavior of the system with a resistance of an increasing value is the following:

• When the resistance value is very low (in the 0 ÷ RX’ range) the cell cannot be written and is isolated from the system so it does not work at all, because the S and SB nodes cannot keep their value. In this case, we have a stuck-at fault.
• When the resistance value is in the RX’ ÷ RX” range, the cell keeps working on until it switches to LPM and then switches again to NM. In this case, the cell cannot preserve its state and flips its value, preserving the faulty value in the achieved NM state. In this case, we have an LPRF.
• When the resistance value is above RX”, the cell works correctly in any case because we have a situation very similar to a fault-free SRAM cell.

This resistive-bridge defect has a certain impact on power consumption. In fact, the presence of a resistive path between the two focused S and SB nodes leads to quite a large current as an effect of the defect. In particular, the unwanted path causes an increase in the absorbed current in the cell that maintains its higher value until either the bit-flip (after switching from LPM to NM) or the changing of the data stored involves a decrease in the non-expected value within the specification of the system. Indeed, this current, starting from VDD and passing through the gate of M3 and then through the S node and the M2 channel as far as the GND node, modifies the expected working behavior of the entire system. In terms of SNM, considering only the middle range, we observe an impact on the noise margin that is very small with respect to the correct graph depicted above.

3.2. Resistive Open on the Cell Transitor Source Terminals (R2)

The other resistance we consider in this study corresponds to a resistive-open defect like R2, inside the cell. In this case, the behavior of the system is not compromised as long as the resistance value is not high enough to produce a failure, where the resistance may be considered almost an open circuit, thus not allowing the cell to handle read and write operations. Considering all the ranges of values that R2 may have, causing a fault in the cell, this defect can cause misbehavior in two cases:

• When the cell is written and then we quickly perform a read operation.
• When the cell is written, then we switch the system to LPM and after switching again to NM we perform a read operation.

The effects of the fault can be analyzed referring to three ranges of values for the size of the resistive defect R2. Assuming the cell is written with a “0” and considering R2 as resistive-open defect injected inside the cell, there are the following cases:

• When the resistance is within the range 0 ÷ RY’ the system works correctly, even if we perform a read operation either in NM or after a transition between LPM and NM.
• When the resistance is within the range RY’ ÷ RY’’ the cell undergoes a failure when a read after write (RAW) operation is performed. This effect can be modeled as a dRDF.
• When the resistance is above RY’’, a failure is visible if we perform a quick RAW (the cell is read right after a write action is performed), even if we keep the cell either in NM or passing through LPM (the associated model is dRDF).

We observe no effect on current consumption for this defect, but we do see an impact on SNM, if we consider the symmetry of the cell. This effect may compromise the quality of the cell, thus increasing the defectivity of the entire system.

3.3. Resistive Open between the Inverters (R3)

The last resistance we consider in this study corresponds to a resistive-open defect modeled by R3 that may occur inside the low-power SRAM cell. It creates a resistive path between M6 and the SB node, thus involving a degradation of the voltage value at the SB node when the cell is written with a “1”.

The failure of the cell has only two different ranges of values compared with the previous defects. Indeed, assuming in this case a “1” is written in the cell, the following behaviors can be observed:

• When the resistance is within the range 0 ÷ RZ’ the system works correctly, even if we perform a read operation either in only the NM or after switching from LPM to NM.
• When the resistance is above RZ’ the cell undergoes a failure when a read operation is performed right after a write operation (RAW) either when the cell is kept in NM or when it is passes through LPM (the associated model is dRDF).

There is no impact on power consumption in this case and a minimal impact on the SNM that may not compromise the reliability of the cell.

3.4. Discussion: Symmetry of the Cell

The study has focused so far on the three main resistive defects that we considered on our analysis, but we have already pointed out the symmetry of the low-power SRAM cell used for our purposes. These other resistive defects may have an impact on the system in similar ways as we focused on before.

Considering the effect of the resistive defects considered so far (R1, R2, and R3), we have the same effects with the other resistive defects (from R4 to R10).

In particular, when a “0” is written in the cell, based on the symmetry of the cell, we can state that:

• We have the same effect of R1 considering the INV-M1,2 with the R8 resistance.
• We have the same effect of R2 considering the INV-M1,2 with the R9 resistance.

The R3 resistance corresponds to R6 when considering the INV-M1,2.

Considering the effect of the other three resistances (R4, R5, and R6), we have the same effect with the other symmetric resistive defects as explained in the following.

When a “1” is written in the cell, based on the symmetry of the cell, we can state that:

• We have the same effect of R1 considering the INV-M1,2 with R4 or R7.
• We have the same effect of R2 considering the INV-M1,2 either with R5 or R10.
• The R6 resistance corresponds to R3 when considering the INV-M3,4.

Moreover, regarding SNM, we notice that the behavior of the cell is symmetric in all cases except for the resistive defects on the pull-down of the case of the inverter. The reason we obtain this difference lies in the reduction of the rail-to-rail value of the supply voltage from the ground, thus increasing the threshold voltage that, in this case, may compromise the correct functionalities of the inverter inside the cell.

Table 1. Defect correspondences due to the symmetry of the cell.

Resistance	Write 0	Write 1
R1	R8	N.A.
R2	R9	N.A.
R3	N.A.	R6
R4	N.A.	R7
R5	N.A.	R10
R6	R3	N.A.

summarizes the correspondence of each resistive defect with each other when a “0” or a “1” is written in the cell.

4. Tests for Resistive Defects in the Low-Power SRAM Cell

In this section, we summarize our analysis of the capability of different test solutions to detect the considered faults caused by resistive defects, considering the different values of each one and the related fault model associated with these defects. To better explain our analysis, it is necessary to list the tests we considered for our purposes:

• March test. A test algorithm that is used for RAM and consists of a sequence of so-called March elements (a write and read action with increasing and decreasing addresses for each cell) that are performed inside the device under test (DUT) [21].
• Low-power retention test (LPR). It corresponds to a few steps that are performed in the cell. First, a “0” or a “1” is written into the cell, then it is switched into LPM, then it is turned back to NM, and finally the cell value stored is read. To decrease the test time for our analysis, we considered only a read action right after switching to NM in the measure of nanoseconds instead of milliseconds. This is because we avoid the time for the entire device to switch in LPM. This test does not cover a read action enacted after a long time.
• IDDQ test. It corresponds to the measurement of the quiescent current during SRAM operations.
• Read Equivalent Stress test (RES) [22,23,24,25]. It is an alternative methodology that can be employed, which does not require current measurements or passages to LPM. This test methodology is based on the Read Equivalent Stress method. The RES test involves repeated reading operations, which cause stress on the faulty cell. These operations are performed not on the faulty cell but on the other cells in the same row. To implement this test solution, we consider a row of cells in the same word line. Firstly, an operation is performed inside the faulty cell, then the other cells are selected. The WL signal continues acting on the other cells but has an impact on the faulty cell because of the stress created by the indirect read action on the same word line. Furthermore, when the system does not select the cell, the pre-charge circuit stays in the active status and continues charging the bit lines at the VDD value. On the other side, when the cell is selected, the pre-charge circuit switches off and an operation can be performed on the cell. It is possible to use a BIST to perform this type of test. Providing that the BIST engine can apply these stimuli, i.e., execute a long enough uninterrupted sequence of selective read operations on the cells of the same row, this method allows an easier and faster way to apply and test than the tests based on Low-power retention or IDDQ. To extend the effectiveness of the technique for our purposes, this test has to be performed at the minimum VDD value admissible by the specifications of the system and the technology.

4.1. R1 Case

In this paragraph, we analyze the two main resistive-bridging defects R1 and R8 that are involved in the test when the cell is written as a “0”, but (as anticipated before) we would find the same results with R4 and R7 when the cell is written as a “1” due to the symmetry of the cell.

The faults caused by the R1 and R8 defects can be tested through different types of techniques. We analyze the test options in each range case, starting from the minimum to the maximum resistance values.

Due to the misbehavior caused by R1 (and R8 for symmetry) in the range 0 ÷ RX’, any test writing and reading a “0” for R1 and R8 can detect it. Therefore, a basic March test is sufficient.

For the defects within the RX’ ÷ RX’’ range, a March test is not suitable. However, it is possible to resort to other kinds of tests, such as:

• Low-power retention (LPR) test.
• IDDQ test. If a defect in this range occurs inside the cell, a higher current consumption by the whole system is detectable in NM; indeed, we have a higher power consumption when we have already written the cell. Then, after switching to LPM and returning to NM, the current consumption decreases, remaining within the specification limits.
• Read Equivalent Stress (RES) test in a particular sub-range.

Above RX’’ (i.e., when the defect approximates an open circuit) no fault is present.

4.2. R2 Case

In this paragraph, we will analyze the two resistive-open defects, R2 and R9, that are involved in the test when the cell is written with a “0”. We would find the same results with R5 and R10 when the cell is written with a “1”.

When considering the fault corresponding to R2 and R9 in the range 0 ÷ RY’ (where RY’ is a relatively small value, depending on the specific cell), there is no functional effect and so no fault to detect.

For R2 and R9 within the RY’ ÷ RY’’ range, a March RAW (read after write) test is sufficient to detect a bit-flip in the cell without passing through LPM.

For R2 and R9 above the RY’’ value, it is possible to resort to the following types of tests:

• LPR test: Write the cell with “0”, then isolate the cell through WL signal by acting on M5 and M6, enter LPM, then return to NM, and at last read the cell value.
• A March RAW (read after write) test without passing through LPM.

4.3. R3 Case

In this paragraph, we analyze the last two resistive-open defects R3 and R6 that are involved in the test when the cell is written with a “1” or a “0”, respectively.

The failure of the cell has two different ranges of values with respect to the previous defect. Indeed, the following behaviors can be observed:

• When the resistance is within the range 0 ÷ RZ’, the system works correctly, even if we perform a read operation either in the NM or after coming back from the LPM.
• When the resistance is above RZ’, the cell undergoes failure in the case of a read operation protocol after a write operation. This failure can occur either if the cell is in NM or passes through LPM, so a March RAW is sufficient to detect the fault.

5. Experimental Results

This section presents the experimental results based on the main simulation of a 6T SRAM cell in 160 nm STMicroelectronics technology, addressing the defects discussed in the previous sections. For our purpose, we used Cadence Virtuoso for the schematics and the ELDO spice simulator for simulations and analysis.

Figure 4 shows a complete low-power SRAM sub-system featuring all the components of a single cell that we used for our simulations. This system is made up of three main components:

• A 6T-SRAM cell with INV-M3,4, INV-M1,2 and two pass-transistors, M5 and M6, through which bit-lines can access the cell when the WL signal is high.
• A back-bias circuit, increasing the VGND value to reduce leakage currents when the cell switches from Normal-Mode (NM) to Low-Power-Mode (LPM).
• A pre-charge circuit (M7, M8, M9), which charges the bit-lines to VDD when the cell is not selected for any operation. It is driven by the PCON signal that works either before an operation when the cell is selected or when the word line is activated, and other cells are selected for any operation.

Figure 4. 6T-SRAM with pre-charge circuit.

Figure 4. 6T-SRAM with pre-charge circuit.

To implement our analysis, we properly drive the WL signal to write the cell, the PDM signal in order to enable/disable the LPM in the cell, the PCON signal to enable/disable the pre-charge circuit, the BLCON signal to enable/disable the bit-lines, and thus the column of the cells (we consider them with high-impedance end).

The experimental results of our analysis for the three main resistive defects (R1, R2, and R3) are illustrated in the following sub-sections for each of the considered defects.

5.1. R1 Case

Figure 5a shows the results of the simulation of an LPR test in the RX’ ÷ RX’’ range, which detects a bit-flip after switching the mode of the cell and reading the data stored with R1 injected in the cell. For the sake of comparison, Figure 5b depicts the behavior of an LPR test of a fault-free SRAM cell. Looking at the figure, we can see that after exiting LPM, the SB voltage node sharply decreases causing a failure in the cell behavior and allowing defect detection when the reading action is performed in the cell. The LPM is usually in the millisecond range at least, but it has been shortened for clarity.

In Figure 6, we considered a resistive value in the sub-range of RX’ ÷ RX’’, in which we simulated the effect of the RES test during which we have a bit-flip after several indirect read operations. To summarize, among all the tests we performed in this range, the considered defect is detected by the RES technique, as well.

This type of simulation was performed using the lowest power supply voltage that allows the system to keep working. The reason behind this choice is that when we consider the sub-range and perform reading operations in the cell, this continues working without any effect. For this reason, and in agreement with the capability of the tester to work with lower power supply voltage, we consider this solution more affordable than the previous one, not only in terms of time but also in terms of costs. The only drawback is the perfect knowledge of the layout of the row of the cell required because we need to know it in order to perform writing/reading actions in the other cell of the same row of the defective one. However, if this test was to be performed with the lowest power supply value that the system allows, the effect could be visible in very few reading operations.

This mechanism is useful because, as we explained in the previous chapters, the device that embeds the SRAM requires milliseconds of time to pass from NM to LPM. With this type of test, we may detect that particular defect in a shorter time.

This particular range could also have an impact on the IDDQ test and the SNM as well. In particular, the IDDQ technique may detect a higher current consumption before any kind of operations may be performed inside the cell.

Looking at Figure 7, we can see the trend of the current during the LPR test simulation with a decreasing R1 defect inserted in the cell. In particular, the green line depicts the current consumption of an LPR test with a fault-free cell. We can see that the quiescent current maintains its low value during the operation inside the cell. The red line depicts the current consumption of an LPR test in the sub-range of RX’ ÷ RX’’. In this case, we can see that the quiescent current is higher than the previous one, that is up to 20% more than the previous one. As the arrow indicates on the figure, the more R1 is increased, the lower the effect on the power consumption we have inside the cell until we have no impact when the R1 value is below RX’ (as the arrow indicates in the figure when we have the bit-flip).

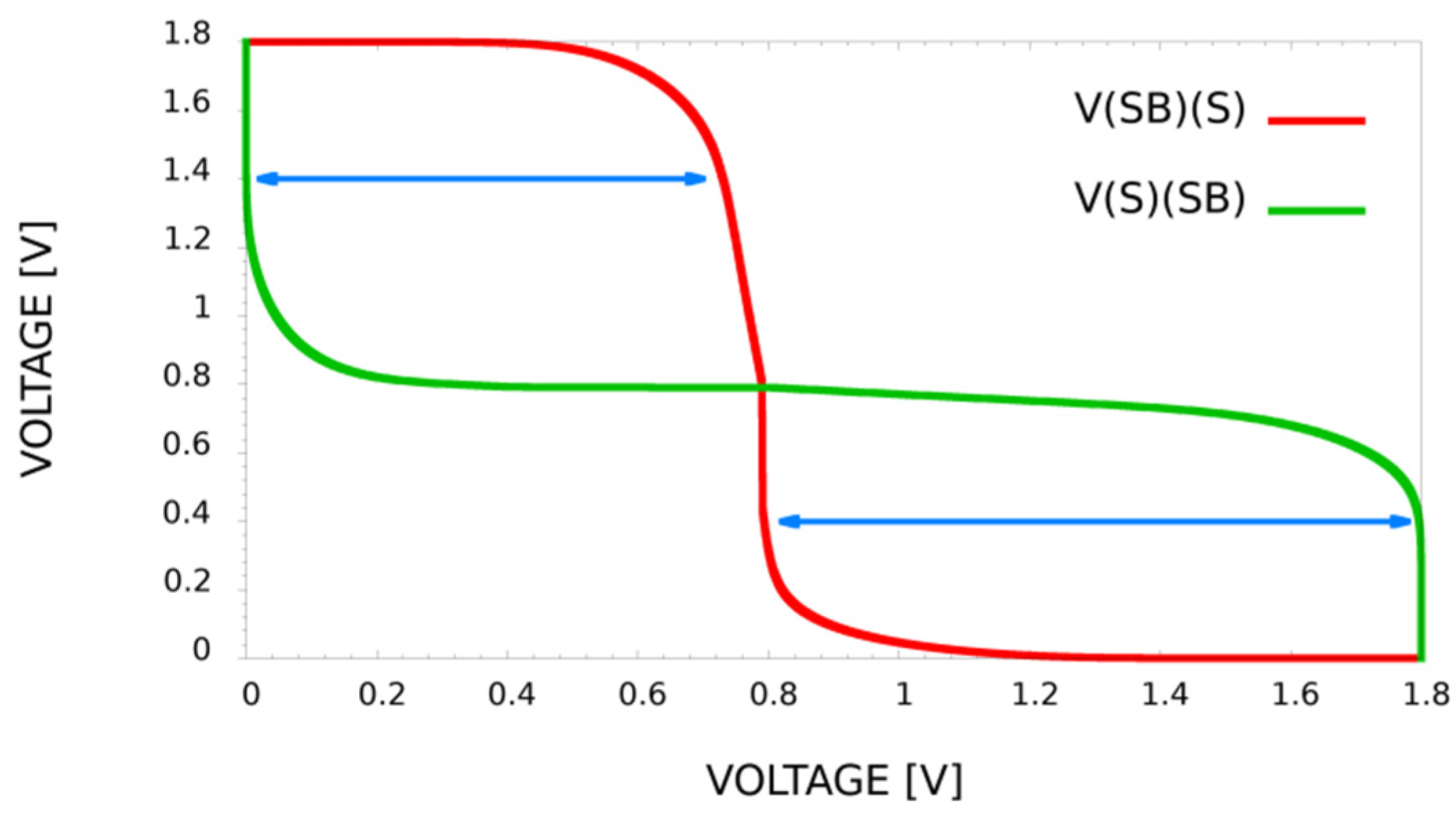
Regarding SNM, Figure 8 shows a simulation that represents the characteristics of SNM when R1 is injected in the cell. Considering R1 in the RX’ ÷ RX’’ value range inserted in the cell, the red line depicts the IN/OUT characteristic of the INV-M3,4 in node SB depending on the S node as a source. Vice-versa, the green line depicts the IN/OUT characteristic of the INV-M1,2 in node S depending on the SB node. By inverting the axes, the butterfly-line graph is produced. As we can see, the defect inside the cell impacts the SNM, reducing the stability of the cell that is up to 30% more affected than the typical one.

According to our simulations, for the considered cells, the values for RX’ and RX’’ are 20 kΩ and 35 kΩ, respectively.

Table 2. Effectiveness of the different test methods with respect to the R1 defect.

	<RX′	RX′÷RX″	>RX″
LPR TEST	Detected	Detected	No Effect
March TEST	Detected	Undetected	No Effect
IDDQ TEST	N.A.	Detected	No Effect
RES TEST	N.A.	Detected	No Effect

summarizes the defect effects and the fault detection capabilities of each test in each range of values. The RES test detects the fault only in a limited sub-range of RX’ ÷ RX’’ (around 30 kΩ).

5.2. R2 Case

Figure 9 shows the results of the simulation of an LPR test considering the R2 defect above the RY’’ value. The simulation detects a bit-flip after reading the stored data when the cell switches from LPM to NM.

In this case, it is useless to use the IDDQ technique due to the impossibility to detect any effect on the power consumption of the cell. For this reason, we did not consider the IDDQ test for this resistive defect.

In this case, we have no effect on SNM for R2, but when considering the R10 resistance in the RY’ ÷ RY’’ range and looking at Figure 10, we can see a large impact on the SNM that may affect the stability of the cell by 40% more than the typical one. This situation is due to a resistance in the VGND node that interferes with the threshold of the inverter and compromises the noise margin of the cell.

According to our simulations, for the considered cells, the values for RY’ and RY’’ are 3 MΩ and 15 MΩ, respectively. The effect of every test when the defect size belongs to each range is summarized in the following

Table 3. Effectiveness of the different test methods with respect to the R2 defect.

	<RY′	RY′ ÷ RY″	>RY″
LPR TEST	No Effect	Undetected	Detected
March TEST	No Effect	Detected	Detected

.

5.3. R3 Case

Figure 11 shows the results of the simulation of an LPR test considering the R3 defect. The simulation shows that the LPR test detects a bit-flip after reading the stored data when the cell switches from LPM to NM.

Even in this case, the IDDQ technique is useless due to the impossibility to detect any kind of effect in the power consumption of the entire cell with the considered R3 resistance.

Figure 12 shows an SNM margin analysis considering an R3 value above RZ’ implemented in the cell where we can see a not-so-explicit impact on the stability of the cell, except for being 15% more affected than the typical SNM of the faulty-free cell.

According to our simulations, for the considered cell, the value for R3’ is 30 kΩ. The effect of every test when the defect size belongs to each range is summarized in

Table 4. Effectiveness of the different test methods with respect to R3.

	<RZ′	>RZ′
LPR TEST	No Effect	Detected
March TEST	No Effect	Detected

.

6. Discussion

We have seen in the previous sections that, for each case, the defects that may occur in the circuit may produce different effects and may be detected by different tests.

The best test strategy must be evaluated case by case considering the technology is used (hence, the likelihood of the different defects, and the range of their values), the product quality objectives, and the maximum costs one can afford.

To summarize the conclusions of our analysis, we can state that traditional retention tests generally require more time than a March test applied via BIST. Similarly, any test based on moving the memory to LPM and back or on the IDDQ current measure may be relatively long and expensive. Other solutions able to more quickly detect the addressed effects are thus highly welcome. The performed analysis allows one to evaluate the pros and cons of each case and choose the best test solution.

To conclude, in

Table 5. Summary of the effectiveness of the different test methods with respect to R1.

R1	<25 KΩ	25 KΩ ÷ 35 KΩ	>35 KΩ
LPR TEST	Detected	Detected	Detected
March TEST	Detected	Undetected	Detected
IDDQ TEST	N.A.	Detected	No Effect
RES TEST	N.A.	Detected	No Effect

,

Table 6. Summary of the effectiveness of the different test methods with respect to R2.

R2	<3 MΩ	3 MΩ ÷ 15 MΩ	>15 MΩ
LPR TEST	No Effect	Undetected	Detected
March TEST	No Effect	Detected	Detected
IDDQ TEST	N.A.	N.A.	N.A.
RES TEST	N.A.	N.A.	N.A.

and

Table 7. Summary of the effectiveness of the different test methods with respect to R3.

R3	<3 MΩ	>15 MΩ
LPR TEST	No Effect	Detected
March TEST	No Effect	Detected
IDDQ TEST	N.A.	N.A.
RES TEST	N.A.	N.A.

, we can see all the possible cases we discussed in this paper considering the real values analyzed through the SRAM model, allowing one to identify the test able to spot a defect in the cell.

7. Conclusions

The present work provides a comprehensive overview, supported by experimental results, on the possible effects of some resistive defects affecting a 160 nm low-power SRAM cell, which uses the back-bias technique to reduce the leakage currents when entering the low-power mode. The analysis focuses on several resistive defects provoking a bit-flip of the cell when moving to LPM, taking into account the symmetry of the entire SRAM cell. Furthermore, the paper reports an evaluation of the effects of each defect and the associated fault models in order to assess the effectiveness and advantages/limitations of different test methods. The analysis can be used by test engineers to more effectively select the test solution(s) to be used for each product. The analysis methodology considering the low-power architecture can also be extended to more advanced technology nodes.

Future works will include:

• The evaluation of the most likely values for such defects through low-level failure analysis of the specific technology.
• The exploration of possible BIST solutions to implement the considered tests.