Methodology for Neural Network-Based Material Card Calibration Using LS-DYNA MAT_187_SAMP-1 Considering Failure with GISSMO
Abstract
:1. Introduction
2. Materials and Methods
2.1. Artificial Neural Networks
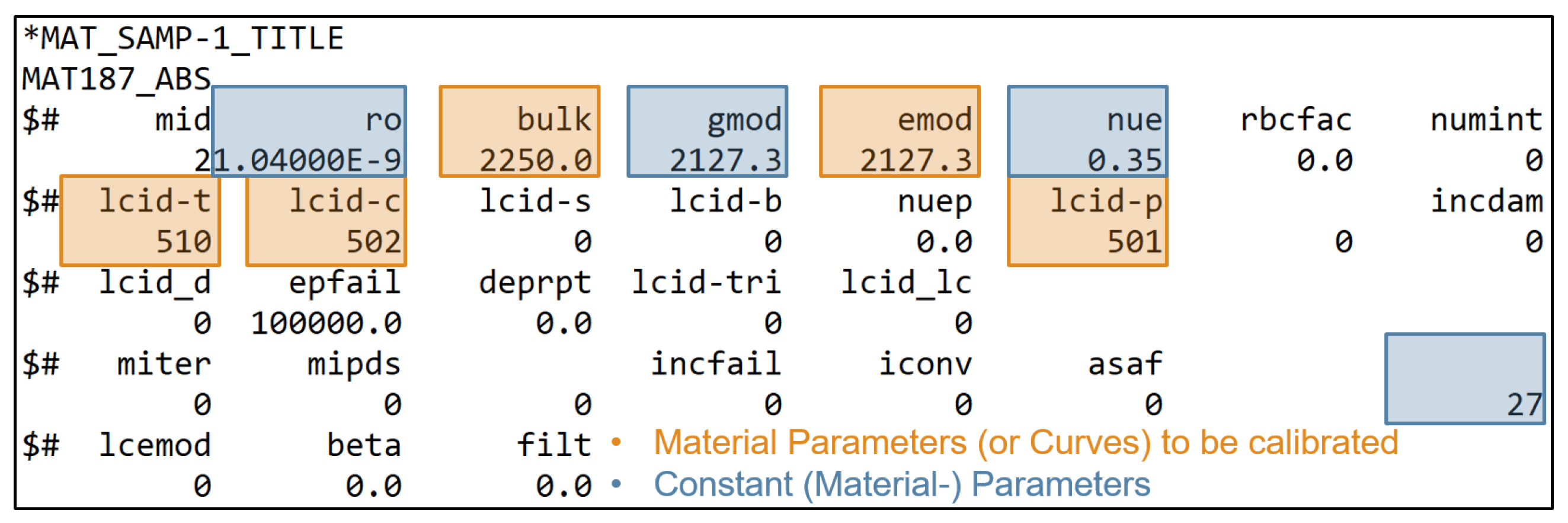
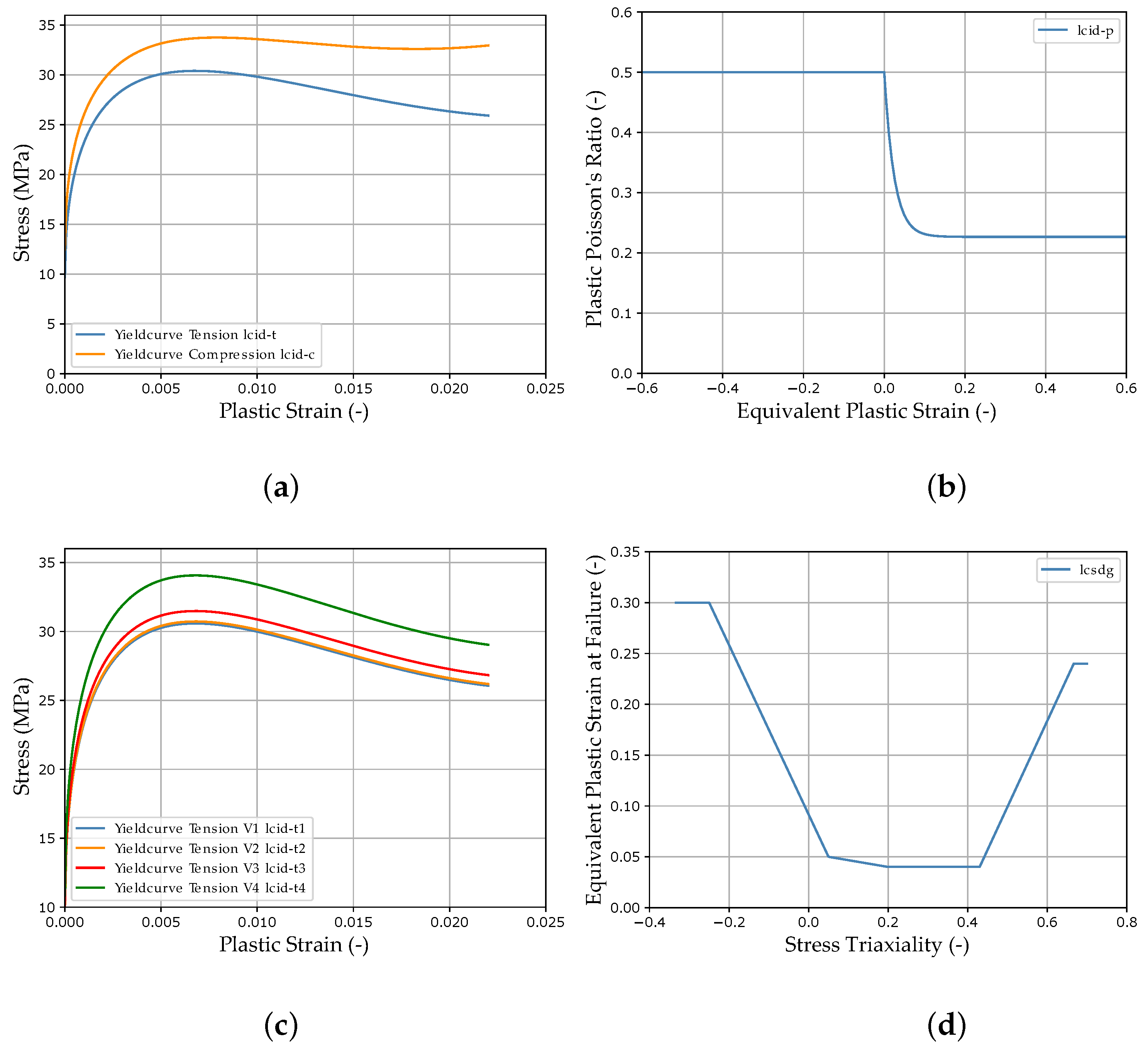
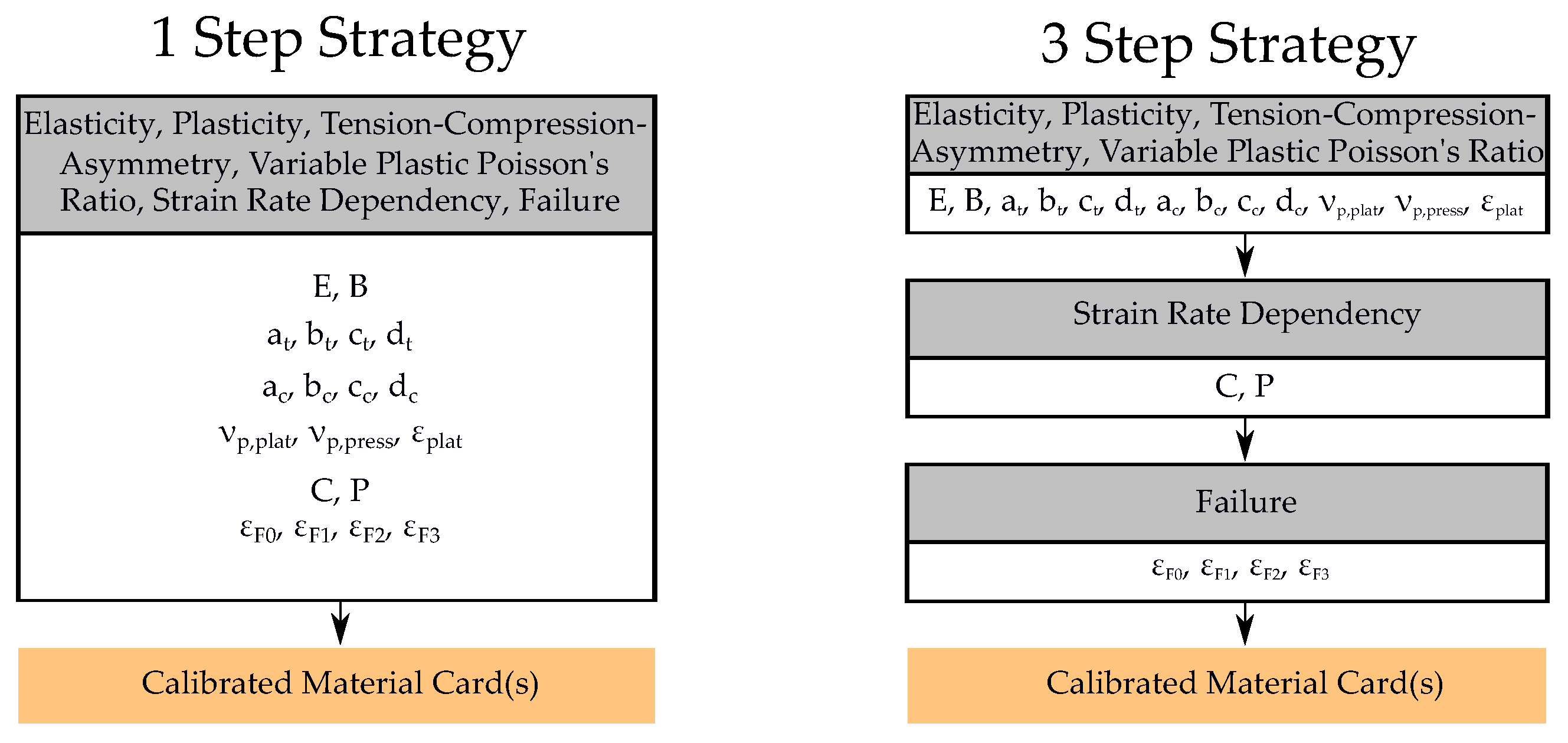
2.2. Description of the Material Behavior with LS-DYNA MAT_187_SAMP-1 and GISSMO
- Elasticity;
- Plasticity;
- Tension–compression asymmetry;
- Variable plastic Poisson’s ratio;
- Strain rate dependency;
- Failure.
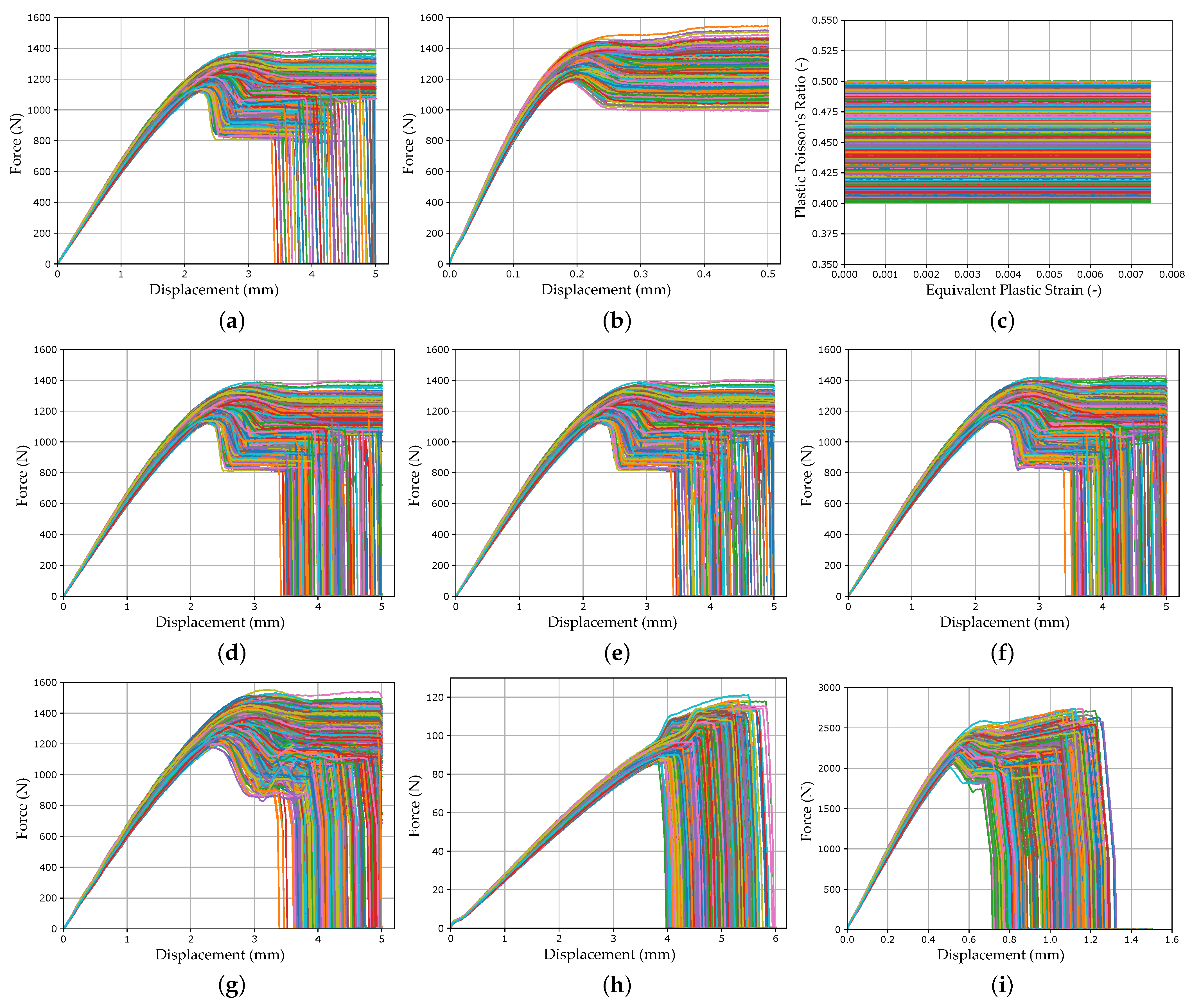
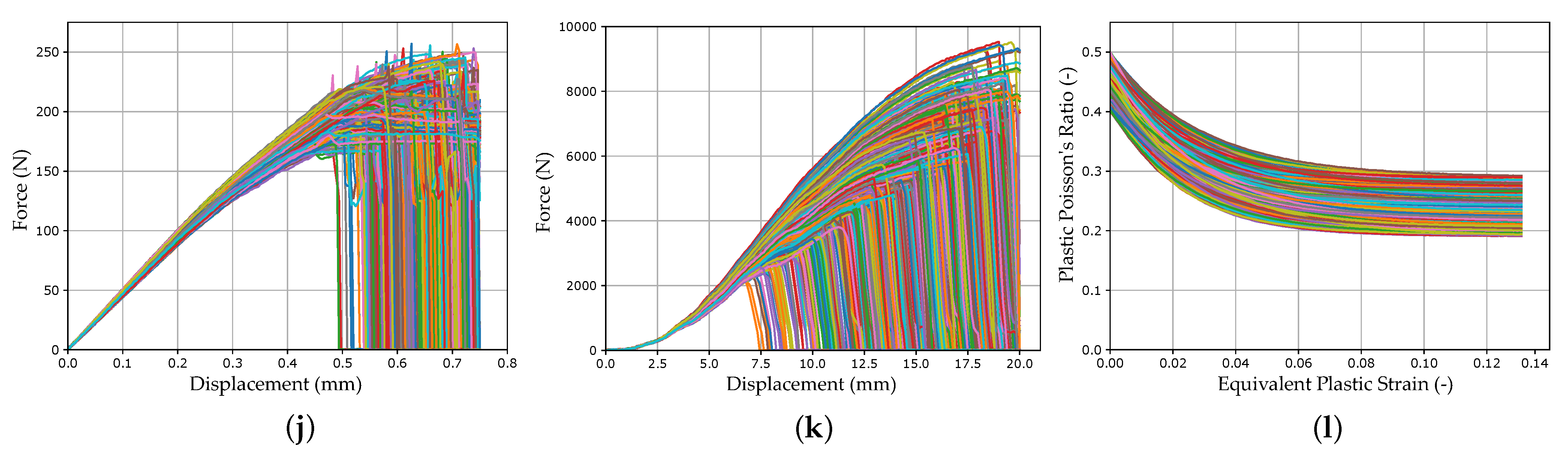
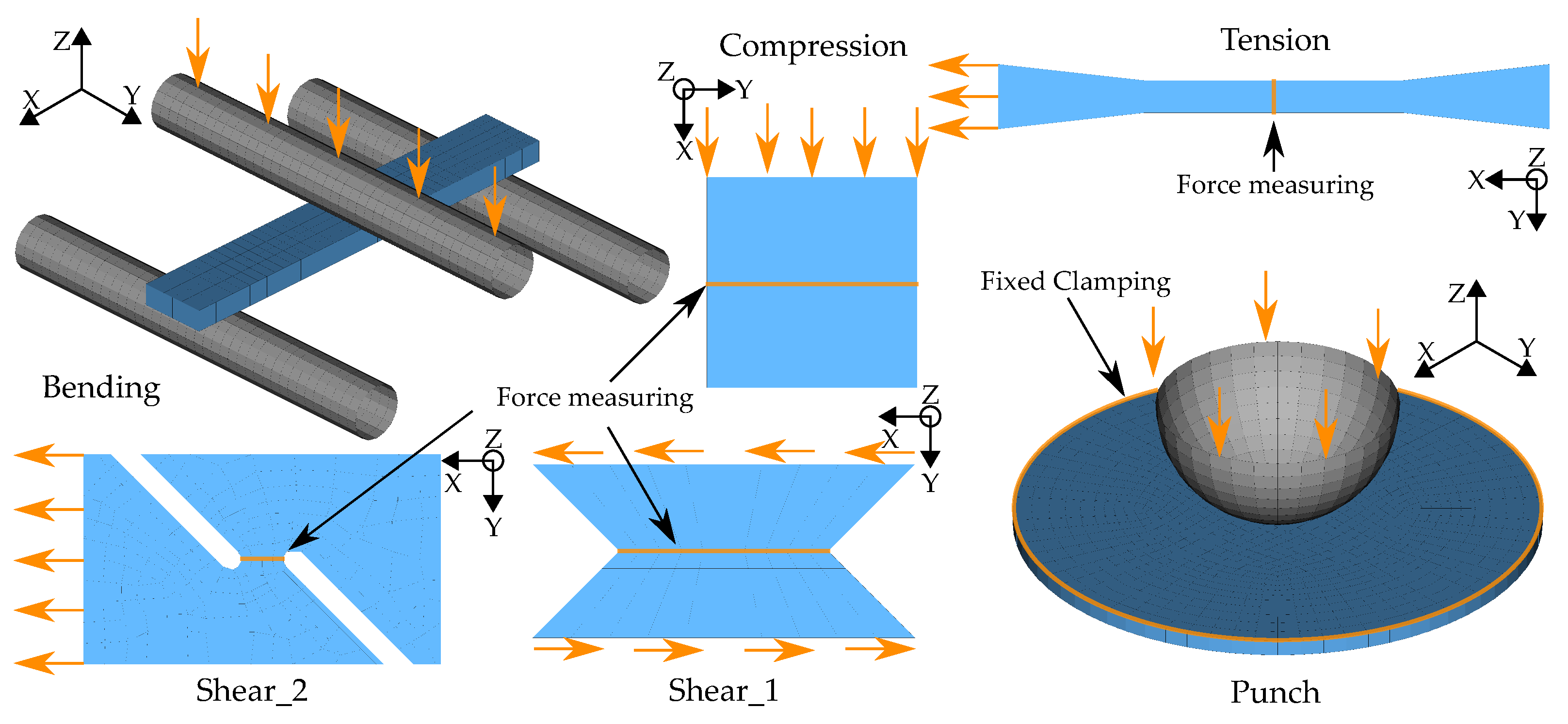
2.3. Finite Element Models
2.4. Material Parameter Setup and Configuration of the Virtual Investigations
2.5. Material Parameter Identification Process
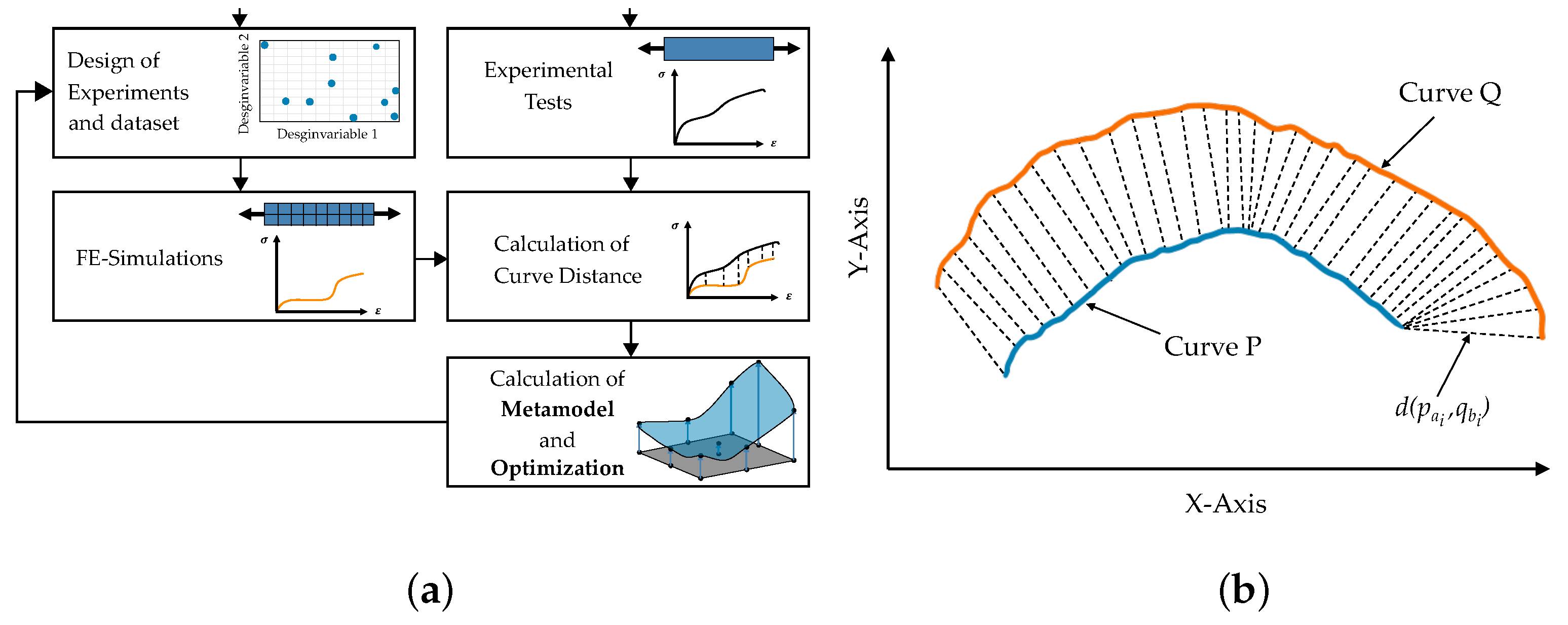
2.5.1. Iterative Optimization-Based Procedure Using LS-OPT
- The results of the optimization process are highly dependent on the choice of starting point, while the ideal location is unknown;
- Finding suitable parameters for sophisticated material models requires many iterations, which lead to high computational costs;
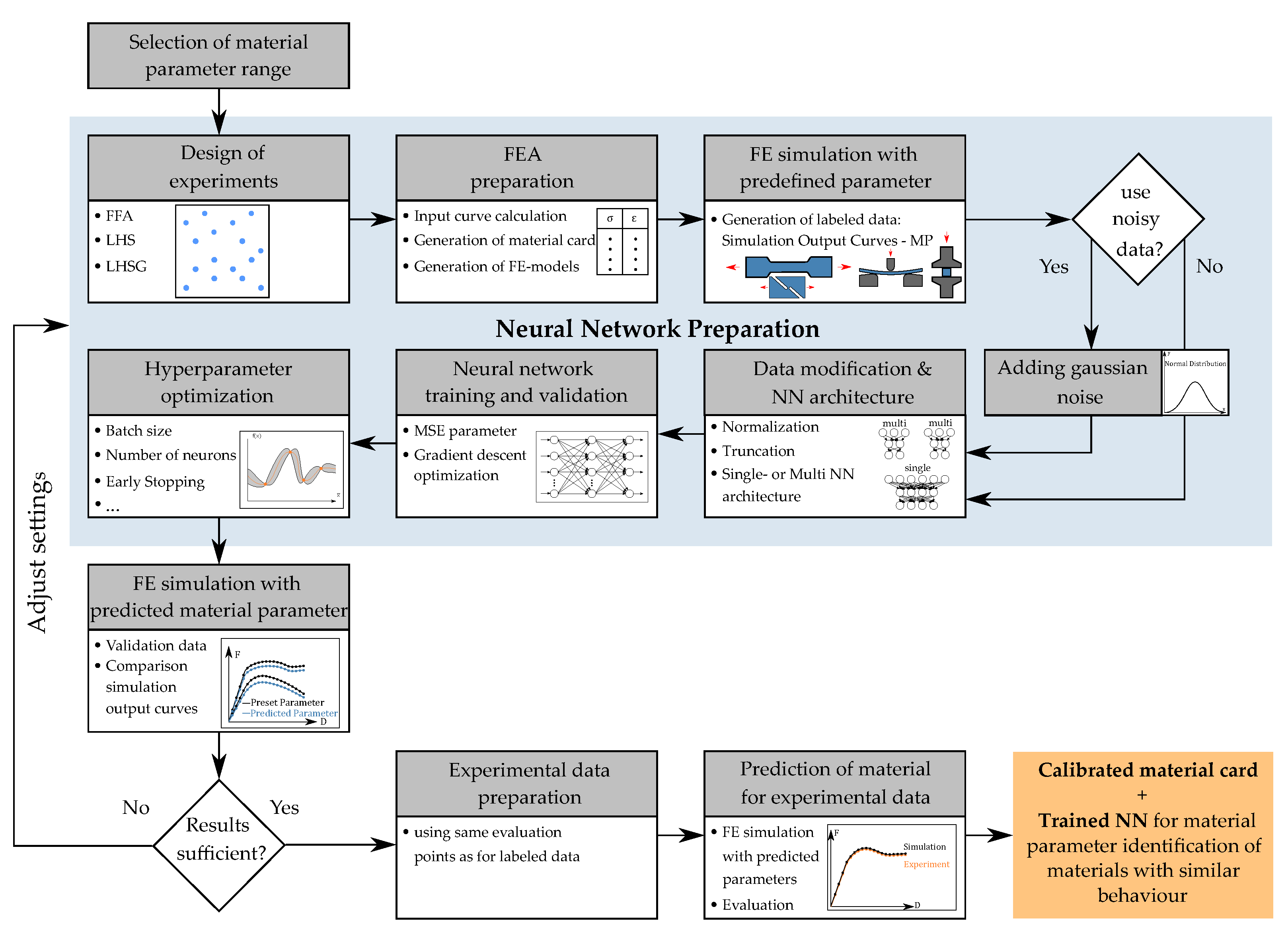
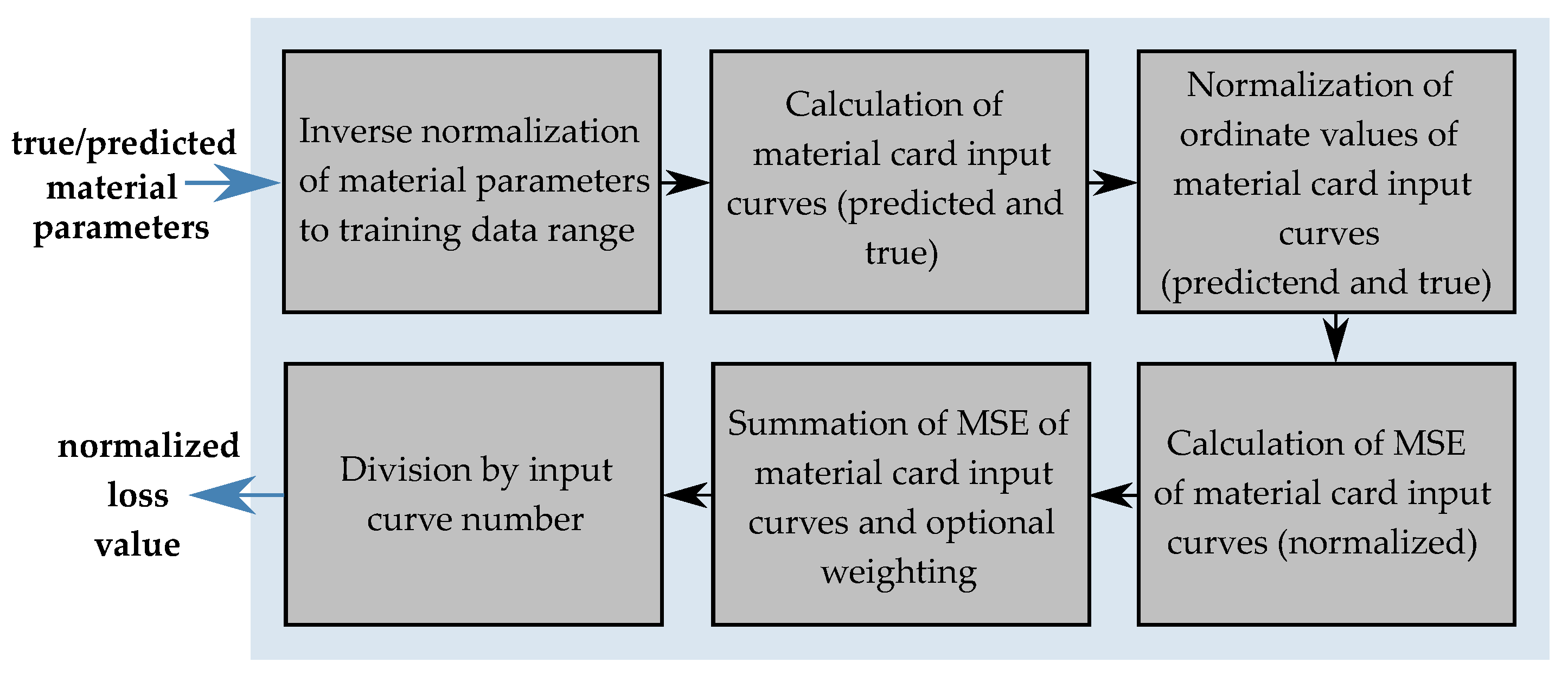
2.5.2. Direct Neural Network-Based Procedure Using Self-Implemented Framework
- Material parameter (NN output);
- Ordinate values of material card input curves;
- Ordinate values of simulation output curves (NN input).
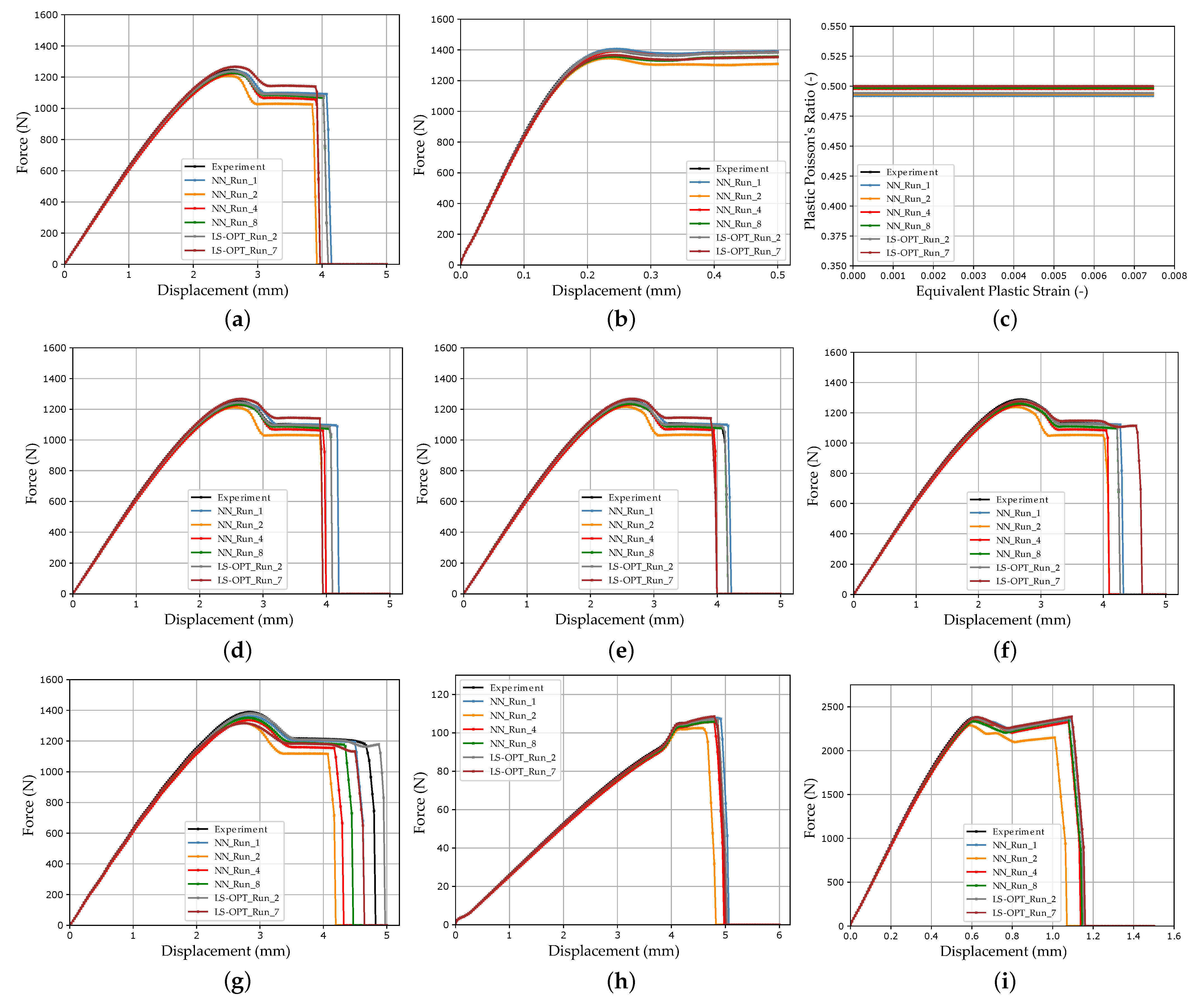
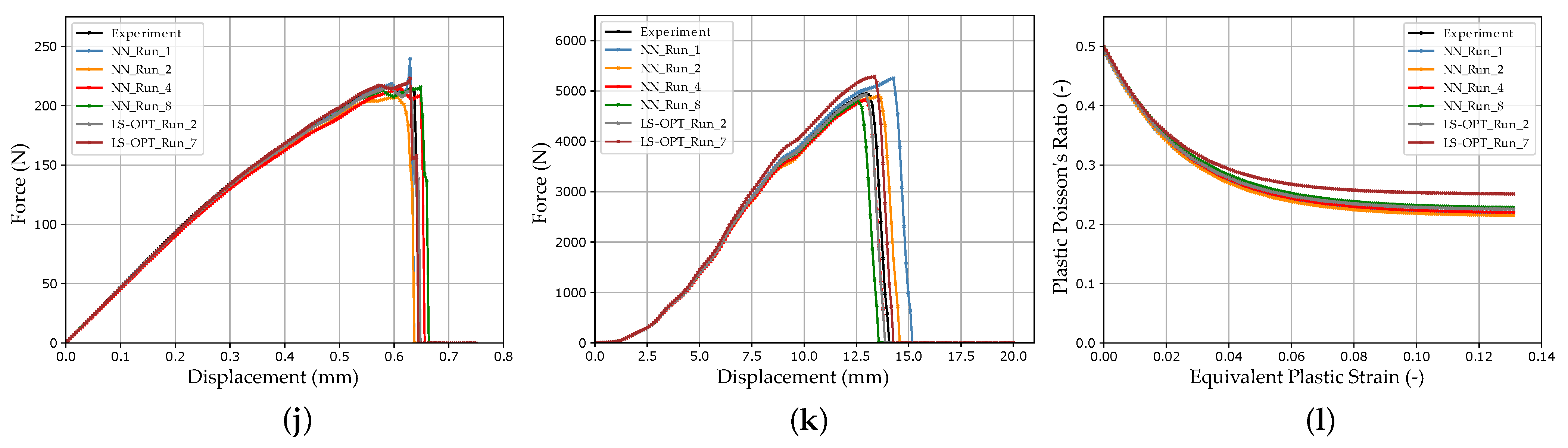
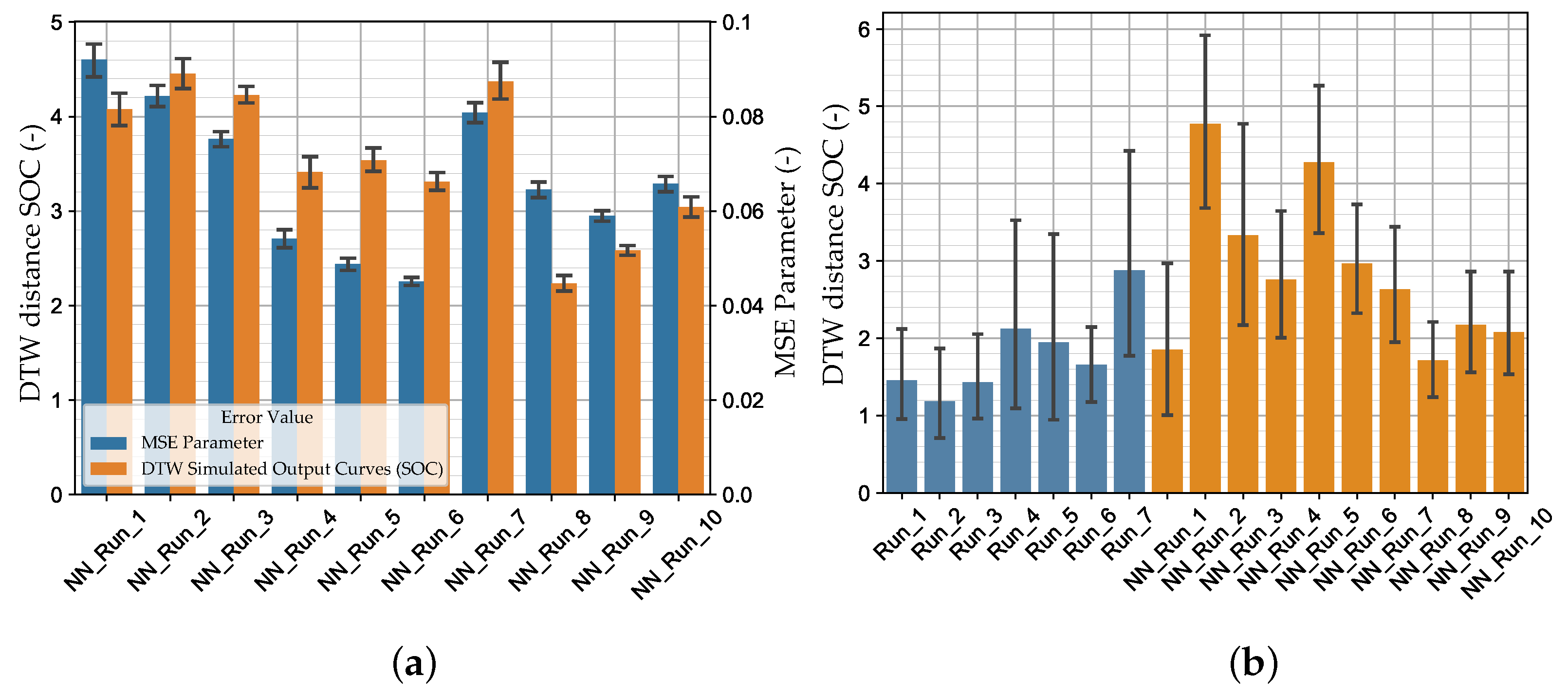
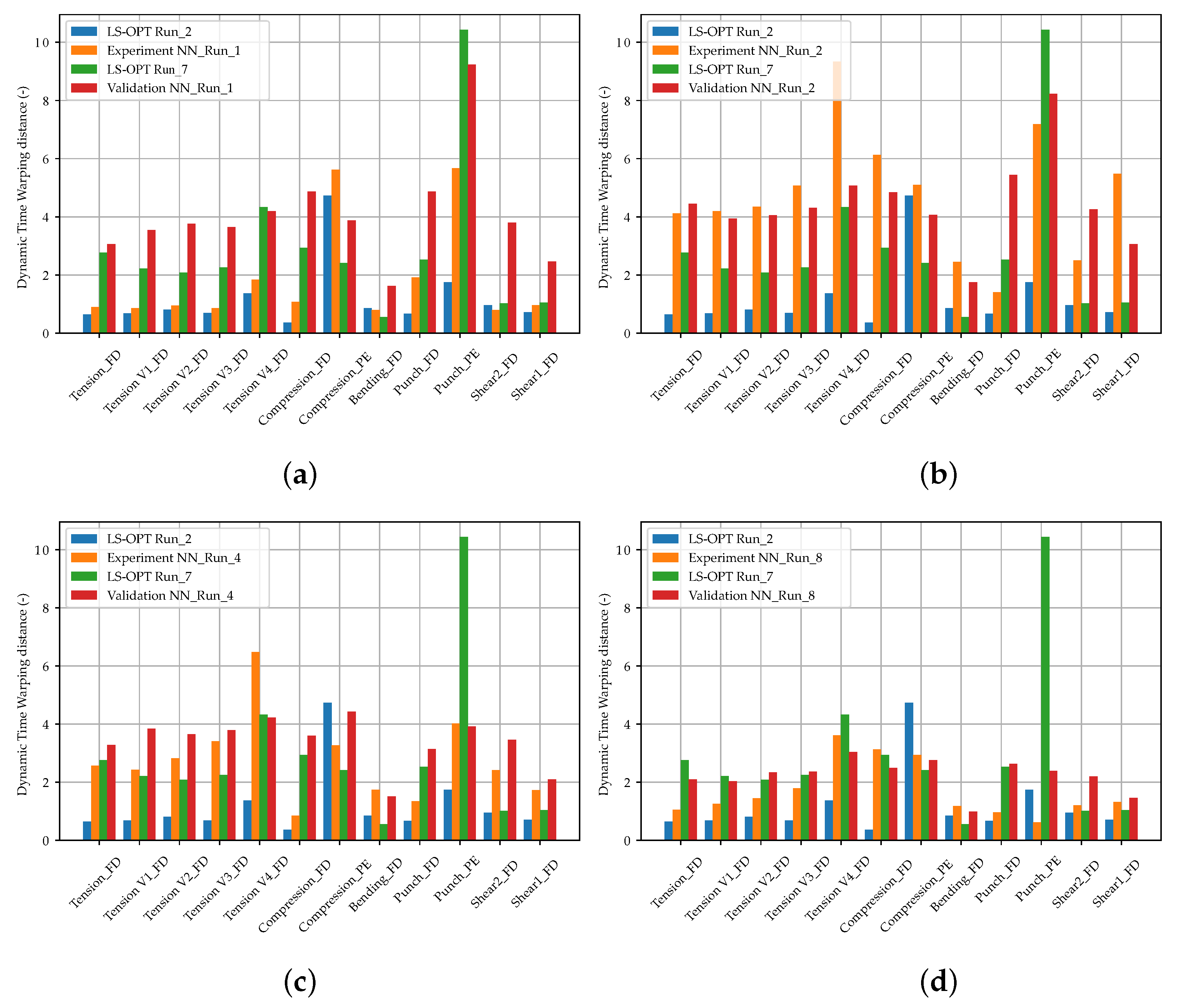
3. Results and Discussion
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile Butadiene Styrene |
| ANN | Artificial Neural Network |
| ASA | Adaptive Simulated Annealing |
| CL | Custom Loss |
| CLF | Custom Loss Function |
| DIC | Digital Image Correlation |
| DOE | Design of Experiments |
| DTW | Dynamic Time Warping |
| EPS | Equivalent Plastic Strain |
| EPSF | Equivalent Plastic Strain at Failure |
| EXP | Experiment |
| FDC | Force–Displacement Curve |
| FE | Finite Element |
| GA | Genetic Algorithm |
| GBM | Gradient-Based Methods |
| GISSMO | Generalized Incremental Stress State-Dependent Damage Model |
| GD | Gradient Descent |
| HL | Hidden Layer |
| HP | Hyperparameter |
| HPO | Hyperparameter Optimization |
| IL | Input Layer |
| LFOP | Leap-Frog Algorithm |
| LH | Latin Hypercube |
| LHS | Latin Hypercube Sampling |
| MDPI | Multidisciplinary Digital Publishing Institute |
| ML | Machine Learning |
| MP | Material Parameter |
| MPI | Material Parameter Identification |
| MSE | Mean Squared Error |
| MCIC | Material Card Input Curve(s) |
| NAN | Not a Number |
| NN | Neural Network |
| OL | Output Layer |
| PEC | Plastic Poisson’s Ratio Equivalent Plastic Strain Curve |
| PI | Parameter Identification |
| PPR | Plastic Poisson’s Ratio |
| RSM | Response Surface Methodology |
| SOC | Simulation Output Curve(s) |
| TRI | Triaxiality |
| VAL | Validation |
| VPPR | Variable Plastic Poisson’s Ratio |
Appendix A

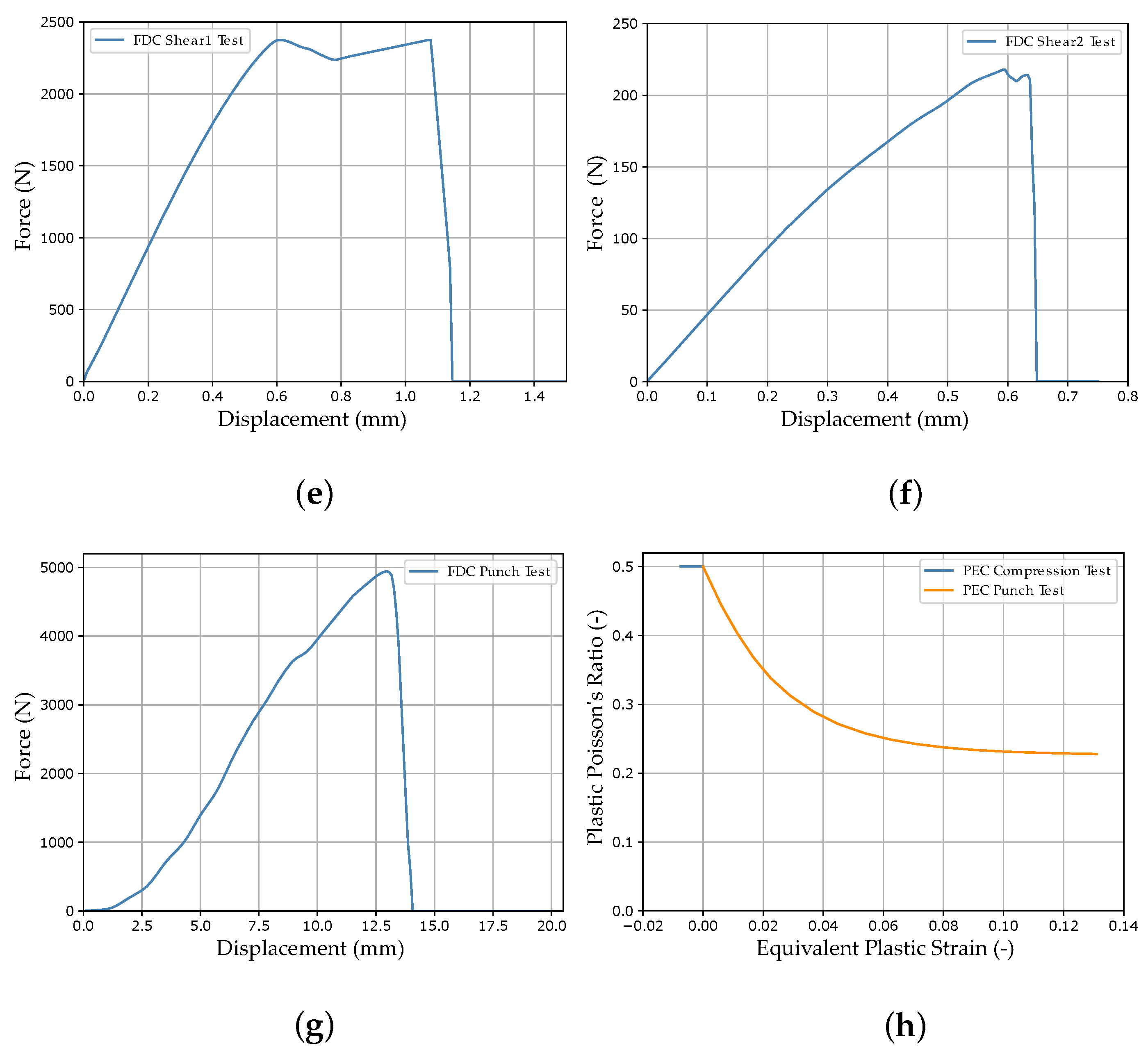

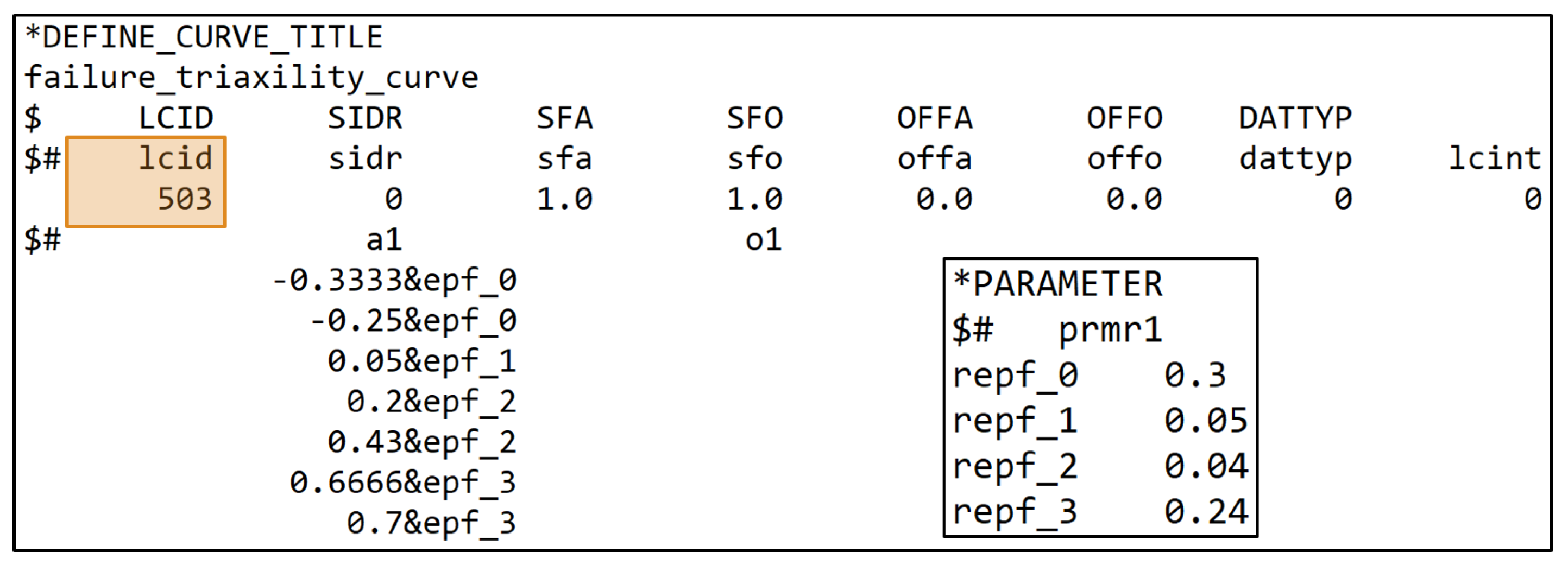
| Setting | Run_1 | Run_2 | Run_3 |
|---|---|---|---|
| Sampling Point Selection | D-Optimal | D-Optimal | D-Optimal |
| Simulations per Iteration | 40 | 100 | 40 |
| Metamodel | Polynomial | Polynomial | Polynomial |
| Metamodel Order | Linear | Elliptic | Linear |
| Distance Measure | DTW * | DTW * | DTW * |
| Optimization Algorithm | ASA/LFOP ** | ASA/LFOP ** | GA/LFOP ** |
| Maximum Iterations | 23 | 9 | 23 |
| Design Change Tolerance | *** | *** | *** |
| Objective Function Tolerance | *** | *** | *** |
| Required Iterations | 23 | 9 | 23 |
| Mean DTW SOC Exp. Set (-) |
| Setting | Run_4 | Run_5 | Run_6 | Run_7 |
|---|---|---|---|---|
| Sampling Point Selection | D-Optimal | D-Optimal | D-Optimal | D-Optimal |
| Simulations per Iteration | 40; 10; 20 | 45; 10; 20 | 40; 10; 20 | 40; 10; 20 |
| Metamodel | Polynomial | Polynomial | Polynomial | Polynomial |
| Metamodel-Order | Linear | Elliptic | Linear | Linear |
| Distance Measure | DTW *; DTW *; DTW * | DTW *; DTW *; DTW * | DTW *; DTW *; DTW * | MSE; MSE; DTW * |
| Optimization Algorithm | ASA/LFOP ** | ASA/LFOP ** | GA/LFOP ** | ASA/LFOP ** |
| Maximum Iterations | 20; 10; 15 | 18; 10; 15 | 20; 10; 15 | 20; 10; 15 |
| Design Change Tolerance | *** | *** | *** | *** |
| Objective Function Tolerance | *** | *** | *** | *** |
| Required Iterations | 18; 10; 14 | 15; 8; 13 | 20; 10; 15 | 20; 2; 15 |
| Mean DTW SOC Exp. Set (-) |
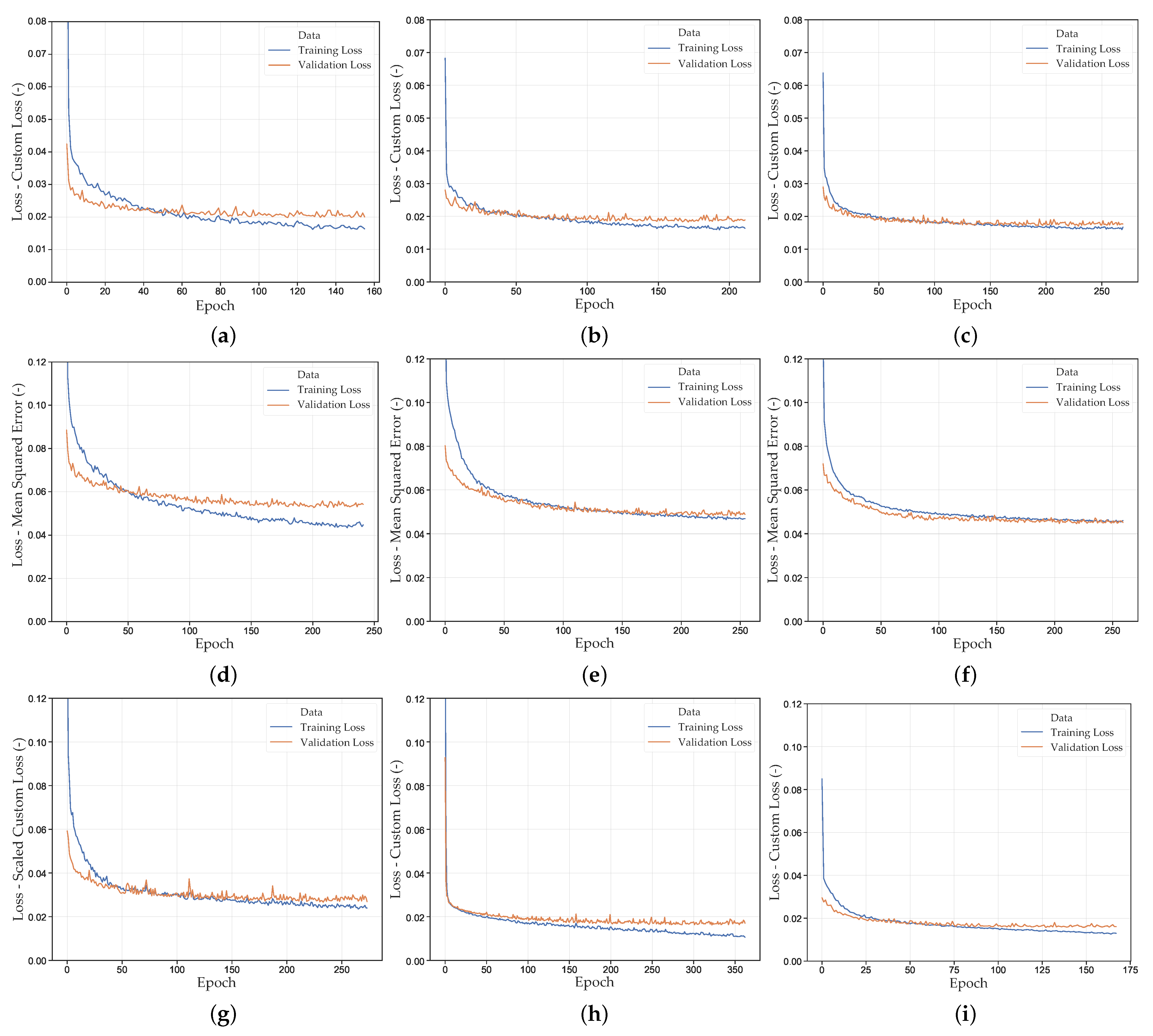
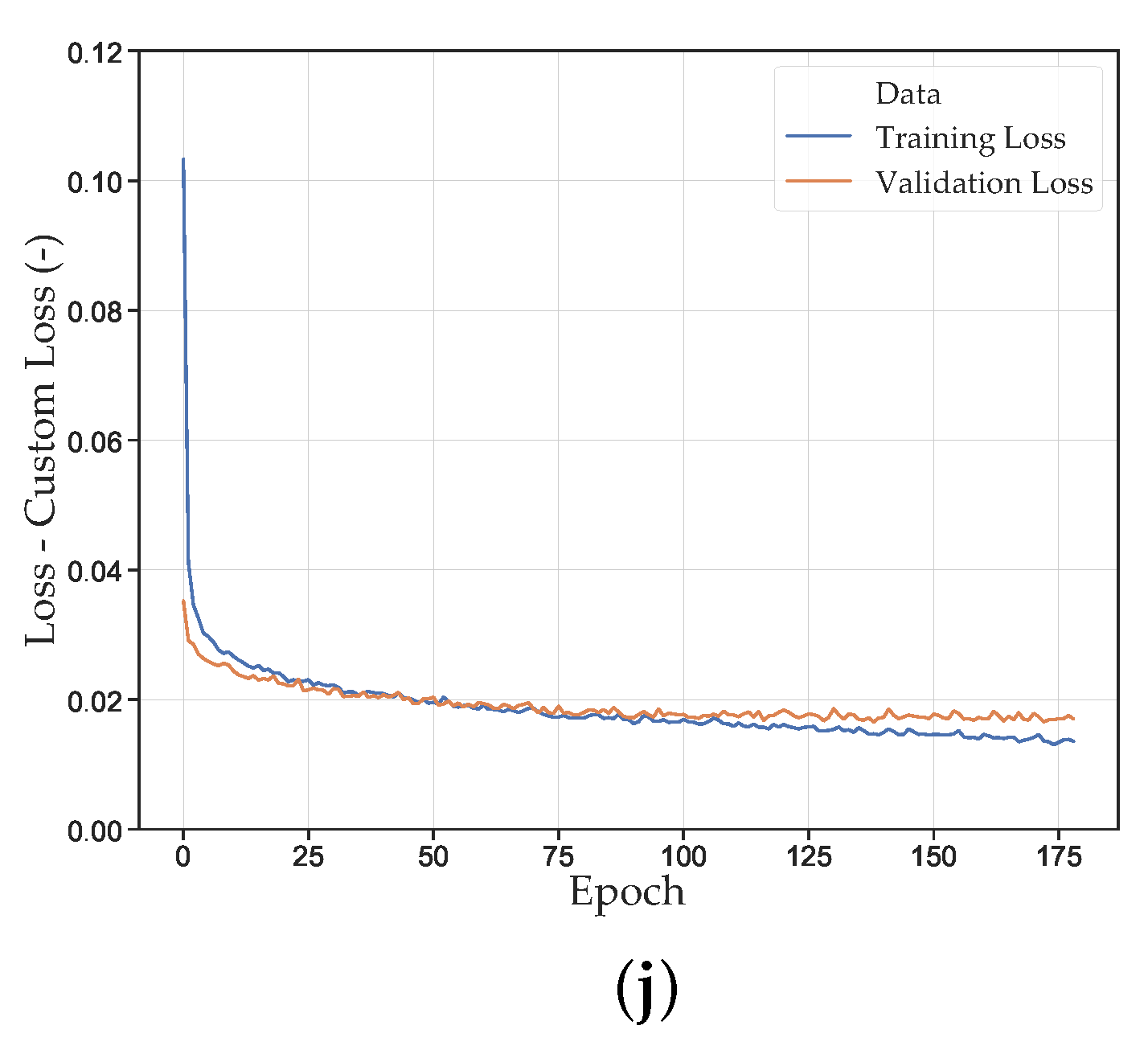
| Run | Dataset | NN | Loss | Early Stopped Epoch | Loss Val. Set (-) | Mean DTW SOC Val. Set (-) | Mean DTW SOC Exp. Set (-) |
|---|---|---|---|---|---|---|---|
| NN_Run_1 | 1 | Default | CL | 157 | |||
| NN_Run_2 | 2 | Default | CL | 212 | |||
| NN_Run_3 | 3 | Default | CL | 270 | |||
| NN_Run_4 | 1 | Default | MSE | 242 | |||
| NN_Run_5 | 2 | Default | MSE | 255 | |||
| NN_Run_6 | 3 | Default | MSE | 260 | |||
| NN_Run_7 | 2 | Default | CL (scaled *) | 274 | |||
| NN_Run_8 | 2 | HPO1 | CL | 363 | |||
| NN_Run_9 | 3 | HPO2 | CL | 168 | |||
| NN_Run_10 | 2 | HPO3 | CL | 179 |
| (Hyper-)Parameter | Setting |
|---|---|
| Batch Size | 25 |
| Maximum Epochs | 400 |
| Early Stopping Patience | 40 |
| Neurons (IL) | 2400 |
| Hidden Layers | 1 |
| Neurons (HL) | 100 |
| Kernel Initializer (HL) | He Uniform |
| Activation (HL) | Hard Sigmoid |
| Dropout (HL) | |
| Neurons (Output Layer) | 19 |
| Kernel Initializer (OL) | He Uniform |
| Activation (OL) | Linear |
| Gradient Descent Optimizer | Adam |
| (Hyper-)Parameter | Search Range |
|---|---|
| Batch Size | 20; 25 *; 30; …; 150 |
| Number HL | 1 *; 2; 3 |
| Neurons (HL1) | 30; 40; 50 *; …; 500 |
| Kernel Initializer (HL) | Normal *; Uniform; Glorot Uniform; Lecun Uniform; Glorot Normal; He Normal; He Uniform |
| Activation (HL1) | Softmax; Softplus; Softsign; Relu *; Sigmoid; Hard Sigmoid |
| Dropout (HL1) | ; ; *; …; |
| Neurons (HL2) | 30; 40; 50 *; …; 500 |
| Kernel Initializer (HL2) | Normal *; Uniform; Glorot Uniform; Lecun Uniform; Glorot Normal; He Normal; He Uniform |
| Activation (HL2) | Softmax; Softplus; Softsign; Relu *; Sigmoid; Hard Sigmoid |
| Dropout (HL2) | ; ; *; …; |
| Neurons (HL3) | 30; 40; 50 *; …; 500 |
| Kernel Initializer (HL3) | Normal *; Uniform; Glorot Uniform; Lecun Uniform; Glorot Normal; He Normal; He Uniform |
| Activation (HL3) | Softmax; Softplus; Softsign; Relu *; Sigmoid; Hard Sigmoid |
| Dropout (HL3) | ; ; *; …; |
| Kernel Initializer (OL) | Normal *; Uniform; Lecun Uniform; Glorot Normal; He Normal; He Uniform |
| GD Optimizer | Adam *; Adagrad; Adamax; Nadam |
| (Hyper-)Parameter | HPO1 | HPO2 | HPO3 |
|---|---|---|---|
| Batch Size | 85 | 25 | 50 |
| Maximum Epochs * | 400 | 400 | 400 |
| Early Stopping Patience * | 40 | 40 | 40 |
| Neurons (IL) * | 2400 | 2400 | 2400 |
| Number HL | 1 | 2 | 2 |
| Neurons (HL1) | 460 | 470 | 450 |
| Kernel Initializer (HL1) | He Uniform | He Uniform | He Normal |
| Activation (HL1) | Hard Sigmoid | Relu | Softplus |
| Dropout (HL1) | |||
| Neurons (HL2) | - | 470 | 310 |
| Kernel Initializer (HL2) | - | Uniform | Normal |
| Activation (HL2) | - | Softplus | Relu |
| Dropout (HL2) | - | ||
| Neurons (OL) * | 19 | 19 | 19 |
| Kernel Initializer (OL) | Lecun Uniform | He Uniform | Uniform |
| Activation (OL) * | Linear | Linear | Linear |
| Loss Function * | Custom Loss | Custom Loss | Custom Loss |
| GD Optimizer | Adamax | Adamax | Adamax |
| HP Optimizer | Bayesian | Bayesian | Random Search |
| Max Trials * | 500 | 500 | 500 |
| Executions per Trial * | 2 | 2 | 2 |
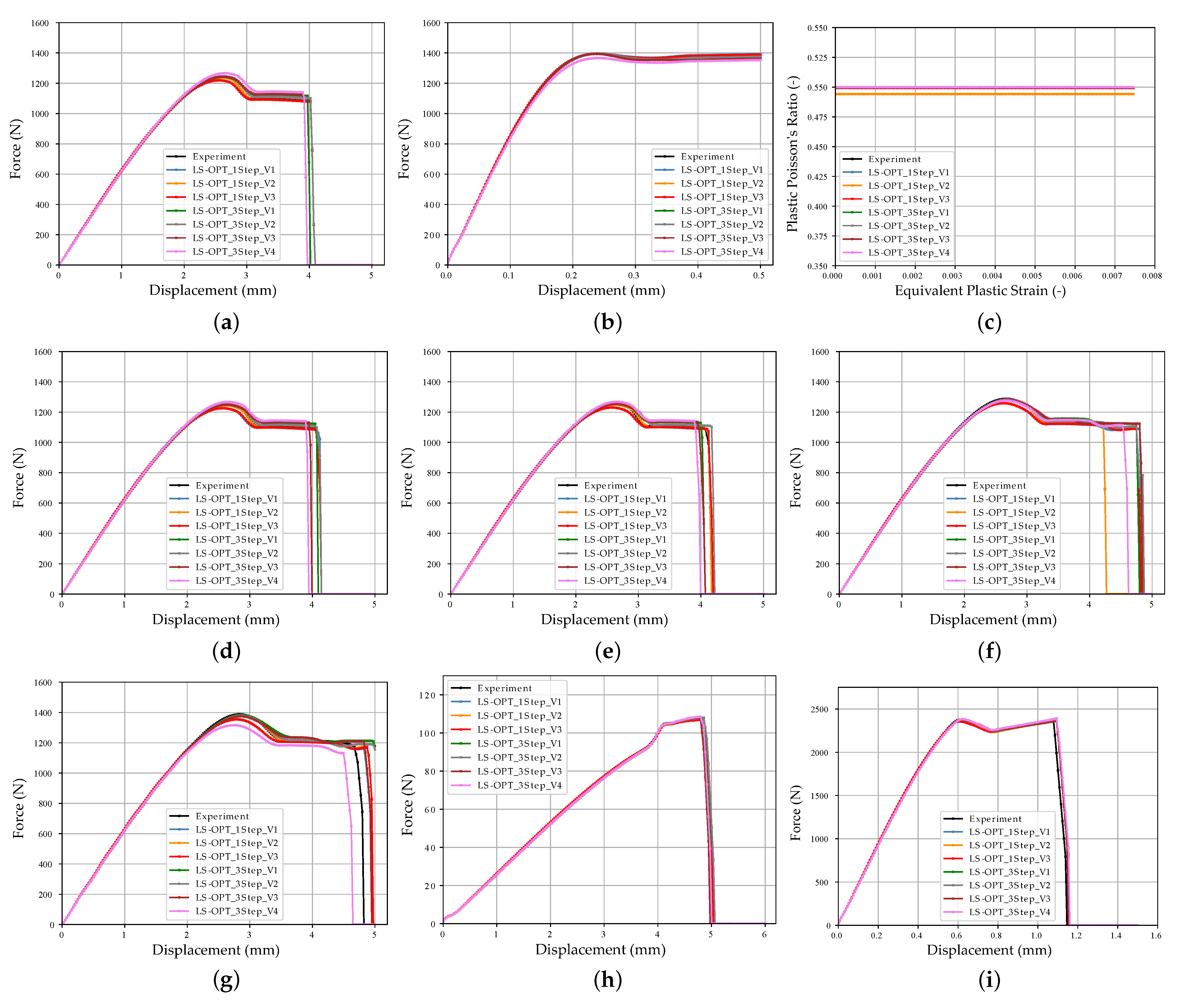
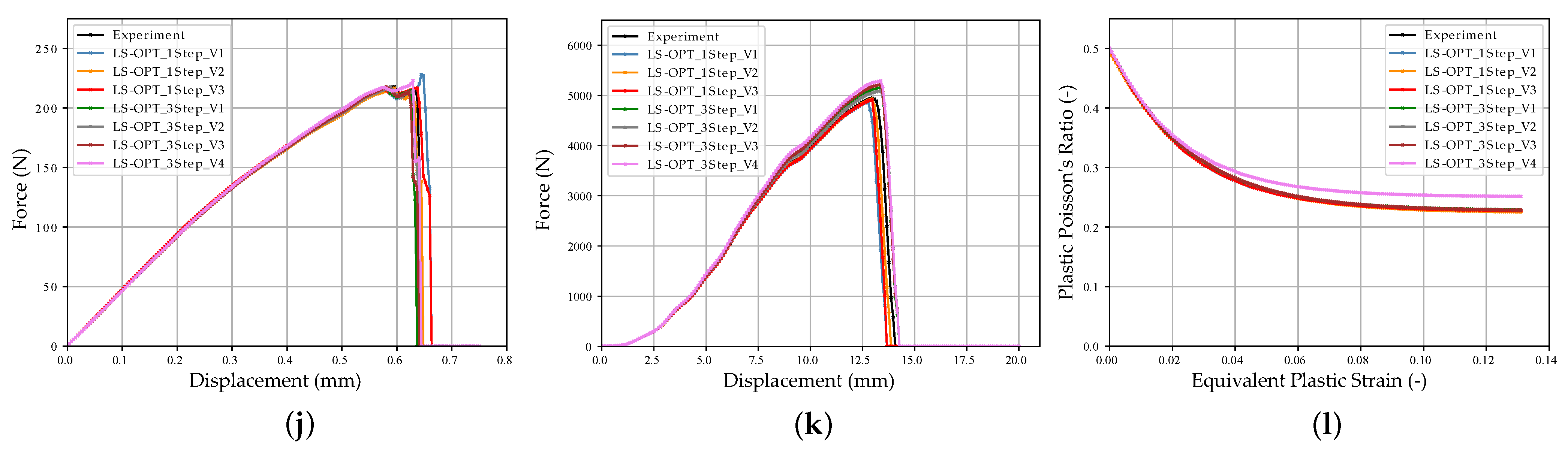
References
- Fonseca, J.H.; Quagliato, L.; Yun, S.; Han, D.; Kim, N.; Lee, H. Preliminary design of an injection-molded recycled-carbon fiber–reinforced plastic/metal hybrid automotive structure via combined optimization techniques. Struct. Multidiscip. Optim. 2021, 64, 2773–2788. [Google Scholar] [CrossRef]
- Winter, J.; Fiebig, S.; Franke, T.; Vietor, T. NURBS-based shape and parameter optimization of structural components with an adaptive amount of control points. In Proceedings of the 13th World Congress of Structural and Multidisciplinary Optimization (WCSMO-13), Beijing, China, 20–24 May 2019. [Google Scholar]
- Werner, Y.; Vietor, T.; Weinert, M.; Erber, T. Multidisciplinary design optimization of a generic b-pillar under package and design constraints. Eng. Optim. 2020, 53, 1884–1901. [Google Scholar] [CrossRef]
- Van de Weg, B.; Greve, L.; Andres, M.; Eller, T.; Rosic, B. Neural network-based surrogate model for a bifurcating structural fracture response. Eng. Fract. Mech. 2021, 241, 107424. [Google Scholar] [CrossRef]
- Kohar, C.P.; Greve, L.; Eller, T.K.; Connolly, D.S.; Inal, K. A machine learning framework for accelerating the design process using CAE simulations: An application to finite element analysis in structural crashworthiness. Comput. Methods Appl. Mech. Eng. 2021, 385, 114008. [Google Scholar] [CrossRef]
- Kolling, S.; Haufe, A.; Feucht, M.; Bois, P.A.D. SAMP-1: A Semi-Analytical Model for the Simulation of Polymers. In Proceedings of the 4th LS-DYNA Anwenderforum, Bamberg, Germany, 20–21 October 2005. [Google Scholar]
- Fröck, H.; Kappis, L.V.; Reich, M.; Kessler, O. A Phenomenological Mechanical Material Model for Precipitation Hardening Aluminium Alloys. Metals 2019, 9, 1165. [Google Scholar] [CrossRef] [Green Version]
- Eggertsen, P.A.; Mattiasson, K.; Hertzman, J. A Phenomenological Model for the Hysteresis Behavior of Metal Sheets Subjected to Unloading/Reloading Cycles. ASME J. Manuf. Sci. Eng. 2011, 133, 061021. [Google Scholar] [CrossRef]
- Morasch, A.; Matias, D.; Baier, H. Material modelling for crash simulation of thin extruded aluminium sections. Int. J. Crashworthiness 2014, 19, 500–513. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. The identification of parameters for visco-plastic models via finite-element methods and gradient methods. Model. Simul. Mater. Sci. Eng. 1994, 2, 597–616. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. A unified approach for parameter identification of inelastic material models in the frame of the finite element method. Comput. Methods Appl. Mech. Eng. 1996, 136, 225–258. [Google Scholar] [CrossRef]
- Morand, L.; Helm, D. A mixture of experts approach to handle ambiguities in parameter identification problems in material modeling. Comput. Mater. Sci. 2019, 167, 85–91. [Google Scholar] [CrossRef]
- Kučerová, A.; Zeman, J. Estimating Parameters of Microplane Material Model Using Soft Computing Methods. In Proceedings of the 6thWorld Congresses of Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazil, 30 May–3 June 2005. [Google Scholar]
- Haufe, A.; Koch, D. First Steps towards Machine-Learning supported Material Parameter Identification. In Proceedings of the 12th European LS-DYNA Conference, Koblenz, Germany, 14–16 May 2019. [Google Scholar]
- Meißner, P.; Watschke, H.; Winter, J.; Vietor, T. Artificial Neural Networks-Based Material Parameter Identification for Numerical Simulations of Additively Manufactured Parts by Material Extrusion. Polymers 2020, 12, 2949. [Google Scholar] [CrossRef] [PubMed]
- Goh, G.D.; Sing, S.L.; Yeong, W.Y. A review on machine learning in 3D printing: Applications, potential, and challenges. Artif. Intell. Rev. 2020, 54, 63–94. [Google Scholar] [CrossRef]
- Mehlig, B. Artifical Neural Networks; Lecture Notes; Department of Physics, University of Gothenburg: Göteborg, Sweden, 2019. [Google Scholar]
- Kučerová, A. Identification of Nonlinear Mechanical Model Parameters Based on Softcomputing Methods. Ph.D. Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2007. [Google Scholar]
- Yao, L.; Sethares, W. Nonlinear parameter estimation via the genetic algorithm. IEEE Trans. Signal Process. 1994, 42, 927–935. [Google Scholar] [CrossRef] [Green Version]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Yagawa, G.; Okuda, H. Neural networks in computational mechanics. Arch. Comput. Methods Eng. 1996, 3, 435–512. [Google Scholar] [CrossRef]
- Jordan, M.I.; Rumelhart, D.E. Forward Models: Supervised Learning with a Distal Teacher. Cogn. Sci. 1992, 16, 307–354. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties fromspherical indentation data using neural networks. Part i: The case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties fromspherical indentation data using neural networks. Part ii: Plasticity with nonlinear isotropic and kinematichardening. J. Mech. Phys. Solids 1999, 47, 1589–1607. [Google Scholar] [CrossRef]
- Nardin, A.; Schrefler, B.; Lefik, M. Application of Artificial Neural Network for Identification of Parameters of a Constitutive Law for Soils. In Developments in Applied Artificial Intelligence, Proceedings of the 16th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems, IEA/AIE 2003, Loughborough, UK, 23–26 June 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 545–554. [Google Scholar] [CrossRef]
- Aguir, H.; Chamekh, A.; BelHadjSalah, H.; Dogui, A.; Hambli, R. Parameter identification of a non-associative elastoplastic constitutive model using ANN and multi-objective optimization. Int. J. Mater. Form. 2009, 2, 75–82. [Google Scholar] [CrossRef]
- Unger, J.F.; Könke, C. An inverse parameter identification procedure assessing the quality of the estimates using Bayesian neural networks. Appl. Soft Comput. 2011, 11, 3357–3367. [Google Scholar] [CrossRef]
- MacKay, D.J.C. A Practical Bayesian Framework for Backpropagation Networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Adeli, E.; Rosić, B.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Bayesian Parameter Determination of a CT-Test Described by a Viscoplastic-Damage Model Considering the Model Error. Metals 2020, 10, 1141. [Google Scholar] [CrossRef]
- Da Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial Neural Networks; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Number Bd. 10 in Neural Networks and Learning Machines; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 16 July 2021).
- Pinto, N.; Doukhan, D.; DiCarlo, J.J.; Cox, D.D. A High-Throughput Screening Approach to Discovering Good Forms of Biologically Inspired Visual Representation. PLoS Comput. Biol. 2009, 5, e1000579. [Google Scholar] [CrossRef] [PubMed]
- Moons, B.; Bankman, D.; Verhelst, M. Embedded Deep Learning; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. Keras Tuner. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 13 October 2021).
- Hutter, F.; Kotthoff, L.; Vanschoren, J. (Eds.) Automated Machine Learning; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kegl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, NIPS’11, Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Li, L.; Jamieson, K.G.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Efficient Hyperparameter Optimization and Infinitely Many Armed Bandits. J. Mach. Learn. Res. 2016. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Reithofer, P.; Fertschej, A.; Hirschmann, B.; Jilka, B.; Rollant, M. Material Models For Thermoplastics in LS-DYNA from Deformation to Failure. In Proceedings of the 15th International LS-DYNA Users Conference, Dearborn, MI, USA, 10–12 June 2018. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Volume II Material Models LS-DYNA, 11th ed.; LSTC: Livermore, CA, USA, 2018. [Google Scholar]
- Andrade, F.X.C.; Feucht, M.; Haufe, A.; Neukamm, F. An incremental stress state dependent damage model for ductile failure prediction. Int. J. Fract. 2016, 200, 127–150. [Google Scholar] [CrossRef]
- Neukamm, F.; Feucht, M.; Haufe, A.D. Considering damage history in crashworthiness simulations. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Basaran, M.; Wölkerling, S.D.; Feucht, M.; Neukamm, F.; Weichert, D. An Extension of the GISSMO Damage Model Based on Lode Angle Dependence. In Proceedings of the 9th LS-DYNA FORUM 2010, Bamberg, Germany, 12–13 October 2010; DYNAmore: Stuttgart, Germany, 2010; pp. 3–17. [Google Scholar]
- Haufe, A.; DuBois, P.; Neukamm, F.; Feucht, M. GISSMO—Material Modeling with a sophisticated Failure Criteria. In Proceedings of the LS-DYNA Info Day, Gothenburg, Sweden, 23–24 May 2011. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]
- Helbig, M.; Haufe, A. Modeling of Crazing in Rubber-toughened Polymers with LS-DYNA. In Proceedings of the 15th International LS-DYNA User Conference, Dearborn, MI, USA, 10–12 June 2018. [Google Scholar]
- Vogler, M.; Dell, H.; Oberhofer, G.; Gese, H. Beschreibung von unverstärkten, kurzfaserverstärkten und endlosfaserverstärkten Kunststoffen in der Crashsimulation. In Proceedings of the Deutsches LS-DYNA Forum, MATFEM Partnerschaft Dr. Grese and Oberhofer, München, Germany, 10–12 October 2016. [Google Scholar]
- Škrlec, A.; Klemenc, J. Estimating the Strain-Rate-Dependent Parameters of the Cowper-Symonds and Johnson-Cook Material Models using Taguchi Arrays. J. Mech. Eng. 2016, 62, 220–230. [Google Scholar] [CrossRef] [Green Version]
- Darlet, A.; Desmorat, R. Stress triaxiality and Lode angle along surfaces of elastoplastic structures. Int. J. Solids Struct. 2015, 67–68, 71–83. [Google Scholar] [CrossRef]
- Bai, Y.; Teng, X.; Wierzbicki, T. On the Application of Stress Triaxiality Formula for Plane Strain Fracture Testing. J. Eng. Mater. Technol. 2009, 131, 021002. [Google Scholar] [CrossRef]
- Hayashi, S. Prediction of Failure Behavior in Polymers Under Multiaxial Stress State. Seikei-Kakou 2013, 25, 476–482. [Google Scholar] [CrossRef] [Green Version]
- Stander, N.; Roux, W.; Eggleston, T.; Craig, K. LS OPT User’s Manual—A Design Optimization and Probabilistic Analysis Tool for the Engeneering Analyst, v. 6.0 ed.; Livermore Software Technology Corporation: Livermore, CA, USA, 2019. [Google Scholar]
- Stander, N.; Craig, K.; Müllerschön, H.; Reichert, R. Material identification in structural optimization using response surfaces. Struct. Multidiscip. Optim. 2005, 29, 93–102. [Google Scholar] [CrossRef]
- Carney, S.D.A.S.K.S. Modeling of Carbon-Fiber-Reinforced Polymer (CFRP) Composites in LS-DYNA with Optimization of Material and Failure Parameters in LS-OPT. In Proceedings of the 15th International LS-DYNA User Conference, Dearborn, MI, USA, 10–12 June 2018. [Google Scholar]
- Stander, M.R.L.N.F.B.N. Shape Optimization of a Vehicle Crash-box using LS-OPT. In Proceedings of the 5th European LS-DYNA Users Conference, Birmingham, UK, 25–26 May 2005. [Google Scholar]
- Maier, G.; Buljak, V.; Garbowski, T.; Cocchetti, G.; Novati, G. Mechanical characterization of materials and diagnosis of structures by inverse analysis: Some innovative procedures and applications. Int. J. Comput. Methods 2014, 11, 1343002. [Google Scholar] [CrossRef]
- Maier, G.; Zavelani-Rossi, A.; Benedetti, D. A finite element approach to optimal design of plastic structures in plane stress. Int. J. Numer. Methods Eng. 1972, 4, 455–473. [Google Scholar] [CrossRef]
- Bolzon, G.; Buljak, V.; Maier, G.; Miller, B. Assessment of elastic–plastic material parameters comparatively by three procedures based on indentation test and inverse analysis. Inverse Probl. Sci. Eng. 2011, 19, 815–837. [Google Scholar] [CrossRef]
- Jekel, C.F.; Venter, G.; Venter, M.P.; Stander, N.; Haftka, R.T. Similarity measures for identifying material parameters from hysteresis loops using inverse analysis. Int. J. Mater. Form. 2018, 12, 355–378. [Google Scholar] [CrossRef]
- Witowski, K.; Stander, N. Parameter Identification of Hysteretic Models Using Partial Curve Mapping. In Proceedings of the 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA,, 17–19 September 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; Technical report; Technische Universität Wien: Vienna, Austria, 1994. [Google Scholar]
- Stander, K.W.N. Modified Dynamic Time Warping for Utilizing Partial Curve Data to Calibrate Material Models. In Proceedings of the 16th International LS-DYNA Users Conference, Detroit, MI, USA, 31 May–2 June 2020. [Google Scholar]
- Giorgino, T. Computing and Visualizing Dynamic Time Warping Alignments inR: ThedtwPackage. J. Stat. Softw. 2009, 31, 1–24. [Google Scholar] [CrossRef] [Green Version]




| MP Name | MPexp | MPMin | MPMax | MPStart | MCIC |
|---|---|---|---|---|---|
| emod (MPa) | - | ||||
| bulk (MPa) | - | ||||
| at (-) | 43,416.1 | 40,000.0 | 46,000.0 | 44,000.0 | lcid-t; lcid-t1-lcid-t4 |
| bt (-) | lcid-t; lcid-t1-lcid-t4 | ||||
| ct (-) | lcid-t; lcid-t1-lcid-t4 | ||||
| dt (-) | lcid-t; lcid-t1-lcid-t4 | ||||
| ac (-) | 51,000.0 | 47,000.0 | 52,000.0 | 50,000.0 | lcid-c |
| bc (-) | lcid-c | ||||
| cc (-) | lcid-c | ||||
| dc (-) | lcid-c | ||||
| p,plat (-) | lcid-p | ||||
| p,press (-) | lcid-p | ||||
| p,plat (-) | lcid-p | ||||
| C () | 27,572.1 | 15,000.0 | 50,000.0 | 30,000.0 | lcid-t1-lcid-t4 |
| P (-) | lcid-t1-lcid-t4 | ||||
| epsf0 (-) | lcsdg | ||||
| epsf1 (-) | lcsdg | ||||
| epsf2 (-) | lcsdg | ||||
| epsf3 (-) | lcsdg |
| Dataset | Sampling | Training Set Size | Validation Set Size | Complete Set Size |
|---|---|---|---|---|
| 1 | LHS | 450 | 300 | 750 |
| 2 | LHS | 900 | 600 | 1500 |
| 3 | LHS | 1800 | 1200 | 3000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meißner, P.; Winter, J.; Vietor, T. Methodology for Neural Network-Based Material Card Calibration Using LS-DYNA MAT_187_SAMP-1 Considering Failure with GISSMO. Materials 2022, 15, 643. https://doi.org/10.3390/ma15020643
Meißner P, Winter J, Vietor T. Methodology for Neural Network-Based Material Card Calibration Using LS-DYNA MAT_187_SAMP-1 Considering Failure with GISSMO. Materials. 2022; 15(2):643. https://doi.org/10.3390/ma15020643
Chicago/Turabian StyleMeißner, Paul, Jens Winter, and Thomas Vietor. 2022. "Methodology for Neural Network-Based Material Card Calibration Using LS-DYNA MAT_187_SAMP-1 Considering Failure with GISSMO" Materials 15, no. 2: 643. https://doi.org/10.3390/ma15020643
APA StyleMeißner, P., Winter, J., & Vietor, T. (2022). Methodology for Neural Network-Based Material Card Calibration Using LS-DYNA MAT_187_SAMP-1 Considering Failure with GISSMO. Materials, 15(2), 643. https://doi.org/10.3390/ma15020643






