A 32-Bit DSP Instruction Pipeline Control Unit Verification Method Based on Instruction Reordering Strategy
Abstract
:1. Introduction
- First, by analyzing the architecture and function points of the IPCU, an efficient and portable abstract model based on the instruction reordering strategy is established. According to the symmetry of input and output of the instruction pipeline, the complex logic inside the hardware design and the external complex interface protocol are shielded, which reduces the complexity of verification;
- Second, we automatically generate random test stimuli with constraints and implement effective intensive testing of different functional points of the design under test (DUT) by directionally adjusting the test stimulus generation method, thereby improving code coverage and functional coverage;
- Finally, according to the symmetry of the DUT and the model, the results of the reference model and the DUT are automatically compared and analyzed by means of assertion, which greatly reduces the manpower and time required for verification and improves the verification efficiency.
2. Related Work
2.1. Simulation-Based Directed Functional Verification
2.2. Formal Verification Based on Random Stimulus
2.3. Verification Method Based on Reference Models
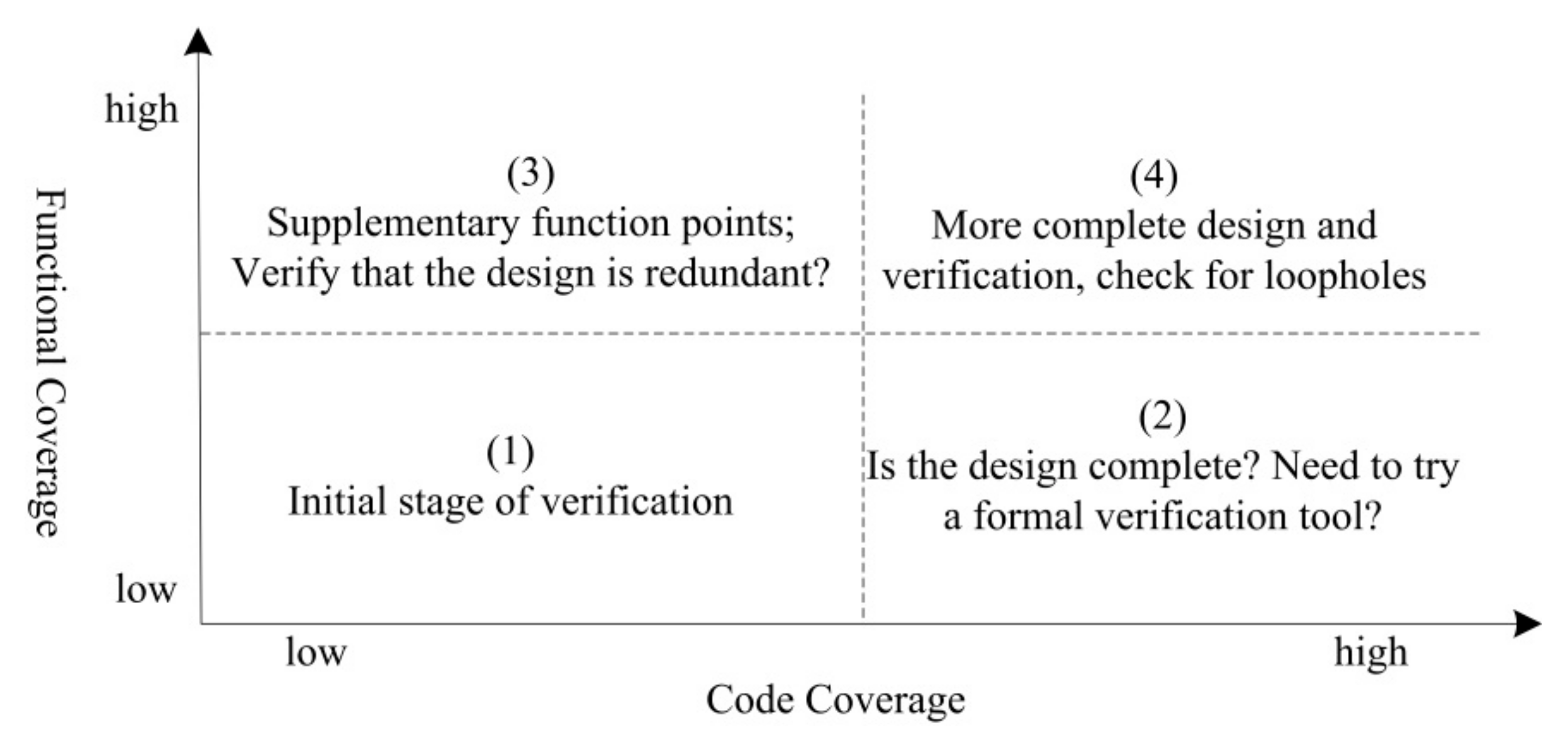
2.4. Validation Effectiveness Evaluation
2.5. Summary
3. Proposed Verification Method
3.1. Overview of IPCU Verification
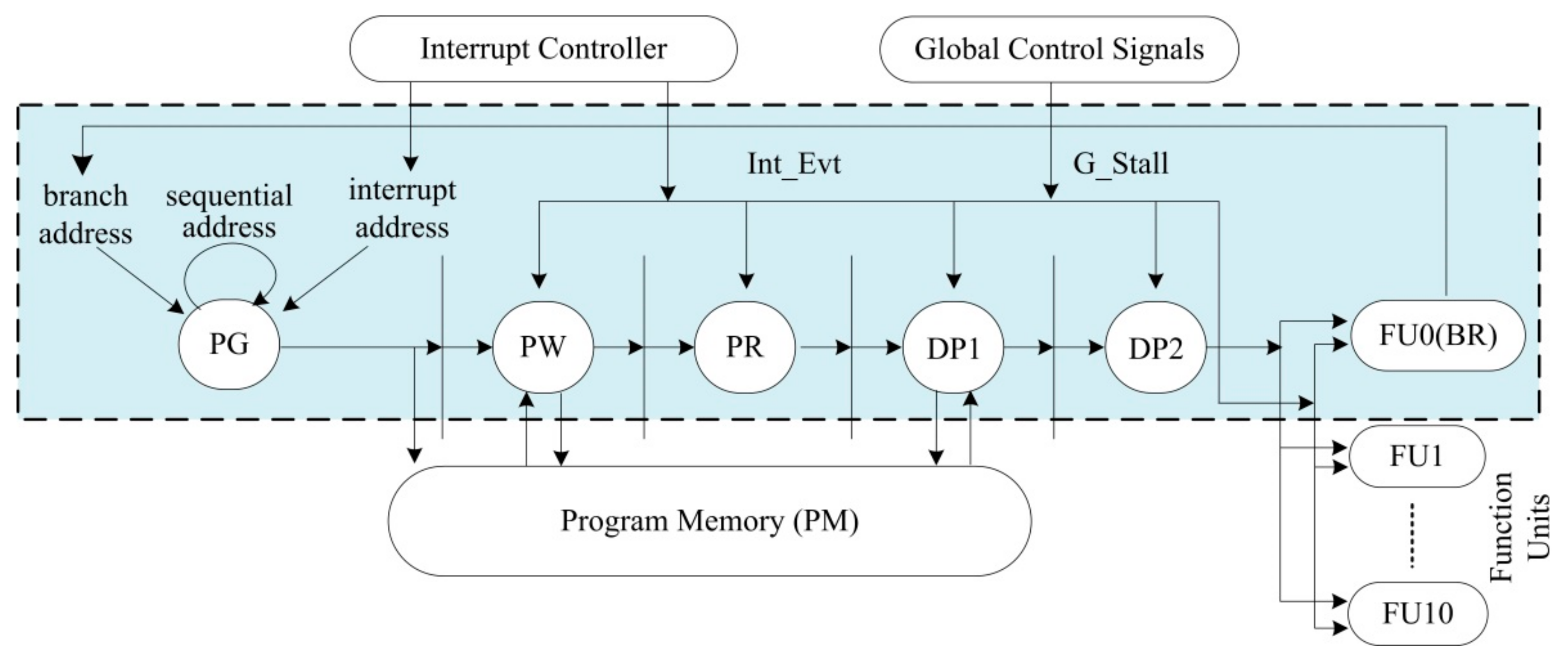
3.1.1. IPCU Architecture of FT-xDSP
3.1.2. Challenges for FT-xDSP IPCU Verification
- Verification of complex protocols: As shown in Figure 2, complex communication occurs between instruction pipelines, which include both control signals and data streams (such as 512-bit FP). When encountering branches and interruptions, it is difficult to traverse the complex states and protocols between pipelines through simple simulation-based verification, and it is also difficult to construct a suitable constraint for a single module (such as BR, PG, DP1, etc.) through formal verification. In addition, whether through simulation verification or formal verification, it is also very difficult to analyze the verification results of the complex control pipeline.
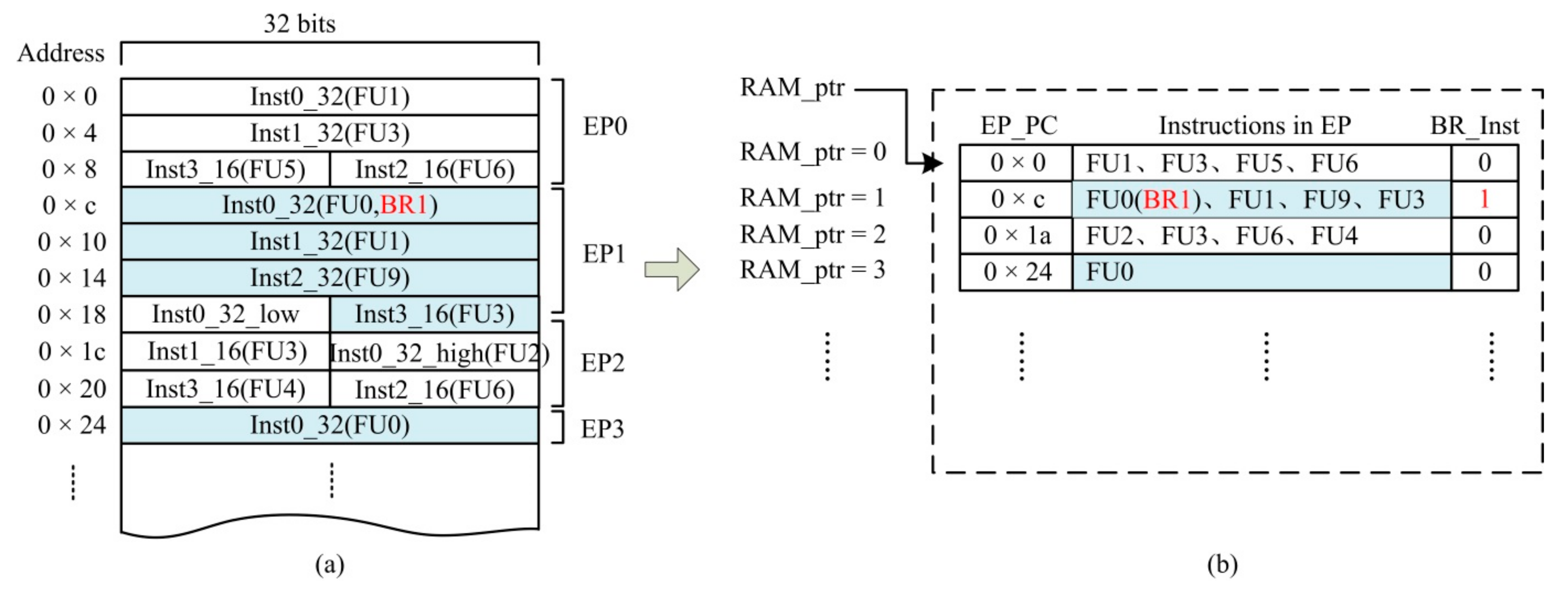
- Traversal verification of EP parallelism: The instruction format of FT-xDSP is illustrated in Figure 3. As the figure shows, the instructions are closely arranged in PM. Instructions that can be issued in parallel in a single clock cycle are referred to as an execution package (EP). In Figure 4, EP0 can be seen to contain two 32-bit instructions and two 16-bit instructions, while EP1 contains one 32-bit instruction and one 16-bit instruction. This tight arrangement can easily cause an instruction (or an EP) to be located on the boundary of two FPs (aligned according to 512 bit).
- Program execution sequence verification: There are three types of program execution sequence functional units in FT-xDSP: sequence, branch jump, and interrupt response. Figure 5 presents a schematic diagram of the corresponding program flow. Here, Figure 5a is the sequence Execute the program; the program does not contain a branch instruction (SBR) and no interrupt event occurs. Figure 5b is a branch jump program, and EP2 contains a conditional branch instruction (the branch instruction has six delay slots). If the branch condition is true, after six branch delay slots, the program jumps to the branch target address (BRT; the example in the figure is EP1). If the branch condition is false, the program will continue to execute downward from EP9. Figure 5c is the interrupt response program: when an interrupt event occurs during the execution of the main program, the currently executing program is interrupted and jumps to the interrupt service program (Int_EPx). Until the interrupt transaction is processed, the program returns to the place at which the main program was interrupted to continue execution. In the verification of the program execution sequence, the branch delay slot processing, branch target EP cross-boundary processing, interrupt address preservation, pipeline emptying, and interrupt return address processing are all difficult points of verification, and are also the points most prone to design bugs in DSP chips. In particular, when the frequency of branches and interrupts is high and there are a large number of cross-boundary EPs, not only does the stimulus structure become complicated, but the analysis of the instruction pipeline execution result also becomes very time-consuming and labor-intensive.
- Build a high-level reference model by means of a reasonable level and function division. This model has a simple input–output relationship, which avoids the need to analyze complex protocols between pipelines and can quickly and accurately obtain the correct results of random test incentives;
- Automatically generate EP parallelism-configurable random instruction test stimuli, and can construct a legal branch program flow and interrupt the program flow via adding legal branch instructions to EP and inserting interrupt events into program flow;
- Automatically compare results and collect the coverage.
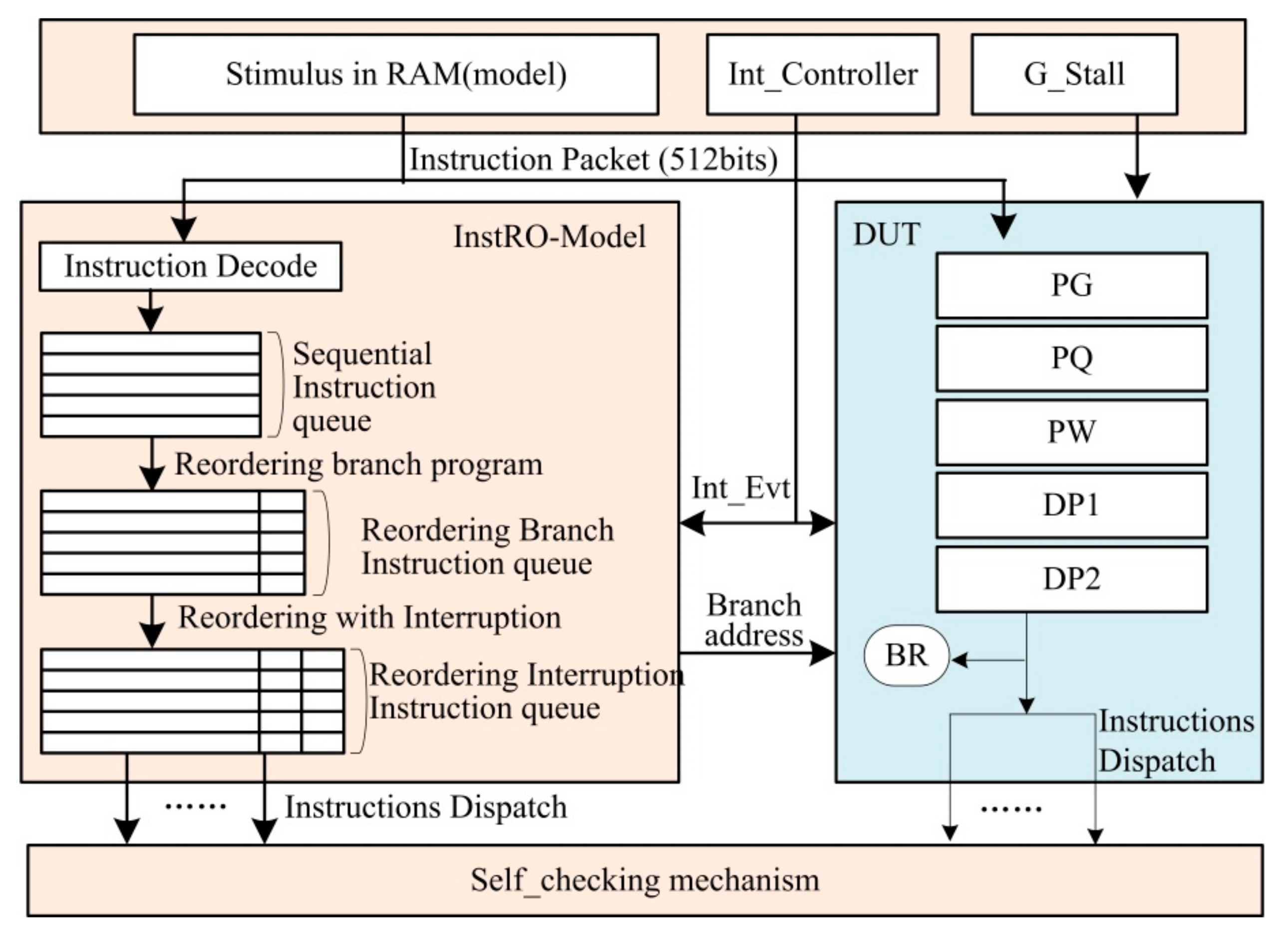
3.1.3. Instruction Reordering (InstRO) Strategy
3.2. Reference Model Based on Instruction Reordering Strategy (InstRO-Model)
3.2.1. Instruction Decoding
3.2.2. Branch Control
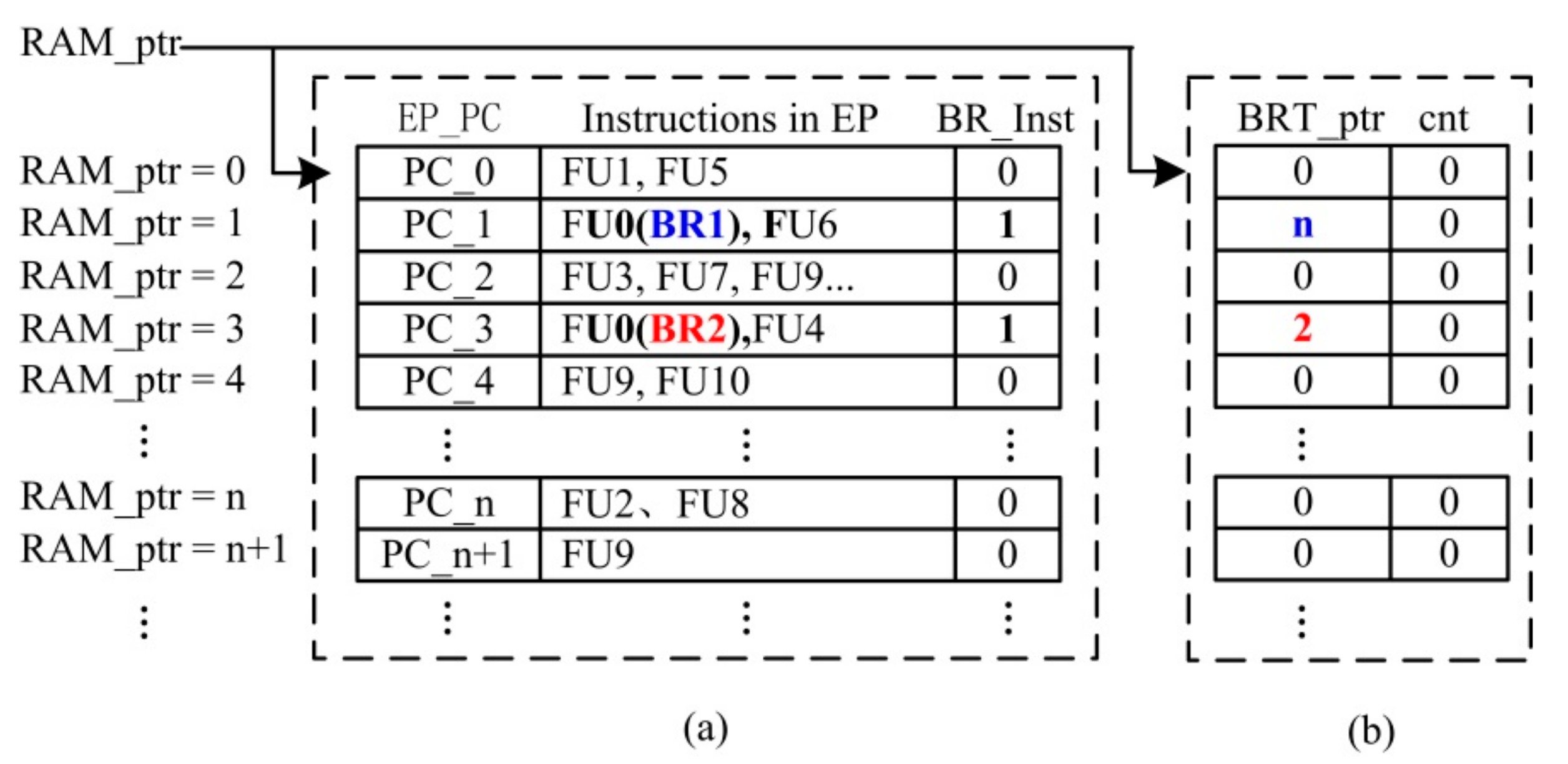
- Branch target address (BRT) generation. In the DUT, the branch target address of the branch instruction is calculated by the OP field of the branch instruction, or determined by the value in the register specified by the OP field. In the InstRO-Model, the OP field of branch instruction code is randomly generated; accordingly, in order to both ensure the legitimacy of the branch target address and reduce the difficulty of verification, the branch target address is randomly generated in all valid EP_PC. Moreover, at the top level of the DUT Bypass, the branch target address is input to the fetch module, so that the branch target address of the DUT is consistent with that in InstRO-Model. That is, in the sequential instruction queue, when a branch instruction (BR_Inst is 1) occurs in the EP pointed to by a RAM_ptr, an EP_PC is randomly selected as the branch target BRT in the sequential instruction queue. The RAM_ptr corresponding to this EP_PC is then saved to the BR_ptr of the line where the branch instruction is located. For example, in Figure 8a, the BRTs of the two branch instructions of BR1 and BR2 are PC_n and PC_2, respectively. The corresponding RAM_ptrs (n and 2) are then recorded in the respective BRT_ptrs.
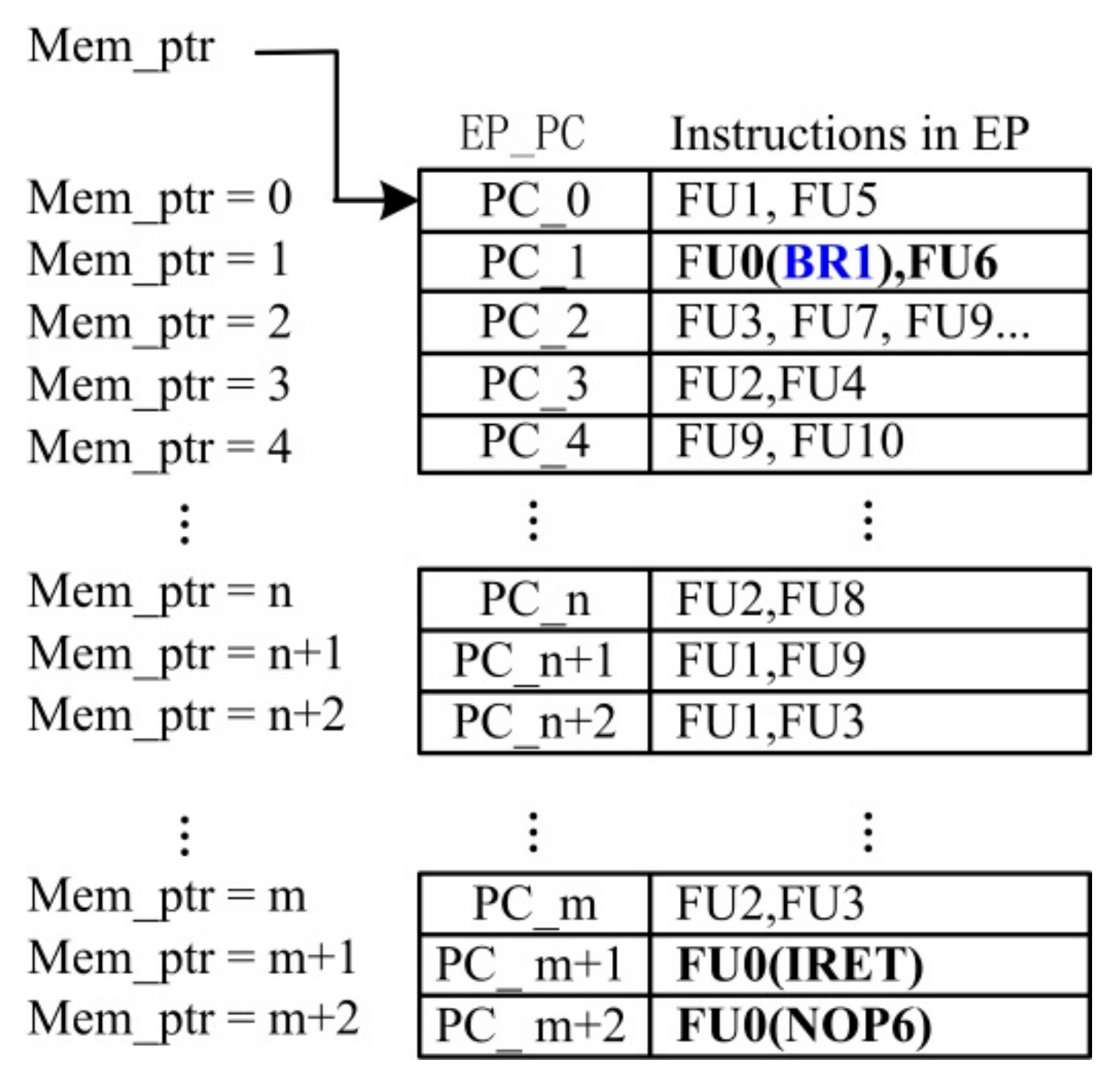
- Branch EP reordering. Based on BRInst and BRT_ptr in Figure 8, InstRO-Model reorders the test program and writes it into a new queue according to the execution order of the execution branch. As shown in Figure 9, the program runs until it reaches the branch instruction BR1. After six delay slots, the program jumps to the random branch target address PC_n of BR1 to continue execution. Subsequently, the program runs to the branch instruction BR2; after six delay slots, the program jumps to the random branch target address PC_2 of BR2 to continue execution. After the branch program pipeline is reordered, the branch control processing queue is also reordered. The new queue pointer is DP_ptr, which represents the actual dispatching order of the DUT. The reordered instruction queue is the standard instruction dispatch result queue of the branch program.
- Branch jump count. In Figure 9, the branch instruction BR2 constructs a loop program: PC_2–PC_9. If the branch jump is not constrained then, in this test stimulus, the entire test process will involve executing this cycle, resulting in a large number of repeated verifications while also preventing other randomly generated EPs from being effectively verified. Therefore, the count (cnt) of branch jumps is added to Figure 9b. Here, cnt accumulates the number of dispatches of the EP containing the branch instruction. The maximum threshold of cnt (cnt_th) is set in the random stimulus constraint, and the branch instruction is executed only when cnt is less than cnt_th. Assuming that the condition of the execution of the branch instruction is BR_Valid, the condition of the branch jump is as follows:
3.2.3. Processing of Interrupt Event
3.3. Automatic Generation of Stimulus
3.3.1. Instruction Code Generation and Parallelism Configuration
3.3.2. Branch/Interrupt Address Generation
3.3.3. Generation of Global Control Signal
3.4. Automatic Results Comparison and Coverage Collection
4. Experiments and Result Analysis
4.1. Configurable Oriented Random Constraints
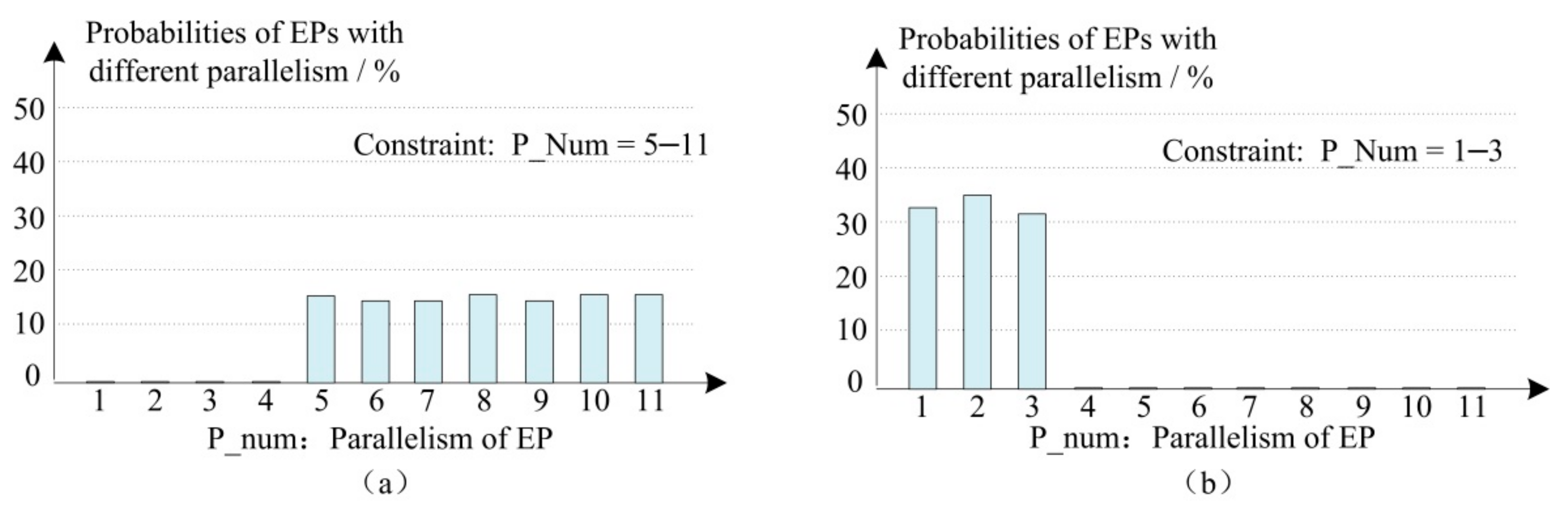
4.1.1. EP Parallelism Configuration
4.1.2. Branch Target Address Range Configuration
4.2. Coverage Assessment
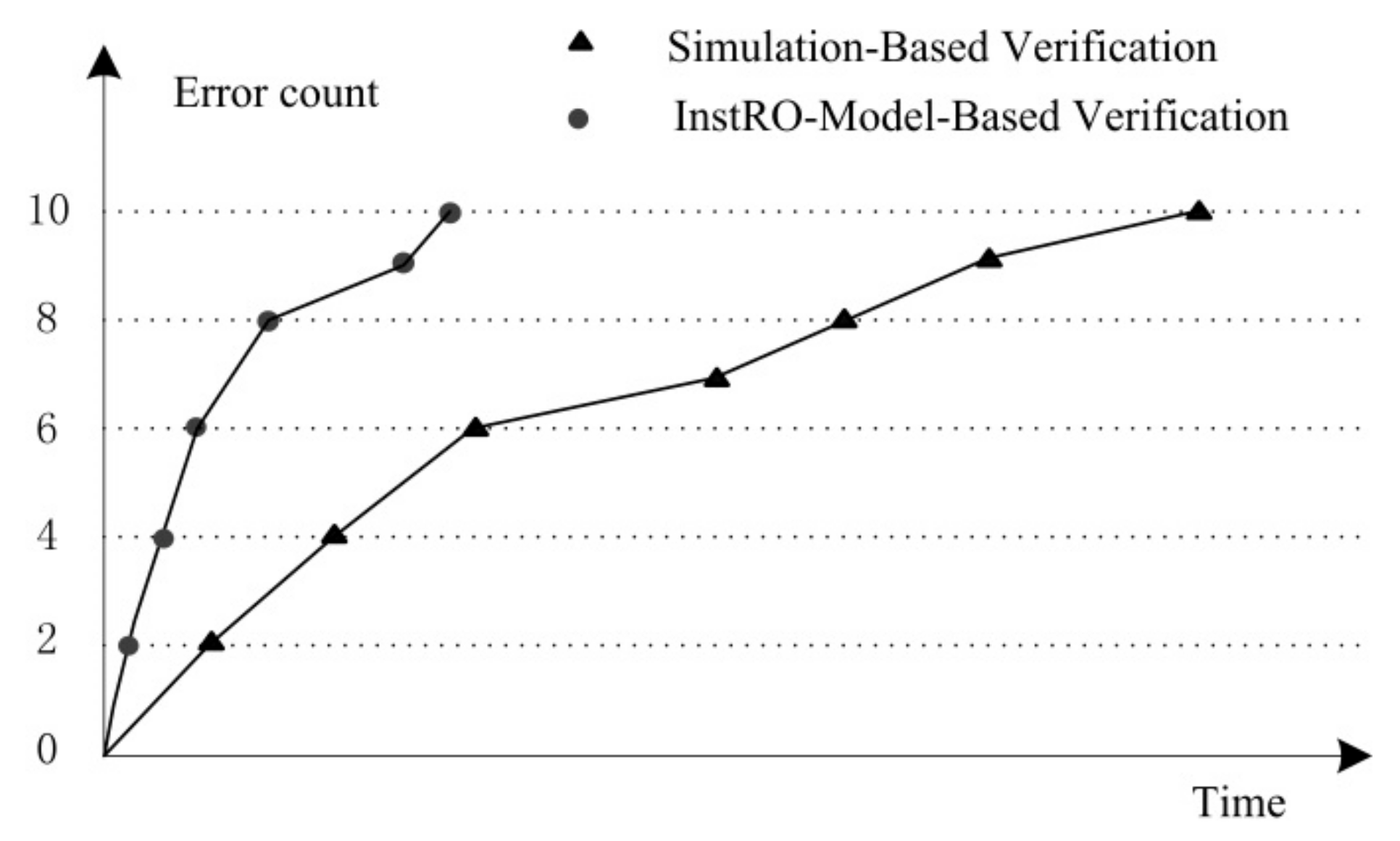
4.3. Simulation Time Analysis
4.4. Portability Analysis
- The processing of the program by the instruction pipeline in the general VLIW DSP can be summarized as sequential execution, branch jump, and interrupt processing. The structure of the InstRO-Model is accordingly suitable for most general-purpose DSPs;
- The InstRO-Model verification method has a higher level of architecture, and moreover does not involve the results of specific instruction execution (such as multiplication, floating-point operations, etc.). In the VLIW DSP structure, regardless of whether or not the internal protocol of the instruction pipeline is the same, its input signals are still instruction codes, branch or interrupt addresses, and global control signals. Therefore, when generating random test stimuli for IPCU of different processors, it is only necessary to make some changes for the difference of functional unit FUx, instruction Type/L/P, etc. By modifying the relevant information, the directional random generation of the input test stimuli can be completed.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hegde, K.; Yu, J.; Agrawal, R.; Yan, M.; Fletcher, C. UCNN: Exploiting computational reuse in deep neural networks via weight repetition. In Proceedings of the 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 2–6 June 2018; pp. 674–687. [Google Scholar]
- Park, E.; Kim, D.; Yoo, S. Energy-Efficient Neural Network Accelerator Based on Outlier-Aware Low-Precision Computation. In Proceedings of the 45th Annual International Symposium on Computer Architecture (ISCA), Los Angeles, CA, USA, 2–6 June 2018; pp. 688–698. [Google Scholar]
- May, C.; Silha, E.; Simpson, R.; Warren, H. The PowerPC Architecture: A Specification for a New Family of RISC Processors; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1994. [Google Scholar]
- Shen, H.H.; Wei, W.L.; Chen, Y.J. A Survey on Coverage Directed Generation Technology. J. Comput.-Aided Des. Comput. Graph. 2009, 21, 419–431. [Google Scholar]
- Spear, C.; Tumbush, G. SystemVerilog for Verification; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Liu, M. Data Coherence Optimization and Verification Platform Research of DMA Accessing in Multi-Core DSP. Master’s Thesis, National University of Defense Technology, Changsha, China, 2016. [Google Scholar]
- Wu, Q.W.; Feng, Y. Research for Constructure and Test Method of the DSP. Comput. Digit. Eng. 2010, 9, 84–87. [Google Scholar]
- Hu, W.W.; Chen, Y.J.; Li, L.; Cheng, Q. Linear Time Memory Consistency Verification. IEEE Trans. Comput. 2012, 61, 502–516. [Google Scholar] [CrossRef]
- Molina, A.; Cadenas, O. Functional verification: Approaches and challenges. Lat. Am. Appl. Res. 2007, 37, 65–69. [Google Scholar]
- Chen, P.H.; Wei, L.H. A Method of Improving DSP Test Coverage Based on ATE. Comput. Sci. Appl. 2021, 11, 1598–1606. [Google Scholar]
- Farimah, F.; Prabhat, M. Automated Test Generation for Debugging Multiple Bugs in Arithmetic Circuits. IEEE Trans. Comput. 2019, 68, 182–197. [Google Scholar]
- Chen, S.M.; Wang, Y.H.; Liu, S.; Wan, J.H.; Chen, H.Y.; Liu, H.Z.; Zhang, K.; Ning, X. FT-Matrix: A Coordination-Aware Architecture for Signal Processing. IEEE Micro 2014, 34, 64–73. [Google Scholar] [CrossRef]
- Sun, J.; Shi, P.F.; Feng, C.Y.; Meng, L.; Zhang, H. Low Power Verification Based on Multi-Cores DSP. Microelectron. Comput. 2015, 12, 116–121. [Google Scholar]
- Chen, Y.J.; Li, L.; Chen, T.S.; Li, L.; Wang, L.; Feng, X.X.; Hu, W.W. Program Regularization in Memory Consistency Verification. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 2163–2174. [Google Scholar] [CrossRef]
- Feig, R.; Weiss, S. Functional verification of instruction processing units through control flow modeling. Microelectron. J. 2002, 33, 285–299. [Google Scholar] [CrossRef]
- Qi, J.Y. A RISC instruction pipeline architecture. Mini-Micro Syst. 1995, 16, 1–5. [Google Scholar]
- Jiang, J. Research and Implementation on Instruction Control Pipeline in General-Purpose EPIC Microprocessor. J. Chin. Comput. Syst. 2006, 27, 1661–1664. [Google Scholar]
- Sabaghian-Bidgoli, H.; Behnam, P.; Alizadeh, B.; Navabi, Z. Reducing Search Space for Fault Diagnosis: A Probability-Based Scoring Approach. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Bochum, Germany, 3–5 July 2017; pp. 545–550. [Google Scholar]
- Akbarpour, B.; Tahar, S. An approach for the formal verification of DSP designs using Theorem proving. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 1441–1457. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.L.; Xu, W.B. Study on Automatic Test Generation of Digital Circuits Using Particle Swarm Optimization. In Proceedings of the 2011 10th International Symposium on Distributed Computing and Applications to Business, Engineering and Science, Wuxi, China, 14–17 October 2011; pp. 324–328. [Google Scholar]
- Cerny, E.; Dudani, S.; Havlicek, J.; Korchemny, D. SVA: The Power of Assertions in SystemVerilog; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Fooladi, M.; Kamran, A. Speed-Up in Test Methods Using Probabilistic Merit Indicators. J. Electron. Test. 2020, 36, 285–296. [Google Scholar] [CrossRef]
- Aghaei, B. A high fault coverage test approach for communication channels in network on chip. Microelectron. Reliab. 2017, 75, 178–186. [Google Scholar] [CrossRef]
- Liu, W.H.; Yu, M.Y.; Wang, J.X. A Graph-model Based Code-coverage-improving Verification Method. Microprocessors 2008, 6, 48–50. [Google Scholar]
- Bin, E.; Emek, R.; Shurek, G.; Ziv, A. Using a Constraint Satisfaction Formulation and Solution Techniques for Random Test Program Generation. IBM Syst. J. 2002, 41, 386–402. [Google Scholar] [CrossRef] [Green Version]
- Braun, G.; Nohl, A.; Hoffmann, A.; Schliebusch, O.; Leupers, R.; Meyr, H. A Universal Technique for Fast and Flexible Instruction-Set Architecture Simulation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 23, 1625–1639. [Google Scholar] [CrossRef]
- Tasiran, S.; Batson, B.; Yu, Y. Linking Simulation with Formal Verification at a Higher Level. IEEE Des. Test Comput. Mag. 2004, 21, 472–482. [Google Scholar] [CrossRef]
- Zhu, D.L.; Guo, D.Y.; Hu, H. Rapid implementation of instruction-level precision VLIW DSP simulator. Comput. Eng. Des. 2013, 34, 256–261. [Google Scholar]
- Monaco, J.; Holloway, D.; Raina, R. Functional verification methodology for the PowerPC 604 microprocessor. In Proceedings of the 33rd Annual Design Automation Conference, Las Vegas, NV, USA, 3–7 June 1996; pp. 319–324. [Google Scholar]
- Shen, J.; Abraham, J.; Baker, D.; Hurson, T.; Kinkade, M.; Gervasio, G.; Chu, C.C.; Hu, G. Functional Verification of the Equator MAP1000 Microprocessor. In Proceedings of the 1999 36th Annual Design Automation Conference (DAC), New Orleans, LA, USA, 21–25 June 1999. [Google Scholar]
- Foote, T.G.; Hoffman, D.E. Testing the 500-MHz IBM S/390 microprocessor. IEEE Des. Test Comput. Mag. 1998, 15, 83–89. [Google Scholar] [CrossRef]
- Bustan, D.; Korchemny, D.; Seligman, E.; Yang, J. SystemVerilog Assertions: Past, Present, and Future SVA Standardization Experience. IEEE Des. Test Comput. 2012, 29, 23–31. [Google Scholar] [CrossRef]
- IEEE STD 1800–2009; IEEE Standard for SystemVerilog—Unified Hardware Design, Specification, and Verification Language. IEEE: New York, NY, USA, 2009.
- Gong, L.K.; Lu, J.F. Verification-Purpose Operating System for Microprocessor System-Level Functions. IEEE Des. Test Comput. 2010, 27, 76–85. [Google Scholar] [CrossRef]
- Hosseini, A.; Mavroidis, D.; Konas, P. Code generation and analysis for the functional verification of microprocessors. In Proceedings of the 33rd Design Automation Conference Proceedings, 1996, Los Angeles, CA, USA, 3–7 June 1996. [Google Scholar]
- Duran, C.; Morales, H.; Rojas, C.; Ruospoy, A.; Sanchezy, E.; Roa, E. Simulation and Formal: The Best of Both Domains for Instruction Set Verification of RISC-V Based Processors. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–4. [Google Scholar]
- Bratt, J.P.; Yan-Tek, H.P.; Joshi, C.S.; Nofal, M.R.; Paul, R.; Scanlon, J.T.A.K. Superscalar Microprocessor Instruction Pipeline Including Instruction Dispatch and Release Control. EP0690372 A1, 12 March 2010. [Google Scholar]
- Momose, T.; Fujita, A.; Kubo, K. Data Processing System with an Enhanced Instruction Pipeline Control. CA1098214 A1, 24 March 1981. [Google Scholar]










| Verification Methods | Advantage | Disadvantage | Scope of Application |
|---|---|---|---|
| Simulation-based directed functional verification | Efficient in the initial stage of verification | Hard to perform state traversal on the DUT, highly time-consuming, and rarely reused | Simple design [13,14,15] |
| Formal verification based on random stimulation | Easy to perform state traversal on the DUT | Problem of exploration space explosion | Simple logic [18,19,20] |
| Verification method based on a reference model | Realize simulation verification or random verification | Realization of the reference model is difficult | Data-intensive design [6,22,23,24,25] or system-level processors [31,36] |
| Line | Pseudocode | Description |
|---|---|---|
| Begin | ||
| 1: | P_min = 5; | 1: Set the minimum parallelism of EP, assuming it is set to 5. |
| 2: | P_max = 11; | 2: Set the maximum parallelism of EP, assuming it is set to 11. |
| 3: | P_min32 = 4; | 3: Set the minimum parallelism of 32-bit length instructions, assuming it is set to 4 (Note: P_min32 ≤ P_min). |
| 4: | for(I = 32′h0; I < 15′d524288; I = I + 1) | 4: After the parameters are set, begin randomly generating 1M EPs. |
| 5: | begin | |
| 6: | P_offset = P_max − P_min + 1; | 6: Calculate the random range of EP parallelism, P_offset = 11 − 5 + 1 = 7. |
| 7: | P_num = P_min + {$random}%P_offset; | 7: For the current randomly generated EP parallelism, assuming $random(seed) is 2022, P_num= 5 + 2022%7 = 11. |
| 8: | P_num32 = P_min32 + {$random}%(P_num − P_min32 + 1); | 8: The number of 32-bit instructions in EP: P_num32 = 4 + 2022%(11 − 4 + 1) = 6. |
| 9: | P_num16 =P_num − P_num32; | 9: The number of 16-bit instructions in EP: P_num16 = 11 − 6 = 5. |
| 10: | Task_Genrate32bitInst (P_num32); | 10: Generate P_num32 32-bit instructions. |
| 11: | Task_Genrate16bitInst (P_num16); | 11: Generate P_num16 16-bit instructions. |
| End | ||
| End |
| Line | SVA Assertions |
|---|---|
| 1: | assert_DP_PC: assert property (@(posedge clk) disable iff (~rst_n) if (!G_Stall) ResultQueue_PC [DP_ptr] == DUT.DP_PC); |
| 2: | assert_U1_Inst: assert property (@(posedge clk) disable iff (~rst_n) if (!G_Stall) ResultQueue_FP [DP_ptr] == {DUT.FU0_Inst, DUT.FU1_Inst, …, DUT.FU10_Inst}); |
| Line | SVA Assertions |
|---|---|
| 1: | cover_IH_Flush_U1: cover property (@(posedge clk) disable iff (~rst_n) if (!G_Stall) FU1_Valid && IH_Flush); |
| 2: | cover_IH_Flush_with_GStall: cover property (@(posedge clk) disable iff (~rst_n) IH_Flush && G_Stall);; |
| Unit in IPCU | Simulation-Based Coverage (%) | InstRO-Model Coverage (%) | Total Coverage (%) | |||
|---|---|---|---|---|---|---|
| Block | Expression | Block | Expression | Block | Expression | |
| Fetch | 96.5 | 82.7 | 99 | 92.8 | 100 | 96.3 |
| Dispatch | 100 | 87.4 | 100 | 96.2 | 100 | 99.5 |
| BR | 100 | 100 | 96.2 | 90.3 | 100 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, S.; Zhang, L. A 32-Bit DSP Instruction Pipeline Control Unit Verification Method Based on Instruction Reordering Strategy. Symmetry 2022, 14, 646. https://doi.org/10.3390/sym14040646
Wang H, Liu S, Zhang L. A 32-Bit DSP Instruction Pipeline Control Unit Verification Method Based on Instruction Reordering Strategy. Symmetry. 2022; 14(4):646. https://doi.org/10.3390/sym14040646
Chicago/Turabian StyleWang, Huili, Sheng Liu, and Ling Zhang. 2022. "A 32-Bit DSP Instruction Pipeline Control Unit Verification Method Based on Instruction Reordering Strategy" Symmetry 14, no. 4: 646. https://doi.org/10.3390/sym14040646
APA StyleWang, H., Liu, S., & Zhang, L. (2022). A 32-Bit DSP Instruction Pipeline Control Unit Verification Method Based on Instruction Reordering Strategy. Symmetry, 14(4), 646. https://doi.org/10.3390/sym14040646





