1. Introduction
Due to continuous increments in greenhouse gases and environmental pollution, there is an ever-increasing interest in the use of renewable energy sources [
1,
2]. The expansion of global renewable energy generation started during the last third of the twentieth century and has been remarkably increasing year by year.
In 2009, the share of renewable energy sources was approximately 8.7% of global total energy consumption. By the end of 2019, it was found to reach 11.2% of the world’s total power generation capacities [
3]. It has a positive effect on employment growth in the sector every year. To adapt to the increasing penetration in grid infrastructure, renewable distributed generation requires coordinated efforts right from the planning stage to the power generation, transmission, distribution, consumption, and protection [
4,
5,
6,
7].
The uncertain nature of renewable energy generation creates many problems in system security [
8]. There is a chance of grid failure if the electrical system is not handled or managed properly in the case of a renewable integrated system. During the past few years, the concept of the electrical system has changed from a regulated to a deregulated model. To date, some countries have developed their internal power structure to implement the deregulated concept properly and other countries are following the leader countries. In the deregulated or competitive power market, several entities have performed their operation. Generation companies (GENCOs), transmission companies (TRANSCOs), distribution companies (DISCOs), retailers, independent system operator (ISO), etc. are the electricity market players. The ISO plays the most vital role in the deregulated system by controlling the entire electricity market. The prices of the electricity are also set by the ISO by optimizing the bidding values that are received from the generator side and demand side.
In the past, some research work has been carried out by several academicians in the field of renewable energy and deregulated systems [
9,
10]. The distribution system is a final delivery stage of a power system and it transforms the high-voltage to lower-voltage power using power transformers and directly feeds that power to different customers/consumers. Previously, distribution substations have taken that power from the transmission network of the power grid. Now, distributed generations (DGs) are becoming more popular because of the efficient utilization of energy and mitigating the global energy crisis [
11]. DG is mainly of two types, i.e., non-renewable energy generation (gas turbines, coal plants, reciprocating engines) and renewable energy generation (solar PV, biomass, wind, tidal, etc.) [
12,
13]. The investment in renewable distributed generation (RDG) units is increasing day by day due to the reduction in gas emissions. By installing distributed generation, voltage stability, reliability, power quality, and efficiency can be improved and peak power demands, operational cost, and transmission loss can be significantly reduced in comparison to the conventional power system operation. To deliver secure, sustainable, and affordable energy, the RDG units will play an important role soon [
14]. They also offer a viable alternative to sites that may not be electrified otherwise [
15]. Wang et al. [
16] used an analytical method to find the optimal location of DG in radial and meshed networked systems considering minimization of the system power loss. For sizing and siting of DG, both systems are essentially required for minimizing system power loss, and this is determined by using an analytical method proposed in [
17]. Additionally, it is important to optimize storage systems that help increase energy security [
18].
Recently, meta-heuristic algorithms have been used to optimally allocate the sizing and location of DG. In ref. [
19], the artificial bee colony (ABC) algorithm was used for finding the DG unit’s size, power factor, and location of the DG in the distributed network considering minimum real power loss as an objective function. Discrete particle swarm optimization (PSO) was used in [
20] to solve the site and sizing problems of DG units. To determine the optimal location and size of DG in the distributed system, a modified teaching-learning-based optimization (MTLBO) algorithm was used in [
21]. In ref. [
22], the loss sensitivity factor and bacterial foraging optimization (BFO) algorithm were used to identify the optimal locations and size of the DG unit, respectively, considering minimization of network power losses, operational costs, and improving voltage stability. To minimize losses, the optimal location and capacity of DG were discussed by using the cuckoo search (CS) algorithm [
23]. To minimize the active power loss and energy loss of distribution lines, the krill herd algorithm was used for the placement of DG by maintaining the bus voltage and voltage stability index within specified limits of the system [
24]. Paper [
25] proposed an ant lion optimization (ALO) algorithm for optimal location and sizing of renewable DG for various distribution systems. Wu et al. [
26] deployed the optimal strategy for the optimized operation of a wind-solar-biogas integrated system. Ref. [
27] displayed the optimization techniques for a solid oxide fuel cell and power to the gas integrated renewable system in a microgrid.
The literature survey shows that a limited amount of work concerning optimal sizing and placement of DGs has been reported in past years. In addition, the critical study of the literature referred to here in this aspect reveals that up until now, no one has considered the economical criterion with technical constraints for deciding on the placement of RDG units. Therefore, a comprehensive attempt has been made to study the techno-economical aspect of RDG units to cope with the competitive electricity market. Here, the total losses of the distribution network along with the overall cost factors and the profit for the investors have been investigated by using different optimization approaches. In addition, the review of the literature highlights many aspects of power system problems but various points that need to be focused on are as follows:
What is the economic impact of RDG units on the electricity grid?
What is the system voltage impact of RDG units in wind-integrated systems?
How do different optimization techniques play an important role in the economic benefit and system voltage profile of the electrical system?
These issues have not been addressed together in recent years by researchers in the field. Therefore, in this work, all these problems have been examined together by proper operation of RDG units.
In a deregulated environment, the integration of RDG units is becoming more and more popular because of their excellent eco-friendly behavior. Therefore, the research interest here is to concentrate on the “optimal operation of renewable distributed generation in a day-ahead power system”. It is also emphasized in this work that the aspect of making it cost-effective is to cope with the competitive electricity market. The prime highlights of this work are as below:
To develop a system model for optimal placement of RDG units in a competitive electricity market.
The economic impact assessment of different wind speeds in a wind-integrated system.
Bus sensitivity factor (BSF) has been considered for equating the optimal position of the wind farm in the integrated system.
Comparative study of SQP, ABC, PSO, ACO, and SMA corresponding to the system profit, system generation cost, and bus voltage profile.
The SMA and ACO have been used for the first time in this type of economic assessment (i.e., impact valuation of LMP) in a deregulated power system, which is the novelty of this work.
3. Objective Functions
The main objective of this work is to assess the economic effect of wind farm integration in a day-ahead electricity market. The economic assessment of an electrical system is divided into two parts, i.e., generation cost of power generation companies and the profit of the customers (i.e., social welfare or social benefit). In the deregulated electrical system, it is desirable that the profit of the power producer must be minimized by a certain amount and that benefit given to the customer by increasing the social benefits. This happens due to the competitiveness among the market players in the deregulated power system. The mathematical expressions of the objective function (F) and social benefits (SB) are as follows:
Here, F is the combination of generator side bidding cost (C
i(P
gi)) and benefit to the consumer (B
j(P
dj)). N
g and N
d are the numbers of generators and loads, respectively. From Equations (4) and (5), it is clear that social benefit is the reciprocal of the objective function. The main objective of this work is to maximize the social benefit, so the objective function (F) must be minimized to fulfill the system requirements. The equation of the supplier’s profit is:
Here, ‘P(m,t)’, ‘TRC(m,t)’, and ‘TGC(m,t)’ are the system profit, total revenue, and total generation cost of the m-th unit at the time ‘t’, respectively.
Here, ‘Pg(i,t)’ and ‘LMP(i,t)’ are the generated power and locational marginal price at the i-th unit at the time ‘t’.
Here, GCTh and GCW are the thermal and wind power generation costs. ‘am’, ‘bm’, and ‘cm’ are the cost co-efficients of thermal generators. To solve the optimal power flow problem, several constraints need to be considered. The constraints are divided into two parts, i.e., equality and inequality constraints.
Here, WGP is wind-generated power. Ploss and PL are the transmission load and power demand. NTL and Nb are the number of transmission lines and the number of buses in the system. Vi, Vj, δi, and δj are the voltage magnitude and voltage angle at the buses i and j. In the inequality function, the upper and lower limit of the voltage magnitude (Vi), voltage angle (ϕi), transmission line flow (TLl), real power generation (Pgi), and reactive power generation (Qgi) have been considered.
The indicating block diagram of the presented approach is shown in
Figure 1.
4. Results and Discussions
A modified IEEE 30-bus test system was used in this work to check the efficiency of the proposed concept. The initial system data were taken from [
34], IEEE 30-bus system. This system has 30 buses, 6 generators, 19 loads, and 41 transmission lines. Bus no. 1 was considered as the slack bus and the system MVA limit was taken as 100 MVA. The modified IEEE 30 bus test system was adapted from [
35,
36] and is shown in
Figure 2. The step-by-step workflow of this work is as follows:
- Step 1:
Check the effect of deregulation in system generation cost, profit, bus voltage, and LMP of a thermal power plant using SQP (without considering the wind farm).
- Step 2:
Comparative study of generation cost, profit, bus voltage, and LMP of a thermal power plant using SQP, ACO, PSO, ABC, and SMA optimization techniques (without considering the wind farm).
- Step 3:
Finding the optimal position of the wind farm using BSF.
- Step 4:
Placement of wind farm in the system and checking all economic parameters, system voltages, and LMPs after and before the wind farm placement using SQP, ACO, PSO, ABC, and SMA.
The entire work was performed in the day-ahead electricity market environment. In this type of electricity environment, the power producers submit their optimal bid for power generation to the system operator (ISO); at the same time, the customer also submits their bid to the ISO for their power consumption. In this situation, the ISO performs the optimal problem solution and fixes the price of the power at an optimal value (LMP), which gives benefit to both the power producer and customer.
It is obvious from the concept of deregulation that the profit of power producers may be reduced due to the competition in the electricity market as well as due to the increment of social benefits. For checking the effect of deregulation in the electrical system, demand-side bidding was performed in this work. Bus nos. 7 and 19 of the modified IEEE 30-bus system were considered for the demand-side bidding.
Table 1 shows the effect of deregulation on system generation cost, profit, and revenue of a thermal power plant using SQP (without considering wind farms).
From
Table 1, it can be seen that the system generation cost has been reduced by a large amount after deregulation. At the same time, supplier profit has been reduced to 138.9077
$/h from 196.9082
$/h. This is due to the maximization of social benefits. In the entire work, profit is considered as the supplier-side profit. Therefore, if profit is minimized then the social benefit will maximize, which is the main motto of deregulation.
Figure 3 and
Figure 4 show the impact of deregulation on system voltage profiles and LMP, respectively.
The voltage profile of the system is improved after the implementation of a deregulated power environment, which can be seen in
Figure 3. Here, maximum bus voltages are trying to reach the optimal voltage value to maintain the system stability. The LMP value is decreasing for all buses after deregulation, which gives benefit to the customers.
In the modified IEEE 30-bus test system, there are six generators in operation. To examine the usefulness of different types of optimization techniques, a comparative study was performed by considering five optimization techniques (i.e., SQP, ACO, PSO, ABC, and SMA).
Table 2 shows the power generation quantity for different generators with all taken optimization techniques. The best optimization techniques always provide an idea about the lowest quantity of power generation. If the system is properly or optimally scheduled, then the system loss is automatically reduced and, as a result, power generation requirement is also minimized.
Table 2 indicates that the SMA provides the best power scheduling among all the considered optimization techniques.
Table 3 depicts the comparison in system economy with the different optimization techniques. It is observed that the system generation cost is reduced using the metaheuristic optimization techniques compared with SQP. The system generation cost is 705.35
$/h using SQP, whereas it is reduced to 688.301
$/h and 688.1534
$/h using ABC and SMA. The supplier profit is also increased using ABC and SMA. We can conclude from the results obtained in
Table 3 that when the system is mathematically validated before the practical operation, then power generator scheduling must be performed by the concept of the SMA algorithm. This will provide more stability to the system economically.
This work was performed by considering the deregulated power environment. The profit shown in
Table 3 is the profit of the generation companies. From the objective function, it is clear that social benefit is maximized when GENCOS profit is minimized. Therefore, SMA provides the best social welfare as compared to the other techniques.
Figure 5,
Figure 6,
Figure 7 and
Figure 8 display the impact of optimization techniques on system voltage profiles and LMP. After the application of ABC and SMA, the system voltage, as well as LMP, are improved for the entire system.
After the detailed study, we can conclude that the system economy, as well as system stability, can be enhanced by using the SMA and ABC optimization techniques. Therefore, in the next part of this work we have used SMA and ABC along with SQP algorithms instead of five optimization techniques. SQP is a linear optimization technique. It is considered for comparative study along with the most superior considered optimization techniques (i.e., ABC and SMA).
In the previous section, we have already seen the importance of different types of optimization techniques in the deregulated power environment. Due to the limitations in future power generation from the thermal power plant, the whole world is now going towards renewable energy sources. At present, renewable energy sources are used as the backup source but in the near future, they will be the prime power generating sources. In this section of the work, an assessment study has been performed for checking the status of the system economy as well as voltage level after the placement of the wind farm.
A factor named ‘bus sensitivity factor (BSF)’ has been used for finding the optimal position of wind farm placement in the system. Equation (3) depicts the mathematical equation of BSF. By using this concept, the BSF values of all buses were calculated, which are shown in
Table 4.
Based on the concept of BSF, the wind farm is placed at the bus that has the lowest value of BSF. The lowest values of BSF indicate the most sensitive bus in the system. It can be observed from the table that bus no. 2 has the lowest BSF value. However, this bus already has the thermal generator, so the wind farm has been placed in the next priority bus, i.e., bus no. 3. The wind speed is variable in nature. When considering this phenomenon, three different wind speeds were used to check the performance of the presented approach. The real-time data for Silchar, Assam, India, for a particular day at midnight, 8 AM, and 4 PM were taken from [
37].
Table 5 shows the real-time wind speed data and wind power calculation for all the considered periods. The operational cost of wind power generation is considered as 2
$/MWh. The wind power operational cost data were chosen after a detailed study about the recent wind investment cost in India.
In the previous section, the entire work was performed without the placement of a wind farm. Now, the wind farm has been placed at the optimal position (optimal location was calculated using the concept of BSF).
Table 6 deploys the comparison result before and after wind farm placement using SQP.
From
Table 6, it can be seen that wind farm placement plays a vital role in a deregulated system. The system generation cost is minimum with the integration of the maximum amount of wind power in the system. This placement also affects the supplier’s profit. The supplier profit is maximum with the placement of a high-value wind farm and profit is minimum without the implementation of the wind farm in the system.
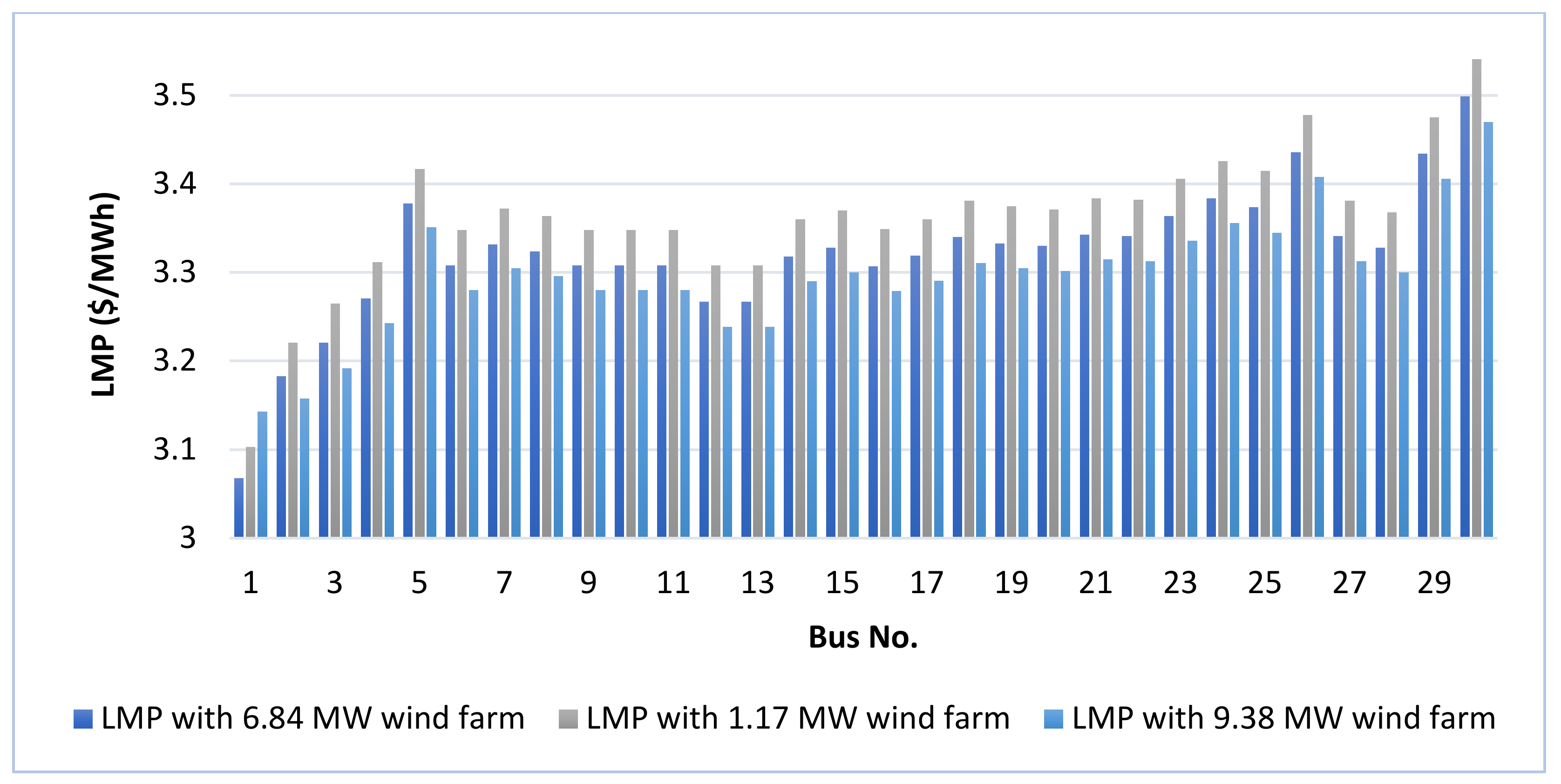
Figure 9,
Figure 10 and
Figure 11 display the LMP after the placement of the wind farm in the system. It can be observed that the maximum amount of wind farm integration provides more economic stability to the system by all the optimization techniques. The highest amount of wind farm integration and the application of the SMA optimization technique provide the most economic result for the wind-integrated deregulated power system.
Table 7 and
Table 8 display the comparison result before and after wind farm placement using ABC and SMA. Like the previous case, economic sustainability is enhanced in this case with the wind farm placement in an integrated deregulated system with the operation of ABC and SMA. The system generation cost approaches the minimum value with the incorporation of the maximum amount of wind power. The supplier profit is supreme with the settlement of high-value wind farms and profit is lowest without the operation of the wind farm in the system.
Figure 12,
Figure 13 and
Figure 14 show the comparative results of system economy with three different optimization techniques. In the results, two cases have been displayed, i.e., without windfarm integration and with wind farm integration. After the incorporation of the wind farm, all the applied optimization techniques show better results towards the economic advancement of the system.
Our main objective is to minimize the system generation cost, which can be achieved by using the SMA. When the generation cost is minimized then social welfare is automatically maximized. From this study, we observed that the maximum amount of wind farm integration along with the optimal concept of SMA provides the highest social welfare and minimum system generation cost. The convergence plots of ABC and SMA with two different situations (i.e., without wind farm and with a maximum capacity of wind farm) are depicted in
Figure 15 and
Figure 16.