The Influence Mechanism of Urban Spatial Structure on Urban Vitality Based on Geographic Big Data: A Case Study in Downtown Shanghai
Abstract
:1. Introduction
2. Literature Review and Theoretical Framework
2.1. Literature Review
2.1.1. Study on Urban Spatial Structure
2.1.2. Study on Urban Vitality
2.1.3. Study on the Interactive Relationship between Urban Spatial Structure and Urban Vitality
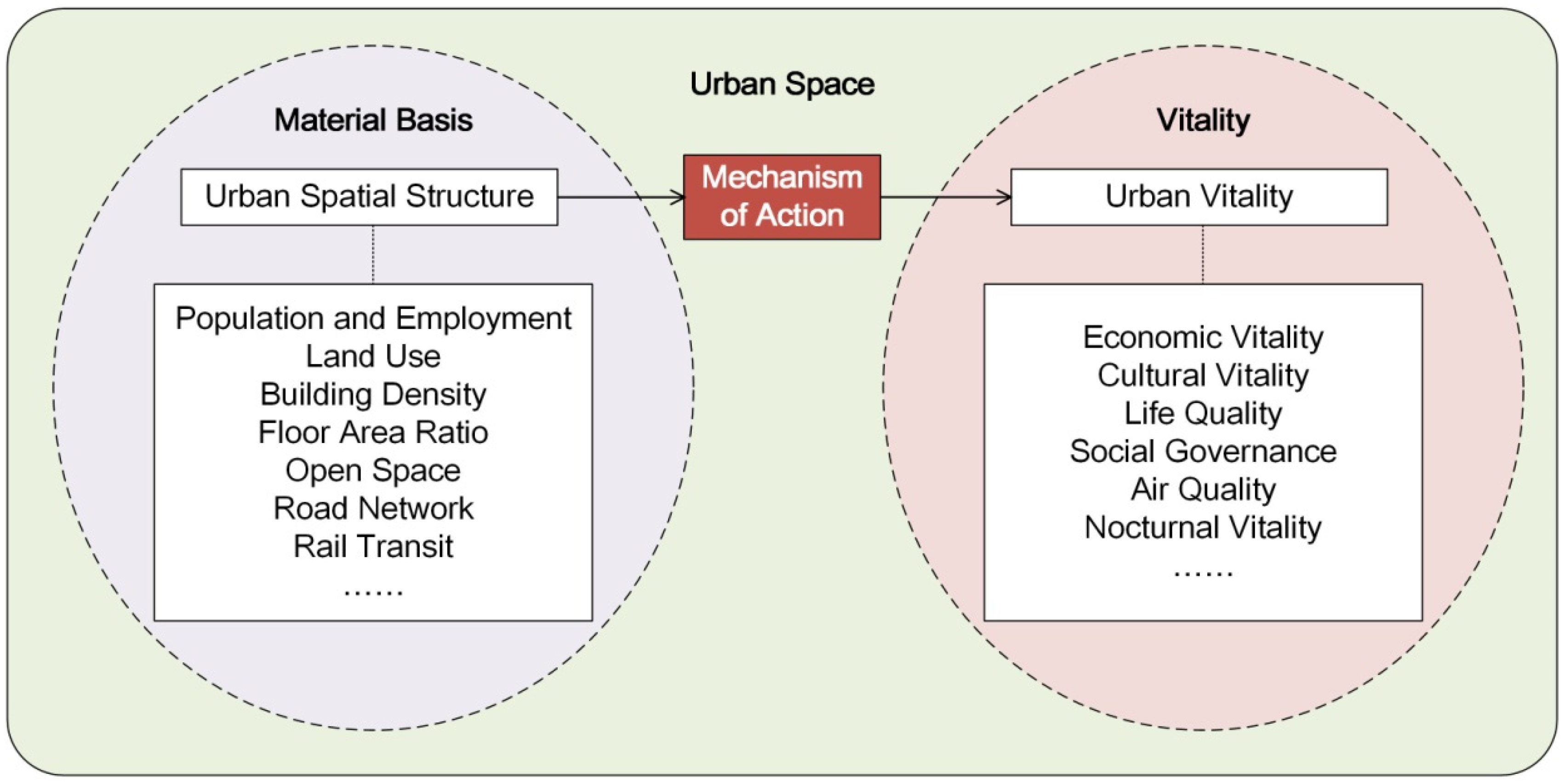
2.2. Theoretical Framework
2.2.1. Theoretical Model
2.2.2. Indicator System
3. Methodology
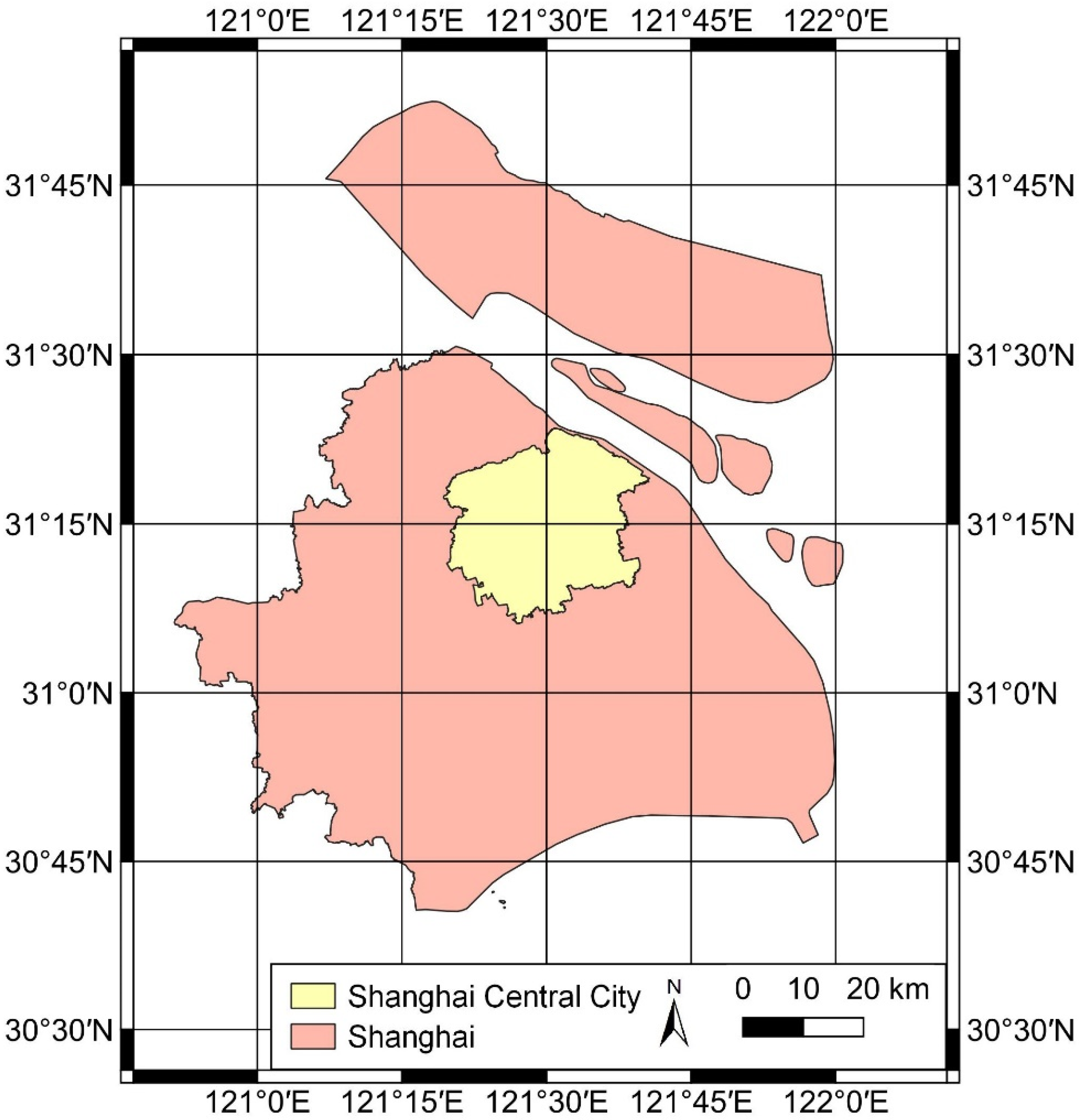
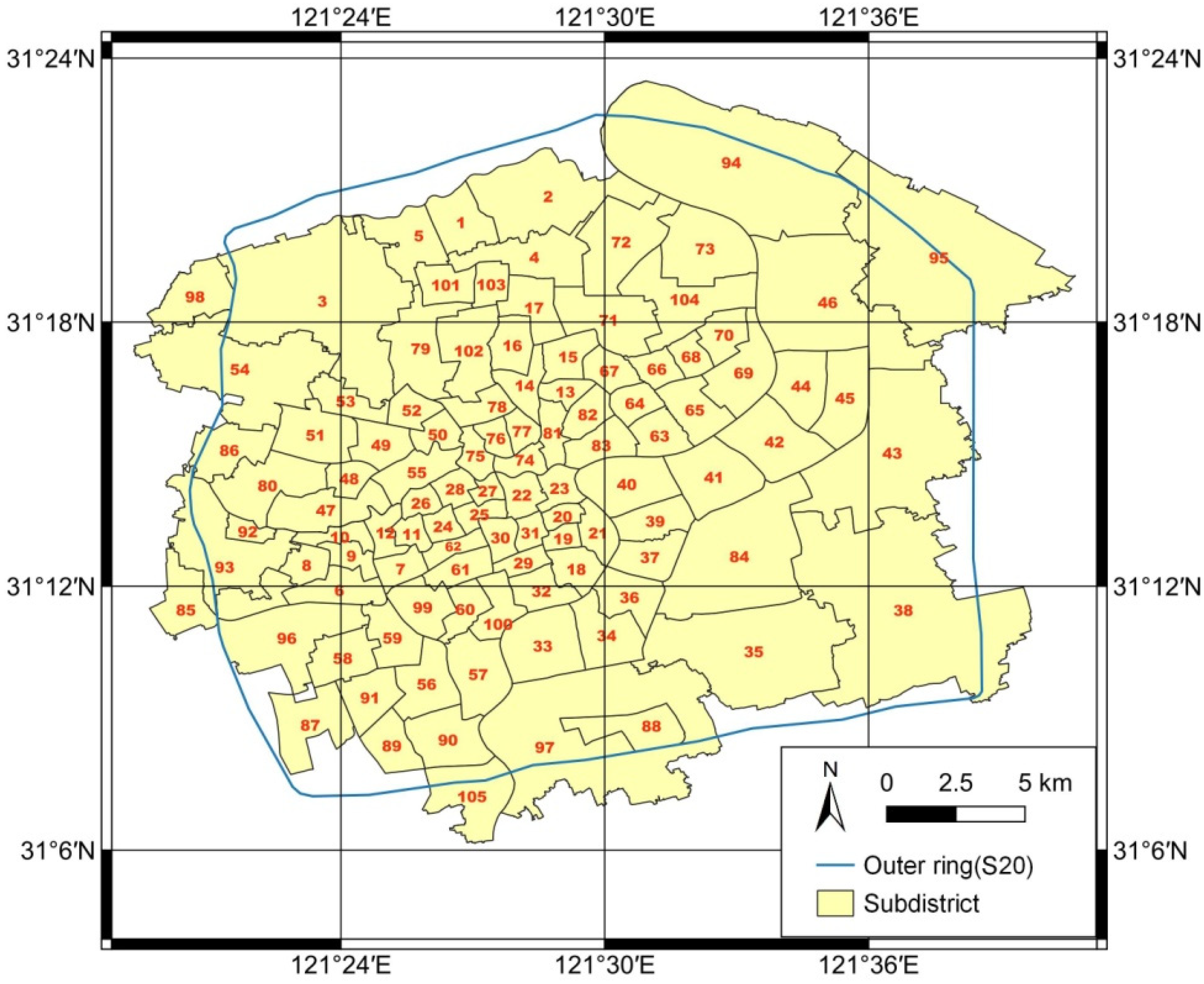
3.1. Study Area
3.2. Data Sources and Preprocessing
3.3. Methods
3.3.1. Comprehensive Evaluation Method of Urban Vitality
- (1)
- Standardization of decision matrix
- (2)
- Calculating entropy weight
- (3)
- General weighted evaluation method with entropy weight
- (4)
- TOPSIS method for comprehensive evaluation.
- Step1:
- Input raw data to calculate second-level indicators of urban vitality of each subdistrict (town).
- Step2:
- Perform min–max standardization on the second-level indicators of urban vitality, calculate the entropy weight, and use the general weighted evaluation method with entropy weight to calculate the first-level indicators of urban vitality of each subdistrict (town).
- Step3:
- Perform vector standardization on the first-level indicators of urban vitality, calculate the entropy weight, and use the entropy weight–TOPSIS method to calculate the comprehensive urban vitality index of each subdistrict (town).
3.3.2. A Binary Correlation Analysis Method of Urban Spatial Structure and Urban Vitality
3.3.3. Eigenvector Space Filtering Regression (ESF Regression)
4. Results
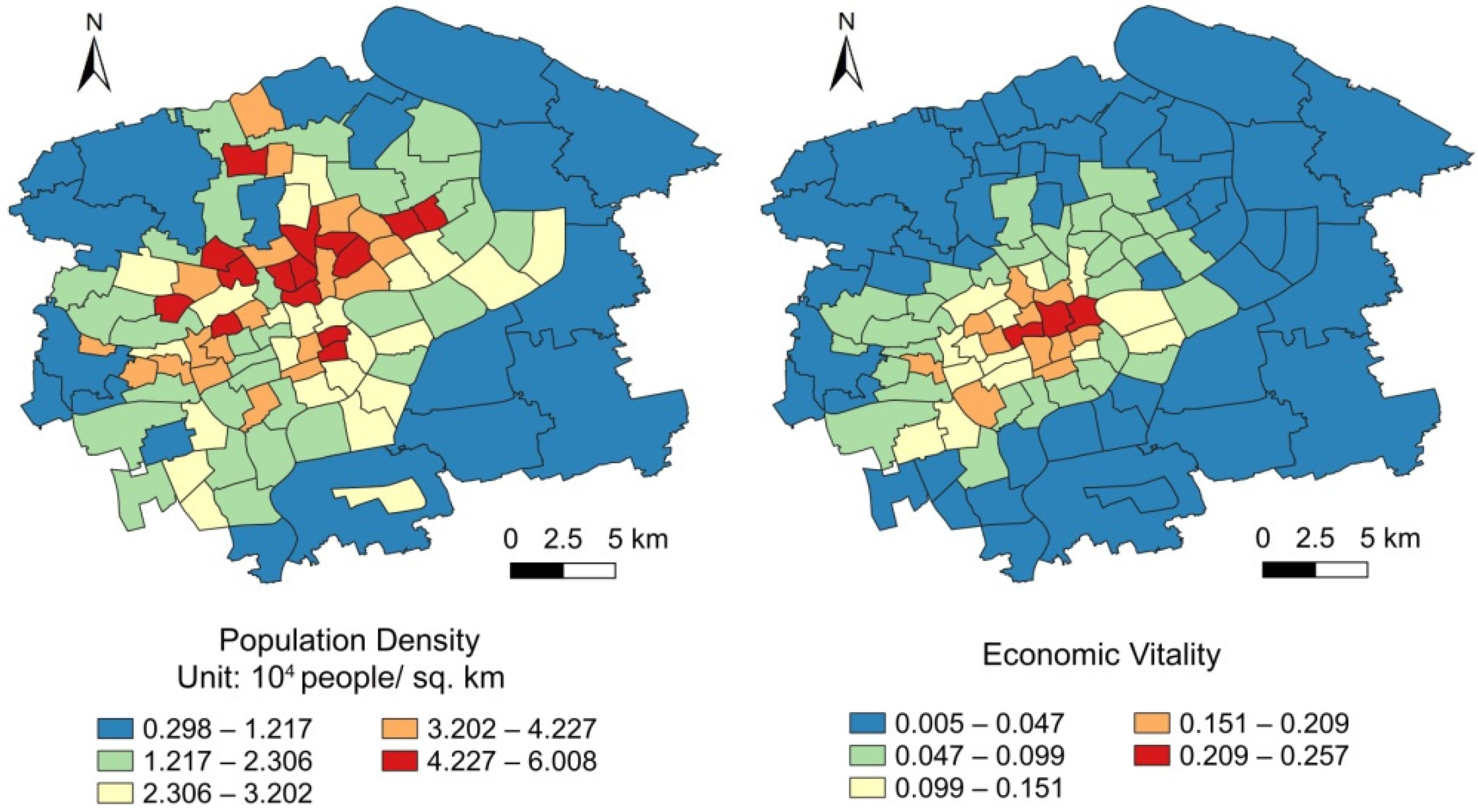
4.1. Data Distribution
4.2. Correlation Analysis of Binary Space
4.3. Combined Impact Analysis
4.3.1. Comprehensive Vitality
4.3.2. Economic Vitality
4.3.3. Cultural Vitality
4.3.4. Nocturnal Vitality
5. Discussion
5.1. Spatial Mismatches between Floor Area Ratio and Population Density
5.2. The Difference in the Impact of Different Spatial Scales on Urban Vitality
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, H.; Roser, M. Urbanization. 2018. Available online: https://ourworldindata.org/urbanization (accessed on 15 November 2021).
- The World Bank. Urban Population (% of Total Population). 2020. Available online: https://data.worldbank.org/indicator/SP.URB.TOTL.IN.ZS (accessed on 1 December 2021).
- Wang, N. The spatial structure defects of megalopolises and the treatment of “urban diseases”. Reg. Econ. Rev. 2015, 30, 153–160. [Google Scholar]
- Shi, Y. The measurement index system of “urban disease” in China and its empirical analysis. Econ. Geogr. 2014, 34, 1–6. [Google Scholar]
- Jin, X.; Long, Y.; Sun, W.; Lu, Y.; Yang, X.; Tang, J. Evaluating cities’ vitality and identifying ghost cities in China with emerging geographical data. Cities 2017, 63, 98–109. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, P.; Liang, J. Urban vitality based on location service data: A case study of the Inner Sixth Ring Road of Beijing. Reg. Res. Dev. 2018, 37, 64–69, 87. [Google Scholar]
- Ta, N.; Zeng, Y.; Zhu, Q.; Wu, J. Analysis of the relationship between built environment and urban vitality in Central Shanghai based on big data. Sci. Geogr. Sin. 2020, 40, 60–68. [Google Scholar]
- Anas, A.; Arnott, R.; Small, K.A. Urban spatial structure. J. Econ. Lit. 1998, 36, 1426–1464. [Google Scholar]
- Arribas-Bel, D.; Sanz-Graica, F. The validity of the monocentric city model in a polycentric age: US metropolitan areas in 1990, 2000 and 2010. Urban Geogr. 2014, 35, 980–997. [Google Scholar] [CrossRef] [Green Version]
- Fujita, M.; Ogawa, H. Multiple equilibria and structural transition of non-monocentric urban configurations. Reg. Sci. Urban Econ. 1982, 12, 161–196. [Google Scholar] [CrossRef]
- Gordon, P.; Richardson, H.W.; Wong, H.L. The distribution of population and employment in a polycentric city: The case of Los Angeles. Environ. Plan. A Econ. Space 1986, 18, 161–173. [Google Scholar] [CrossRef]
- Song, S. Monocentric and Polycentric Density Functions and Their Required Commutes; Working Papers UCTC No. 198; The University of California Transportation Center: Berkeley, CA, USA, 1992. [Google Scholar]
- Li, Y.; Liu, X. How did urban polycentricity and dispersion affect economic productivity? A case study of 306 Chinese cities. Landsc. Urban Plan. 2018, 173, 51–59. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, W.; Wang, X. Does polycentric and compact development alleviate urban traffic congestion? A case study of 98 Chinese cities. Cities 2019, 88, 100–111. [Google Scholar] [CrossRef]
- Botequilha-Leit, O.A. Eco-polycentric urban systems: An ecological region perspective for network cities. Challenges 2012, 3, 1–42. [Google Scholar] [CrossRef]
- Champion, A.G. A changing demographic regime and evolving poly centric urban regions: Consequences for the size, composition and distribution of city populations. Urban Stud. 2001, 38, 657–677. [Google Scholar] [CrossRef]
- Loibl, W.; Tötzer, T.; Köstl, M.; Steinnocher, K. Simulation of Polycentric Urban Growth Dynamics through Agents. In Modelling Land-Use Change; Koomen, E., Stillwell, J., Bakema, A., Scholten, H.J., Eds.; Springer: Dordrecht, The Netherlands, 2007; Volume 90, pp. 219–236. [Google Scholar]
- Wei, S.; Chen, Y.; Lu, S. Urban sprawl, polycentric agglomeration and productivity. China Ind. Econ. 2016, 30, 58–75. [Google Scholar]
- Yang, Q.; Shi, Y.; Zhou, L. Did industrial centralization strategy in Shanghai’s suburbs lead to economic growth? Sustainability 2022, 14, 856. [Google Scholar] [CrossRef]
- Scheer, B.C.; Petkov, M. Edge city morphology: A comparison of commercial centers. J. Am. Plan. Assoc. 1998, 64, 298–310. [Google Scholar] [CrossRef]
- Lee, J.; Kurisu, K.H.; An, K.; Hanaki, K. Development of the compact city index and its application to Japanese cities. Urban Stud. 2015, 52, 1054–1070. [Google Scholar] [CrossRef]
- Ibrahim, A. Investigation of the Relationship between Urban Spatial Structure and Travel Demand in the GTA. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 1997. [Google Scholar]
- Clark, L.P.; Millet, D.B.; Marshall, J.D. Air quality and urban form in US urban areas: Evidence from regulatory monitors. Environ. Sci. Technol. 2011, 45, 7028–7035. [Google Scholar] [CrossRef]
- Lin, J.J.; Yang, A.T. Structural analysis of how urban form impacts travel demand: Evidence from Taipei. Urban Stud. 2009, 46, 1951–1967. [Google Scholar] [CrossRef]
- Bento, A.M.; Cropper, M.L.; Mobarak, A.M.; Vinha, K. The effects of urban spatial structure on travel demand in the United States. Rev. Econ. Stat. 2005, 87, 466–478. [Google Scholar] [CrossRef]
- Kenworthy, J.; Hu, G. Transport and urban form in Chinese cities: An international comparative and policy perspective with implications for sustainable urban transport in China. disP-Plan. Rev. 2002, 38, 4–14. [Google Scholar] [CrossRef]
- Holden, E.; Norland, I.T. Three challenges for the compact city as a sustainable urban form: Household consumption of energy and transport in eight residential areas in the greater Oslo region. Urban Stud. 2005, 42, 2145–2166. [Google Scholar] [CrossRef]
- Song, Y.; Knaap, G.J. Measuring urban form: Is Portland winning the war on sprawl? J. Am. Plan. Assoc. 2004, 70, 210–225. [Google Scholar] [CrossRef]
- Salomons, E.M.; Pont, M.B. Urban traffic noise and the relation to urban density, form, and traffic elasticity. Landsc. Urban Plan. 2012, 108, 2–16. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Li, B.; Peng, Z.R.; Fu, Q. Investigating the relationship between air pollution variation and urban form. Build. Environ. 2019, 147, 559–568. [Google Scholar] [CrossRef]
- Coogan, P.F.; White, L.F.; Evans, S.R.; Adler, T.J.; Hathaway, K.M.; Palmer, J.R.; Rosenberg, L. Longitudinal assessment of urban form and weight gain in African-American women. Am. J. Prev. Med. 2011, 40, 411–418. [Google Scholar] [CrossRef] [Green Version]
- Stone, B.; Hess, J.J.; Frumkin, H. Urban form and extreme heat events: Are sprawling cities more vulnerable to climate change than compact cities? Environ. Health Perspect. 2010, 118, 1425–1428. [Google Scholar] [CrossRef] [Green Version]
- Frank, L.; Bradley, M.; Kavage, S.; Chapman, J.; Lawton, T.K. Urban form, travel time, and cost relationships with tour complexity and mode choice. Transportation 2008, 35, 37–54. [Google Scholar] [CrossRef]
- Ma, J.; Liu, Z.; Chai, Y. The impact of urban form on CO2 emission from work and non-work trips: The case of Beijing, China. Habitat Int. 2015, 47, 1–10. [Google Scholar] [CrossRef]
- Asami, Y.; Kubat, A.S.; Istek, C. Characterization of the street networks in the traditional Turkish urban form. Environ. Plan. B Plan. Des. 2001, 28, 777–795. [Google Scholar] [CrossRef]
- Nass, P. Urban form, sustainability and health: The case of greater Oslo. Eur. Plan. Stud. 2014, 22, 1524–1543. [Google Scholar] [CrossRef] [Green Version]
- Gong, P.; Yang, J. Spatial structure of urban agglomerations in China based on Microblog data. Urban Dev. Res. 2020, 27, 1–8, 61, 181. [Google Scholar]
- Zhou, C.; Li, S.; Wang, S. Examining the impacts of urban form on air pollution in developing countries: A case study of China’s megacities. Int. J. Environ. Res. Public Health 2018, 15, 1565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hui, E.C.M.; Li, X.; Chen, T.; Lang, W. Deciphering the spatial structure of China’s megacity region: A new bay area—The Guangdong-Hong Kong-Macao greater bay area in the making. Cities 2020, 105, 102168. [Google Scholar] [CrossRef]
- Xue, B.; Xiao, Q.; Li, J.; Xie, X. Analysis of urban spatial structure in Northeast China based on point of interest (POI) big data. Sci. Geogr. Sin. 2020, 40, 691–700. [Google Scholar]
- Chen, Z.; Yu, B.; Song, W.; Liu, H.; Wu, Q.; Shi, K.; Wu, J. A new approach for detecting urban centers and their spatial structure with nighttime light remote sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6305–6319. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, T.; He, Z.; Wang, R. Urban spatial structure and motorization in China. J. Reg. Sci. 2017, 57, 470–486. [Google Scholar] [CrossRef]
- Ding, L.; Song, X.; Niu, X. Discussion on the functional relation characteristics of urban spatial structure: A case study of central Shanghai. City Plan. Rev. 2019, 43, 107–116. (In Chinese) [Google Scholar]
- Lee, C. Impacts of two-scale urban form and their combined effects on commute modes in US metropolitan areas. J. Transp. Geogr. 2020, 88, 102821. [Google Scholar] [CrossRef]
- Ryu, H.; Park, I.K.; Chun, B.S.; Chang, S.I. Spatial statistical analysis of the effects of urban form indicators on road-traffic noise exposure of a city in South Korea. Appl. Acoust. 2017, 115, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, J. The Death and Life of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar]
- Crull, S.R.; Cook, C.C. Housing and economic vitality in rural Midwestern counties. Hous. Soc. 2000, 27, 16–32. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, B. Modelling of index system of economic vitality during the COVID-19 Epidemic. JOJ Wildl. Biodivers. 2021, 3, 91–112. [Google Scholar]
- Ravenscroft, N. The vitality and viability of town centres. Urban Stud. 2000, 37, 2533–2549. [Google Scholar] [CrossRef]
- Jackson, M.R.; Green, F.K.; Herranz, J. Cultural Vitality in Communities: Interpretation and Indicators; The Urban Institute: Washington, DC, USA, 2006. [Google Scholar]
- Ortega-Villa, L.M.; Ley-Garcia, J. Analysis of cultural indicators: A comparison of their conceptual basis and dimensions. Soc. Indic. Res. 2018, 137, 413–439. [Google Scholar] [CrossRef]
- Yang, Z.; Su, M.; Chen, B. Change of urban ecosystem development: A case study of Beijing, China. Procedia Environ. Sci. 2010, 2, 681–688. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Yang, Z.; Chen, B.; Zhang, Y.; Zhang, L. Emergy-based urban ecosystem health assessment: A case study of Baotou city. Acta Ecol. Sin. 2008, 28, 1720–1728. [Google Scholar] [CrossRef]
- Scott, K. Community Vitality: Canadian Index of Wellbeing; University of Waterloo: Waterloo, ON, Canada, 2010. [Google Scholar]
- Etuk, L.E.; Acock, A. Toward a rural community vitality measurement practice. Community Dev. 2017, 48, 141–153. [Google Scholar] [CrossRef]
- Lan, F.; Gong, X.; Da, H.; Wen, H. How do population inflow and social infrastructure affect urban vitality? Evidence from 35 large-and medium-sized cities in China. Cities 2020, 100, 102454. [Google Scholar] [CrossRef]
- Pan, H.; Yang, C.; Quan, L.; Liao, L. A new insight into understanding urban vitality: A case study in the Chengdu-Chongqing area twin-city economic circle, China. Sustainability 2021, 13, 10068. [Google Scholar] [CrossRef]
- Li, Q.; Cui, C.; Liu, F.; Wu, Q.; Run, Y.; Han, Z. Multidimensional urban vitality on streets: Spatial patterns and influence factor identification using multisource urban data. ISPRS Int. J. Geo-Inf. 2021, 11, 2. [Google Scholar] [CrossRef]
- Wu, W.; Niu, X.; Li, M. Influence of built environment on street Vitality: A case study of West Nanjing Road in Shanghai based on mobile location data. Sustainability 2021, 13, 1840. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Long, Y.; Long, Y.; Xu, M. A new urban vitality analysis and evaluation framework based on human activity modeling using multi-source big data. ISPRS Int. J. Geo-Inf. 2020, 9, 617. [Google Scholar] [CrossRef]
- Zhang, A.; Li, W.; Wu, J.; Lin, J.; Chu, J.; Xia, C. How can the urban landscape affect urban vitality at the street block level? A case study of 15 metropolises in China. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 1245–1262. [Google Scholar] [CrossRef]
- Xia, C.; Yeh, A.G.O.; Zhang, A. Analyzing spatial relationships between urban land use intensity and urban vitality at street block level: A case study of five Chinese megacities. Landsc. Urban Plan. 2020, 193, 103669. [Google Scholar] [CrossRef]
- Long, Y.; Huang, C.C. Does block size matter? The impact of urban design on economic vitality for Chinese Cities. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 406–422. [Google Scholar] [CrossRef] [Green Version]
- Mao, G.; Zhou, W.; Cai, A. Enterprise density, industrial association and industrial cluster transfer. J. Huaiyin Norm. Univ. Nat. Sci. Ed. 2015, 14, 323–330, 341. [Google Scholar]
- Shao, J. Research on the Collaborative Mechanism Construction of China’s Social Governance. Ph.D. Thesis, Jilin University, Jilin, China, June 2014. [Google Scholar]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M. Development of TOPSIS method to solve complicated decision-making problems—An overview on developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, D. Relationship between urban new business indexes and the business environment of Chinese cities: A study based on Entropy-TOPSIS and a Gaussian Process Regression model. Sustainability 2020, 12, 10422. [Google Scholar] [CrossRef]
- Lee, S.I. Developing a bivariate spatial association measure: An integration of Pearson’s r and Moran’s I. J. Geogr. Syst. 2001, 3, 369–385. [Google Scholar] [CrossRef]
- Dou, Y.; Luo, X.; Dong, L.; Wu, C.; Liang, H.; Ren, J. An empirical study on transit-oriented low-carbon urban land use planning: Exploratory Spatial Data Analysis (ESDA) on Shanghai, China. Habitat Int. 2016, 53, 379–389. [Google Scholar] [CrossRef]
- Fischer, M.M.; Getis, A. Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Griffith, D.A. A linear regression solution to the spatial autocorrelation problem. J. Geogr. Syst. 2000, 2, 141–156. [Google Scholar] [CrossRef]
- Cao, J.; Chen, Y.; Wilson, J.P.; Tan, H.; Yang, J.; Xu, Z. Modeling China’s prefecture-level economy using VIIRS imagery and spatial methods. Remote Sens. 2020, 12, 839. [Google Scholar] [CrossRef] [Green Version]
- Griffith, D.A. Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR). Environ. Plan. A 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial Autocorrelation and Spatial Filtering: Gaining Understanding through Theory and Scientific Visualization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Helbich, M.; Jokar Arsanjani, J. Spatial eigenvector filtering for spatiotemporal crime mapping and spatial crime analysis. Cartogr. Geogr. Inf. Sci. 2015, 42, 134–148. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D.A.; Lee, M.; Sinha, P. Eigenvector selection with stepwise regression techniques to construct eigenvector spatial filters. J. Geogr. Syst. 2016, 18, 67–85. [Google Scholar] [CrossRef]
- Ge, W.; Yang, H.; Zhu, X.; Ma, M.; Yang, Y. Ghost city extraction and rate estimation in China based on NPP-VIIRS night-time light data. ISPRS Int. J. Geo-Inf. 2018, 7, 219. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Jiang, D.; Huang, Y. China kilometer grid population distribution dataset. Acta Geogr. Sin. 2014, 69, 41–44. [Google Scholar]


| Dimension | Index | Implication | Computational Formula | Symbolic Meaning |
|---|---|---|---|---|
| Population dimension | Population density | The number of people per unit area | is the population density of unit , is the permanent population of unit , is the area of unit | |
| Job–housing balance | The relationship between the size of jobs and the number of houses | is the job–housing balance of unit , is the employed population of unit , is the employed population of the entire study area, is the permanent population of unit , is the permanent population of the entire study area | ||
| Land use dimension | The mixed degree of land use | Measurement of functional mixing of urban land use | is the mixed degree of land use of unit , is the ratio of type in land use types, is the number of land use categories | |
| Average block area | The average size of blocks in the study area | is average block area of unit , is the total area of unit , is the number of blocks of unit | ||
| Building density | The proportion of the base area of a building and the land area | is the building bottom area of unit , is the occupied land area of unit | ||
| Floor area ratio | The ratio of the gross building area to the land area | is the gross building area of unit , is the occupied land area of unit | ||
| Open space ratio | The ratio of open space to total land area | is the open space area of unit , is the total land area of unit | ||
| Open space fragmentation | Degree of fragmentation of open space | is the number of patches of open space of unit , is the total land area of unit | ||
| Traffic dimension | Road density | Ratio of total road length to total area | is the total road length of unit , is the total land area of unit | |
| Rail transit station density | Number of rail transit stations per unit area | is the number of rail transit stations of unit , is the total land area of unit | ||
| Accessibility of rail transit stations | Distance from the nearest rail transit station | The ISO area function of QNEAT3 (https://root676.github.io/, accessed on 15 December 2020) plug-in in QGIS 3.8 (QGIS Development Team, URL https://qgis.org/, accessed on 15 December 2020) was selected to realize the calculation of this index. | ||
| Data Category | Data Type | Data Sources |
|---|---|---|
| Population spatial structure data | Permanent population data | The Sixth National Population Census (2010) |
| Employment population data | The Third National Economic Census (2013) | |
| Data of spatial structure of land use | Land use data | Shanghai Urban Master Plan (2017–2035) |
| Public open space data | Map World (https://www.tianditu.gov.cn/, accessed on 20 June 2019) | |
| Building floor and height data | Urban Data Party (https://www.udparty.com/, accessed on 10 September 2017) | |
| Traffic spatial structure data | Road network data | Openstreetmap (https://www.openstreetmap.org/, accessed on 14 April 2020) |
| Rail transit station data | Map World (https://www.tianditu.gov.cn/, accessed on 12 May 2020) | |
| Urban vitality data | Points of interest (POI) data | Gaode Map (https://www.amap.com/, accessed on 17 June 2018) |
| Housing price data | ShanghaiLianjia.com (https://sh.lianjia.com/, accessed on 6 September 2018) | |
| Remote sensing data of night light | High Resolution Earth Observation System Hubei Data and Application Network (http://www.hbeos.org.cn/, accessed on 14 May 2020) | |
| PM2.5 data | Atmospheric Composition Analysis Group, Dalhousie University (http://fizz.phys.dal.ca/~atmos/martin/, accessed on 26 April 2020) |
| Urban Spatial Structure Indicators | Unit | Symbol | Minimum Value | Median | Maximum Value | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|---|
| Population density | 104 people/km2 | PD | 0.298 | 2.537 | 6.008 | 2.650 | 1.330 |
| Job–housing balance | - | JH | 0.003 | 0.784 | 10.055 | 1.406 | 1.677 |
| Mixed degree of land use | - | LUM | 0.580 | 0.791 | 0.960 | 0.783 | 0.104 |
| Building density | - | BD | 0.102 | 0.239 | 0.384 | 0.239 | 0.061 |
| Floor area ratio | - | FAR | 0.428 | 1.608 | 2.632 | 1.585 | 0.523 |
| Average block area | km2 | MBA | 0.020 | 0.121 | 0.444 | 0.139 | 0.090 |
| Open space ratio | % | OSR | 0.000 | 4.003 | 16.198 | 4.894 | 3.909 |
| Open space fragmentation | - | OSF | 0.000 | 0.547 | 27.265 | 1.079 | 2.776 |
| Road density | km/km2 | RD | 4.382 | 9.134 | 22.849 | 9.904 | 3.681 |
| Rail transit station density | one per km2 | RSD | 0.000 | 0.514 | 1.856 | 0.592 | 0.383 |
| The nearest distance to the rail transit station | km | RSA | 0.404 | 0.761 | 3.896 | 0.931 | 0.532 |
| Urban Vitality Indicators | Symbol | Minimum Value | Median | Maximum Value | Average Value | Standard Deviation |
|---|---|---|---|---|---|---|
| Comprehensive vitality | Comp_V | 0.014 | 0.146 | 0.908 | 0.203 | 0.176 |
| Economic vitality | Econ_V | 0.005 | 0.059 | 0.257 | 0.077 | 0.060 |
| Cultural vitality | Cult_V | 0.001 | 0.044 | 0.365 | 0.067 | 0.071 |
| Quality of life | Life_Q | 0.001 | 0.066 | 0.248 | 0.079 | 0.057 |
| Social governance | Soc_G | 0.002 | 0.066 | 0.222 | 0.081 | 0.055 |
| Air quality | Air_Q | 0.091 | 0.098 | 0.105 | 0.098 | 0.004 |
| Nocturnal vitality | Night_V | 0.011 | 0.03 | 0.414 | 0.059 | 0.078 |
| Variables | ESF Regression | OLS Regression | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | t Value | p Value | VIF | Coefficient | t Value | p Value | VIF | |
| PD | −0.071 | −2.113 | * | 2.806 | −0.079 | −2.079 | * | 2.553 |
| LUM | −1.218 | −3.438 | *** | 1.934 | −1.466 | −3.746 | *** | 1.639 |
| Ln(FAR) | 1.284 | 9.870 | *** | 3.573 | 1.084 | 7.794 | *** | 2.839 |
| OSR | 0.028 | 3.400 | *** | 1.430 | 0.022 | 2.357 | * | 1.317 |
| RD | 0.085 | 8.649 | *** | 1.875 | 0.093 | 8.613 | *** | 1.571 |
| RSA | −0.371 | −5.202 | *** | 2.047 | −0.450 | −6.346 | *** | 1.735 |
| EV1 | 1.314 | 4.448 | *** | 1.194 | N/A | |||
| EV2 | −1.012 | −3.237 | ** | 1.338 | N/A | |||
| EV9 | −0.603 | −2.182 | * | 1.046 | N/A | |||
| EV14 | 0.662 | 2.198 | * | 1.241 | N/A | |||
| EV18 | 0.547 | 1.954 | 0.054 | 1.071 | N/A | |||
| EV24 | 0.569 | 1.942 | 0.055 | 1.176 | N/A | |||
| R2 | 0.922 | 0.880 | ||||||
| AICc | 40.027 | 69.827 | ||||||
| Model Test | ESF Regression | OLS Regression | ||
|---|---|---|---|---|
| Test Value | p Value | Test Value | p Value | |
| White test | 99.040 | 0.241 | 36.345 | 0.108 |
| Ramsey RESET test | 0.511 | 0.675 | 2.719 | 0.049 |
| Jarque–Bera test for residuals | 3.709 | 0.156 | 0.303 | 0.860 |
| Moran index of residuals | 0.076 | 0.093 | 0.278 | 0.001 |
| Variables | ESF Regression | OLS Regression | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | t Value | p Value | VIF | Coefficient | t Value | p Value | VIF | |
| JH | 0.107 | 0.018 | *** | 1.260 | 0.117 | 5.871 | *** | 1.149 |
| FAR | 0.536 | 0.069 | *** | 1.877 | 0.517 | 6.485 | *** | 1.790 |
| MBA | −1.860 | 0.525 | ** | 3.185 | −1.601 | −2.659 | ** | 2.997 |
| RD | 0.038 | 0.012 | ** | 2.755 | 0.056 | 4.148 | *** | 2.506 |
| RSA | −0.396 | 0.067 | *** | 1.827 | −0.451 | −5.815 | *** | 1.750 |
| EV1 | 1.515 | 5.149 | *** | 1.197 | N/A | |||
| EV14 | 0.770 | 2.758 | ** | 1.078 | N/A | |||
| EV17 | 0.665 | 2.413 | * | 1.050 | N/A | |||
| EV35 | −0.555 | −1.996 | * | 1.071 | N/A | |||
| R2 | 0.910 | 0.868 | ||||||
| AICc | 34.415 | 64.299 | ||||||
| Model Test | ESF Regression | OLS Regression | ||
|---|---|---|---|---|
| Test Value | p Value | Test Value | p Value | |
| White test | 57.706 | 0.340 | 28.431 | 0.100 |
| Ramsey RESET test | 1.235 | 0.302 | 2.475 | 0.066 |
| Jarque–Bera test for residuals | 4.572 | 0.102 | 0.092 | 0.955 |
| Moran index of residuals | −0.083 | 0.114 | 0.105 | 0.032 |
| Variables | ESF Regression | OLS Regression | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | t Value | p Value | VIF | Coefficient | t Value | p Value | VIF | |
| PD2 | −0.021 | −2.578 | * | 2.407 | −0.017 | −1.963 | 0.053 | 1.959 |
| LUM | −1.802 | −3.095 | ** | 2.295 | −1.607 | −2.577 | * | 1.808 |
| FAR | 0.701 | 5.314 | *** | 2.981 | 0.898 | 6.244 | *** | 2.431 |
| OSR | 0.047 | 3.909 | *** | 1.379 | 0.050 | 3.616 | *** | 1.257 |
| RD | 0.043 | 3.022 | ** | 1.733 | 0.060 | 3.579 | *** | 1.606 |
| RSA | −0.900 | −9.044 | *** | 1.751 | −0.845 | −7.278 | *** | 1.639 |
| EV1 | 1.400 | 3.101 | ** | 1.225 | N/A | |||
| EV5 | 1.416 | 2.718 | ** | 1.631 | N/A | |||
| EV7 | 0.844 | 2.046 | * | 1.022 | N/A | |||
| EV14 | 1.694 | 3.799 | ** | 1.196 | N/A | |||
| EV16 | 1.591 | 3.670 | ** | 1.130 | N/A | |||
| R2 | 0.864 | 0.792 | ||||||
| AICc | 124.860 | 157.302 | ||||||
| Model Test | ESF Regression | OLS Regression | ||
|---|---|---|---|---|
| Test Value | p Value | Test Value | p Value | |
| White test | 91.517 | 0.124 | 62.320 | <0.001 |
| Ramsey RESET test | 1.385 | 0.252 | 3.617 | 0.016 |
| Jarque–Bera test for residuals | 3.587 | 0.166 | 2.122 | 0.346 |
| Moran index of residuals | −0.004 | 0.457 | 0.228 | 0.001 |
| Variables | ESF Regression | OLS Regression | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | t Value | p Value | VIF | Coefficient | t Value | p Value | VIF | |
| PD | −0.221 | −4.488 | *** | 3.374 | −0.218 | −3.779 | *** | 3.339 |
| JH | 0.077 | 2.627 | ** | 1.909 | 0.103 | 3.094 | ** | 1.764 |
| FAR | 0.490 | 4.060 | *** | 3.116 | 0.471 | 3.388 | ** | 3.008 |
| RD | 0.147 | 10.995 | *** | 1.907 | 0.154 | 10.006 | *** | 1.815 |
| RSA | −0.227 | −2.601 | * | 1.686 | −0.276 | −2.721 | ** | 1.652 |
| EV1 | 1.221 | 3.061 | ** | 1.199 | N/A | |||
| EV4 | 1.446 | 3.934 | *** | 1.019 | N/A | |||
| EV7 | 0.758 | 2.061 | * | 1.019 | N/A | |||
| EV11 | −1.155 | −3.132 | *** | 1.024 | N/A | |||
| EV21 | 0.762 | 2.056 | * | 1.036 | N/A | |||
| R2 | 0.848 | 0.779 | ||||||
| AICc | 99.688 | 126.563 | ||||||
| Model Test | ESF Regression | OLS Regression | ||
|---|---|---|---|---|
| Test Value | p Value | Test Value | p Value | |
| White test | 74.661 | 0.193 | 27.616 | 0.119 |
| Ramsey RESET test | 1.986 | 0.122 | 1.543 | 0.208 |
| Jarque–Bera test for residuals | 1.102 | 0.576 | 4.184 | 0.123 |
| Moran index of residuals | −0.016 | 0.464 | 0.190 | 0.001 |
| Variables | Coefficient | t Value | p Value | VIF |
|---|---|---|---|---|
| ln(PD) | 0.310 | 4.655 | ** | 2.441 |
| LUM | −0.931 | −2.522 | * | 1.714 |
| OSR | 0.010 | 1.107 | 0.271 | 1.385 |
| RD | 0.087 | 8.598 | *** | 1.625 |
| RSA | −0.494 | −6.466 | *** | 1.920 |
| EV1 | 1.416 | 4.347 | *** | 1.185 |
| EV5 | 2.153 | 6.289 | *** | 1.310 |
| EV8 | −0.818 | −2.653 | ** | 1.062 |
| EV14 | 0.820 | 2.519 | * | 1.183 |
| EV21 | 0.600 | 1.992 | * | 1.012 |
| EV22 | −0.726 | −2.420 | * | 1.005 |
| R2 | 0.903 | |||
| AICc | 59.809 | |||
| Model Test | Test Value | p Value |
|---|---|---|
| White test | 76.864 | 0.483 |
| Ramsey RESET test | 1.091 | 0.357 |
| Jarque–Bera test for residuals | 1.505 | 0.471 |
| Moran index of residuals | 0.013 | 0.337 |
| Variables | Subdistrict Scale | Grid Scale | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | t Value | p Value | VIF | Coefficient | t Value | p Value | VIF | |
| PD | −0.323 | −6.669 | *** | 3.374 | 0.113 | 2.895 | ** | 1.686 |
| FAR | 0.651 | 4.945 | *** | 3.116 | 0.228 | 3.624 | *** | 1.852 |
| RD | 0.171 | 11.491 | *** | 1.907 | 0.112 | 13.441 | *** | 1.518 |
| RSA | −0.311 | −2.959 | ** | 1.686 | −0.137 | −3.625 | *** | 1.410 |
| R2 | 0.758 | 0.440 | ||||||
| AICc | 133.959 | 1507.785 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Shi, Y. The Influence Mechanism of Urban Spatial Structure on Urban Vitality Based on Geographic Big Data: A Case Study in Downtown Shanghai. Buildings 2022, 12, 569. https://doi.org/10.3390/buildings12050569
Liu D, Shi Y. The Influence Mechanism of Urban Spatial Structure on Urban Vitality Based on Geographic Big Data: A Case Study in Downtown Shanghai. Buildings. 2022; 12(5):569. https://doi.org/10.3390/buildings12050569
Chicago/Turabian StyleLiu, Danxuan, and Yishao Shi. 2022. "The Influence Mechanism of Urban Spatial Structure on Urban Vitality Based on Geographic Big Data: A Case Study in Downtown Shanghai" Buildings 12, no. 5: 569. https://doi.org/10.3390/buildings12050569
APA StyleLiu, D., & Shi, Y. (2022). The Influence Mechanism of Urban Spatial Structure on Urban Vitality Based on Geographic Big Data: A Case Study in Downtown Shanghai. Buildings, 12(5), 569. https://doi.org/10.3390/buildings12050569






