Estimating Risks of Heat Strain by Age and Sex: A Population-Level Simulation Model
Abstract
:1. Introduction
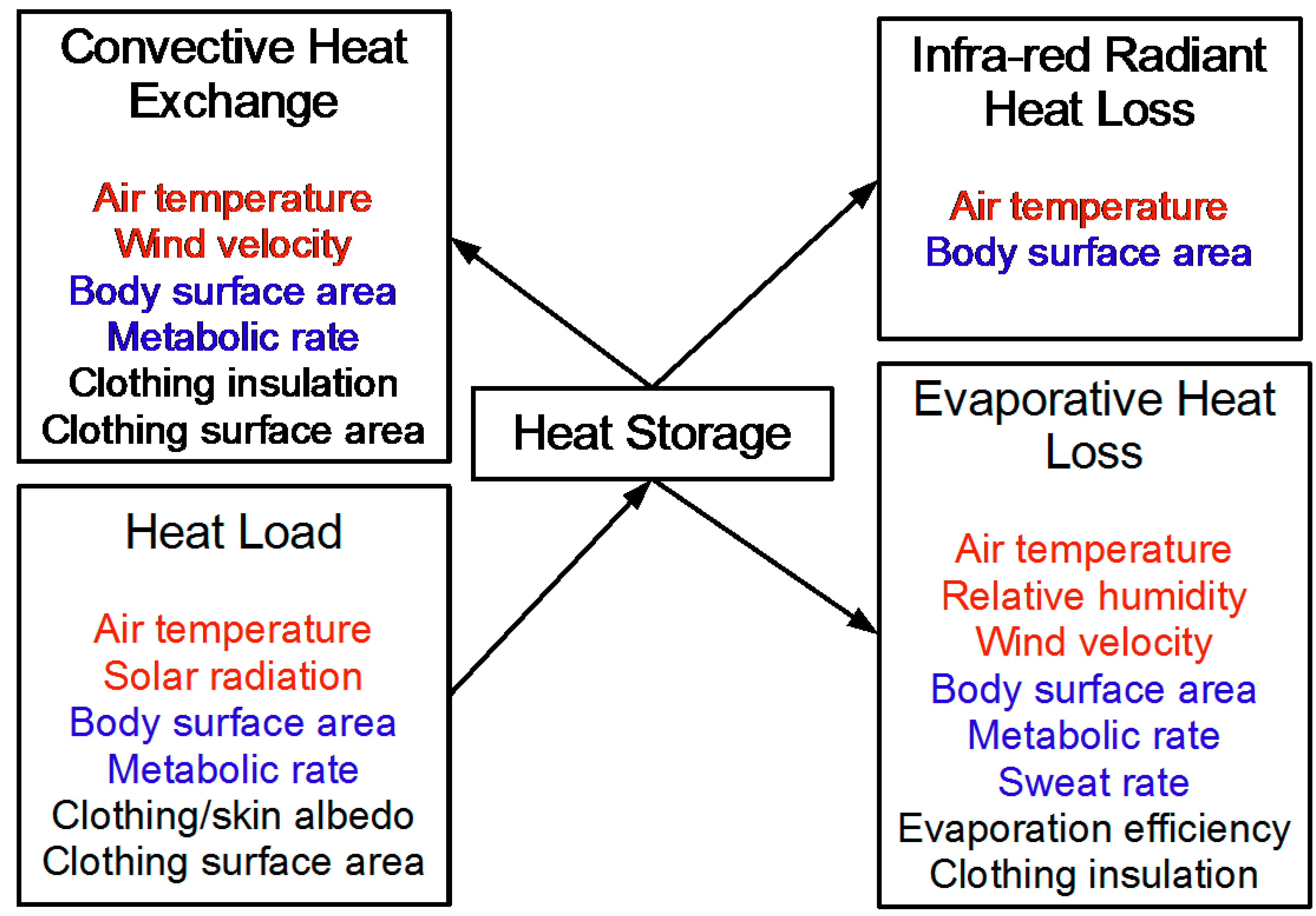
2. Materials and Methods
| Characteristic | Description | Value |
|---|---|---|
| Clothing albedo * | reflecting power of clothing | 0.3 |
| Clothed proportion | proportion of body covered | 0.4 |
| Clothing surface area ratio | factor increase in surface area for clothed area | 1.08 |
| Evaporation efficiency | proportion of sweat that evaporates | 0.85 |
| Insulation of clothing ** | basic dry thermal insulation of clothing | 0.093 m2∙W−1∙K |
| Skin albedo *** | reflecting power of skin | 0.3 |
| Skin temperature | kept fixed to simplify sweating model (see text and Maloney and Forbes [39]) | 36 °C |
2.1. Weather Variables
2.2. Individual Level Characteristics
2.3. Scaling from Individuals to Populations
2.4. Outcome Variables
2.5. Model Testing
3. Results



4. Discussion
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group 1 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- McMichael, A.J.; Woodruff, R.E.; Hales, S. Climate change and human health: Present and future risks. Lancet 2006, 367, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Kovats, S.; Hajat, S. Heat stress and public health: A critical review. Annu. Rev. Public Health 2008, 29, 41–55. [Google Scholar] [CrossRef] [PubMed]
- Knowlton, K.; Rotkin-Ellman, M.; King, G.; Margolis, H.G.; Smith, D.; Solomon, G.; Trent, R.; English, P. The 2006 California heat wave: Impacts on hospitalizations and emergency department visits. Environ. Health Perspect. 2009, 117, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Anderson, G.B.; Bell, M.L. Heat waves in the United States: Mortality risk during heat waves and effect modification by heat wave characteristics in 43 U.S. communities. Environ. Health Perspect. 2011, 119, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Fouillet, A.; Rey, G.; Wagner, V.; Laaidi, K.; Empereur-Bissonnet, P.; Le Tertre, A.; Frayssinet, P.; Bessemoulin, P.; Laurent, F.; de Crouy-Chanel, P.; et al. Has the impact of heat waves on mortality changed in France since the European heat wave of summer 2003? A study of the 2006 heat wave. Int. J. Epidemiol. 2008, 37, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Sherwood, S.C.; Huber, M. An adaptability limit to climate change due to heat stress. PNAS 2010, 107, 9552–9555. [Google Scholar] [CrossRef] [PubMed]
- Rey, G.; Fouillet, A.; Bessemoulin, P.; Frayssinet, P.; Dufour, A.; Jougla, E.; Hémon, D. Heat exposure and socio-economic vulnerability as synergistic factors in heat-wave-related mortality. Eur. J. Epidemiol. 2009, 24, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Hansen, A.; Bi, P.; Nitschke, M.; Pisaniello, D.; Newbury, J.; Kitson, A. Perceptions of heat-susceptibility in older persons: Barriers to adaptation. Int. J. Environ. Res. Public Health 2011, 8, 4714–4728. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Kan, H.; Kovats, S. The impact of the 2003 heat wave on mortality in Shanghai, China. Sci. Total Environ. 2010, 408, 2418–2420. [Google Scholar] [CrossRef] [PubMed]
- D’Ippoliti, D.; Michelozzi, P.; Marino, C.; de’Donato, F.; Menne, B.; Katsouyanni, K.; Kirchmayer, U.; Analitis, A.; Medina-Ramón, M.; Paldy, A.; et al. The impact of heat waves on mortality in 9 European cities: Results from the EuroHEAT project. Environ. Health Perspect. 2010, 9. [Google Scholar] [CrossRef]
- Lefevre, C.E.; Bruine de Bruin, W.; Taylor, A.L.; Dessai, S.; Kovats, S.; Fischhoff, B. Heat protection behaviors and positive affect during the 2013 heat wave in the United Kingdom. Soc. Sci. Med. 2015, 128, 282–289. [Google Scholar] [CrossRef] [PubMed]
- The Climate Institute. Sport and Climate Impacts: How Much Heat Can Sport Handle; The Climate Institute: Sydney, Australia, 2015; p. 21. [Google Scholar]
- Yard, E.E.; Gilchrist, J.; Haileyesus, T.; Murphy, M.; Collins, C.; McIlvain, N.; Comstock, R.D. Heat illness among high school athletes—United States, 2005–2009. J. Saf. Res. 2010, 41, 471–474. [Google Scholar]
- Hanna, E.G.; Kjellstrom, T.; Bennett, C.; Dear, K. Climate change and rising heat: Population health implications for working people in Australia. Asia Pac. J. Public Health 2011, 23, 14S–26S. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Hanna, E.G.; Kjellstrom, T. Working in Australia’s heat: Health promotion concerns for health and productivity. Health Promot. Int. 2013, 5, 1–12. [Google Scholar]
- Séguin, J.; Berry, P. Human Health in a Changing Climate: A Canadian Assessment of Vulnerabilities and Adaptive Capacity. Synthesis Report; Health Canada: Ottawa, ON, Canada, 2008. [Google Scholar]
- Eubank, S.; Guclu, H.; Kumar, V.S.A.; Marathe, M.V.; Srinivasan, A.; Toroczkai, Z.; Wang, N. Modelling disease outbreaks in realistic urban social networks. Nature 2004, 429, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Cummings, D.A.; Cauchemez, S.; Fraser, C.; Riley, S.; Meeyai, A.; Iamsirithaworn, S.; Burke, D.S. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 2005, 437, 209–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Longini, I.M.; Nizam, A.; Xu, S.; Ungchusak, K.; Hanshaoworakul, W.; Cummings, D.A.; Halloran, M.E. Containing pandemic influenza at the source. Science 2005, 309, 1083–1087. [Google Scholar] [CrossRef]
- Gilbert, N.; Terna, T.P. How to build and use agent-based models in social science. Mind Soc. 2000, 1, 57–72. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. PNAS 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Weng, W.G.; Han, X.F.; Fu, M. An extended multi-segmented human bioheat model for high temperature environments. Int. J. Heat Mass Transf. 2014, 75, 504–513. [Google Scholar] [CrossRef]
- Myrup, L.O.; Morgan, D.L. Numerical model of the urban atmosphere, Volume 1. The city-surface interface. In Contributions in Atmospheric Science No 4; University of California: Davis, CA, USA, 1972. [Google Scholar]
- Havenith, G. Individualized model of human thermoregulation for the simulation of heat stress response. J. Appl. Physiol. 2001, 90, 1943–1954. [Google Scholar] [PubMed]
- Gagge, A.P.; Stolwijk, J.A.J.; Nish, Y. An effective temperature scale based on a simple model of human physiological regulatory response. ASHRAE Trans. 1971, 77, 247–263. [Google Scholar]
- Ferreira, M.S.; Yanagihara, J.I. A transient three-dimensional heat transfer model of the human body. Int. Commun. Heat Mass Transf. 2009, 36, 718–724. [Google Scholar] [CrossRef]
- Wyndham, C.H.; Atkins, A.R. A physiological scheme and mathematical model of temperature regulation in man. Pflügers Archiv. 1968, 303, 14–30. [Google Scholar] [CrossRef] [PubMed]
- Takada, S.; Kobayashi, H.; Matsushita, T. Thermal model of human body fitted with individual characteristics of body temperature regulation. Build. Environ. 2009, 44, 463–470. [Google Scholar] [CrossRef]
- Kenny, G.; Gagnon, D.; Dorman, L.E.; Hardcastle, S.G.; Jay, O. Heat balance and cumulative heat storage during exercise performed in the heat in physically active younger and middle-aged men. Eur. J. Appl. Physiol. 2010, 109, 81–92. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, D.; Jay, O.; Lemire, B.; Dorman, L.; Kenny, G.P. Sex-related differences in dynamic heat balance: Metabolic heat production considerations. Med. Sci. Sports Exerc. 2008, 40. [Google Scholar] [CrossRef]
- Cramer, M.; Jay, O. Heat production per unit mass, not relative exercise intensity, determines the core temperature response during exercise in compensable conditions. In Proceedings of the 15th International Conference on Environmental Ergonomics, Queenstown, New Zealand, 11–15 February 2013.
- Bar-Or, O. Effects of age and gender on sweating pattern during exercise. Int. J. Sports Med. 1998, 19, S106–S107. [Google Scholar] [CrossRef] [PubMed]
- Bergeron, M.F. Youth sports in the heat. Sports Med. 2009, 39, 513–522. [Google Scholar] [CrossRef] [PubMed]
- Åström, D.O.; Forsberg, B.; Rocklöv, J. Heat wave impact on morbidity and mortality in the elderly population: A review of recent studies. Maturitas 2011, 99–105. [Google Scholar] [CrossRef]
- Hansen, A.; Bi, P.; Ryan, P.; Nitschke, M.; Pisaniella, D.; Tucker, G. The effect of heat waves on hospital admissions for renal disease in a temperate city of Australia. Int. J. Epidemiology 2008, 37, 1359–1365. [Google Scholar] [CrossRef]
- Judson, O.P. The rise of the individual-based model in ecology. TREE 1994, 9, 9–14. [Google Scholar] [PubMed]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef] [PubMed]
- Maloney, S.K.; Forbes, C.F. What effect will a few degrees of climate change have on human heat balance? Implications for human activity. Int. J. Biometeorol. 2011, 55, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Kenny, N.A.; Warland, J.S.; Brown, R.D.; Gillespie, T.G. Estimating the radiation absorbed by a human. Int. J. Biometeorol. 2008, 52, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Australian Government Bureau of Meteorology. Daily Weather Observations. Available online: http://www.bom.gov.au/climate/dwo/index.shtml (accessed on 10 April 2015).
- Baldwin, P; Maynard, A. A survey of wind speeds in indoor workplaces. Ann. Occup. Hyg. 1998, 42, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, C.G.; Kenney, W.L. Effects of age and acclimation on responses to passive heat exposure. J. Appl. Physiol. 1993, 75, 2162–2167. [Google Scholar] [PubMed]
- Anderson, R.K.; Kenney, W.L. Effect of age on heat-activated sweat gland density and flow during exercise in dry heat. J. Appl. Physiol. 1987, 63, 1089–1094. [Google Scholar] [PubMed]
- Inoue, Y.; Havenith, G.; Kenney, W.L.; Loomis, J.L.; Buskirk, E.R. Exercise- and methylcholine-induced sweating responses in older and younger men: Effect of heat acclimation and aerobic fitness. Int. J. Biometeorol. 1999, 42, 210–216. [Google Scholar] [CrossRef] [PubMed]
- Inbar, O.; Morris, N.; Epstein, Y.; Gass, G. Comparison of thermoregulatory responses to exercise in dry heat among prepubertal boys, young adults and older males. Exp. Physiol. 2004, 89, 691–700. [Google Scholar] [CrossRef] [PubMed]
- Green, J.M.; Bishop, P.A.; Muir, I.H.; Lomax, R.G. Gender differences in sweat lactate. Eur. J. Appl. Physiol. 2000, 82, 230–235. [Google Scholar] [CrossRef] [PubMed]
- Foster, K.G.; Ellis, F.P.; Doré, C.; Exton-Smith, A.N.; Weiner, J.S. Sweat responses in the aged. Age Ageing 1976, 5, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Mehnert, P.; Bröde, P.; Griefahn, B. Gender-related difference in sweat loss and its impact on exposure limits to heat stress. Int. J. Ind. Ergon. 2002, 29, 343–351. [Google Scholar] [CrossRef]
- Rowland, T. Thermoregulation during exercise in the heath in children: Old concepts revisited. J. Appl. Physiol. 2008, 105, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Weyand, P.G.; Smith, B.R; Sandell, R.F. Assessing the metabolic cost of walking: The influence of baseline subtractions. In Proceedings of the 31st annual international conference of the IEEE, Minneapolis, MN, USA, 3–6 September 2009.
- Nitschke, M.; Hansen, A.; Bi, P.; Pisaniello, D.; Newbury, J.; Kitson, A.; Tucker, G.; Avery, J.; Grande, E.D. Risk factors, health effects and behaviour in older people during extreme heat: A survey in South Australia. Int. J. Environ. Res. Public Health 2013, 10, 6721–6733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Havenith, G.; Holmer, I.; den Hartog, E.A.; Parsons, K.C. Clothing evaporative heat resistence—Proposal for improved representation in standards and models. Ann. Occup. Hyg. 1999, 43, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Australian Bureau of Statistics. Household Energy Consumption Survey, Australia: Summary of Results, 2012. Available online: http://www.abs.gov.au/ausstats/abs@.nsf/Lookup/4670.0main+features100072012 (accessed on 14 May 2015).
- University of Queensland. Keeping Cool (or Warm) Sustainably at Work. Available online: http://www.uq.edu.au/sustainability/air-conditioning-at-uq (accessed on 14 May 2015).
- Australian Bureau of Statistics. Overweight and Obesity in Adults in Australia: A Snapshot, 2011. Available online: http://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/4842.0.55.001Main+Features12007%E2%80%9308?OpenDocument (accessed on 14 May 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glass, K.; Tait, P.W.; Hanna, E.G.; Dear, K. Estimating Risks of Heat Strain by Age and Sex: A Population-Level Simulation Model. Int. J. Environ. Res. Public Health 2015, 12, 5241-5255. https://doi.org/10.3390/ijerph120505241
Glass K, Tait PW, Hanna EG, Dear K. Estimating Risks of Heat Strain by Age and Sex: A Population-Level Simulation Model. International Journal of Environmental Research and Public Health. 2015; 12(5):5241-5255. https://doi.org/10.3390/ijerph120505241
Chicago/Turabian StyleGlass, Kathryn, Peter W. Tait, Elizabeth G. Hanna, and Keith Dear. 2015. "Estimating Risks of Heat Strain by Age and Sex: A Population-Level Simulation Model" International Journal of Environmental Research and Public Health 12, no. 5: 5241-5255. https://doi.org/10.3390/ijerph120505241
APA StyleGlass, K., Tait, P. W., Hanna, E. G., & Dear, K. (2015). Estimating Risks of Heat Strain by Age and Sex: A Population-Level Simulation Model. International Journal of Environmental Research and Public Health, 12(5), 5241-5255. https://doi.org/10.3390/ijerph120505241





