The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus
Abstract
:1. Introduction
2. Method
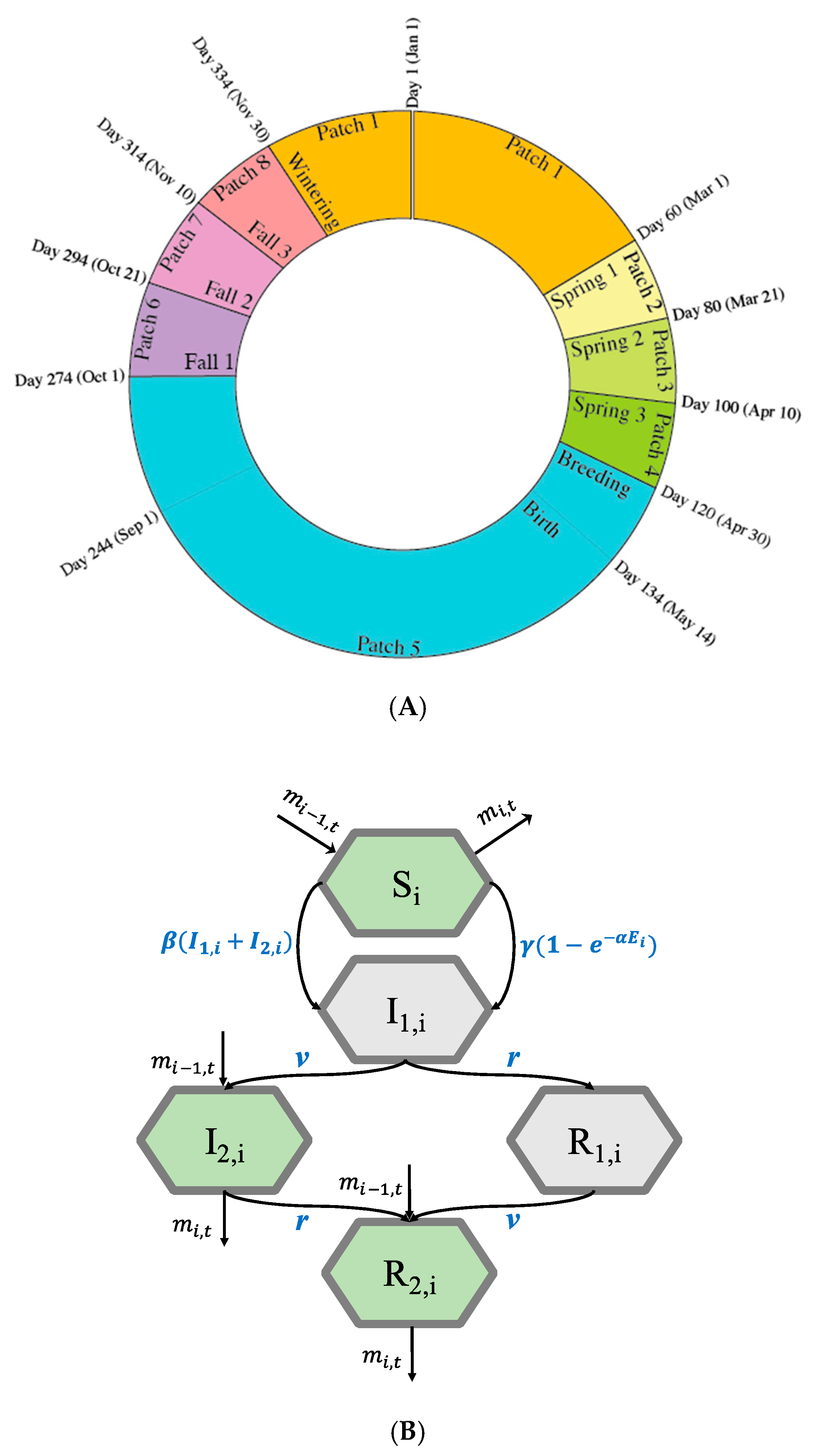
2.1. The Model
2.2. Simulations and Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Webster, R.G.; Peiris, M.; Chen, H.; Guan, Y. H5N1 outbreaks and enzootic influenza. Biodiversity 2006, 7, 51–55. [Google Scholar] [CrossRef]
- WHO Influenza (Avian and Other Zoonotic). Available online: http://www.who.int/news-room/fact-sheets/detail/influenza-(avian-and-other-zoonotic) (accessed on 13 November 2018).
- WHO Cumulative Number of Confirmed Human Cases for Avian Influenza A(H5N1) Reported to WHO, 2003–2018. Available online: http://www.who.int/influenza/human_animal_interface/2018_07_20_tableH5N1.pdf?ua=1 (accessed on 23 October 2018).
- Kilpatrick, A.M.; Chmura, A.A.; Gibbons, D.W.; Fleischer, R.C.; Marra, P.P.; Daszak, P. Predicting the global spread of H5N1 avian influenza. Proc. Natl. Acad. Sci. USA 2006, 103, 6075–6076. [Google Scholar] [CrossRef]
- Si, Y.; Skidmore, A.K.; Wang, T.; De Boer, W.F.; Debba, P.; Toxopeus, A.G.; Li, L.; Prins, H.H.T. Spatio-temporal dynamics of global H5N1 outbreaks match bird migration patterns. Geospat. Health 2009, 4, 65–78. [Google Scholar] [CrossRef] [Green Version]
- El-Shesheny, R.; Kandeil, A.; Bagato, O.; Maatouq, A.M.; Moatasim, Y.; Rubrum, A.; Song, M.S.; Webby, R.J.; Ali, M.A.; Kayali, G. Molecular characterization of avian influenza H5N1 virus in Egypt and the emergence of a novel endemic subclade. J. Gen. Virol. 2014, 95, 1444. [Google Scholar] [CrossRef]
- Duan, L.; Bahl, J.; Smith, G.J.D.; Wang, J.; Vijaykrishna, D.; Zhang, L.J.; Zhang, J.X.; Li, K.S.; Fan, X.H.; Cheung, C.L.; et al. The development and genetic diversity of H5N1 influenza virus in China, 1996–2006. Virology 2008, 380, 243–254. [Google Scholar] [CrossRef]
- Guan, Y.; Poon, L.L.M.; Cheung, C.Y.; Ellis, T.M.; Lim, W.; Lipatov, A.S.; Chan, K.H.; Sturm-Ramirez, K.M.; Cheung, C.L.; Leung, Y.H.C.; et al. H5N1 influenza: A protean pandemic threat. Proc. Natl. Acad. Sci. USA 2004, 101, 8156–8161. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-I.; Pascua, P.N.Q.; Kwon, H.-I.; Lim, G.-J.; Kim, E.-H.; Yoon, S.-W.; Park, S.-J.; Kim, S.M.; Choi, E.-J.; Si, Y.-J.; et al. Pathobiological features of a novel, highly pathogenic avian influenza A(H5N8) virus. Emerg. Microbes Infect. 2014, 3, 1–12. [Google Scholar] [CrossRef]
- Lycett, S.J.; Bodewes, R.; Pohlmann, A.; Banks, J.; Bányai, K.; Boni, M.F.; Bouwstra, R.; Breed, A.C.; Brown, I.H.; Chen, H.; et al. Role for migratory wild birds in the global spread of avian influenza H5N8. Science 2016, 354, 213–217. [Google Scholar] [Green Version]
- Lee, D.-H.; Torchetti, M.K.; Winker, K.; Ip, H.S.; Song, C.-S.; Swayne, D.E. Intercontinental Spread of Asian-Origin H5N8 to North America through Beringia by Migratory Birds. J. Virol. 2015, 89, 6521–6524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pasick, J.; Berhane, Y.; Joseph, T.; Bowes, V.; Hisanaga, T.; Handel, K.; Alexandersen, S. Reassortant Highly Pathogenic Influenza A H5N2 Virus Containing Gene Segments Related to Eurasian H5N8 in British Columbia, Canada, 2014. Sci. Rep. 2015, 5, srep09484. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.S.; Chen, L.H.; Chen, Y.P.; Liu, Y.P.; Li, W.C.; Lin, Y.L.; Lee, F. Highly pathogenic avian influenza viruses H5N2, H5N3, and H5N8 in Taiwan in 2015. Vet. Microbiol. 2016, 187, 50–57. [Google Scholar] [CrossRef]
- Van Den Brand, J.M.A.; Verhagen, J.H.; Kroeze, E.J.B.V.; Van De Bildt, M.W.G.; Bodewes, R.; Herfst, S.; Richard, M.; Lexmond, P.; Bestebroer, T.M.; Fouchier, R.A.M.; et al. Wild ducks excrete highly pathogenic avian influenza virus H5N8 (2014–2015) without clinical or pathological evidence of disease. Emerg. Microbes Infect. 2018, 7, 67. [Google Scholar] [PubMed]
- Russell, B.C.A. Sick birds don’t fly…or do they? Science 2016, 354, 174–175. [Google Scholar] [CrossRef] [PubMed]
- Olsen, B.; Munster, V.J.; Wallensten, A.; Waldenström, J.; Osterhaus, A.D.M.E.; Fouchier, R.A.M. Global Patterns of Influenza A Virus in Wild Birds. Science 2006, 312, 384–388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sims, L.D.; Domenech, J.; Benigno, C.; Kahn, S.; Kamata, A.; Lubroth, J.; Martin, V.; Roeder, P. Origin and evolution of highly pathogenic H5N1 avian influenza in Asia. Vet. Rec. 2005, 157, 159–164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, H.; Zhou, S.; Dong, L.; Van Boeckel, P.; Cui, Y.; Wu, Y.; Cazelles, B.; Huang, S.; Yang, R.; Grenfell, B.T.; et al. Avian influenza H5N1 viral and bird migration networks in Asia. Proc. Natl. Acad. Sci. USA 2015, 112, 172–177. [Google Scholar] [CrossRef]
- Prosser, D.J.; Hungerford, L.L.; Erwin, R.M.; Ottinger, M.A.; Takekawa, J.Y.; Ellis, E.C. Mapping avian influenza transmission risk at the interface of domestic poultry and wild birds. Front. Public Health 2013, 1, 28. [Google Scholar] [CrossRef]
- Sun, H.; Pu, J.; Hu, J.; Liu, L.; Xu, G.; Gao, G.F.; Liu, X.; Liu, J. Characterization of clade 2.3.4.4 highly pathogenic H5 avian influenza viruses in ducks and chickens. Vet. Microbiol. 2016, 182, 116–122. [Google Scholar] [CrossRef]
- Bevins, S.N.; Dusek, R.J.; White, C.L.; Gidlewski, T.; Bodenstein, B.; Mansfield, K.G.; DeBruyn, P.; Kraege, D.; Rowan, E.; Gillin, C.; et al. Widespread detection of highly pathogenic H5 influenza viruses in wild birds from the Pacific Flyway of the United States. Sci. Rep. 2016, 6, 28980. [Google Scholar] [CrossRef]
- Jeong, J.; Kang, H.M.; Lee, E.K.; Song, B.M.; Kwon, Y.K.; Kim, H.R.; Choi, K.S.; Kim, J.Y.; Lee, H.J.; Moon, O.K.; et al. Highly pathogenic avian influenza virus (H5N8) in domestic poultry and its relationship with migratory birds in South Korea during 2014. Vet. Microbiol. 2014, 173, 249–257. [Google Scholar] [CrossRef]
- Li, X.; Xu, B.; Shaman, J. Pathobiological features favouring the intercontinental dissemination of highly pathogenic avian influenza virus. R. Soc. Open Sci. 2019, 6, 190276. [Google Scholar] [CrossRef] [Green Version]
- Breban, R.; Drake, J.M.; Stallknecht, D.E.; Rohani, P. The Role of Environmental Transmission in Recurrent Avian Influenza Epidemics. PLoS Comput. Biol. 2009, 5, e1000346. [Google Scholar] [CrossRef]
- Rohani, P.; Breban, R.; Stallknecht, D.E.; Drake, J.M. Environmental transmission of low pathogenicity avian influenza viruses and its implications for pathogen invasion. Proc. Natl. Acad. Sci. USA 2009, 106, 10365–10369. [Google Scholar] [CrossRef] [Green Version]
- Galsworthy, S.J.; Bosch, Q.A.; Hoye, B.J.; Heesterbeek, J.A.P.; Klinkenberg, D. Effects of Infection-Induced Migration Delays on the Epidemiology of Avian Influenza in Wild Mallard Populations. PLoS ONE 2011, 6, e26118. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Li, Z.; Shi, J.; Shinya, K.; Deng, G.; Qi, Q.; Tian, G.; Fan, S.; Zhao, H.; et al. Properties and Dissemination of H5N1 Viruses Isolated during an Influenza Outbreak in Migratory Waterfowl in Western China. J. Virol. 2006, 80, 5976–5983. [Google Scholar] [CrossRef] [Green Version]
- Hénaux, V.; Samuel, M.D. Avian Influenza Shedding Patterns in Waterfowl: Implications for Surveillance, Environmental Transmission, and Disease Spread. J. Wildl. Dis. 2011, 47, 566–578. [Google Scholar] [CrossRef] [PubMed]
- Van Gils, J.A.; Munster, V.J.; Radersma, R.; Liefhebber, D.; Fouchier, R.A.M.; Klaassen, M. Hampered foraging and migratory performance in swans infected with low-pathogenic avian influenza A virus. PLoS ONE 2007, 2, e184. [Google Scholar] [CrossRef] [PubMed]
- Hirschfeld, A.; Heyd, A. Mortality of migratory birds caused by hunting in Europe: Bag statistics and proposals for the conservation of birds and animal welfare. Berichte zum Vogelschutz 2005, 42, 47–74. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics With S-PLUS; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Handel, A.; Brown, J.; Stallknecht, D.; Rohani, P. A Multi-scale Analysis of Influenza A Virus Fitness Trade-offs due to Temperature-dependent Virus Persistence. PLoS Comput. Biol. 2013, 9, e1002989. [Google Scholar] [CrossRef]



| Parameter | Description | Value | Unit | Reference |
|---|---|---|---|---|
| Contact transmission rate in Flock A | For , ; for , | [26,27] | ||
| Contact transmission rate in Flock B | For , ; for , | [26,27] | ||
| Infection recovery rate in Flock A | [1/13, 1/3] | [26,28] | ||
| Infection recovery rate in Flock B | [1/13, 1/3] | [26,28] | ||
| Infection-induced mortality rate in Flock A | ||||
| Infection-induced mortality rate in Flock B | ||||
| Migration recovery rate in Flock A | [1/100, 1/1] | [26,29] | ||
| Migration recovery rate in Flock B | [1/100, 1/1] | [26,29] | ||
| Natural mortality rate | [26] | |||
| Hunting mortality rate | For , | [26,30] | ||
| Migration matrix of Flock A | Shown in Figure 1. | [26] | ||
| Migration matrix of Flock B | Defined by and . | [26] | ||
| Birth rate | For and 162 , , otherwise | [26] | ||
| c | Persistence of virions | [24,25] | ||
| Exposure rate | [24,25] | |||
| Re-scaled environmental infectiousness | [24,25] | |||
| The time lag in migration schedule of Flock A and Flock B |
| Variables | Definition | Initial Value |
|---|---|---|
| Susceptible birds in Flock A | ||
| Susceptible birds in Flock B | ||
| Infectious birds without migration ability in Flock A | ||
| Infectious birds without migration ability in Flock B | ||
| Infectious birds with migration ability in Flock A | ||
| Infectious birds with migration ability in Flock B | ||
| Recovered birds without migration ability in Flock A | ||
| Recovered birds without migration ability in Flock B | ||
| Recovered birds with migration ability in Flock A | ||
| Recovered birds with migration ability in Flock B | ||
| E | Virions in the environment divided by shedding rate) |
| Parameter | Patch 3 | Patch 5 | ||
|---|---|---|---|---|
| PRCC | p Value | PRCC | p Value | |
| 0.5133 | 0.00 | 0.4149 | 0.00 | |
| 0.2225 | 0.00 | 0.2911 | 0.00 | |
| −0.6562 | 0.00 | −0.6948 | 0.00 | |
| −0.1097 | 0.00 | −0.2305 | 0.00 | |
| −0.4969 | 0.00 | −0.4062 | 0.00 | |
| −0.1478 | 0.00 | −0.1980 | 0.00 | |
| 0.3595 | 0.00 | 0.3255 | 0.00 | |
| 0.0284 | 0.00 | 0.0614 | 0.00 | |
| Parameter | Patch 3 | Patch 5 | ||
|---|---|---|---|---|
| PRCC | p Value | PRCC | p Value | |
| c | −0.0072 | 0.47 | −0.0063 | 0.53 |
| 0.1201 | 0.00 | 0.1437 | 0.00 | |
| −0.0060 | 0.55 | −0.0074 | 0.46 | |
| time lag | 0.0179 | 0.07 | 0.0109 | 0.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, B.; Shaman, J. The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus. Int. J. Environ. Res. Public Health 2019, 16, 1890. https://doi.org/10.3390/ijerph16111890
Li X, Xu B, Shaman J. The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus. International Journal of Environmental Research and Public Health. 2019; 16(11):1890. https://doi.org/10.3390/ijerph16111890
Chicago/Turabian StyleLi, Xueying, Bing Xu, and Jeffrey Shaman. 2019. "The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus" International Journal of Environmental Research and Public Health 16, no. 11: 1890. https://doi.org/10.3390/ijerph16111890
APA StyleLi, X., Xu, B., & Shaman, J. (2019). The Impact of Environmental Transmission and Epidemiological Features on the Geographical Translocation of Highly Pathogenic Avian Influenza Virus. International Journal of Environmental Research and Public Health, 16(11), 1890. https://doi.org/10.3390/ijerph16111890




