Application of the Spline Interpolation in Simulating the Distribution of Phytoplankton in a Marine NPZD Type Ecosystem Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Marine Ecosystem Model
2.2. The Adjoint Model
2.3. Independent Points Scheme and Interpolation Methods
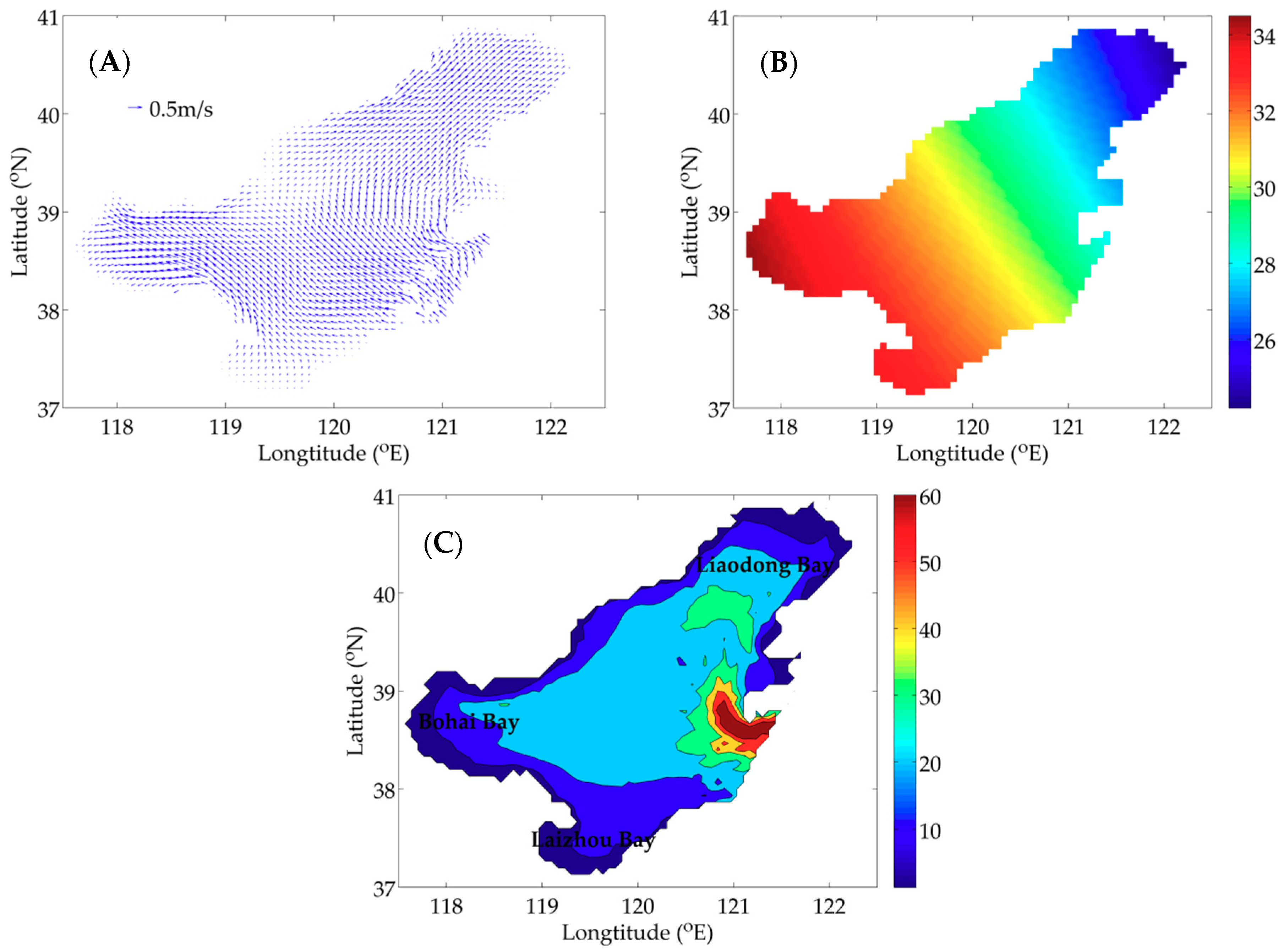
2.4. Data
3. Results
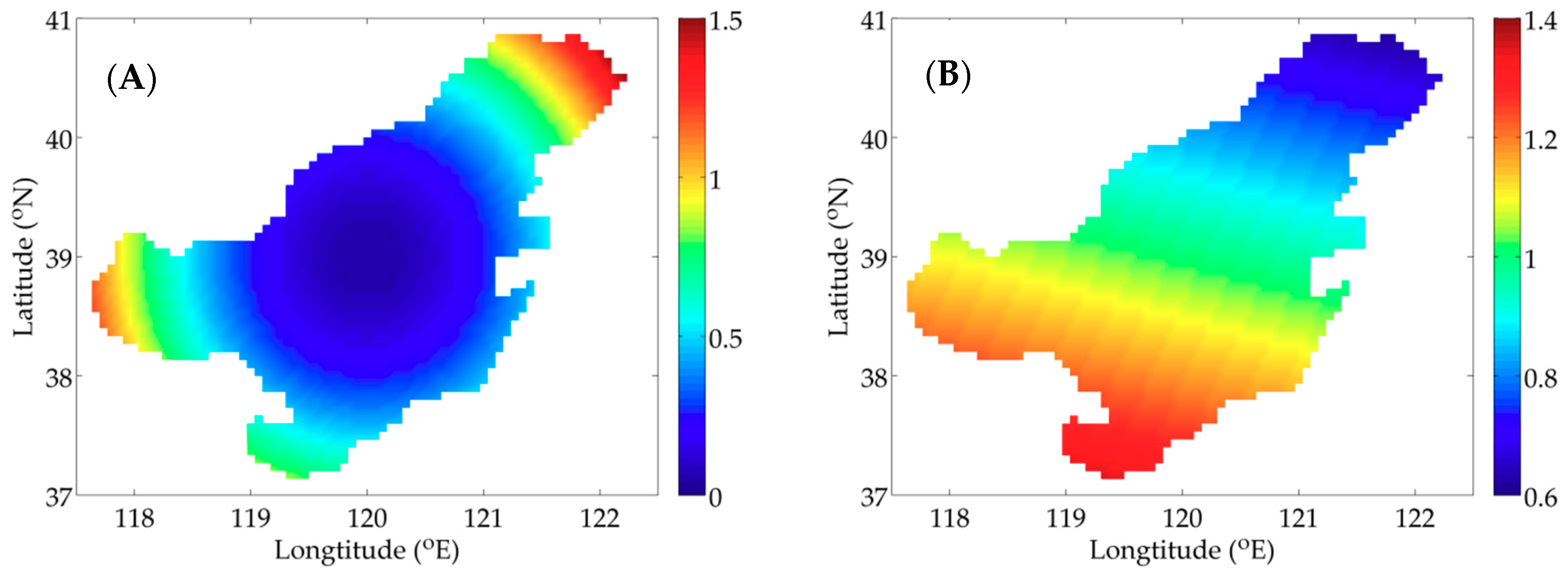
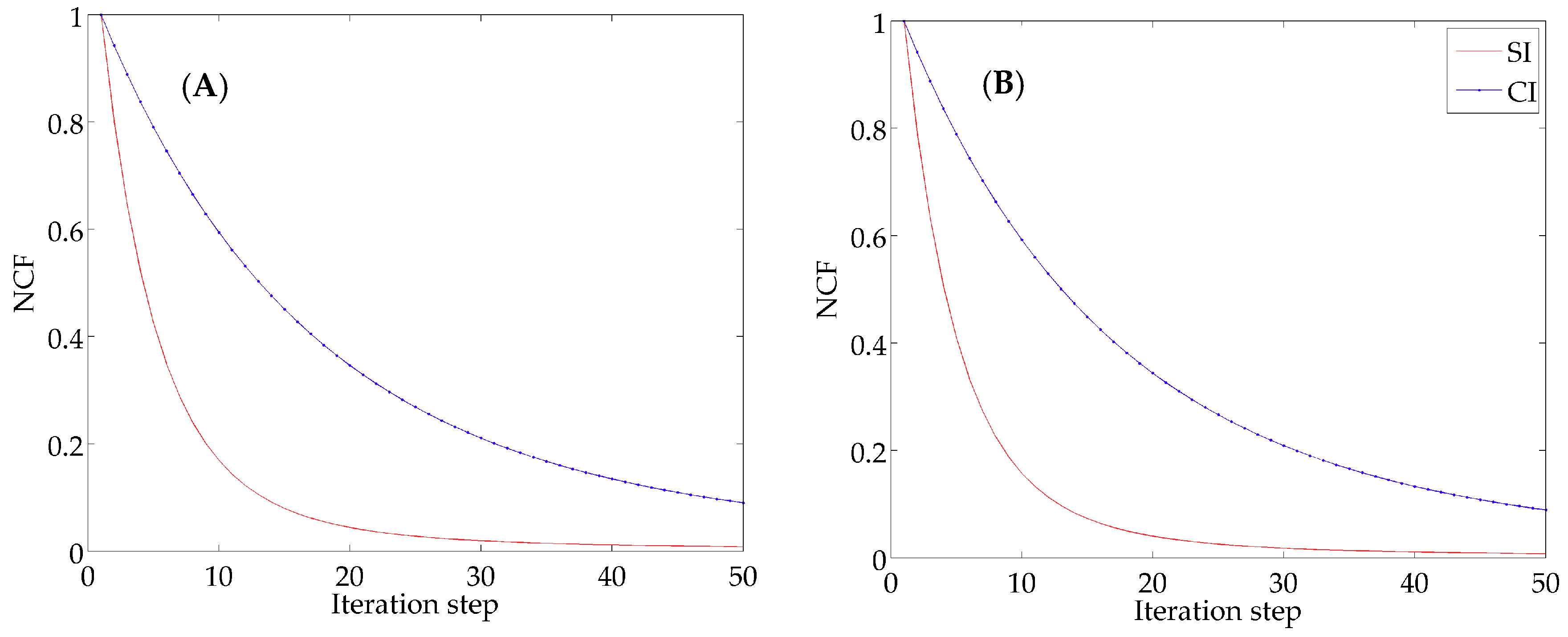
3.1. Idealized Twin Experiments
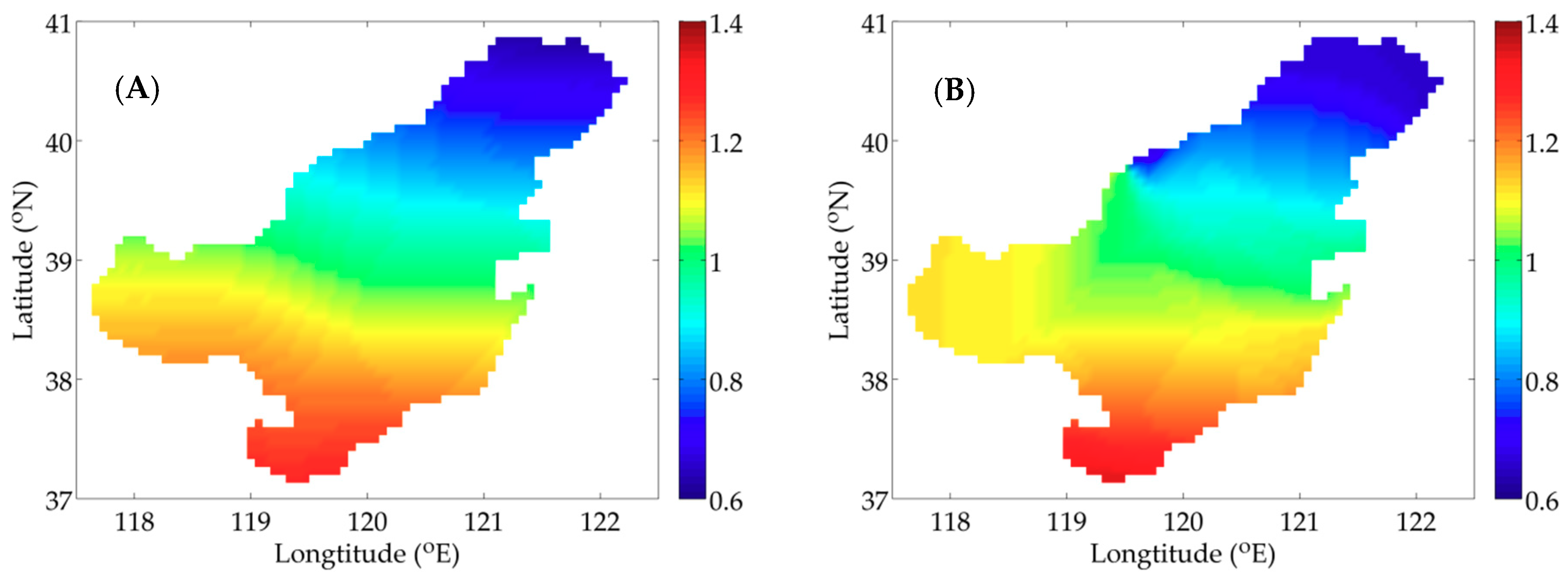
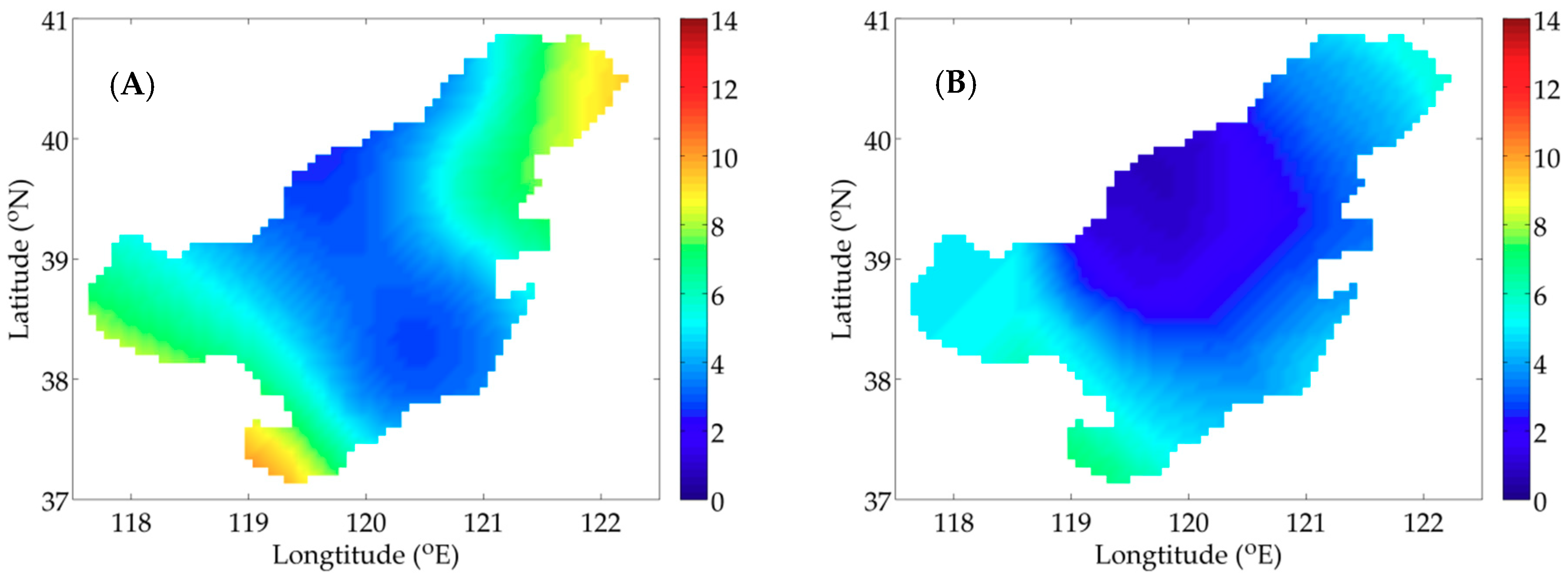
3.2. Practical Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The NPZD Model
Appendix B. The Adjoint Model
References
- Riley, G.A.; Stommel, H.; Bumpus, D.F. Quantitative ecology of plankton of Western North atlantic. Bull. Bingham Oceanogr. Collect. 1949, 12, 1–69. [Google Scholar]
- Moll, A.; Radach, G. Review of three-dimensional ecological modelling related to the North Sea shelf system: Part 1: Models and their results. Prog. Oceanogr. 2003, 57, 175–217. [Google Scholar] [CrossRef]
- Kishi, M.J.; Ikeda, S. Population dynamics of ‘red tide’ organisms in eutrophicated coastal waters—Numerical experiment of phytoplankton bloom in the East Seto Inland Sea, Japan. Ecol. Model. 1986, 31, 145–174. [Google Scholar] [CrossRef]
- Walsh, J.J.; Dieterle, D.A.; Meyers, M.B. A simulation analysis of the fate of phytoplankton within the Mid-Atlantic Bight. Cont. Shelf Res. 1988, 8, 757–787. [Google Scholar] [CrossRef][Green Version]
- Baretta, J.W.; Ebenhoh, W.; Ruardij, P. The European regional seas ecosystem model, a complex marine ecosystem model. Neth. J. Sea Res. 1995, 33, 233–246. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, H.D.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Gregg, W.W.; Ginoux, P.; Schopf, P.S.; Casey, N.W. Phytoplankton and iron: Validation of a global three-dimensional ocean biogeochemical model. Deep Sea Res. Part II 2003, 50, 3143–3169. [Google Scholar] [CrossRef]
- Kantha, L.H. A general ecosystem model for applications to primary productivity and carbon cycle studies in the global oceans. Ocean Model. 2004, 6, 285–334. [Google Scholar] [CrossRef]
- Franks, P.J.S. NPZ models of plankton dynamics: Their construction, coupling to physics, and application. J. Oceanogr. 2002, 58, 379–387. [Google Scholar] [CrossRef]
- Franks, P.J.S.; Chen, C.S. A 3-D prognostic numerical model study of the Georges Bank ecosystem. Part II: Biological-physical model. Deep Sea Res. Part II 2001, 48, 457–482. [Google Scholar] [CrossRef]
- Fan, W.; Lv, X.Q. Data assimilation in a simple marine ecosystem model based on spatial biological parameterizations. Ecol. Model. 2009, 220, 1997–2008. [Google Scholar] [CrossRef]
- Li, K.Q.; Zhang, L.; Li, Y.; Zhang, L.J.; Wang, X.L. A three-dimensional water quality model to evaluate the environmental capacity of nitrogen and phosphorus in Jiaozhou Bay, China. Mar. Pollut. Bull. 2015, 91, 306–316. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.L.; Li, K.Q.; Liang, S.K.; Lin, G.H.; Wang, X.L. A coastal three-dimensional water quality model of nitrogen in Jiaozhou Bay linking field experiments with modelling. Mar. Pollut. Bull. 2017, 114, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Lawson, L.M.; Hofmann, E.E.; Spitz, Y.H. Time series sampling and data assimilation in a simple marine ecosystem model. Deep Sea Res. Part II 1996, 43, 625–651. [Google Scholar] [CrossRef]
- Gunson, J.; Oschlies, A.; Garcon, V. Sensitivity of ecosystem parameters to simulated satellite ocean color data using a coupled physical-biological model of the North Atlantic. J. Mar. Res. 1999, 57, 613–639. [Google Scholar] [CrossRef][Green Version]
- Fennel, K.; Losch, M.; Schroter, J.; Wenzel, M. Testing a marine ecosystem model: Sensitivity analysis and parameter optimization. J. Mar. Syst. 2001, 28, 45–63. [Google Scholar] [CrossRef]
- Friedrichs, M.A.M. A data assimilative marine ecosystem model of the central equatorial Pacific: Numerical twin experiments. J. Mar. Res. 2001, 59, 859–894. [Google Scholar] [CrossRef]
- Zhao, L.; Wei, H.; Xu, Y.; Feng, S. An adjoint data assimilation approach for estimating parameters in a three-dimensional ecosystem model. Ecol. Model. 2005, 186, 234–249. [Google Scholar] [CrossRef]
- Zhang, L.; Constantinescu, E.M.; Sandu, A.; Tang, Y.; Chai, T.; Carmichael, G.R.; Byun, D.; Olaguer, E. An adjoint sensitivity analysis and 4D-Var data assimilation study of Texas air quality. Atmos. Environ. 2008, 42, 5787–5804. [Google Scholar] [CrossRef]
- Gao, X.M.; Wei, Z.X.; Lv, X.Q.; Wang, Y.G.; Fang, G.H. Numerical study of tidal dynamics in the South China Sea with adjoint method. Ocean Model. 2015, 92, 101–114. [Google Scholar] [CrossRef]
- Kuroda, H.; Kishi, M.J. A data assimilation technique applied to estimate parameters for the NEMURO marine ecosystem model. Ecol. Model. 2004, 172, 69–85. [Google Scholar] [CrossRef]
- Tjiputra, J.F.; Polzin, D.; Winguth, A.M.E. Assimilation of seasonal chlorophyll and nutrient data into an adjoint three-dimensional ocean carbon cycle model: Sensitivity analysis and ecosystem parameter optimization. Glob. Biogeochem. Cycles 2007, 21, GB1001. [Google Scholar] [CrossRef]
- Yaremchuk, M.; Martin, P.; Beattie, C. A hybrid approach to generating search subspaces in dynamically constrained 4-dimensional data assimilation. Ocean Model. 2017, 117, 41–51. [Google Scholar] [CrossRef]
- Li, X.N.; Xu, M.J.; Lv, X.Q.; Fu, K. A study of the transport of marine pollutants using adjoint method of data assimilation with method of characteristics. Adv. Math. Phys. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Bargaoui, Z.K.; Chebbi, A. Comparison of two kriging interpolation methods applied to spatiotemporal rainfall. J. Hydrol. 2009, 365, 56–73. [Google Scholar] [CrossRef]
- Erxleben, J.; Elder, K.; Davis, R.E. Comparison of spatial interpolation methods for estimating snow distribution in the Colorado Rocky Mountains. Hydrol. Process. 2002, 16, 3627–3649. [Google Scholar] [CrossRef]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. UK 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Orùs, R.; Hernández-Pajares, M.; Juan, J.M.; Sanz, J. Improvement of global ionospheric VTEC maps by using kriging interpolation technique. J. Atmos. Sol. Terr. Phys. 2005, 67, 1598–1609. [Google Scholar] [CrossRef]
- Xie, Y.F.; Chen, T.B.; Lei, M.; Yang, J.; Guo, Q.J.; Song, B.; Zhou, X.Y. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertain analysis. Chemosphere 2011, 82, 468–476. [Google Scholar] [CrossRef]
- Wang, C.H.; Li, X.Y.; Lv, X.Q. Nmerical study on initial field of pollution in the Bohai Sea with the adjoint method. Math. Probl. Eng. 2016, 4, 389–405. [Google Scholar]
- Liu, Y.Z.; Yu, J.; Shen, Y.L.; Lv, X.Q. A modified interpolation method for surface total nitrogen in the Bohai Sea. J. Atmos. Ocean. Technol. 2016, 33, 1509–1517. [Google Scholar] [CrossRef]
- Pan, H.D.; Guo, Z.; Lv, X.Q. Inversion of Tidal Open Boundary Conditions of the M2 Constituent in the Bohai and Yellow Seas. J. Atmos. Ocean. Technol. 2017, 34, 1661–1672. [Google Scholar] [CrossRef]
- Zong, X.L.; Xu, M.J.; Xu, J.L.; Lv, X.Q. Improvement of the ocean pollutant transport model by using the surface spline interpolation. Tellus Ser. A Dyn. Meteorol. Oceanogr. 2018, 70, 1–13. [Google Scholar] [CrossRef]
- Qi, P.; Wang, C.H.; Li, X.Y.; Lv, X.Q. Numerical study on spatially varying control parameters of a marine ecosystem dynamical model with the adjoint method. Acta. Oceanol. Sin. 2011, 30, 7–14. [Google Scholar] [CrossRef]
- Zhang, J.C.; Lu, X.Q.; Wang, P.; Wang, Y.P. Study on linear and nonlinear bottom friction parameterizations for regional tidal models using data assimilation. Cont. Shelf Res. 2011, 31, 555–573. [Google Scholar] [CrossRef]
- Zhang, J.C.; Wang, Y.P. A method for inversion of periodic open boundary conditions in two-dimensional tidal models. Comput. Methods Appl. Mech. Eng. 2014, 275, 20–38. [Google Scholar] [CrossRef]
- Guo, Z.; Pan, H.D.; Fan, W.; Lv, X.Q. Application of surface spline interpolation in version of bottom friction coefficients. J. Atmos. Ocean. Technol. 2017, 34, 2021–2028. [Google Scholar] [CrossRef]
- Li, Z.J.; Chao, Y.; McWilliams, J.C.; Ide, K. A three-dimensional variational data assimilation scheme for the Regional Ocean Modeling System: Implementation and basic experiments. J. Geophys. Res. 2008, 113, C05002. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Newcombe, S.K.; Black, A.F.; Kirby, N.E. The ABDMAP (Algal Bloom Detection, Monitoring and Prediction) concerted action. Int. J. Remote Sens. 2001, 22, 205–247. [Google Scholar] [CrossRef]
- Waston, W.G.; Nancy, W.C. Global and regional evaluation of the SeaWiFS chlorophyll data set. Remote Sens. Environ. 2004, 93, 463–479. [Google Scholar]
- Semovski, S.V.; Wozniak, B. Model of the annual phytoplankton cycle in the marine ecosystem-assimilation of monthly satellite chlorophyll data for the North Atlantic and Baltic. Oceanologia 1995, 37, 3–31. [Google Scholar]
- Redfield, A.C.; Ketchum, B.H.; Richards, F.A. The influence of organisms on the composition of sea-water. Sea Ideas Obs. Prog. Study Seas 1963, 2, 26–77. [Google Scholar]



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Maximum growth rate of phytoplankton | Vm | 1.0 | day−1 |
| Maximum grazing rate of zooplankton | Gm | 0.5 | day−1 |
| Mortality rate of phytoplankton | Dp | 0.1 | day−1 |
| Mortality rate of zooplankton | Dz | 0.2 | day−1 |
| Remineralization rate of detritus | e | 0.05 | day−1 |
| Temperature coefficient for phytoplankton growth at 10 °C | AQ10 | 2.08 | - |
| Temperature coefficient for zooplankton growth at 10 °C | BQ10 | 3.10 | - |
| Assimilation ratio of zooplankton | γ | 0.75 | - |
| Excretion ratio of zooplankton | θ | 0.03 | - |
| Attenuation coefficient of light | Kext | 1.0 | m−1 |
| Optimum irradiance | Io | 100 | W m−2 |
| Sinking velocity of phytoplankton | wp | 0.73 | m day−1 |
| Sinking velocity of detritus | wd | 1.00 | m day−1 |
| Half-saturation constant for nutrient uptake | Ks | 1.0 | mmol m−3 |
| Ivlev constant of zooplankton | f | 0.2 | m3(mmol N)−1 |
| Interpolation Method | NCF | MAE (mmol N m−3) | RMSE (mmol N m−3) | SC |
|---|---|---|---|---|
| SI | 8.3 × 10−3 | 0.050 | 0.190 | 0.84 |
| CI | 9.0 × 10−2 | 0.178 | 0.295 | 0.77 |
| Interpolation Method | NCF | MAE (mmol N m-3) | RMSE (mmol N m-3) | SC |
|---|---|---|---|---|
| SI | 7.8 × 10-3 | 0.034 | 0.096 | 0.88 |
| CI | 8.9 × 10-2 | 0.120 | 0.183 | 0.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zheng, Q.; Lv, X. Application of the Spline Interpolation in Simulating the Distribution of Phytoplankton in a Marine NPZD Type Ecosystem Model. Int. J. Environ. Res. Public Health 2019, 16, 2664. https://doi.org/10.3390/ijerph16152664
Li X, Zheng Q, Lv X. Application of the Spline Interpolation in Simulating the Distribution of Phytoplankton in a Marine NPZD Type Ecosystem Model. International Journal of Environmental Research and Public Health. 2019; 16(15):2664. https://doi.org/10.3390/ijerph16152664
Chicago/Turabian StyleLi, Xiaona, Quanxin Zheng, and Xianqing Lv. 2019. "Application of the Spline Interpolation in Simulating the Distribution of Phytoplankton in a Marine NPZD Type Ecosystem Model" International Journal of Environmental Research and Public Health 16, no. 15: 2664. https://doi.org/10.3390/ijerph16152664
APA StyleLi, X., Zheng, Q., & Lv, X. (2019). Application of the Spline Interpolation in Simulating the Distribution of Phytoplankton in a Marine NPZD Type Ecosystem Model. International Journal of Environmental Research and Public Health, 16(15), 2664. https://doi.org/10.3390/ijerph16152664




