Spatial Characteristics and Factor Analysis of Pollution Emission from Heavy-Duty Diesel Trucks in the Beijing–Tianjin–Hebei Region, China
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Acquisition and Management
3. Methods
3.1. Construction of Pollutant Emission Inventory for HDDTs
3.2. Spatial Autocorrelation Analysis
3.3. Regression Analysis
3.4. Geographical Detector Technique
4. Results
4.1. Spatial Distribution Characteristics of Pollutant Emissions from HDDTs in the BTH Region
4.1.1. Spatial Distribution Pattern of Pollutant Emissions from HDDTs in the BTH Region
4.1.2. Spatial Autocorrelation Characteristics of HDDT Emissions in the BTH Region
4.2. Analysis of Related Factors of HDDT Emissions in the BTH Region
4.2.1. Significances and Directions of Related Factors
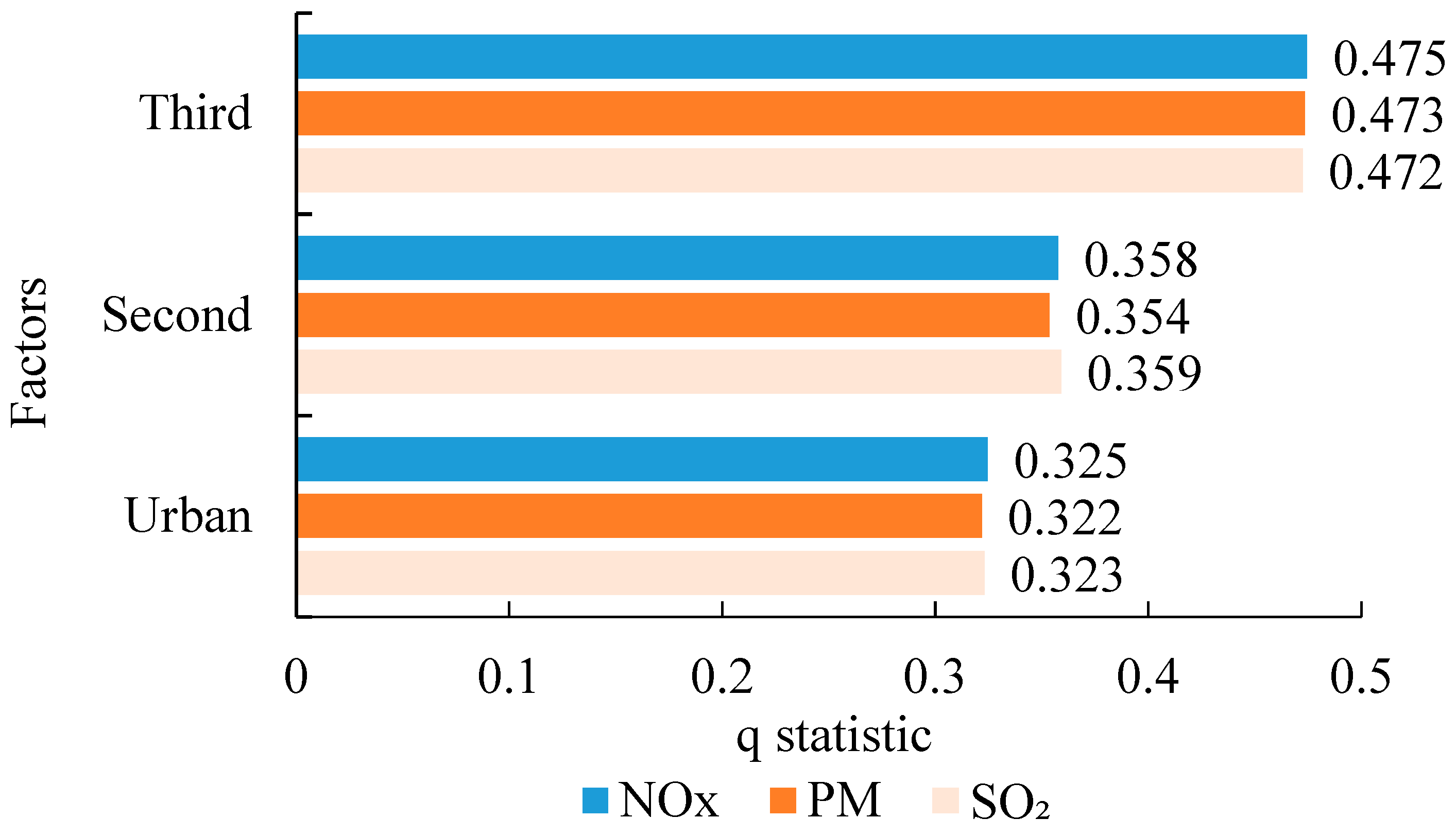
4.2.2. Strengths of Significant Related Factors
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, H.; Zhang, Q.; Shi, Y.; Wang, D. On-road remote sensing measurements and fuel-based motor vehicle emission inventory in Hangzhou, China. Atmos. Environ. 2007, 41, 3095–3107. [Google Scholar] [CrossRef]
- Xie, R.; Wei, D.; Han, F.; Lu, Y.; Fang, J.; Liu, Y.; Wang, J. The effect of traffic density on smog pollution: Evidence from Chinese cities. Technol. Forecast. Soc. Chang. 2019, 144, 421–427. [Google Scholar] [CrossRef]
- Tischer, V.; Fountas, G.; Polette, M.; Rye, T. Environmental and economic assessment of traffic-related air pollution using aggregate spatial information: A case study of Balneário Camboriú, Brazil. J. Transp. Health 2019, 14, 100592. [Google Scholar] [CrossRef]
- Lejri, D.; Can, A.; Schiper, N.; Leclercq, L. Accounting for traffic speed dynamics when calculating COPERT and PHEM pollutant emissions at the urban scale. Transp. Res. Part D Transp. Environ. 2018, 63, 588–603. [Google Scholar] [CrossRef] [Green Version]
- Kan, Z.; Tang, L.; Kwan, M.-P.; Zhang, X. Estimating vehicle fuel consumption and emissions using GPS big data. Int. J. Environ. Res. Public Health 2018, 15, 566. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Wu, Y.; Liu, H.; Wu, X.; Zhou, Y.; Yao, Z.; Fu, L.; He, K.; Hao, J. Historical evaluation of vehicle emission control in Guangzhou based on a multi-year emission inventory. Atmos. Environ. 2013, 76, 32–42. [Google Scholar] [CrossRef]
- Yang, X.F.; Liu, H.; Man, H.Y.; He, K.B. Characterization of road freight transportation and its impact on the national emission inventory in China. Atmos. Chem. Phys. 2015, 15, 2105–2118. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Huang, C.; Jing, Q.; Wang, H.; Pan, H.; Li, L.; Zhao, J.; Dai, Y.; Huang, H.; Schipper, L.; et al. On-road emission characteristics of heavy-duty diesel vehicles in Shanghai. Atmos. Environ. 2007, 41, 5334–5344. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, S.J.; Li, M.L.; Ge, Y.S.; Shu, J.W.; Zhou, Y.; Xu, Y.Y.; Hu, J.N.; Liu, H.; Fu, L.X.; et al. The challenge to NOx emission control for heavy-duty diesel vehicles in China. Atmos. Chem. Phys. 2012, 12, 9365–9379. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Niu, T.; Wu, Y.; Zhang, K.M.; Wallington, T.J.; Xie, Q.; Wu, X.; Xu, H. Fine-grained vehicle emission management using intelligent transportation system data. Environ Pollut. 2018, 241, 1027–1037. [Google Scholar] [CrossRef]
- Wang, X.; Westerdahl, D.; Wu, Y.; Pan, X.; Zhang, K.M. On-road emission factor distributions of individual diesel vehicles in and around Beijing, China. Atmos. Environ. 2011, 45, 503–513. [Google Scholar] [CrossRef]
- China’s State Council. 2018 China Motor Vehicle Environmental Management Annual Report. Available online: http://www.gov.cn/guoqing/2019-04/09/content_5380744.htm (accessed on 9 April 2019).
- Ministry of Ecology and Environment of the People’s Republic of China. Diesel Truck Pollution Control Battle Plan. Available online: http://www.mee.gov.cn/xxgk2018/xxgk/xxgk03/201901/W020190104656772362578.pdf (accessed on 4 January 2019). (In Chinese)
- Gong, M.; Yin, S.; Gu, X.; Xu, Y.; Jiang, N.; Zhang, R. Refined 2013-based vehicle emission inventory and its spatial and temporal characteristics in Zhengzhou, China. Sci. Total Environ. 2017, 599–600, 1149–1159. [Google Scholar] [CrossRef] [PubMed]
- Requia, W.J.; Dalumpines, R.; Adams, M.D.; Arain, A.; Ferguson, M.; Koutrakis, P. Modeling spatial patterns of link-based PM 2.5 emissions and subsequent human exposure in a large canadian metropolitan area. Atmos. Environ. 2017, 158, 172–180. [Google Scholar] [CrossRef]
- Sun, S.; Wei, J.; Gao, W. Vehicle emission trends and spatial distribution in Shandong province, China, from 2000 to 2014. Atmos. Environ. 2016, 147, 190–199. [Google Scholar] [CrossRef]
- Yang, W.; Yu, C.; Yuan, W.; Wu, X.; Zhang, W.; Wang, X. High-resolution vehicle emission inventory and emission control policy scenario analysis, a case in the Beijing-Tianjin-Hebei (BTH) region, China. J. Clean. Prod. 2018, 203, 530–539. [Google Scholar] [CrossRef]
- Liu, Y.H.; Ma, J.L.; Li, L.; Lin, X.F.; Xu, W.J.; Ding, H. A high temporal-spatial vehicle emission inventory based on detailed hourly traffic data in a medium-sized city of China. Environ. Pollut. 2018, 236, 324–333. [Google Scholar] [CrossRef]
- Song, X.; Hao, Y.; Zhang, C.; Peng, J.; Zhu, X. Vehicular emission trends in the Pan-Yangtze River Delta in China between 1999 and 2013. J. Clean. Prod. 2016, 137, 1045–1054. [Google Scholar] [CrossRef]
- Huo, H.; Zhang, Q.; He, K.; Yao, Z.; Wang, X.; Zheng, B.; Streets, D.G.; Wang, Q.; Ding, Y. Modeling vehicle emissions in different types of Chinese cities: Importance of vehicle fleet and local features. Environ. Pollut. 2011, 159, 2954–2960. [Google Scholar] [CrossRef]
- Conte, M.; Contini, D. Size-resolved particle emission factors of vehicular traffic derived from urban eddy covariance measurements. Environ. Pollut. 2019, 251, 830–838. [Google Scholar] [CrossRef]
- Réquia, W.J., Jr.; Koutrakis, P.; Roig, H.L. Spatial distribution of vehicle emission inventories in the Federal District, Brazil. Atmos. Environ. 2015, 112, 32–39. [Google Scholar] [CrossRef]
- Requia, W.J.; Roig, H.L.; Koutrakis, P.; Adams, M.D. Modeling spatial patterns of traffic emissions across 5,570 municipal districts in Brazil. J. Clean. Prod. 2017, 148, 845–853. [Google Scholar] [CrossRef]
- Sun, D.J.; Zhang, K.; Shen, S. Analyzing spatiotemporal traffic line source emissions based on massive didi online car-hailing service data. Transp. Res. Part D Transp. Environ. 2018, 62, 699–714. [Google Scholar] [CrossRef]
- Requia, W.J.; Koutrakis, P.; Roig, H.L.; Adams, M.D.; Santos, C.M. Association between vehicular emissions and cardiorespiratory disease risk in Brazil and its variation by spatial clustering of socio-economic factors. Environ. Res. 2016, 150, 452–460. [Google Scholar] [CrossRef] [PubMed]
- Tuia, D.; de Eicker, M.O.; Zah, R.; Osses, M.; Zarate, E.; Clappier, A. Evaluation of a simplified top-down model for the spatial assessment of hot traffic emissions in mid-sized cities. Atmos. Environ. 2007, 41, 3658–3671. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhang, S.; Wu, Y.; Li, Z.; Zhou, Y.; Fu, L.; Hao, J. Real-world emissions and fuel consumption of diesel buses and trucks in Macao: From on-road measurement to policy implications. Atmos. Environ. 2015, 120, 393–403. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, M.; Zhang, B. The effects of urbanization on PM2.5 concentrations in China’s Yangtze River Economic Belt: New evidence from spatial econometric analysis. J. Clean. Prod. 2019, 239, 118065. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, J.; Wang, S. Examining the effects of socioeconomic development on fine particulate matter (PM2.5) in China’s cities using spatial regression and the geographical detector technique. Sci. Total Environ. 2018, 619, 436–445. [Google Scholar] [CrossRef]
- Dong, K.; Hochman, G.; Kong, X.; Sun, R.; Wang, Z. Spatial econometric analysis of China’s PM10 pollution and its influential factors: Evidence from the provincial level. Ecol. Indic. 2019, 96, 317–328. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Liu, Y.; Yang, R. The spatial characteristics and formation mechanisms of county level urbanization in China. Acta Geogr. Sin. 2012, 67, 1011–1020. [Google Scholar]
- Chen, L.; Shi, M.; Li, S.; Gao, S.; Zhang, H.; Sun, Y.; Mao, J.; Bai, Z.; Wang, Z.; Zhou, J. Quantifying public health benefits of environmental strategy of PM2.5 air quality management in Beijing–Tianjin–Hebei region, China. J. Environ. Sci. 2017, 57, 33–40. [Google Scholar] [CrossRef] [PubMed]
- National Road Freight Vehicle Supervision and Service Platform. Available online: https://www.gghypt.net/ (accessed on 30 June 2018).
- Cheng, S.; Zhang, B.; Peng, P.; Yang, Z.; Lu, F. Spatiotemporal evolution pattern detection for heavy-duty diesel truck emissions using trajectory mining: A case study of Tianjin, China. J. Clean. Prod. 2020, 244, 118654. [Google Scholar] [CrossRef]
- Cheng, S.; Lu, F.; Peng, P.; Wu, S. A spatiotemporal multi-view-based learning method for short-term traffic forecasting. ISPRS Int. J. Geo Inf. 2018, 7, 218. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Lu, F.; Peng, P.; Wu, S. Short-term traffic forecasting: An adaptive ST-KNN model that considers spatial heterogeneity. Comput. Environ. Urban 2018, 71, 186–198. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment of the People’s Republic of China. Technical Guide for the Preparation of Air Pollutant Emission Inventory of Road Vehicles. Available online: http://www.mee.gov.cn/gkml/hbb/bgg/201501/W020150107594587831090.pdf (accessed on 31 December 2014). (In Chinese)
- Beijing Regional Statistical Yearbook. 2018. Available online: http://tjj.beijing.gov.cn/nj/qxnj/2018/zk/indexch.htm (accessed on 15 February 2019).
- Tianjin Statistical Yearbook. 2018. Available online: http://61.181.81.253/nianjian/2018nj/zk/indexch.htm (accessed on 13 February 2019).
- Hebei Economic Yearbook. 2018. Available online: http://tjj.hebei.gov.cn/res/nj2018/zk/indexch.htm (accessed on 1 February 2019).
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Anselin, L. Lagrange multiplier test diagnostics for spatial dependence and spatial heterogeneity. Geogr. Anal. 1988, 20, 1–17. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.D. The spatial-temporal hierarchy of regional inequality of China. Appl. Geogr. 2010, 30, 303–316. [Google Scholar] [CrossRef]
- Cheng, S.; Lu, F.; Peng, P.; Wu, S. Multi-task and multi-view learning based on particle swarm optimization for short-term traffic forecasting. Knowl. Based Syst. 2019, 180, 116–132. [Google Scholar] [CrossRef]
- Patton, A.P.; Perkins, J.; Zamore, W.; Levy, J.I.; Brugge, D.; Durant, J.L. Spatial and temporal differences in traffic-related air pollution in three urban neighborhoods near an interstate highway. Atmos. Environ. 2014, 99, 309–321. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Zhou, W.; Li, W.; Li, L. Impact of urbanization level on urban air quality: A case of fine particles (PM2.5) in Chinese cities. Environ. Pollut. 2014, 194, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Marshall, J.; Sander, H.; Manson, S. Air pollution and urban form: Evidence from satellite data. In Proceedings of the 5th WSEAS International Conference on Environment, Ecosystem and Development, Tenerife, Spain, 14–16 December 2017; pp. 477–479. [Google Scholar]
- Xie, W.; Deng, H.; Chong, Z. The spatial and heterogeneity impacts of population urbanization on fine particulate (PM2.5) in the Yangtze River Economic Belt, China. Int. J. Environ. Res. Public Health 2019, 16, 1058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donateo, A.; Conte, M.; Grasso, F.M.; Contini, D. Seasonal and diurnal behaviour of size segregated particles fluxes in a suburban area. Atmos. Environ. 2019, 219, 117052. [Google Scholar] [CrossRef]




| Time | Longitude | Latitude | Vehicle ID | Speed (km/h) | Tonnage (t) | Emission Standards |
|---|---|---|---|---|---|---|
| 15 April 2018 00:01:29 | 114.793419 | 37.773788 | 101203 | 67.24 | 31.0 | Euro IV |
| 15 April 2018 00:01:44 | 118.388985 | 39.673519 | 102576 | 44.37 | 24.8 | Euro III |
| 15 April 2018 00:01:59 | 117.524101 | 35.917999 | 257364 | 59.82 | 20.5 | Euro V |
| 15 April 2018 00:02:39 | 114.101501 | 36.595001 | 432576 | 87.83 | 15.9 | Euro IV |
| … | … | … | … | … | … | … |
| Explanatory Variable | Abbreviation | Symbol Predictions | Minimum | Maximum | Mean | SD | Moran’s I |
|---|---|---|---|---|---|---|---|
| Per capital GDP (ten thousand) | GDP | + | 1.22 | 32.14 | 5.00 | 0.29 | 0.45 *** |
| Population density (people/km2) | People | + | 41.77 | 41,967 | 1986.92 | 355.76 | 0.53 *** |
| Urbanization rate (%) | Urban | + | 15.78 | 100.00 | 57.63 | 1.49 | 0.43 *** |
| Proportion of secondary industries (%) | Second | + | 1.43 | 68.63 | 41.20 | 1.03 | 0.27 *** |
| Proportion of tertiary industries (%) | Third | − | 24.36 | 98.57 | 47.43 | 1.19 | 0.44 *** |
| Pollutant | Unit | Minimum | Maximum | Average | SD |
|---|---|---|---|---|---|
| NOX | kg/km2 | 0.0207 | 6.5042 | 1.1272 | 0.9096 |
| PM | g/km2 | 0.0625 | 20.3228 | 3.4235 | 2.7907 |
| SO2 | kg/km2 | 0.0014 | 0.4396 | 0.0774 | 0.0619 |
| Independent Variables | Classification 1 | Classification 2 | Classification 3 | Classification 4 | Classification 5 |
|---|---|---|---|---|---|
| lnGDP | ≤0.8 | 0.8–1.2 | 1.2–1.7 | 1.7–2.4 | 2.4–3.5 |
| lnpeople | ≤5.0 | 5.0–6.0 | 6.0–7.0 | 7.0–8.3 | 8.3–10.7 |
| lnurban | ≤3.5 | 3.5–3.8 | 3.8–4.0 | 4.0–4.3 | 4.3–4.7 |
| lnsecond | ≤2.2 | 2.2–3.2 | 3.2–3.6 | 3.6–3.9 | 3.9–4.3 |
| lnthird | ≤3.3 | 3.3–3.4 | 3.4–3.5 | 3.5–3.6 | 3.6–3.9 |
| Pollutant | Moran’s I | Z Score | p-Value |
|---|---|---|---|
| NOX | 0.2808 | 6.6048 | <0.01 |
| PM | 0.2775 | 6.5398 | <0.01 |
| SO2 | 0.2851 | 6.6985 | <0.01 |
| Pollutant | Variable | OLS | SLM | SEM |
|---|---|---|---|---|
| CONSTANT | 4.5533 * | 29.7975 *** | 35.952 *** | |
| lnGDP | 0.0983 | 0.0957 | 0.1650 | |
| lnpeople | 0.0002 | 0.0354 | −0.1931* | |
| NOX | lnurban | 1.2703 *** | 1.4544 *** | 1.8731 *** |
| lnsecond | 1.1472 *** | 0.9339 *** | 0.8451 *** | |
| lnthird | −8.7645 *** | −9.1260 *** | −9.4088 ** | |
| Wln NOX | 0.3916 *** | |||
| CONSTANT | 28.3899 *** | 26.4641 *** | 30.3236 *** | |
| lnGDP | 0.0986 | 0.0955 | 0.1683 | |
| lnpeople | 0.0021 | 0.0368 | −0.1918 * | |
| PM | lnurban | 1.3109 *** | 1.4835 *** | 1.8983 *** |
| lnsecond | 1.1390 *** | 0.9292 *** | 0.8392 *** | |
| lnthird | −8.8786 *** | −9.2130 *** | −9.4854 *** | |
| W ln PM | 0.3924 *** | |||
| CONSTANT | 37.9129 *** | 32.0907 *** | 39.9361 *** | |
| lnGDP | 0.1058 | 0.1013 | 0.1705 | |
| lnpeople | −0.0010 | 0.0341 | −0.1933 * | |
| SO2 | lnurban | 1.2540 *** | 1.4376 *** | 1.8598 *** |
| lnsecond | 1.1369 *** | 0.9254 *** | 0.8360 *** | |
| lnthird | −8.6586 *** | −9.0186 *** | −9.3125 *** | |
| W ln SO2 | 0.3913 *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Wu, S.; Cheng, S.; Lu, F.; Peng, P. Spatial Characteristics and Factor Analysis of Pollution Emission from Heavy-Duty Diesel Trucks in the Beijing–Tianjin–Hebei Region, China. Int. J. Environ. Res. Public Health 2019, 16, 4973. https://doi.org/10.3390/ijerph16244973
Zhang B, Wu S, Cheng S, Lu F, Peng P. Spatial Characteristics and Factor Analysis of Pollution Emission from Heavy-Duty Diesel Trucks in the Beijing–Tianjin–Hebei Region, China. International Journal of Environmental Research and Public Health. 2019; 16(24):4973. https://doi.org/10.3390/ijerph16244973
Chicago/Turabian StyleZhang, Beibei, Sheng Wu, Shifen Cheng, Feng Lu, and Peng Peng. 2019. "Spatial Characteristics and Factor Analysis of Pollution Emission from Heavy-Duty Diesel Trucks in the Beijing–Tianjin–Hebei Region, China" International Journal of Environmental Research and Public Health 16, no. 24: 4973. https://doi.org/10.3390/ijerph16244973
APA StyleZhang, B., Wu, S., Cheng, S., Lu, F., & Peng, P. (2019). Spatial Characteristics and Factor Analysis of Pollution Emission from Heavy-Duty Diesel Trucks in the Beijing–Tianjin–Hebei Region, China. International Journal of Environmental Research and Public Health, 16(24), 4973. https://doi.org/10.3390/ijerph16244973







