Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Materials
2.2. Methodology
2.2.1. Processing Geospatial Data
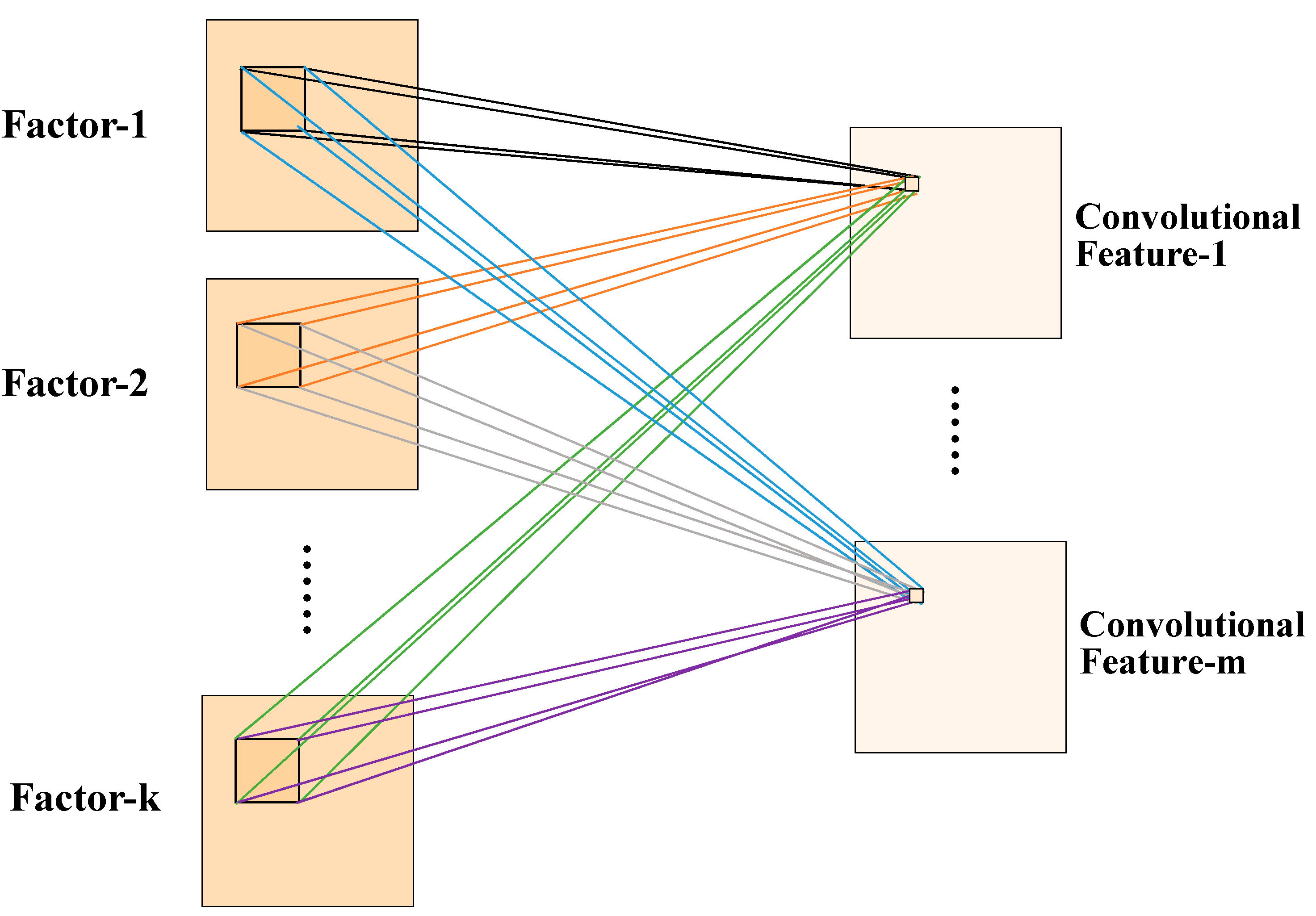
2.2.2. A Developed Deep Convolutional Neural Network Model
3. Results
3.1. Integrated Spatial Influencing Feature
3.2. Single Spatial Influencing Feature
3.3. Comparation with the GWR Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geng, J.; Wang, H.; Fan, J.; Ma, X. Deep supervised and contractive neural network for SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2442–2459. [Google Scholar] [CrossRef]
- Van, D.A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global estimates of fine particulate matter using a combined geophysical-statistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar]
- Center for International Earth Science Information Network—CIESIN—Columbia University. Gridded Population of the World, Version 4 (gpwv4): Population Density Adjusted to Match 2015 Revision UN WPP Country Totals; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2016. [Google Scholar]
- Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-temporal variation of PM2.5 concentrations and their relationship with geographic and socioeconomic factors in China. Int. J. Environ. Res. Public Health 2013, 11, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Alain, G.; Bengio, Y. Understanding intermediate layers using linear classifier probes. arXiv, 2016; arXiv:1610.01644. [Google Scholar]
- Ward, S.; Bond, P. The Earth Observation Handbook; European Space Agency: Paris, France, 2008; Volume 1315. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley: Hoboken, NJ, USA, 1993; pp. 321–323. [Google Scholar]
- Haining, R. Spatial Data Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Anselin, L. Local indicators of spatial association—Lisa. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Boots, B. Local measures of spatial association. Écoscience 2002, 9, 168–176. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Anselin, L. Spatial econometric: Methods and models. J. Am. Stat. Assoc. 1990, 85, 160. [Google Scholar]
- Anselin, L.; Bera, A.K.; Florax, R.; Yoon, M.J. Simple diagnostic tests for spatial dependence. Reg. Sci. Urban Econ. 1996, 26, 77–104. [Google Scholar] [CrossRef]
- Gschlößl, S. Hierarchical Bayesian Spatial Regression Models with Applications to Non-Life Insurance. Ph.D. Thesis, Technische Universität München, München, Germany, 2006. [Google Scholar]
- Feuillet, T.; Commenges, H.; Menai, M.; Salze, P.; Perchoux, C.; Reuillon, R.; Kesse-Guyot, E.; Enaux, C.; Nazare, J.-A.; Hercberg, S. A massive geographically weighted regression model of walking-environment relationships. J. Transp. Geogr. 2018, 68, 118–129. [Google Scholar] [CrossRef]
- Sampson, P.D.; Guttorp, P. Nonparametric estimation of nonstationary spatial covariance structure. J. Am. Stat. Assoc. 1992, 87, 108–119. [Google Scholar] [CrossRef]
- Duarte-Cunha, M.; Almeida, A.S.d.; Cunha, G.M.d.; Souza-Santos, R. Geographic weighted regression: Applicability to epidemiological studies of leprosy. Rev. Soc. Bras. Med. Trop. 2016, 49, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Fischer, E.; Pahan, D.; Chowdhury, S.; Richardus, J. The spatial distribution of leprosy cases during 15 years of a leprosy control program in Bangladesh: An observational study. BMC Infect. Dis. 2008, 8, 126. [Google Scholar] [CrossRef]
- Lesage, J.P. A Family of Geographically Weighted Regression Models; Springer: Berlin/Heidelberg, Germany, 2004; pp. 241–264. [Google Scholar]
- Zheng, Y.; Liu, F.; Hsieh, H.P. U-air: When urban air quality inference meets big data. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 1436–1444. [Google Scholar]
- Yan, L.; Zhou, M.; Wu, Y.; Yan, L. Long short term memory model for analysis and forecast of PM2.5. In Proceedings of the International Conference on Cloud Computing and Security, Haikou, China, 8–10 June 2018; Springer: Berlin/Heidelberg, Germany, 2004; pp. 623–634. [Google Scholar]
- Suleiman, A.; Tight, M.; Quinn, A. Applying machine learning methods in managing urban concentrations of traffic-related particulate matter (PM10 and PM2.5). Atmos. Pollut. Res. 2019, 10, 134–144. [Google Scholar] [CrossRef]
- Hsieh, H.P.; Lin, S.D.; Zheng, Y. Inferring air quality for station location recommendation based on urban big data. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 437–446. [Google Scholar]
- He, Q.; Geng, F.; Li, C. Long-term variation of satellite-based PM2.5 and influence factors over east China. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef]
- Hajiloo, F.; Hamzeh, S.; Gheysari, M. Impact assessment of meteorological and environmental parameters on PM2.5 concentrations using remote sensing data and GWR analysis (case study of Tehran). Environ. Sci. Pollut. Res. 2018, 1–15. [Google Scholar]
- Yang, D.; Wang, X.; Xu, J.; Xu, C.; Lu, D.; Ye, C.; Wang, Z.; Bai, L. Quantifying the influence of natural and socioeconomic factors and their interactive impact on PM2.5 pollution in China. Environ. Pollut. 2018, 241, 475–483. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems, Doha, Qatar, 12–15 November 2012; pp. 1097–1105. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 142–158. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Ni, L.; Zhang, T.; Wang, Q. Deep learning based feature selection for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2321–2325. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, L.; Zhao, J.; Gu, J.; Zhao, J. Discriminant deep belief network for high-resolution SAR image classification. Pattern Recognit. 2017, 61, 686–701. [Google Scholar] [CrossRef]
- Liang, H.; Li, Q. Hyperspectral imagery classification using sparse representations of convolutional neural network features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef]
- Nogueira, K.; Penatti, O.A.B.; Santos, J.A.D. Towards better exploiting convolutional neural networks for remote sensing scene classification. Pattern Recognit. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D. Dense semantic labeling of subdecimeter resolution images with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, PP, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Du, K.; Deng, Y.; Wang, R.; Zhao, T.; Li, N. Sar atr based on displacement- and rotation-insensitive CNN. Remote Sens. Lett. 2016, 7, 895–904. [Google Scholar] [CrossRef]



| Spatial Correlation Parameter, n | Training Accuracy | Validation Accuracy |
|---|---|---|
| 1 | 67.94% | 80.17% |
| 2 | 77.71% | 82.37% |
| 3 | 88.08% | 86.11% |
| 4 | 92.01% | 90.50% |
| 5 | 94.51% | 91.83% |
| 6 | 96.53% | 92.14% |
| 7 | 97.35% | 92.90% |
| 8 | 98.30% | 92.46% |
| 9 | 98.71% | 93.29% |
| 10 | 98.87% | 92.40% |
| 11 | 99.29% | 93.28% |
| 12 | 99.53% | 93.25% |
| 96,337 Pixels | Original Annual Concentration () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <10 | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 | >100 | ||
| Estimated annual concentration () | <10 | 18,395 | 337 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10~20 | 112 | 11,792 | 70 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 20~30 | 2 | 83 | 21,891 | 86 | 12 | 1 | 0 | 2 | 0 | 0 | 0 | |
| 30~40 | 0 | 3 | 101 | 10,804 | 89 | 3 | 0 | 0 | 0 | 0 | 0 | |
| 40~50 | 0 | 6 | 18 | 115 | 13,971 | 60 | 5 | 0 | 0 | 0 | 0 | |
| 50~60 | 0 | 0 | 1 | 5 | 62 | 4103 | 57 | 4 | 0 | 0 | 0 | |
| 60~70 | 0 | 0 | 0 | 0 | 0 | 49 | 3650 | 62 | 0 | 0 | 0 | |
| 70~80 | 0 | 0 | 2 | 0 | 0 | 1 | 142 | 3598 | 159 | 0 | 0 | |
| 80~90 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 296 | 4563 | 60 | 0 | |
| 90~100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 38 | 1332 | 7 | |
| >100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3 | 166 | |
| Accuracy | 99.38% | 96.49% | 99.13% | 98.10% | 98.85% | 97.27% | 94.36% | 90.81% | 95.84% | 95.48% | 95.95% | |
| 96,337 Pixels | Original Annual Concentrations ( ) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <10 | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 | >100 | ||
| Estimated annual concentration () | <10 | 17,974 | 535 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10~20 | 161 | 11,775 | 135 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 20~30 | 3 | 129 | 21,622 | 129 | 20 | 0 | 1 | 6 | 0 | 0 | 0 | |
| 30~40 | 1 | 3 | 177 | 10,869 | 128 | 4 | 1 | 1 | 2 | 0 | 0 | |
| 40~50 | 1 | 1 | 27 | 181 | 13,991 | 90 | 8 | 1 | 8 | 0 | 0 | |
| 50~60 | 0 | 0 | 2 | 3 | 81 | 4099 | 93 | 3 | 1 | 0 | 0 | |
| 60~70 | 0 | 0 | 4 | 1 | 5 | 75 | 3491 | 75 | 1 | 1 | 0 | |
| 70~80 | 0 | 0 | 1 | 0 | 1 | 1 | 181 | 3395 | 193 | 1 | 0 | |
| 80~90 | 0 | 0 | 1 | 0 | 2 | 0 | 17 | 462 | 4445 | 108 | 0 | |
| 90~100 | 0 | 0 | 0 | 0 | 5 | 0 | 5 | 4 | 101 | 1290 | 40 | |
| >100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 158 | |
| Accuracy | 99.08% | 94.63% | 98.42% | 97.17% | 98.30% | 96.02% | 91.94% | 86.01% | 93.56% | 91.88% | 79.80% | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Jin, M.; Li, H. Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model. Int. J. Environ. Res. Public Health 2019, 16, 454. https://doi.org/10.3390/ijerph16030454
Li J, Jin M, Li H. Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model. International Journal of Environmental Research and Public Health. 2019; 16(3):454. https://doi.org/10.3390/ijerph16030454
Chicago/Turabian StyleLi, Junming, Meijun Jin, and Honglin Li. 2019. "Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model" International Journal of Environmental Research and Public Health 16, no. 3: 454. https://doi.org/10.3390/ijerph16030454
APA StyleLi, J., Jin, M., & Li, H. (2019). Exploring Spatial Influence of Remotely Sensed PM2.5 Concentration Using a Developed Deep Convolutional Neural Network Model. International Journal of Environmental Research and Public Health, 16(3), 454. https://doi.org/10.3390/ijerph16030454





