Eutrophication Assessment Based on the Cloud Matter Element Model
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Cloud-Matter Element (CME) Model
2.3. Eutrophication Assessment with CME Model
- Determine the m eutrophication evaluation indicators and n classification levels, and the scopes of each evaluation indicator classified as certain eutrophication level.
- 2.
- Calculate parameter groups (i = 1, 2, …, m, j = 1, 2, …, n) of cloud model by Equations (4)–(6), and shown in Table 3, which are in accordance with the eutrophication classification of five indicators presented in Table 2. The parameters Smin and Smax are boundary values of the indicators corresponding to a certain eutrophication level, obtained from Table 2. Since the upper boundaries of Chl-a, CODMn, TP, and TN for level VI, as well as upper boundary of SD for level I are not available, non-linear regression analysis was performed with the assumption of upper boundary values increases with the level. The results obtained for upper boundary were 255.36 mg/m3, 28.71 mg/L, 731.07 mg/m3, 7770 mg/m3, and 18.68 m for Chl-a, CODMn, TP, TN, and SD, respectively.
- 3.
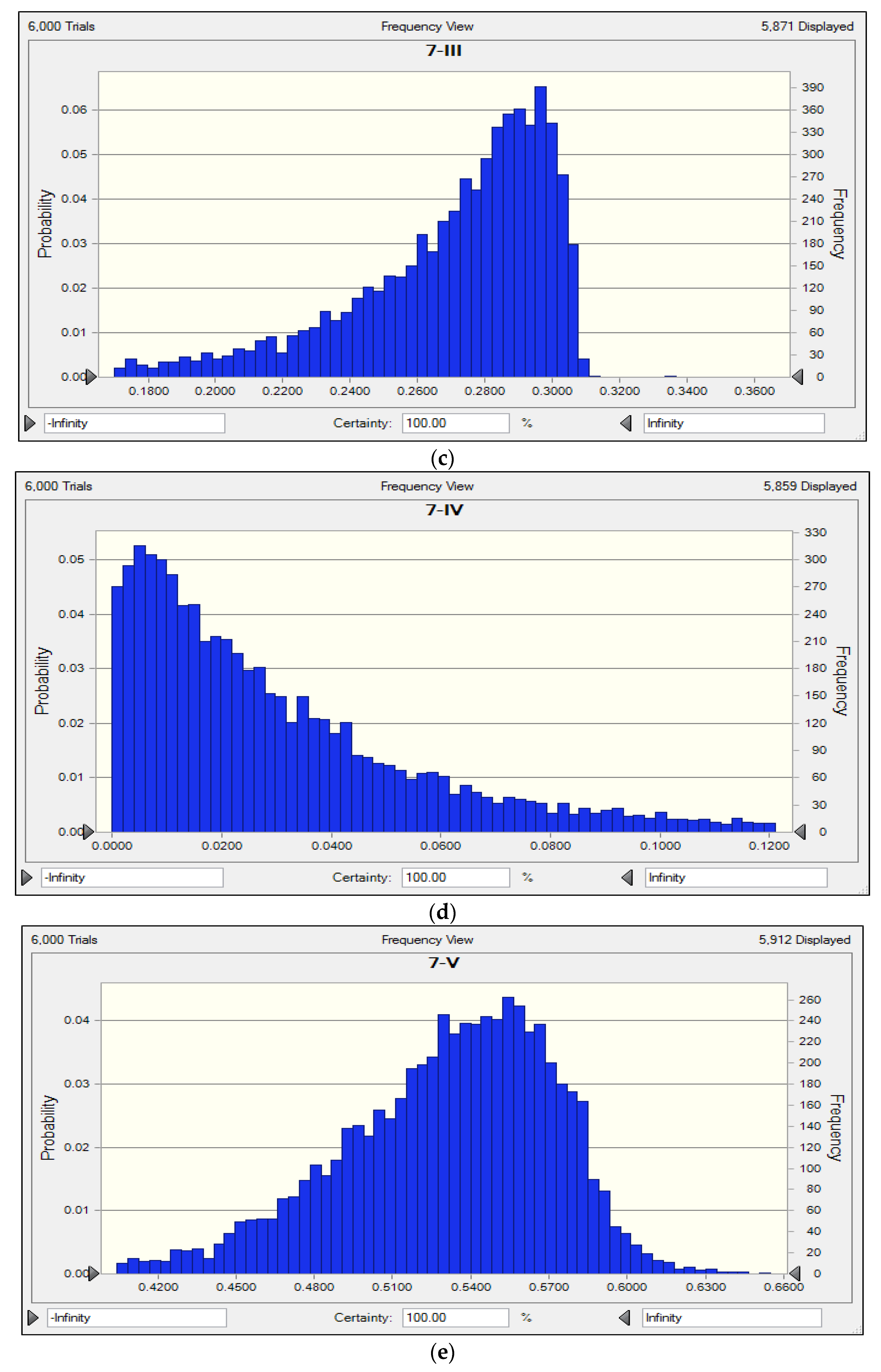
- Establish CME matrix with consideration of m evaluation factors belonging to certain eutrophication level. Generate the normal random number with the expectation value of and standard deviation of . Therefore, the CME model can be expressed by Equation (7) as follows:where is the CME matrix of the kth evaluated object and is the membership degree with distribution parameters of the ith indicator to the jth level for the kth evaluated object calculated by Equation (3) [30,31]. Substitute the eigenvector value into cloud models repeatedly to obtain the distributions of certainty degree and final outcomes corresponding to all classifications.
- 4.
- Repeat above steps N times to get N certainty degrees in CME model.
- 5.
- Calculate weights of indicators by combined weight method.
- 6.
- Calculate neartude of evaluated lakes/reservoirs to certain eutrophication level.
3. Results and Discussions
3.1. Eutrophication Evaluation Results
3.2. Comparison with Other Methods
- (1)
- The results of CME model were consistent with other methods, which verify the validity of the CME model. For example, for Bosten Lake (S3), Ci Lake (S8), Chao Lake (S10), Dianchi Lake (Outer sea) (S11), Dianchi Lake (Cao Sea) (S12), Mogu Lake (S15), Li Lake (S16), Dongshan Lake (S17), Moshui Lake (S18), Liwan Lake (S19), Liuhua Lake (S20), Xuanwu Lake (S21), Jingpo Lake (S22), Nan Lake (S23), and Qionghai Lake (S24), the results of CME model are consistent with the results of all the other evaluation methods. For Yuqiao reservoir (S5), Gucheng Lake (S6), and Nansi Lake (S7), Dali Lake (S9), and West Lake (S13), the results of the CME model are consistent with the results of most of other evaluation methods.
- 2)
- In addition, the CME model makes up the limitations of other evaluation methods.
- 1)
- The comprehensive index (CI) method can evaluate eutrophication status comprehensively with consideration of all evaluated indicators. Since the tropical level index (TLI) for CODMn, TP, TN, and SD have close relationships to concentrations of Chl-a, if Chl-a concentration is abnormal by external effects, the evaluation results are inaccurate, which is the limitation of CI method. The results of Dianshan Lake (S4), Yuqiao reservoir (S5), Gucheng Lake (S6), West Lake (S13), and Gantang Lake (S14) obtained by the CI method and the CME model are different. For Dianshan Lake (S4), Yuqiao reservoir (S5), West Lake (S13), and Gantang Lake (S14), the eutrophication levels obtained by the CI method are IV, IV, V, and V, respectively, while the eutrophication levels obtained by the CME model are V, V, VI, and VI, respectively. As such, for most lakes, the eutrophication levels obtained by the CI method are lower than eutrophication levels obtained by the CME model, which proved that the CI method is more conservative than the CME model.
- 2)
- Models of matter element (ME), fuzzy matter element (FME), and cloud matter element (CME) take the eutrophication evaluation process as multi-criteria decision-making process and reflect the impact of all indicators comprehensively and objectively [6].
- (3)
- Through calculation of neartudes, the eutrophication levels of lakes/reservoirs can be determined more directly. For example, the eutrophication indicators are in different eutrophication levels for Yuqiao Reservoir (S5), i.e., eutrophication levels V, IV, III, V, and IV for Chl-a, CODMn, TP, TN, and SD, respectively. Through the neartude calculation of the CME model, the neartudes of S5 corresponding to each eutrophication level are 0.0000, 0.0000, 0.0311, 0.3604, 0.6022, and 0.0064 for I, II, III, IV, V, and VI, respectively. Therefore, according to the principle of maximum neartude, the eutrophication levels of S5 were level V.
- (4)
- The CME model can judge the eutrophication trend of different lakes and reservoirs with the same eutrophication level. Taking Gantang Lake (S14) and Mogu Lake (S15) as examples, the neartudes of S14 were to level V and VI were 0.3760 and 0.6239, while the neartudes of S15 were to level V and VI were 0.2513 and 0.7486. The levels of both lakes were level VI, however, the eutrophication trend of S15 was more obvious than S14, which is similar to other research results [35]. For the other methods, it is difficult to judge eutrophication degree of different waters with the same eutrophication level.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Evaluated Objects | Methods | Certainty Degree/Neartude to Levels | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |||
| Dianchi Lake (Cao Sea) (S1) | ME model | −0.58 | −0.53 | −0.14 | 0.19 | −0.42 | −0.73 | |
| FME model | 0.00 | 0.01 | 0.53 | 0.41 | 0.25 | 0.22 | ||
| CME model | Mean | 0.00 | 0.00 | 0.50 | 0.45 | 0.05 | 0.00 | |
| S.D. | 0.00 | 0.00 | 0.02 | 0.04 | 0.04 | 0.00 | ||
| Liwan Lake (S2) | ME model | −0.57 | −0.49 | −0.10 | −0.16 | −0.46 | −0.74 | |
| FME model | 0.00 | 0.01 | 0.58 | 0.28 | 0.21 | 0.21 | ||
| CME model | Mean | 0.00 | 0.31 | 0.43 | 0.24 | 0.01 | 0.00 | |
| S.D. | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | ||
| Liwan Lake (S3) | ME model | −0.60 | −0.57 | −0.40 | −0.03 | −0.06 | −0.60 | |
| FME model | 0.00 | 0.00 | 0.17 | 0.45 | 0.44 | 0.25 | ||
| CME model | Mean | 0.00 | 0.00 | 0.04 | 0.06 | 0.04 | 0.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S4) | ME model | −0.60 | −0.57 | −0.23 | −0.15 | −0.39 | −0.49 | |
| FME model | 0.00 | 0.01 | 0.39 | 0.40 | 0.54 | 0.26 | ||
| CME model | Mean | 0.00 | 0.00 | 0.31 | 0.33 | 0.36 | 0.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | ||
| Liwan Lake (S5) | ME model | −0.61 | −0.58 | −0.45 | −0.21 | 0.12 | −0.53 | |
| FME model | 0.00 | 0.00 | 0.16 | 0.32 | 0.54 | 0.25 | ||
| CME model | Mean | 0.00 | 0.00 | 0.03 | 0.36 | 0.60 | 0.01 | |
| S.D. | 0.00 | 0.00 | 0.03 | 0.03 | 0.01 | 0.00 | ||
| Liwan Lake (S6) | ME model | −0.61 | −0.59 | −0.43 | −0.15 | −0.44 | −0.58 | |
| FME model | 0.00 | 0.00 | 0.10 | 0.48 | 0.33 | 0.42 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.53 | 0.13 | 0.35 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | 0.00 | ||
| Liwan Lake (S7) | ME model | −0.61 | −0.59 | −0.41 | −0.38 | −0.28 | −0.32 | |
| FME model | 0.00 | 0.00 | 0.23 | 0.14 | 0.54 | 0.41 | ||
| CME model | Mean | 0.00 | 0.00 | 0.27 | 0.03 | 0.53 | 0.17 | |
| S.D. | 0.00 | 0.00 | 0.03 | 0.03 | 0.04 | 0.04 | ||
| Liwan Lake (S8) | ME model | −0.61 | −0.60 | −0.53 | −0.36 | 0.01 | −0.20 | |
| FME model | 0.00 | 0.00 | 0.05 | 0.06 | 0.77 | 0.30 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.06 | 0.94 | 0.01 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.02 | 0.02 | 0.00 | ||
| Liwan Lake (S9) | ME model | −0.65 | −0.62 | −0.55 | −0.24 | −0.24 | −0.22 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.31 | 0.51 | 0.44 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.31 | 0.49 | 0.21 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S10) | ME model | −0.62 | −0.61 | −0.55 | −0.41 | −0.14 | −0.56 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.06 | 0.53 | 0.46 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.07 | 0.59 | 0.35 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.02 | 0.02 | 0.01 | ||
| Liwan Lake (S11) | ME model | −0.62 | −0.61 | −0.57 | −0.47 | 0.16 | −0.21 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.91 | 0.40 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | 0.01 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Liwan Lake (S12) | ME model | −0.88 | −0.88 | −0.88 | −0.86 | −0.81 | −0.52 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.05 | 0.81 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S13) | ME model | −0.62 | −0.62 | −0.59 | −0.53 | −0.32 | 0.10 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.38 | 0.54 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.29 | 0.71 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.04 | ||
| Liwan Lake (S14) | ME model | −0.59 | −0.57 | −0.51 | −0.38 | 0.06 | −0.08 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.55 | 0.61 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | 0.62 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | ||
| Liwan Lake (S15) | ME model | −0.62 | −0.62 | −0.59 | −0.53 | −0.34 | 0.22 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.23 | 0.55 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.75 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S16) | ME model | −0.62 | −0.60 | −0.58 | −0.53 | −0.36 | 0.09 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.20 | 0.63 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.87 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | ||
| Liwan Lake (S17) | ME model | −0.68 | −0.68 | −0.67 | −0.64 | −0.55 | 0.05 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.06 | 0.84 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S18) | ME model | −0.77 | −0.77 | −0.76 | −0.75 | −0.68 | −0.26 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.03 | 0.81 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S19) | ME model | −0.67 | −0.66 | −0.65 | −0.62 | −0.52 | 0.11 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.08 | 0.80 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.0016 | ||
| Liwan Lake (S20) | ME model | −0.88 | −0.88 | −0.88 | −0.88 | −0.85 | −0.48 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.02 | 0.94 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Liwan Lake (S21) | ME model | −0.70 | −0.69 | −0.68 | −0.63 | −0.48 | 0.01 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.23 | 0.79 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.17 | 0.83 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Liwan Lake (S22) | ME model | −0.61 | −0.59 | −0.46 | −0.24 | −0.16 | −0.26 | |
| FME model | 0.00 | 0.00 | 0.11 | 0.24 | 0.65 | 0.32 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.30 | 0.55 | 0.15 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | ||
| Liwan Lake (S23) | ME model | −0.62 | −0.62 | −0.60 | −0.56 | −0.30 | −0.11 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.27 | 0.64 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.81 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Liwan Lake (S24) | ME model | −0.52 | −0.30 | −0.15 | −0.20 | −0.45 | −0.71 | |
| FME model | 0.04 | 0.28 | 0.59 | 0.15 | 0.29 | 0.23 | ||
| CME model | Mean | 0.30 | 0.01 | 0.44 | 0.11 | 0.15 | 0.00 | |
| S.D. | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | ||
Appendix B
| Evaluated Objects | Methods | Certainty Degree/Neartude to Levels | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |||
| Erhai Lake (S1) | Cloud model | 0.18 | 0.25 | 0.79 | 0.86 | 0.59 | 0.49 | |
| CME model | Mean | 0.00 | 0.00 | 0.50 | 0.45 | 0.05 | 0.00 | |
| S. D. | 0.00 | 0.00 | 0.02 | 0.04 | 0.04 | 0.00 | ||
| Gaoshan Lake (S2) | Cloud model | 0.21 | 0.50 | 0.77 | 0.87 | 0.65 | 0.48 | |
| CME model | Mean | 0.00 | 0.31 | 0.43 | 0.24 | 0.01 | 0.00 | |
| S. D. | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | ||
| Nansi Lake (S3) | Cloud model | 0.17 | 0.21 | 0.48 | 0.86 | 0.71 | 0.51 | |
| CME model | Mean | 0.00 | 0.00 | 0.04 | 0.06 | 0.04 | 0.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S4) | Cloud model | 0.16 | 0.35 | 0.66 | 0.85 | 0.86 | 0.51 | |
| CME model | Mean | 0.00 | 0.00 | 0.31 | 0.33 | 0.36 | 0.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | ||
| Nansi Lake (S5) | Cloud model | 0.16 | 0.18 | 0.31 | 0.70 | 0.82 | 0.52 | |
| CME model | Mean | 0.00 | 0.00 | 0.03 | 0.36 | 0.60 | 0.01 | |
| S. D. | 0.00 | 0.00 | 0.03 | 0.03 | 0.01 | 0.00 | ||
| Nansi Lake (S6) | Cloud model | 0.16 | 0.18 | 0.51 | 0.82 | 0.81 | 0.74 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.53 | 0.13 | 0.35 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | 0.00 | ||
| Nansi Lake (S7) | Cloud model | 0.16 | 0.26 | 0.47 | 0.57 | 0.68 | 0.69 | |
| CME model | Mean | 0.00 | 0.00 | 0.27 | 0.03 | 0.53 | 0.17 | |
| S. D. | 0.00 | 0.00 | 0.03 | 0.03 | 0.04 | 0.04 | ||
| Nansi Lake (S8) | Cloud model | 0.16 | 0.17 | 0.19 | 0.62 | 0.92 | 0.55 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.06 | 0.94 | 0.01 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.02 | 0.02 | 0.00 | ||
| Nansi Lake (S9) | Cloud model | 0.16 | 0.16 | 0.29 | 0.52 | 0.69 | 0.68 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.31 | 0.49 | 0.21 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S10) | Cloud model | 0.16 | 0.16 | 0.17 | 0.54 | 0.86 | 0.78 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.07 | 0.59 | 0.35 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.02 | 0.02 | 0.01 | ||
| Nansi Lake (S11) | Cloud model | 0.16 | 0.16 | 0.18 | 0.32 | 0.86 | 0.67 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | 0.01 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Nansi Lake (S12) | Cloud model | 0.16 | 0.16 | 0.16 | 0.18 | 0.20 | 1.00 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S13) | Cloud model | 0.16 | 0.16 | 0.17 | 0.21 | 0.54 | 0.83 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.29 | 0.71 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.04 | ||
| Nansi Lake (S14) | Cloud model | 0.16 | 0.16 | 0.17 | 0.29 | 0.70 | 0.81 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | 0.62 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | ||
| Nansi Lake (S15) | Cloud model | 0.16 | 0.16 | 0.18 | 0.21 | 0.48 | 0.78 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.75 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S16) | Cloud model | 0.16 | 0.16 | 0.17 | 0.21 | 0.32 | 0.90 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.87 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.03 | ||
| Nansi Lake (S17) | Cloud model | 0.16 | 0.16 | 0.16 | 0.18 | 0.21 | 0.98 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S18) | Cloud model | 0.15 | 0.16 | 0.16 | 0.17 | 0.19 | 0.99 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S19) | Cloud model | 0.16 | 0.16 | 0.17 | 0.19 | 0.22 | 0.96 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S20) | Cloud model | 0.15 | 0.16 | 0.16 | 0.17 | 0.18 | 1.00 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| Nansi Lake (S21) | Cloud model | 0.16 | 0.16 | 0.17 | 0.22 | 0.25 | 0.94 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.17 | 0.83 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Nansi Lake (S22) | Cloud model | 0.16 | 0.19 | 0.44 | 0.66 | 0.73 | 0.57 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.30 | 0.55 | 0.15 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | ||
| Nansi Lake (S23) | Cloud model | 0.15 | 0.16 | 0.16 | 0.22 | 0.42 | 0.93 | |
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.81 | |
| S. D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | ||
| Nansi Lake (S24) | Cloud model | 0.41 | 0.49 | 0.73 | 0.59 | 0.59 | 0.49 | |
| CME model | Mean | 0.30 | 0.01 | 0.44 | 0.11 | 0.15 | 0.00 | |
| S. D. | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.00 | ||
References
- Li, F.X. Application of triangle relational degree model for evaluation of lake eutrophication. Adv. Mater. Res. 2012, 518–523, 1113–1116. [Google Scholar] [CrossRef]
- Primpas, I.; Tsirtsis, G.; Karydis, M.; Kokkoris, G.D. Principal component analysis: Development of a multivariate index for assessing eutrophication according to the European water framework directive. Ecol. Indic. 2010, 10, 178–183. [Google Scholar] [CrossRef]
- Zhang, X.P.; Chen, W.G.; Xu, W.J. The Application of fuzzy variable sets theory in Eutrophication evaluation for urban lake. Adv. Mater. Res. 2012, 446–449, 2667–2672. [Google Scholar] [CrossRef]
- Deng, X.; Xu, Y.; Han, L.; Yu, Z.; Yang, M.; Pan, G. Assessment of river health based on an improved entropy-based fuzzy matter-element model in the Taihu Plain, China. Ecol. Indic. 2015, 57, 85–95. [Google Scholar] [CrossRef]
- He, Y.X.; Dai, A.Y.; Zhu, J.; He, H.Y.; Li, F. Risk assessment of urban network planning in china based on the matter-element model and extension analysis. Int. J. Electr. Power Energy Syst. 2011, 33, 775–782. [Google Scholar] [CrossRef]
- Liu, D.; Zou, Z. Water quality evaluation based on improved fuzzy matter-element method. J. Environ. Sci. 2012, 24, 1210–1216. [Google Scholar] [CrossRef]
- Wang, G.Z.; Ren, L.L.; Wang, B.; Yu, Z. Lake eutrophication evaluation model based on projection pursuit method. Water Resour. Prot. 2009, 25, 13–18. (In Chinese) [Google Scholar]
- Han, H.G.; Chen, Q.L.; Qiao, J.F. An efficient self-organizing RBF neural network for water quality prediction. Neural Netw. 2011, 24, 717–725. [Google Scholar] [CrossRef]
- García-Nieto, P.J.; García-Gonzalo, E.; Fernández, J.A.; Muñiz, C.D. Predictive modelling of eutrophication in the Pozon de la Dolores lake (Northern Spain) by using an evolutionary support vector machines approach. J. Math. Biol. 2017, 76, 817–840. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Hörmann, G.; Huang, J.; Fohrer, N.; Zhang, L. Combining multivariate statistical techniques and random forests model to assess and diagnose the trophic status of Poyang Lake in China. Ecol. Indic. 2017, 83, 74–83. [Google Scholar] [CrossRef]
- Peng, L.; Lu, F.C.; Li, N.Y.; Huang, H.P.; Xie, Q. Study on fault diagnosis for power transformer based on cloud matter element analysis principle and DGA. In Proceedings of the IEEE 9th International Conference on Properties and Applications of Dielectric Materials, Harbin, China, 19–23 July 2009. [Google Scholar]
- Men, B.H.; Yang, X.G.; Dong, X.M. Application of matter element model in water eutrophication evaluation of lake and reservoir. Water Resour. Hydropower Northeast 2002, 9, 42–44. (In Chinese) [Google Scholar]
- Yan, H.; Wu, D.; Huang, Y.; Wang, G.; Shang, M.; Xu, J.; Zhao, Y. Water eutrophication assessment based on rough set and multidimensional cloud model. Chemom. Intell. Lab. Syst. 2017, 164, 103–112. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Hörmann, G. Dynamic water quality evaluation based on fuzzy matter-element model and functional data analysis, a case study in Poyang Lake. Environ. Sci. Pollut. Res. Int. 2017, 24, 19138–19148. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Xu, C.; Li, D. Generic normal cloud model. Inf. Sci. 2014, 280, 1–15. [Google Scholar] [CrossRef]
- Wang, J.Q.; Peng, L.; Zhang, H.Y.; Chen, X.H. Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information. Inf. Sci. 2014, 274, 177–191. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, W. Comprehensive Eutrophication assessment based on fuzzy matter element model and Monte Carlo-triangular fuzzy numbers approach. Int. J. Environ. Res. Public Health 2019, 16, 1769. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Ou, C.; Li, Q.; Zhang, X.; Zhang, C.; Zhu, D. Fuzzy synthetic evaluation of soil nutrients in cultivated land based on cloud model in Da’an City, Jilin Province. Trans. Chin. Soc. Agric. Mach. 2018, 49, 251–257. (In Chinese) [Google Scholar]
- Jia, C.Y.; Bai, T.; Shan, X.Y.; Cui, F.J.; Xu, S.J. Cloud neutral fuzzy PID hybrid integrated algorithm of flatness control. J. Iron Steel Res. Int. 2014, 21, 559–564. [Google Scholar] [CrossRef]
- Li, D. Membership clouds and membership cloud generators. Comput. Res. Dev. 1995, 32, 15–20. [Google Scholar]
- Li, F.X.; Lu, M.; Yi, S.J. Eutrophication evaluation of lake based on cloud model. Adv. Mater. Res. 2014, 955, 1653–1656. [Google Scholar] [CrossRef]
- Shu, J. Assessment of eutrophication in main lakes of China. Oceanol. Limnol. Sin. 1993, 24, 616–620. (In Chinese) [Google Scholar]
- Lu, H.; Ren, L.; Chen, Y.; Tian, P.; Liu, J. A cloud model based multi-attribute decision making approach for selection and evaluation of groundwater management schemes. J. Hydrol. 2017, 555, 881–893. [Google Scholar] [CrossRef]
- Wang, S.; Li, D.; Shi, W.; Li, D.; Wang, X. Cloud model-based spatial data mining. Geogr. Inf. Sci. 2003, 9, 60–70. [Google Scholar] [CrossRef]
- Qin, K.; Xu, K.; Liu, F.; Li, D. Image segmentation based on histogram analysis utilizing the cloud model. Comput. Math. Appl. 2011, 62, 2824–2833. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Liu, S.; Zhang, W.; Wang, L.; Wang, J. General multidimensional cloud model and its application on spatial clustering in Zhanjiang, Guangdong. J. Geogr. Sci. 2010, 20, 787–798. [Google Scholar] [CrossRef]
- Liu, D.; Wang, D.; Wu, J.; Wang, Y.; Wang, L.; Zou, X.; Chen, X. A risk assessment method based on RBF artificial neural network—Cloud model for urban water hazard. J. Intell. Fuzzy Syst. 2014, 27, 2409–2416. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Meng, Y. Prediction of rock burst classification using the technique of cloud models with attribution weight. Nat. Hazards 2013, 68, 549–568. [Google Scholar] [CrossRef]
- Cheng, K.; Fu, Q.; Meng, J.; Li, T.X.; Pei, W. Analysis of the spatial variation and identification of factors affecting the water resources carrying capacity based on the cloud model. Water Resour. Manag. 2018, 32, 2767–2781. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.; Ding, H.; Singh, V.P.; Wang, Y.; Zeng, X.; Wu, J.; Wang, L. A cloud model-based approach for water quality assessment. Environ. Res. 2016, 148, 24–35. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Y. Evaluation model of fracture hazard of concrete dam based on cloud matter element. Water Resour. Power 2017, 35, 71. (In Chinese) [Google Scholar]
- Liu, C.; Shen, Z.Z.; Gan, L.; Xiong, S.F.; Lu, J. Comprehensive evaluation of rehabilitation degree of dangerous reservoir based on fuzzy gray clustering and combination weighting method. Adv. Sci. Technol. Water Resour. 2018, 38, 36–41. (In Chinese) [Google Scholar]
- Wong, H.; Hu, B.Q. Application of improved extension evaluation method to water quality evaluation. J. Hydrol. 2014, 509, 539–548. [Google Scholar] [CrossRef]
- Monte Carlo Simulation in Crystal Ball 7.3. Available online: https://medarbejdere.au.dk/fileadmin/www.asb.dk/servicekatalog/IT/Analysevaerktoejer/Crystal_Ball/Crystal_Ball_7.3_UK.pdf (accessed on 30 October 2019).
- Wang, D.; Zeng, D.; Singh, V.P.; Xu, P.; Liu, D.; Wang, Y.; Wang, L. A multi-dimension cloud model-based approach for water quality assessment. Environ. Res. 2016, 149, 113–121. [Google Scholar] [CrossRef] [PubMed]






| Cases | Names | Location (Province/City) | Chl-a (mg/m3) | CODMn (mg/L) | TP (mg/m3) | TN (mg/m3) | SD (m) |
|---|---|---|---|---|---|---|---|
| S1 | Erhai Lake | Yunnan | 4.33 | 3.38 | 21 | 180 | 2.40 |
| S2 | Gaozhou Reservoir | Guangdong | 1.49 | 1.47 | 46 | 358 | 1.72 |
| S3 | Bosten Lake | Xinjiang | 4.91 | 5.42 | 50 | 969 | 1.46 |
| S4 | Dianshan Lake | Shanghai | 3.00 | 2.87 | 29 | 1086 | 0.67 |
| S5 | Yuqiao Reservoir | Tianjin | 16.20 | 5.16 | 26 | 1020 | 1.16 |
| S6 | Gucheng Lake | Jiangsu | 4.99 | 2.75 | 52 | 2374 | 0.28 |
| S7 | Nansi Lake | Shandong | 3.77 | 6.96 | 194 | 3201 | 0.44 |
| S8 | Ci Lake | Hubei | 15.38 | 4.4 | 87 | 1540 | 0.65 |
| S9 | Dali Lake | Inner Mongolia | 7.24 | 16.25 | 153 | 1671 | 0.48 |
| S10 | Chao Lake | Anhui | 14.56 | 4.34 | 140 | 2270 | 0.27 |
| S11 | Dianchi Lake (Outer sea) | Yunnan | 44.43 | 7.11 | 108 | 1309 | 0.49 |
| S12 | Dianchi Lake (Cao Sea) | Yunnan | 298.86 | 16.58 | 931 | 15,273 | 0.23 |
| S13 | West Lake | Zhejiang | 95.94 | 10.18 | 136 | 2230 | 0.37 |
| S14 | Gantang Lake | Jiangxi | 77.70 | 6.96 | 135 | 2140 | 0.36 |
| S15 | Mogu Lake | Xinjiang | 82.40 | 14.60 | 332 | 2660 | 0.49 |
| S16 | Li Lake | Guangdong | 119.51 | 9.92 | 372 | 3038 | 0.34 |
| S17 | Dongshan Lake | Guangdong | 185.10 | 14.80 | 670 | 7200 | 0.26 |
| S18 | Moshui Lake | Hubei | 262.40 | 13.60 | 500 | 16,050 | 0.15 |
| S19 | Liwan Lake | Guangdong | 162.92 | 14.46 | 743 | 7337 | 0.31 |
| S20 | Liuhua Lake | Guangdong | 323.51 | 25.26 | 643 | 6777 | 0.15 |
| S21 | Xuanwu Lake | Jiangsu | 202.10 | 8.86 | 708 | 6790 | 0.31 |
| S22 | Jingpo Lake | Jilin | 4.96 | 5.96 | 316 | 1270 | 0.73 |
| S23 | Nan Lake | Jilin | 120.60 | 8.22 | 228 | 2630 | 0.22 |
| S24 | Qionghai Lake | Sichuan | 0.88 | 1.43 | 130 | 410 | 2.98 |
| Rank | Chl-a (mg/m3) | CODMn (mg/L) | TP (mg/m3) | TN (mg/m3) | SD (m) |
|---|---|---|---|---|---|
| I | ≤0.5 | ≤0.15 | ≤1 | ≤20 | ≥10 |
| II | ≤1 | ≤0.4 | ≤4 | ≤50 | ≥5 |
| III | ≤4 | ≤2.0 | ≤25 | ≤300 | ≥1.5 |
| IV | ≤10 | ≤4.0 | ≤50 | ≤500 | ≥1.0 |
| V | ≤64 | ≤10.0 | ≤200 | ≤2000 | ≥0.4 |
| VI | >64 | >10 | >200 | >2000 | <0.4 |
| Rank | Chl-a (mg/m3) | CODMn (mg/L) | TP (mg/m3) | TN (mg/m3) | SD (m) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ex | En | He | Ex | En | He | Ex | En | He | Ex | En | He | Ex | En | He | |
| I | 0.50 | 0.17 | 0.02 | 0.08 | 0.03 | 0.00 | 1.25 | 0.42 | 0.04 | 15.00 | 5.00 | 0.50 | 14.34 | 1.45 | 0.14 |
| II | 1.50 | 0.17 | 0.02 | 0.28 | 0.07 | 0.01 | 3.75 | 0.42 | 0.04 | 40.00 | 3.33 | 0.33 | 7.50 | 0.83 | 0.08 |
| III | 3.00 | 0.33 | 0.03 | 1.20 | 0.33 | 0.03 | 15.00 | 3.33 | 0.33 | 175.00 | 41.67 | 4.17 | 3.25 | 0.58 | 0.06 |
| IV | 7.00 | 1.00 | 0.10 | 3.00 | 0.67 | 0.07 | 37.50 | 4.17 | 0.42 | 400.00 | 33.33 | 3.33 | 1.25 | 0.08 | 0.01 |
| V | 37.50 | 9.17 | 0.92 | 7.00 | 1.67 | 0.17 | 125.00 | 25.00 | 2.50 | 1250.00 | 250.00 | 25.00 | 0.70 | 0.10 | 0.01 |
| VI | 160.18 | 31.73 | 3.17 | 19.36 | 4.79 | 0.48 | 465.54 | 88.51 | 8.85 | 4885.00 | 961.67 | 96.17 | 0.20 | 0.07 | 0.01 |
| Indicators | Entropy | Entropy Weights | AHP Weights | Combined Weights |
|---|---|---|---|---|
| Chl-a | 3.185 | 0.151 | 0.460 | 0.309 |
| CODMn | 4.739 | 0.259 | 0.150 | 0.203 |
| TP | 3.826 | 0.196 | 0.090 | 0.142 |
| TN | 3.024 | 0.140 | 0.050 | 0.094 |
| SD | 4.661 | 0.254 | 0.250 | 0.252 |
| Cases | Neartude | Eutrophication Levels | |||||
|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | ||
| Erhai Lake (S1) | 0.00 | 0.00 | 0.50 | 0.45 | 0.05 | 0.00 | III |
| Gaoshan Lake (S2) | 0.00 | 0.31 | 0.43 | 0.24 | 0.02 | 0.00 | III |
| Bosten Lake (S3) | 0.00 | 0.00 | 0.06 | 0.57 | 0.37 | 0.01 | IV |
| Dianshan Lake (S4) | 0.00 | 0.00 | 0.31 | 0.33 | 0.36 | 0.00 | V |
| Yuqiao reservoir (S5) | 0.00 | 0.00 | 0.03 | 0.36 | 0.60 | 0.01 | V |
| Gucheng Lake (S6) | 0.00 | 0.00 | 0.00 | 0.53 | 0.13 | 0.35 | IV |
| Nansi Lake (S7) | 0.00 | 0.00 | 0.27 | 0.03 | 0.53 | 0.17 | V |
| Ci Lake (S8) | 0.00 | 0.00 | 0.00 | 0.06 | 0.94 | 0.01 | V |
| Dali Lake (S9) | 0.00 | 0.00 | 0.00 | 0.31 | 0.49 | 0.21 | V |
| Chao Lake (S10) | 0.00 | 0.00 | 0.00 | 0.07 | 0.59 | 0.35 | V |
| Dianchi Lake (Outer sea) (S11) | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | 0.01 | V |
| Dianchi Lake (Cao Sea) (S12) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | VI |
| West Lake (S13) | 0.00 | 0.00 | 0.00 | 0.00 | 0.29 | 0.71 | VI |
| Gantang Lake (S14) | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | 0.62 | VI |
| Mogu Lake (S15) | 0.00 | 0.00 | 0.00 | 0.00 | 0.25 | 0.75 | VI |
| Li Lake (S16) | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.87 | VI |
| Dongshan Lake (S17) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | VI |
| Moshui Lake (S18) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | VI |
| Liwan Lake (S19) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | VI |
| Liuhua Lake (S20) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | VI |
| Xuanwu Lake (S21) | 0.00 | 0.00 | 0.00 | 0.00 | 0.17 | 0.83 | VI |
| Jingpo Lake (S22) | 0.00 | 0.00 | 0.00 | 0.30 | 0.55 | 0.15 | V |
| Nan Lake (S23) | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.81 | VI |
| Qionghai Lake (S24) | 0.30 | 0.01 | 0.44 | 0.11 | 0.15 | 0.01 | III |
| Cases | Relevant Weighted Nutrition State Comprehensive Index Method | Matter Element (ME) Model | Fuzzy Matter Element (FME) Model | Cloud Model | Cloud Matter Element (CME) Model | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Chl-a | CODMn | TP | TN | SD | Comprehensive Index (CI) Method | |||||
| Erhai Lake (S1) | IV | III | III | III | III | III | IV | III | IV | III |
| Gaoshan Lake (S2) | III | II | IV | III | IV | III | IV | III | IV | III |
| Bosten Lake (S3) | IV | IV | IV | V | IV | IV | IV | IV | IV | IV |
| Dianshan Lake (S4) | III | III | III | V | V | IV | IV | V | V | V |
| Yuqiao reservoir (S5) | V | IV | III | V | IV | IV | V | V | V | V |
| Gucheng Lake (S6) | IV | III | IV | V | VI | V | IV | IV | IV | IV |
| Nansi Lake (S7) | III | V | V | VI | V | V | V | V | VI | V |
| Ci Lake (S8) | V | IV | V | V | V | V | V | V | V | V |
| Dali Lake (S9) | IV | VI | V | V | V | V | VI | V | V | V |
| Chao Lake (S10) | V | IV | V | V | VI | V | V | V | V | V |
| Dianchi Lake (Outer sea) (S11) | V | V | V | V | V | V | V | V | V | V |
| Dianchi Lake (Cao Sea) (S12) | VI | VI | VI | VI | VI | VI | VI | VI | VI | VI |
| West Lake (S13) | VI | V | V | V | VI | V | VI | VI | VI | VI |
| Gantang Lake (S14) | VI | V | V | V | VI | V | V | VI | VI | VI |
| Mogu Lake (S15) | VI | VI | VI | VI | V | VI | VI | VI | VI | VI |
| Li Lake (S16) | VI | V | VI | VI | VI | VI | VI | VI | VI | VI |
| Dongshan Lake (S17) | VI | VI | VI | VI | VI | VI | VI | VI | VI | VI |
| Moshui Lake (S18) | VI | VI | VI | VI | VI | VI | VI | VI | VI | VI |
| Liwan Lake (S19) | VI | VI | VI | VI | VI | VI | VI | VI | VI | VI |
| Liuhua Lake (S20) | VI | VI | VI | VI | VI | VI | VI | VI | VI | VI |
| Xuanwu Lake (S21) | VI | V | VI | VI | VI | VI | VI | VI | VI | VI |
| Jingpo Lake (S22) | IV | IV | VI | V | V | V | V | V | V | V |
| Nan Lake (S23) | VI | V | VI | VI | VI | VI | VI | VI | VI | VI |
| Qionghai Lake (S24) | III | II | V | III | III | III | III | III | III | III |
| Evaluated Objects | Methods | Certainty Degree/Neartude to Levels | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |||
| Dianchi Lake (Cao Sea) (S12) | ME model | −0.88 | −0.88 | −0.88 | −0.86 | −0.81 | −0.52 | |
| FME model | 0.00 | 0.00 | 0.03 | 0.00 | 0.05 | 0.81 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.0000 | ||
| Liwan Lake (S19) | ME model | −0.67 | −0.66 | −0.65 | −0.62 | −0.52 | 0.11 | |
| FME model | 0.00 | 0.00 | 0.04 | 0.00 | 0.08 | 0.80 | ||
| CME model | Mean | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.99 | |
| S.D. | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.0016 | ||
| Evaluated Objects | Methods | Certainty Degree/Neartude to Levels | Eutrophication Level | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | ||||
| Erhai Lake (S1) | Cloud model | 0.18 | 0.25 | 0.79 | 0.86 | 0.59 | 0.49 | IV | |
| CME model | Mean | 0.00 | 0.00 | 0.50 | 0.45 | 0.05 | 0.00 | III | |
| S. D. | 0.00 | 0.00 | 0.02 | 0.04 | 0.04 | 0.00 | |||
| Gaoshan Lake (S2) | Cloud model | 0.21 | 0.50 | 0.77 | 0.87 | 0.65 | 0.48 | IV | |
| CME model | Mean | 0.00 | 0.31 | 0.43 | 0.24 | 0.01 | 0.00 | III | |
| S. D. | 0.00 | 0.00 | 0.01 | 0.01 | 0.01 | 0.00 | |||
| Nansi Lake (S7) | Cloud model | 0.16 | 0.26 | 0.47 | 0.57 | 0.68 | 0.69 | VI | |
| CME model | Mean | 0.00 | 0.00 | 0.27 | 0.03 | 0.53 | 0.17 | V | |
| S. D. | 0.00 | 0.00 | 0.03 | 0.03 | 0.04 | 0.04 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, X.; Wu, Y. Eutrophication Assessment Based on the Cloud Matter Element Model. Int. J. Environ. Res. Public Health 2020, 17, 334. https://doi.org/10.3390/ijerph17010334
Wang Y, Zhang X, Wu Y. Eutrophication Assessment Based on the Cloud Matter Element Model. International Journal of Environmental Research and Public Health. 2020; 17(1):334. https://doi.org/10.3390/ijerph17010334
Chicago/Turabian StyleWang, Yumin, Xian’e Zhang, and Yifeng Wu. 2020. "Eutrophication Assessment Based on the Cloud Matter Element Model" International Journal of Environmental Research and Public Health 17, no. 1: 334. https://doi.org/10.3390/ijerph17010334
APA StyleWang, Y., Zhang, X., & Wu, Y. (2020). Eutrophication Assessment Based on the Cloud Matter Element Model. International Journal of Environmental Research and Public Health, 17(1), 334. https://doi.org/10.3390/ijerph17010334






