Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation
Abstract
:1. Introduction
2. Materials and Methods
- Three-dimensional finite element model of the eye and material models for ocular tissues
- Three-dimensional CFD turbulence model of the air puff impinging on the cornea
- Fluid–structure interaction (FSI) coupling between the two models
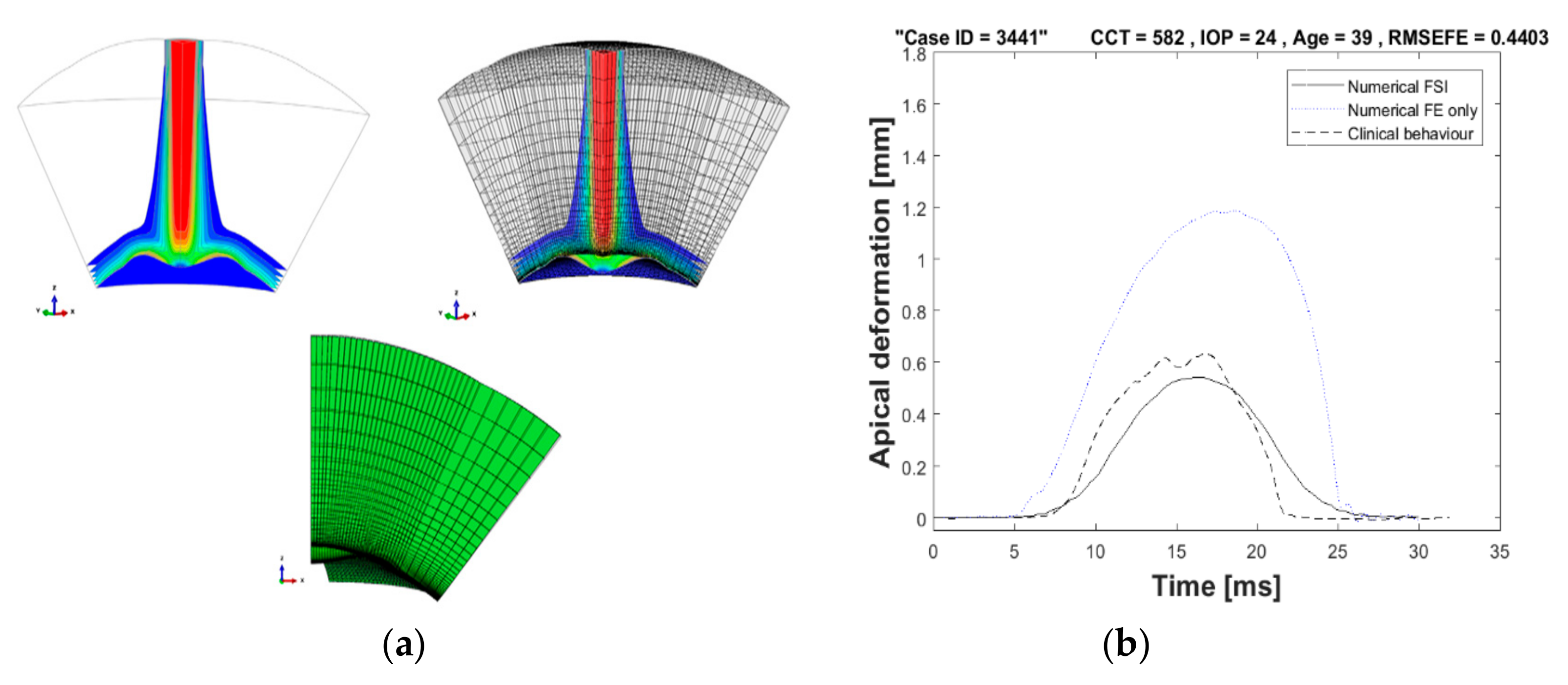
2.1. Three-Dimensional Eye Model
2.2. Three-Dimensional CFD Turbulence Model of the Air Puff
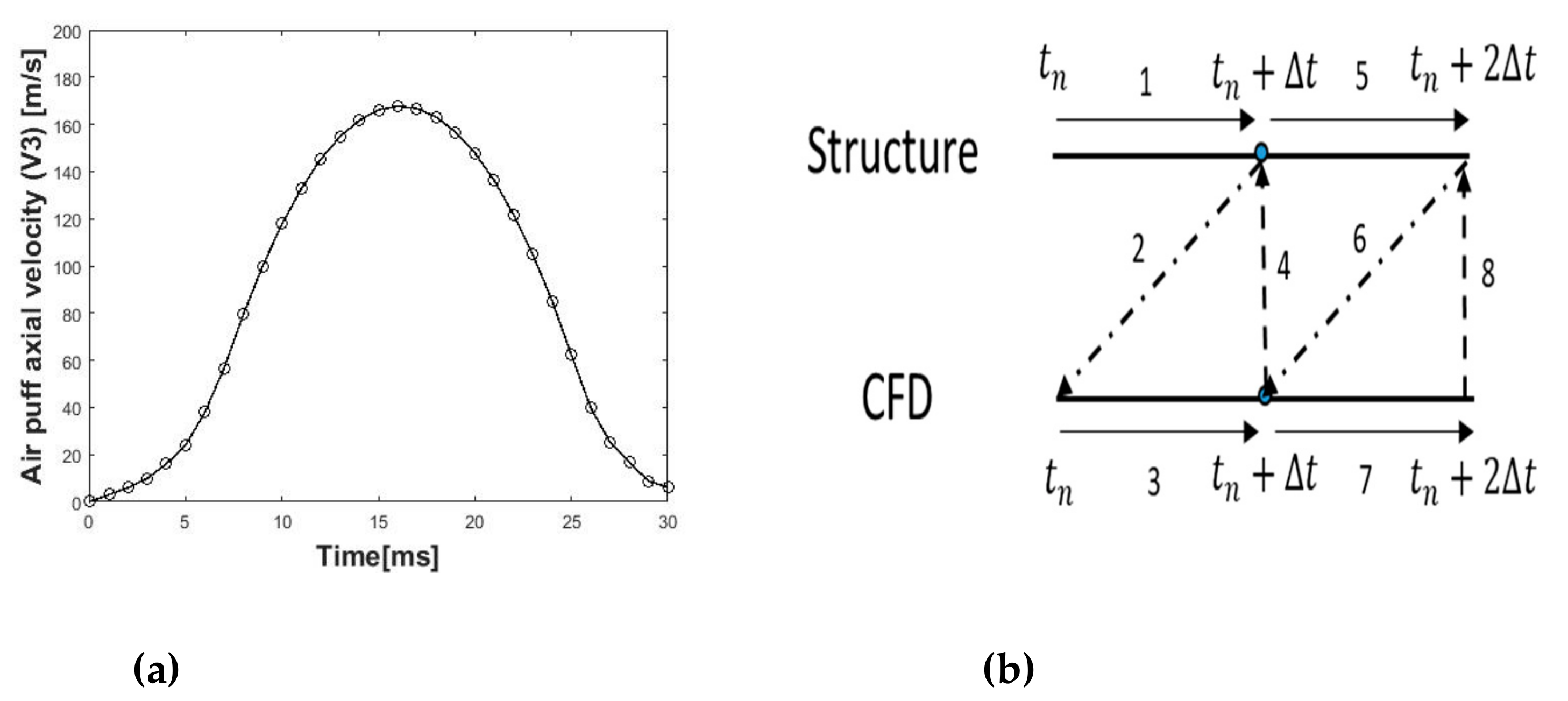
2.3. Fluid–Structure Interaction Co-Simulation
Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh
2.4. Clinical Dataset
2.5. Ethical Statement
3. Results
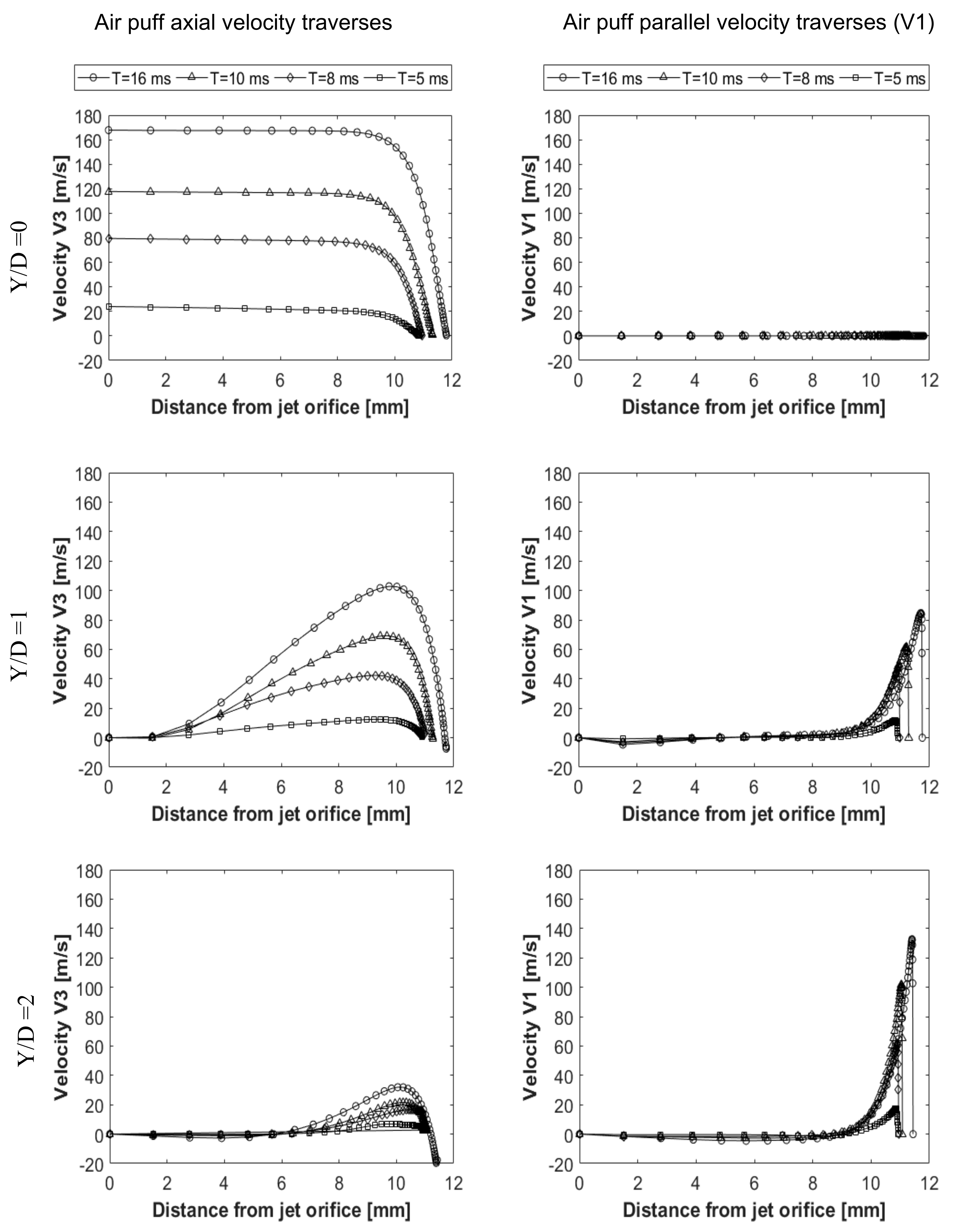
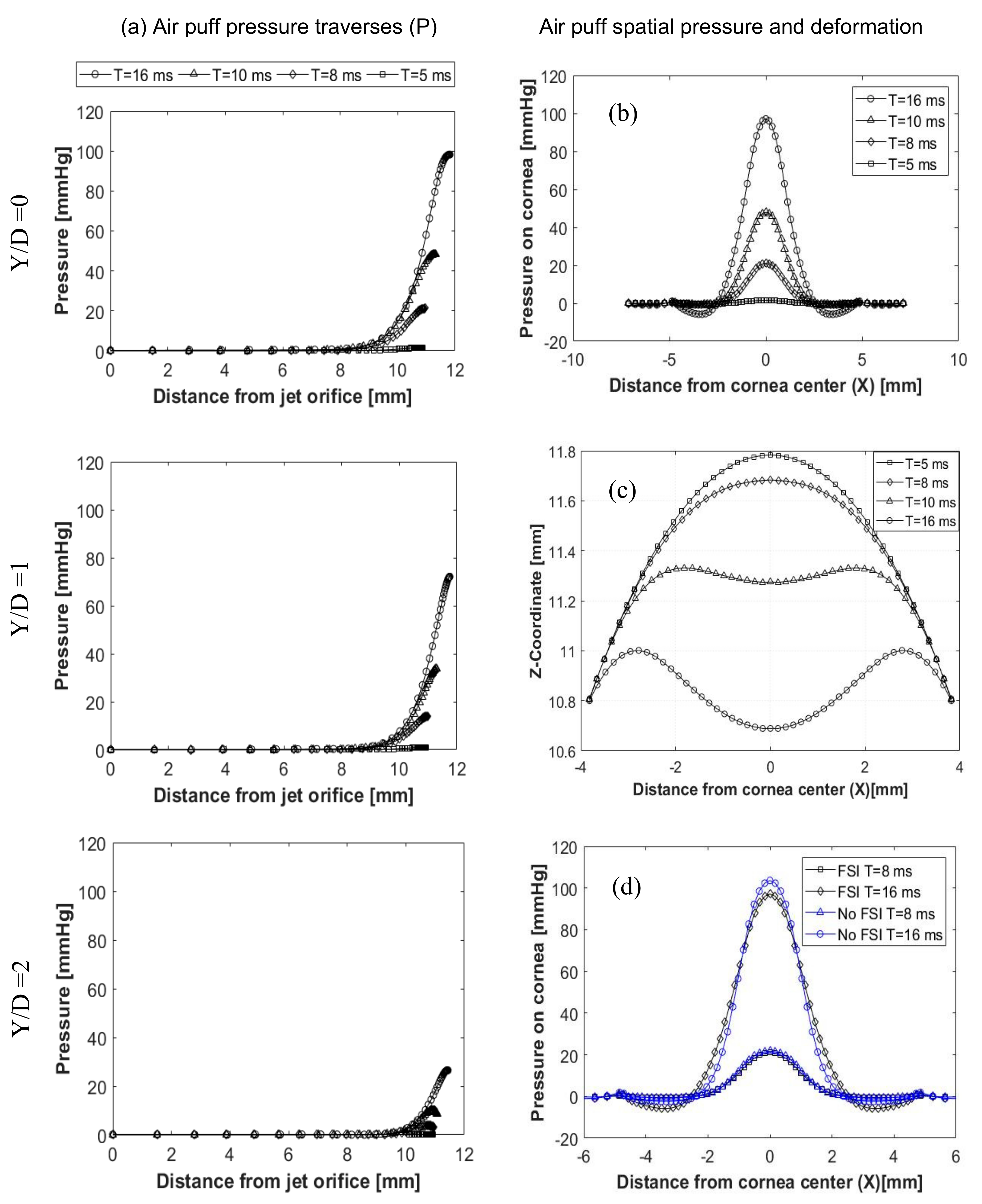
3.1. Air Puff Traverses
3.2. Parametric Study Results
- Cornea material stiffness coefficient (μ)
- Central corneal thickness (CCT)
- Corneal curvature radius (R)
- Intraocular pressure (IOP)
3.3. Clinical Validation of Numerical Results
4. Discussion
5. Conclusions
- To validate the numerical method on a wider range of eye model parameters.
- To see how air puff pressure value and distribution are affected by corneal parameters change.
- To know which corneal response parameters are affected by IOP and material changes.
- To produce estimation algorithms for IOP and corneal material.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| IOP | Intraocular Pressure |
| CCT | Central Corneal Thickness |
| CFD | Computational Fluid Dynamics |
| FE | Finite Element |
| FSI | Fluid–Structure Interaction |
| ALE | Arbitrary Lagrangian–Eulerian |
| CorVis-ST | Corneal Visualisation Scheimpflug Technology |
| ORA | Ocular Response Analyser |
| RE | Reynolds number |
| HCR | Highest Concavity Radius |
| PD | Peak Distance |
| SP-HC | Stiffness Parameter at highest concavity |
| CDR | Corneal Deformation Response |
Appendix A
| Interval to check convergence | 1 |
| Maximum number of iterations | 250 | |
| Linear convergence limit | 1 × 10−7 | |
| Time integration method | THETA |
| Energy equation and dependent variable | No Energy | |
| Linear convergence limit | 1 × 10−7 | |
Spalart-Allmaras model | 0.136 | |
| 0.622 | ||
| 7.100 | ||
| 3.239 | ||
| 0.300 | ||
| 2.000 | ||
| σ | 0.667 | |
| κ | 0.410 | |
| E (Law of the wall coefficient) | 8.432 | |
| Turbulent Prandtl number | 0.889 | |
| Turbulent Schmidt number | 1.000 | |
| Positivity rate | 0.200 | |
Fixed CFL incrementation | Start time | 0 |
| Termination time | 0.03 | |
| Initial time step | 0.01 | |
| Scale factor for time step growth | 0.25 | |
| Maximum CFL number | 0.45 | |
| Iteration limit | 250 |
| Smoother type for coarse grid solver | ICC | |
| Solver type for krylov space solver | CG | |
| Linear convergence limit | 1 × 10−5 | |
| Maximum CFL number | 0.45 | |
Diagonally-scaled FGMRES solver parameters | Iteration limit | 50 |
| Number of restart vectors | 15 | |
| Linear convergence limit | 1 × 10−5 |
References
- Fundamentals of Biomechanics; Springer: Boston, MA, USA, 2007.
- Liu, J.; Roberts, C.J. Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J. Cataract Refract. Surg. 2005, 31, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Hanselaer, P. The Human Eye. Nature 1874, 10, 243. [Google Scholar]
- Surgery for Refractive Errors. Lancet 1985, 325, 435–436. [CrossRef]
- Cochrane, G.M.; Toit, R.D.; le Mesurier, R.T. Management of refractive errors. BMJ 2010, 340, 855–860. [Google Scholar] [CrossRef] [Green Version]
- Luce, D. Air–Jet Temporal and Spatial Pressure Properties of the Reichert Ocular Response Analyzer (ORA). Investig. Ophthalmol. Vis. Sci. 2005, 46, 5009. [Google Scholar]
- Luce, D.A. Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J. Cataract Refract. Surg. 2005, 31, 156–162. [Google Scholar] [CrossRef]
- Ambrósio, R.; Ramos, I.; Luz, A.; Faria, F.C.; Steinmueller, A.; Krug, M.; Belin, M.W.; Roberts, C.J. Dynamic ultra high speed scheimpflug imaging for assessing corneal biomechanical properties. Rev. Bras. Oftalmol. 2013, 72, 99–102. [Google Scholar] [CrossRef] [Green Version]
- Kwon, T.-H.; Ghaboussi, J.; Pecknold, D.A.; Hashash, Y. Role of corneal biomechanical properties in applanation tonometry measurements. J. Refract. Surg. 2010, 26, 512–519. [Google Scholar] [CrossRef]
- Elsheikh, A.; McMonnies, C.W.; Whitford, C.; Boneham, G.C. In vivo study of corneal responses to increased intraocular pressure loading. Eye Vis. 2015, 2, 20. [Google Scholar] [CrossRef] [Green Version]
- Abitbol, O.; Bouden, J.; Doan, S.; Hoang-Xuan, T.; Gatinel, D. Corneal hysteresis measured with the ocular response analyzer® in normal and glaucomatous eyes. Acta Ophthalmol. 2010, 88, 116–119. [Google Scholar] [CrossRef]
- Andreassen, T.T.; Simonsen, A.H.; Oxlund, H. Biomechanical properties of keratoconus and normal corneas. Exp. Eye Res. 1980, 31, 435–441. [Google Scholar] [CrossRef]
- Vinciguerra, R.; Ambrósio, R.; Elsheikh, A.; Roberts, C.J.; Lopes, B.; Morenghi, E.; Azzolini, C.; Vinciguerra, P. Detection of Keratoconus With a New Biomechanical Index. J. Refract. Surg. 2016, 32, 803–810. [Google Scholar] [CrossRef] [Green Version]
- Eliasy, A.; Chen, K.J.; Vinciguerra, R.; Maklad, O.; Vinciguerra, P.; Ambrósio, R.; Roberts, C.J.; Elsheikh, A. Ex-vivo experimental validation of biomechanically-corrected intraocular pressure measurements on human eyes using the CorVis ST. Exp. Eye Res. 2018, 175, 98–102. [Google Scholar] [CrossRef] [PubMed]
- Bao, F.; Geraghty, B.; Wang, Q.; Elsheikh, A. Consideration of corneal biomechanics in the diagnosis and management of keratoconus: Is it important? Eye Vis. 2016, 3, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piñero, D.P.; Alcón, N. Corneal biomechanics: A review. Clin. Exp. Optom. 2015, 98, 107–116. [Google Scholar] [CrossRef]
- Kerautret, J.; Colin, J.; Touboul, D.; Roberts, C. Biomechanical characteristics of the ectatic cornea. J. Cataract Refract. Surg. 2008, 34, 510–513. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Tao, C.; Zhou, D.; Sun, Y.; Zhou, C.; Ren, Q.; Roberts, C.J. Air Puff Induced Corneal Vibrations: Theoretical Simulations and Clinical Observations. J. Refract. Surg. 2014, 30, 208–213. [Google Scholar] [CrossRef] [Green Version]
- Simonini, I.; Angelillo, M.; Pandolfi, A. Theoretical and numerical analysis of the corneal air puff test. J. Mech. Phys. Solids 2016, 93, 118–134. [Google Scholar] [CrossRef]
- Kaneko, M.; Tokuda, K.; Kawahara, T. Dynamic sensing of human eye. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2871–2876. [Google Scholar]
- Kling, S.; Bekesi, N.; Dorronsoro, C.; Pascual, D.; Marcos, S. Corneal viscoelastic properties from finite-element analysis of in vivo air-puff deformation. PLoS ONE 2014, 9, e104904. [Google Scholar] [CrossRef]
- Ariza-Gracia, M.; Zurita, J.F.; Piñero, D.P.; Rodriguez-Matas, J.F.; Calvo, B. Coupled biomechanical response of the cornea assessed by non-contact tonometry. A simulation study. PLoS ONE 2015, 10, e0121486. [Google Scholar] [CrossRef] [Green Version]
- Muench, S.; Roellig, M.; Spoerl, E.; Balzani, D. Numerical and Experimental Study of the Spatial Stress Distribution on the Cornea Surface During a Non-Contact Tonometry Examination. Exp. Mech. 2018, 59, 1285–1297. [Google Scholar] [CrossRef]
- Montanino, A.; Angelillo, M.; Pandolfi, A. Modelling with a meshfree approach the cornea-aqueous humor interaction during the air puff test. J. Mech. Behav. Biomed. Mater. 2018, 77, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Montanino, A.; Angelillo, M.; Pandolfi, A. A 3D fluid-solid interaction model of the air puff test in the human cornea. J. Mech. Behav. Biomed. Mater. 2019, 94, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Ariza-Gracia, M.Á.; Wu, W.; Calvo, B.; Malvè, M.; Büchler, P.; Matas, J.F.R. Fluid–structure simulation of a general non-contact tonometry. A required complexity? Comput. Methods Appl. Mech. Eng. 2018, 340, 202–215. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.A.; Roberts, C.J.; Reilly, M.A. Biomechanical Impact of the Sclera on Corneal Deformation Response to an Air-Puff: A Finite-Element Study. Front. Bioeng. Biotechnol. 2019, 6, 1–8. [Google Scholar] [CrossRef]
- Looneytand, M.K. Mean-flow and turbulent characteristics of free and impinging jet flaws. J. Fluid Mech. 2018, 147, 397–429. [Google Scholar]
- Craft, T.J.; Graham, L.J.W.; Launder, B.E. Impinging jet studies for turbulence model assessment—II. An examination of the performance of four turbulence models. Int. J. Heat Mass Transf. 1993, 36, 2685–2697. [Google Scholar] [CrossRef]
- Gauntner, J.W.; Livingood, J.N.B.; Hrycak, P. Survey of Literature on Flow Characteristics of a Single Turbulent Jet Impinging on a Flat Plate; NASA Lewis Research Center: Cleveland, OH, USA, 1970.
- Donaldson, C.; Snedeker, R. A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 1971, 45, 281–319. [Google Scholar] [CrossRef]
- Hammad, K.J.; Milanovic, I. Flow Structure in the Near-Wall Region of a Submerged Impinging Jet. J. Fluids Eng. 2011, 133, 091205. [Google Scholar] [CrossRef]
- Larras, J. Plane turbulent impinging jets. J. Hydraul. Res. 1974, 12, 279–282. [Google Scholar] [CrossRef]
- Meek, K.M.; Campanelli, M.; Geraghty, B.; Elsheikh, A.; Rama, P. Characterization of age-related variation in corneal biomechanical properties. J. R. Soc. Interface 2010, 7, 1475–1485. [Google Scholar]
- Eliasy, A.; Chen, K.-J.; Vinciguerra, R.; Lopes, B.T.; Abass, A.; Vinciguerra, P.; Ambrósio, R., Jr.; Roberts, C.J.; Elsheikh, A. Determination of Corneal Biomechanical Behavior in-vivo for Healthy Eyes Using CorVis ST Tonometry: Stress-Strain Index. Front. Bioeng. Biotechnol. 2019, 7, 105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elsheikh, A.; Whitford, C.; Hamarashid, R.; Kassem, W.; Joda, A.; Büchler, P. Stress free configuration of the human eye. Med. Eng. Phys. 2013, 35, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Kotecha, A.; Elsheikh, A.; Roberts, C.R.; Zhu, H.; Garway-Heath, D.F. Corneal thickness- and age-related biomechanical properties of the cornea measured with the ocular response analyzer. Investig. Ophthalmol. Vis. Sci. 2006, 47, 5337–5347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elsheikh, A.; Geraghty, B.; Alhasso, D.; Knappett, J.; Campanelli, M.; Rama, P. Regional variation in the biomechanical properties of the human sclera. Exp. Eye Res. 2010, 90, 624–633. [Google Scholar] [CrossRef]
- Ogden, R.W. Compressible Rubberlike Solids Large deformation isotropic elasticity: On the correlation of theory and experiment for compressible rubberlike solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Pandolfi, A.; Holzapfel, G.A. Three-Dimensional Modeling and Computational Analysis of the Human Cornea Considering Distributed Collagen Fibril Orientations. J. Biomech. Eng. 2008, 130, 061006. [Google Scholar] [CrossRef] [Green Version]
- Abaqus. ABAQUS/Standard Analysis User’s Manual v14.2. SIMULIA. 2014. Available online: http://130.149.89.49:2080/v6.14/pdf_books/CAE.pdf (accessed on 20 June 2016).
- van Wylen, G.J.J.; Sonntag, R.E. Fundamentals of Classical Thermodynamics; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Villamarin, A.; Roy, S.; Hasballa, R.; Vardoulis, O.; Reymond, P.; Stergiopulos, N. 3D simulation of the aqueous flow in the human eye. Med. Eng. Phys. 2012, 34, 1462–1470. [Google Scholar] [CrossRef]
- Maklad, O.; Theofilis, V.; Elsheikh, A. Fluid Structure Interaction (FSI) Simulation of the human eye under the air puff tonometry using Computational Fluid Dynamics (CFD) in ICCFD10 2018, no. ICCFD10-017. Available online: http://www. iccfd. org/iccfd10/proceedings. html (accessed on 23 April 2019).
- NASA. Turbulence Modeling Resource: The Spalart-allmaras Turbulence. Recherche 2011, 41, 1–8. Available online: https://turbmodels.larc.nasa.gov/ (accessed on 25 February 2016).
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Fluid flow handbook: McGraw-Hill, NY, USA, 1995. [Google Scholar]
- Shpilrain, E.E. AIR (PROPERTIES OF). A–Z Guid. Thermodyn. Heat Mass Transf. Fluids Eng. 2006. [Google Scholar] [CrossRef]
- Rigden, P.J. Viscosity of air [15]. Nature 1938, 141, 82. [Google Scholar] [CrossRef]
- Joda, A.A.; Shervin, M.M.S.; Kook, D.; Elsheikh, A. Development and validation of a correction equation for Corvis tonometry. Comput. Methods Biomech. Biomed. Engin. 2015, 19, 943–953. [Google Scholar] [CrossRef] [PubMed]
- Shirokoff, D.; Rosales, R.R. An efficient method for the incompressible Navier-Stokes equations on irregular domains with no-slip boundary conditions, high order up to the boundary. J. Comput. Phys. 2010, 230, 8619–8646. [Google Scholar] [CrossRef] [Green Version]
- Kelley, C.T. Iterative Methods for Linear and Nonlinear Equations. Society 1995, 16, 166. [Google Scholar]
- Drkošová, J.; Greenbaum, A.; Rozložník, M.; Strakoš, Z. Numerical stability of GMRES. BIT Numer. Math. 1995, 35, 309–330. [Google Scholar] [CrossRef]
- Pueyo, A.; Zingg, D.W. Efficient Newton-Krylov Solver for Aerodynamic Computations. AIAA J. 1998, 36, 1991–1997. [Google Scholar]
- Su, G.W.; Geller, J.T.; Hunt, J.R.; Pruess, K. A review of algebraic multigrid.pdf. Vadose Zo. J. 2004, 3, 592–601. [Google Scholar] [CrossRef]
- Kincaid, D.R.; Respess, J.R.; Young, D.M.; Grimes, R.R. Algorithm 586: ITPACK 2C: A FORTRAN Package for Solving Large Sparse Linear Systems by Adaptive Accelerated Iterative Methods. ACM Trans. Math. Softw. 1982, 8, 302–322. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Cambridge Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Courant, R.; Lewy, H.; Friedrichs, K. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- de Moura, C.A.; Kubrusly, C.S. (Eds.) The Courant–Friedrichs–Lewy (CFL) Condition; Birkhäuser: Boston, MA, USA, 2013. [Google Scholar]
- Laney, C.B. Computational Gasdynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Kcharik, M.; Liska, R.; Váchal, P.; Shashkov, M. Arbitrary Lagrangian-Eulerian (ALE) Method in Compressible Fluid Dynamics. Available online: https://eudml.org/doc/271298 (accessed on 19 December 2019).
- Hron, J.; Turek, S. A Monolithic FEM/Multigrid Solver for an ALE Formulation of Fluid-Structure Interaction with Applications in Biomechanics. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 146–170. [Google Scholar]
- Donea, J.; Huerta, A.; Ponthot, J.-P.; Rodríguez-Ferran, A. Arbitrary Lagrangian-Eulerian Methods. In Encyclopedia of Computational Mechanics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2017; pp. 1–23. [Google Scholar] [CrossRef]
- Souli, M.; Zolesio, J.P. Arbitrary Lagrangian-Eulerian and free surface methods in fluid mechanics. Comput. Methods Appl. Mech. Eng. 2001, 191, 451–466. [Google Scholar] [CrossRef]
- Ambrósio, R.; Lopes, B.T.; Faria-Correia, F.; Salomão, M.Q.; Bühren, J.; Roberts, C.J.; Elsheikh, A.; Vinciguerra, R.; Vinciguerra, P. Integration of Scheimpflug-Based Corneal Tomography and Biomechanical Assessments for Enhancing Ectasia Detection. J. Refract. Surg. 2017, 33, 434–443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villavicencio, O.F.; Gilani, F.; Henriquez, M.A.; Izquierdo, L.; Ambrósio, R.R. Independent Population Validation of the belin/Ambrósio Enhanced Ectasia display: Implications for Keratoconus studies and screening. Int. J. Keratoconus Ectatic Corneal Dis. 2014, 3, 1. [Google Scholar] [CrossRef]
- Dupps, W.J.; Wilson, S.E. Biomechanics and wound healing in the cornea. Exp. Eye Res. 2006, 83, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Pandolfi, A.; Fotia, G.; Manganiello, F. Finite element simulations of laser refractive corneal surgery. Eng. Comput. 2009, 25, 15–24. [Google Scholar] [CrossRef]
- Gefen, A.; Shalom, R.; Elad, D.; Mandel, Y. Biomechanical analysis of the keratoconic cornea. J. Mech. Behav. Biomed. Mater. 2009, 2, 224–236. [Google Scholar] [CrossRef]
- Roy, A.S.; Kurian, M.; Matalia, H.; Shetty, R. Air-puff associated quantification of non-linear biomechanical properties of the human cornea in vivo. J. Mech. Behav. Biomed. Mater. 2015, 48, 173–182. [Google Scholar]




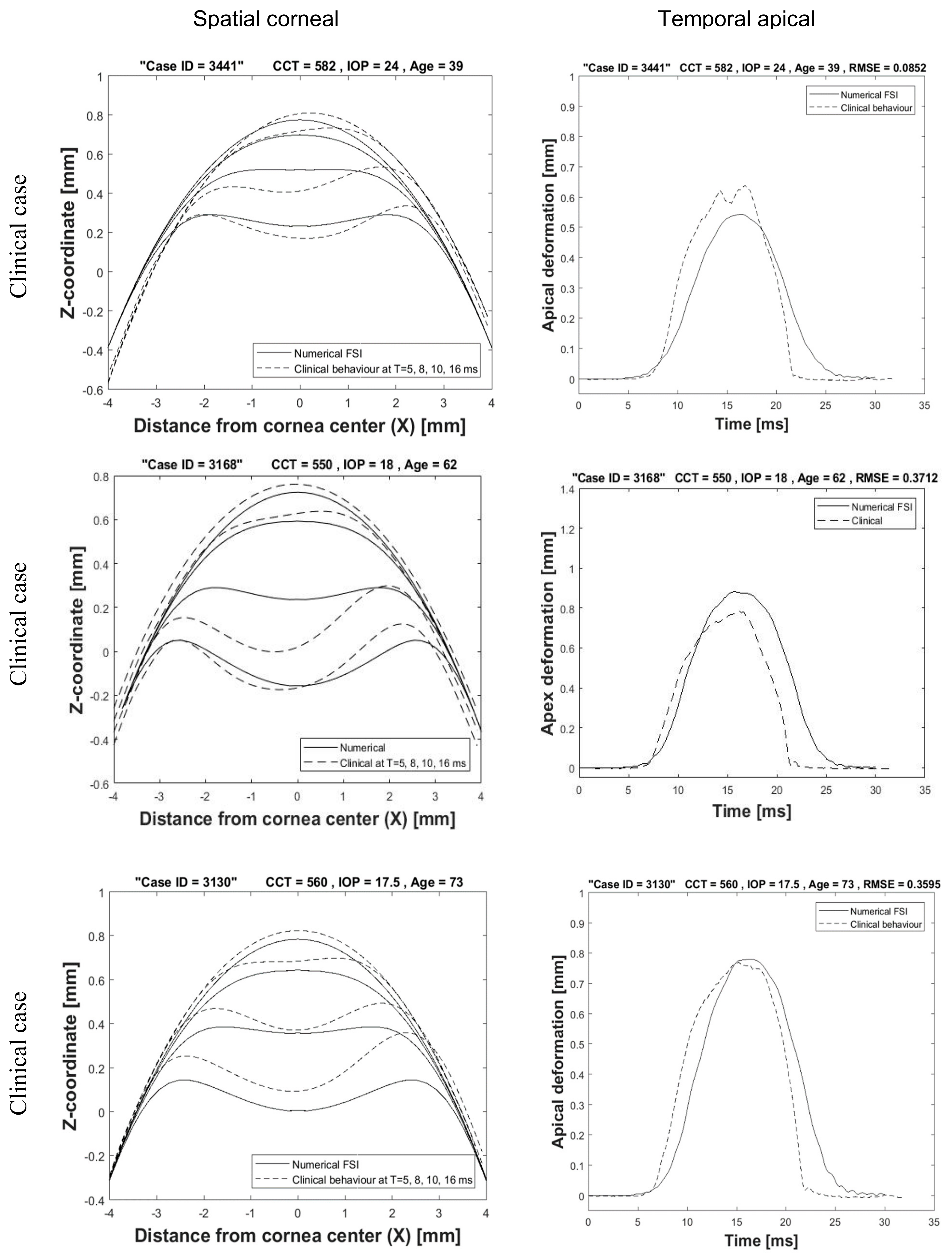
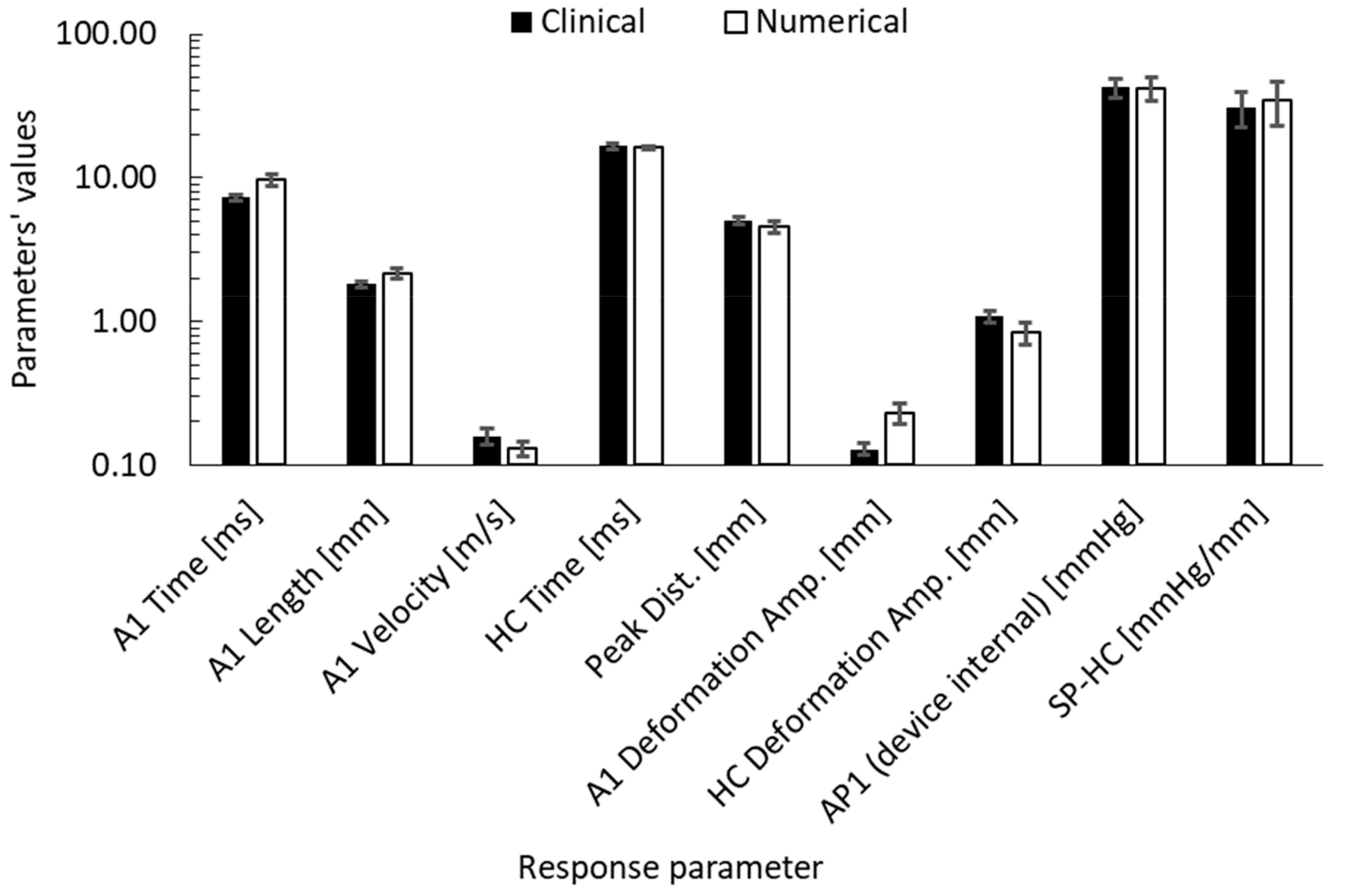
| Datasets | Participants | Age (years) | CCT (μm) | CVS-IOP (mmHg) |
|---|---|---|---|---|
| Dataset 1 (Milan) | 225 | 38 ± 17.2 (7–91) | 543 ± 31.5 (458–635) | 15.7 ± 2.35 (11–25) |
| Dataset 2 (Rio) | 251 | 43 ± 16.5 (8–87) | 539 ± 33.2 (454–629) | 14.8 ± 3.06 (6–34) |
| Variable | Mean | Std. Deviation | Minimum | Maximum |
|---|---|---|---|---|
| IOP (mmHg) | 18.36 | 6.25 | 10 | 25 |
| CCT (µm) | 550.45 | 73.99 | 445 | 645 |
| µ | 0.0712 | 0.0236 | 0.0422 | 0.1082 |
| R (mm) | 7.82 | 0.33 | 7.4 | 8.4 |
| A1 Time (ms) | 9.66 | 0.97 | 7.81 | 12.47 |
| A1 Length (mm) | 2.15 | 0.19 | 1.91 | 2.62 |
| A1 Velocity (mm/s) | 0.13 | 0.04 | 0.06 | 0.21 |
| HC Time (ms) | 16.21 | 0.36 | 15.3 | 16.9 |
| Peak Distance (mm) | 4.58 | 0.95 | 2.46 | 6.62 |
| A1 Def. Amp. (mm) | 0.23 | 0.05 | 0.17 | 0.39 |
| HC Def. Amp. (mm) | 0.84 | 0.3 | 0.42 | 1.77 |
| AP1(mmHg) | 42.09 | 12.09 | 18.82 | 75.24 |
| SP-HC | 34.69 | 21.92 | 5 | 109.59 |
| Variable | A1 Time (ms) | A1 Length mm) | A1 Velocity (mm/s) | HC Time (ms) | Peak Dist. (mm) | A1 Deformation Amp. (mm) | HC Deformation Amp. (mm) | AP1 (mmHg) | SP-HC Stiffness parameter | |
|---|---|---|---|---|---|---|---|---|---|---|
| IOP (mmHg) | Pearson Correlation (r) | 0.725 ** | −0.455 ** | −0.731 ** | −0.255 ** | −0.616 ** | −0.403 ** | −0.635 ** | 0.736 ** | 0.442 ** |
| Sig. (two-tailed) | 0.000 | 0.000 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| CCT (µm) | Pearson Correlation (r) | 0.382 ** | 0.637 ** | −0.206 * | −0.122 | −0.500 ** | 0.673 ** | −0.493 ** | 0.385 ** | 0.468 ** |
| Sig. (two-tailed) | 0.000 | 0.000 | 0.031 | 0.204 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| μ | Pearson Correlation (r) | 0.338 ** | 0.471 ** | −0.367 ** | −0.280 ** | −0.407 ** | 0.432 ** | −0.377 ** | 0.355 ** | 0.434 ** |
| Sig. (two-tailed) | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| R (mm) | Pearson Correlation (r) | −0.007 | −0.056 | −0.067 | 0.032 | 0.088 | −0.253 ** | −0.052 | 0.007 | −0.088 |
| Sig. (two-tailed) | 0.946 | 0.564 | 0.486 | 0.741 | 0.362 | 0.008 | 0.592 | 0.945 | 0.362 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maklad, O.; Eliasy, A.; Chen, K.-J.; Theofilis, V.; Elsheikh, A. Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation. Int. J. Environ. Res. Public Health 2020, 17, 54. https://doi.org/10.3390/ijerph17010054
Maklad O, Eliasy A, Chen K-J, Theofilis V, Elsheikh A. Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation. International Journal of Environmental Research and Public Health. 2020; 17(1):54. https://doi.org/10.3390/ijerph17010054
Chicago/Turabian StyleMaklad, Osama, Ashkan Eliasy, Kai-Jung Chen, Vassilios Theofilis, and Ahmed Elsheikh. 2020. "Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation" International Journal of Environmental Research and Public Health 17, no. 1: 54. https://doi.org/10.3390/ijerph17010054
APA StyleMaklad, O., Eliasy, A., Chen, K.-J., Theofilis, V., & Elsheikh, A. (2020). Simulation of Air Puff Tonometry Test Using Arbitrary Lagrangian–Eulerian (ALE) Deforming Mesh for Corneal Material Characterisation. International Journal of Environmental Research and Public Health, 17(1), 54. https://doi.org/10.3390/ijerph17010054








