Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment
Abstract
:1. Introduction
- (1)
- A novel concept of the Spherical normal fuzzy (SpNoFS) set is defined, between which the new score, the accuracy function, and some improved operational rules are established.
- (2)
- Some new information aggregation operators based on operational rules of SpNoFS, including the Spherical normal fuzzy Bonferroni mean (SpNoFBM) operator and the Spherical normal fuzzy weighted Bonferroni mean (SpNoFGBM) operator, are proposed.
- (3)
- A new MCDM method for selecting an antivirus mask over the COVID-19 pandemic in light of the SpNoFBM operator and the SpNoFGBM operator is constructed.
2. Literature Review
2.1. The Healthcare and Medical Decision Making Problems Based on the Fuzzy MCDM Method
2.2. The MCDM Methods Based on Fuzzy Set Theories
2.3. Spherical Fuzzy Set
3. Preliminaries
4. The Spherical Normal Fuzzy Number and Its Operations
5. Spherical Normal Fuzzy Bonferroni Mean Operators
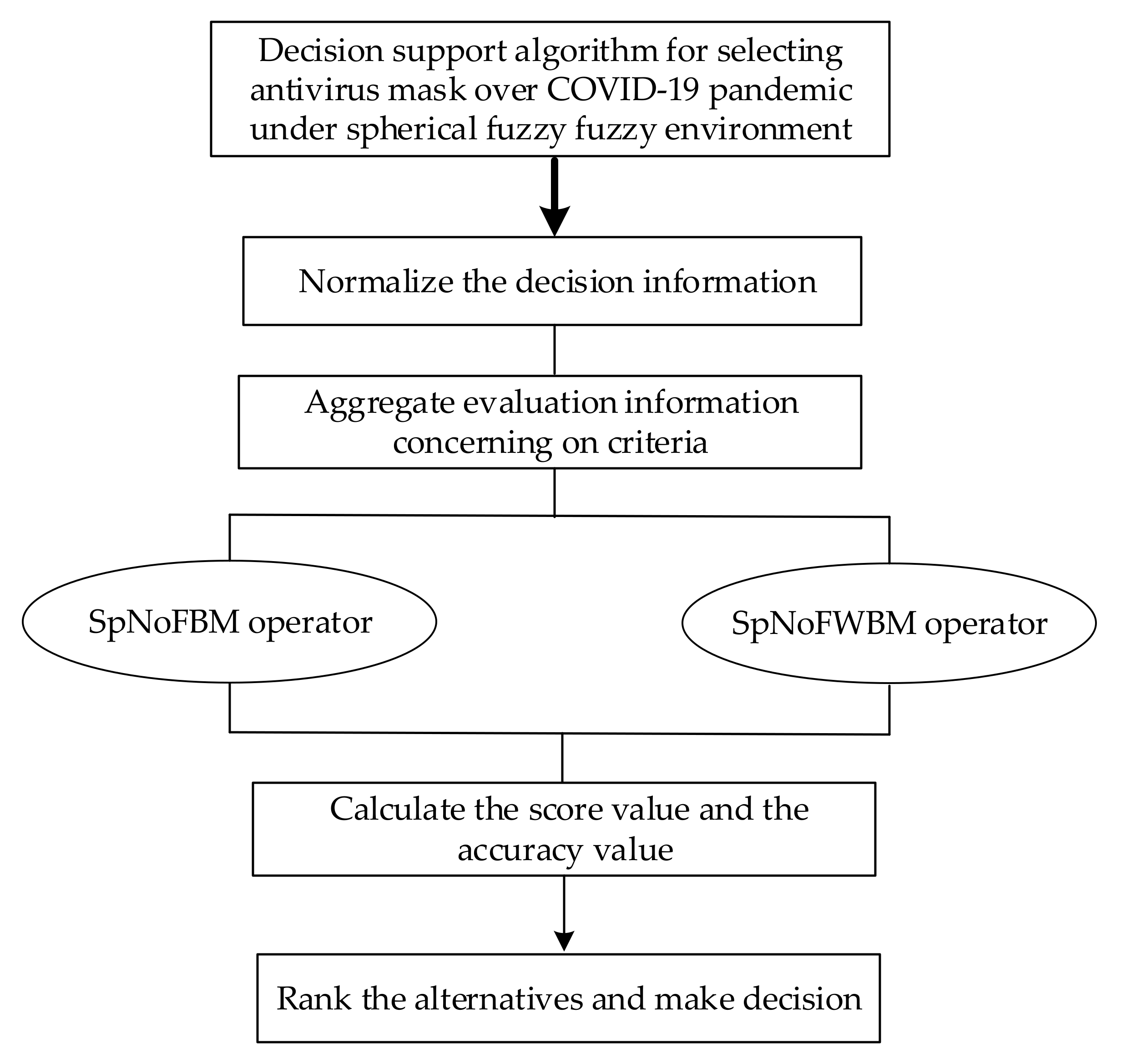
6. A Novel MCDM Model Based on Proposed Aggregation Operators
7. The Case on Antivirus Mask Selecting over the COVID-19 Pandemic
7.1. Decision Procedure
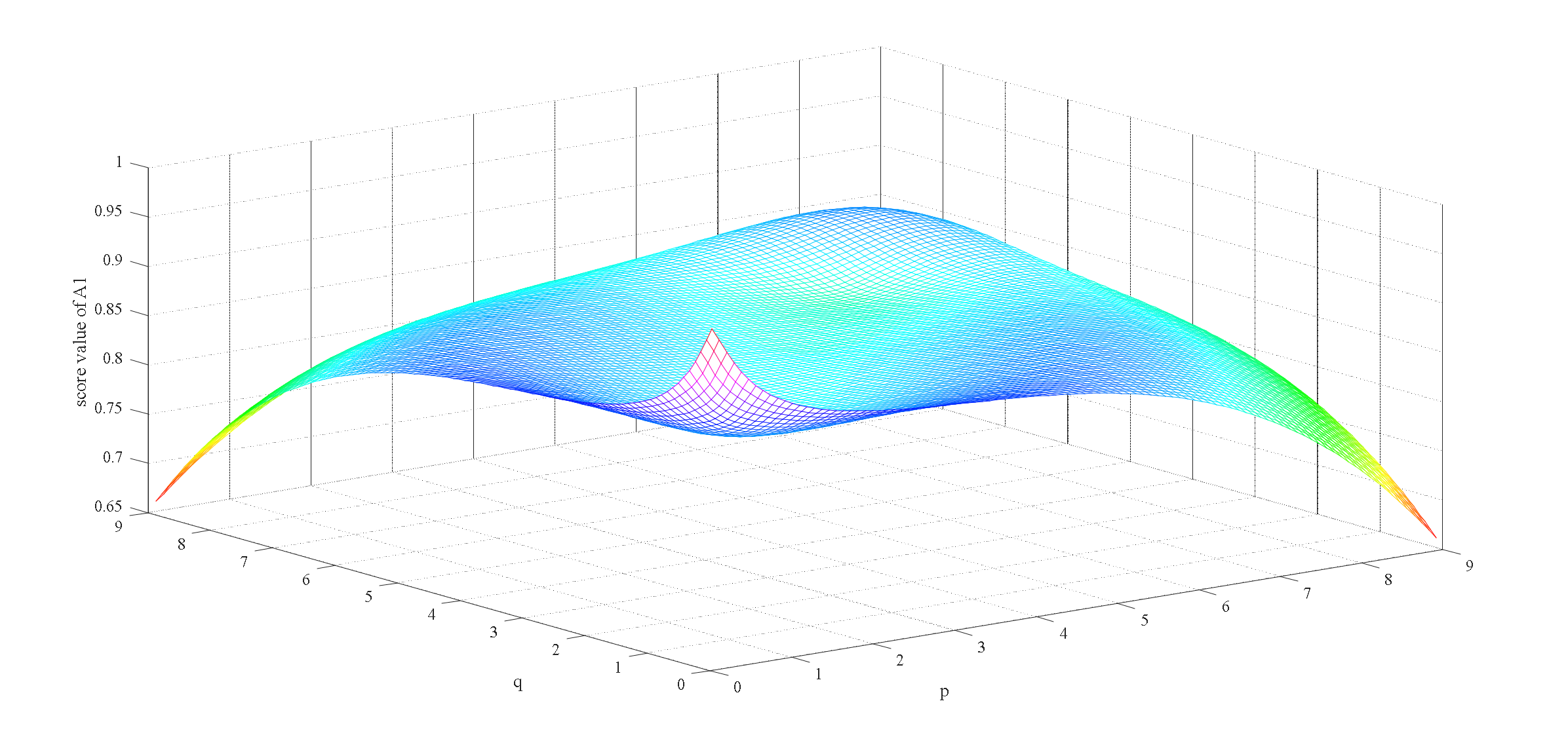
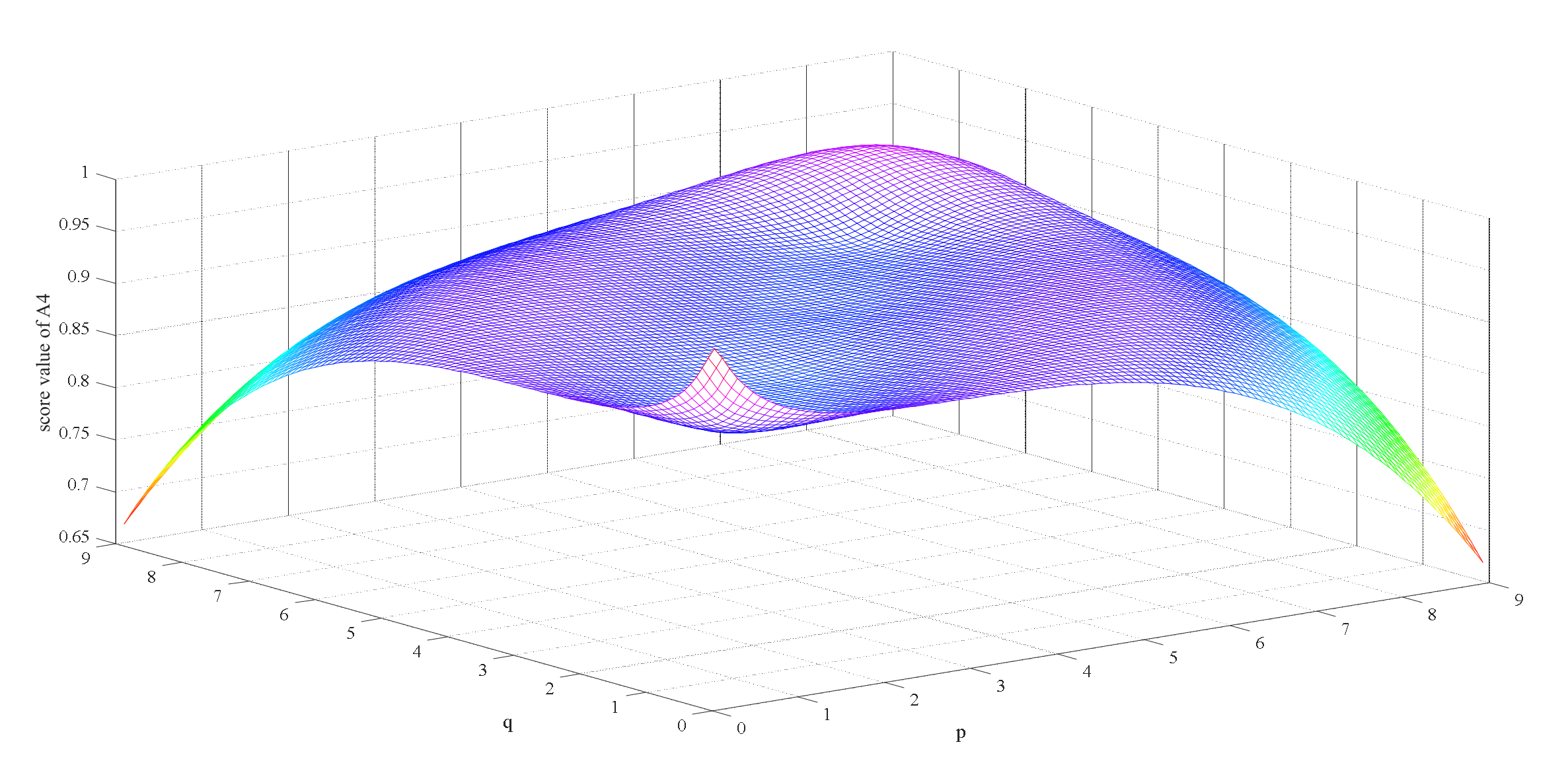
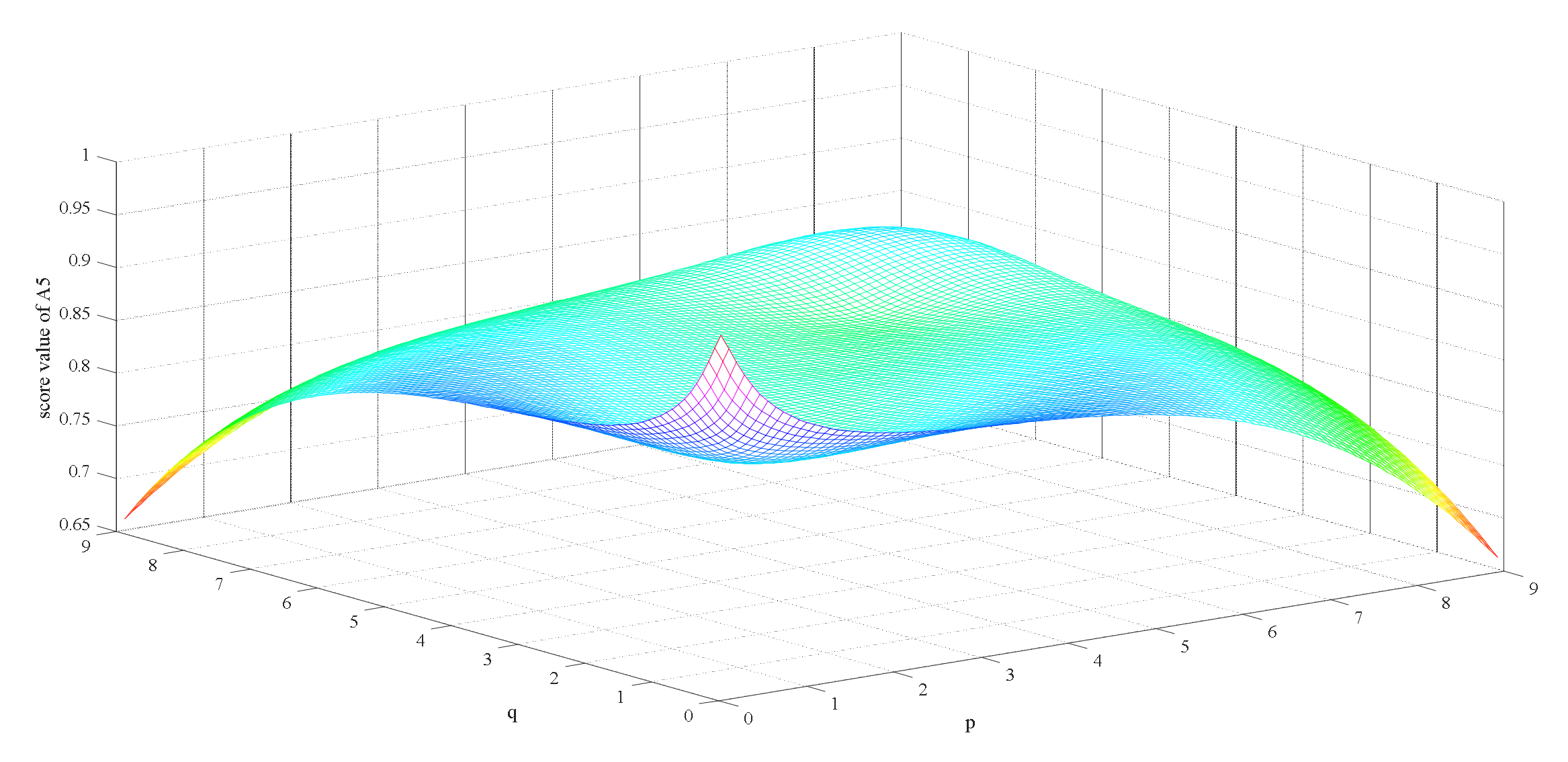
7.2. Sensitive Analysis
7.3. Comparative Analysis
8. Conclusions
- (1)
- The proposed method simultaneously considers both subjective evaluation information of decision makers and objective information of target criteria by combining SpFN with NFN. Compared with the existing methods, our methods are more general and powerful.
- (2)
- The proposed MCMD method and information aggregation operators are based on the BM operator; it pays more attention to the interrelationship between any two different SpNoFNs and also to the influence of the interrelationships on the decision result. The decision procedure of our proposed method is more in line with the real situation.
- (3)
- There are three parameters, namely , and , in the proposed method, the value of which can be adjusted by the decision makers based on subjective preferences and real situation to obtain corresponding decision results. As such, the method of our study renders the process of decision and information aggregation more flexible.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Singer, H.M. Short-term predictions of country-specific Covid-19 infection rates based on power law scaling exponents. arXiv 2020, arXiv:2003.11997. [Google Scholar]
- Coleman, C.M.; Sisk, J.M.; Mingo, R.M.; Nelson, E.A.; White, J.M.; Frieman, M.B. ABL kinase inhibitors are potent inhibitors of SARS-CoV and MERS-CoV fusion. J. Virol. 2016, 90, 8924–8933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Björn, W.S.; Dagmar, M.S.; Kun, Q.; Juan, L.; Zheng, H.; Li, X. COVID-19 and computer audition: An overview on what speech & sound analysis could contribute in the SARS-CoV-2 corona crisis. arXiv 2020, arXiv:2003.11117. [Google Scholar]
- Hu, Z.; Ge, Q.; Li, S.; Boerwincle, E.; Jin, L.; Xiong, M. Forecasting and evaluating intervention of Covid-19 in the World. arXiv 2020, arXiv:2003.09800. [Google Scholar]
- Akram, M.; Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 7. [Google Scholar] [CrossRef]
- Hashmi, M.R.; Riaz, M.; Smarandache, F. m-Polar neutrosophic topology with applications to multi-criteria decision-making in medical diagnosis and clustering analysis. Int. J. Fuzzy Syst. 2020, 22, 273–292. [Google Scholar] [CrossRef]
- Zhou, Q.; Mo, H.; Deng, Y. A new divergence measure of Pythagorean fuzzy sets based on belief function and its application in medical diagnosis. Mathematics 2020, 8, 142. [Google Scholar] [CrossRef] [Green Version]
- Yucesan, M.; Gul, M. Hospital service quality evaluation: An integrated model based on Pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Comput. 2020, 24, 3237–3255. [Google Scholar] [CrossRef]
- Lee, Y.C.; Chung, P.H.; Shyu, J.Z. Performance evaluation of medical device manufacturers using a hybrid fuzzy MCDM. J. Sci. Ind. Res. 2017, 76, 28–31. [Google Scholar]
- Nilashi, M.; Samad, S.; Manaf, A.A.; Ahmadi, H.; Rashid, T.A.; Munshi, A.; Almukadi, W.; Ibrahim, O.; Ahmed, O.H.; Hassan, O. Factors influencing medical tourism adoption in Malaysia: A DEMATEL-Fuzzy TOPSIS approach. Comput. Ind. Eng. 2019, 137, 106005. [Google Scholar] [CrossRef]
- Mardani, A.; Hooker, R.; Ozkul, S.; Yifan, S.; Nilashi, M.; Sabzi, H.Z.; Fei, G.C. Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments. Expert Syst. Appl. 2019, 137, 202–231. [Google Scholar] [CrossRef]
- Gao, H.; Ran, L.; Wei, G.; Wei, C.; Wu, J. VIKOR method for MAGDM based on q-rung interval-valued orthopair fuzzy information and its application to supplier selection of medical consumption products. Int. J. Environ. Res. Public Health 2020, 17, 525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garg, H.; Kaur, G. Quantifying gesture information in brain hemorrhage patients using probabilistic dual hesitant fuzzy sets with unknown probability information. Comput. Ind. Eng. 2020, 140, 106211. [Google Scholar] [CrossRef]
- Yang, Z.; Ouyang, T.; Fu, X.; Peng, X. A decision-making algorithm for online shopping using deep-learning–based opinion pairs mining and q-rung orthopair fuzzy interaction Heronian mean operators. Int. J. Intell. Syst. 2020, 35, 783–825. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hong, W.C.; Li, J. Electric load forecasting by hybrid self-recurrent support vector regression model with variational mode decomposition and improved cuckoo search algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Kundra, H.; Sadawarti, H. Hybrid algorithm of cuckoo search and particle swarm optimization for natural terrain feature extraction. Res. J. Inf. Technol. 2015, 7, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Lee, A.; Kang, H. A multi-criteria decision-making model for evaluating senior daycare center locations. Int. J. Environ. Res. Public Health 2019, 16, 5031. [Google Scholar] [CrossRef] [Green Version]
- Qu, G.; Xue, R.; Li, T.; Qu, W.; Xu, Z. A stochastic multi-attribute method for measuring sustainability performance of a supplier based on a triple bottom line approach in a dual hesitant fuzzy linguistic environment. Int. J. Environ. Res. Public Health 2020, 17, 2138. [Google Scholar] [CrossRef] [Green Version]
- Fathima, P.F.A.; John, S.J.; Bibitha, K.V.; Garg, H. Spherical fuzzy soft sets and its application in decision making process. J. Intell. Fuzzy Syst. 2019, 37, 8237–8250. [Google Scholar]
- Garg, H.; Kaur, G. Novel distance measures for cubic intuitionistic fuzzy sets and their applications to pattern recognitions and medical diagnosis. Granul. Comput. 2020, 5, 169–184. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Hussain, A.; Mahmood, T.; Ali, M.I. Rough Pythagorean fuzzy ideals in semigroups. Comput. Appl. Math. 2019, 38. [Google Scholar] [CrossRef]
- Verma, R.; Merigo, J.M. On generalized similarity measures for Pythagorean fuzzy sets and their applications to multiple attribute decision-making. Int. J. Intell. Syst. 2019, 34, 2556–2583. [Google Scholar] [CrossRef]
- He, T.; Wei, G.; Lu, J.; Wei, C.; Lin, R. Pythagorean 2-Tuple Linguistic Taxonomy Method for Supplier Selection in Medical Instrument Industries. Int. J. Environ. Res. Public Health 2019, 16, 4875. [Google Scholar] [CrossRef] [Green Version]
- Haktanir, E.; Kahraman, C. A novel interval-valued Pythagorean fuzzy QFD method and its application to solar photovoltaic technology development. Comput. Ind. Eng. 2019, 132, 361–372. [Google Scholar] [CrossRef]
- Chen, T.Y. A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment. Neural Comput. Appl. 2019, 31, 3969–3999. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies (Wict), Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets-first results. Part 1. Seminar “neuro-fuzzy systems with applications”. J. Comput. Sci. Cybernetics. 2014, 4, 409–420. [Google Scholar]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S. Spherical aggregation operators and their application in multiattribute group decision-making. Int. J. Intell. Syst. 2019, 34, 493–523. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng. Appl. Artif. Intel. 2019, 85, 307–323. [Google Scholar] [CrossRef]
- Jin, H.H.; Ashraf, S.; Abdullah, S.; Qiyas, M.; Bano, M.; Zeng, S. Linguistic spherical fuzzy aggregation operators and their applications in multi-attribute decision making problems. Mathematics 2019, 7, 413. [Google Scholar] [CrossRef] [Green Version]
- Gundogdu, F.K.; Kahraman, C. Extension of WASPAS with spherical fuzzy sets. Informatica 2019, 30, 269–292. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Ashraf, S.; Abdullah, S. Spherical fuzzy logarithmic aggregation operators based on entropy and their application in decision support systems. Entropy 2019, 21, 628. [Google Scholar] [CrossRef] [Green Version]
- Rafiq, M.; Shahzaib, A.; Saleem, A.; Tahir, M.; Shakoor, M. The cosine similarity measures of spherical fuzzy sets and their applications in decision making. J. Intell. Fuzzy Syst. 2019, 36, 6059–6073. [Google Scholar] [CrossRef]
- Zeng, S.Z.; Hussain, A.; Tahir, M.; Ali, M.I.; Munir, M.; Ashraf, S. Covering-based spherical fuzzy rough set model hybrid with TOPSIS for multi-attribute decision-making. Symmetry 2019, 11, 547. [Google Scholar] [CrossRef] [Green Version]
- Ashraf, S.; Abdullah, S.; Abdullah, L. Child development influence environmental factors determined using spherical fuzzy distance measures. Mathematics 2019, 7, 661. [Google Scholar] [CrossRef] [Green Version]
- Gundogdu, F.K.; Kahraman, C. A novel VIKOR method using spherical fuzzy sets and its application to warehouse site selection. J. Intell. Fuzzy Syst. 2019, 37, 1197–1211. [Google Scholar] [CrossRef]
- Yang, M.S.; Ko, C.H. On a class of fuzzy c-numbers clustering procedures for fuzzy data. Fuzzy Set. Syst. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, C.Y. Study on the universality of the normal cloud model. Eng. Sci. 2004, 6, 28–34. [Google Scholar]
- Wang, J.Q.; Li, K.J.; Zhang, H.Y. Multi-criteria decision-making method based on induced intuitionistic normal fuzzy related aggregation operators. Int. J. Uncertain Fuzz. 2012, 20, 559–578. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, K.J.; Zhang, H.Y.; Chen, X.H. A score function based on relative entropy and its application in intuitionistic normal fuzzy multiple criteria decision making. J. Intell. Fuzzy Syst. 2013, 25, 567–576. [Google Scholar] [CrossRef]
- Wang, J.Q.; Zhou, P.; Li, K.J.; Zhang, H.Y.; Chen, X.H. Multi-criteria decision-making method based on normal intuitionistic fuzzy-induced generalized aggregation operator. Top 2014, 22, 1103–1122. [Google Scholar] [CrossRef]
- Liu, P.D.; Teng, F. Multiple criteria decision making method based on normal interval-valued intuitionistic fuzzy generalized aggregation operator. Complexity 2016, 21, 277–290. [Google Scholar] [CrossRef]
- Yang, Z.; Li, J.; Huang, L.; Shi, Y. Developing dynamic intuitionistic normal fuzzy aggregation operators for multi-attribute decision-making with time sequence preference. Expert Syst. Appl. 2017, 82, 344–356. [Google Scholar] [CrossRef]
- Zhang, G.F.; Zhang, Z.M.; Kong, H. Some normal intuitionistic fuzzy Heronian mean operators using Hamacher operation and their application. Symmetry 2018, 10, 199. [Google Scholar] [CrossRef] [Green Version]
- Bonferroni, C. Sulle medie multiple di potenze. Bolletino Matematica Italiana 1950, 5, 267–270. [Google Scholar]
- Parkan, C.; Wu, M.L. Decision-making and performance measurement models with applications to robot selection. Comput. Ind. Eng. 1999, 36, 503–523. [Google Scholar] [CrossRef]




medical surgical mask () | <(135,11.8), (0.29,0.54,0.61)> | <(48,4.2), (0.54,0.44,0.63)> | <(68,5.7), (0.27,0.65,0.68)> | <(6.6,0.63), (0.3,0.22,0.63)> |
particulate respirator () | <(140,12.5), (0.54,0.55,0.49)> | <(40,3.7), (0.44,0.59,0.56)> | <(69,5.8), (0.61,0.48,0.54)> | <(9,1.1), (0.73,0.43,0.42)> |
medical protective mask () | <(105,9), (0.53,0.48,0.29)> | <(36,3.3), (0.45,0.46,0.66)> | <(75,7.1), (0.73,0.55,0.44)> | <(7.5,0.72), (0.6,0.47,0.63)> |
disposable medical mask () | <(120,11), (0.73,0.48,0.29)> | <(35,3.2), (0.8,0.21,0.12)> | <(85,7.6), (0.28,0.55,0.44)> | <(8,0.9), (0.28,0.65,0.68)> |
ordinary non-medical mask () | <(125,11.3), (0.39,0.58,0.64)> | <(45,4.3), (0.34,0.66,0.43)> | <(90,8.2), (0.45,0.68,0.31)> | <(7.2,0.71), (0.23,0.61,0.61)> |
gas mask () | <(115,10.1), (0.1,0.7,0.25)> | <(37,3.4), (0.32,0.64,0.27)> | <(79,7.3), (0.43,0.65,0.37)> | <(8.3,0.82), (0.6,0.42,0.6)> |
| <(0.964,0.083), (0.29,0.54,0.61)> | <(1, 0.085), (0.54,0.44,0.63)> | <(0.756, 0.058), (0.27,0.65,0.68)> | <(0.733,0.05), (0.3,0.22,0.63)> | |
| <(1, 0.089), (0.54,0.55,0.49)> | <(0.833, 0.08), (0.44,0.59,0.56)> | <(0.767, 0.059), (0.61,0.48,0.54)> | <(1,0.12), (0.73,0.43,0.42)> | |
| <(0.75, 0.062), (0.53,0.48,0.29)> | <(0.75, 0.07), (0.45,0.46,0.66)> | <(0.838, 0.082), (0.73,0.55,0.44)> | <(0.833,0.06), (0.6,0.47,0.63)> | |
| <(0.857, 0.081), (0.73,0.48,0.29)> | <(0.729, 0.068), (0.8,0.21,0.12)> | <(0.944, 0.083), (0.28,0.55,0.44)> | <(0.889, 0.09), (0.28,0.65,0.68)> | |
| <(0.893, 0.082), (0.39,0.58,0.64)> | <(0.938, 0.096), (0.34,0.66,0.43)> | <(1, 0.091), (0.45,0.68,0.31)> | <(0.8,0.06), (0.23,0.61,0.61)> | |
| <(0.821, 0.071), (0.1,0.7,0.25)> | <(0.771, 0.073), (0.32,0.64,0.27)> | <(0.878, 0.082), (0.43,0.65,0.37)> | <(0.922,0.07), (0.6,0.42,0.6)> |
| The Value of p, q | The Ranking Result |
|---|---|
| = 0.3 | |
| = 1 | |
| = 7 | |
| = 9 | |
| = 0.1, = 5 | |
| = 5, = 0.1 | |
| = 1, = 9 | |
| = 9, = 1 |
| The Ranking Result | |
|---|---|
| = 0.85, = = = 0.05 | |
| = 0.85, = = = 0.05 | |
| = 0.85, = = = 0.05 | |
| = 0.85, = = = 0.05 |
| Methods | Information by SpFN | Information by NFN | Whether Considered the Interrelationships between Arguments |
|---|---|---|---|
| Yager [23]’s method based on PyFS | no | no | no |
| Cuong [29,30]’s method based on PtFS | no | no | no |
| Wang et al. [44]’s method based on INFN and entropy | no | yes | no |
| Yang et al. [47]’s method based on INFN | no | yes | no |
| Zhang et al. [48]’s method based on INFN and Heronian Mean Operator | no | yes | yes |
| The proposed method | yes | yes | yes |
| Ranking Results | ||||||||
|---|---|---|---|---|---|---|---|---|
| The proposed method (P1) | 5 | 4 | 2 | 1 | 6 | 3 | ||
| The method using Archimedean operator by [32] (P2) | 5 | 4 | 3 | 1 | 6 | 2 | ||
| The method using logarithmic operation by [36] (P3) | 5 | 3 | 2 | 1 | 6 | 4 | ||
| The method using cosine similarity measures by [37] (P4) | 3 | 2 | 4 | 1 | 5 | 6 | ||
| The method using induced generalized aggregation operator by [45] (P5) | 2 | 4 | 1 | 3 | 5 | 6 | ||
| Ranking Difference | Spearman’s Test Results | |||||||
| Z | ||||||||
| P1-P2 | 0 | 0 | 1 | 0 | 0 | 1 | 0.943 | 2.108 |
| P1-P3 | 0 | 1 | 0 | 0 | 0 | 1 | 0.943 | 2.108 |
| P1-P4 | 2 | 2 | 2 | 0 | 1 | 3 | 0.371 | 0.831 |
| P1-P5 | 3 | 0 | 1 | 2 | 1 | 3 | 0.314 | 0.703 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, X.; Garg, H.; Qi, M. Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment. Int. J. Environ. Res. Public Health 2020, 17, 3407. https://doi.org/10.3390/ijerph17103407
Yang Z, Li X, Garg H, Qi M. Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment. International Journal of Environmental Research and Public Health. 2020; 17(10):3407. https://doi.org/10.3390/ijerph17103407
Chicago/Turabian StyleYang, Zaoli, Xin Li, Harish Garg, and Meng Qi. 2020. "Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment" International Journal of Environmental Research and Public Health 17, no. 10: 3407. https://doi.org/10.3390/ijerph17103407
APA StyleYang, Z., Li, X., Garg, H., & Qi, M. (2020). Decision Support Algorithm for Selecting an Antivirus Mask over COVID-19 Pandemic under Spherical Normal Fuzzy Environment. International Journal of Environmental Research and Public Health, 17(10), 3407. https://doi.org/10.3390/ijerph17103407







