Effects of Slip Length and Inertia on the Permeability of Fracture with Slippery Boundary Condition
Abstract
:1. Introduction
2. Methodology
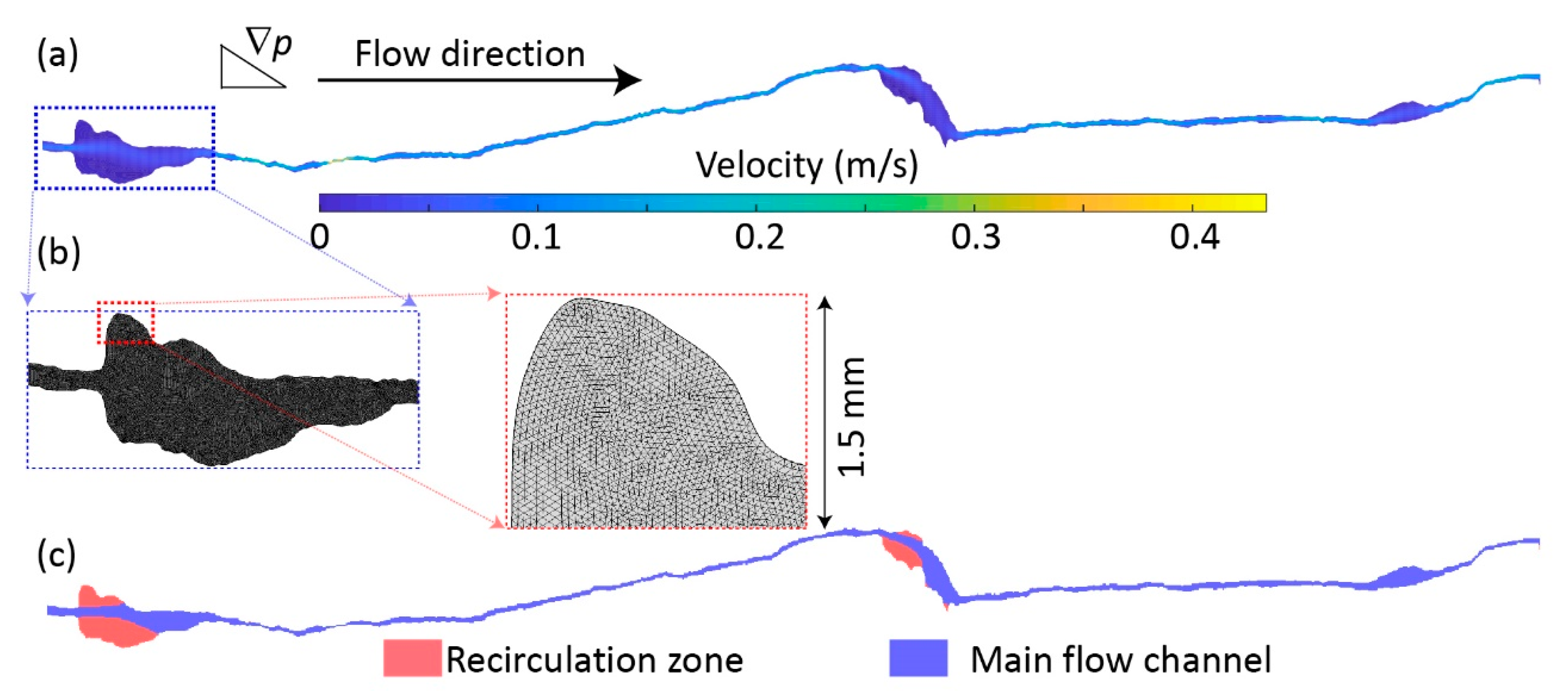
2.1. Fracture Data and Computational Fluid Dynamics
2.2. Automatic Recirculation Zone Quantification
2.3. Fracture Permeability Analysis
3. Results and Discussion
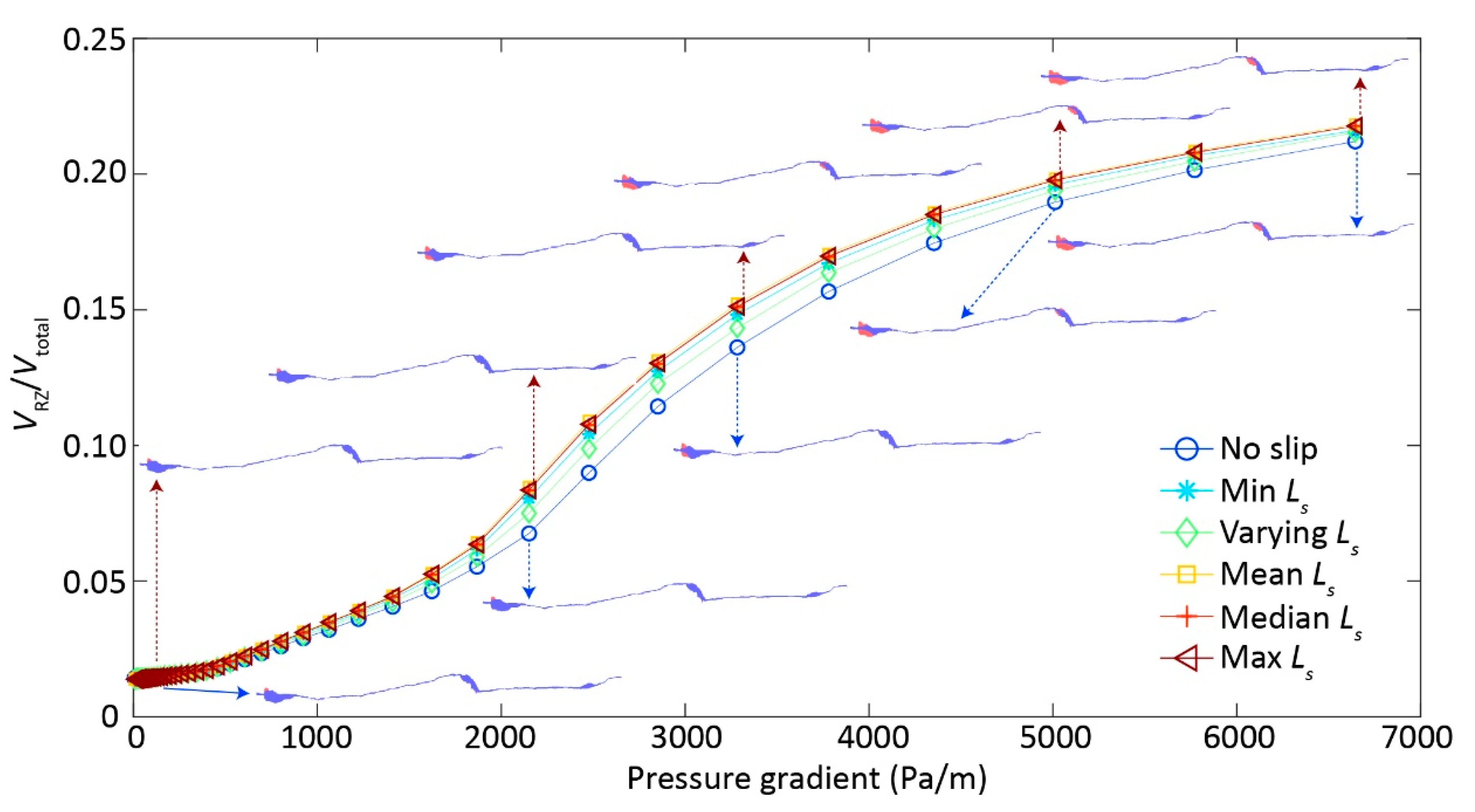
3.1. Fracture Nonlinear Flow Behavior
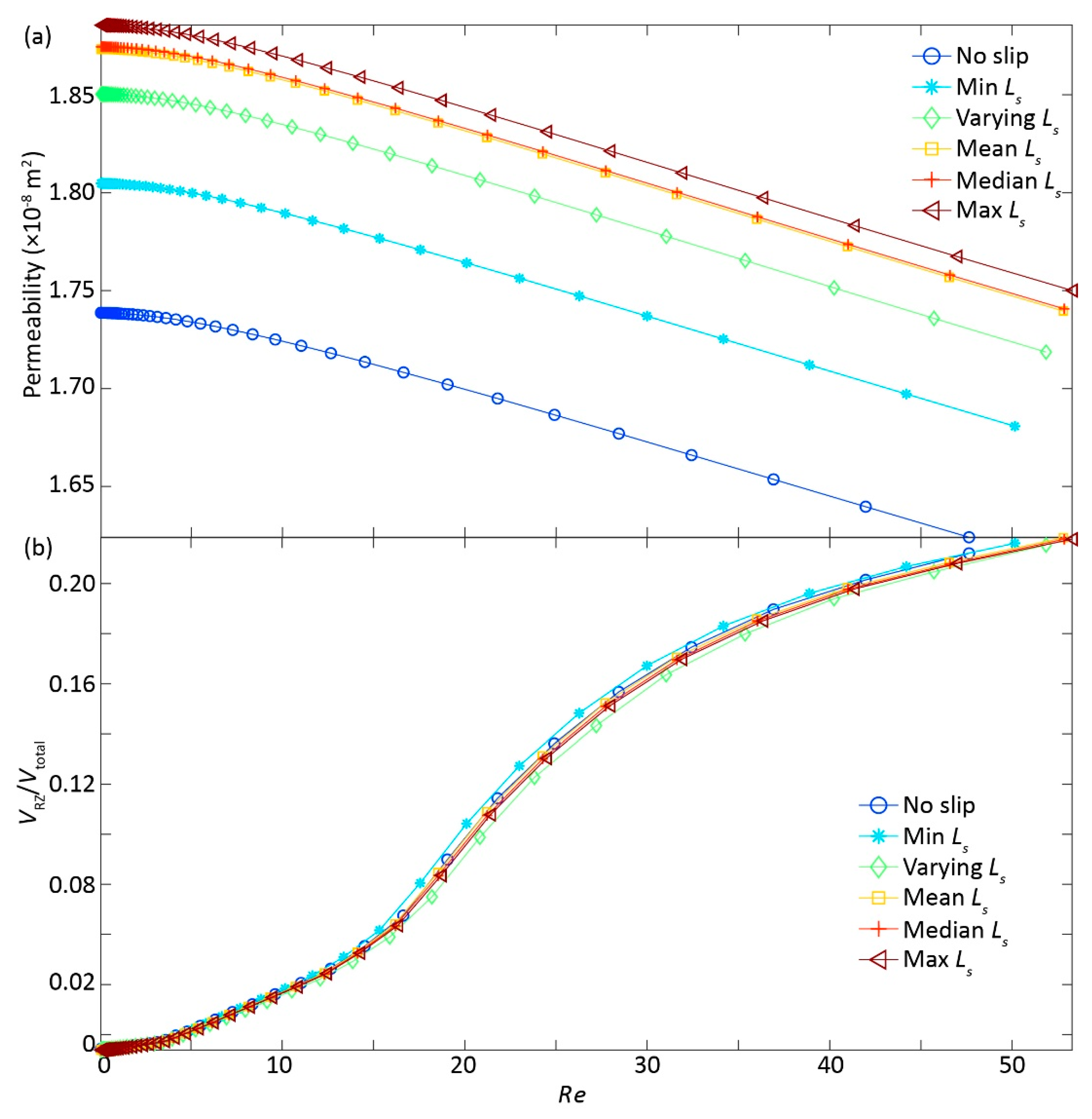
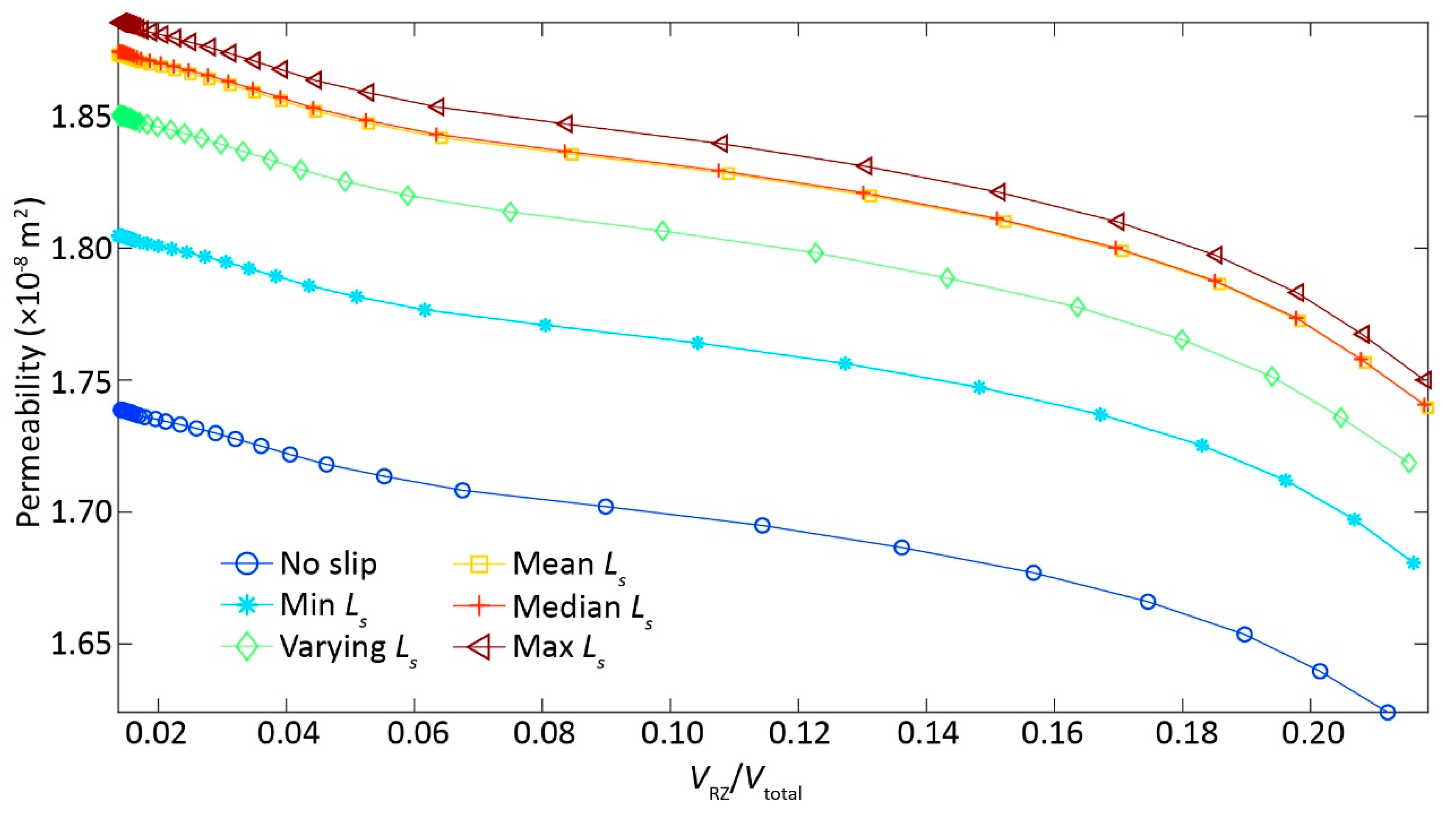
3.2. Inertial Effects on Reducing Permeability
3.3. Slippery Effects on Enhancing Permeability
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Christensen, M.; Tanino, Y. Enhanced permeability due to apparent oil/brine slippage in limestone and its dependence on wettability. Geophys. Res. Lett. 2017, 44, 6116–6123. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Wang, L. Scale-dependent Poiseuille flow alternatively explains enhanced dispersion in geothermal environments. Hydrol. Process. 2019, 33, 527–534. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, L.; James, S.C. When can the local advection–dispersion equation simulate non-Fickian transport through rough fractures? Stoch. Environ. Res. Ris. Assess. 2019, 33, 931–938. [Google Scholar] [CrossRef]
- Yang, Z.; Niemi, A.; Fagerlund, F.; Illangasekare, T.; Detwiler, R.L. Dissolution of dense non-aqueous phase liquids in vertical fractures: Effect of finger residuals and dead-end pools. J. Contam. Hydrol. 2013, 149, 88–99. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cardenas, M.B. Non-Fickian transport through two-dimensional rough fractures: Assessment and prediction. Water Resour. Res. 2014, 50, 871–884. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Nowamooz, A.; Radilla, G.; Fourar, M. Non-Darcian two-phase flow in a transparent replica of a rough-walled rock fracture. Water Resour. Res. 2009, 45, W07406. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B. Linear permeability evolution of expanding conduits due to feedback between flow and fast phase change. Geophys. Res. Lett. 2017, 44, 4116–4123. [Google Scholar] [CrossRef]
- Elkhoury, J.E.; Ameli, P.; Detwiler, R.L. Dissolution and deformation in fractured carbonates caused by flow of CO2-rich brine under reservoir conditions. Int. J. Greenh. Gas. Cont. 2013, 16, S203–S215. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B. Connecting Pressure-Saturation and Relative Permeability Models to Fracture Properties: The Case of Capillary-Dominated Flow of Supercritical CO2 and Brine. Water Resour. Res. 2018, 54, 6965–6982. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L.; Shao, J.; Liu, X.; Hao, Q.; Xing, L.; Zheng, L.; Xiao, Y. Parallel Processing Transport Model MT3DMS by Using OpenMP. Int. J. Environ. Res. Public Health 2018, 15, 1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M. Modification of the Local Cubic Law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 2015, 51, 2064–2080. [Google Scholar] [CrossRef]
- Brush, D.J.; Thomson, N.R. Fluid flow in synthetic rough-walled fractures: Navier-Stokes, Stokes, and local cubic law simulations. Water Resour. Res. 2003, 39, 1085. [Google Scholar] [CrossRef]
- Chaudhary, K.; Cardenas, M.B.; Deng, W.; Bennett, P.C. The role of eddies inside pores in the transition from Darcy to Forchheimer flows. Geophys. Res. Lett. 2011, 38, L24405. [Google Scholar] [CrossRef]
- Qian, J.; Chen, Z.; Zhan, H.; Guan, H. Experimental study of the effect of roughness and Reynolds number on fluid flow in rough-walled single fractures: A check of local cubic law. Hydrol. Process. 2011, 25, 614–622. [Google Scholar] [CrossRef]
- Qian, J.; Zhan, H.; Chen, Z.; Ye, H. Experimental study of solute transport under non-Darcian flow in a single fracture. J. Hydrol. 2011, 399, 246–254. [Google Scholar] [CrossRef]
- Zhou, J.-Q.; Chen, Y.F.; Wang, L.C.; Cardenas, M.B. Universal Relationship between Viscous and Inertial Permeability of Geologic Porous Media. Geophys. Res. Lett. 2019, 46, 1441–1448. [Google Scholar] [CrossRef]
- Lee, H.-B.; Yeo, I.W.; Lee, K.-K. Water flow and slip on NAPL-wetted surfaces of a parallel-walled fracture. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Zhou, J.-Q.; Wang, L.; Li, C.; Tang, H.; Wang, L. Effect of fluid slippage on eddy growth and non-Darcian flow in rock fractures. J. Hydrol. 2020, 581, 124440. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, L.; Wang, T.; Singh, K.; Wang, Z.-L.; Chen, X. Can homogeneous slip boundary condition affect effective dispersion in single fractures with Poiseuille flow? J. Hydrol. 2020, 581, 124385. [Google Scholar] [CrossRef]
- Zhou, J.-Q.; Wang, L.; Chen, Y.-F.; Cardenas, M.B. Mass Transfer between Recirculation and Main Flow Zones: Is Physically Based Parameterization Possible? Water Resour. Res. 2019, 55, 345–362. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.Q.; Wang, M.; Wang, L.C.; Chen, Y.F.; Zhou, C.B. Emergence of nonlinear laminar flow in fractures during shear. Rock Mech. Rock Eng. 2018, 51, 3635–3643. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Navier-Stokes flow and transport simulations using real fractures shows heavy tailing due to eddies. Geophys. Res. Lett. 2007, 34, L14404. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zhan, H.; Liu, Y.; Qi, H.; Huang, L.; Wei, Z.; Liu, Z. Effects of Slip Length and Inertia on the Permeability of Fracture with Slippery Boundary Condition. Int. J. Environ. Res. Public Health 2020, 17, 3817. https://doi.org/10.3390/ijerph17113817
Liu B, Zhan H, Liu Y, Qi H, Huang L, Wei Z, Liu Z. Effects of Slip Length and Inertia on the Permeability of Fracture with Slippery Boundary Condition. International Journal of Environmental Research and Public Health. 2020; 17(11):3817. https://doi.org/10.3390/ijerph17113817
Chicago/Turabian StyleLiu, Benhua, Hao Zhan, Yiran Liu, Huan Qi, Linxian Huang, Zhengrun Wei, and Zhizheng Liu. 2020. "Effects of Slip Length and Inertia on the Permeability of Fracture with Slippery Boundary Condition" International Journal of Environmental Research and Public Health 17, no. 11: 3817. https://doi.org/10.3390/ijerph17113817
APA StyleLiu, B., Zhan, H., Liu, Y., Qi, H., Huang, L., Wei, Z., & Liu, Z. (2020). Effects of Slip Length and Inertia on the Permeability of Fracture with Slippery Boundary Condition. International Journal of Environmental Research and Public Health, 17(11), 3817. https://doi.org/10.3390/ijerph17113817



