A Universal Physics-Based Model Describing COVID-19 Dynamics in Europe
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Proposed Self-Organizing Diffusion Model (SODM)
- The control parameter is defined as the density , where Q is the total charge distributed over the whole lattice, expressed in charge units (Q = Σqij), and P is the total population; i.e., the number of sites of the (L × L) lattice, with L being the length of the lattice.
- The percentage of the active sites S over the lattice population P defines the order parameter . The sites corresponding to those carriers (M) are named active sites. As a result, by following the evolution of M, a good quantitative description about the evolution of the diffusion can be obtained.
- As mentioned above, for an n-level diffusion, each site can dispense its charge (n/4) to each of its nearest neighbors, regardless of how many charge units it owns (qij). This charge transfer is controlled by a random process; thus, the process occurs with a probability of 0.5.
- This version of the model is closed; thus, it is not externally supplied with charge at all. This does not exclude the possibility of being considered as an open system after the proper modification to the rules concerning its perimeter points.
- Regarding the initial conditions, these have significant roles in the model, and they are distinguished into two categories:
- ○
- In the first category, the available charge is initially distributed over the lattice sites in a random, uniform way [30]. As a result, some sites will initially be found with zero charge, while others will present a large amount of charge. Then, the initially distributed charge will be diffused over the whole lattice.
- ○
- In the second category, the initially available charge is again randomly distributed, but this time only at the lattice boundary-sites. In this case, the charge is expected to diffuse from the perimeter towards the interior of the lattice.
- Sweeping all lattice sites is a recurrent procedure. The order parameter—i.e., the percentage of the active carriers—as a function of the algorithmic time is registered (each unit of the algorithmic time is considered to be one lattice sweep). Thus, a time series corresponding to the temporal evolution of the percentage of the active sites is generated and comprises the simulation’s output.
- Isolation between all lattice sites can be implemented in a four-level communication approach, meaning that the capability to pass charge (communications) from one lattice site to its nearest neighbors (comprising its environment) can be reduced. In this model version (a square lattice), the possible contact reduction levels are as follows:
- ○
- 75% reduction; i.e., each site transfers charge to 1 out of 4 of its nearest neighbors.
- ○
- 50% reduction; i.e., each site transfers charge to 2 out of 4 of its nearest neighbors.
- ○
- 25% reduction; i.e., each site transfers charge to 3 out of 4 of its nearest neighbors.
- ○
- No reduction—in this case, charge may be transferred to all four nearest neighbors.
2.2. SODM and the COVID-19 Viral Epidemic
- The active lattice sites of the SODM correspond to the infected active population due to an epidemic.
- The algorithmic time is measured in time units. Each time unit corresponds to a lattice sweep. It is apparent that the epidemic real time in days matches a number of lattice sweeps; i.e., a number of algorithmic time units.
- The charge in each site (qij) in the SODM equivalently corresponds to the infection charge transferred during the spread of an epidemic and not to the virus charge in the medical sense (in the human body).
- The SODM models the infection diffusion and not the viral (in the medical sense) spread.
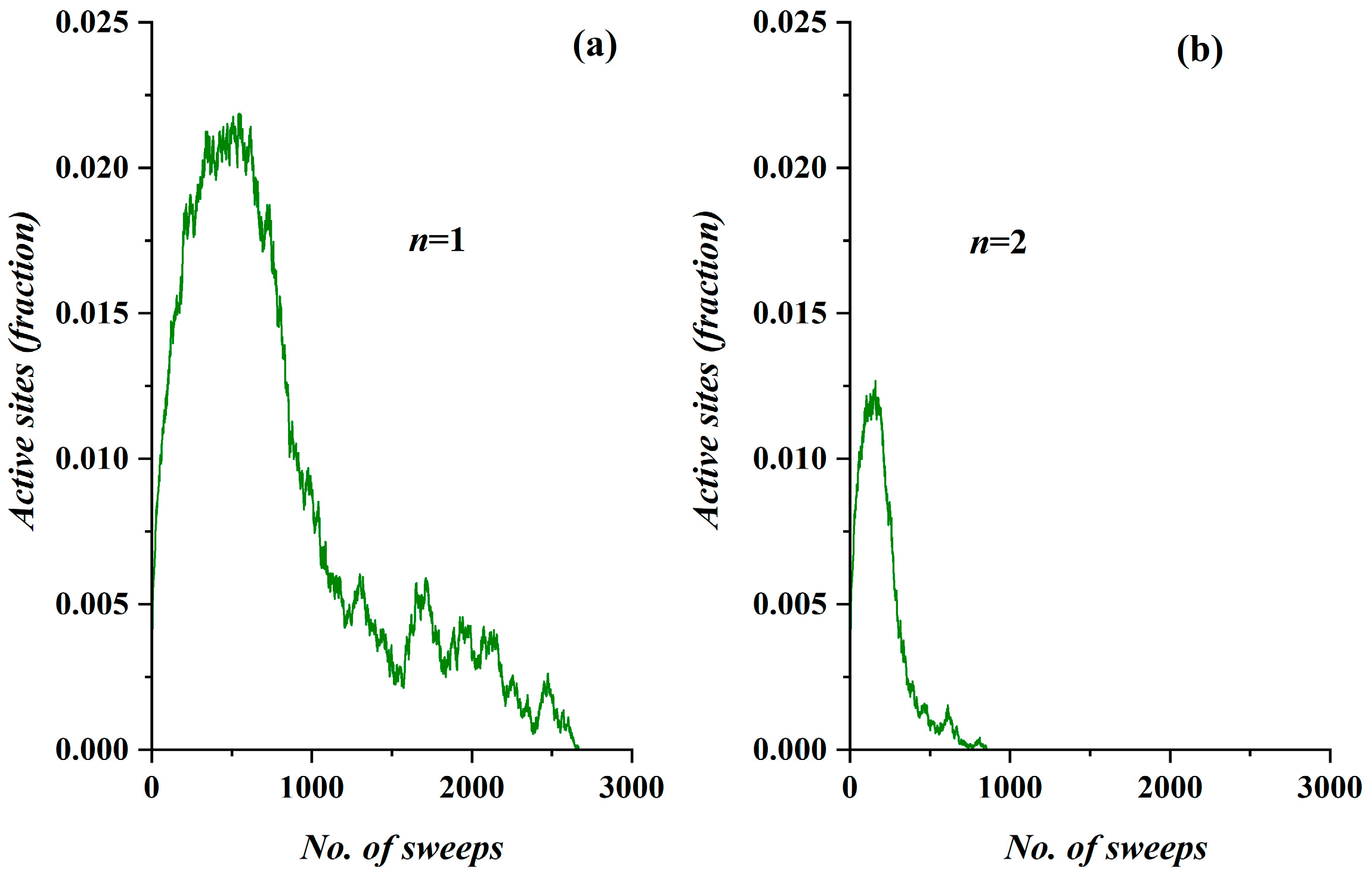
- The model incorporates four activity levels regarding the capability of a site to pass charge to its nearest neighbors. The strongest site activity (n = 1) means that even the site with the least charge (qij = 1 charge unit) is capable of diffusing its charge. For an epidemic, this means that even the carrier with the least virus charge (which should not be confused with the virus charge in the medical sense) can transmit the virus and indeed does so. Such a behavior could describe the most aggressive and easily diffused viruses, such as COVID-19. Thus, within the frame of the SODM, an activity level of n = 1 could describe epidemics caused by aggressive viruses. The diffusion of various, less aggressive, seasonal viruses, according to their characteristics, could be described by the other levels of activity with n > 1; for instance, for a less aggressive virus corresponding to activity level n = 2, the sites that have a charge qij = 1 charge unit are inactive, and so on.
- The effect of measures restricting physical contact (physical or social distancing) is also incorporated within the proposed SODM. As already described above, this is modeled in four levels due to the form of the lattice, which is a square. As a result, the allowed communication of a site with 1 out of its 4 nearest neighbors corresponds to restrictive measures of 75% (strict isolation policies), while less stringent distancing measures could be considered within the proposed SODM.
3. Results
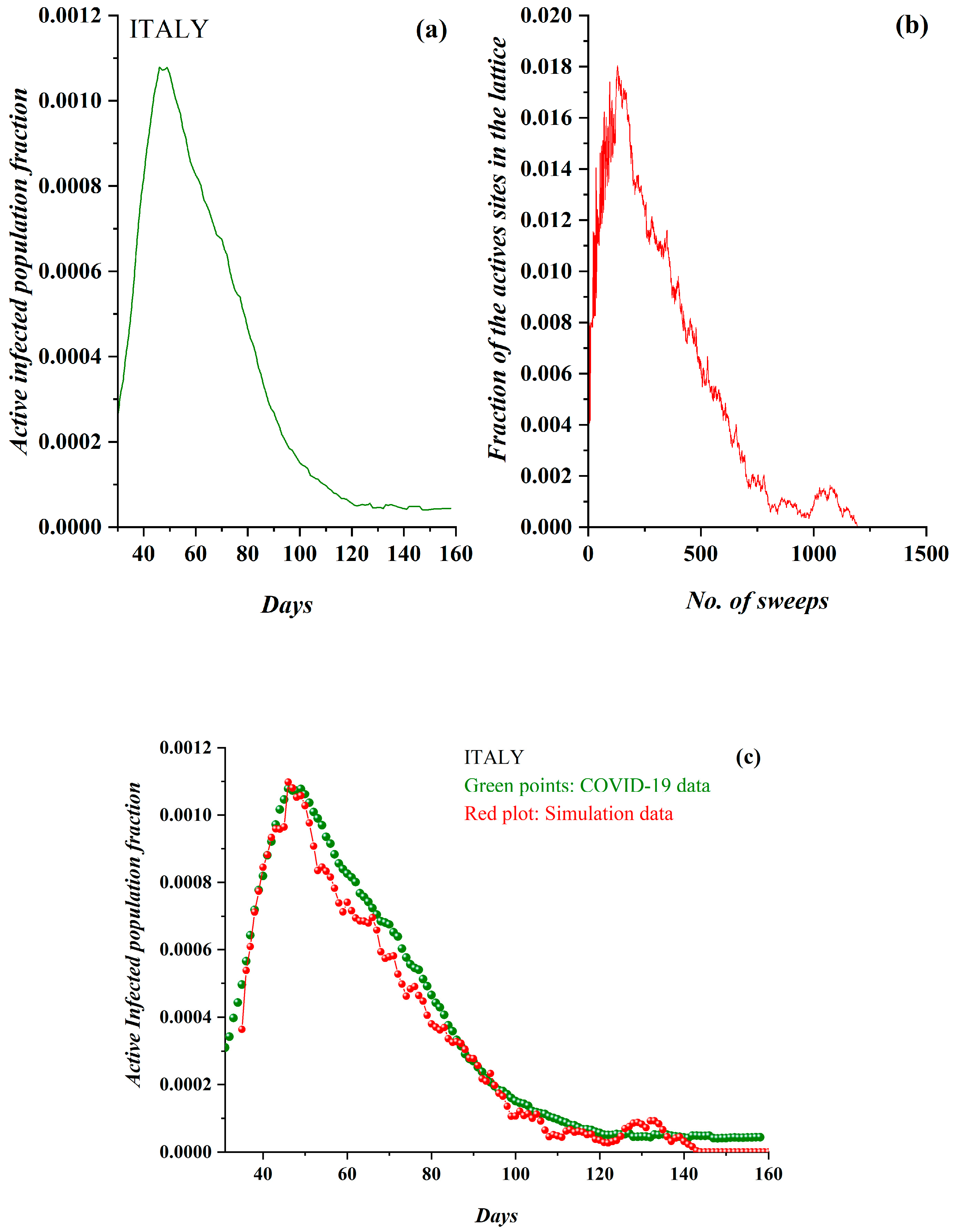
3.1. Comparative Results of the SODM and Real COVID-19 Epidemic Data
3.2. Autocorrelation Function of Epidemic Spread
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Ion, S.; Marinoschi, G. A self-organizing criticality mathematical model for contamination and epidemic spreading. Discret. Contin. Dyn. Syst. B 2017, 22, 383–405. [Google Scholar] [CrossRef] [Green Version]
- Rhodes, C.; Jensen, H.J.; Anderson, R.M. On the critical behaviour of simple epidemics. Proc. R. Soc. B Biol. Sci. 1997, 264, 1639–1646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van de Leemput, I.A.; Wichers, M.; Cramer, A.O.J.; Borsboom, D.; Tuerlinckx, F.; Kuppens, P.; van Nes, E.H.; Viechtbauer, W.; Giltay, E.J.; Aggen, S.H.; et al. Critical slowing down as early warning for the onset and termination of depression. Proc. Natl. Acad. Sci. USA 2014, 111, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Stollenwerk, N. Self-organized criticality in human epidemiology. AIP Conf. Proc. 2005, 779, 191–194. [Google Scholar]
- Brett, T.S.; Ajelli, M.; Liu, Q.-H.; Krauland, M.G.; Grefenstette, J.J.; Van Panhuis, W.G.; Vespignani, A.; Drake, J.M.; Rohani, P. Detecting critical slowing down in high-dimensional epidemiological systems. PLoS Comput. Biol. 2020, 16, e1007679. [Google Scholar] [CrossRef] [Green Version]
- Melin, P.; Monica, J.C.; Sanchez, D.; Castillo, O. Analysis of Spatial Spread Relationships of Coronavirus (COVID-19) Pandemic in the World using Self Organizing Maps. Chaos Solitons Fractals 2020, 138, 109917. [Google Scholar] [CrossRef]
- Nadim, S.K.S.; Ghosh, I.; Chattopadhyay, J. Short-term predictions and prevention strategies for COVID-19: A model-based study. arXiv 2020, arXiv:2003.018150. [Google Scholar]
- Holmdahl, I.; Buckee, C. Wrong but Useful—What Covid-19 Epidemiologic Models Can and Cannot Tell Us. N. Engl. J. Med. 2020, 383, 303–305. [Google Scholar] [CrossRef]
- Weitz, J.S.; Beckett, S.J.; Coenen, A.R.; Demory, D.; Dominguez-Mirazo, M.; Dushoff, J.; Leung, C.-Y.; Li, G.; Măgălie, A.; Park, S.W.; et al. Modeling shield immunity to reduce COVID-19 epidemic spread. Nat. Med. 2020, 26, 849–854. [Google Scholar] [CrossRef]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.Y.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, eaba9757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, S.; Chen, H. Modeling the epidemic dynamics and control of COVID-19 outbreak in China. Quant. Biol. 2020, 8, 11–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Franco, E.; Mohler, G.; Short, M.B.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 202006520. [Google Scholar] [CrossRef]
- Tsiotas, D.; Magafas, L. The Effect of Anti-COVID-19 Policies on the Evolution of the Disease: A Complex Network Analysis of the Successful Case of Greece. Physics 2020, 2, 17. [Google Scholar] [CrossRef]
- Maugeri, A.; Barchitta, M.; Battiato, S.; Agodi, A. Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy. Int. J. Environ. Res. Public Health 2020, 17, 4964. [Google Scholar] [CrossRef]
- Demertzis, K.; Tsiotas, D.; Magafas, L. Modeling and Forecasting the COVID-19 Temporal Spread in Greece: An Exploratory Approach based on Complex Network Defined Splines. Int. J. Environ. Res. Public Health 2020, 17, 4693. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, C.; Anderson, R. Epidemic Thresholds and Vaccination in a Lattice Model of Disease Spread. Theor. Popul. Biol. 1997, 52, 101–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keeling, M.J.; Eames, K.T.D. Νetworks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosmidis, K.; Macheras, P. A fractal kinetics SI model can explain the dynamics of COVID-19 epidemics. PLoS ONE 2020, 15, e0237304. [Google Scholar] [CrossRef]
- Huang, K.; Holbrow, C.H. Statistical Mechanics. Phys. Today 1965, 18, 92. [Google Scholar] [CrossRef]
- Wong, C.-Y. Introduction to High-Energy Heavy-Ion Collisions; World Scientific Publishing: Singapore, 1994. [Google Scholar]
- Contoyiannis, Y.; Stavrinides, S.G.; Hanias, M.P.; Kampitakis, M.; Papadopoulos, P.; Picos, R.; Potirakis, S.M. Critical Lattice-Dynamics in Self-Organized Diffusion, Manuscript in preparation. 2020.
- Contoyiannis, Y.; Diakonos, F. Criticality and intermittency in the order parameter space. Phys. Lett. A 2000, 268, 286–292. [Google Scholar] [CrossRef]
- Contoyiannis, Y.F.; Diakonos, F.K.; Malakis, A. Intermittent Dynamics of Critical Fluctuations. Phys. Rev. Lett. 2002, 89, 35701. [Google Scholar] [CrossRef]
- Contoyiannis, Y.F.; Diakonos, F.K. Abrupt transition in a sandpile model. Phys. Rev. E 2006, 73, 031303. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wu, Y.; Zhang, W. Comprehensive identification and isolation policies have effectively suppressed the spread of COVID-19. Chaos Solitons Fractals 2020, 139, 110041. [Google Scholar] [CrossRef]
- Our World in Data. Available online: https://ourworldindata.org/coronavirus-data-explorer?zoomToSelection=true&casesMetric=true&interval=total (accessed on 31 July 2020).
- Hassani, H.; Leonenko, N.; Patterson, K. The sample autocorrelation function and the detection of long-memory processes. Phys. A Stat. Mech. Appl. 2012, 391, 6367–6379. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef] [Green Version]
- Beckley, R.; Weatherspoon, C.; Alexander, M.; Chandler, M.; Johnson, A.; Batt Ghan, S. Modeling Epidemics with Differential Equations; Tennessee State University Internal Report 2013; Tennessee State University: Nashville, TN, USA, 2020. [Google Scholar]
- Miller, J.C. Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes. Infect. Dis. Model. 2017, 2, 35–55. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Teng, Z.; Nieto, J.J.; Torres, A. Analysis of an SIR Epidemic Model with Pulse Vaccination and Distributed Time Delay. J. Biomed. Biotechnol. 2007, 2007, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Croccolo, F.; Roman, H.E. Spreading of infections on random graphs: A percolation-type model for COVID-19. Chaos Solitons Fractals 2020, 139, 110077. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Zhang, D.; Peng, L.; Zhuge, C.; Hong, L. Rational evaluation of various epidemic models based on the COVID-19 data of China 2020. arXiv 2020, arXiv:2003.05666. [Google Scholar]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1997, 49, 435479. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contoyiannis, Y.; Stavrinides, S.G.; P. Hanias, M.; Kampitakis, M.; Papadopoulos, P.; Picos, R.; M. Potirakis, S. A Universal Physics-Based Model Describing COVID-19 Dynamics in Europe. Int. J. Environ. Res. Public Health 2020, 17, 6525. https://doi.org/10.3390/ijerph17186525
Contoyiannis Y, Stavrinides SG, P. Hanias M, Kampitakis M, Papadopoulos P, Picos R, M. Potirakis S. A Universal Physics-Based Model Describing COVID-19 Dynamics in Europe. International Journal of Environmental Research and Public Health. 2020; 17(18):6525. https://doi.org/10.3390/ijerph17186525
Chicago/Turabian StyleContoyiannis, Yiannis, Stavros G. Stavrinides, Michael P. Hanias, Myron Kampitakis, Pericles Papadopoulos, Rodrigo Picos, and Stelios M. Potirakis. 2020. "A Universal Physics-Based Model Describing COVID-19 Dynamics in Europe" International Journal of Environmental Research and Public Health 17, no. 18: 6525. https://doi.org/10.3390/ijerph17186525
APA StyleContoyiannis, Y., Stavrinides, S. G., P. Hanias, M., Kampitakis, M., Papadopoulos, P., Picos, R., & M. Potirakis, S. (2020). A Universal Physics-Based Model Describing COVID-19 Dynamics in Europe. International Journal of Environmental Research and Public Health, 17(18), 6525. https://doi.org/10.3390/ijerph17186525








