Abstract
There are multiple formulas for estimating the percentage of body fat (BF%). Clínica Universidad de Navarra-Body Adiposity Estimator (CUN-BAE) is one of the most used formulas because of its accuracy and its association with cardiovascular pathologies. Equation Córdoba for Estimation of Body Fat (ECORE-BF) was developed to simplify the calculation of BF% while maintaining a similar level of accuracy. The objective was to compare ECORE-BF in a large sample of Spanish workers using CUN-BAE as a reference. A cross-sectional study was carried out on 196,844 participants. The BF% was estimated using different formulas: relative fat mass (RFM), Palafolls, Deurenberg, and ECORE-BF. The accuracy of the estimation was determined using Lin’s concordance correlation coefficient (CCC) and the Bland–Altman method, using CUN-BAE as the reference method. ECORE-BF reached the highest concordance (CCC = 0.998). It also showed the lowest mean difference (−0.0077) and the tightest agreement limits (−0.9723, 0.9569) in the Bland–Altman test. In both analyses, it remained robust even when separating the analyses by sex, nutritional status, or age. ECORE-BF presented as the most straightforward and most accurate equation for the estimation of BF%, remaining robust regardless of population characteristics.
1. Introduction
Overweight and obesity, defined as the accumulation of fatty tissue, are global public health problems [1,2] and their prevalence has increased steadily in recent years [3]. This epidemic has made chronic diseases increasingly common worldwide, showing high rates in clinical and community settings. An abnormal amount of fat tissue is a risk factor for type 2 diabetes mellitus, hypertension, atherogenic dyslipidemia, and cardiovascular disease, among others [4,5,6].
Body Mass Index (BMI) has been traditionally used for the assessment of nutritional status. However, its use in isolation is controversial because it does not address the distribution of body compartments. Moreover, it does not consider the influence of other variables such as age or sex, which are fundamental in estimating body composition [7]. These issues cause it to have a low correlation and concordance with body fat (BF) [8,9]. Therefore, the same BMI value can be associated with a wide range of body fat percentages, from healthy to pathological, making clinical assessment difficult [10].
Many tools are available to obtain BF accurately, such as dual-energy X-ray absorptiometry (DXA), magnetic resonance imaging (MRI), and air displacement plethysmography (ADP), among others [11]. However, their large size (which makes them difficult to transport), high cost, complexity, and the use of radiation, among other problems, make them challenging to use in many clinical and community settings [8,12]. Different formulas and other indices from anthropometric variables have been proposed in various populations to avoid these problems, and they have shown a higher correlation with BF than BMI [13,14,15]. Additionally, these equations are simple to use, accessible, and have shown a strong association with various chronic diseases [16].
Among these different equations, the Clínica Universidad de Navarra-Body Adiposity Estimator (CUN-BAE) stands out. CUN-BAE was validated using ADP as a gold standard, and it is widely used in clinical studies to discriminate against various cardiovascular pathologies [16,17]. The complexity of the formula, composed of nine components, makes it challenging to use in real clinical settings where the appropriate software is not available. Several authors have developed alternatives to the equation in order to respect Ockam’s razor principle and facilitate accessibility in any condition [15,18]. In our group, the Equation Córdoba for Estimation of Body Fat (ECORE-BF) was developed [15]. It shows a very high concordance (0.960) with CUN-BAE and requires only three components for its calculation. However, the equation has not been tested in a large sample with different characteristics from those used for its development.
Therefore, the objective of the study is to compare ECORE-BF with different BF prediction equations in a large sample of Spanish workers.
2. Materials and Methods
2.1. Study Design, Population, and Sample
A cross-sectional study was carried out on the working population of the Balearic Islands (Spain) belonging to different productive sectors (public administration, services industries, healthcare, or postal office). The sample was selected from the workers who carried out health surveillance in the period from 2012 to 2016. Prior to each occupational health examination day, workers were assigned a number, and half of them were selected using a random number table. Workers who had been selected were invited to participate in the study during the occupational health examination. The following inclusion criteria were considered: aged 18 to 65 years, agreement to participate in the study, and gainfully employed. A total of 196,844 workers participated in the study sample.
2.2. Study Variables and Measurement
The body fat percentage (BF%) was estimated through different formulas that have calculations based on BMI, waist circumference (WC), or both. The formulas used were CUN-BAE (gold standard) [17], an equation formed by nine components and that uses age, BMI, and sex for its calculation; ECORE-BF [15], which works with natural logarithm of body mass index (lnBMI), age, and sex; relative fat mass (RFM) [13], which includes height, WC, and sex; Palafolls [14], which uses BMI, WC, and sex; and Deurenberg [19], which utilizes BMI, sex, and age. The formulas used are specified in Table 1.

Table 1.
Estimation formulas.
In addition, age (years), sex (female/male), height (cm), weight (kg), BMI (kg/m2), and WC (cm) were collected. Nutritional status was classified according to the WHO criteria for BMI [20]. CUN-BAE and cut-off points for Caucasians were used for BF% (for women: normal weight, <30%; overweight, 30.1–35%; obese, >35.1%; and for men: normal weight, <20%; overweight, 20.1–25%; obese, >25.1%) [21].
Anthropometric variables were measured according to the recommendations of the International Standards for Anthropometric Assessment of International Society for the Advancement of Kinanthropometry (ISAK) [22]. The weight was measured with an electronic scale (Seca 700 scale, Seca GmbH, Hambrug) with an accuracy of 0.1 kg. The height was measured with a stadiometer (Seca 220 (CM) telescopic height rod for column scales, Seca GmbH, Hamburg) with an accuracy of 0.5 cm. The WC was measured at the midpoint between the last rib and the iliac crest. All measurements were made by trained staff to minimize the coefficient of variation. Each measurement was made three times, and the average was registered.
2.3. Ethical and Legal Aspects
All of the workers were informed, verbally and in writing, of the research objectives before being enrolled. Informed consent was obtained from each in compliance with the current regulations. The study’s protocol complied with the Declaration of Helsinki for conducting medical research involving human subjects and was approved by the Balearic Ethical Committee of Clinical Research (CEI-IB Ref. No:1887). No patients were involved in data analysis or manuscript writing, and the results of the research will not be disseminated to the patients.
2.4. Statistical Analysis
The quantitative variables are presented as the mean and standard deviation, and the qualitative values displayed as absolute and relative frequencies.
To contrast the goodness-of-fit to a normal distribution of the data from the quantitative variables, the Kolmogorov–Smirnov test with the Lilliefors correction was employed. The Student’s t-test for two means and ANOVA for three or more means was performed for the bivariate hypothesis contrast. For the correlation between the quantitative variables, the Pearson’s correlation coefficient (r) was used.
We also analyzed the degree of concordance with the reference method quantitatively, computing the Lin’s concordance correlation coefficient (CCC), and graphically, with the Bland–Altman method. Correlation and concordance analyses were computed according to sex, nutritional status (BMI), and quartiles of age.
For all of the statistical analyses, the probability of an α error of below 5% (p < 0.05) was considered statistically significant. Confidence intervals were calculated at 95%. For the statistical analysis, IBM SPSS Statistics 22.0 software (IBM, Chicago, IL, USA) and Epidat 4.2. (Department of Sanidade, Xunta de Galicia, Galicia, Spain) were used.
3. Results
Of the 196,844 workers, 41.7% were women. The overall mean age was 40 (SD 10.6) years. The BF% was 29.5% (SD 8.2) and higher in women (p < 0.001). Following the BMI criteria, 36.1% (95% CI: 35.9–36.3) and 17.8% (95% CI: 17.6–18) of the subjects were overweight and obese, respectively. All variables analyzed showed statistically significant differences between men and women (p < 0.001) (Table 2).

Table 2.
Descriptive characteristics of the sample.
3.1. Comparison of the Different Estimation Formulas and Adiposity Indexes
3.1.1. Correlations between the Different Formulas and CUN-BAE
ECORE-BF showed the highest correlation values with CUN-BAE in general, in women, and in men, followed by Palafolls and Deurenberg. In the case of these latter formulas, the correlation decreased when the analysis was separated by sex. Additionally, the analysis of linear correlations according to the BMI categories and age showed that ECORE-BF was the most robust equation. Palafolls and Deurenberg showed similar values, although lower than that of ECORE-BF. Finally, RFM was the equation with the lowest correlation values, especially when separating the analysis according to sex and in participants with a healthy weight (Table 3).

Table 3.
Bivariate correlations between study formulas and CUN-BAE.
3.1.2. Lin’s Concordance between the Different Formulas and CUN-BAE
ECORE-BF achieved the highest concordance, remaining robust after separating the analysis between men and women, BMI categories, and age. Something similar was observed in the case of Deurenberg, although the CCC values were lower. Palafolls showed a concordance of 0.836 in the total sample. However, when the analysis was separated according to sex, BMI categories, and age, the CCC decreased in most groups, especially in men, participants with a normal weight, and those under 32 years old. The CCC increased in the case of obesity status and those over 49 years old. Finally, RFM showed the lowest concordance values, a tendency highlighted by a CCC of 0.527 for the obesity group (Table 4).

Table 4.
Lin’s concordance correlation coefficient between study formulas and CUN-BAE.
The Bland–Altman graphics (Figure 1) showed that ECORE-BF was the prediction equation with the smallest difference in means and the tightest agreement limits (Table 5). In other words, the estimations with ECORE-BF were those that showed the smallest dispersion when compared with those of CUN-BAE; moreover, the results remained consistent in men, women, all BMI categories, and all age groups. The rest of the equations studied showed higher mean differences, as well as more open limits of agreement, evidenced by a higher dispersion according to CUN-BAE.
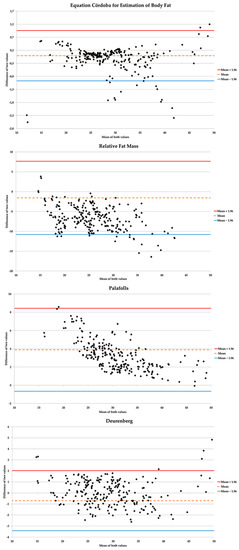
Figure 1.
Concordance graphs between study formulas and CUN-BAE (gold standard).

Table 5.
Mean differences between formulas and CUN-BAE.
4. Discussion
Our study indicates that ECORE-BF shows a high concordance with CUN-BAE, a widely used method to estimate body fat percentage in the general population. The estimation and distribution of body fat have been widely studied, mainly because of its involvement in the development of various chronic diseases [23]. In this context, several formulas based on anthropometric measurements have been developed to replace more complicated and expensive tools [13,14,15].
ECORE-BF is shown to be an accessible and easy to calculate alternative that has a high predictive capacity [15]. Our results show an excellent clinical concordance with CUN-BAE, reaching a value of 0.998 in the total sample, which is higher than that observed in the original study (Intraclass Correlation Coefficient= 0.960). This concordance remained stable in all performed analyses, which confirms its robustness regardless of the population where it is applied. Furthermore, a mean difference close to 0 was found, with very close agreement limits (Low Limit of Agreement (LLA) = −0.9723, Upper Limit of Agreement (ULA) = 0.9569), improving the results found in the development of the equation (Mean Difference (MD) = 1.819; LLA = −2.256, ULA = 5.895) [15]. It should also be noted that of the rest of the formulas studied, the one proposed by Deurenberg et al. was the only one that showed a similar agreement to ECORE-BF (CCC = 0.981), although the dispersion in the estimate was higher (MD = 0.70; LLA = −3.42, ULA = 2.02) than ECORE-BF.
Although BMI alone correlates significantly with BF%, it has a low predictive capacity [7,24,25]. However, when other variables, such as sex and age, are incorporated into the analysis, the accuracy improves [12,15,17]. Hastuti et al. developed several formulas using anthropometric measurements. They showed that equations using BMI and sex produced good results in explaining variability (R2 = 0.668) and in the limits of agreement (−0.2 ± 4.3 in men and 0.4 ± 5.4 in women) [24]. The rest of the formulas developed by these authors presented similar precision results. However, for their calculation, they required variables that were difficult to obtain, such as skin folds [24].
Another variable used for the estimation of the BF% is WC. When WC is included in the regression models, it achieves positive results in explained variability and concordance but maintains a high dispersion in the estimates [26]. Palafolls and RFM are two formulas that incorporate WC into their analyses. Palafolls, which uses BMI, sex, and WC, was developed following the same methodology as that used for ECORE-BF, but in a smaller sample [14]. Our results show that the CCC was 0.836, although the dispersion in the estimate was higher than that shown by ECORE-BF (MD = 3.88; LLA = 0.66, UPA = 8.43). The dispersion decreased in three of the four age groups in which the analysis was separated. Furthermore, RFM, developed using the DXA as a reference, showed the worst results of the equations studied. Although the linear correlation with CUN-BAE was good (r = 0.821), RFM showed the lowest degree of agreement (CCC = 0.765), results that align with those shown by other authors. Paek et al. studied the validity of RFM in a sample of Korean adults; the results showed that it had a high dispersion in the estimate, with a tendency to overestimate, and a predictive capacity similar to that shown by the BMI [27]. Although Guzmán-León et al. stated that RFM presents greater consistency in the estimation of BF% than BMI, they did not carry out a study of clinical, quantitative, or graphic concordance, and conclusions had been drawn from the estimates obtained through a new linear regression model. In other words, to determine the accuracy of RFM in their sample, they carried out a new regression model with the equation, which implies an adjustment with new beta coefficients. This calculation guarantees that the formula explains a higher variability than what would be achieved without the original equation’s adjustment [28]. Additionally, our results show that the degree of agreement with CUN-BAE was higher in participants with normal weight and overweight (CCC = 0.741 and CCC = 0.767, respectively), dropping more than 0.2 points in those with obesity (CCC = 0.527). This decrease is because the BF% estimate is made using a central obesity indicator (WC), which means that it is not entirely accurate in people with a high overall BF%. Other developed equations that use WC as the adjustment variable also introduce weight, ensuring that a measure is available that accounts for total body mass [29].
Several authors have developed formulas for the estimation of BF% composed of a large number of variables. However, the results obtained do not improve on those achieved by simpler models, such as ECORE-BF [30]. Therefore, making the equations more complex does not guarantee greater precision in the estimation. Accessible models should be developed that help clinical staff diagnose overweight and obesity easily [31]. As mentioned above, equations based on anthropometric measurements (e.g., BMI) have shown good results [15,17,18,26]. However, these equations generally have limitations and are less accurate than those based on skin folds [32]. Nevertheless, they are widely used in the scientific literature and are good indicators of cardiovascular health [16,33,34]. ECORE-BF is, therefore, an alternative that can be used in specific clinical settings where qualified personnel are not available to take complex anthropometric measurements (e.g., skin folds). In short, all tools (DXA, ADP, equations based on anthropometry) may have some limitations [35,36], but knowing them and identifying which situations to use them in can be useful when interpreting the results they provide.
5. Study Limitations and Strengths
The main limitation of the study is that a gold standard, such as DXA or ADP, was not used. Future studies should validate ECORE-BF by using more accurate methods. However, ECORE-BF has demonstrated robustness in working populations regardless of characteristics and sample size. Finally, it is important to emphasize that ECORE-BF is validated only in the working Caucasian population. Therefore, in order to extend its use to populations with other characteristics, it must be validated in those populations or adapted to them, as has been done previously with other equations [37].
6. Conclusions
ECORE-BF has only three components, which makes it easy to calculate, regardless of the clinical setting in which it is used. Furthermore, the simplicity of obtaining the variables involved in the estimation reduces the need for highly qualified personnel trained in anthropometric measurement. Finally, the robustness found in men, women, and any age group or nutritional status guarantees the accuracy of the results in any worker to whom it is applied.
Author Contributions
Conceptualization, R.M.-L., M.R.-S., and G.M.-R.; methodology, A.M.Y., M.B.-V., and A.-A.L.-G.; formal analysis, R.M.-L.; investigation, A.-A.L.-G., A.M.Y., and M.B.-V.; data curation, A.M.Y. and M.B.-V.; original draft preparation, R.M.-L.; review and editing, A.M.Y., M.B.-V., M.R.-S., G.M.-R., and A.-A.L.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the field staff and participants of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haslam, D.; James, W.P.T. Obesity. Lancet 2005, 366, 1197–1209. [Google Scholar] [CrossRef]
- Blüher, M. Obesity: Global epidemiology and pathogenesis. Nat. Rev. Endocrinol. 2019, 15, 288–298. [Google Scholar] [CrossRef] [PubMed]
- NCD Risk Factor Collaboration. Worldwide trends in body-mass index, underweight, overweight, and obesity from 1975 to 2016: A pooled analysis of 2416 population-based measurement studies in 128·9 million children, adolescents, and adults. Lancet 2017, 390, 2627–2642. [Google Scholar] [CrossRef]
- Romero-Saldaña, M.; Fuentes-Jiménez, F.; Vaquero-Abellán, M.; Álvarez-Fernández, C.; Molina-Recio, G.; López-Miranda, J. New non-invasive method for early detection of metabolic syndrome in the working population. Eur. J. Cardiovasc. Nurs. 2016, 15, 549–558. [Google Scholar] [CrossRef]
- Kahn, S.E.; Hull, R.L.; Utzschneider, K.M. Mechanisms Linking Obesity to Insulin Resistance and Type 2 Diabetes. Nature 2006, 444, 840–846. [Google Scholar] [CrossRef]
- Lorenzatti, A.J.; Toth, P.P. New Perspectives on Atherogenic Dyslipidaemia and Cardiovascular Disease. Eur. Cardiol. 2020, 15, e04. [Google Scholar] [CrossRef] [PubMed]
- Ranasinghe, C.; Gamage, P.; Katulanda, P.; Andraweera, N.; Thilakarathne, S.; Tharanga, P. Relationship between Body mass index (BMI) and body fat percentage, estimated by bioelectrical impedance, in a group of Sri Lankan adults: A cross sectional study. BMC Public Health 2013, 13, 797. [Google Scholar] [CrossRef] [PubMed]
- Belarmino, G.; Horie, L.; Sala, P.; Torrinhas, R.; Heymsfield, S.; Waitzberg, D. Body adiposity index performance in estimating body fat in a sample of severely obese Brazilian patients. Nutr. J. 2015, 14, 130. [Google Scholar] [CrossRef]
- Silva, D.; Petroski, E.; Peres, M. Is high body fat estimated by body mass index and waist circumference a predictor of hypertension in adults? A population-based study. Nutr. J. 2012, 11, 112. [Google Scholar] [CrossRef] [PubMed]
- Smalley, K.J.; Knerr, A.N.; Kendrick, Z.V.; Colliver, J.A.; Owen, O.E. Reassessment of Body Mass Indices. Am. J. Clin. Nutr. 1990, 52, 405–408. [Google Scholar] [CrossRef] [PubMed]
- Borga, M.; West, J.; Bell, J.; Harvey, N.; Romu, T.; Heymsfield, S.B.; Leinhard, O.D. Advanced body composition assessment: From body mass index to body composition profiling. J. Investig. Med. 2018, 66, 1–9. [Google Scholar] [CrossRef]
- Chambers, A.; Parise, E.; Mccrory, J.; Cham, R. A comparison of prediction equations for the estimation of body fat percentage in non-obese and obese older Caucasian adults in the United States. J. Nutr. Health Aging 2014, 18, 586–590. [Google Scholar] [CrossRef]
- Woolcott, O.O.; Bergman, R.N. Relative fat mass (RFM) as a new estimator of whole-body fat percentage—A cross-sectional study in American adult individuls. Sci. Rep. 2018, 8, 10980. [Google Scholar] [CrossRef]
- Mill-Ferreyra, E.; Cameno-Carrillo, V.; Saúl-Gordo, H.; Camí-Lavado, M.C. Estimación del porcentaje de grasa corporal en función del índice de masa corporal y perímetro abdominal: Fórmula Palafolls. Semergen 2019, 45, 101–108. [Google Scholar] [CrossRef]
- Molina-Luque, R.; Romero-Saldaña, M.; Álvarez-Fernández, C.; Bennasar-Veny, M.; Álvarez-López, A.; Molina-Recio, G. Equation Córdoba: A Simplified Method for Estimation of Body Fat (ECORE-BF). Int. J. Environ. Res. Public Health 2019, 16, 4529. [Google Scholar] [CrossRef]
- Suliga, E.; Ciesla, E.; Gluszek-Osuch, M.; Rogula, T.; Gluszek, S.; Koziel, D. The Usefulness of Anthropometric Indices to Identify the Risk of Metabolic Syndrome. Nutrients 2019, 11, 2598. [Google Scholar] [CrossRef]
- Gomez-Ambrosi, J.; Silva, C.; Catalan, V.; Rodriguez, A.; Galofre, J.; Escalada, J.; Valentí, V.; Rotellar, F.; Romero, S.; Ramírez, B.; et al. Clinical Usefulness of a New Equation for Estimating Body Fat. Diabetes Care 2011, 35, 383–388. [Google Scholar] [CrossRef]
- Fuster-Parra, P.; Bennasar-Veny, M.; Tauler, P.; Yañez, A.; López-González, A.; Aguiló, A. A Comparison between Multiple Regression Models and CUN-BAE Equation to Predict Body Fat in Adults. PLoS ONE 2015, 10, e0122291. [Google Scholar] [CrossRef]
- Deurenberg, P.; Weststrate, J.A.; Seidell, J.C. Body mass index as a measure of body fatness: Age—And sex- specific prediction formulas. Br. J. Nutr. 1991, 65, 105–114. [Google Scholar] [CrossRef]
- World Health Organization. Body Mass Index-BMI. Available online: http://www.euro.who.int/en/health-topics/disease-prevention/nutrition/a-healthy-lifestyle/body-mass-index-bmi (accessed on 23 January 2019).
- Gómez-Ambrosi, J.; Silva, C.; Galofré, J.; Escalada, J.; Santos, S.; Millán, D.; Vila, N.; Ibañez, P.; Gil, M.J.; Valentí, V.; et al. Body mass index classification misses subjects with increased cardiometabolic risk factors related to elevated adiposity. Int. J. Obes. 2011, 36, 286–294. [Google Scholar] [CrossRef]
- Stewart, A.D.; Marfell-Jones, M.; Olds, T.; De Ridder, J. International Standards for Anthropometric Assessment; ISAK: Lower Hutt, New Zealand, 2011. [Google Scholar]
- Corbatón, A.; Martínez-Larrad, M.T.; Serrano-García, I.; Fernández, C.; Serrano-Ríos, M. Body fat anthropometric indexes: Which of those identify better high cardiovascular risk subjects? A comparative study in Spanish population. PLoS ONE 2019, 14, e0216877. [Google Scholar] [CrossRef]
- Hastuti, J.; Kagawa, M.; Byrne, N.M.; Hills, A.P. Anthropometry to assess body fat in Indonesian adults. Asia Pac. J. Clin. Nutr. 2018, 27, 592–598. [Google Scholar]
- Castro-Porras, L.V.; Rojas-Russell, M.E.; Villanueva-Sánchez, J.; López-Cervantes, M. An anthropometry-based equation of fat mass percentage as a valid discriminator of obesity. Public Health Nutr. 2019, 22, 1250–1258. [Google Scholar] [CrossRef]
- Lahav, Y.; Epstein, Y.; Kedem, R.; Schermann, H. A novel body circumferences-based estimation of percentage body fat. Br. J. Nutr. 2018, 119, 720–725. [Google Scholar] [CrossRef]
- Paek, J.K.; Kim, J.; Kim, K.; Lee, S.Y. Usefulness of relative fat mass in estimating body adiposity in Korean adult population. Endocr. J. 2019, 66, 723–729. [Google Scholar] [CrossRef]
- Guzmán-León, A.E.; Velarde, A.G.; Vidal-Salas, M.; Urquijo-Ruiz, L.G.; Caraveo-Gutiérrez, L.A.; Valencia, M.E. External validation of the relative fat mass (RFM) index in adults from north-west Mexico using different reference methods. PLoS ONE 2019, 14, e0226767. [Google Scholar] [CrossRef]
- Lee, D.H.; Keum, N.; Hu, F.B.; Orav, E.J.; Rimm, E.B.; Sun, Q.; Willett, W.C.; Giovannucci, E.L. Development and validation of anthropometric prediction equations for lean body mass, fat mass and percent fat in adults using the National Health and Nutrition Examination Survey (NHANES) 1999–2006. Br. J. Nutr. 2017, 118, 858–866. [Google Scholar] [CrossRef]
- Sousa, C.M.; Santana, E.; Lopes, M.V.; Lima, G.; Azoubel, L.; Carneiro, É.; Barros, A.K.; Pires, N. Development of a Computational Model to Predict Excess Body Fat in Adolescents through Low Cost Variables. Int. J. Environ. Res. Public Health 2019, 6, 2962. [Google Scholar] [CrossRef]
- Henry, C.J.; Ponnalagu, S.; Tan, S.Y. New Equations to Predict Body Fat in Asian-Chinese Adults Using Age, Height, Skinfold Thickness, and Waist Circumference. J. Acad. Nutr. Diet 2018, 118, 1263–1269. [Google Scholar] [CrossRef]
- Nickerson, B.S.; Esco, M.R.; Bishop, P.A.; Fedewa, M.V.; Snarr, R.L.; Kliszczewicz, B.M.; Park, K.S. Validity of BMI-Based Body Fat Equations in Men and Women: A 4-Compartment Model Comparison. J. Strength Cond. Res. 2018, 32, 121–129. [Google Scholar] [CrossRef]
- Głuszek, S.; Ciesla, E.; Głuszek-Osuch, M.; Kozieł, D.; Kiebzak, W.; Wypchło, Ł.; Suliga, E. Anthropometric indices and cut-off points in the diagnosis of metabolic disorders. PLoS ONE 2020, 15, e0235121. [Google Scholar] [CrossRef] [PubMed]
- Chung, W.; Park, J.H.; Chung, H.S.; Yu, J.M.; Kim, D.S.; Moon, S. Utility of the Z-score of log-transformed A Body Shape Index (LBSIZ) in the assessment for sarcopenic obesity and cardiovascular disease risk in the United States. Sci. Rep. 2019, 9, 9292. [Google Scholar] [CrossRef] [PubMed]
- McLester, C.N.; Nickerson, B.S.; Kliszczewicz, B.M.; Hicks, C.S.; Williamson, C.M.; Bechke, E.E.; McLester, J.R. Validity of DXA body volume equations in a four-compartment model for adults with varying body mass index and waist circumference classifications. PLoS ONE 2018, 13, e0206866. [Google Scholar] [CrossRef]
- Tewari, N.; Awad, S.; Macdonald, I.A.; Lobo, D.N. A comparison of three methods to assess body composition. Nutrition 2018, 47, 1–5. [Google Scholar] [CrossRef]
- Leal, L.; Barbosa, G.; Ferreira, R.; Avelino, E.B.; Bezerra, A.N.; Vale, S.; Maciel, B. Cross-validation of prediction equations for estimating body composition in ballet dancers. PLoS ONE 2019, 14, e0219045. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).