Impact of Urban Morphology and Climate on Heating Energy Consumption of Buildings in Severe Cold Regions
Abstract
:1. Introduction
2. Materials and Methods
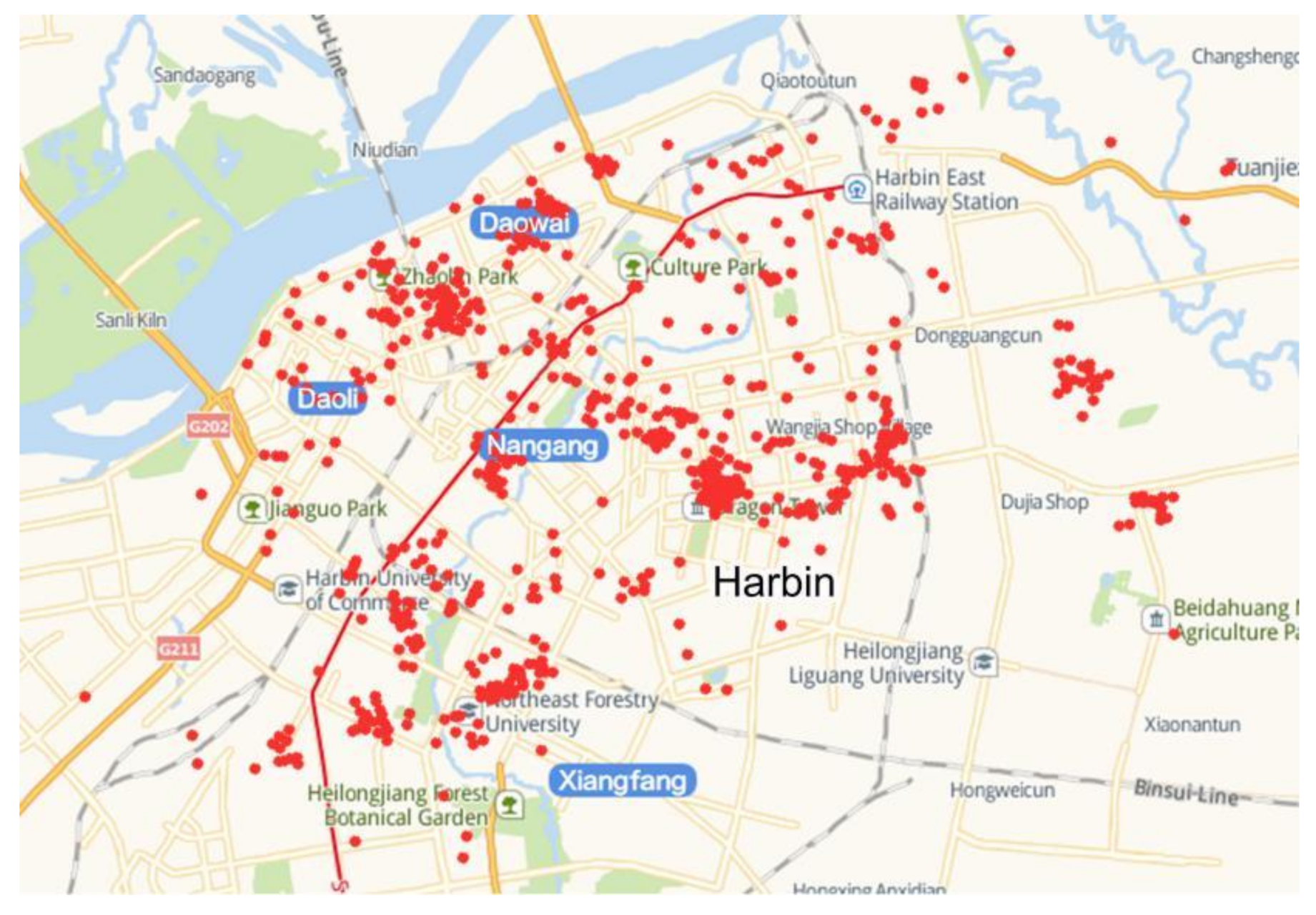
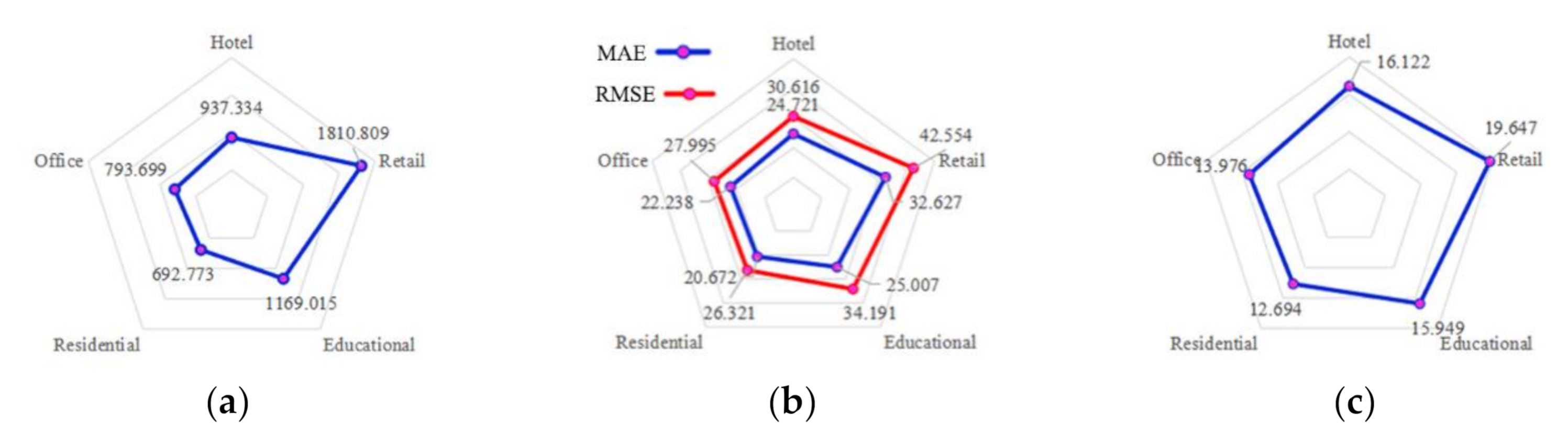
2.1. Energy Consumption Data
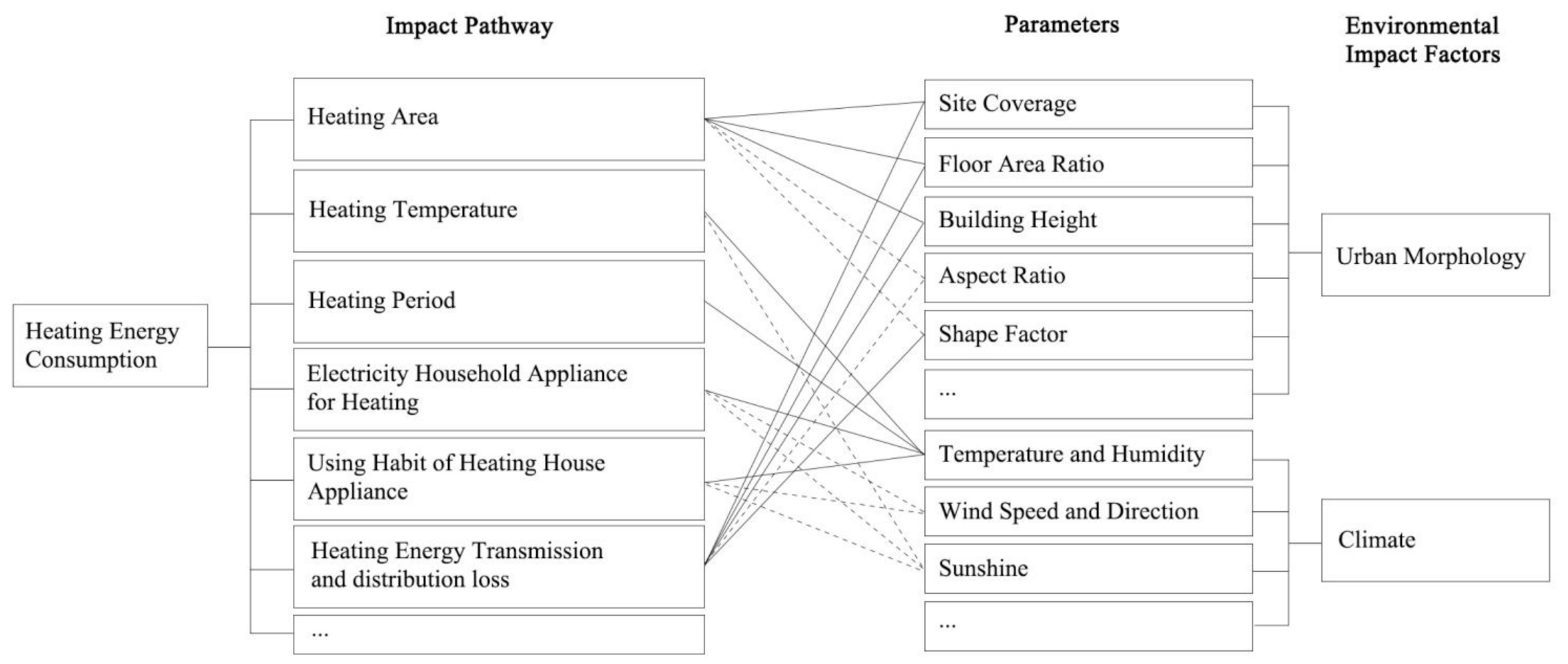
2.2. Environmental Impact Parameters
2.2.1. Urban Morphological Parameters
Building Density (BD)
Floor Area Ratio (FAR)
Aspect Ratio (AR)
Building Height (BH)
Shape Factor (SF)
2.2.2. Climatic Parameters
Temperature
Wind Speed
Relative Humidity
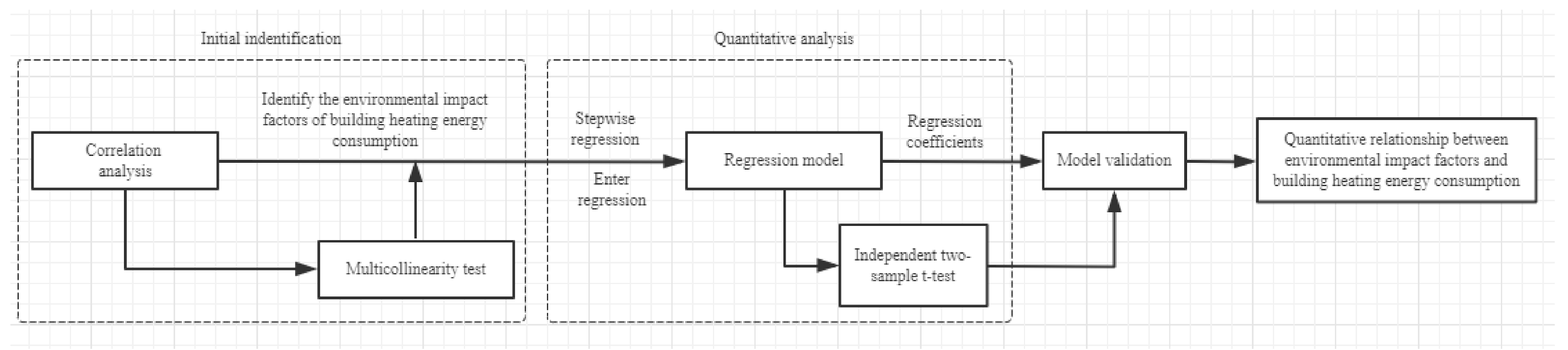
2.3. Statistical Analysis Framework
2.3.1. Correlation Analysis
2.3.2. Multicollinearity Test
2.3.3. Stepwise Regression
2.3.4. Independent Two-Sample T-Test
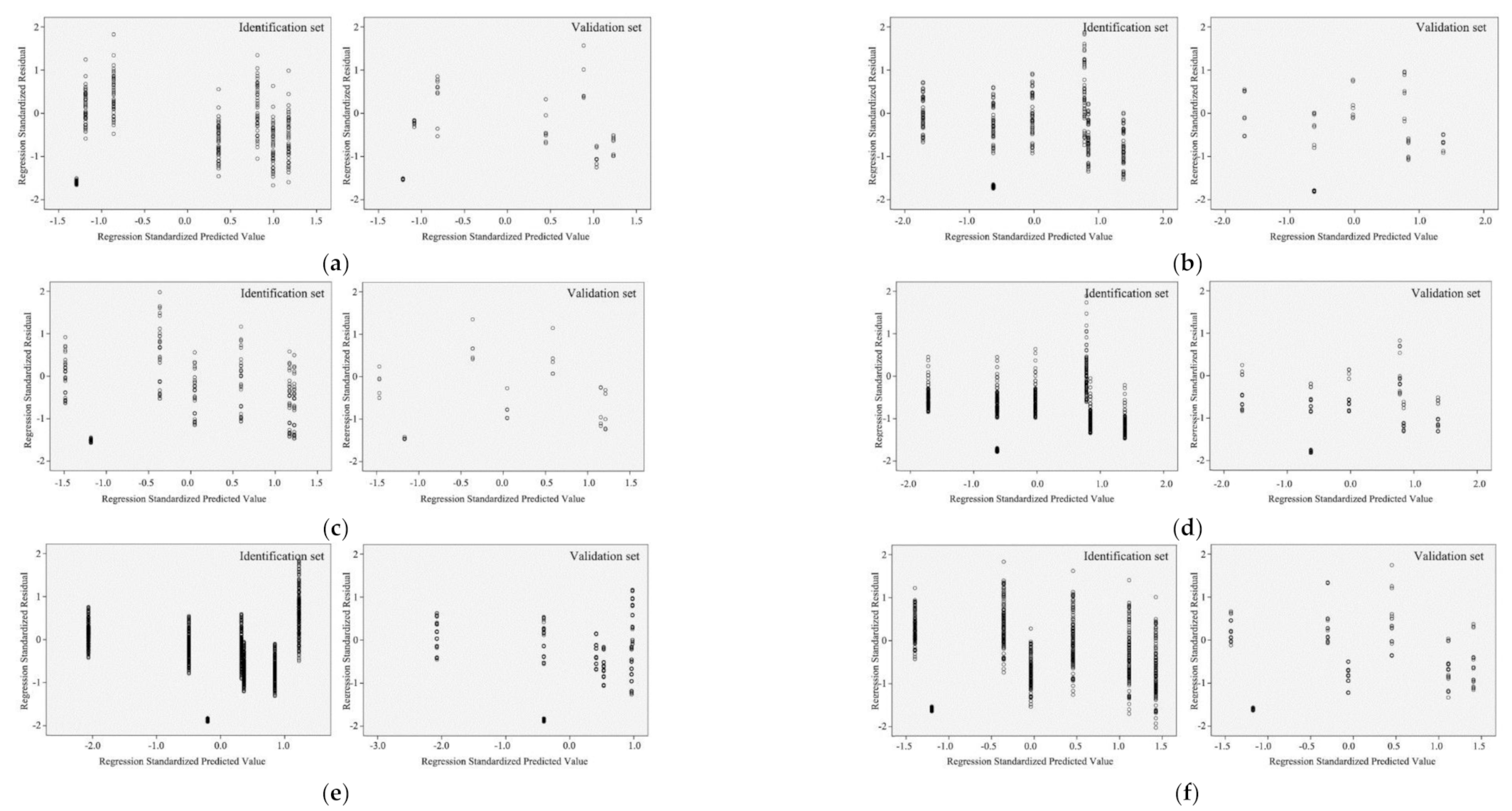
2.3.5. Model Validation
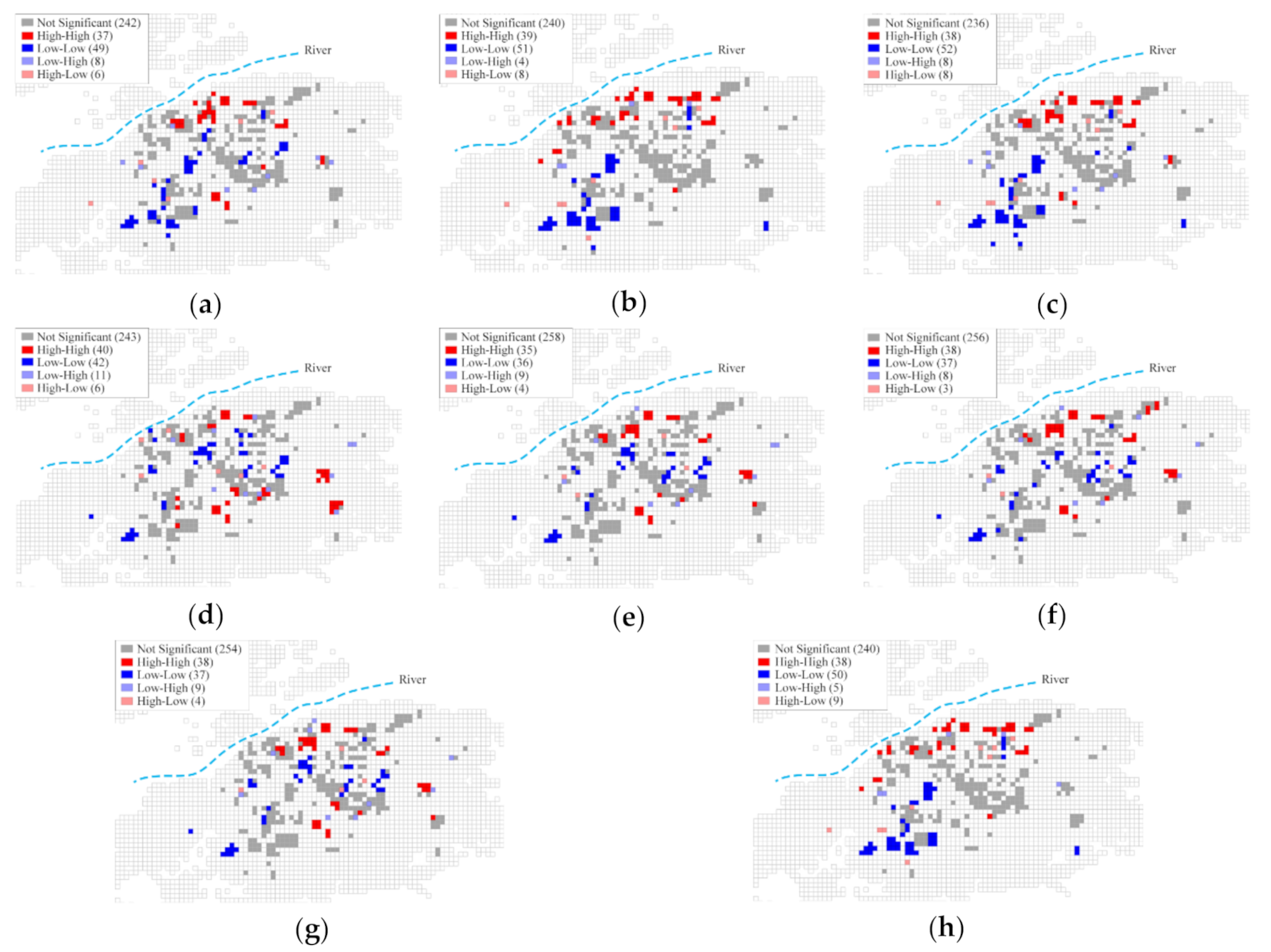
2.4. Cluster Analysis
- “High-high” describes an area of high value surrounded by areas of high values.
- “Low-low” describes an area of low value surrounded by areas of low values.
- “Low-high” describes an area of low value surrounded by areas of high values.
- “High-low” describes an area of high value surrounded by areas of low values.
- “Not significant” describes an area whose p-value of local Moran’s I > 0.05.
3. Results
3.1. Result of Initial Identification
3.2. Result of Regression Models
3.2.1. Urban Morphological Parameters
3.2.2. Climatic Parameters
3.3. Validation of Regression Models
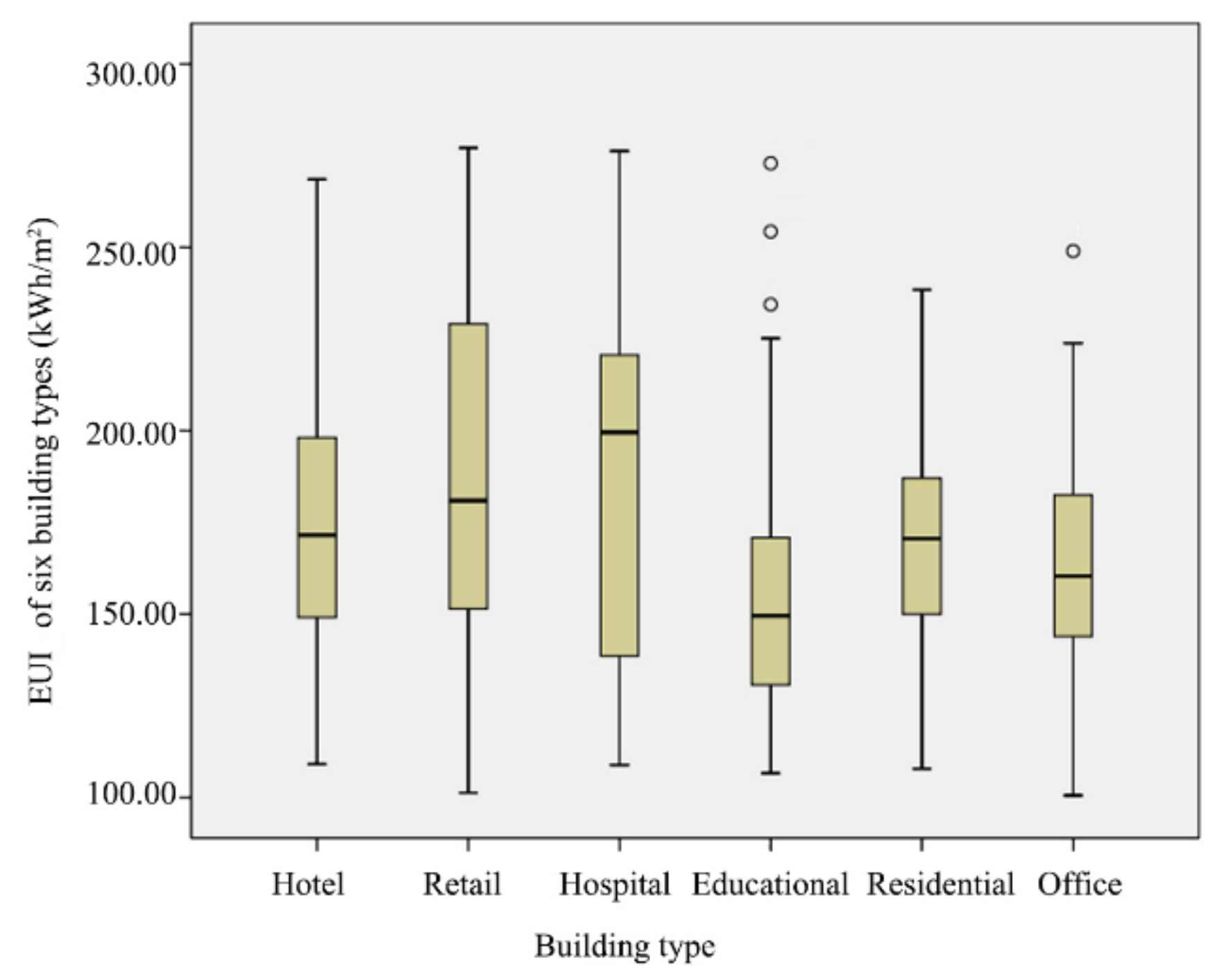
3.4. Distribution Characteristics of Heating EUI
4. Discussion
4.1. Discussion of the Results
4.1.1. Impact of Urban Morphology
Building Height (BH)
Aspect Ratio (AR) and Floor Area Ratio (FAR)
Shape Factor (SF)
4.1.2. Impact of Climate
4.1.3. Impact of Location
4.2. Study Limitations and Further Research Lines
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEA. 2019 Global Status Report for Buildings and Construction; International Energy Agency: Paris, France, 2019; Volume 224, ISBN 9789280737684. [Google Scholar]
- Chang, C.; Zhu, N.; Yang, K.; Yang, F. Data and analytics for heating energy consumption of residential buildings: The case of a severe cold climate region of China. Energy Build. 2018, 172, 104–115. [Google Scholar] [CrossRef]
- Cai, W. 2018 Report of China Building Energy Consumption. China Association of Building Energy Efficiency. Available online: http://www.cabee.org/site/content/23568.html (accessed on 20 March 2020).
- Cai, W. 2017 Report of China Building Energy Consumption. China Association of Building Energy Efficiency. Available online: https://mp.weixin.qq.com/s/XpPPN5xwpJoaWW9G7FQ5sw (accessed on 20 March 2020).
- Corgnati, S.P.; Fabrizio, E.; Filippi, M. The impact of indoor thermal conditions, system controls and building types on the building energy demand. Energy Build. 2008, 40, 627–636. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Miró, L.; Martínez, M.; Fernández, A.I.; Urge-Vorsatz, D. Affordable construction towards sustainable buildings: Review on embodied energy in building materials. Curr. Opin. Environ. Sustain. 2013, 5, 229–236. [Google Scholar] [CrossRef]
- Kim, D.B.; Kim, D.D.; Kim, T. Energy performance assessment of HVAC commissioning using long-term monitoring data: A case study of the newly built office building in South Korea. Energy Build. 2019, 204, 109465. [Google Scholar] [CrossRef]
- Hu, S.; Yan, D.; Guo, S.; Cui, Y.; Dong, B. A survey on energy consumption and energy usage behavior of households and residential building in urban China. Energy Build. 2017, 148, 366–378. [Google Scholar] [CrossRef]
- Rafsanjani, H.N.; Ahn, C.R.; Chen, J. Linking building energy consumption with occupants’ energy-consuming behaviors in commercial buildings: Non-intrusive occupant load monitoring (NIOLM). Energy Build. 2018, 172, 317–327. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Olsthoorn, D.; Torjan, M.; Haghighat, F. Urban neighborhood characteristics influence on a building indoor environment. Sustain. Cities Soc. 2015, 19, 403–413. [Google Scholar] [CrossRef] [Green Version]
- Lee, G.; Jeong, Y. Impact of Urban and Building Form and Microclimate on the Energy Consumption of Buildings—Based on Statistical Analysis. J. Asian Archit. Build. Eng. 2017, 16. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xie, Y.; Luan, B.; Chen, X. Urban macro-level impact factors on Direct CO2 Emissions of urban residents in China. Energy Build. 2015, 107, 131–143. [Google Scholar] [CrossRef]
- Mouzourides, P.; Kyprianou, A.; Neophytou, M.K.A.; Ching, J.; Choudhary, R. Linking the urban-scale building energy demands with city breathability and urban form characteristics. Sustain. Cities Soc. 2019, 49, 101460. [Google Scholar] [CrossRef]
- de Lemos Martins, T.A.; Faraut, S.; Adolphe, L. Influence of context-sensitive urban and architectural design factors on the energy demand of buildings in Toulouse, France. Energy Build. 2019, 190, 262–278. [Google Scholar] [CrossRef]
- Gros, A.; Bozonnet, E.; Inard, C.; Musy, M. Simulation tools to assess microclimate and building energy—A case study on the design of a new district. Energy Build. 2016, 114, 112–122. [Google Scholar] [CrossRef]
- Ahn, Y.J.; Sohn, D.W. The effect of neighbourhood-level urban form on residential building energy use: A GIS-based model using building energy benchmarking data in Seattle. Energy Build. 2019, 196, 124–133. [Google Scholar] [CrossRef]
- de Martins, T.A.L.; Adolphe, L.; Bastos, L.E.G.; de Martins, M.A.L. Sensitivity analysis of urban morphology factors regarding solar energy potential of buildings in a Brazilian tropical context. Sol. Energy 2016, 137, 11–24. [Google Scholar] [CrossRef]
- Xie, X.; Sahin, O.; Luo, Z.; Yao, R. Impact of neighbourhood-scale climate characteristics on building heating demand and night ventilation cooling potential. Renew. Energy 2020, 150, 943–956. [Google Scholar] [CrossRef]
- Frank, T. Climate change impacts on building heating and cooling energy demand in Switzerland. Energy Build. 2005, 37, 1175–1185. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Ren, Z. Assessment of climate change impact on residential building heating and cooling energy requirement in Australia. Build. Environ. 2010, 45, 1663–1682. [Google Scholar] [CrossRef]
- Xu, P.; Joe, Y.; Miller, N.; Schlegel, N.; Shen, P. Impacts of climate change on building heating and cooling energy patterns in California. EGY 2012, 44, 792–804. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Q. Impact of climate change heating and cooling energy use in buildings in the United States. Energy Build. 2014, 82, 428–436. [Google Scholar] [CrossRef] [Green Version]
- Berger, T.; Amann, C.; Formayer, H.; Korjenic, A.; Pospischal, B.; Neururer, C.; Smutny, R. Impacts of climate change upon cooling and heating energy demand of office buildings in Vienna, Austria. Energy Build. 2014, 80, 517–530. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Li, Z.; Han, Y.; Xu, P. Methods for benchmarking building energy consumption against its past or intended performance: An overview. Appl. Energy 2014, 124, 325–334. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Holcomb, D.; Li, W.; Seshia, S.A. Algorithms for Green Buildings: Learning-Based Techniques for Energy Prediction and Fault Diagnosis. Technical Report No. UCB/EECS-2009-138. University of California at Berkeley. Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=35B4E692951D9F1AFFEE6C0707261B3F?doi=10.1.1.432.1494&rep=rep1&type=pdf (accessed on 2 May 2020).
- Al-Homoud, M.S. Computer-aided building energy analysis techniques. Build. Environ. 2001, 36, 421–433. [Google Scholar] [CrossRef]
- Zhao, H.X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G. Re-evaluation of building cooling load prediction models for use in humid subtropical area. Energy Build. 2013, 62, 442–449. [Google Scholar] [CrossRef]
- Amiri, S.S.; Mottahedi, M.; Asadi, S. Using multiple regression analysis to develop energy consumption indicators for commercial buildings in the U.S. Energy Build. 2015, 109, 209–216. [Google Scholar] [CrossRef]
- Song, S.-Y.; Leng, H. Modeling the Household Electricity Usage Behavior and Energy-Saving Management in Severely Cold Regions. Energies 2020, 13, 5581. [Google Scholar] [CrossRef]
- Tellier, L.N. Characterizing urban form by means of the Urban Metric System. Land Use Policy 2020, 104672. [Google Scholar] [CrossRef]
- Equere, V.; Mirzaei, P.A.; Riffat, S. Definition of a new morphological parameter to improve prediction of urban heat island. Sustain. Cities Soc. 2020, 56. [Google Scholar] [CrossRef]
- Xu, X.; AzariJafari, H.; Gregory, J.; Norford, L.; Kirchain, R. An integrated model for quantifying the impacts of pavement albedo and urban morphology on building energy demand. Energy Build. 2020, 211. [Google Scholar] [CrossRef]
- Salvati, A.; Coch, H.; Morganti, M. Effects of urban compactness on the building energy performance in Mediterranean climate. Energy Procedia 2017, 122, 499–504. [Google Scholar] [CrossRef] [Green Version]
- Ramponi, R.; Blocken, B.; de Coo, L.B.; Janssen, W.D. CFD simulation of outdoor ventilation of generic urban configurations with different urban densities and equal and unequal street widths. Build. Environ. 2015, 92, 152–166. [Google Scholar] [CrossRef] [Green Version]
- Shen, P.; Wang, Z. How neighborhood form influences building energy use in winter design condition: Case study of Chicago using CFD coupled simulation. J. Clean. Prod. 2020, 261, 121094. [Google Scholar] [CrossRef]
- Liu, J.; Heidarinejad, M.; Gracik, S.; Srebric, J. The impact of exterior surface convective heat transfer coefficients on the building energy consumption in urban neighborhoods with different plan area densities. Energy Build. 2015, 86, 449–463. [Google Scholar] [CrossRef]
- Allen-dumas, M.R.; Rose, A.N.; New, J.R.; Omitaomu, O.A.; Yuan, J.; Branstetter, M.L.; Sylvester, L.M.; Seals, M.B.; Carvalhaes, T.M.; Adams, M.B.; et al. Impacts of the morphology of new neighborhoods on microclimate and building energy. Renew. Sustain. Energy Rev. 2020, 133, 110030. [Google Scholar] [CrossRef]
- Steemers, K. Energy and the city: Density, buildings and transport. Energy Build. 2003, 35, 3–14. [Google Scholar] [CrossRef]
- Sanaieian, H.; Tenpierik, M.; Van Den Linden, K.; Mehdizadeh Seraj, F.; Mofidi Shemrani, S.M. Review of the impact of urban block form on thermal performance, solar access and ventilation. Renew. Sustain. Energy Rev. 2014, 38, 551–560. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F.; Nakhaie, A.A.; Yagouti, A.; Giguère, M.; Keusseyan, R.; Coman, A. Indoor thermal condition in urban heat Island - Development of a predictive tool. Build. Environ. 2012, 57, 7–17. [Google Scholar] [CrossRef]
- Ashtiani, A.; Mirzaei, P.A.; Haghighat, F. Indoor thermal condition in urban heat island: Comparison of the artificial neural network and regression methods prediction. Energy Build. 2014, 76, 597–604. [Google Scholar] [CrossRef]
- Sailor, D.J.; Dietsch, N. The urban heat island Mitigation Impact Screening Tool (MIST). Environ. Model. Softw. 2007, 22. [Google Scholar] [CrossRef] [Green Version]
- Giridharan, R.; Lau, S.S.Y.; Ganesan, S.; Givoni, B. Urban design factors influencing heat island intensity in high-rise high-density environments of Hong Kong. Build. Environ. 2007, 42, 3669–3684. [Google Scholar] [CrossRef]
- Katrutsa, A.; Strijov, V. Comprehensive study of feature selection methods to solve multicollinearity problem according to evaluation criteria. Expert Syst. Appl. 2017, 76, 1–11. [Google Scholar] [CrossRef]
- Walter, T.; Sohn, M.D. A regression-based approach to estimating retrofit savings using the Building Performance Database. Appl. Energy 2016, 179, 996–1005. [Google Scholar] [CrossRef] [Green Version]
- Shacham, M.; Brauner, N. Application of stepwise regression for dynamic parameter estimation. Comput. Chem. Eng. 2014, 69, 26–38. [Google Scholar] [CrossRef]
- Silhavy, R.; Silhavy, P.; Prokopova, Z. Analysis and selection of a regression model for the Use Case Points method using a stepwise approach. J. Syst. Softw. 2017, 125, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Gurney, K.R. The variation of climate change impact on building energy consumption to building type and spatiotemporal scale. Energy 2016, 111, 137–153. [Google Scholar] [CrossRef] [Green Version]
- Seya, H. Global and local indicators of spatial associations. In Spatial Analysis Using Big Data; Elsevier: Amsterdam, The Netherlands, 2007; pp. 33–53. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Ueki, M.; Kawasaki, Y. Multiple choice from competing regression models under multicollinearity based on standardized update. Comput. Stat. Data Anal. 2013, 63, 31–41. [Google Scholar] [CrossRef]
- Resch, E.; Bohne, R.A.; Kvamsdal, T.; Lohne, J. Impact of Urban Density and Building Height on Energy Use in Cities. Energy Procedia 2016, 96, 800–814. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Gou, Z.; Lau, S.S.-Y.; Qin, H. The Impact of Urban Design Descriptors on Outdoor Thermal Environment: A Literature Review. Energies 2017, 10, 2151. [Google Scholar] [CrossRef] [Green Version]
- Giannopoulou, K.; Santamouris, M.; Livada, I.; Georgakis, C.; Caouris, Y. The impact of canyon geometry on intra Urban and Urban: Suburban night temperature differences under warm weather conditions. Pure Appl. Geophys. 2010, 167, 1433–1449. [Google Scholar] [CrossRef]
- Erell, E.; Pearlmutter, D.; Williamson, T.J. Urban Microclimate: Designing the Spaces Between Buildings, 1st ed.; Earthscan: London, UK; Washington, DC, USA, 2010. [Google Scholar]
- Niachou, K.; Livada, I.; Santamouris, M. Experimental study of temperature and airflow distribution inside an urban street canyon during hot summer weather conditions—Part I: Air and surface temperatures. Build. Environ. 2007, 43, 1383–1392. [Google Scholar] [CrossRef]
- Andreou, E.; Axarli, K. Investigation of urban canyon microclimate in traditional and contemporary environment. Experimental investigation and parametric analysis. Renew. Energy 2012, 43, 354–363. [Google Scholar] [CrossRef]
- Johansson, E. Influence of urban geometry on outdoor thermal comfort in a hot dry climate: A study in Fez, Morocco. Build. Environ. 2006, 41, 1326–1338. [Google Scholar] [CrossRef]
- Perini, K.; Magliocco, A. Effects of vegetation, urban density, building height, and atmospheric conditions on local temperatures and thermal comfort. Urban For. Urban Green. 2014, 13, 495–506. [Google Scholar] [CrossRef]
- Skarbit, N.; Stewart, I.D.; Unger, J.; Gál, T. Employing an urban meteorological network to monitor air temperature conditions in the “local climate zones” of Szeged, Hungary. Int. J. Climatol. 2017, 37, 582–596. [Google Scholar] [CrossRef]
- Wang, Y.; Berardi, U.; Akbari, H. Comparing the effects of urban heat island mitigation strategies for Toronto, Canada. Energy Build. 2016, 114, 2–19. [Google Scholar] [CrossRef]
- Stamenković, M.G.; Miletić, M.J.; Kosanović, S.M.; Vučković, G.D.; Glišović, S.M. Impact of a building shape factor on space cooling energy performance in the green roof concept implementation. Therm. Sci. 2018, 22, 687–698. [Google Scholar] [CrossRef]
- Ratti, C.; Raydan, D.; Steemers, K. Building form and environmental performance: Archetypes, analysis and an arid climate. Energy Build. 2003, 35, 49–59. [Google Scholar] [CrossRef]
- Liu, J.; Heidarinejad, M.; Nikkho, S.K.; Mattise, N.W.; Srebric, J. Quantifying impacts of urban microclimate on a building energy consumption-a case study. Sustainability 2019, 11, 4921. [Google Scholar] [CrossRef] [Green Version]
- Malys, L.; Musy, M.; Inard, C. Microclimate and building energy consumption: Study of different coupling methods. Adv. Build. Energy Res. 2015, 9, 151–174. [Google Scholar] [CrossRef]
- Wu, Z.; Qin, M.; Zhang, M. Phase change humidity control material and its impact on building energy consumption. Energy Build. 2018, 174, 254–261. [Google Scholar] [CrossRef]
- Wang, H. Huge energy saving potential of heating in northern cities and towns. Constr. Archit. 2015, 8, 11–12. [Google Scholar] [CrossRef]
- Leng, H.; Yuan, Q.; Guo, E. Study of the Design Tactics of “Winter-friendly” for Civic Amenity in Cold Region. Archit. J. 2016, 9, 22–26. [Google Scholar]
- Llantoy, N.; Chàfer, M.; Cabeza, L.F. A comparative life cycle assessment (LCA) of different insulation materials for buildings in the continental Mediterranean climate. Energy Build. 2020, 225, 110323. [Google Scholar] [CrossRef]
- Heravi, G.; Mahdi, M.; Rostami, M. Identifying cost—Optimal options for a typical residential nearly zero energy building’s design in developing countries. Clean Technol. Environ. Policy 2020. [Google Scholar] [CrossRef]
- Tomholt, L.; Geletina, O.; Alvarenga, J.; Shneidman, A.V.; Weaver, J.C.; Fernandes, M.C.; Mota, S.A.; Bechthold, M.; Aizenberg, J. Tunable infrared transmission for energy-efficient pneumatic building façades. Energy Build. 2020, 226, 110377. [Google Scholar] [CrossRef]
- Kosonen, A.; Keskisaari, A. Zero-energy log house—Future concept for an energy efficient building in the Nordic conditions. Energy Build. 2020, 228, 110449. [Google Scholar] [CrossRef]




| Title | Test of Normality | Minimum (kWh/m2) | Maximum (kWh/m2) | Mean (kWh/m2) | Std. Deviation (kWh/m2) |
|---|---|---|---|---|---|
| Sig | |||||
| Heating EUI | 0.006 | 100.52 | 298.78 | 168.93 | 35.66 |
| Building Type | Building Height (m) | Total Floor Area (m2) | Footprint Area (m2) | Annual Heating EUI (kWh/m2) | Monthly Heating EUI (kWh/m2) |
|---|---|---|---|---|---|
| Hotel | 5.92–108.73 | 941.13–6036.59 | 172.00–4018.23 | 109.1–268.59 | 1.20–57.31 |
| Retail building | 6.00–97.00 | 1536.60–238,437.16 | 269.12–101,453.12 | 101.25–275.39 | 0.91–68.49 |
| Hospital | 3.29–57.42 | 810.65–76,286.13 | 223.51–3632.20 | 108.84–273.45 | 1.14–61.98 |
| Educational building | 3.49–57.00 | 503.04–85,500.63 | 174.10–6276.32 | 106.63–272.90 | 1.02–74.67 |
| Residential building | 11.39–111.84 | 158.06–45,679.20 | 158.06–5279.00 | 107.83–238.41 | 1.03–63.34 |
| Office | 4.00–115.25 | 941.61–106,209.65 | 50.30–5373.42 | 100.52–248.98 | 0.78–50.91 |
| Heating EUI | Urban Morphology | Climate | ||||||
|---|---|---|---|---|---|---|---|---|
| BD | AR | BH | FAR | SF | WSP | TEMP | RH | |
| Hotel | 0.347 * | −0.400 ** | −0.435 ** | −0.054 | 0.275 | −0.387 ** | −0.604 ** | 0.564 ** |
| Retail | 0.189 | 0.324 * | 0.07 | −0.236 | 0.365 * | −0.357 ** | −0.310 ** | 0.347 ** |
| Hospital | −0.156 | −0.227 | −0.267 | 0.05 | −0.1 | −0.394 ** | −0.442 ** | 0.435 ** |
| Educational | 0.013 | −0.270 ** | −0.271 ** | 0.056 | 0.075 | −0.301 ** | −0.220 ** | 0.279 ** |
| Residential | 0.254 ** | −0.160 * | −0.232 ** | 0.259 ** | 0.359 ** | −0.322 ** | −0.234 ** | 0.302 ** |
| Office | 0.105 | −0.302 ** | −0.355 ** | −0.087 | 0.09 | −0.620 ** | −0.743 ** | 0.677 ** |
| Title | Hotel | Retail | Educational | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BD | AR | BH | VIF | AR | SF | VIF | AR | BH | VIF | |
| BD | 1 | −0.186 | −0.172 | 1.036 | - | - | - | - | - | - |
| AR | −0.186 | 1 | 0.907 ** | 5.650 | 1 | −0.126 | 1.016 | 1 | 0.853 ** | 3.676 |
| BH | −0.172 | 0.907 ** | 1 | 5.618 | - | - | - | 0.853 ** | 1 | 3.676 |
| FAR | - | - | - | - | - | - | - | - | - | - |
| SF | - | - | - | - | −0.126 | 1 | 1.016 | - | - | - |
| Title | Residential | Office | |||||||
|---|---|---|---|---|---|---|---|---|---|
| BD | AR | BH | FAR | SF | VIF | AR | BH | VIF | |
| BD | 1 | 0.049 | −0.035 | 0.762 ** | 0.109 | 2.433 | - | - | - |
| AR | 0.049 | 1 | 0.877 ** | 0.122 | −0.314 ** | 4.505 | 1 | 0.865 ** | 3.968 |
| BH | −0.035 | 0.877 ** | 1 | 0.044 | −0.392 ** | 4.739 | 0.865 ** | 1 | 3.968 |
| FAR | 0.762 ** | 0.122 | 0.044 | 1 | 0.037 | 2.427 | - | - | - |
| SF | 0.109 | −0.314 ** | −0.392 ** | 0.037 | 1 | 1.199 | - | - | - |
| WSP | TEMP | RH | VIF | |
|---|---|---|---|---|
| WSP | 1 | 0.810 * | −0.830 * | 3.300 |
| TEMP | 0.810 * | 1 | −0.938 ** | 8.475 |
| RH | −0.830 * | −0.938 ** | 1 | 9.346 |
| Building Type | Independent Variable | Constant | α | R2 | t-Test |
|---|---|---|---|---|---|
| Hotel | BH | 192.037 | −0.601 | 0.189 | 0.006 |
| Retail building | AR | 105.508 | 51.45 | 0.272 | 0.000 |
| SF | 239.71 | 0.000 | |||
| Educational | BH | 170.211 | −0.65 | 0.074 | 0.000 |
| Residential building | FAR | 99.013 | 9.516 | 0.190 | 0.000 |
| SF | 217.762 | 0.000 | |||
| Office | BH | 179.642 | −0.369 | 0.126 | 0.000 |
| Building Type | Independent Variable | Constant | α | R2 | t-Test |
|---|---|---|---|---|---|
| Hotel | WSP | −1.074 | 6.856 | 0.394 | 0.005 |
| TEMP | −1.003 | 0.001 | |||
| Retail building | WSP | 57.233 | −10.281 | 0.127 | 0.003 |
| Hospital | TEMP | 23.458 | −0.639 | 0.196 | 0.000 |
| Educational building | WSP | 43.923 | −7.303 | 0.091 | 0.010 |
| Residential building | WSP | 0.553 | −7.187 | 0.134 | 0.011 |
| TEMP | 0.627 | 0.001 | |||
| RH | 0.792 | 0.000 | |||
| Office | WSP | 44.302 | −2.342 | 0.558 | 0.001 |
| TEMP | −1.060 | 0.001 | |||
| RH | −0.315 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Leng, H.; Xu, H.; Guo, R.; Zhao, Y. Impact of Urban Morphology and Climate on Heating Energy Consumption of Buildings in Severe Cold Regions. Int. J. Environ. Res. Public Health 2020, 17, 8354. https://doi.org/10.3390/ijerph17228354
Song S, Leng H, Xu H, Guo R, Zhao Y. Impact of Urban Morphology and Climate on Heating Energy Consumption of Buildings in Severe Cold Regions. International Journal of Environmental Research and Public Health. 2020; 17(22):8354. https://doi.org/10.3390/ijerph17228354
Chicago/Turabian StyleSong, Shiyi, Hong Leng, Han Xu, Ran Guo, and Yan Zhao. 2020. "Impact of Urban Morphology and Climate on Heating Energy Consumption of Buildings in Severe Cold Regions" International Journal of Environmental Research and Public Health 17, no. 22: 8354. https://doi.org/10.3390/ijerph17228354





