Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China
Abstract
1. Introduction
2. Methodology and Materials
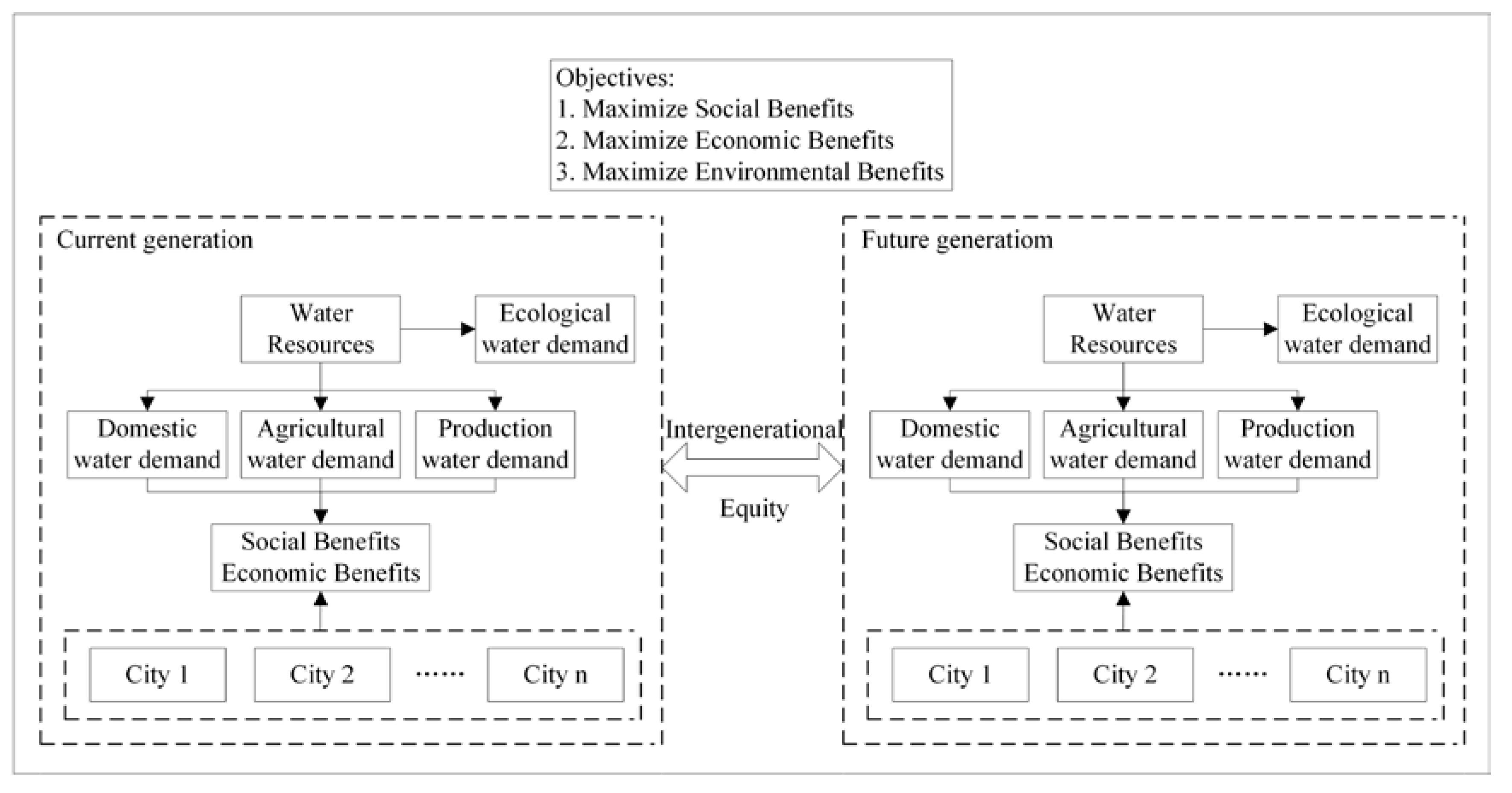
2.1. Key Problem Statement
2.2. Scenario Setting
2.3. Area of Study
2.4. Data Source
3. Modeling
3.1. Model Construction
3.1.1. Objective Functions
- (1)
- Maximize Social Benefits
- (2)
- Maximize Economic Benefits
- (3)
- Maximize Environmental Benefits
3.1.2. Constraint Setting
- (1)
- Intergenerational equity restriction
- (2)
- Water supply restriction
- (3)
- Water demand constraint
- (4)
- Water supply capacity constraints
- (5)
- Reservoir cap.acity constraints
3.1.3. Global Model
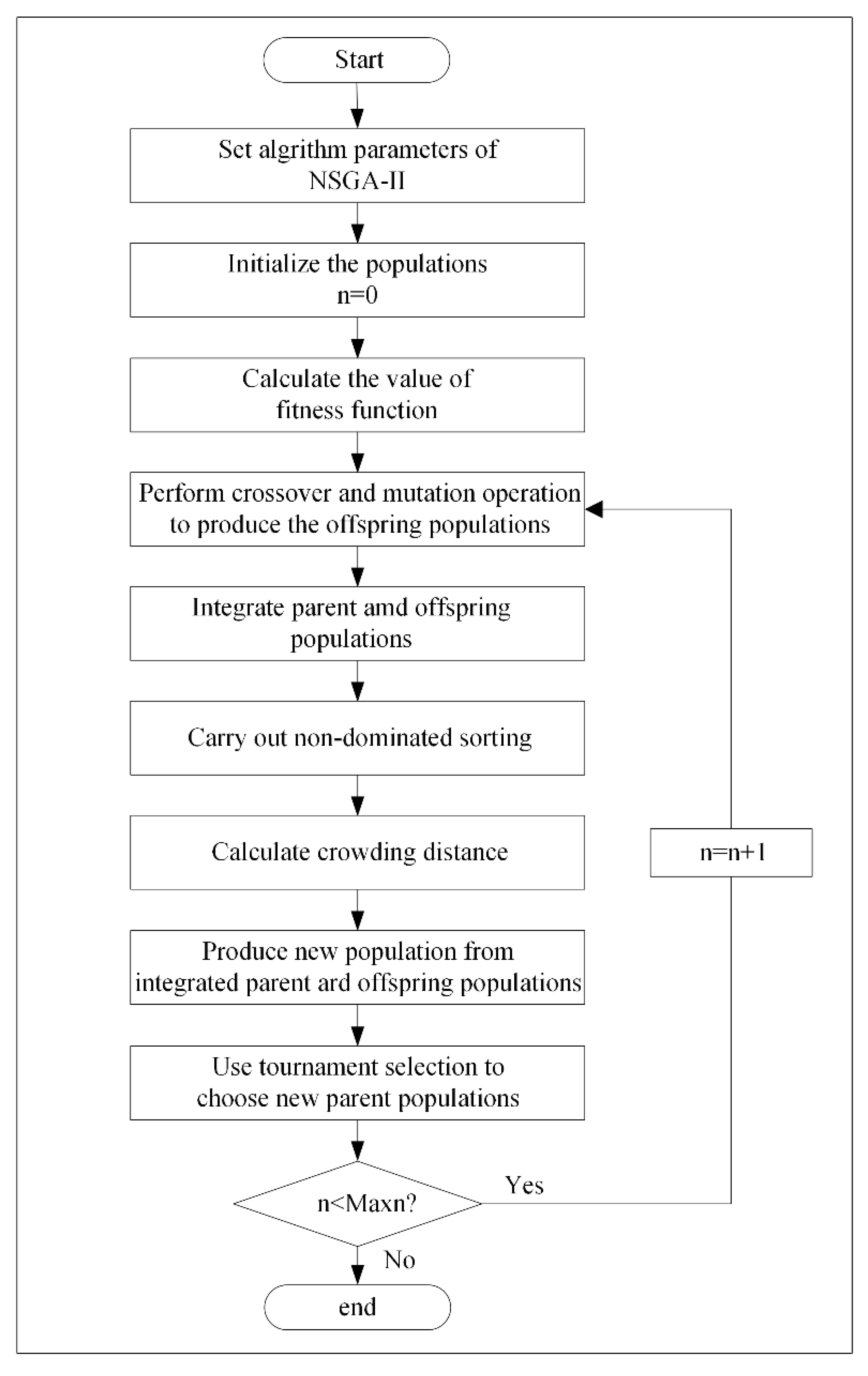
3.2. Modern Solution
3.3. NSGA-2 Design
4. Result and Recommendation
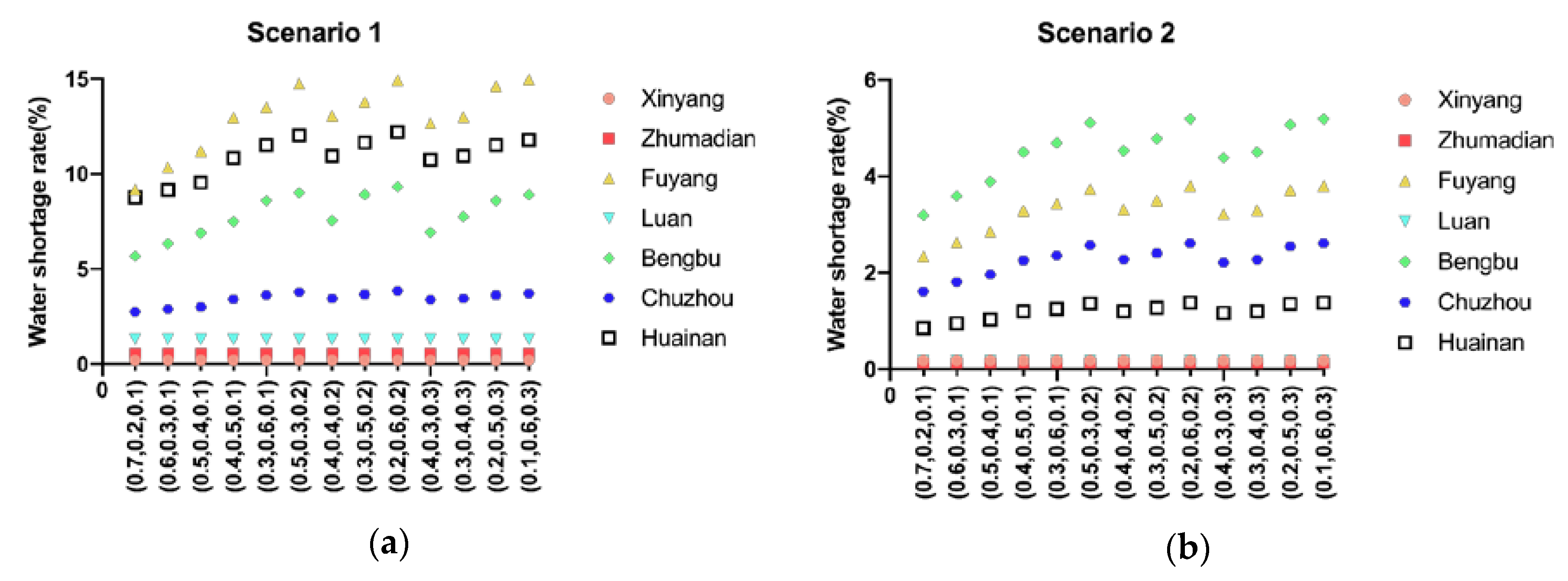
4.1. Water Demand Forecast of the Middle and Upper Reaches of Huaihe River Basin
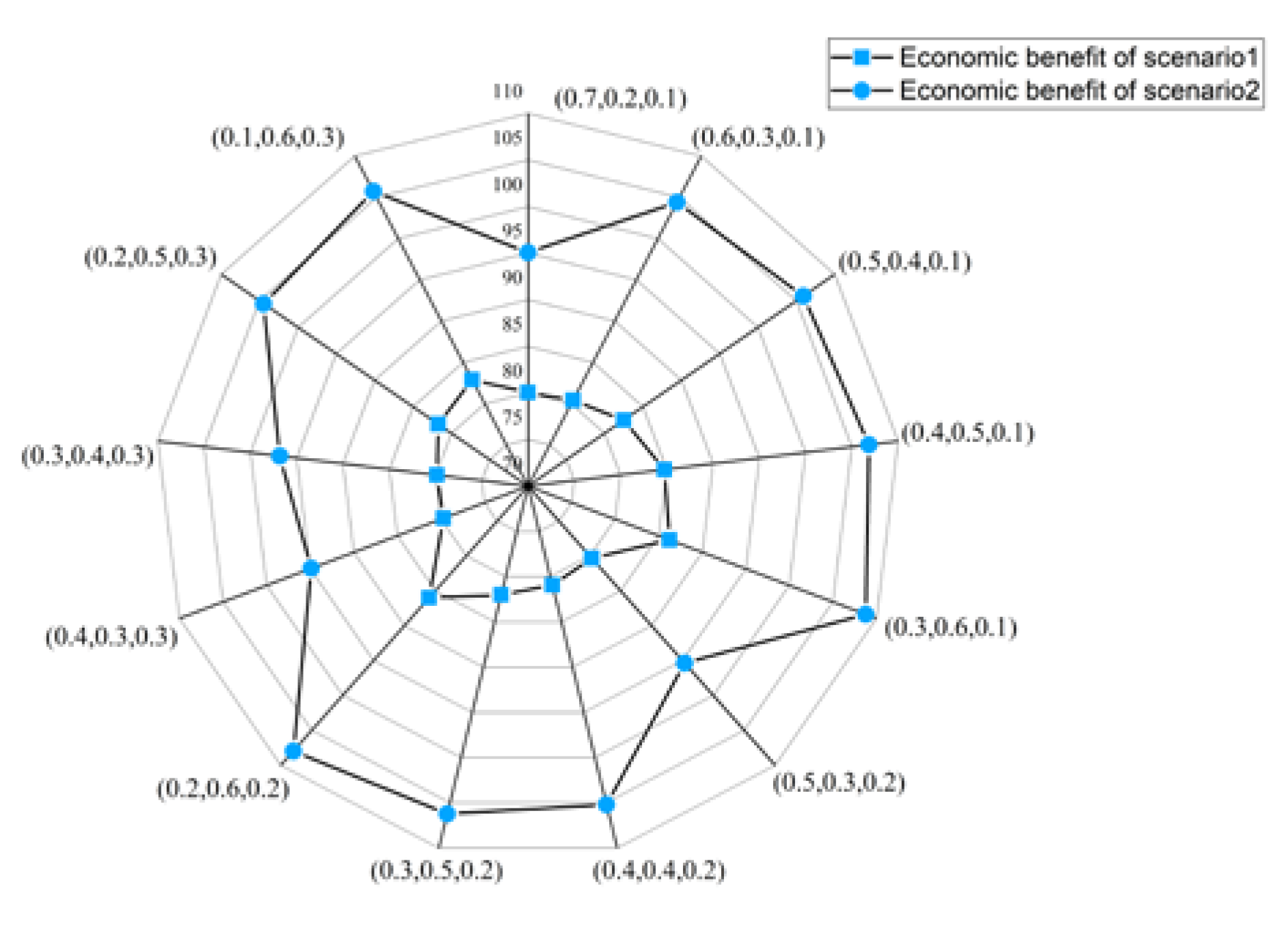
4.2. Benefit Analysis
4.3. Total Economic Benefits Analysis
4.4. Water Resources Allocation Strategies Analysis of Different Generations
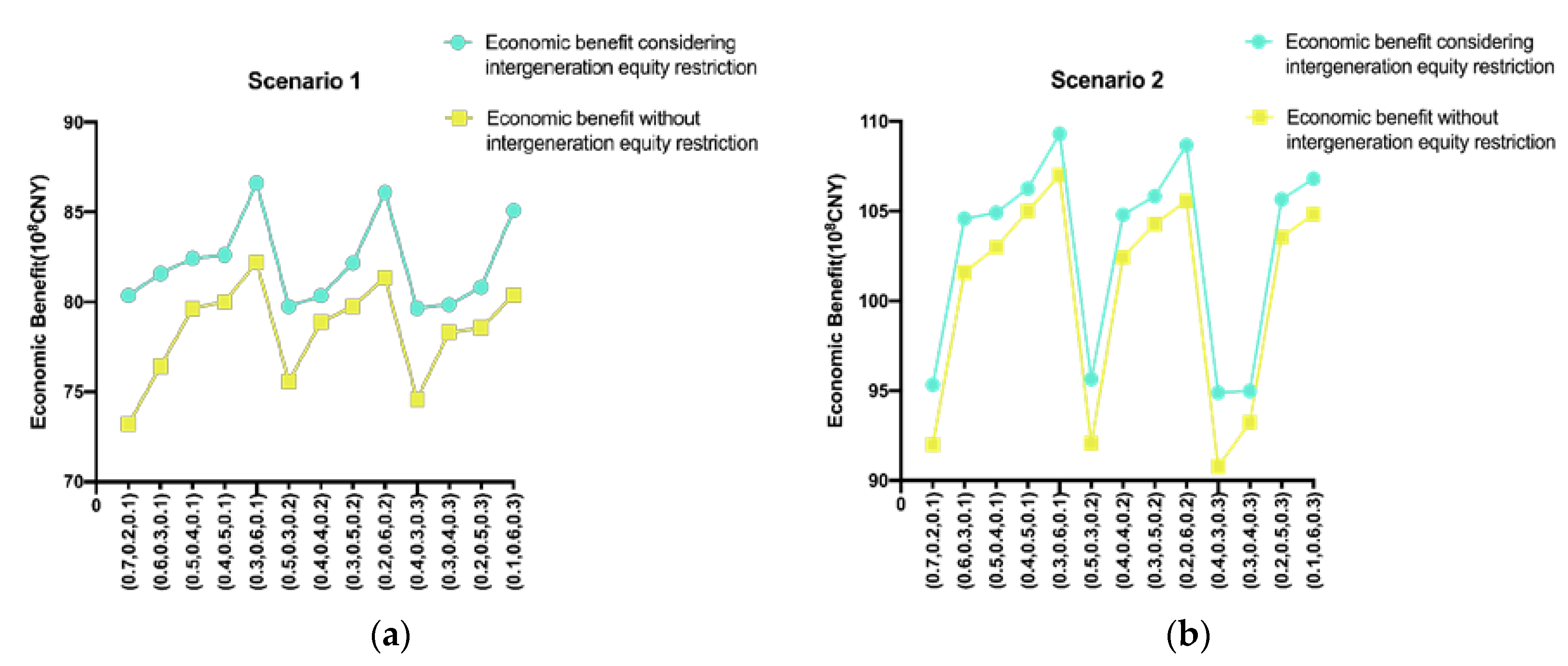
4.5. Results of Considering and Not Considering Intergenerational Equity
4.6. Analysis of Specific Scheme under Balanced Weights (,,)
4.6.1. Specific Water Resources Allocation Scheme under Balanced Weights
4.6.2. Social Benefits Analysis
4.6.3. Economic Benefits Analysis and Intergeneration Equity Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eliasson, J. The rising pressure of global water shortages. Nat. Cell Biol. 2014, 517, 6–7. [Google Scholar] [CrossRef] [PubMed]
- Gheewala, S.H.; Silalertruksa, T.; Nilsalab, P.; Lecksiwilai, N.; Sawaengsak, W.; Mungkung, R.; Ganasut, J. Water stress index and its implication for agricultural land-use policy in Thailand. Int. J. Environ. Sci. Technol. 2017, 15, 833–846. [Google Scholar] [CrossRef]
- Yang, G.; Dong, Z.; Feng, S.; Li, B.; Sun, Y.; Chen, M. Early warning of water resource carrying status in Nanjing City based on coordinated development index. J. Clean. Prod. 2020. [Google Scholar] [CrossRef]
- Abdi, R.; Yasi, M. Evaluation of environmental flow requirements using eco-hydrologic–hydraulic methods in perennial rivers. Water Sci. Technol. 2015, 72, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, X.; Guo, H.; Ma, W. Multi-Water Resources Optimal Allocation Based on Multi-Objective Uncertain Chance-Constrained Programming Model. Water Resour. Manag. 2020, 34, 4881–4899. [Google Scholar] [CrossRef]
- Qiu, Y.; Liu, Y.; Liu, Y.; Chen, Y.; Li, Y. An Interval Two-Stage Stochastic Programming Model for Flood Resources Allocation under Ecological Benefits as a Constraint Combined with Ecological Compensation Concept. Int. J. Environ. Res. Public Health 2019, 16, 1033. [Google Scholar] [CrossRef]
- Li, M.; Xu, Y.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Efficient irrigation water allocation and its impact on agricultural sustainability and water scarcity under uncertainty. J. Hydrol. 2020, 586, 124888. [Google Scholar] [CrossRef]
- Li, F.; Wu, F.-P.; Chen, L.-X.; Zhao, Y.; Chen, X.-N.; Shao, Z.-Y. Fair and Reasonable Allocation of Trans-Boundary Water Resources Based on an Asymmetric Nash Negotiation Model from the Satisfaction Perspective: A Case Study for the Lancang–Mekong River Bain. Int. J. Environ. Res. Public Health 2020, 17, 7638. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Z.; Chen, L.; Ding, T. Optimization of Regional Water-Energy-Food Systems Based on Interval Number Multi-Objective Programming: A Case Study of Ordos, China. Int. J. Environ. Res. Public Health 2020, 17, 7508. [Google Scholar] [CrossRef]
- Divakar, L.; Babel, M.S.; Perret, S.; Das Gupta, A. Optimal allocation of bulk water supplies to competing use sectors based on economic criterion—An application to the Chao Phraya River Basin, Thailand. J. Hydrol. 2011, 401, 22–35. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S. Optimization model for the allocation of water resources based on the maximization of employment in the agriculture and industry sectors. J. Hydrol. 2016, 533, 430–438. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S. Multi-Objective Optimization Model for the Allocation of Water Resources in Arid Regions Based on the Maximization of Socioeconomic Efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Xu, J.; Lv, C.; Yao, L.; Hou, S. Intergenerational equity based optimal water allocation for sustainable development: A case study on the upper reaches of Minjiang River, China. J. Hydrol. 2019, 568, 835–848. [Google Scholar] [CrossRef]
- Jiang, S.; Ning, S.; Cao, X.; Jin, J.; Song, F.; Yuan, X.; Zhang, L.; Xu, X.; Udmale, P. Optimal Water Resources Regulation for the Pond Irrigation System Based on Simulation—A Case Study in Jiang-Huai Hilly Regions, China. Int. J. Environ. Res. Public Health 2019, 16, 2717. [Google Scholar] [CrossRef] [PubMed]
- Garrido, A. A mathematical programming model applied to the study of water markets within the Spanish agricultural sector. Ann. Oper. Res. 2000, 94, 105–123. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, J.; Zhang, Z.; Liu, K.; Gao, X.; Wang, Z. Regional Spatial Management Based on Supply–Demand Risk of Ecosystem Services—A Case Study of the Fenghe River Watershed. Int. J. Environ. Res. Public Health 2020, 17, 4112. [Google Scholar] [CrossRef]
- Chen, J.; Yu, C.; Cai, M.; Wang, H.; Zhou, P. Multi-Objective Optimal Allocation of Urban Water Resources While Considering Conflict Resolution Based on the PSO Algorithm: A Case Study of Kunming, China. Sustain. 2020, 12, 1337. [Google Scholar] [CrossRef]
- Bithas, K. The sustainable residential water use: Sustainability, efficiency and social equity. The European experience. Ecol. Econ. 2008, 68, 221–229. [Google Scholar] [CrossRef]
- Gleeson, T.; Alley, W.M.; Allen, D.M.; Sophocleous, M.A.; Zhou, Y.; Taniguchi, M.; Vandersteen, J. Towards Sustainable Groundwater Use: Setting Long-Term Goals, Backcasting, and Managing Adaptively. Ground Water 2011, 50, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Syme, G. Acceptable risk and social values: Struggling with uncertainty in Australian water allocation. Stoch. Environ. Res. Risk Assess. 2013, 28, 113–121. [Google Scholar] [CrossRef]
- Bahrami-Yarahmadi, M.; Pagliara, S.; Yabarehpour, E.; Najafi, N. Study of Scour and Flow Patterns around Triangular-Shaped Spur Dikes. KSCE J. Civ. Eng. 2020, 24, 3279–3288. [Google Scholar] [CrossRef]
- Chichilnisky, G. An axiomatic approach to sustainable development. Soc. Choice Welf. 1996, 13, 231–257. [Google Scholar] [CrossRef]
- Winter-Nelson, A. Discount rates, natural resources, and the measurement of aggregate economic growth in Africa. Ecol. Econ. 1996, 17, 21–32. [Google Scholar] [CrossRef]
- Pope, C.; Perry, G. Individual versus social discount rates in allocating depletable natural resources over time. Econ. Lett. 1989, 29, 257–264. [Google Scholar] [CrossRef]
- Sieveking, M.; Semmler, W. The present value of resources with large discount rates. Appl. Math. Optim. 1997, 35, 283–309. [Google Scholar] [CrossRef]
- Farzin, Y.H. The Effect of the Discount Rate on Depletion of Exhaustible Resources. J. Political Econ. 1984, 92, 841–851. [Google Scholar] [CrossRef]
- Rodriguez, C.A.; Turner, B.M.; McClure, S.M. Intertemporal Choice as Discounted Value Accumulation. PLoS ONE 2014, 9, e90138. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Shokri, A.; Bozorg-Haddad, O.; Mariño, M.A. Multi-Objective Quantity–Quality Reservoir Operation in Sudden Pollution. Water Resour. Manag. 2014, 28, 567–586. [Google Scholar] [CrossRef]
- Ahmadi, M.; Bozorg-Haddad, O.; Loáiciga, H.A. Adaptive Reservoir Operation Rules Under Climatic Change. Water Resour. Manag. 2014, 29, 1247–1266. [Google Scholar] [CrossRef]
- Gu, X.; Yu, Y.; Li, J.; Li, Y.; Alamdari, M.M. Semi-active storey isolation system employing MRE isolator with parameter identification based on NSGA-II with DCD. Earthq. Struct. 2016, 11, 1101–1121. [Google Scholar] [CrossRef]
- Cai, Y.; Yue, W.; Xu, L.; Yang, Z.; Rong, Q. Sustainable urban water resources management considering life-cycle environmental impacts of water utilization under uncertainty. Resour. Conserv. Recycl. 2016, 108, 21–40. [Google Scholar] [CrossRef]
- Xu, Z.; Pan, B.; Han, M.; Zhu, J.; Tian, L. Spatial–temporal distribution of rainfall erosivity, erosivity density and correlation with El Niño–Southern Oscillation in the Huaihe River Basin, China. Ecol. Inform. 2019, 52, 14–25. [Google Scholar] [CrossRef]
- The Huaihe River Commission of the Ministry of Water Resources, P.R.C. Water Resources Bulletin of Huaihe River Basin. Available online: http://www.hrc.gov.cn/main/szygb/158093.jhtml (accessed on 25 May 2020).
- Cao, Q.; Hao, Z.; Yuan, F.; Berndtsson, R.; Xu, S.; Gao, H.; Hao, J. On the Predictability of Daily Rainfall during Rainy Season over the Huaihe River Basin. Water 2019, 11, 916. [Google Scholar] [CrossRef]
- Collentine, D. Water Resource Economics: The Analysis of Scarcity, Policies and Projects. Eur. Rev. Agric. Econ. 2006, 33, 437–439. [Google Scholar] [CrossRef]
- Eum, H.-I.; Simonovic, S.P. Integrated Reservoir Management System for Adaptation to Climate Change: The Nakdong River Basin in Korea. Water Resour. Manag. 2010, 24, 3397–3417. [Google Scholar] [CrossRef]
- Jia, W.; Dong, Z.; Duan, C.; Ni, X.; Zhu, Z. Ecological reservoir operation based on DFM and improved PA-DDS algorithm: A case study in Jinsha river, China. Hum. Ecol. Risk Assess. Int. J. 2019, 26, 1723–1741. [Google Scholar] [CrossRef]
- Chen, M.; Dong, Z.; Jia, W.; Ni, X.; Yao, H. Multi-Objective Joint Optimal Operation of Reservoir System and Analysis of Objectives Competition Mechanism: A Case Study in the Upper Reach of the Yangtze River. Water 2019, 11, 2542. [Google Scholar] [CrossRef]
- Dai, C.; Qin, X.; Chen, Y.; Guo, H. Dealing with equality and benefit for water allocation in a lake watershed: A Gini-coefficient based stochastic optimization approach. J. Hydrol. 2018, 561, 322–334. [Google Scholar] [CrossRef]




| Scenario 1 | Domestic Water Demand | Agricultural Water Demand | Production Water Demand | Ecological Water Demand | Total |
| Xinyang | 2.30 | 31.05 | 2.69 | 0.11 | 36.16 |
| Zhumadian | 2.69 | 8.02 | 3.31 | 0.11 | 14.13 |
| Fuyang | 3.67 | 23.04 | 5.14 | 0.24 | 32.10 |
| Luan | 1.99 | 21.55 | 4.23 | 0.14 | 27.90 |
| Bengbu | 1.99 | 11.34 | 5.64 | 0.19 | 19.15 |
| Chuzhou | 0.61 | 5.73 | 0.83 | 0.04 | 7.21 |
| Huainan | 1.08 | 6.71 | 1.55 | 0.10 | 9.44 |
| Scenario 2 | Domestic Water Demand | Agricultural Water Demand | Production Water Demand | Ecological Water Demand | Total |
| Xinyang | 3.28 | 31.23 | 4.02 | 0.24 | 38.77 |
| Zhumadian | 3.15 | 8.35 | 3.38 | 0.16 | 15.04 |
| Fuyang | 3.83 | 20.72 | 5.96 | 0.36 | 30.88 |
| Luan | 2.14 | 17.87 | 4.23 | 0.17 | 24.40 |
| Bengbu | 2.17 | 8.37 | 5.79 | 0.23 | 16.56 |
| Chuzhou | 0.70 | 5.62 | 0.90 | 0.05 | 7.26 |
| Huainan | 1.20 | 5.03 | 1.66 | 0.12 | 8.01 |
| Scenario 1 | Domestic Water | Agricultural Water | Production Water | Ecological Water | Total |
| Xinyang | 2.30 | 30.99 | 2.69 | 0.11 | 36.08 |
| Zhumadian | 2.67 | 7.98 | 3.29 | 0.11 | 14.05 |
| Fuyang | 3.18 | 19.97 | 4.46 | 0.24 | 27.85 |
| Luan | 1.96 | 21.22 | 4.16 | 0.14 | 27.48 |
| Bengbu | 1.82 | 10.37 | 5.16 | 0.19 | 17.53 |
| Chuzhou | 0.59 | 5.54 | 0.80 | 0.04 | 6.97 |
| Huainan | 0.97 | 6.01 | 1.39 | 0.10 | 8.46 |
| Scenario 2 | Domestic Water | Agricultural Water | Production Water | Ecological Water | Total |
| Xinyang | 3.28 | 31.18 | 4.01 | 0.24 | 38.70 |
| Zhumadian | 3.15 | 8.33 | 3.37 | 0.16 | 15.01 |
| Fuyang | 3.70 | 20.02 | 5.76 | 0.36 | 29.84 |
| Luan | 2.13 | 17.84 | 4.22 | 0.17 | 24.36 |
| Bengbu | 2.07 | 7.98 | 5.52 | 0.23 | 15.80 |
| Chuzhou | 0.68 | 5.49 | 0.88 | 0.05 | 7.10 |
| Huainan | 1.18 | 4.95 | 1.64 | 0.12 | 7.89 |
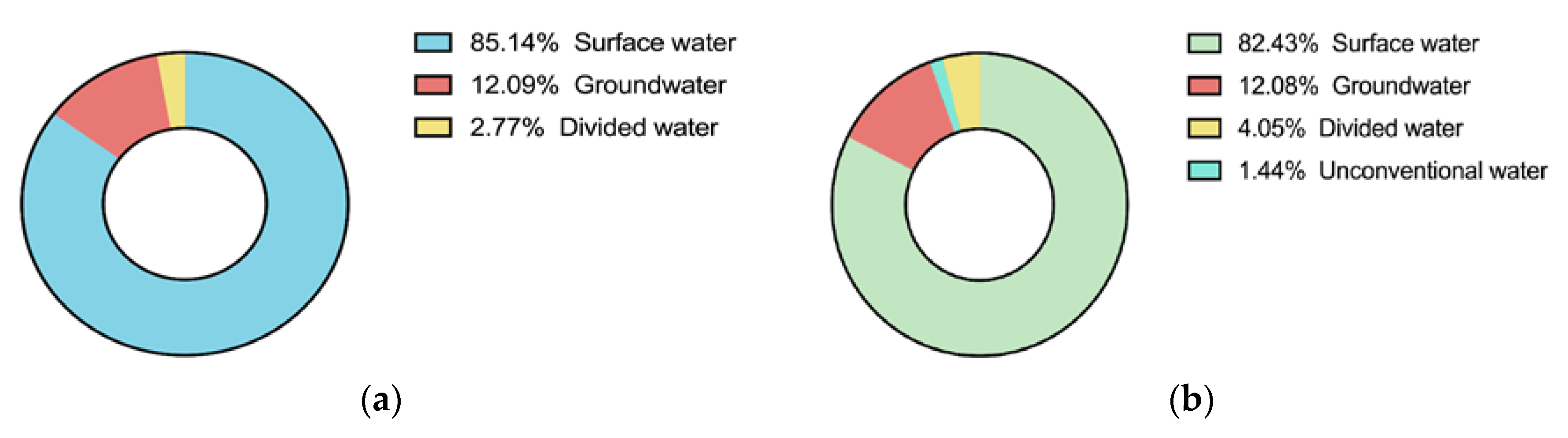
| Scenario 1 | Surface Water | Ground Water | Divided Water | Unconventional Water | Total |
| Xinyang | 34.9 | 1.18 | 0 | 0 | 36.08 |
| Zhumadian | 11.32 | 2.73 | 0 | 0 | 14.05 |
| Fuyang | 16.34 | 7.69 | 0 | 3.83 | 27.85 |
| Luan | 27.18 | 0.29 | 0 | 0 | 27.48 |
| Bengbu | 14.28 | 3.25 | 0 | 0 | 17.53 |
| Chuzhou | 6.62 | 0.35 | 0 | 0 | 6.97 |
| Huainan | 7.21 | 1.25 | 0 | 0 | 8.46 |
| Scenario 2 | Surface Water | Ground Water | Divided Water | Unconventional Water | Total |
| Xinyang | 37.45 | 1.18 | 0 | 0 | 38.7 |
| Zhumadian | 12.28 | 2.73 | 0 | 0 | 15.01 |
| Fuyang | 16.66 | 8.09 | 0 | 5.1 | 29.84 |
| Luan | 24.07 | 0.29 | 0 | 0 | 24.36 |
| Bengbu | 12.64 | 3.15 | 0 | 0 | 15.8 |
| Chuzhou | 5.96 | 0.15 | 1 | 0 | 7.1 |
| Huainan | 5.22 | 1.15 | 1 | 0.52 | 7.89 |
| Economic Benefits | Discount Value of Economic Benefits | |
|---|---|---|
| Scenario 1 | 79.46 | 79.46 |
| Scenario 2 | 168.3 | 80.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Dong, Z.; Chen, T. Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China. Int. J. Environ. Res. Public Health 2020, 17, 9289. https://doi.org/10.3390/ijerph17249289
Zhang J, Dong Z, Chen T. Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China. International Journal of Environmental Research and Public Health. 2020; 17(24):9289. https://doi.org/10.3390/ijerph17249289
Chicago/Turabian StyleZhang, Jitao, Zengchuan Dong, and Tian Chen. 2020. "Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China" International Journal of Environmental Research and Public Health 17, no. 24: 9289. https://doi.org/10.3390/ijerph17249289
APA StyleZhang, J., Dong, Z., & Chen, T. (2020). Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China. International Journal of Environmental Research and Public Health, 17(24), 9289. https://doi.org/10.3390/ijerph17249289







