Exposure of Live-Line Workers to Magnetic Fields: A Dosimetric Analysis
Abstract
1. Introduction
- ▪
- More evolved anatomical models adopted, making reference to the version 3.1 of the Virtual Population [32];
- ▪
- The 2013/35/EU Directive, referring to health and sensory ELVs, taking also into account suggestions provided by the 2010 ICNIRP Guidelines;
- ▪
- More evolved filtering techniques applied to filter the raw computed data of the induced electric field, before comparing them with the ELVs;
- ▪
- New scenarios of workers exposure.
2. Materials and Methods
2.1. Model for in-Silico Simulations
2.2. Finite Element Solvers for the Dosimetric Analysis
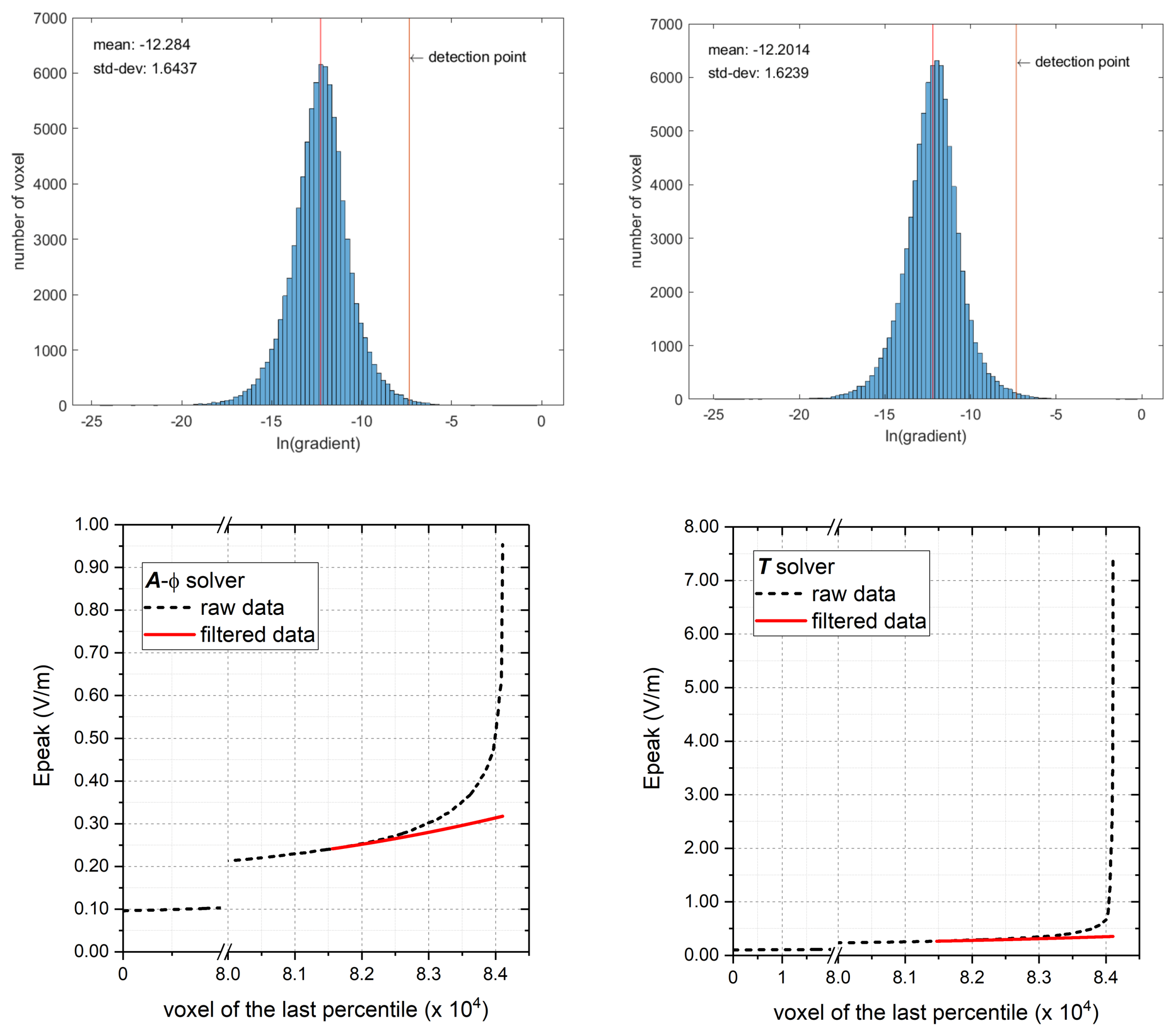
2.3. Numerical Artefacts and Filtering Techniques
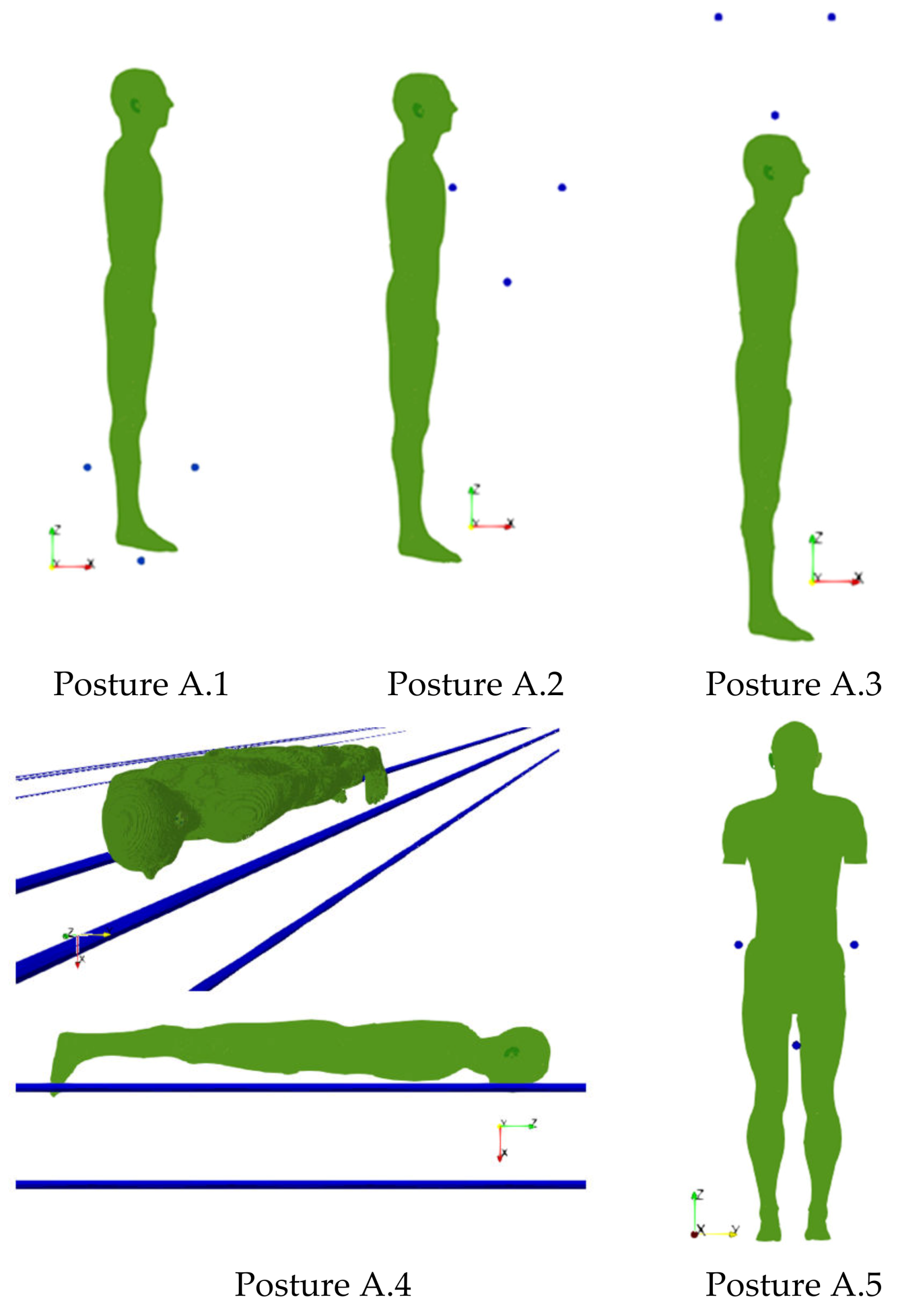
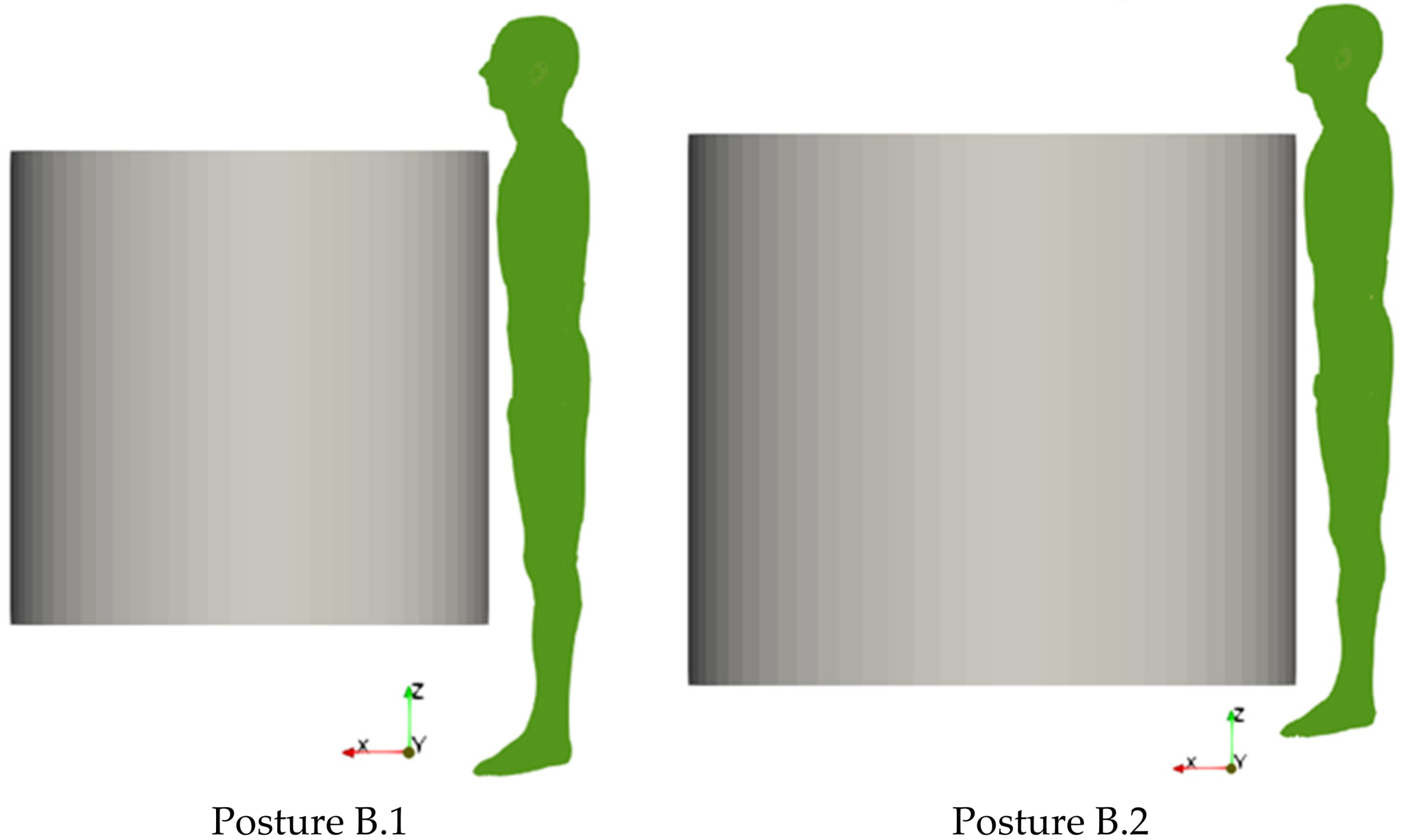
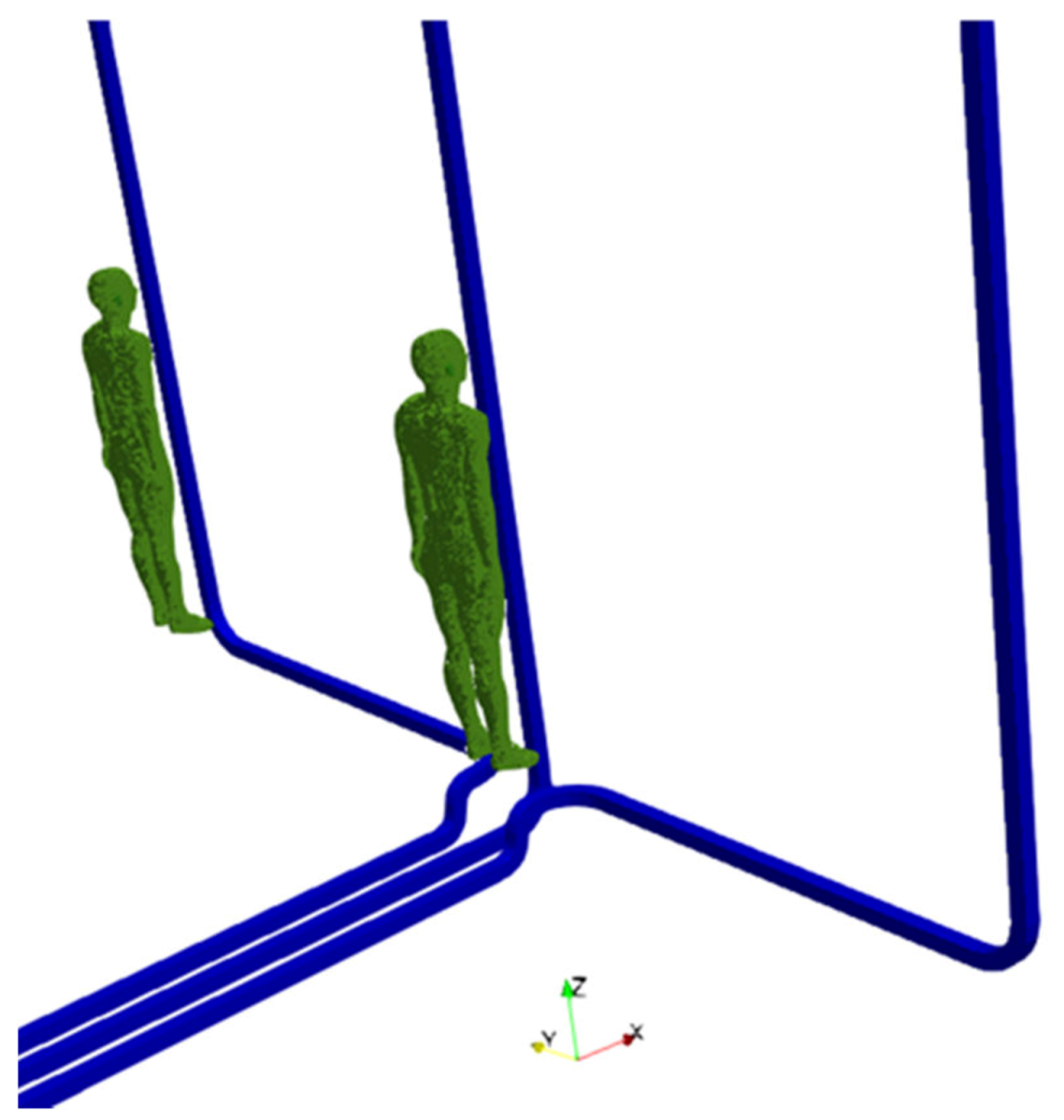
2.4. Exposure Scenarios
3. Results and Discussion
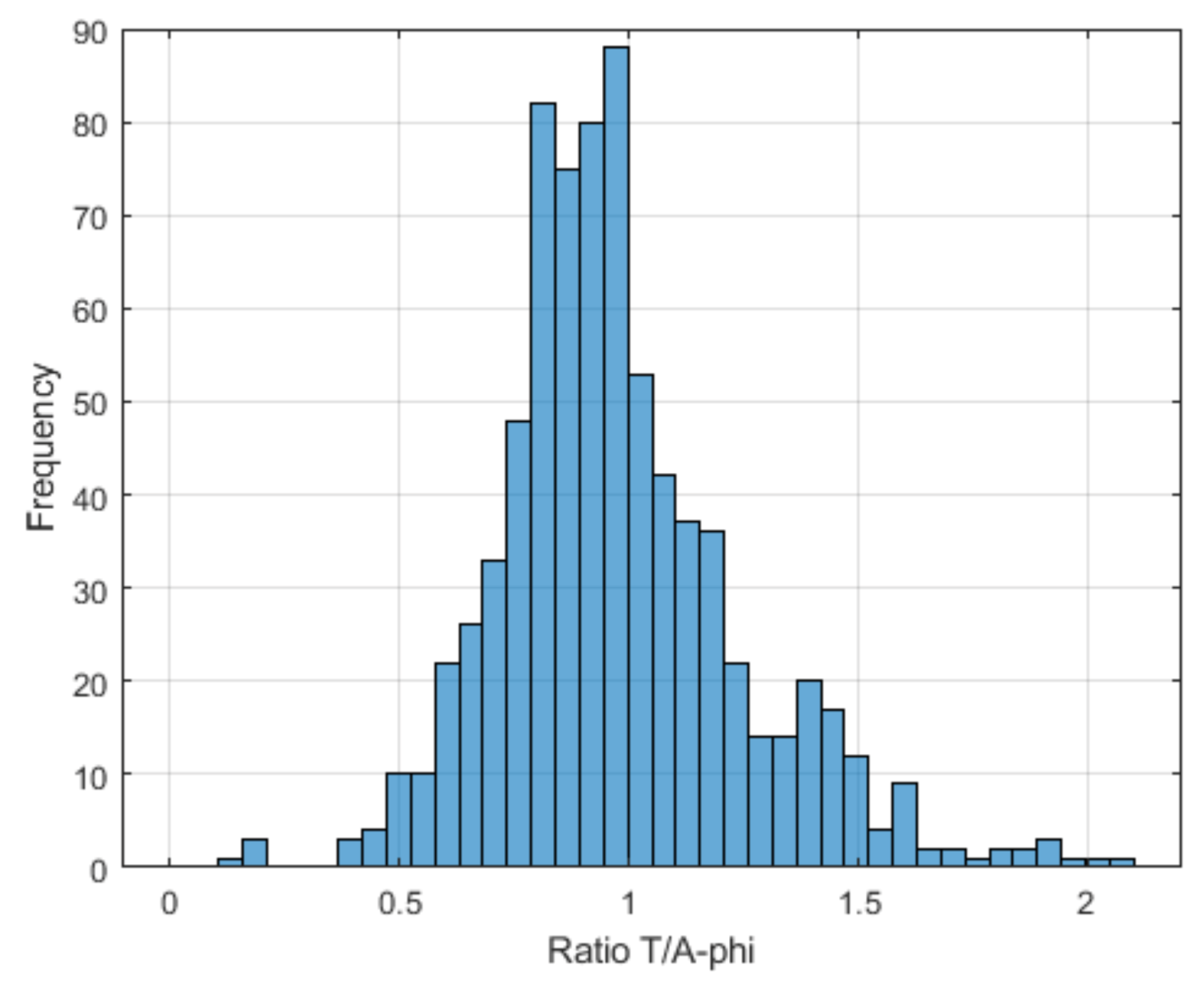
3.1. Considerations about Results Accuracy
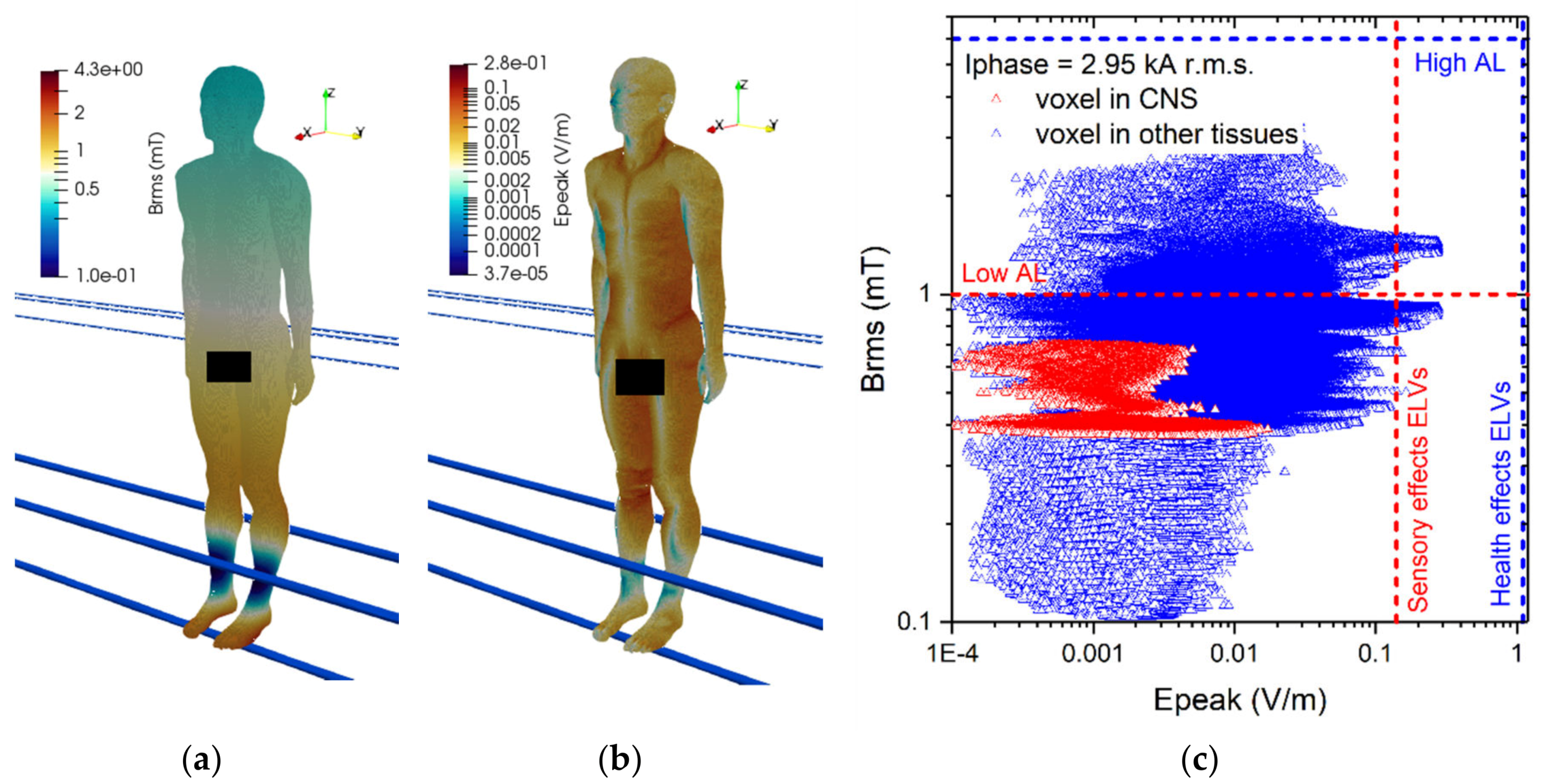
3.2. Results about the Exposure Scenario A
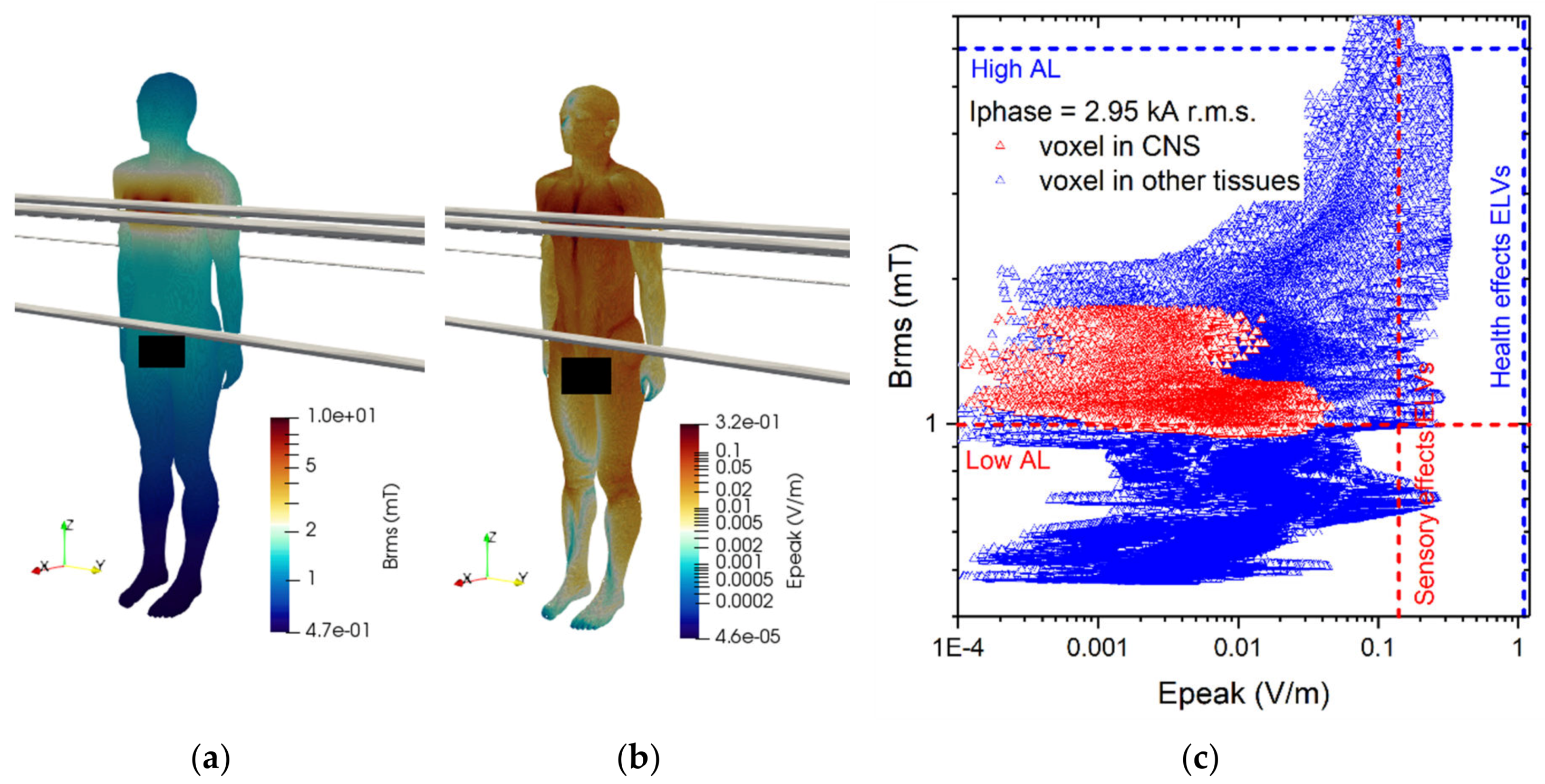
3.3. Results about the Exposure Scenario B
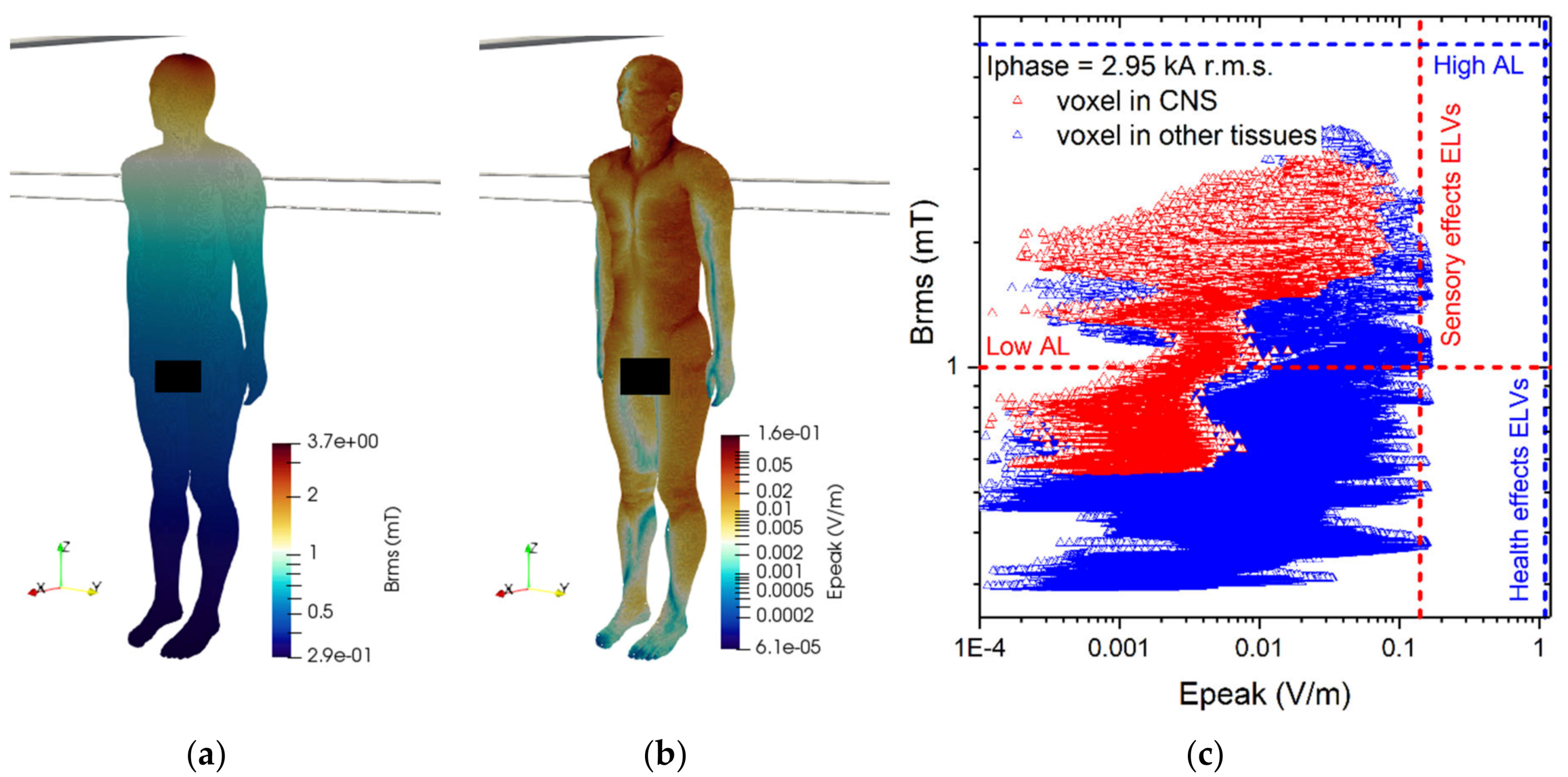
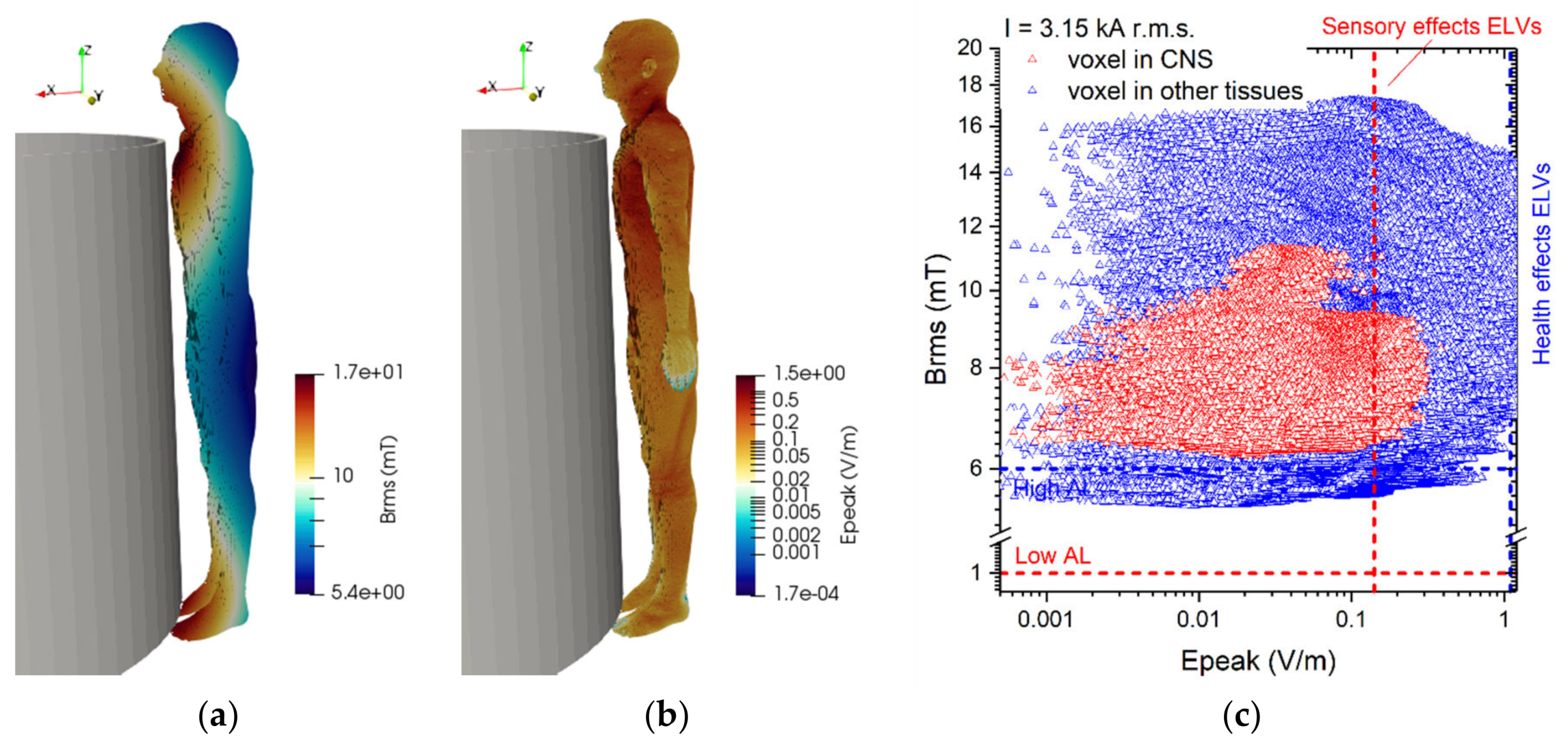
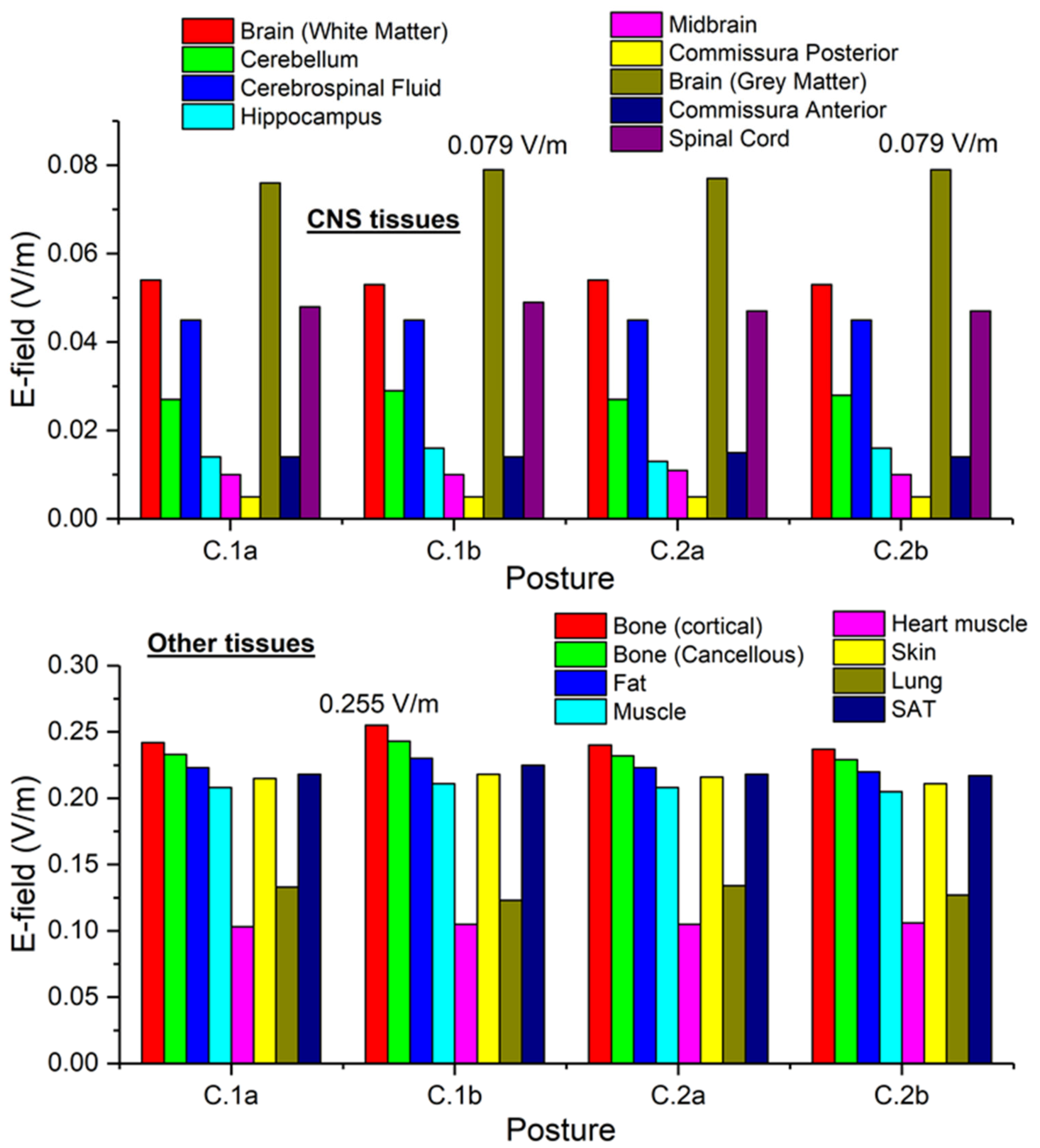
3.4. Results Concerning Exposure Scenario C
3.5. Analysis of Sensitivity to Body-Conductor Relative Position
- (a)
- For the exposure scenario A, posture A.3 that gives rise to the worst exposure conditions. The human body has been moved in order to reduce (resp. increase) the distance between the worker’s head and the closest conductor at 25 mm (resp. 75 mm). These cases are identified as A.3#1 and A.3#2, respectively. Moreover, the body has been moved along the transversal direction of conductors (x-axis in Figure 1) of−50 mm (case A.3#3) and + 50 mm (case A.3#4).
- (b)
- For the exposure scenario B, the case of 380 kV line trap coil (B.2), that gives rise to the worst exposure conditions. The human body has been moved in order to reduce (resp. increase) the distance between the worker’s thorax and the coil at 5 mm (resp. 15 mm). These cases are identified as B.2#1 and B.2#2, respectively. Moreover, the body has been moved along the vertical axis (z-axis in Figure 2) of −200 mm (case B.2#3) and of +200 mm (case B.2#4).
- (c)
- For the exposure scenario C, the case of phase conductors at a distance of 2.5 m and the worker placed in front of the lateral conductor (C.1b), that gives rise to the worst exposure conditions. The human body has been moved in order to reduce (resp. increase) the distance between the worker’s thorax and the coil at 30 mm (resp. 110 mm). These cases are identified as C.1b#1 and C.1b#2, respectively.
4. Conclusions
- For scenario (A) the results obtained showed that the worst position is when the conductors are placed near the operator’s head, assuming a conductor - head distance equal to 50 mm. Considering a value of current equal to 2950 A r.m.s, in any analyzed position the ELVs for CNS tissues and all other tissues are never exceeded, despite in some cases the ALs are exceeded in non-CNS tissues. Considering this high current value, which is not normally achieved on overhead lines in Italy, it is not necessary to take further precautions for workers.
- For Scenario (B), only the typical work positions for the 220 kV and 380 kV voltage level have been studied. In both cases the parts of the body that are mainly involved are chest, neck and head. If the current flowing through the line trap exceeds the value of 1000 A, the E-field peak values could be higher than the regulatory limits. At present, in the Italian experience, this kind of job is actually done in conditions of out of service of the power line (dead working). In case of live-line working, the results obtained suggest the requirement that the activity is carried on with a continuous monitoring of the current values, in order to immediately stop the work if the value of 1000 A is exceeded.
- For scenario (C) the worst position, from the point of view of the exposure to the magnetic field, is the one with the operator in front of a lateral conductor. The E-field peak values induced in the body, with a current value equal to 1600 A r.m.s. used for the computation, are always found lower than regulatory limits. It is therefore not necessary to take further precautions for workers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tamus, Z.A.; Németh, B.; Novák, B.; Kimpián, A.; Kiss, I.; Szűcs, L.; Berta, I. Examination of electric field exposure of live line workers. In Proceedings of the XVII International Symposium on High Voltage Engineering, Hannover, Germany, 22–26 August 2011. [Google Scholar]
- The European Parliament and the Council of the European Union. Directive 2013/35/EU on the Minimum Health and Safety Requirements Regarding the Exposure of Workers to the Risks Arising from Physical Agents (Electromagnetic Fields); European Union: Brussels, Belgium, 2013. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for limiting exposure to time varying electric and magnetic fields (1 Hz to 100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines on limits of exposure to static magnetic fields. Health Phys. 2009, 96, 504–514. [Google Scholar] [CrossRef] [PubMed]
- Habiballah, I.O.; Abdel-Galil, T.K.; Dawoud, M.M.; Belhadj, C.A.; Arif Abdul-Majeed, M.; Al-Betairi, T.A. ELF Electric and Magnetic Fields Exposure Assessment of Live-Line Workers for 132 kV Transmission Line of SEC. In Proceedings of the 2006 IEEE/PES Transmission and Distribution Conference and Exposition Latin America, Caracas, Venezuela, 15–18 August 2016. [Google Scholar] [CrossRef]
- Dehghan, H.; Rizi, H.A.Y. Health problems from radiation of high-voltage facilities. Int. J. Environ. Health. Eng. 2013, 2, 1. [Google Scholar] [CrossRef]
- Korpinen, L.; Kuisti, H.; Pääkkönen, R.; Vanhala, P.; Elovaara, J. Occupational Exposure to Electric and Magnetic Fields While Working at Switching and Transforming Stations of 110 kV. Ann. Occup. Hyg. 2011, 55, 526–536. [Google Scholar]
- Belhadj, C.A.; Dawoud, M.M.; Maalej, N.; Habiballah, I.O.; Abdel-Galil, T.K. Electric & Magnetic Field Assessment for Live-Line Workers Next to A 132 KV Transmission Line Conductor. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition: Latin America, Bogota, Colombia, 13–15 August 2008. [Google Scholar] [CrossRef]
- Tourab, W.; Babouri, A. Measurement and Modeling of Personal Exposure to the Electric and Magnetic Fields in the Vicinity of High Voltage Power Lines. Saf. Heal. Work. 2015, 7, 102–110. [Google Scholar] [CrossRef]
- Korpinen, L.; Pääkkönen, R.; Farrugia, L.; Tarao, H.; Gobba, F. Directive 2013/35/EU for electromagnetic fields of workers’ exposure and working from the ladder near a 400 kV power line. In Proceedings of the Progress in Electromagnetics Research Symposium, PIERS 2016, Shanghai, China, 8–11 August 2016; pp. 2106–2108, Article number 7734883. [Google Scholar]
- Ozen, S.; Helhel, S.; Carlak, H.F. Occupational exposure assessment of power frequency magnetic field in 154/31.5kV electric power substation in Turkey. In Proceedings of the Progress in Electromagnetics Research Symposium, Prague, Czech Republic, 6–9 July 2015; pp. 1440–1443. [Google Scholar]
- Nunes, F.O.; Margato, E.F. Risk assessment of chronic exposure to magnetic fields near electrical apparatus. In Proceedings of the 9th International Symposium on Occupational Safety and Hygiene, SHO 2013, Guimaraes, Portugal, 14–15 February 2013; pp. 389–394, Article code: 96254. [Google Scholar]
- Lindh, T.O.; Tornqvist, S.G.; Andersson, L.-I.K. Exposure to Electric and Magnetic Fields among Employees in the Electric Utility Industry. Appl. Occup. Environ. Hyg. 1997, 12, 293–301. [Google Scholar] [CrossRef]
- Li, L.; Xiong, D.-F.; Liu, J.-W.; Li, Z.-X.; Zeng, G.-C.; Li, H.-L. No effects of power line frequency extremely low frequency electromagnetic field exposure on selected neurobehavior tests of workers inspecting transformers and distribution line stations versus controls. Australas. Phys. Eng. Sci. Med. 2013, 37, 37–44. [Google Scholar] [CrossRef]
- Dawson, T.W.; Caputa, K.; Stuchly, M.A. Magnetic field exposures for UK live-line workers. Phys. Med. Boil. 2002, 47, 995–1012. [Google Scholar] [CrossRef]
- Zubal, I.G.; Harrell, C.R.; Smith, E.O.; Rattner, Z.; Gindi, G.; Hoffer, P.B. Computerized three-dimensional segmented human anatomy. Med. Phys. 1994, 21, 299–302. [Google Scholar] [CrossRef]
- US National Library of Medicine. Available online: https://www.nlm.nih.gov/research/visible/visiblehuman.html (accessed on 1 March 2020).
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for limiting exposure to time varying electric, magnetic and electromagnetic fields (up to 300 GHz). Health Phys. 1998, 74, 494–522. [Google Scholar]
- ElBidweihy, H.; Anis, H. Comparative Exposure to Magnetic Fields of Live-Line Workers on Power Lines. In Proceedings of the 2012 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Orlando, FL, USA, 7–10 May 2012. [Google Scholar] [CrossRef]
- Ghania, S.M. Evaluation of Electromagnetic Fields Exposure during Live Line Working Conditions Inside High Voltage Substations. IRACST Eng. Sci. Technol. An Int. J. (ESTIJ) 2013, 3, 2250–3498. [Google Scholar]
- Korpinen, L.; Elovaara, J.A.; Kuisti, H.A. Evaluation of current densities and total contact currents in occupational exposure at 400 kV substations and power lines. Bioelectromagnetics 2009, 30, 231–240. [Google Scholar] [CrossRef] [PubMed]
- Krajewski, W. Estimation of the electromagnetic field exposure during LLW on a HV tower with cable heads. Electr. Power Syst. Res. 2016, 140, 121–131. [Google Scholar] [CrossRef]
- Krajewski, W. Numerical assessment of electromagnetic exposure during live-line works on high-voltage objects. IET Sci. Meas. Technol. 2009, 3, 27–38. [Google Scholar] [CrossRef]
- Göcsei, G.; Kiss, I.; Németh, B. Effects of magnetic fields during high voltage live-line maintenance. J. Phys. Conf. Ser. 2015, 646, 012026. [Google Scholar] [CrossRef]
- Maalej, N.M.; Belhadj, C.A. External and internal electromagnetic exposures of workers near high voltage power lines. Progress Electromagn. Res. C 2011, 19, 191–205. [Google Scholar] [CrossRef]
- IEC/EN 62233. Measurement Methods for Electromagnetic Fields of Household Appliances and Similar Apparatus with Regard to Human Exposure; IEC: Geneva, Sweitzerland, 2005. [Google Scholar]
- Krajewski, W. Validation of a Numerical Approach to the Analysis of a Live-line Worker Exposure to the Electric Field. Prog. Electromagn. Res. 2011, 119, 315–333. [Google Scholar] [CrossRef][Green Version]
- Yordanova, M.; Mehmed-Hamza, M.; Abraham, A.; Kovalev, S.; Tarassov, V.; Snasel, V.; Vasileva, M.; Sukhanov, A. A Computing Approach to Risk Assessment Related to Electromagnetic Field Exposure from Overhead Power Lines. Adv. Intell. Syst. Comput. 2017, 680, 220–227. [Google Scholar]
- Dimbylow, P. Development of the female voxel phantom, NAOMI, and its application to calculations of induced current densities and electric fields from applied low frequency magnetic and electric fields. Phys. Med. Boil. 2005, 50, 1047–1070. [Google Scholar] [CrossRef]
- Dimbylow, P.J. Induced current densities from low-frequency magnetic fields in a 2 mm resolution, anatomically realistic model of the body. Phys. Med. Boil. 1998, 43, 221–230. [Google Scholar] [CrossRef]
- Nagaoka, T.; Watanabe, S.; Sakurai, K.; Kunieda, E.; Watanabe, S.; Taki, M.; Yamanaka, Y. Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic-field dosimetry. Phys. Med. Boil. 2004, 49, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Christ, A.; Kainz, W.; Hahn, E.G.; Honegger, K.; Zefferer, M.; Neufeld, E.; Rascher, W.; Janka, R.; Bautz, W.; Chen, J.; et al. The Virtual Family—Development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Boil. 2009, 55, N23–N38. [Google Scholar] [CrossRef] [PubMed]
- 4D Extended Cardiac-Torso (XCAT) Phantom, Version 2.0, Duke University (UK). Available online: https://olv.duke.edu/industry-investors/available-technologies/xcat/ (accessed on 1 March 2020).
- Findlay, R.P. Induced electric fields in the MAXWEL surface-based human model from exposure to external low frequency electric fields. Radiat. Prot. Dosim. 2013, 162, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Magne, I.; Deschamps, F. Electric field induced in the human body by uniform 50 Hz electric or magnetic fields: Bibliography analysis and method for conservatively deriving measurable limits. J. Radiol. Prot. 2016, 36, 419–436. [Google Scholar] [CrossRef] [PubMed]
- Dawson, T.; Potter, M.; Stuchly, M. Evaluation of modeling accuracy of power frequency field interactions with the human body. Appl. Comput. Electromagn. Soc. J. 2001, 16, 162–172. [Google Scholar]
- Hirata, A.; Yamazaki, K.; Hamada, S.; Kamimura, Y.; Tarao, H.; Wake, K.; Suzuki, Y.; Hayashi, N.; Fujiwara, O. Intercomparison of induced fields in Japanese male model for ELF magnetic field exposures: Effect of different computational methods and codes. Radiat. Prot. Dosim. 2009, 138, 237–244. [Google Scholar] [CrossRef]
- Aga, K.; Hirata, A.; Laakso, I.; Tarao, H.; Diao, Y.; Ito, T.; Sekiba, Y.; Yamazaki, K. Intercomparison of In Situ Electric Fields in Human Models Exposed to Spatially Uniform Magnetic Fields. IEEE Access 2018, 6, 70964–70973. [Google Scholar] [CrossRef]
- Poljak, D.; Cvetković, M.; Bottauscio, O.; Hirata, A.; Laakso, I.; Neufeld, E.; Reboux, S.; Warren, C.; Giannopolous, A.; Costen, F. On the Use of Conformal Models and Methods in Dosimetry for Nonuniform Field Exposure IEEE Trans. Electromagn. Compat. 2018, 60, 328–337. [Google Scholar] [CrossRef]
- Arduino, A.; Bottauscio, O.; Chiampi, M.M.; Laakso, I.; Zilberti, L. Computational Low-Frequency Electromagnetic Dosimetry Based on Magnetic Field Measurements. IEEE J. Electromagn. RF Microwaves Med. Boil. 2018, 2, 302–309. [Google Scholar] [CrossRef]
- Gomez-Tames, J.; Laakso, I.; Haba, Y.; Hirata, A.; Poljak, D.; Yamazaki, K. Computational Artifacts of the In Situ Electric Field in Anatomical Models Exposed to Low-Frequency Magnetic Field. IEEE Trans. Electromagn. Compat. 2017, 60, 589–597. [Google Scholar] [CrossRef]
- Arduino, A.; Bottauscio, O.; Chiampi, M.; Giaccone, L.; Liorni, I.; Kuster, N.; Zilberti, L.; Zucca, M. Accuracy Assessment of Numerical Dosimetry for the Evaluation of Human Exposure to Electric Vehicle Inductive Charging Systems. IEEE Trans. Electromagn. Compat. 2020, 1–12. [Google Scholar] [CrossRef]
- IEEE C95. 1-2019-IEEE Approved Draft Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic and Electromagnetic Fields, 0 Hz to 300 GHz; IEEE: Piscataway Township, NJ, USA, 2019. [Google Scholar]
- Hasgall, P.A.; Neufeld, E.; Gosselin, M.C.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues; Version 4.0; IT’S Foundation: Zurich, Switzerland, 15 May 2018. [Google Scholar] [CrossRef]
- Chen, X.-L.; Benkler, S.; Chavannes, N.; De Santis, V.; Bakker, J.; Van Rhoon, G.; Mosig, J.; Kuster, N. Analysis of human brain exposure to low-frequency magnetic fields: A numerical assessment of spatially averaged electric fields and exposure limits. Bioelectromagnetics 2013, 34, 375–384. [Google Scholar] [CrossRef]
- Peratta, C.; Peratta, A. Modelling the Human Body Exposure to ELF Electric Fields; WIT Press: Southampton, UK; Boston, MA, USA, 2010; Volume 47, p. 24. [Google Scholar]
- Åström, M.; Lemaire, J.-J.; Wardell, K. Influence of heterogeneous and anisotropic tissue conductivity on electric field distribution in deep brain stimulation. Med. Boil. Eng. 2011, 50, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Saad, Y.; Schultz, M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Golias, N.; Tsiboukis, T. Magnetostatics with edge elements: A numerical investigation in the choice of the tree. IEEE Trans. Magn. 1994, 30, 2877–2880. [Google Scholar] [CrossRef]
- Kos, B.; Valič, B.; Kotnik, T.; Gajšek, P. Occupational exposure assessment of magnetic fields generated by induction heating equipment—The role of spatial averaging. Phys. Med. Boil. 2012, 57, 5943–5953. [Google Scholar] [CrossRef]
- Zucca, M.; Bottauscio, O.; Chiampi, M.; Zilberti, L. Operator Safety and Field Focality in Shielded Transcranial Magnetic Stimulation. IEEE Trans. Magn. 2017, 53, 5100704. [Google Scholar] [CrossRef]
- CIGRE. Guide for Thermal Rating Calculations of Overhead Lines; Technical Brochure 601, Study Committee B2; CIGRE: Paris, France, 2012. [Google Scholar]
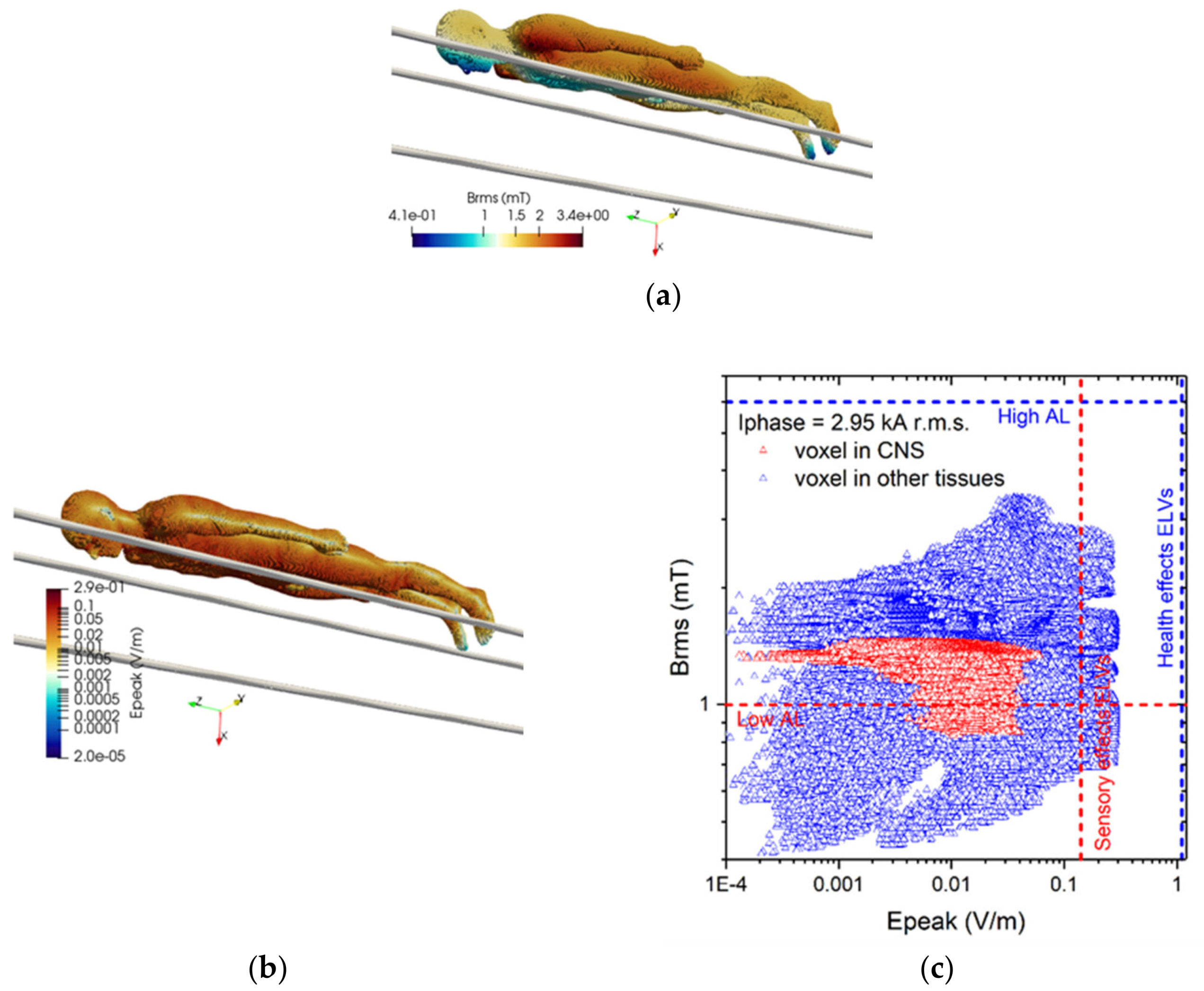
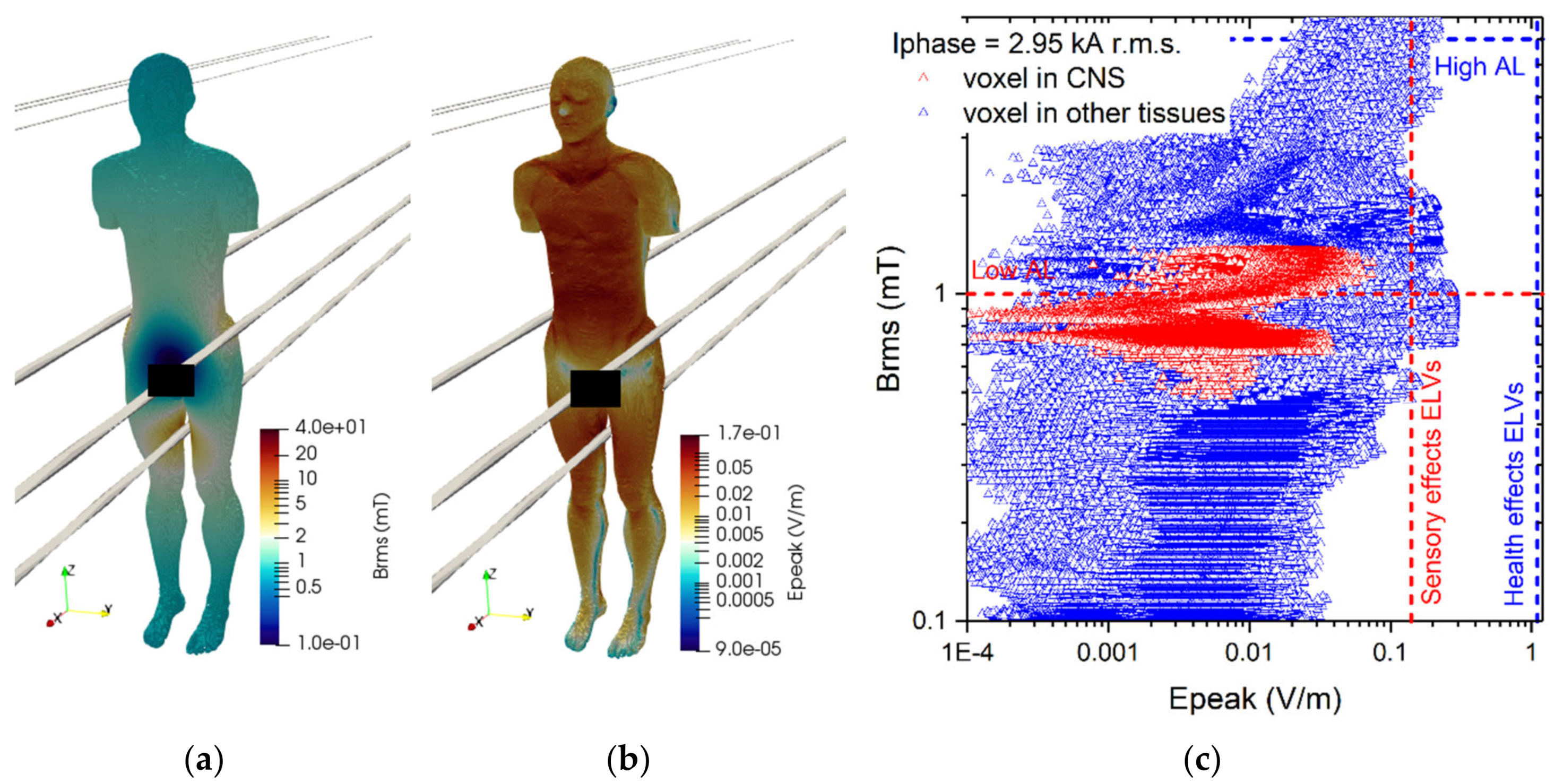
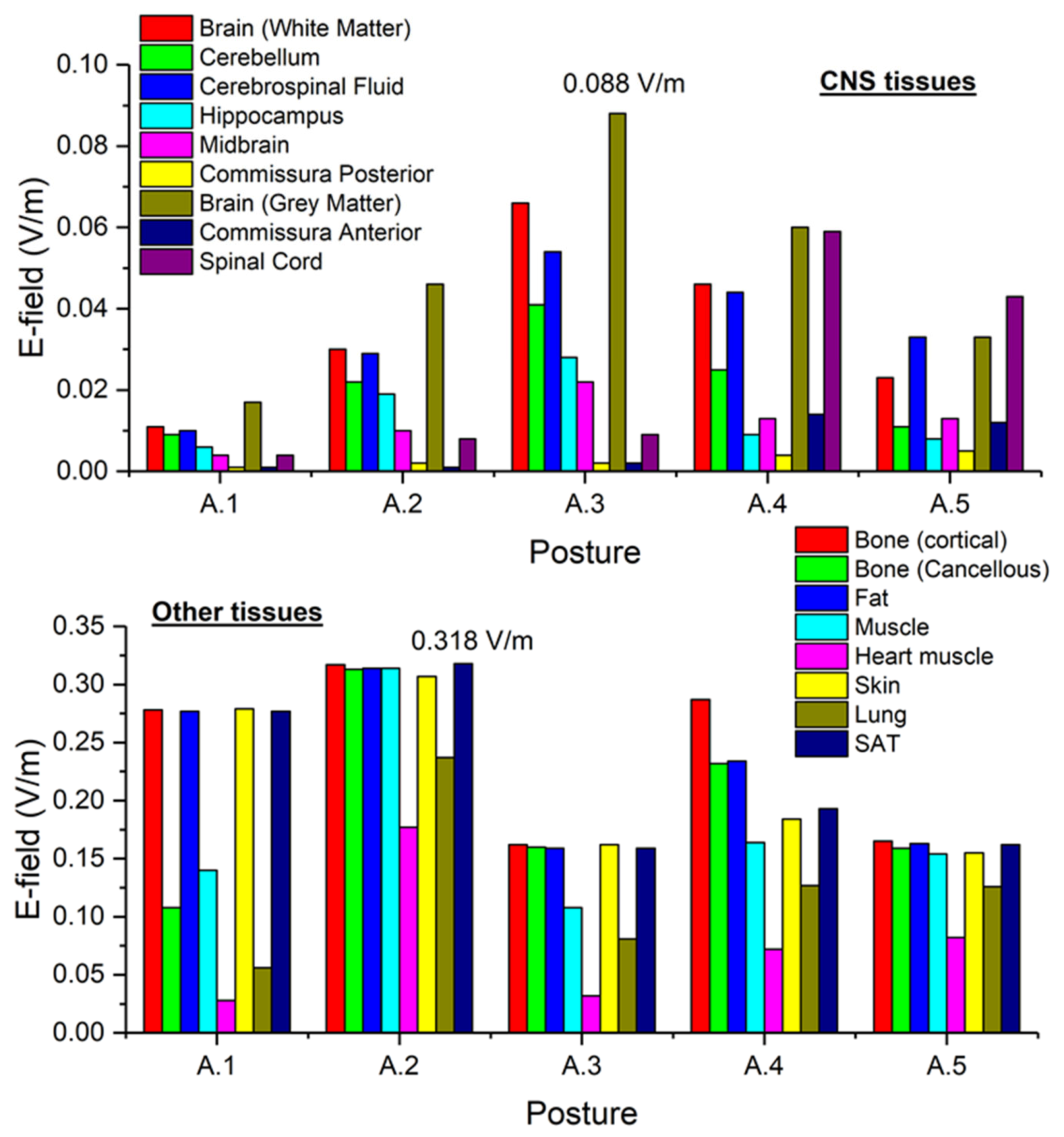
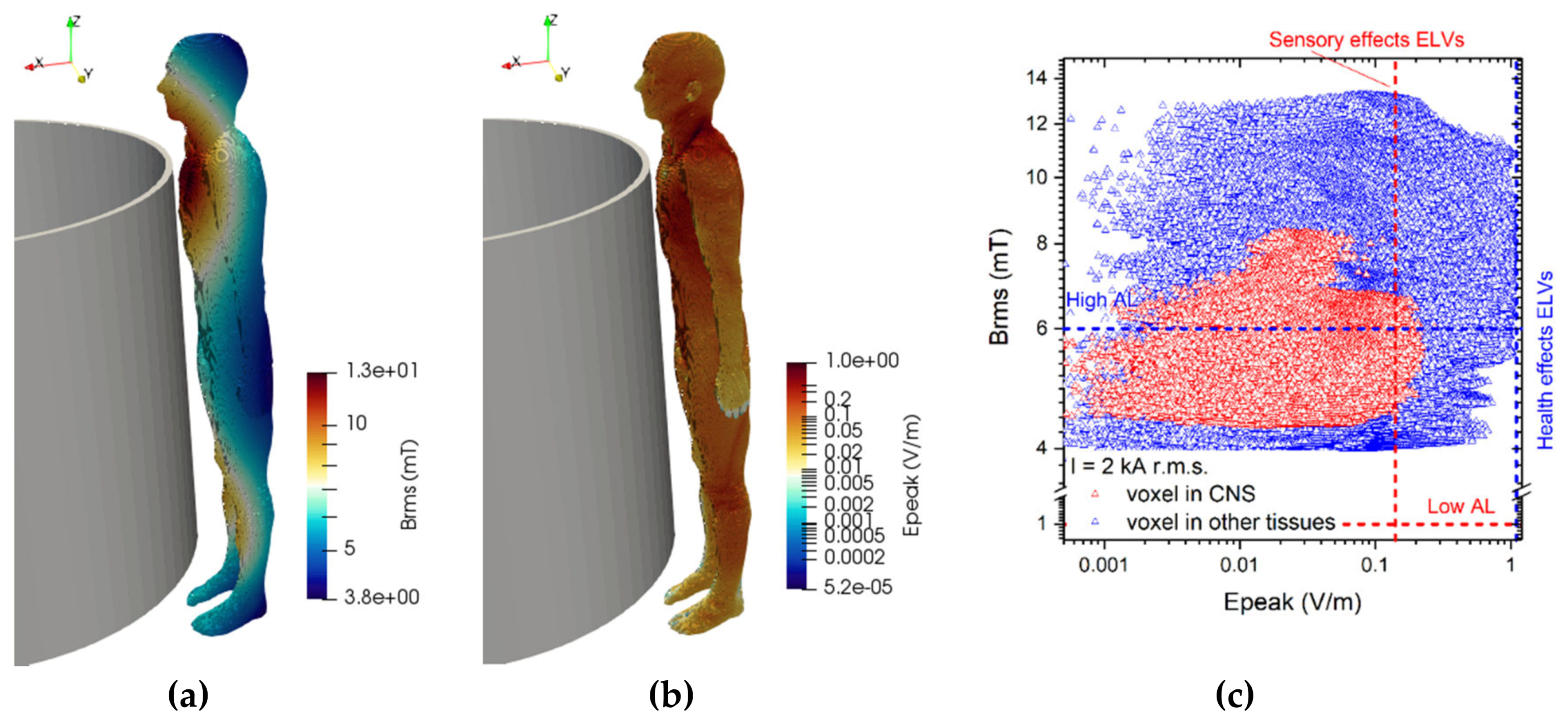


| Tissue | Electrical Conductivity (S/m) |
|---|---|
| Central nervous system (CNS) | |
| Brain (White Matter) | 0.265 |
| Cerebellum | 0.660 |
| Cerebrospinal Fluid | 1.777 |
| Hippocampus | 0.276 |
| Midbrain | 0.234 |
| Commissura Posterior | 0.265 |
| Brain (Grey Matter) | 0.239 |
| Commissura Anterior | 0.265 |
| Spinal Cord | 0.234 |
| Other tissues | |
| Bone (Cortical) | 0.0035 |
| Bone (Cancellous) | 0.0821 |
| Fat | 0.0573 |
| Muscle | 0.355 |
| Heart Muscle | 0.381 |
| Skin | 0.170 |
| Lung | 0.105 |
| Subcutaneous Adipose Tissue (SAT) | 0.057 |
| Voltage (kV) | Diameter (mm) | Height (mm) | Number of Turns |
|---|---|---|---|
| 220 | 1090 | 1120 | 17 |
| 380 | 1450 | 1350 | 15 |
| Posture | E-Field After Outlier Removal | E-Field 99th Percentile | ||||
|---|---|---|---|---|---|---|
| E_outA-ϕ (V/m) | E_outT (V/m) | Ratio E_outT/E_outA-ϕ | E_99A-ϕ (V/m) | E_99T (V/m) | Ratio E_99T/E_99A-ϕ | |
| A.1 | 0.279 | 0.201 | 0.72 | 0.060 | 0.057 | 0.95 |
| A.2 | 0.318 | 0.354 | 1.11 | 0.096 | 0.103 | 1.07 |
| A.3 | 0.162 | 0.259 | 1.60 | 0.060 | 0.065 | 1.08 |
| A.4 | 0.288 | 0.285 | 0.99 | 0.076 | 0.077 | 1.01 |
| A.5 | 0.166 | 0.221 | 1.34 | 0.071 | 0.066 | 0.93 |
| B.1 | 1.042 | 1.616 | 1.55 | 0.414 | 0.441 | 1.07 |
| B.2 | 1.474 | 2.192 | 1.49 | 0.578 | 0.611 | 1.06 |
| C.1a | 0.243 | 0.393 | 1.62 | 0.082 | 0.083 | 1.01 |
| C.1b | 0.255 | 0.364 | 1.42 | 0.081 | 0.083 | 1.03 |
| C.2a | 0.240 | 0.370 | 1.54 | 0.083 | 0.083 | 1.00 |
| C.2b | 0.238 | 0.347 | 1.46 | 0.082 | 0.083 | 1.01 |
| Tissue | Reference Position (A.3) | Case A.3#1 | Case A.3#2 | Case A.3#3 | Case A.3#4 |
|---|---|---|---|---|---|
| Brain (White Matter) | 0.066 | 0.080 | 0.057 | 0.055 | 0.062 |
| Cerebellum | 0.041 | 0.045 | 0.037 | 0.038 | 0.041 |
| Cerebrospinal Fluid | 0.054 | 0.067 | 0.048 | 0.052 | 0.054 |
| Hippocampus | 0.028 | 0.031 | 0.026 | 0.025 | 0.030 |
| Midbrain | 0.022 | 0.025 | 0.020 | 0.022 | 0.019 |
| Commissura Posterior | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Brain (Grey Matter) | 0.088 | 0.104 | 0.077 | 0.085 | 0.084 |
| Commissura Anterior | 0.002 | 0.002 | 0.002 | 0.003 | 0.001 |
| Spinal Cord | 0.009 | 0.009 | 0.008 | 0.009 | 0.009 |
| Tissue | Reference Position (B.2) | Case B.2#1 | Case B.2#2 | Case B.2#3 | Case B.2#4 |
|---|---|---|---|---|---|
| Brain (White Matter) | 0.223 | 0.220 | 0.226 | 0.334 | 0.155 |
| Cerebellum | 0.187 | 0.184 | 0.189 | 0.247 | 0.126 |
| Cerebrospinal Fluid | 0.200 | 0.197 | 0.202 | 0.291 | 0.150 |
| Hippocampus | 0.119 | 0.118 | 0.120 | 0.184 | 0.075 |
| Midbrain | 0.104 | 0.102 | 0.105 | 0.126 | 0.073 |
| Commissura Posterior | 0.016 | 0.016 | 0.016 | 0.017 | 0.010 |
| Brain (Grey Matter) | 0.385 | 0.382 | 0.389 | 0.576 | 0.245 |
| Commissura Anterior | 0.025 | 0.025 | 0.026 | 0.015 | 0.019 |
| Spinal Cord | 0.095 | 0.093 | 0.097 | 0.063 | 0.080 |
| Tissue | Reference Position (C.1b) | Case C.1b#1 | Case C.1b#2 |
|---|---|---|---|
| Brain (White Matter) | 0.053 | 0.067 | 0.044 |
| Cerebellum | 0.029 | 0.035 | 0.024 |
| Cerebrospinal Fluid | 0.045 | 0.064 | 0.037 |
| Hippocampus | 0.016 | 0.021 | 0.014 |
| Midbrain | 0.010 | 0.011 | 0.009 |
| Commissura Posterior | 0.005 | 0.005 | 0.004 |
| Brain (Grey Matter) | 0.079 | 0.112 | 0.062 |
| Commissura Anterior | 0.014 | 0.017 | 0.012 |
| Spinal Cord | 0.049 | 0.057 | 0.042 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottauscio, O.; Arduino, A.; Bavastro, D.; Capra, D.; Guarneri, A.; Parizia, A.A.; Zilberti, L. Exposure of Live-Line Workers to Magnetic Fields: A Dosimetric Analysis. Int. J. Environ. Res. Public Health 2020, 17, 2429. https://doi.org/10.3390/ijerph17072429
Bottauscio O, Arduino A, Bavastro D, Capra D, Guarneri A, Parizia AA, Zilberti L. Exposure of Live-Line Workers to Magnetic Fields: A Dosimetric Analysis. International Journal of Environmental Research and Public Health. 2020; 17(7):2429. https://doi.org/10.3390/ijerph17072429
Chicago/Turabian StyleBottauscio, Oriano, Alessandro Arduino, Davide Bavastro, Davide Capra, Arianna Guarneri, Alessandro A. Parizia, and Luca Zilberti. 2020. "Exposure of Live-Line Workers to Magnetic Fields: A Dosimetric Analysis" International Journal of Environmental Research and Public Health 17, no. 7: 2429. https://doi.org/10.3390/ijerph17072429
APA StyleBottauscio, O., Arduino, A., Bavastro, D., Capra, D., Guarneri, A., Parizia, A. A., & Zilberti, L. (2020). Exposure of Live-Line Workers to Magnetic Fields: A Dosimetric Analysis. International Journal of Environmental Research and Public Health, 17(7), 2429. https://doi.org/10.3390/ijerph17072429





