Automated Detection and Screening of Traumatic Brain Injury (TBI) Using Computed Tomography Images: A Comprehensive Review and Future Perspectives
Abstract
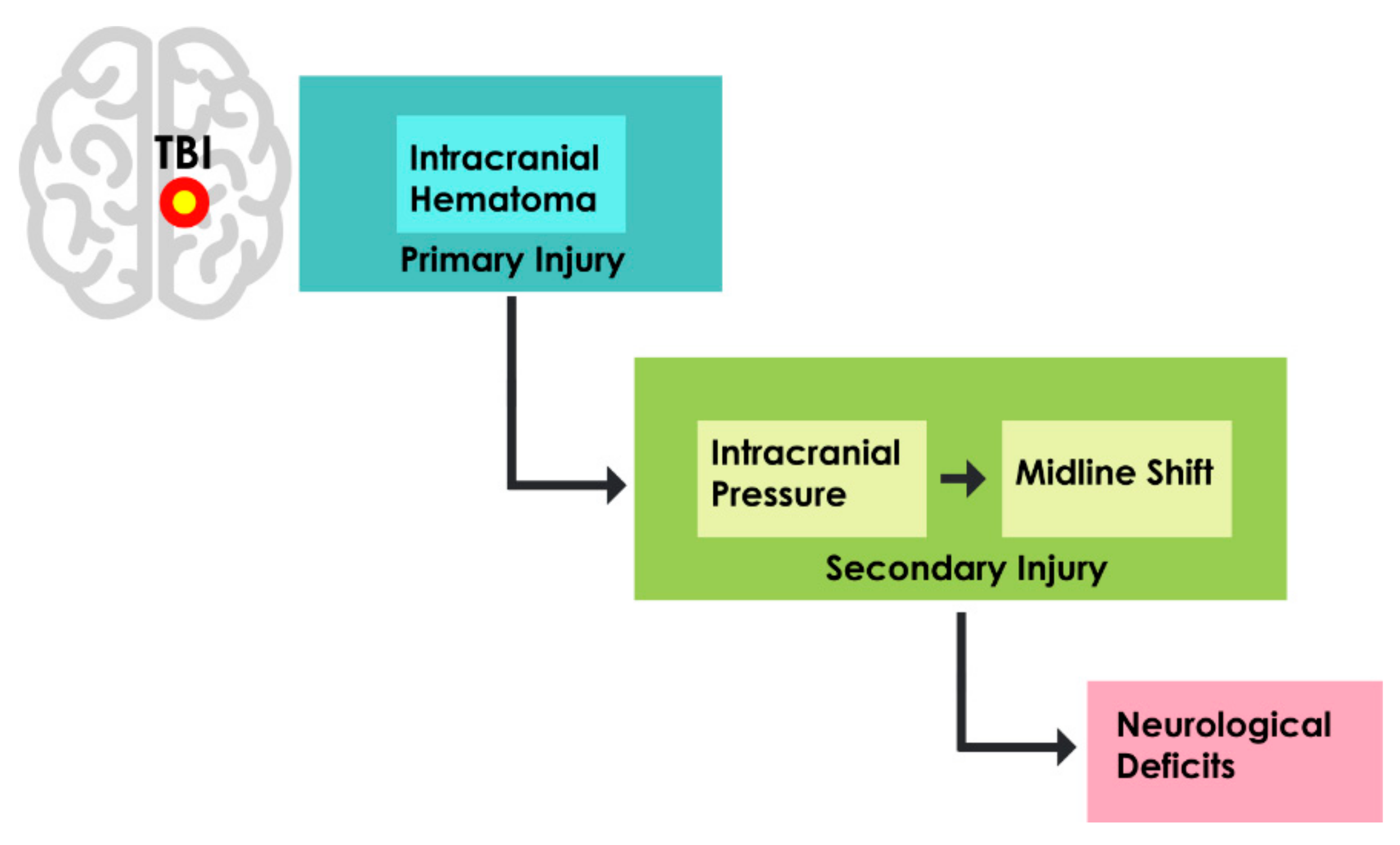
:1. Introduction
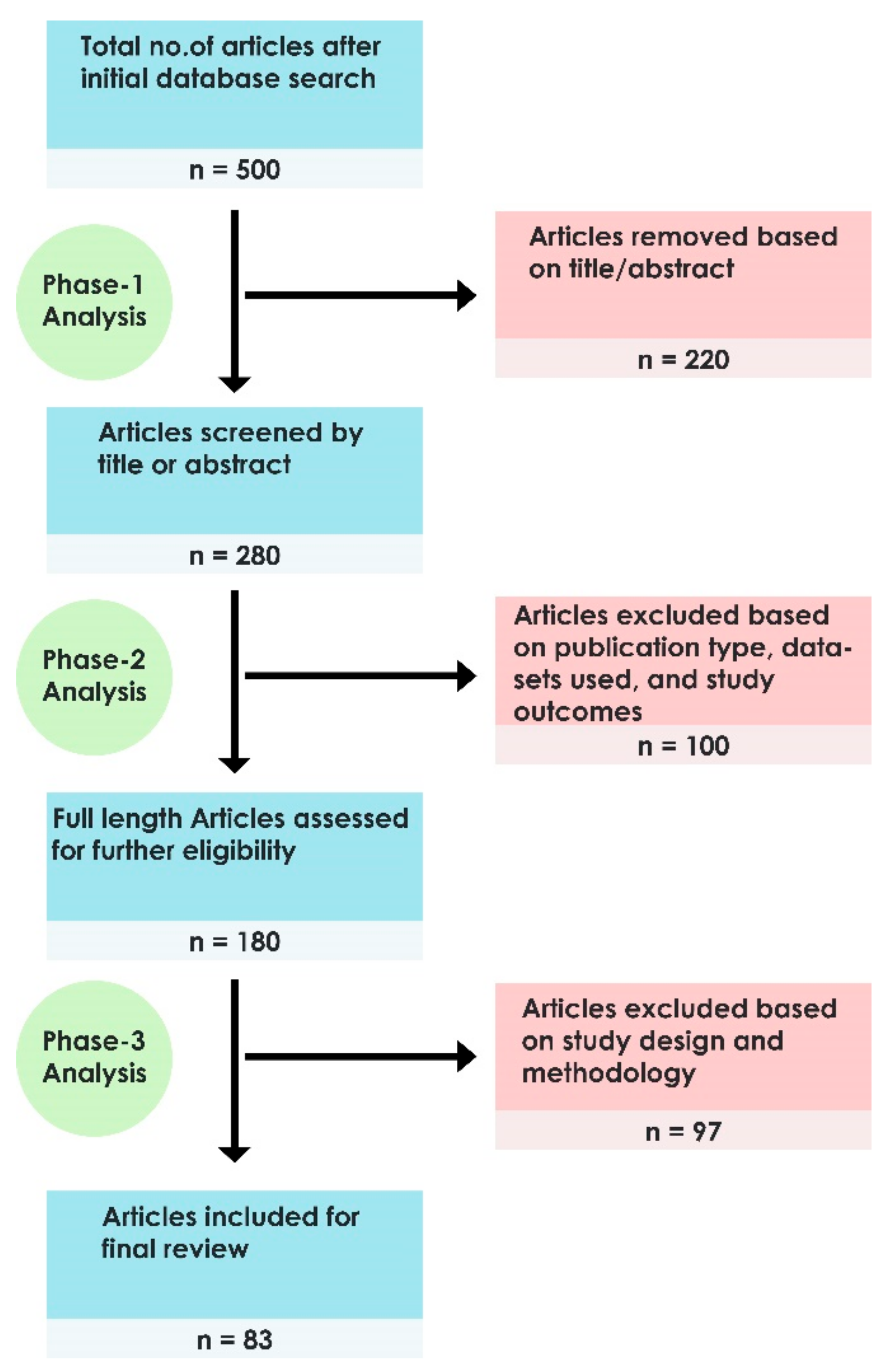
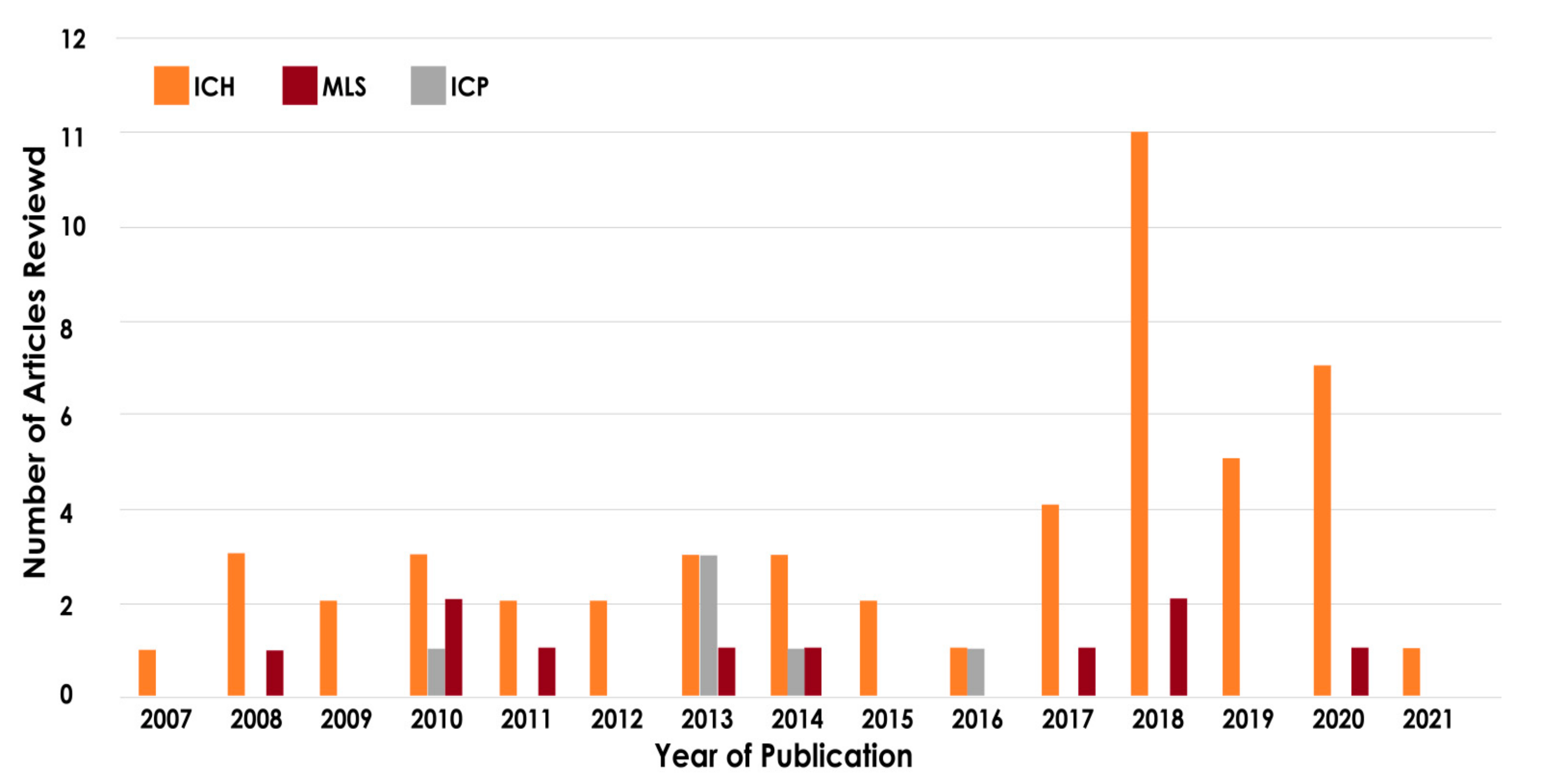
2. Search Strategy and Organisation of the Review
3. Open Source Datasets
3.1. CQ500 Dataset
3.2. RSNA Dataset
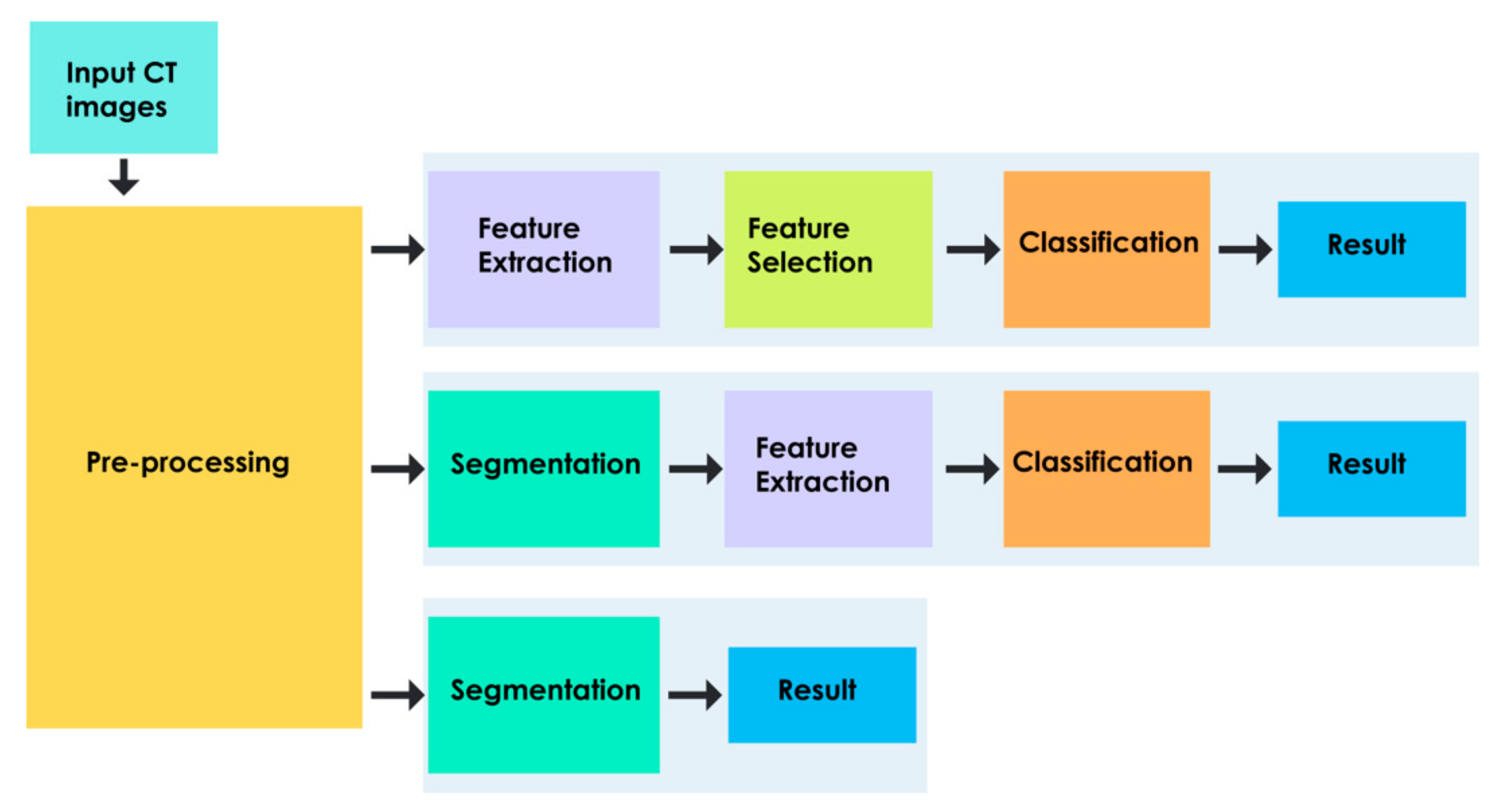
4. Generics of Computer Aided Diagnosis
- Feature Learning-Based Approach
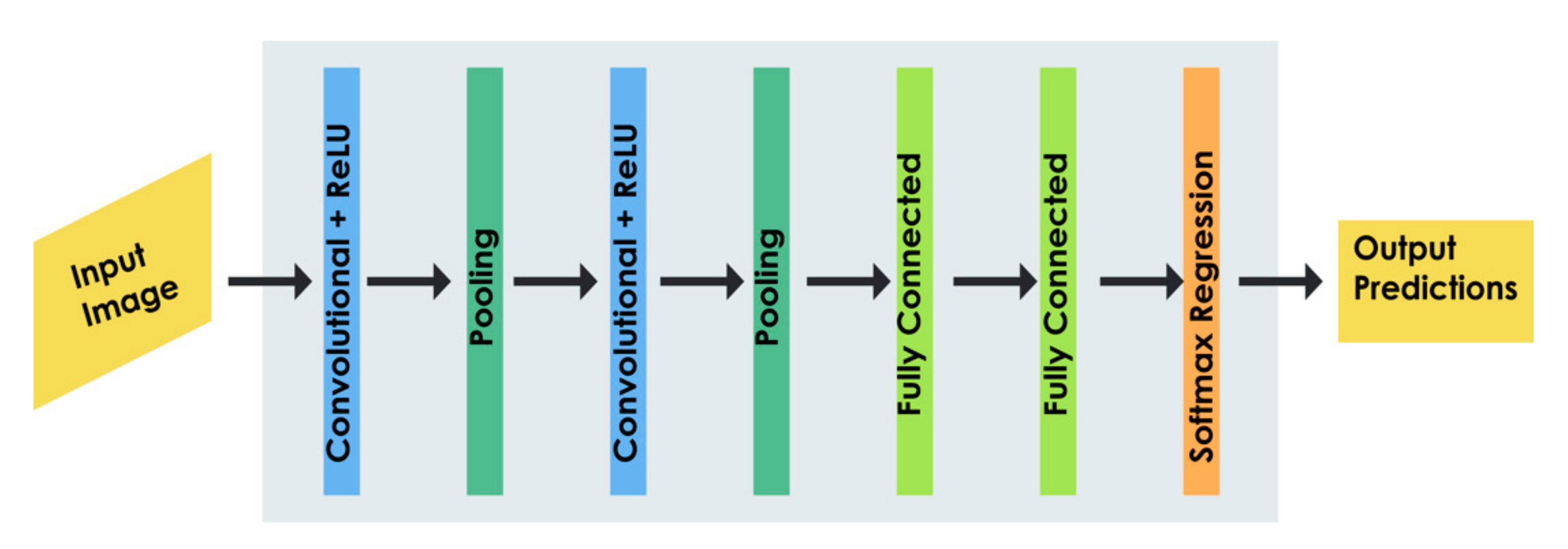
- Deep Learning-Based Approach
4.1. Pre-Processing
4.2. Feature Extraction
4.3. Segmentation
4.4. Feature Dimensionality Reduction
4.5. Classification
4.6. Deep Learning for Hematoma Detection
4.7. Hematoma Volume Estimation
4.8. Automated Intracranial Pressure Prediction
4.9. Automated Midline Estimation
5. Discussion
5.1. Open Issues for Future Development
5.1.1. CAD Models Based on Large and Diverse Datasets
5.1.2. CAD Models for Detection, Classification, and Estimation of TBI-Related Pathologies
5.1.3. CAD Models Based on Clinical Guidelines
5.1.4. Limitations of the Study
- Multiple research databases were searched to obtain the final set of papers for review. The searching process was limited to the set of keywords and their synonyms. Therefore, the study may have neglected some of the relevant works related to the automated detection and assessment of TBI-related abnormalities, like ICH, ICP, and MLS.
- The study consists of papers that are published in the English language. Hence, we have not considered relevant studies in other languages.
- TBI can result in different kinds of primary and secondary injuries, and hence, the paper is limited to CAD systems for the detection and assessment of hematoma, intracranial pressure, and midline shift.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Langlois, J.A.; Rutland-Brown, W.; Wald, M.M. The epidemiology and impact of traumatic brain injury: A brief overview. J. Head Trauma Rehabil. 2006, 21, 375–378. [Google Scholar] [CrossRef] [Green Version]
- Dewan, M.C.; Rattani, A.; Gupta, S.; Baticulon, R.E.; Hung, Y.C.; Punchak, M.; Agrawal, A.; Adeleye, A.O.; Shrime, M.G.; Rubiano, A.M.; et al. Estimating the global incidence of traumatic brain injury. J. Neurosurg. 2018, 1080, 130–1097. [Google Scholar] [CrossRef] [Green Version]
- Finkelstein, E.; Corso, P.S.; Miller, T.R. The Incidence and Economic Burden of Injuries in The United States; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Indian Head Injury Foundation. Traumatic Brain Injury. Available online: http://indianheadinjuryfoundation.org/traumatic-brain-injury/ (accessed on 10 January 2021).
- Kaur, P.; Sharma, S. Recent advances in pathophysiology of traumatic brain injury. Curr. Neuropharmacol. 2018, 1224, 16–1238. [Google Scholar] [CrossRef] [PubMed]
- McKee, C.; Daneshvar, D.H. The neuropathology of traumatic brain injury. Handb. Clin. Neurol. 2015, 127, 45–66. [Google Scholar]
- Kim, J.J.; Gean, A.D. Imaging for the diagnosis and management of traumatic brain injury. Neurotherapeutics 2011, 8, 39–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ayaz, H.; Izzetoglu, M.; Izzetoglu, K.; Onaral, B.; Ben, B. Early diagnosis of traumatic intracranial hematomas. J. Biomed. Opt. 2021, 24, 051411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Mufti, F.; Thabet, A.M.; Singh, T.; El-Ghanem, M.; Amuluru, K.; Gandhi, C.D. Clinical and radiographic predictors of intracerebral hemorrhage outcome. Interv. Neurol. 2018, 7, 118–136. [Google Scholar] [CrossRef] [Green Version]
- Wilkinson, M.; Kung, T.F.C.; Jickling, G.C.; Colbourne, F. A translational perspective on intracranial pressure responses following intracerebral haemorrhage in animal models. Brain Hemorrhages 2020, 2, 34–48. [Google Scholar] [CrossRef]
- Oswal, A.; Toma, A.K. Intracranial pressure and cerebral haemodynamics. Anaesth. Intensive Care Med. 2017, 18, 259–263. [Google Scholar] [CrossRef]
- Monro, A. Observations on the Structure and Function of the Nervous System; Creech & Johnson: Edinburgh, UK, 1783. [Google Scholar]
- Feigin, V.L.; Lawes, C.M.; Bennett, D.A.; Barker-Collo, S.L.; Parag, V. Worldwide stroke incidence and early case fatality reported in 56 population-based studies: A systematic review. Lancet Neurol. 2009, 8, 355–369. [Google Scholar] [CrossRef]
- Fernando, S.M.; Tran, A.; Cheng, W.; Rochwerg, B.; Taljaard, M.; Kyeremanteng, K.; English, S.W.; Sekhon, M.S.; Griesdale, D.E.; Dowlatshahi, D.; et al. A diagnosis of elevated intracranial pressure in critically ill adults: Systematic review and meta-analysis. BMJ 2019, 366, 4225. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.; Tang, X.; Zhang, M.; Li, Q.; Xing, X.; Zhou, X.S.; Xue, Z.; Zhu, W.; Chen, Z.; Shi, F. The delineation of largely deformed brain midline using regression-based line detection network. Med. Phys. 2020, 47, 5531–5542. [Google Scholar] [CrossRef]
- Marshall, L.F.; Marshall, S.B.; Klauber, M.R.; Clark, M.V.; Eisenberg, H.M.; Jane, J.A.; Luerssen, T.G.; Marmarou, A.; Foulkes, M.A. A new classification of head injury based on computerized tomography. J. Neurosurg. 1991, 75, S14–S20. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.; Newberg, A. Neuroimaging in traumatic brain imaging. NeuroRx 2005, 2, 372–383. [Google Scholar] [CrossRef]
- Muschelli, J.; Sweeney, E.M.; Ullman, N.L.; Vespa, P.; Hanley, D.F.; Crainiceanu, C.M. PItcHPERFeCT: Primary Intracranial Hemorrhage Probability Estimation using Random Forests on CT. NeuroImage Clin. 2017, 14, 379–390. [Google Scholar] [CrossRef]
- Tavakoli, S.; Peitz, G.; Ares, W.; Hafeez, S.; Grandhi, R. Complications of invasive intracranial pressure monitoring devices in neurocritical care. Neurosurg. Focus 2017, 43, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muralidharan, R. External ventricular drains: Management and complications. Surg. Neurol. Int. 2015, 6, S271–S274. [Google Scholar] [CrossRef] [PubMed]
- Tabaddor, K.; Danziger, A.; Wisoff, H.S. Estimation of intracranial pressure by CT scan in closed head trauma. Surg. Neurol. 1982, 18, 212–215. [Google Scholar] [CrossRef]
- Kumar, M.; Saunak, N.; Anup, C.; Sadhu, K.; Chatterjee, J.; Ghosh, N. Computer-assisted delineation of hematoma from CT volume using autoencoder and Chan Vese model. Int. J. Comput. Assist. Radiol. Surg. 2018, 14, 259–269. [Google Scholar]
- Chan, T. Computer aided detection of small acute intracranial hemorrhage on computer tomography of brain. Comput. Med. Imaging Grap. 2007, 31, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Strub, W.M.; Leach, J.L.; Tomsick, T.; Vagal, A. Overnight preliminary head CT interpretations provided by residents: Locations of misidentified intracranial hemorrhage. Am. J. Neuroradiol. 2007, 28, 1679–1682. [Google Scholar] [CrossRef] [Green Version]
- Lal, N.R.; Murray, U.M.; Eldevik, O.P.; Desmond, J.S. Clinical consequences of misinterpretations of neuroradiologic CT scans by on-call radiology residents. Am. J. Neuroradiol. 2000, 21, 124–129. [Google Scholar]
- Cho, J.; Park, K.S.; Karki, M.; Lee, E.; Ko, S.; Kim, J.K.; Lee, D.; Choe, J.; Son, J.; Kim, M.; et al. Improving Sensitivity on identification and delineation of intracranial hemorrhage lesion using cascaded deep learning models. J. Digit. Imaging 2019, 32, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Prakash, K.N.B.; Zhou, S.; Morgan, T.C.; Hanley, D.F.; Nowinski, W.L. Segmentation and quantification of intra-ventricular/cerebral hemorrhage in CT scans by modified distance regularized level set evolution technique. Int. J. Comput. Assist. Radiol. Surg. 2012, 7, 785–798. [Google Scholar] [CrossRef] [Green Version]
- Hooshmand, M.; Soroushmehr, S.M.R. Automatic Midline Shift Detection in Traumatic Brain Injury. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI, USA, 17–21 July 2018. [Google Scholar]
- Chen, W.; Smith, R.; Nabizadeh, N.; Ward, K.; Cockrell, C.; Ha, J.; Najarian, K. Texture Analysis of Brain CT Scans for ICP Prediction. In Proceedings of the International Conference on Image and Signal Processing, Berlin, Germany, 30 June–2 July 2010. [Google Scholar]
- Liao, C.-C.; Xiao, F.; Wong, J.-M.; Chiang, I.-J. Automatic recognition of midline shift on brain CT images. Comput. Biol. Med. 2010, 40, 331–339. [Google Scholar] [CrossRef]
- Castellino, R.A. Computer aided detection (CAD): An overview. Cancer Imaging 2005, 5, 17–19. [Google Scholar] [CrossRef] [Green Version]
- Karthik, R.; Menaka, R.; Johnson, A.; Anand, S. Neuroimaging and deep learning for brain stroke detection—A review of recent advancements and future prospects. Comput. Methods Programs Biomed. 2020, 197, 105728. [Google Scholar] [CrossRef]
- Bhatele, K.R.; Bhadauria, S.S. Brain structural disorders detection and classification approaches: A review. Artif. Intell. Rev. 2020, 53, 3349–3401. [Google Scholar] [CrossRef]
- Gudigar, A.; Raghavendra, U.; Hegde, A.; Kalyani, M.; Ciaccio, E.J.; Acharya, U.R. Brain pathology identification using computer aided diagnostic tool: A systematic review. Comput. Methods Programs Biomed. 2020, 187, 105205. [Google Scholar] [CrossRef]
- Flanders, A.E.; Prevedello, L.M.; Shih, G.; Halabi, S.S.; Kalpathy-Cramer, J.; Ball, R.; Mongan, J.T.; Stein, A.; Kitamura, F.C.; Lungren, M.P.; et al. Construction of a machine learning dataset through collaboration: The RSNA 2019 brain CT hemorrhage challenge. Radiol. Artif. Intell. 2020, 2, e190211. [Google Scholar] [CrossRef]
- Chilamkurthy, S.; Ghosh, R.; Tanamala, S.; Biviji, M.; Campeau, N.G.; Venugopal, V.K.; Mahajan, V.; Rao, P.; Warier, P. Deep learning algorithms for detection of critical findings in head CT scans: A retrospective study. Lancet 2018, 392, 2388–2396. [Google Scholar] [CrossRef]
- Doi, K. Historical review, current status and future potential. Comput. Med. Imaging Graph. 2008, 31, 198–211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Sonka, M.; Hlavac, V.; Boyle, R. Image pre-processing. In Image Processing, Analysis and Machine Vision; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Wang, X.; Paliwal, K.K. Feature extraction and dimensionality reduction algorithms and their applications in vowel recognition. Pattern Recognit. 2003, 36, 2429–2439. [Google Scholar] [CrossRef]
- Ray, S.; Kumar, V.; Ahuja, C.; Khandelwal, N. Intensity population based unsupervised hemorrhage segmentation from brain CT images. Expert Syst. Appl. 2018, 97, 325–335. [Google Scholar] [CrossRef]
- Shahangian, B.; Pourghassem, H. Automatic brain hemorrhage segmentation and classification algorithm based on weighted grayscale histogram feature in a hierarchical classification structure. Biocybern. Biomed. Eng. 2015, 36, 217–232. [Google Scholar] [CrossRef]
- Sharma, B.; Venugopalan, K. Classification of Hematomas in Brain CT Images Using Neural Network. In Proceedings of the International Conference on Issues and Challenges in Intelligent Computing Techniques, Ghaziabad, India, 7–8 February 2014. [Google Scholar]
- Rajini, N.H.; Bhavani, R. Automatic classification of computed tomography brain images using ANN, k-NN and SVM. AI Soc. 2013, 29, 97–102. [Google Scholar] [CrossRef]
- Dawud, M.; Yurtkan, K.; Oztoprak, H. Application of deep learning in neuroradiology: Brain haemorrhage classification using transfer learning. Comput. Intell. Neurosci. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.-A.; Vincent, P.; Bengio, S. Why does unsupervised pre-training help deep learning? J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Ciresan, D.; Meier, U.; Masci, J.; Schmidhuber, J. A Committee of Neural Networks for Traffic Sign Classification. In Proceedings of the International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011. [Google Scholar]
- Raghavendra, U.; Fujita, H.; Bhandary, S.V.; Gudigar, A.; Tan, J.H.; Rajendra, U.A. Deep convolution neural network for accurate diagnosis of glaucoma using digital fundus images. Inf. Sci. 2018, 441, 41–49. [Google Scholar] [CrossRef]
- Sun, H.; Sun, H. A novel measure method of cerebral hematoma volume. Interdiscip. Neurosurg. 2018, 14, 42–46. [Google Scholar] [CrossRef]
- Sáenz, F.; Vera, M.; Huerfano, Y.; Molina, V.; Martinez, L.; Salazar, W.; Gelvez, E.; Salazar, J.; Valbuena, O.; Robles, H.; et al. Brain hematoma computational segmentation Brain hematoma computational segmentation. J. Phys. Conf. Ser. 2018, 1126, 012071. [Google Scholar] [CrossRef] [Green Version]
- Tong, H.; Faizal, M.; Fauzi, A.; Haw, S. Automated Hemorrhage Slices Detection for CT Brain Images. In Proceedings of the International Visual Informatics Conference, Selangor, Malaysia, 9–11 November 2011. [Google Scholar]
- Jacobs, B.; Beems, T.; Van Der Vliet, T.M.; Diaz-Arrastia, R.R.; Borm, G.F.; Vos, P.E. Computed tomography and outcome in moderate and severe traumatic brain injury: Hematoma volume and midline shift revisited. J. Neurotrauma 2011, 28, 203–215. [Google Scholar] [CrossRef]
- Gautam, A.; Raman, B. Automatic Segmentation of Intracerebral Hemorrhage from Brain CT Images. In Machine Intelligence and Signal Analysis. Advances in Intelligent Systems and Computing; Tanveer, M., Pachori, R., Eds.; Springer: Singapore, Singapore, 2019; Volume 748. [Google Scholar] [CrossRef]
- Kumar, I.; Bhatt, C.; Singh, K.U. Entropy based automatic unsupervised brain intracranial hemorrhage segmentation using CT images. J. King Saud Univ. Comput. Inf. Sci. 2020, in press, Corrected Proof. [Google Scholar] [CrossRef]
- Bhadauria, H.S.; Singh, A.; Dewal, M.L. An integrated method for hemorrhage segmentation from brain CT Imaging. Comput. Electr. Eng. 2013, 39, 1527–1536. [Google Scholar] [CrossRef]
- Li, Y.H.; Zhang, L.; Hu, Q.M.; Li, H.W.; Jia, F.C.; Wu, J.H. Automatic subarachnoid space segmentation and hemorrhage detection in clinical head CT scans. Int. J. Comput. Assist. Radiol. Surg. 2012, 7, 507–516. [Google Scholar] [CrossRef]
- Farzaneh, N.; Williamson, C.A.; Jiang, C.; Srinivasan, A.; Bapuraj, J.R.; Gryak, J.; Najarian, K.; Soroushmehr, S.M. Automated segmentation and severity analysis of subdural hematoma for patients with traumatic brain injuries. Diagnostics 2020, 10, 773. [Google Scholar] [CrossRef] [PubMed]
- Farzaneh, N.; Soroushmehr, S.R.; Williamson, C.A.; Jiang, C.; Srinivasan, A.; Bapuraj, J.R.; Ward, K.R.; Korley, F.K.; Najarian, K. Automated Subdural Hematoma Segmentation for Traumatic Brain Injured (TBI) Patients. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017. [Google Scholar]
- Yao, H.; Williamson, C.; Gryak, J.; Najarian, K. Brain Hematoma Segmentation Using Active Learning and an Active Contour Model. In Proceedings of the International Work-Conference on Bioinformatics and Biomedical Engineering, Granada, Spain, 8–10 May 2019. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.K.; Farrokhnia, F. Unsupervised texture segmentation using gabor filters. Pattern Recognit. 1991, 24, 1167–1186. [Google Scholar] [CrossRef] [Green Version]
- Rahim, A.; Azam, S.; Hossain, N.; Islam, R. Face recognition using Local Binary Patterns (LBP). Glob. J. Comput. Sci. Technol. Graph. Vis. 2013, 13, 1–8. [Google Scholar]
- Pourghassem, H.; Ghassemian, H. Content-based medical image classification using a new hierarchical merging scheme. Comput. Med. Imaging Graph 2008, 32, 651–661. [Google Scholar] [CrossRef]
- Hassanzade, S.; Pourghassem, H. A novel logo detection and recognition framework for separated part logos in document images. Aust. J Basic Appl. Sci. 2011, 5, 936–946. [Google Scholar]
- Wickerhauser, M.V.; Jensen, A.; La Cour-Harbo, A.; Boggess, A.; Narcowich, F.J. Ripples in Mathematics: The Discrete Wavelet Transform; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Rao, A.; Noushath, S. Subspace methods for face recognition. J. Comput. Sci. Rev. 2010, 4, 1–17. [Google Scholar]
- Al-AyyouB, M.; Alawad, D.; Al-Darabsah, K.; Aljarrah, I. Automatic detection and classification of brain hemorrhages. Lect. Notes Comput. Sci. 2018, 10752, 417–427. [Google Scholar]
- Cordes, M.S.J.; Younsi, A.; Sahin, Y.A.; Götz, M.; Möhlenbruch, M.; Stock, C.; Bösel, J.; Unterberg, A.; Maier-Hein, K.; Orakcioglu, B. Development and validation of an automatic segmentation algorithm for quantification of intracerebral hemorrhage. Stroke 2016, 47, 2776–2782. [Google Scholar]
- Chawla, M.; Sharma, S.; Sivaswamy, J.; Kishore, L.T. A method for Automatic Detection and Classification of Stroke from Brain CT Images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 2–6 September 2009. [Google Scholar]
- Raghavendra, U.; Gudigar, A.; Vidhya, V.; Rao, B.N.; Sabut, S.; Wei, J.K.; Ciaccio, E.J.; Acharya, U.R. Novel and accurate non—linear index for the automated detection of haemorrhagic brain stroke using CT images. Complex Intell. Syst. 2021, 7, 929–940. [Google Scholar] [CrossRef]
- Liu, R.; Tan, C.L.; Leong, T.Y. Hemorrhage Slices Detection in Brain CT Images. In Proceedings of the 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8 December 2008. [Google Scholar]
- Quattrocchi, K.B.; Prasad, P.; Willits, N.H.; Wagner, F.C. Quantification of midline shift as a predictor of poor outcome following head injury. Surg. Neurol. 1991, 35, 183–188. [Google Scholar] [CrossRef]
- Xiao, C.-C.; Liao, J.; Wong, M.; Chiang, I.J. Automatic diagnosis of intracranial hematoma on brain ct using knowledge discovery techniques: Is finer resolution better? Biomed. Eng. Appl. Basis Commun. 2008, 20, 401–408. [Google Scholar] [CrossRef]
- Yuh, E.L.; Gean, A.D.; Manley, G.T.; Callen, A.L.; Wintermark, M. Computer-aided assessment of head computed tomography (CT) studies in patients with suspected traumatic brain injury. J. Neurotrauma 2008, 1172, 1163–1172. [Google Scholar] [CrossRef] [PubMed]
- Diyana, W.M.; Zaki, M.F.; Fauzi, A.; Besar, R.; Ahmad, W.S.H.M.W. Abnormalities detection in serial computed tomography brain images using multi-level segmentation approach. Multimed. Tools Appl. 2011, 54, 321–340. [Google Scholar]
- Qureshi, N. Semi-automated classification of CT Scans in Traumatic brain injury patients. Int. J. Comput. Appl. 2015, 113, 1–8. [Google Scholar]
- Gillebert, R.; Humphreys, G.W.; Mantini, D. Automated delineation of stroke lesions using brain CT images. NeuroImage Clin. 2014, 4, 540–548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bardera, A.; Boada, I.; Feixas, M.; Remollo, S.; Blasco, G.; Silva, Y.; Pedraza, S. Semi-automated method for brain hematoma and edema quantification using computed tomography. Comput. Med. Imaging Graph. 2009, 33, 304–311. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.; Hu, Q.; Huang, W. Detection and quantification of intracerebral and intraventricular hemorrhage from computed tomography images with adaptive thresholding and case-based reasoning. Int. J Comput. Assist. Radiol. Surg. 2013, 8, 917–992. [Google Scholar] [CrossRef]
- Liao, C.-C.; Xiao, F.; Wong, J.-M.; Chiang, I.-J. A multiresolution binary level set method and its application to intracranial hematoma segmentation. Comput. Med. Imaging Graph. 2009, 33, 423–430. [Google Scholar] [CrossRef]
- Renyi, A. On Measures of Entropy and Information. In Proceedings of the 4th Berkeley symposium on mathematical statistics and probability, Berkeley, CA, USA, 20 June–30 July 1960. [Google Scholar]
- Wang, X.; Tang, X. A unified framework for subspace face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1222–1228. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Jones, N. The learning machines. Nature 2014, 505, 146–148. [Google Scholar] [CrossRef] [Green Version]
- Prevedello, L.M.; Erdal, B.S.; Ryu, J.L.; Little, K.J.; Demirer, M.; Qian, S.; White, R.D. Automated critical test findings identification and online notification system using artificial intelligence in imaging. Radiology 2017, 285, 923–931. [Google Scholar] [CrossRef]
- Arbabshirani, M.R.; Fornwalt, B.K.; Mongelluzzo, G.J.; Seuver, J.D.; Geise, D.B.; Patel, A.A.; Moore, G.J. Advanced machine learning in action: Identification of intracranial hemorrhage on computed tomography scans of the head with clinical work flow integration. NPJ Digit. Med. 2017, 1, 1–7. [Google Scholar] [CrossRef]
- Titano, J.J.; Badgeley, M.; Schefflein, J.; Pain, M.; Su, A.; Cai, M.; Swinburne, N.; Zech, J.; Kim, J.; Bederson, J.; et al. Automated deep-neural-network surveillance of cranial images for acute neurologic events. Nat. Med. 2018, 24, 1337–1341. [Google Scholar] [CrossRef]
- Grewal, M.; Srivastava, M.M.; Kumar, P.; Varadarajan, S. RADnet: Radiologist Level Accuracy Using Deep Learning for Hemorrhage Detection in CT Scans. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 281–284. [Google Scholar]
- Majumdar, A.; Brattain, L.J.; Telfer, B.A.; Farris, C.; Scalera, J. Detecting Intracranial Hemorrhage with Deep Learning. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA; Volume 2018, pp. 583–587. [Google Scholar]
- Lee, H.; Yune, S.; Mansouri, M.; Kim, M.; Tajmir, S.H.; Guerrier, C.E.; Ebert, S.A.; Pomerantz, S.R.; Romero, J.M.; Kamalian, S.; et al. An explainable deep-learning algorithm for the detection of acute intracranial haemorrhage from small datasets. Nat. Biomed. Eng. 2018, 3, 173–182. [Google Scholar] [CrossRef]
- Ye, H.; Gao, F.; Yin, Y.; Guo, D.; Zhao, P.; Lu, Y.; Wang, X.; Bai, J.; Cao, K.; Song, Q.; et al. Precise diagnosis of intracranial hemorrhage and subtypes using a three-dimensional joint convolutional and recurrent neural network. Eur. Radiol. 2019, 29, 6191–6201. [Google Scholar] [CrossRef] [Green Version]
- Kuo, W.; Häne, C.; Mukherjee, P.; Malik, J.; Yuh, E.L. Expert-level detection of acute intracranial hemorrhage on head computed tomography using deep learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22737–22745. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Williamson, C.; Soroushmehr, R.; Gryak, J.; Najarian, K. Hematoma Segmentation Using Dilated Convolutional Neural Network. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; Volume 2018, pp. 5902–5905. [Google Scholar]
- Yao, H.; Williamson, C.; Gryak, J.; Najarian, K. Automated hematoma segmentation and outcome prediction for patients with traumatic brain injury. Artif. Intell. Med. 2020, 107. [Google Scholar] [CrossRef] [PubMed]
- He, J. Automated Detection of Intracranial Hemorrhage on Head Computed Tomography with Deep Learning. In Proceedings of the 2020 10th International Conference on Biomedical Engineering and Technology, Tokyo, Japan, 25–28 March 2020. [Google Scholar]
- Ko, H.; Chung, H.; Lee, H.; Lee, J. Feasible Study on Intracranial Hemorrhage Detection and Classification using a CNN-LSTM Network. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; Volume 2020, pp. 1290–1293. [Google Scholar]
- Chang, P.; Kuoy, E.; Grinband, J.; Weinberg, B.; Thompson, M.; Homo, R.; Chen, J.; Abcede, H.; Shafie, M.; Sugrue, L.; et al. Hybrid 3D/2D convolutional neural network for hemorrhage evaluation on head CT. Am. J. Neuroradiol. 2018, 39, 1609–1616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arab, A.; Chinda, B.; Medvedev, G.; Siu, W.; Guo, H.; Gu, T.; Moreno, S.; Hamarneh, G.; Ester, M.; Song, X. A fast and fully-automated deep-learning approach for accurate hemorrhage segmentation and volume quantification in non-contrast whole-head CT. Sci. Rep. 2020, 10, 19389. [Google Scholar] [CrossRef] [PubMed]
- Desai, V.; Flanders, A.E.; Lakhani, P. Application of deep learning in neuroradiology: Automated detection of basal ganglia hemorrhage using 2D-convolutional neural networks. arXiv 2017, arXiv:1710.03823. [Google Scholar]
- Hssayeni, M.D.; Croock, M.S.; Salman, A.D.; Al-Khafaji, H.F.; Yahya, Z.A.; Ghoraani, B. Intracranial hemorrhage segmentation using a deep convolutional model. Data 2020, 5, 14. [Google Scholar] [CrossRef] [Green Version]
- Irene, K.; Ma’Sum, M.A.; Yunus, R.E.; Jatmiko, W. Segmentation and Approximation of Blood Volume in Intracranial Hemorrhage Patients Based on Computed Tomography Scan Images Using Deep Learning Method. In Proceedings of the 2020 International Workshop on Big Data and Information Security (IWBIS), Depok, Indonesia, 17–18 October 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 65–72. [Google Scholar]
- Anupama, C.S.S.; Sivaram, M.; Lydia, E.L.; Gupta, D.; Shankar, K. Synergic deep learning model–based automated detection and classification of brain intracranial hemorrhage images in wearable networks. Pers. Ubiquitous Comput. 2020, 1–10. [Google Scholar] [CrossRef]
- Watanabe, Y.; Tanaka, T.; Nishida, A.; Takahashi, H.; Fujiwara, M.; Fujiwara, T.; Arisawa, A.; Yano, H.; Tomiyama, N.; Nakamura, H.; et al. Improvement of the diagnostic accuracy for intracranial haemorrhage using deep learning–based computer-assisted detection. Neuroradiology 2021, 63, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Sharrock, M.F.; Mould, W.A.; Ali, H.; Hildreth, M.; Awad, I.A.; Hanley, D.F.; Muschelli, J. 3D deep neural network segmentation of intracerebral hemorrhage: Development and validation for clinical trials. Neuroinformatics 2020, 1–13. [Google Scholar] [CrossRef]
- Mansour, R.F.; Aljehane, N.O. An optimal segmentation with deep learning based inception network model for intracranial hemorrhage diagnosis. Neural Comput. Appl. 2021, 1–13. [Google Scholar] [CrossRef]
- Kuang, H.; Menon, B.K.; Qiu, W. Segmenting Hemorrhagic and Ischemic Infarct Simultaneously From Follow-Up Non-Contrast CT Images in Patients with Acute Ischemic Stroke. IEEE Access 2019, 7, 39842–39851. [Google Scholar] [CrossRef]
- Broderick, J.P.; Brott, T.G.; Duldner, J.E.; Tomsick, T.; Huster, G. Volume of intracerebral hemorrhage. A powerful and easy-to-use predictor of 30-day mortality. Stroke 1993, 24, 987–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zimmerman, R.; Maldjian, J.; Brun, N.; Horvath, B.; Skolnick, B. Radiologic Estimation of Hematoma Volume in Intracerebral Hemorrhage Trial by CT Scan. Am. J. Neuroradiol. 2006, 27, 666–670. [Google Scholar] [PubMed]
- Kothari, R.U.; Brott, T.; Broderick, J.P.; Barsan, W.G.; Sauerbeck, L.R.; Zuccarello, M.; Khoury, J. The ABCs of Measuring Intracerebral Hemorrhage Volumes. Stroke 1996, 27, 1304–1305. [Google Scholar] [CrossRef]
- Webb, J.S.; Ullman, N.L.; Morgan, T.C.; Muschelli, J.; Kornbluth, J.; Awad, I.A.; Mayo, S.; Rosenblum, M.; Ziai, W.; Zuccarrello, M.; et al. Accuracy of the ABC/2 score for intracerebral hemorrhage: Systematic review and analysis of MISTIE, CLEAR-IVH, and CLEAR III. Stroke 2015, 46, 2470–2476. [Google Scholar] [CrossRef] [Green Version]
- Maeda, A.K.; Aguiar, L.R.; Martins, C.; Bichinho, G.L.; Gariba, M.A. Hematoma volumes of spontaneous intracerebral haem-orrhage: The ellipse (ABC/2) method yielded volumes smaller than those measured using the planimetric method. Arq. Neuropsiquiatr. 2013, 71, 540–544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daunis-I-Estadella, J.; Boada, I.; Bardera, A.; Castellanos, M.; Serena, J.; Castellanos, M.D.M. Reliability of the ABC/2 method in determining acute infarct volume. J. Neuroimaging 2011, 22, 155–159. [Google Scholar]
- Hussein, H.M.; Tariq, N.A.; Palesch, Y.Y.; Qureshi, A.I. Reliability of hematoma volume measurement at local sites in a multi-centre acute intracerebral haemorrhage clinical trial Haitham. Bones 2008, 28, 1–7. [Google Scholar]
- Jain, S.; Vyvere, T.V.; Terzopoulos, V.; Sima, D.M.; Roura, E.; Maas, A.; Wilms, G.; Verheyden, J. Automatic quantification of computed tomography features in acute traumatic brain injury. J. Neurotrauma 2019, 36, 1794–1803. [Google Scholar] [CrossRef]
- Zhang, J.G.W.X.; Medow, J.E.; Iskandar, B.J.; Wang, F.; Shokouejnejad, M.; Koueik, J. Invasive and non-invasive means of measuring intracranial pressure: A review. Physiol. Meas. 2017, 143–182. [Google Scholar] [CrossRef]
- Farhadi, A.; Chern, J.J.; Hirsh, D.; Davis, T.; Jo, M.; Maier, F.; Rasheed, K. Intracranial pressure forecasting in children using dynamic averaging of time series data. J. Forecast. 2018, 1, 47–58. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.-J.; Jeong, E.-J.; Kim, H.; Czosnyka, M.; Kim, D.-J. Morphological feature extraction from a continuous intracranial pressure pulse via a peak clustering algorithm. IEEE Trans. Biomed. Eng. 2015, 63, 2169–2176. [Google Scholar]
- Scalzo, F.; Liebeskind, D.; Hu, X. Reducing false intracranial pressure alarms using morphological waveform features. IEEE Trans. Biomed. Eng. 2013, 60, 235–239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scalzo, F.; Asgari, S.; Kim, S.; Bergsneider, M.; Hu, X. Bayesian tracking of intracranial pressure signal morphology. Artif. Intell. Med. 2012, 54, 115–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scalzo, F.; Asgari, S.; Kim, S.; Bergsneider, M.; Hu, X. Robust peak recognition in intracranial pressure signals biomed. Eng. Online 2010, 9, 1–19. [Google Scholar]
- Hu, X.; Xu, P.; Scalzo, F.; Vespa, P.; Bergsneider, M. Morphological clustering and analysis of continuous intracranial pressure. IEEE Trans. Biomed. Eng. 2008, 56, 696–705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calisto, A.; Galeano, M.; Serrano, S.; Azzerboni, B. A new approach for investigating intracranial pressure signal: Filtering and morphological features extraction from continuous recording. IEEE Trans. Biomed. Eng. 2013, 60, 830–837. [Google Scholar] [CrossRef]
- Asgari, S.; Xu, P.; Bergsneider, M.; Hu, X. A subspace decomposition approach toward recognizing valid pulsatile signals. Physiol. Meas. 2009, 30, 1211–1225. [Google Scholar] [CrossRef] [Green Version]
- Kasprowicz, M.; Asgari, S.; Bergsneider, M.; Czosnyka, M.; Hamilton, R.; Hu, X. Pattern recognition of overnight intracranial pressure slow waves using morphological features of intracranial pressure pulse. J. Neurosci. Methods 2010, 190, 310–318. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Cockrell, C.H.; Ward, K.; Najarian, K. Predictability of intracranial pressure level in traumatic brain injury: Features extraction, statistical analysis and machine learning-based evaluation. Int. J. Data Min. Bioinform. 2013, 8, 480–494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pappu, S.; Lerma, J.; Khraishi, T. Brain CT to assess intracranial pressure in patients with traumatic brain injury. J. Neuroimaging 2015, 26, 37–40. [Google Scholar] [CrossRef]
- Aghazadeh, B.S.; Khaleghi, M.; Pidaparti, R.; Najarian, K. Intracranial pressure (ICP) level estimation using textural features of brain CT images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2013, 1, 130–137. [Google Scholar] [CrossRef]
- Qi, X.; Belle, A.; Shandilya, S.K.; Najarian, K.; Chen, W.; Hargraves, R.S.H.; Cockrell, C. Automated Intracranial Pressure Prediction Using Multiple Features Sources. In Proceedings of the 2013 International Conference on Information Science and Applications (ICISA), Suwon, Korea, 24–26 June 2013; pp. 1–4. [Google Scholar]
- Chen, W.; Belle, A.; Cockrell, C.; Ward, K.R.; Najarian, K. Automated midline shift and intracranial pressure estimation based on Brain CT Images. J. Vis. Exp. 2013, 74, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Liao, C.C.; Chen, Y.; Xiao, F. Brain midline shift measurement and its automation: A review of techniques and algorithms. Int. J. Biomed. Imaging. 2018, 2018, 4303161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, R.; Li, S.; Su, B.; Tan, C.L.; Leong, T.Y.; Pang, B.C.; Lim, C.T.; Lee, C.K. Automatic detection and quantification of brain midline shift using anatomical marker model. Comput. Med Imaging Graph. 2014, 38, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, S.; Tan, C.L.; Pang, B.C.; Lim, C.T.; Lee, C.K.; Tian, Q.; Zhang, Z. From Hemorrhage to Midline Shift: A New Method of Tracing the Deformed Midline in Traumatic Brain Injury CT Images. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 2637–2640. [Google Scholar]
- Wang, H.; Ho, S.; Xiao, F.; Chou, J. A simple fast and fully automated approach for midline shift measurement on brain computed tomography. arXiv 2017, arXiv:1703.00797. [Google Scholar]
- Nag, M.K.; Gupta, A.; Hariharasudhan, A.; Sadhu, A.K.; Das, A.; Ghosh, N. Quantitative analysis of brain herniation from non-contrast CT images using deep learning. J. Neurosci. Methods 2021, 349, 109033. [Google Scholar] [CrossRef] [PubMed]
- Marshall, L.F.; Becker, D.P.; Bowers, S.A.; Cayard, C.; Eisenberg, H.M.; Gross, C.R.; Grossman, R.G.; Jane, J.A.; Kunitz, S.C.; Rimel, R.W.; et al. The national traumatic coma data bank. J. Neurosurg. 1983, 59, 276–284. [Google Scholar] [CrossRef] [PubMed]
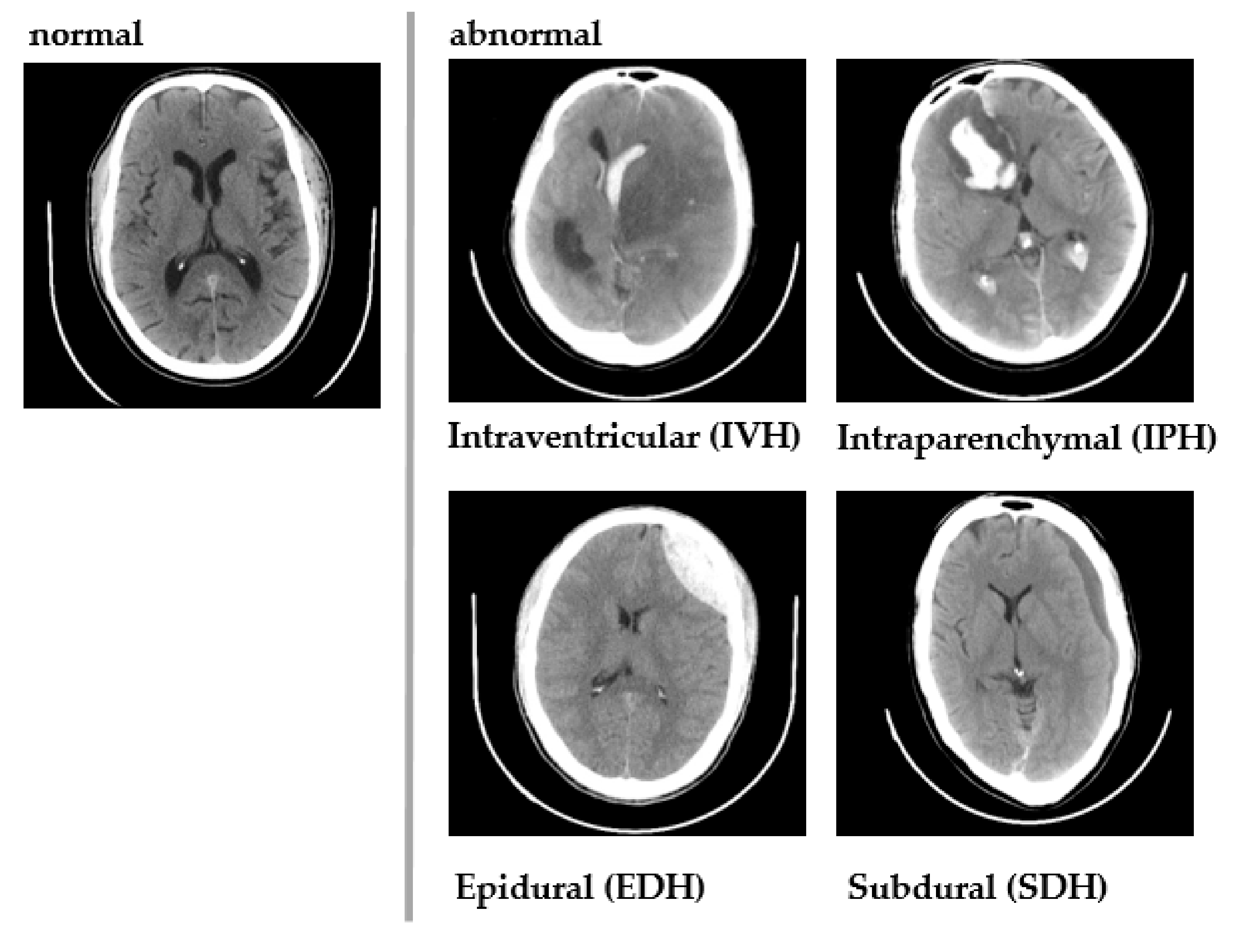
| Pathology | CAD Approaches | Techniques | TBI-Associated Abnormalities | |||
|---|---|---|---|---|---|---|
| ICH Detection | ICH Volume Estimation | ICP | MLS | |||
| TBI | Feature learning based | Feature based | ✓ | ✓ | ✓ | - |
| Segmentation as pixel-wise/voxel-wise classification task | ✓ | - | - | - | ||
| Segmentation based on image delineation | ✓ | - | - | - | ||
| Landmark and symmetry based | - | - | - | ✓ | ||
| Deep learning based | Classification | ✓ | ✓ | - | ✓ | |
| Segmentation | ✓ | - | - | - | ||
| Segmentation and classification | ✓ | - | - | - | ||
| Publication Category | Inclusion Criteria | Exclusion Criteria |
|---|---|---|
| Datasets used and study outcomes |
|
|
| Research design and methodology |
|
|
| Type | Peer reviewed journals, conference proceedings, and systematic reviews | Scientific abstracts, letters to the editor, and articles without full text |
| Period | 2007–2021 | Before 2007 |
| Language | English | Written in other languages |
| Authors | CT Dataset | Method | Classifier | Performance |
|---|---|---|---|---|
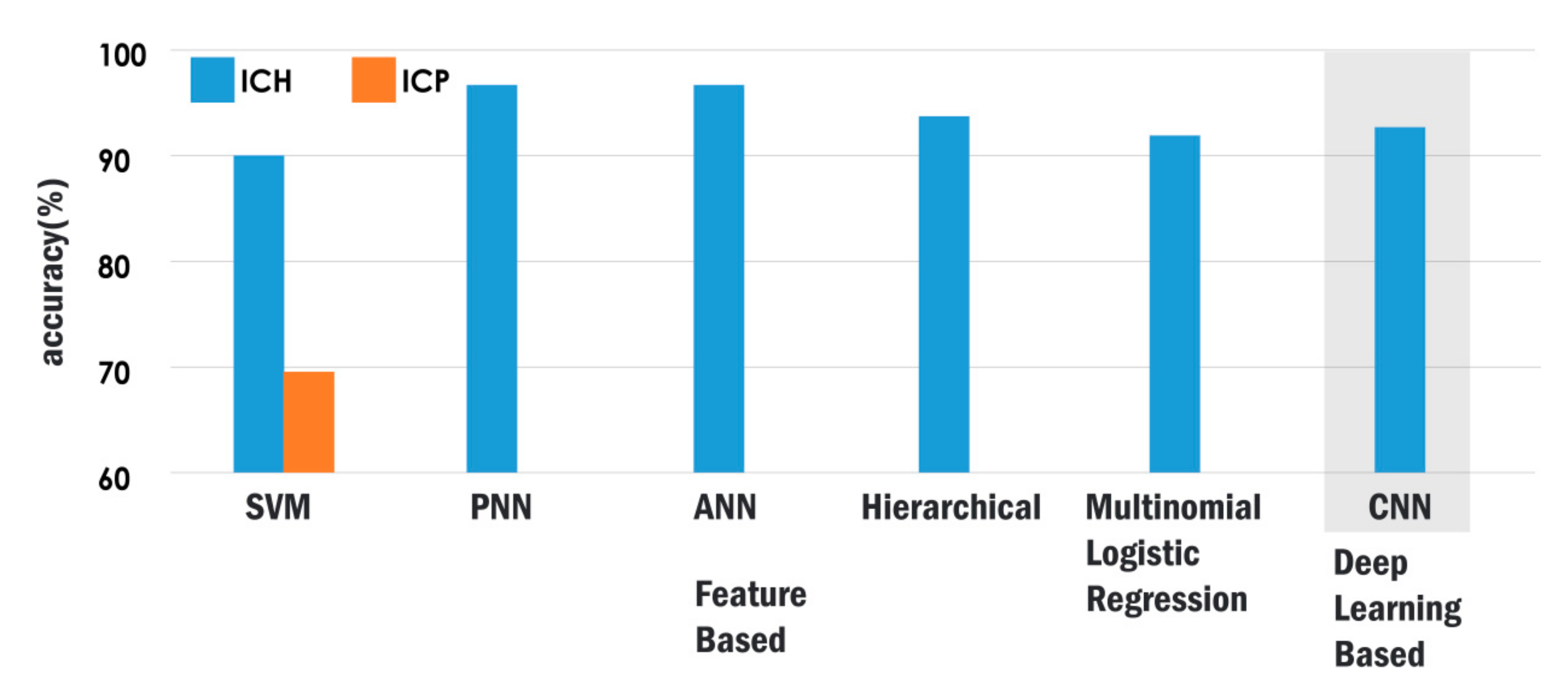
| Raghavendra et al. [70] | 1603 | Entropy-based nonlinear features | PNN | Acc: 97.37 Sen: 96.94 Spec: 97.83 |
| Liu et al. [71] | 11011 | DWT features, statistical features, GLCM texture features | SVM | Acc: 80 Precision: 80.32 Recall: 88.22 Five-class |
| Sharma and Venugopalan [43] | 100 | Shape, intensity, and GLCM texture features | ANN | Acc: 97 Three-class |
| Tong et al. [51] | 450 | LBP texture features and histogram features | SVM | Acc: 90 Precision: 0.8486 Recall: 0.9682 Five-class |
| Rajini and Bhavani [44] | 80 | DWT features | SVM | Acc: 98 Sen: 98 Spec: 100 |
| Li et al. [56] | 129 | Distance features based on landmarks | Bayesian | Sen: 100 Spec: 89.7 |
| Chawla et al. [69] | 35 | Dissimilarity of intensity features in brain hemispheres | - | Acc: 90 Precision: 91 Recall: 90 |
| Shahangian et al. [42] | 627 | MDRLSE + texture and shape features | Hierarchical classifier | Acc: 94.13 Four-class |
| Al-Ayoob et al. [67] | 76 | Thresholding + region growing + shape features | Multinomial Logistic Regression | Acc: 92 Precision: 92.5 Recall: 92.2 Three-class |
| Xiao et al. [73] | 48 | Multi-resolution thresholding + region growing + primary and derived features based on long and short axes | C4.5 | Acc: 0.975 Three-class |
| Yuh et al. [74] | 273 | Thresholding, spatial filtering, and cluster analysis and classification based on location, size, and shape of clusters | - | Sen: 98 Spec: 59 Three-class |
| Zaki et al. [75] | 720 | FCM + multi-level thresholding + location and intensity features | - | Sen: 82.5% |
| Authors | CT Dataset | Method | Performance |
|---|---|---|---|
| Chan [23] | 62 | Top-hat transformation and symmetry detection for candidate detection + knowledge-based classification of normalised CT images | Sen: 100 Spec: 84.1 |
| Liao et al. [80] | 48 | Multiresolution binary level set method + decision rules | Overlap rate: 82 Sen: 0.81 |
| Ray et al. [41] | 590 | Knowledge driven thresholding + morphological operations + data fusion | Acc: 92.45 Sen: 93.95 Spec: 100 |
| Farzaneh et al. [57] | 110 | SLIC + texture, spatial, and deep features + random forest + morphological operations + Gaussian smoothing | Precision: 76.12 Recall: 78.61 Dice coefficient: 75.35 |
| Farzaneh et al. [58] | 866 | DRLSE + textural, statistical, and geometrical features + tree bagger classifier + multi-level thresholding | Sen: 85.02 Spec: 73.74 |
| Scherer et al. [68] | 58 | First- and second-order statistics + texture and threshold features + random forest methodology + morphological operations + Gaussian smoothing | Concordance correlation coefficient = 0.98 |
| Muschelli et al. [18] | 10 | Intensity-based predictors + random forest classifier + thresholding | DSI: 0.899 |
| Qureshi et al. [76] | 866 | ANN and active contours | Jaccard Index: 0.8689 ± 0.042 Dice coefficient: 0.9169 ± 0.02 |
| Yao et al. [59] | 2433 | SLIC + texture and statistical features + SVM + active contour model | Acc: 97 Precision: 0.59 Recall: 0.60 |
| Gillebert et al. [77] | 500 | Threshold-based clustering + voxel-wise comparison of normalised and control Ct images using Crawford–Howell parametric t-test + thresholding | DSI: 0.89 |
| Kumar et al. [54] | 35 | FCM clustering + entropy-based thresholding + DRLSE | Acc: 99.87 Sen: 87.06 Spec: 99.98 |
| Gautam and Raman [53] | 20 | WMFCM clustering + wavelet-based thresholding | DSI: 0.82 |
| Nag et al. [22] | 48 | Fuzzy-based intensifier + auto encoder + active contour Chan-Vese Model | Sen: 0.71 Jaccard Index: 0.55 |
| Saenz et al. [50] | 12 | Hough transform + region growing | Jaccard Index: 0.9005 |
| Bhadauria et al. [55] | 100 | FCM clustering + region-based active contour method | Sen: 79.48 Spec: 99.42 Dice coefficient = 0.8748 |
| Prakash et al. [27] | 200 | Modified distance regularised level set evolution (MDRLSE) | Sen: 79.6 Spec: 99.9 AUC: 0.88 |
| Bardera et al. [78] | 18 | Region growing | Matching ratio: 0.96 |
| Zhang et al. [79] | 10 | Adaptive thresholding and case-based reasoning | Acc: 0.950 ± 0.015 Recall: 83.5 |
| Authors | CT Dataset | Method | Performance |
|---|---|---|---|
| Prevedello et al. [85] | 76 | AI-based deep learning approach | Sen: 90 Spec: 85 AUC: 0.91 |
| Arbabshirani et al. [86] | 46,583 | DCNN | Sen: 71.5 Spec: 83.5 AUC: 0.846 |
| Titano et al. [87] | 37,236 | 3D-CNN | AUC: 0.88 |
| Grewal et al. [88] | 77 | Recurrent Attention DenseNet (RADnet) | Acc: 81.82 Sen: 88 Precision: 81 |
| Chilamkurthy et al. [36] | 21,095 in Qure25k and 491 in CQ500 | U-Net-based architecture + modified ResNet18 + random forest classifier | Sen: 92 Spec: 70 AUC: 0.87 Five-class |
| Dawud et al. [45] | 12,635 | Modified pre-trained AlexNet SVM model | Acc: 93.48 Sen: 95 Spec: 90 Four-class |
| Majumdar et al. [89] | 134 | Modified U-Net model | Sen: 81 Spec: 98 |
| Lee et al. [90] | 904 | Ensemble model comprised of VGG16, ResNet-50, Inception-v3, and Inception-ResNet-v2 | Sen: 78.3 Spec: 92.9 AUC: 95.9 Five-class |
| Ye et al. [91] | 76,621 | 3D CNN-RNN | Sen: 80 Spec: 93.2 AUC: 0.93 Five-class |
| Kuo et al. [92] | 4396 | PatchFCN | AUC = 0.991 ± 0.006 Five-class |
| Yao et al. [93] | 2433 | Dilated CNN | Sen: 0.81 Spec: 0.96 Dice coefficient: 0.62 |
| Yao et al. [94] | 828 | Multi-view CNN + volume and shape features + random forest classifier | Dice coefficient: 0.697 |
| Cho et al. [26] | 135,974 | Cascaded CNN and dual fully convolutional networks (FCNs) | Sen: 97.91 Spec: 98.76 Five-class |
| He [95] | 874,039 (RSNA dataset) | SE—ResNeXt50 and EfficientNet-B3 CNN architectures | Logarithmic Loss = 0.0548 Five-class |
| Ko et al. [96] | 5,244,234 (RSNA dataset) | CNN-LSTM | Logarithmic Loss = 0.075 Acc: 93 |
| Chang et al. [97] | 536,266 | Hybrid 3D/2D mask ROI-based CNN | Sen: 95 Spec: 97 AUC: 0.97 Four-class |
| Arab et al. [98] | 64 | CNN—DS | Precision: 0.85 Recall: 0.83 Dice coefficient: 0.84 |
| Desai et al. [99] | 170 | Pre-trained augmented Google Net | AUC = 1.00 |
| Hssayeni et al. [100] | 82 | U-Net | Sen: 97.28 Spec: 50.4 Dice coefficient: 0.31 Five-class |
| Irene et al. [101] | 27 | DGCNN | Sen: 97.8 Spec: 95.6 |
| Anupama et al. [102] | 82 | GrabCut-based segmentation and synergic deep learning (GC- SDL) | Acc: 95.73 Sen: 94.01 Spec: 97.78 Five-class |
| Watanabe et al. [103] | 40 | U-Net | Acc: 87.5 Sen: 89.6 Spec: 81.2 Reading Time: 43 sec |
| Sharrock et al. [104] | 500 | 3D VNET 128 | Median Dice coefficient: 0.919 |
| Mansour et al. [105] | 82 | Kapoor’s thresholding + elephant herd optimisation + Inception v4 network + multilayer perceptron | Acc: 95.06 Sen: 93.56 Spec: 97.56 |
| Kuang et al. [106] | 30 | U-Net + multi-region contour evolution | Dice coefficient: 0.72 |
| Authors | CT Dataset | Method | Performance |
|---|---|---|---|
| Farzaneh et al. [57] | 110 | 3D resolution of the segmented ICH mask | F1: 98.22 Recall: 98.81 Spec: 92.31 |
| Sun and Sun [49] | 20 | Gengon and truncated pyramid approximations | Processing time <2 s |
| Saenz et al. [50] | 12 | Voxel size multiplied by the number of voxels | - |
| Scherer et al. [68] | 58 | Summing of voxel volumes | Concordance correlation coefficient with manual estimation = 0.99 |
| Bardera et al. [78] | 18 | Individual voxel volume multiplied by the number of voxels | Mean correspondence ratio = 0.74 and mean matching ratio = 0.80 |
| Deep Learning-Based Methods | |||
| Chang et al. [97] | 536,266 | Hybrid 3D/2D mask ROI-based CNN | Pearson correlation coefficients: IPH = 0.999 EDH = 0.987 SAH = 0.953 |
| Arab et al. [98] | 64 | CNN—DS | Average disagreement rate = 0.08 ± 0.02 |
| Jain et al. [114] | 39 | U-Net based FCN | Acc: 0.92 Sen: 0.75 |
| Irene et al. [101] | 27 | DGCNN + SVM with RBF kernel | Mean square error = 3.67 × 104 |
| Sharrock et al. [104] | 500 | 3D VNET 128 | Volume correlation of 0.979 Avg. volume difference = 1.7 mL |
| Authors | CT Dataset | Method | Performance |
|---|---|---|---|
| Chen et al. [29] | 56 | Texture features + SVM | Acc: 81.79 Sen: 82.25 Spec: 81.20 |
| Chen et al. [125] | 57 | MLS, hematoma volume, textural patterns, and patient medical data + SVM | Acc: 70.2 Sen: 65.2 Spec: 73.7 |
| Pappu et al. [126] | 20 | Segmentation of brain parenchyma + ratio of CSF to the size of intracranial vault computations (CSFv/ICVv) | Acc: 67 |
| Aghazadeh et al. [127] | 59 | Fully anisotropic Morlet wavelet transform + KNN | Acc: 86.5 |
| Qi et al. [128] | 57 | MLS, intracranial air cavities, ventricle size, texture patterns, blood amount, and clinical data + SVM | Acc: 73.7 Sen: 68.6 Spec: 76.6 |
| Chen et al. [129] | 391 | MLS, hematoma volume, texture features, demographic information, and severity score + SVM | Acc: 70 Sen: 65 Spec: 73 |
| Authors | CT Dataset | Method | Performance |
|---|---|---|---|
| Landmark-Based Methods | |||
| Yuh et al. [74] | 273 | CT density (Hounsfield units) thresholds, spatial filtering, and cluster analysis | Sen: 100 Spec: 98 |
| Xiao et al. [80] | 80 | Multiresolution binary level set method and Hough transform | Maximal error: 2 mm Root mean square error: 0.57 mm |
| Chen et al. [129] | 391 | Gaussian mixture model + EM + multiple regions shape matching + texture feature extraction | Acc: 70 Sen: 65 Spec: 73 |
| Liu et al. [102] | 7040 | Anatomical marker model and marker candidate selection using spatial features | Area ratio: 0.0766 Maximum distance: 4.738 |
| Hooshmand et al. [28] | 170 | Ventricular geometric patterns and anatomical information | Acc: 68 Sen: 0.75 Spec: 0.65 |
| Symmetry-Based Methods | |||
| Liu et al. [132] | 11 | H-MLS | - |
| Liao et al. [30] | 86 | Bezier Curve and GA | Acc: 95 |
| Wang et al. [133] | 41 | Weighted midline + maximum distance | Acc: 92.68 AUC: 0.9577 |
| CNN-based Methods | |||
| Chilamkurthy et al. [36] | 21,095 in Qure25k and 491 in CQ500 | Modified ResNet18 + random forest classifier | Sen: 0.9385 Spec: 0.907 AUC = 0.9697 |
| Jain et al. [114] | 38 | U-Net based FCN | Acc: 0.89 |
| Wei et al. [15] | 640 (CQ500 and external dataset) | Regression-based line detection network (RLDN) | F1 score: 0.78 Column distance error: 1.17 Max shift distance error: 2.27 |
| Nag et al. [134] | 80 | U-Net | Average error by location = 1.29 mm area = 66.4 mm2 volume = 253.73 mm3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
V., V.; Gudigar, A.; Raghavendra, U.; Hegde, A.; Menon, G.R.; Molinari, F.; Ciaccio, E.J.; Acharya, U.R. Automated Detection and Screening of Traumatic Brain Injury (TBI) Using Computed Tomography Images: A Comprehensive Review and Future Perspectives. Int. J. Environ. Res. Public Health 2021, 18, 6499. https://doi.org/10.3390/ijerph18126499
V. V, Gudigar A, Raghavendra U, Hegde A, Menon GR, Molinari F, Ciaccio EJ, Acharya UR. Automated Detection and Screening of Traumatic Brain Injury (TBI) Using Computed Tomography Images: A Comprehensive Review and Future Perspectives. International Journal of Environmental Research and Public Health. 2021; 18(12):6499. https://doi.org/10.3390/ijerph18126499
Chicago/Turabian StyleV., Vidhya, Anjan Gudigar, U. Raghavendra, Ajay Hegde, Girish R. Menon, Filippo Molinari, Edward J. Ciaccio, and U. Rajendra Acharya. 2021. "Automated Detection and Screening of Traumatic Brain Injury (TBI) Using Computed Tomography Images: A Comprehensive Review and Future Perspectives" International Journal of Environmental Research and Public Health 18, no. 12: 6499. https://doi.org/10.3390/ijerph18126499
APA StyleV., V., Gudigar, A., Raghavendra, U., Hegde, A., Menon, G. R., Molinari, F., Ciaccio, E. J., & Acharya, U. R. (2021). Automated Detection and Screening of Traumatic Brain Injury (TBI) Using Computed Tomography Images: A Comprehensive Review and Future Perspectives. International Journal of Environmental Research and Public Health, 18(12), 6499. https://doi.org/10.3390/ijerph18126499







