Modeling Provincial Covid-19 Epidemic Data Using an Adjusted Time-Dependent SIRD Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data on COVID-19 in Italy
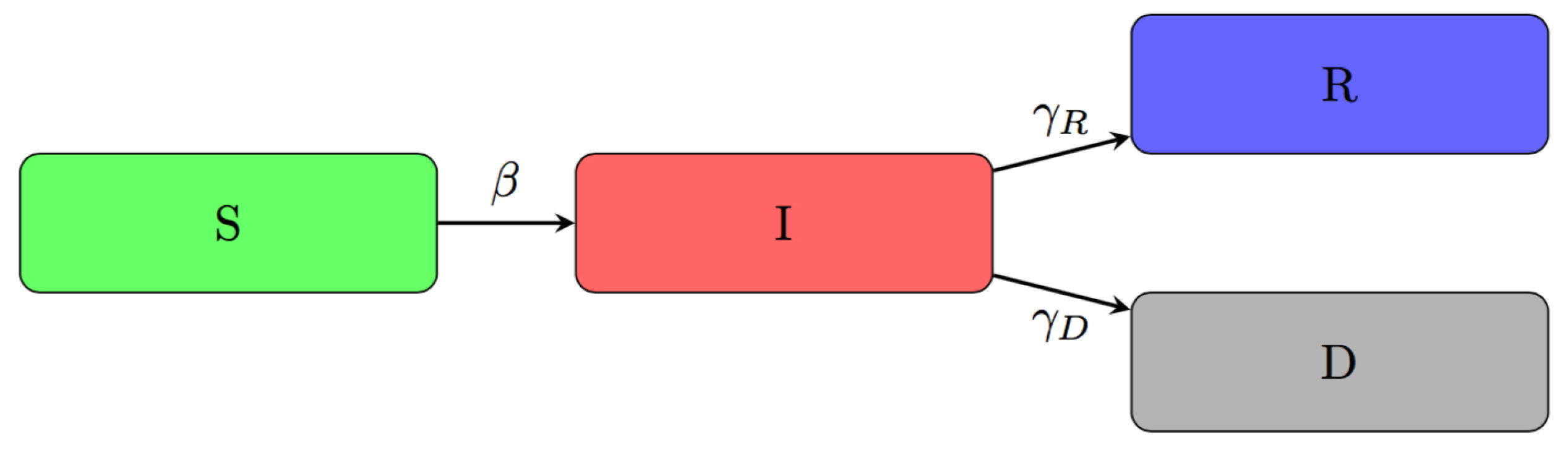
2.2. An Adjusted Time-Dependent SIRD Model
2.3. Adjusted Training Process
2.4. Bootstrap Prediction Intervals
2.5. Model Evaluation
2.6. Model Extensions
3. Results
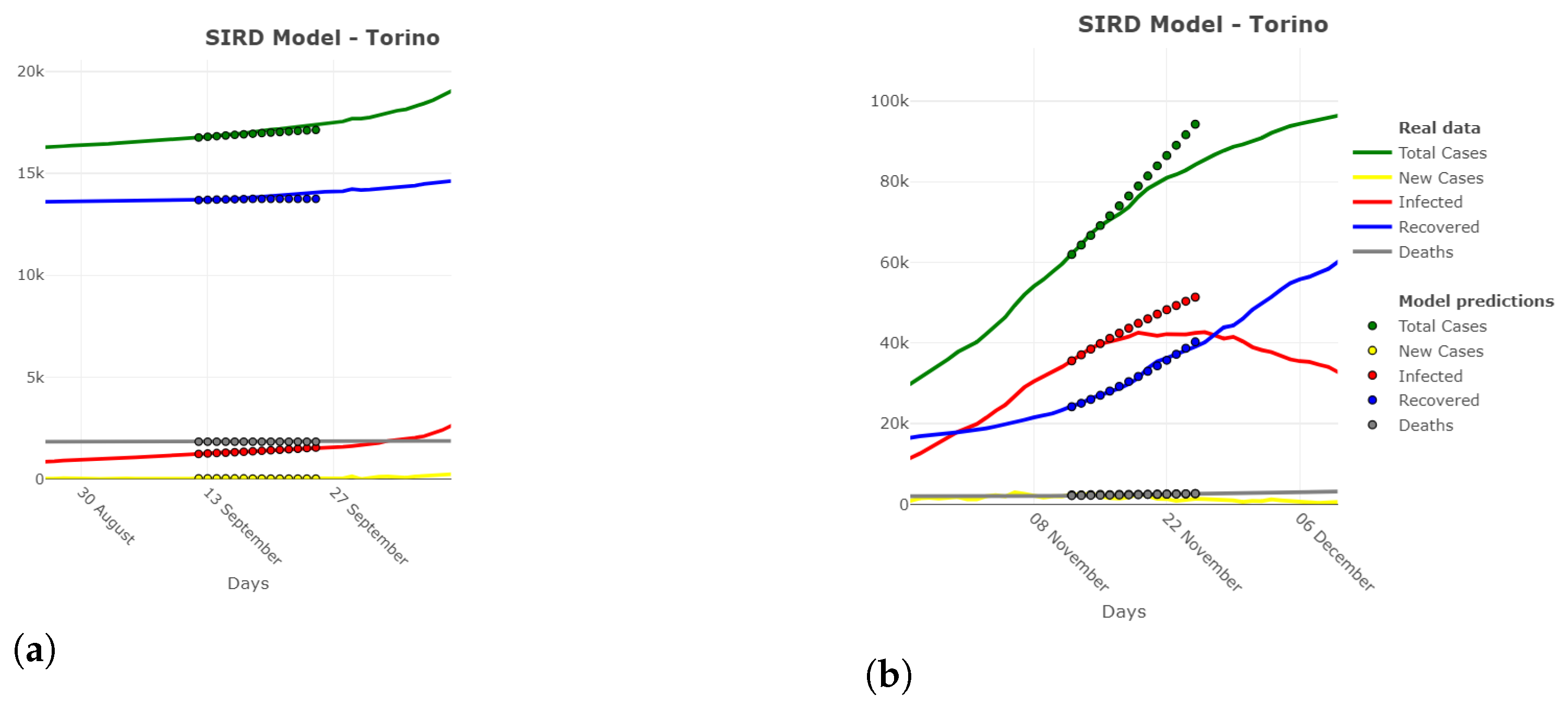
3.1. Model Accuracy Evaluation: Day-By-Day Forecasting Evaluation
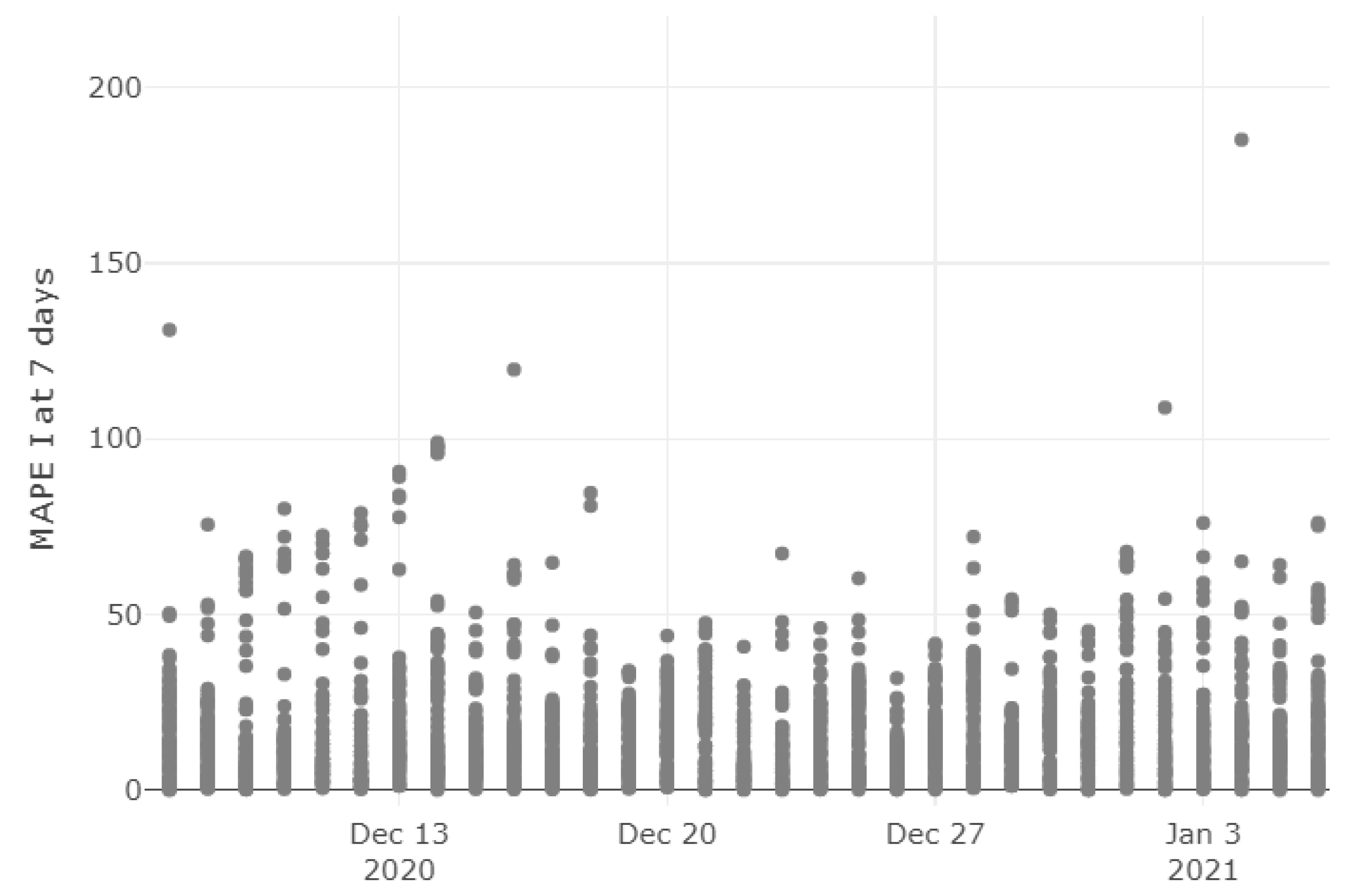
3.2. Model Accuracy Evaluation: Error Distribution across Provinces
3.3. Clustering the Provinces by One-Week Errors on I
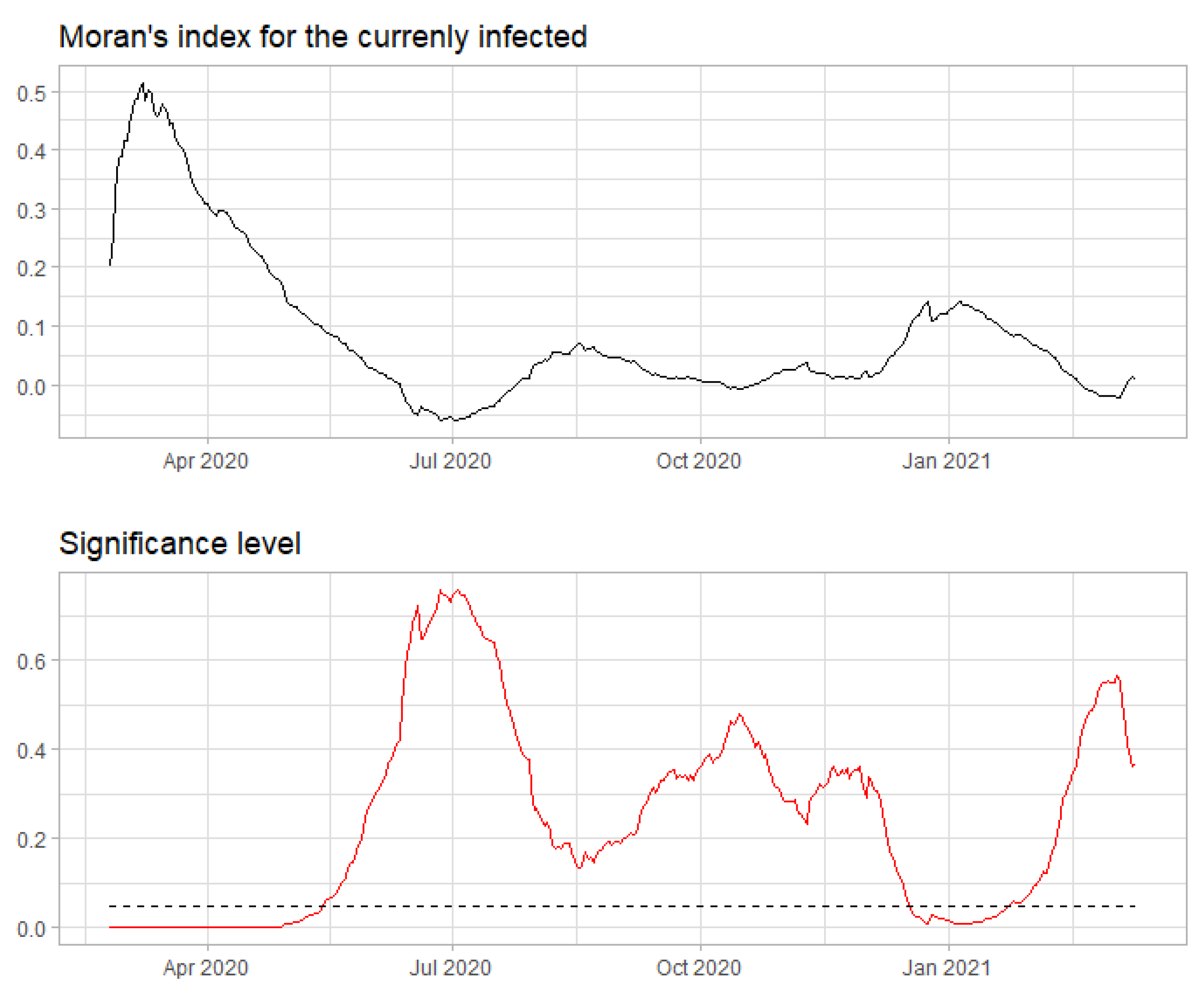
3.4. Spatial Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DTW | Dynamic Time Warping |
| SIRD | Susceptible-Infectious-Recovered-Deceased |
| CPA | Civil Protection Agency |
| FIR | Finite Impulse Response |
| MAPE | Mean Absolute Percentage Error |
| MPE | Mean Percentage Error |
| STARMA | Space Time AutoRegressive Moving Average |
References
- Guzzetta, G.; Poletti, P.; Ajelli, M.; Trentini, F.; Marziano, V.; Cereda, D.; Tirani, M.; Diurno, G.; Bodina, A.; Barone, A.; et al. Potential short-term outcome of an uncontrolled COVID-19 epidemic in Lombardy, Italy, February to March 2020. Eurosurveillance 2020, 25, 1–4. [Google Scholar] [CrossRef]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef]
- Rivieccio, B.A.; Micheletti, A.; Maffeo, M.; Zignani, M.; Comunian, A.; Nicolussi, F.; Salini, S.; Manzi, G.; Auxilia, F.; Giudici, M.; et al. CoViD-19, learning from the past: A wavelet and cross-correlation analysis of the epidemic dynamics looking to emergency calls and Twitter trends in Italian Lombardy region. PLoS ONE 2021, 16, e0247854. [Google Scholar] [CrossRef]
- Castaldi, S.; Maffeo, M.; Rivieccio, B.A.; Zignani, M.; Manzi, G.; Nicolussi, F.; Salini, S.; Micheletti, A.; Gaito, S.; Biganzoli, E. Monitoring emergency calls and social networks for COVID-19 surveillance. To learn for the future: The outbreak experience of the Lombardia region in Italy. Acta Biomed. 2020, 91, 29–33. [Google Scholar] [PubMed]
- Castaldi, S.; Luconi, E.; Rivieccio, B.A.; Boracchi, P.; Marano, G.; Pariani, E.; Romano, L.; Auxilia, F.; Nicolussi, F.; Micheletti, A.; et al. Are epidemiological estimates able to describe the ability of Health Systems to cope with COVID-19 epidemic? Risk Manag. Healthc. Policy 2021, 14, 2221–2229. [Google Scholar] [CrossRef]
- Capasso, V. Mathematical Structures of Epidemic Systems, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Lavezzo, E.; Franchin, E.; Ciavarella, C.; Cuomo-Dannenburg, G.; Barzon, L.; Del Vecchio, C.; Rossi, L.; Manganelli, R.; Loregian, A.; Navarin, N.; et al. Suppression of COVID-19 outbreak in the municipality of Vo, Italy. Nature 2020, 584, 425–429. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Arenas, A.; Cota, W.; Gomez-Gardeñes, J.; Gómez, S.; Granell, C.; Matamalas, J.T.; Soriano-Paños, D.; Steinegger, B. Modeling the Spatiotemporal Epidemic Spreading of COVID-19 and the Impact of Mobility and Social Distancing Interventions. Phys. Rev. X 2020, 10, 1–21. [Google Scholar]
- Bertuzzo, E.; Mari, L.; Pasetto, D.; Miccoli, S.; Casagrandi, R.; Gatto, M.; Rinaldo, A. The geography of COVID-19 spread in Italy and implications for the relaxation of confinement measures. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- Gaeta, G. A simple SIR model with a large set of asymptomatic infectives. arXiv 2020, arXiv:2003.08720. [Google Scholar]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Sebastiani, G.; Massa, M.; Riboli, E. Covid-19 epidemic in Italy: Evolution, projections and impact of government measures. Eur. J. Epidemiol. 2020, 35, 341–345. [Google Scholar] [CrossRef]
- Roosa, K.; Chowell, G. Assessing parameter identifiability in compartmental dynamic models using a computational approach: Application to infectious disease transmission models. Theor. Biol. Med. Model. 2019, 16, 1–15. [Google Scholar] [CrossRef]
- Micheletti, A.; Aletti, G.; Ferrandi, G.; Bertoni, D.; Cavicchioli, D.; Pretolani, R. A weighted χ2 test to detect the presence of a major change point in non-stationary Markov chains. Stat. Methods Appl. 2020, 29, 899–912. [Google Scholar] [CrossRef]
- Calafiore, G.C.; Novara, C.; Possieri, C. A time-varying SIRD model for the COVID-19 contagion in Italy. Annu. Rev. Control 2020, 50, 361–372. [Google Scholar] [CrossRef]
- Amaral, F.; Casaca, W.; Oishi, C.M.; Cuminato, J.A. Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil. Sensors 2021, 21, 540. [Google Scholar] [CrossRef]
- Menchetti, F.; Noirjean, S. Guida alla Lettura e All’interpretazione dei Dati COVID-19 [A Guide to Reading and Interpreting COVID-19 Data]; Technical Report; University of Florence: Florence, Italy, 2020. [Google Scholar]
- Bartoszek, K.; Guidotti, E.; Iacus, S.M.; Okrój, M. Are official confirmed cases and fatalities counts good enough to study the COVID-19 pandemic dynamics? A critical assessment through the case of Italy. Nonlinear Dyn. 2020, 101, 1951–1979. [Google Scholar] [CrossRef]
- Seaman, S.; De Angelis, D. Adjusting COVID-19 Deaths to Account for Reporting Delay; Technical Report MRC-Biostatistics Unit: Cambridge, UK, 2020. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A time-dependent SIR model for COVID-19 with undetectable infected persons. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression iterative estimation of the biasing parameter. Commun. Stat. Theory Methods 1976, 5, 77–88. [Google Scholar] [CrossRef]
- Boguá, M.; Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in complex networks with degree correlations. In Statistical Mechanics of Complex Networks; Pastor-Satorras, R., Rubi, M., Diaz-Guilera, A., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 625, pp. 127–147. [Google Scholar]
- Bastos, S.B.; Cajueiro, D.O. Modeling and forecasting the early evolution of the Covid-19 pandemic in Brazil. Nat. Sci. Rep. 2020, 10, 19457. [Google Scholar] [CrossRef]
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T.; Webster, S.; Cameron-Blake, E.; Hallas, L.; Majumdar, S.; et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef] [PubMed]
- Stone, M. An Asymptotic Equivalence of Choice of Model by Cross-Validation and Akaike’s Criterion. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 44–47. [Google Scholar] [CrossRef]
- Geler, Z.; Kurbalija, V.; Ivanović, M.; Radovanović, M.; Dai, W. Dynamic Time Warping: Itakura vs Sakoe-Chiba. In Proceedings of the IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Sofia, Bulgaria, 3–5 July 2019. [Google Scholar]
- Ferrari, L.; Gerardi, G.; Manzi, G.; Micheletti, A.; Nicolussi, F.; Salini, S. COVID-19 in Italy: An app for a province-based analysis. arXiv 2020, arXiv:2004.12779. [Google Scholar]
- Politis, D.N.; Romano, J.P. The Stationary Bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Aregay, M.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Carroll, R.; Watjou, K. Multiscale measurement error models for aggregated small area health data. Stat. Methods Med. Res. 2016, 25, 1201–1223. [Google Scholar] [CrossRef]
- Prates, M.O. Spatial extreme learning machines: An application on prediction of disease counts. Stat. Methods Med. Res. 2019, 28, 2583–2594. [Google Scholar] [CrossRef]
- McKenzie, J. Mean absolute percentage error and bias in economic forecasting. Econ. Lett. 2011, 113, 259–262. [Google Scholar] [CrossRef]
- Shapiro, M.B.; Karim, F.; Muscioni, G.; Augustine, A.S. Adaptive Susceptible-Infectious-Removed Model for Continuous Estimation of the COVID-19 Infection Rate and Reproduction Number in the United States: Modeling Study. J. Med. Internet Res. 2020, 23, e24389. [Google Scholar] [CrossRef]
- Law, K.B.; Peariasamy, K.M.; Gill, B.S.; Singh, S.; Sundram, B.M.; Rajendran, K.; Dass, S.C.; Lee, Y.L.; Goh, P.P.; Ibrahim, H.; et al. Tracking the early depleting transmission dynamics of COVID-19 with a time-varying SIR model. Nat. Sci. Rep. 2021, 10, 21721. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Zhang, W.; Zhang, D.; Yu, S.; Hao, Y. Estimating the basic reproduction rate of HFMD using the time series SIR model in Guangdong, China. PLoS ONE 2021, 12, e0179623. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.; Koehler, A. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Rathod, S.; Gurung, B.; Singh, K.N.; Ray, M. An improved Space-Time Autoregressive Moving Average (STARMA) model for Modelling and Forecasting of Spatio-Temporal time-series data. J. Indian Soc. Agric. Stat. 2018, 72, 14–25. [Google Scholar]
- Pfeifer, P.E.; Deutsch, S.J. A Three-Stage Iterative Procedure for Space-Time Modeling. Technometrics 1980, 22, 35–47. [Google Scholar] [CrossRef]
- Glasbey, C.A.; Allcroft, D.J. A spatiotemporal auto-regressive moving average model for solar radiation. J. R. Stat. Soc. Ser. C Appl. Stat. 2008, 57, 343–355. [Google Scholar] [CrossRef]
- Wang, X.; Guo, X.; Xin, Q.; Pan, Y.; Hu, Y.; Li, J.; Chu, Y.; Feng, Y.; Wang, Q. Neutralizing Antibodies Responses to SARS-CoV-2 in COVID-19 Inpatients and Convalescent Patients. Clin. Infect. Dis. 2020, 71, 2688–2694. [Google Scholar] [CrossRef]
- Zimmer, C.; Leuba, S.I.; Cohen, T.; Yaesoubi, R. Accurate quantification of uncertainty in epidemic parameter estimates and predictions using stochastic compartmental models. Stat. Methods Med. Res. 2019, 28, 3591–3608. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, D.; Presanis, A.M.; Birrell, P.J.; Scalia Tomba, G.; House, T. Four key challenges in infectious disease modelling using data from multiple sources. Epidemics 2015, 10, 83–87. [Google Scholar] [CrossRef] [PubMed]


| Region | Main Source |
|---|---|
| Valle d’Aosta | https://github.com/pcm-dpc/COVID-19 (accessed on 31 May 2021) |
| Pedmont | https://www.regione.piemonte.it (accessed on 31 May 2021) |
| Lombardy | https://www.laprovinciacr.it (only for Cremona province) (accessed on 31 May 2021) |
| Veneto | https://www.ilgiornaledivicenza.it (accessed on 31 May 2021) |
| Friuli-Venezia-Giulia | https://www.regione.fvg.it (accessed on 31 May 2021) |
| Trentino-Alto-Adige | https://github.com/pcm-dpc/COVID-19 (accessed on 31 May 2021) |
| Emilia-Romagna | https://www.regione.emilia-romagna.it (accessed on 31 May 2021) |
| Liguria | https://www.regione.liguria.it (accessed on 31 May 2021) |
| Tuscany | https://www.toscana-notizie.it (accessed on 31 May 2021) |
| Marche | http://www.regione.marche.it (accessed on 31 May 2021) |
| Umbria | https://public.tableau.com/ (accessed on 31 May 2021) |
| https://regione.umbria.it (accessed on 31 May 2021) | |
| Lazio | https://www.romatoday.it (accessed on 31 May 2021) |
| https://www.facebook.com/SaluteLazio (accessed on 31 May 2021) | |
| Abruzzo | https://www.regione.abruzzo.it (accessed on 31 May 2021) |
| Molise | https://www.molisenews24.it/regione (accessed on 31 May 2021) |
| Puglia | http://www.regione.puglia.it (accessed on 31 May 2021) |
| Basilicata | https://www.regione.basilicata.it (accessed on 31 May 2021) |
| Calabria | https://www.regione.calabria.it (accessed on 31 May 2021) |
| Sicily | https://www.regione.sicilia.it (accessed on 31 May 2021) |
| Sardinia | https://www.regione.sardegna.it (accessed on 31 May 2021) |
| Province | 1 April 2020 | 2 April 2020 | 3 April 2020 | 4 April 2020 |
|---|---|---|---|---|
| Ancona | 7 | 10 | 6 | 7 |
| Pesaro-Urbino | 10 | 20 | 7 | 14 |
| Fermo | 0 | 0 | 2 | 3 |
| Ascoli Piceno | 0 | 1 | 1 | 0 |
| Macerata | 9 | 0 | 1 | 1 |
| “From other regions” | 0 | 0 | 0 | 0 |
| Marche (from provincial deaths) | 26 | 31 | 17 | 25 |
| Marche (from CPA reporting) | 25 | 26 | 54 | 17 |
| Province | 1 April 2020 | 2 April 2020 | 3 April 2020 | 4 April 2020 |
|---|---|---|---|---|
| Piacenza | 25 | 19 | 18 | 12 |
| Parma | 24 | 11 | 9 | 25 |
| Reggio-Emilia | 9 | 9 | 14 | 15 |
| Modena | 10 | 18 | 9 | 6 |
| Bologna | 3 | 7 | 31 | 10 |
| Ferrara | 1 | 3 | 3 | 1 |
| Ravenna | 4 | 1 | 0 | 2 |
| Forlì.Cesena | 4 | 3 | 2 | 1 |
| Rimini | 5 | 4 | 4 | 2 |
| “From other regions” | 3 | 4 | 1 | 1 |
| Emilia-Romagna (from provincial deaths) | 85 | 75 | 90 | 74 |
| Emilia-Romagna (from CPA reporting) | 88 | 79 | 91 | 75 |
| Horizon Days | I | I | R | R | D | D |
|---|---|---|---|---|---|---|
| without s.i. | with s.i. | without s.i. | with s.i. | without s.i. | with s.i. | |
| 1 | 2.78 | 2.79 | 1.46 | 1.46 | 1.08 | 1.07 |
| 2 | 5.19 | 5.24 | 2.69 | 2.70 | 1.96 | 1.95 |
| 3 | 7.79 | 7.88 | 4.00 | 4.01 | 2.82 | 2.81 |
| 4 | 10.48 | 10.64 | 5.39 | 5.42 | 3.67 | 3.67 |
| 5 | 13.18 | 13.48 | 6.88 | 6.94 | 4.52 | 4.53 |
| 6 | 15.73 | 16.30 | 8.54 | 8.61 | 5.33 | 5.34 |
| 7 | 17.55 | 18.48 | 9.90 | 10.07 | 6.00 | 6.03 |
| 8 | 19.64 | 20.64 | 11.00 | 11.37 | 6.69 | 6.73 |
| 9 | 21.97 | 22.98 | 11.90 | 12.41 | 7.37 | 7.43 |
| 10 | 24.35 | 25.39 | 12.80 | 13.39 | 8.04 | 8.10 |
| 11 | 26.72 | 27.85 | 13.64 | 14.27 | 8.71 | 8.77 |
| 12 | 29.09 | 30.36 | 14.40 | 15.05 | 9.36 | 9.45 |
| 13 | 31.33 | 32.80 | 15.12 | 15.78 | 10.02 | 10.13 |
| 14 | 33.55 | 35.37 | 15.88 | 16.53 | 10.64 | 10.77 |
| Horizon Days | MAPE D |
|---|---|
| 1 | 0.987 |
| 2 | 1.785 |
| 3 | 2.560 |
| 4 | 3.346 |
| 5 | 4.115 |
| 6 | 4.846 |
| 7 | 5.458 |
| 8 | 6.073 |
| 9 | 6.706 |
| 10 | 7.342 |
| 11 | 7.986 |
| 12 | 8.609 |
| 13 | 9.245 |
| 14 | 9.881 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari, L.; Gerardi, G.; Manzi, G.; Micheletti, A.; Nicolussi, F.; Biganzoli, E.; Salini, S. Modeling Provincial Covid-19 Epidemic Data Using an Adjusted Time-Dependent SIRD Model. Int. J. Environ. Res. Public Health 2021, 18, 6563. https://doi.org/10.3390/ijerph18126563
Ferrari L, Gerardi G, Manzi G, Micheletti A, Nicolussi F, Biganzoli E, Salini S. Modeling Provincial Covid-19 Epidemic Data Using an Adjusted Time-Dependent SIRD Model. International Journal of Environmental Research and Public Health. 2021; 18(12):6563. https://doi.org/10.3390/ijerph18126563
Chicago/Turabian StyleFerrari, Luisa, Giuseppe Gerardi, Giancarlo Manzi, Alessandra Micheletti, Federica Nicolussi, Elia Biganzoli, and Silvia Salini. 2021. "Modeling Provincial Covid-19 Epidemic Data Using an Adjusted Time-Dependent SIRD Model" International Journal of Environmental Research and Public Health 18, no. 12: 6563. https://doi.org/10.3390/ijerph18126563
APA StyleFerrari, L., Gerardi, G., Manzi, G., Micheletti, A., Nicolussi, F., Biganzoli, E., & Salini, S. (2021). Modeling Provincial Covid-19 Epidemic Data Using an Adjusted Time-Dependent SIRD Model. International Journal of Environmental Research and Public Health, 18(12), 6563. https://doi.org/10.3390/ijerph18126563






