Evaluation of COVID-19 Mitigation Policies in Australia Using Generalised Space-Time Autoregressive Intervention Models
Abstract
:1. Introduction
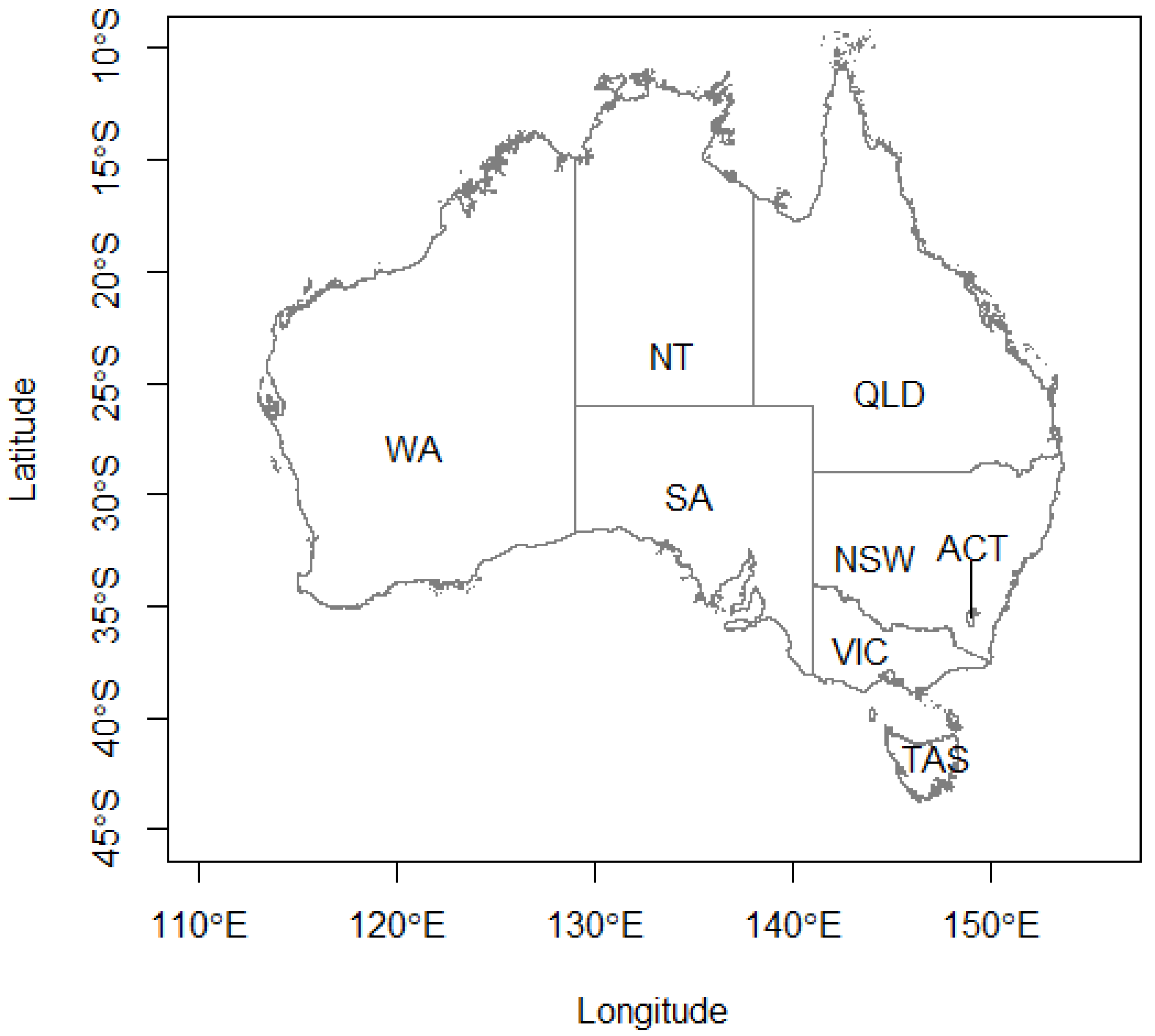
2. Data
2.1. Number of COVID-19 Cases in Australia
2.2. Policies
3. Methods
3.1. The GSTARX Model
- p is the autoregressive order,
- is the spatial order for k-th autoregressive term,
- is an weight matrix which specifies the ℓ-th order spatial weights (see Section 3.3 for further details),
- is an diagonal matrix with elements where each is an autoregressive parameter to be estimated,
- is a diagonal matrix with the i-th diagonal element being representing the q-th exogenous variable observed at time at location i,
- is the vector of the coefficients associated with the q-th exogenous variable, and
- represents the random error terms, assumed to follow the N-dimensional multivariate normal distribution with a mean of and a covariance matrix .
3.2. Model Specifications
3.3. Spatial Weight Matrix
- (a)
- , the identity matrix of size N;
- (b)
- for , the weights are non-zero only when locations i and j are ℓ-th order neighbours, and for all i as a site is not a neighbour of itself by definition; and
- (c)
- the weights are normalised in the sense that the sum of weights in each row of is 1, i.e., .
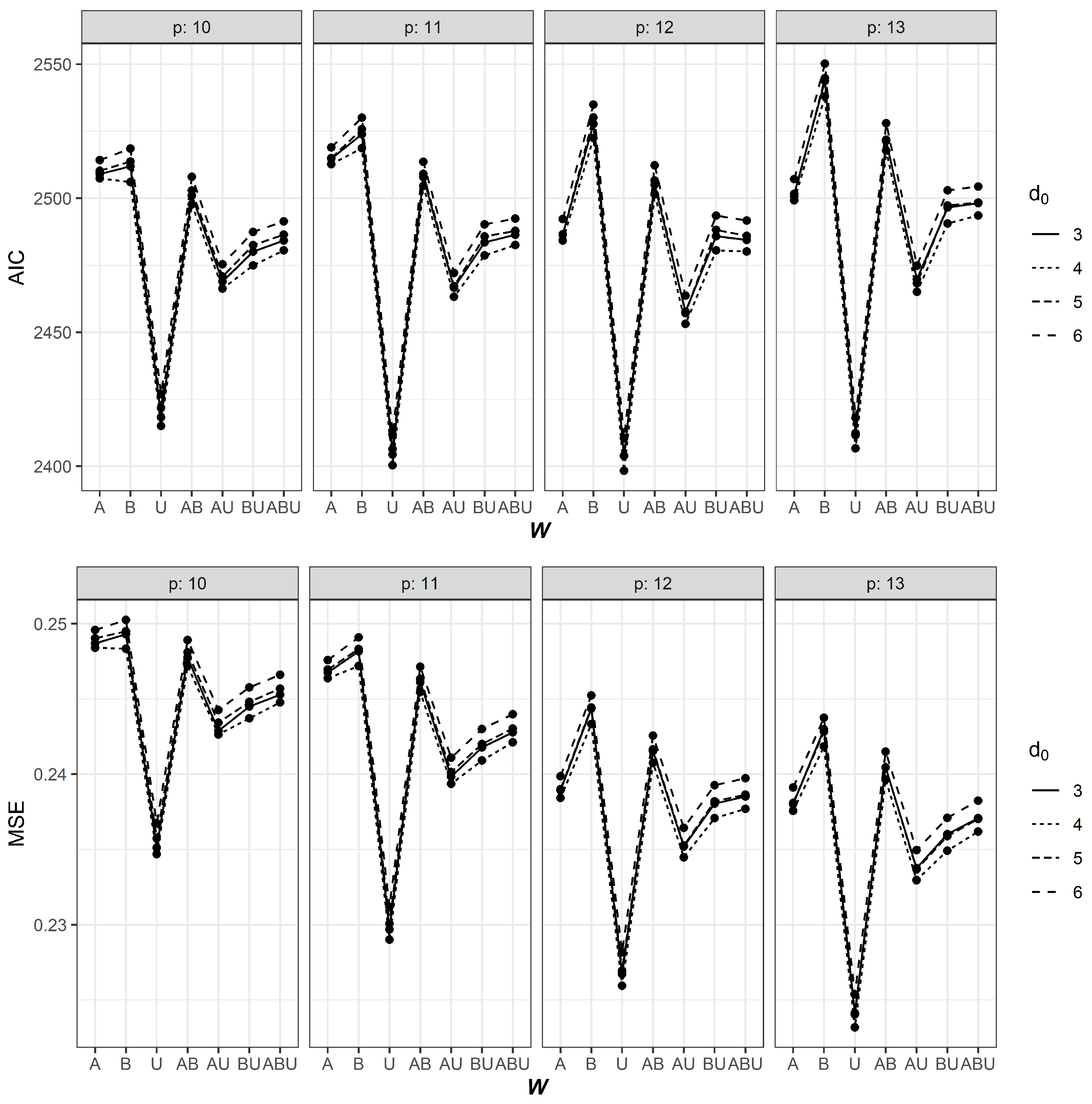
3.4. Estimation
3.5. Statistical Software
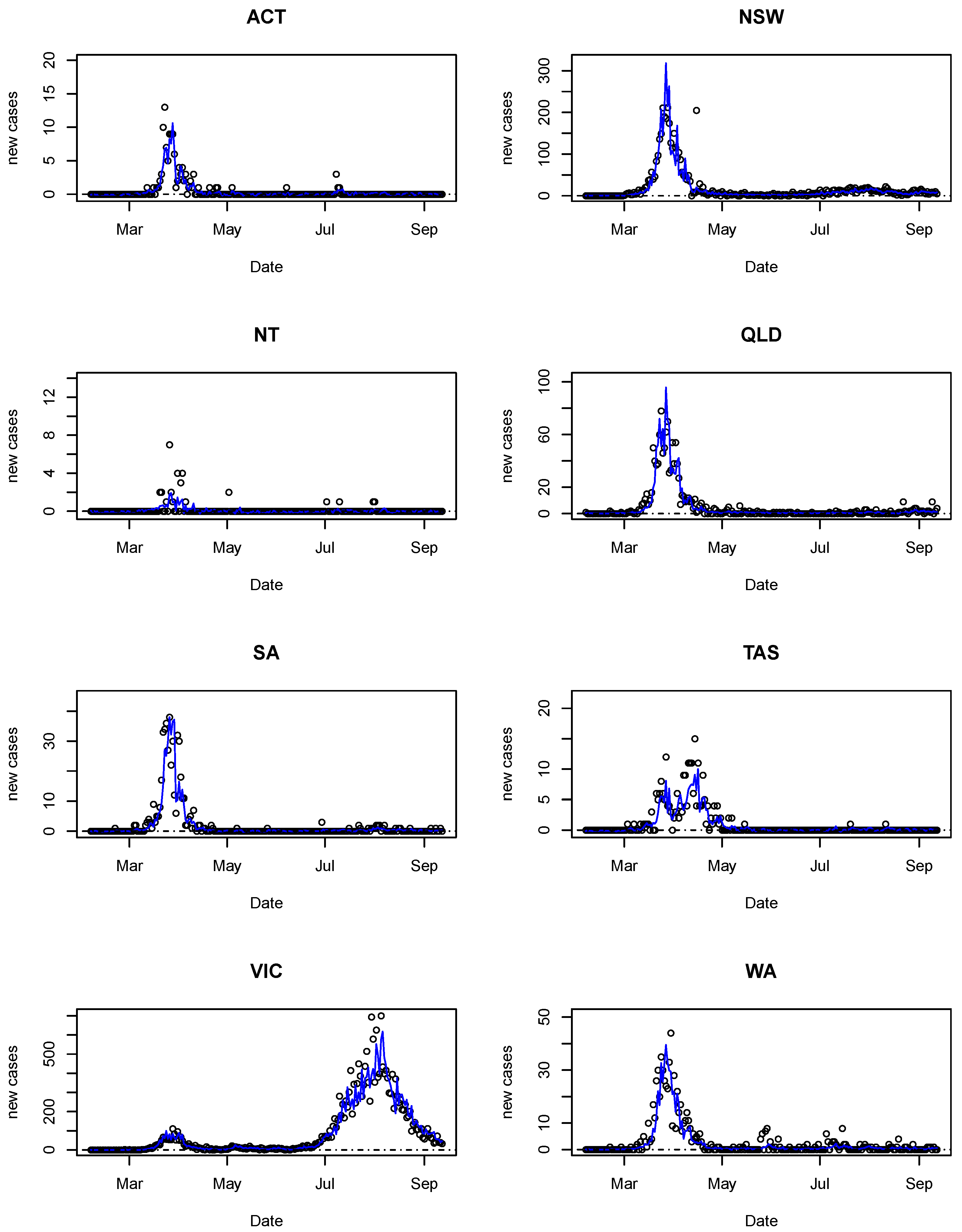
4. Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johns Hopkins University. Johns Hopkins University & Medicine Coronavirus Resource Centre. Available online: https://coronavirus.jhu.edu/ (accessed on 13 November 2020).
- Yan, Z. Unprecedented pandemic, unprecedented shift, and unprecedented opportunity. Hum. Behav. Emerg. Technol. 2020, 2, 110–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ebrahim, S.H.; Ahmed, Q.A.; Gozzer, E.; Schlagenhauf, P.; Memish, Z.A. Covid-19 and community mitigation strategies in a pandemic. BMJ 2020, 368, m1066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fong, M.W.; Gao, H.; Wong, J.Y.; Xiao, J.; Shiu, E.Y.C.; Ryu, S.; Cowling, B.J. Nonpharmaceutical Measures for Pandemic Influenza in Nonhealthcare Settings—Social Distancing Measures. Emerg. Infect. Dis. 2020, 26, 976–984. [Google Scholar] [CrossRef]
- Inoue, H.; Todo, Y. The propagation of the economic impact through supply chains: The case of a mega-city lockdown to contain the spread of Covid-19. Covid Econ. 2020, 2, 43–59. [Google Scholar] [CrossRef] [Green Version]
- Makridis, C.A.; Hartley, J.S. The Cost of COVID-19: A Rough Estimate of the 2020 US GDP Impact; Special Edition Policy Brief; Mercatus Centre George Mason University: Fairfax, VA, USA, 2020. [Google Scholar] [CrossRef]
- Bhuiyan, A.K.M.; Sakib, N.; Pakpour, A.H.; Griffiths, M.D.; Mamun, M.A. COVID-19-related suicides in Bangladesh due to lockdown and economic factors: Case study evidence from media reports. Int. J. Ment. Health Addict. 2020. [Google Scholar] [CrossRef]
- Rossi, R.; Socci, V.; Talevi, D.; Mensi, S.; Niolu, C.; Pacitti, F.; Di Marco, A.; Rossi, A.; Siracusano, A.; Di Lorenzo, G. COVID-19 Pandemic and Lockdown Measures Impact on Mental Health Among the General Population in Italy. Front. Psychiatry 2020, 11, 790. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Roy, D.; Sinha, K.; Parveen, S.; Sharma, G.; Joshi, G. Impact of COVID-19 and lockdown on mental health of children and adolescents: A narrative review with recommendations. Psychiatry Res. 2020, 293, 113429. [Google Scholar] [CrossRef]
- Department of Health, Commonwealth of Australia. Coronavirus (COVID-19) Current Situation and Case Numbers. Available online: https://www.health.gov.au/news/health-alerts/novel-coronavirus-2019-ncov-health-alert/coronavirus-covid-19-current-situation-and-case-numbers (accessed on 18 November 2020).
- Department of Parliamentary Services, Parliament of Australia. COVID-19 Australian Government Roles and Responsibilities: An Overview. Available online: https://parlinfo.aph.gov.au/parlInfo/download/library/prspub/7346878/upload_binary/7346878.pdf. (accessed on 18 November 2020).
- Maclean, H.; Elphick, K. COVID-19 Legislative response—Human Biosecurity Emergency Declaration Explainer. Available online: https://www.aph.gov.au/About_Parliament/Parliamentary_Departments/Parliamentary_Library/FlagPost/2020/March/COVID-19_Biosecurity_Emergency_Declaration. (accessed on 18 November 2020).
- Parliament of Australia. Border Restrictions. Available online: https://parlinfo.aph.gov.au/parlInfo/download/media/pressrel/7250185/upload_binary/7250185.PDF;fileType=application%2Fpdf#search=%22media/pressrel/7250185%22 (accessed on 18 November 2020).
- Prime Minister of Australia. Update on Coronavirus Measures. Media Statement 20 March 2020. Available online: https://www.pm.gov.au/media/update-coronavirus-measures-0 (accessed on 18 November 2020).
- Storen, R.; Corrigan, N. COVID-19: A Chronology of State and Territory Government Announcements (up until 30 June 2020). Available online: https://parlinfo.aph.gov.au/parlInfo/download/library/prspub/7614514/upload_binary/7614514.pdf (accessed on 18 November 2020).
- Box, G.E.P.; Reinsel, G.C.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Cliff, A.D.; Ord, J. Spatial Autocorrelation; Pioneer: London, UK, 1973. [Google Scholar]
- Pfeifer, P.E.; Deutsch, S.J. A three stage iterative procedure for space-time modeling. Technometrics 1980, 22, 35–47. [Google Scholar] [CrossRef]
- Huang, D.; Anh, V.V. Estimation of spatial ARMA models. Aust. J. Stat. 1992, 34, 513–530. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Di Giacinto, V. A generalized space-time ARMA model with an application to regional unemployment analysis in Italy. Int. Reg. Sci. Rev. 2006, 29, 159–198. [Google Scholar] [CrossRef]
- Nurhayati, N.; Pasaribu, U.S.; Neswan, O. Application of generalized space-time autoregressive model on GDP data in west European countries. J. Probab. Stat. 2012, 2012, 867056. [Google Scholar] [CrossRef]
- Stoffer, D.S. Estimation and Identification of Space-Time ARMAX Models in the Presence of Missing Data. J. Am. Stat. Assoc. 1986, 81, 762–772. [Google Scholar] [CrossRef]
- Suhartono, S.R.; Wahyuningrum, S.; Akbar, M.S. GSTARX-GLS model for spatio-temporal data forecasting. Malays. J. Math. Sci. 2016, 10, 91–103. [Google Scholar]
- Biglan, A.; Ary, D.; Wagenaar, A.C. The value of interrupted time-series experiments for community intervention research. Prev. Sci. 2000, 1, 31–49. [Google Scholar] [CrossRef]
- Gilmour, S.; Degenhardt, L.; Hall, W.; Day, C. Using intervention time series analyses to assess the effects of imperfectly identifiable natural events: A general method and example. BMC Med. Res. Methodol. 2006, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Clement, L.; Thas, O.; Vanrolleghem, P.A.; Ottoy, J. Spatio-temporal statistical models for river monitoring networks. Water Sci. Technol. 2006, 53, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Ip, R.H.L.; Li, W.K.; Leung, K.M.Y. Seemingly unrelated intervention time series models for effectiveness evaluation of large scale environmental remediation. Mar. Pollut. Bull. 2013, 74, 56–65. [Google Scholar] [CrossRef]
- Bernal, J.L.; Cummins, S.; Gasparrini, A. Interrupted time series regressipon for the evaluation of public health interventions: A tutorial. Int. J. Epidemiol. 2017, 46, 348–355. [Google Scholar] [PubMed] [Green Version]
- Australia Bureau of Statistics. National, State and Territory Population, Reference Period March 2020 (ABS. cat. no. 3101.0). Available online: https://www.abs.gov.au/statistics/people/population/national-state-and-territory-population/latest-release (accessed on 18 November 2020).
- ACT Government. COVID-19 Updates. Available online: https://www.covid19.act.gov.au/updates (accessed on 18 November 2020).
- NSW Health. Public Health Orders and Restrictions. Available online: https://www.health.nsw.gov.au/Infectious/covid-19/Pages/public-health-orders.aspx (accessed on 18 November 2020).
- Northern Territory Government. Coronavirus (COVID-19) Updates. Available online: https://coronavirus.nt.gov.au/updates (accessed on 18 November 2020).
- Queensland Government. Latest updates—Coronavirus (COVID-19). Available online: https://www.qld.gov.au/health/conditions/health-alerts/coronavirus-covid-19/current-status (accessed on 18 November 2020).
- SA Health, Government of South Australia. COVID-19 Response and Restrictions. Available online: https://www.sahealth.sa.gov.au/wps/wcm/connect/public+content/sa+health+internet/conditions/infectious+diseases/covid-19/response+and+restrictions (accessed on 18 November 2020).
- Tasmanian Government. Coronavirus Disease (COVID-19) Current Restrictions. Available online: https://coronavirus.tas.gov.au/families-community/current-restrictions (accessed on 18 November 2020).
- Department of Health and Human Services, State Government of Victoria. Updates about the Outbreak of the Coronavirus Disease (COVID-19). Available online: https://www.dhhs.vic.gov.au/coronavirus/updates (accessed on 18 November 2020).
- The Government of Western Australia. COVID-19 Coronavirus. Available online: https://www.wa.gov.au/government/covid-19-coronavirus (accessed on 18 November 2020).
- Borovkova, S.; Lopuhaä, H.P.; Ruchjana, B.N. Consistency and Asymptotic Normality of Least Estimators in Generalized STAR Models. Stat. Neerl. 2008, 62, 482–508. [Google Scholar] [CrossRef]
- Zellner, A. An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias. J. Am. Stat. Assoc. 1962, 57, 348–368. [Google Scholar] [CrossRef]
- Zellner, A. Estimators for Seemingly Unrelated Regression Equations: Some Exact Finite Sample Results. J. Am. Stat. Assoc. 1963, 58, 977–992. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Dwivedi, T.D. Estimation of seemingly unrelated regression equations: A brief survey. J. Econom. 1979, 10, 15–32. [Google Scholar] [CrossRef]
- Liu, A. Efficient estimation of two seemingly unrelated regression equations. J. Multivar. Anal. 2002, 82, 445–456. [Google Scholar] [CrossRef] [Green Version]
- Henderson, H.V.; Pukelsheim, F.; Searle, S.R. On the history of the kronecker product. Linear Multilinear Algebra 1983, 14, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Amemiya, T. Advanced Econometrics; Harvard University Press: Cambridge, UK, 1985. [Google Scholar]
- Greene, W.H. Econometric Analysis; Pearson Education India: Delhi, India, 2003. [Google Scholar]
- Lever, J.; Kryzwinski, M.; Altman, N. Model selection and overfitting. Nat. Methods 2016, 13, 703–704. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, J. Spatial Processes: Models and Applications; Pioneer: London, UK, 1981. [Google Scholar]
- Department of Infrastructure, Transport, Regional Development and Communications, Australia Government. Australian Domestic Aviation Activity Monthly Publications. Available online: https://www.bitre.gov.au/publications/ongoing/domestic_airline_activity-monthly_publications (accessed on 18 November 2020).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020, 5, 323–337. [Google Scholar]
- Dhouib, W.; Maatoug, J.; Ayouni, I.; Zammit, N.; Ghammem, R.; Fredj, S.B.; Ghannem, H. The incubation period during the pandemic of COVID-19: A systematic review and meta-analysis. Syst. Rev. 2021, 10, 101. [Google Scholar] [CrossRef]
- World Health Organization. Coronavirus Disease 2019 (COVID-19) Situation Report—55. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200315-sitrep-55-covid-19.pdf (accessed on 18 November 2020).
- Hu, M.; Lin, H.; Wang, J.; Xu, C.; Tatem, A.J.; Meng, B.; Zhang, X.; Liu, Y.; Wang, P.; Wu, G.; et al. Risk of Coronavirus Disease 2019 Transmission in Train Passengers: An Epidemiological and Modeling Study. Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Ip, R.H.L.; Li, W.K. Time varying spatio-temporal covariance models. Spat. Stat. 2015, 14, 269–285. [Google Scholar] [CrossRef] [Green Version]
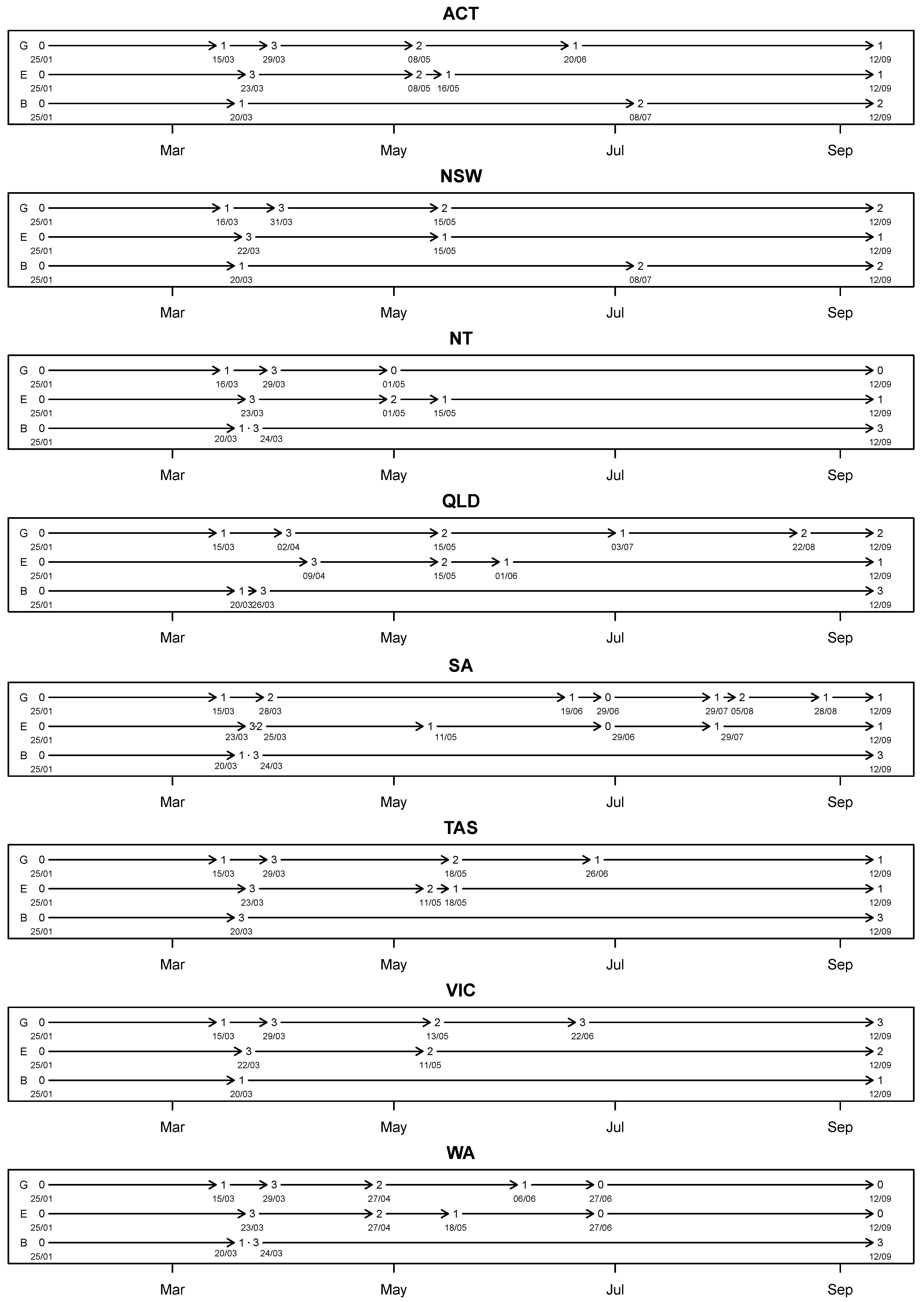

| Policy | Description |
|---|---|
| Gathering | |
| Level 0 | No upper limit on the number of people allowed. |
| Level 1 (Soft) | The upper limit was between 51 and 500. |
| Level 2 (Moderate) | The upper limit was between 3 and 50. |
| Level 3 (Strict) | The upper limit was 2. |
| Economy | |
| Level 0 | No restrictions were imposed. |
| Level 1 (Soft) | Sit-down dining (with varying upper limit) at cafes, restaurants, pubs and clubs was allowed. Indoor religious gatherings (with varying upper limit) were allowed. Most indoor facilities such as gyms, libraries, museums were allowed to operate as long as some kind of “COVID Safe Plan” was enforced. |
| Level 2 (Moderate) | Access to some non-essential and leisure services allowed. Examples include outdoor, non-contact activities such as training and pools (indoor and outdoor), public spaces and lagoons, libraries, parks, playground equipment, skate parks and outdoor gyms. Recreational travel (possibly within certain distance from the place of residence) may be allowed. |
| Level 3 (Strict) | Mandatory closure of all non-essential services. Closure of places of social gathering, including registered and licensed clubs, licensed premises in hotels and bars and entertainment venues. Cafes and restaurants remain open but limited to only takeaway food. “Non-essential” businesses or activities including cinemas, casinos, concerts, indoor sports, gyms, playgrounds, campgrounds, libraries must not be operated. |
| Border Control | |
| Level 0 | No restriction or international travel ban imposed on certain countries. |
| Level 1 | Closure of international border. No interstate border control was in place. |
| Level 2 | Closure of international border. Interstate border control was applied to one state or territory. |
| Level 3 | Closure of international border. Interstate border control was applied to multiple states and territories. |
| AIC | MSE | AIC | MSE | AIC | MSE | AIC | MSE | AIC | MSE | AIC | MSE | AIC | MSE | ||
| 0 | 11 | 2530.2 | 0.249 | 2533.7 | 0.248 | 2416.2 | 0.231 | 2522.5 | 0.248 | 2479.0 | 0.242 | 2494.4 | 0.243 | 2499.6 | 0.245 |
| 12 | 2500.1 | 0.241 | 2536.6 | 0.245 | 2414.5 | 0.229 | 2519.0 | 0.243 | 2469.2 | 0.237 | 2496.5 | 0.239 | 2497.4 | 0.240 | |
| 13 | 2514.9 | 0.240 | 2552.1 | 0.243 | 2424.2 | 0.226 | 2535.1 | 0.242 | 2481.8 | 0.236 | 2507.2 | 0.237 | 2511.2 | 0.239 | |
| 1 | 9 | 2513.3 | 0.253 | 2514.0 | 0.251 | 2418.4 | 0.238 | 2508.0 | 0.251 | 2469.8 | 0.247 | 2478.8 | 0.247 | 2486.8 | 0.249 |
| 11 | 2523.1 | 0.250 | 2526.5 | 0.250 | 2410.7 | 0.231 | 2514.7 | 0.248 | 2474.6 | 0.242 | 2488.6 | 0.243 | 2493.6 | 0.244 | |
| 12 | 2494.0 | 0.241 | 2530.2 | 0.245 | 2410.0 | 0.228 | 2511.9 | 0.243 | 2465.4 | 0.237 | 2491.1 | 0.239 | 2491.8 | 0.240 | |
| 2 | 11 | 2518.0 | 0.248 | 2527.3 | 0.249 | 2407.1 | 0.230 | 2511.9 | 0.247 | 2469.3 | 0.240 | 2486.6 | 0.242 | 2489.9 | 0.244 |
| 12 | 2490.5 | 0.240 | 2530.9 | 0.245 | 2405.8 | 0.227 | 2509.6 | 0.242 | 2460.6 | 0.236 | 2489.0 | 0.239 | 2488.5 | 0.239 | |
| 13 | 2505.6 | 0.239 | 2546.3 | 0.243 | 2414.8 | 0.225 | 2525.7 | 0.241 | 2473.1 | 0.234 | 2499.4 | 0.237 | 2502.1 | 0.238 | |
| 3 | 9 | 2504.1 | 0.251 | 2510.1 | 0.251 | 2411.2 | 0.236 | 2499.6 | 0.246 | 2461.0 | 0.240 | 2472.6 | 0.242 | 2478.3 | 0.243 |
| 11 | 2509.0 | 0.249 | 2511.9 | 0.249 | 2404.4 | 0.230 | 2507.9 | 0.242 | 2466.6 | 0.235 | 2483.5 | 0.238 | 2486.4 | 0.239 | |
| 12 | 2486.5 | 0.239 | 2527.7 | 0.244 | 2403.9 | 0.227 | 2505.0 | 0.240 | 2457.7 | 0.234 | 2485.9 | 0.236 | 2484.4 | 0.237 | |
| 4 | 11 | 2512.7 | 0.246 | 2518.7 | 0.247 | 2400.4 | 0.229 | 2504.6 | 0.245 | 2463.3 | 0.239 | 2478.7 | 0.241 | 2482.6 | 0.242 |
| 12 | 2484.2 | 0.238 | 2522.5 | 0.243 | 2398.3 | 0.226 | 2501.6 | 0.241 | 2453.2 | 0.234 | 2480.6 | 0.237 | 2480.1 | 0.238 | |
| 13 | 2499.2 | 0.238 | 2538.0 | 0.242 | 2406.7 | 0.223 | 2517.8 | 0.240 | 2465.1 | 0.233 | 2490.6 | 0.235 | 2493.5 | 0.236 | |
| 5 | 11 | 2515.0 | 0.247 | 2525.8 | 0.248 | 2406.4 | 0.230 | 2509.1 | 0.246 | 2467.2 | 0.240 | 2485.7 | 0.242 | 2487.8 | 0.243 |
| 12 | 2486.4 | 0.239 | 2530.1 | 0.244 | 2404.0 | 0.227 | 2506.6 | 0.242 | 2457.2 | 0.235 | 2488.2 | 0.238 | 2486.0 | 0.239 | |
| 13 | 2500.7 | 0.238 | 2544.8 | 0.243 | 2411.6 | 0.224 | 2521.8 | 0.240 | 2468.3 | 0.234 | 2497.3 | 0.236 | 2498.4 | 0.237 | |
| 6 | 11 | 2518.9 | 0.248 | 2530.1 | 0.249 | 2411.9 | 0.231 | 2513.6 | 0.247 | 2472.1 | 0.241 | 2490.3 | 0.243 | 2492.4 | 0.244 |
| 12 | 2492.2 | 0.240 | 2534.9 | 0.245 | 2410.5 | 0.228 | 2512.3 | 0.243 | 2463.7 | 0.236 | 2493.5 | 0.239 | 2491.7 | 0.240 | |
| 13 | 2507.1 | 0.239 | 2550.2 | 0.244 | 2418.0 | 0.225 | 2528.0 | 0.241 | 2474.8 | 0.235 | 2502.9 | 0.237 | 2504.4 | 0.238 | |
| 7 | 11 | 2524.2 | 0.248 | 2537.5 | 0.249 | 2413.5 | 0.231 | 2520.0 | 0.248 | 2475.0 | 0.241 | 2495.2 | 0.243 | 2497.2 | 0.244 |
| 12 | 2497.7 | 0.240 | 2541.1 | 0.245 | 2410.6 | 0.228 | 2517.7 | 0.243 | 2465.2 | 0.236 | 2497.5 | 0.239 | 2495.3 | 0.240 | |
| 13 | 2511.7 | 0.239 | 2555.0 | 0.243 | 2418.3 | 0.225 | 2532.5 | 0.242 | 2476.6 | 0.235 | 2506.6 | 0.237 | 2507.8 | 0.238 | |
| AIC | |||||||||
| 2403.9 | 2401.3 | 2401.5 | 2402.4 | 2399.5 | 2400.3 | 2408.2 | 2406.0 | 2406.2 | |
| 2402.8 | 2400.4 | 2400.6 | 2400.9 | 2398.3 | 2398.9 | 2406.8 | 2405.0 | 2405.2 | |
| 2401.8 | 2399.9 | 2399.7 | 2399.5 | 2397.4 | 2397.7 | 2405.3 | 2404.0 | 2404.0 | |
| MSE | |||||||||
| 0.2267 | 0.2263 | 0.2263 | 0.2265 | 0.2259 | 0.2260 | 0.2273 | 0.2270 | 0.2270 | |
| 0.2267 | 0.2264 | 0.2264 | 0.2265 | 0.2259 | 0.2260 | 0.2274 | 0.2271 | 0.2271 | |
| 0.2265 | 0.2262 | 0.2263 | 0.2262 | 0.2258 | 0.2258 | 0.2271 | 0.2269 | 0.2269 | |
| ACT | NSW | NT | QLD | SA | TAS | VIC | WA | |
| 1 | 0.364 *** | 0.317 *** | 0.099 | 0.228 *** | 0.3 *** | 0.141 ** | 0.425 *** | 0.201 *** |
| (0.064) | (0.067) | (0.066) | (0.065) | (0.067) | (0.066) | (0.066) | (0.066) | |
| 2 | 0.138 ** | 0.085 | −0.072 | 0.166 ** | 0.032 | 0.353 *** | 0.06 | 0.132 * |
| (0.068) | (0.071) | (0.066) | (0.067) | (0.07) | (0.066) | (0.072) | (0.067) | |
| 3 | 0.008 | 0.035 | 0.075 | 0.051 | 0.123 * | 0.146 ** | 0.396 *** | 0.159 ** |
| (0.068) | (0.071) | (0.067) | (0.07) | (0.069) | (0.07) | (0.072) | (0.068) | |
| 4 | 0.135 ** | 0.156 ** | −0.221 *** | 0.072 | 0.004 | 0.034 | 0.052 | 0.006 |
| (0.068) | (0.07) | (0.064) | (0.071) | (0.067) | (0.07) | (0.076) | (0.069) | |
| 5 | 0.096 | 0.158 ** | 0.174 *** | 0.138 * | −0.067 | −0.021 | 0.187 ** | 0.141 ** |
| (0.067) | (0.07) | (0.067) | (0.071) | (0.068) | (0.069) | (0.075) | (0.07) | |
| 6 | −0.007 | 0.028 | 0.028 | 0.086 | 0.117 * | 0.052 | −0.055 | 0.047 |
| (0.067) | (0.072) | (0.066) | (0.07) | (0.067) | (0.069) | (0.076) | (0.07) | |
| 7 | −0.077 | −0.002 | 0.264 *** | 0.12 * | 0.092 | −0.06 | −0.037 | −0.076 |
| (0.067) | (0.16) | (0.065) | (0.071) | (0.068) | (0.069) | (0.076) | (0.071) | |
| 8 | −0.234 *** | 0.173 ** | −0.039 | 0.098 | −0.025 | 0.041 | −0.102 | −0.057 |
| (0.067) | (0.073) | (0.067) | (0.07) | (0.069) | (0.069) | (0.075) | (0.071) | |
| 9 | −0.038 | −0.145 ** | −0.116 * | 0.011 | 0.068 | 0.056 | −0.19 ** | −0.042 |
| (0.065) | (0.072) | (0.066) | (0.071) | (0.069) | (0.068) | (0.074) | (0.071) | |
| 10 | 0.16 ** | 0.106 | 0.027 | −0.088 | 0.07 | −0.134 ** | 0.071 | 0.066 |
| (0.065) | (0.071) | (0.07) | (0.072) | (0.069) | (0.068) | (0.07) | (0.07) | |
| 11 | −0.093 | −0.014 | −0.071 | 0.028 | −0.092 | 0.051 | 0.031 | −0.011 |
| (0.064) | (0.07) | (0.069) | (0.071) | (0.069) | (0.064) | (0.069) | (0.07) | |
| 12 | 0.135 ** | −0.044 | −0.1 | −0.105 | 0.025 | 0.031 | 0.097 | −0.013 |
| (0.06) | (0.067) | (0.069) | (0.069) | (0.065) | (0.06) | (0.064) | (0.068) | |
| ACT | NSW | NT | QLD | SA | TAS | VIC | WA | |
| 1 | 0.345 *** | 0.345 ** | -0.114 | 0.508 *** | 0.352 *** | 0.573 *** | 0.018 | 0.374 ** |
| (0.134) | (0.14) | (0.261) | (0.142) | (0.133) | (0.128) | (0.067) | (0.162) | |
| 2 | 0.449 *** | −0.253 | 0.434 | −0.053 | 0.371 ** | 0.161 | 0.068 | −0.09 |
| (0.152) | (0.162) | (0.315) | (0.159) | (0.149) | (0.152) | (0.077) | (0.185) | |
| 3 | −0.081 | 0.336 ** | −0.124 | −0.011 | −0.02 | 0.04 | −0.204 *** | 0.079 |
| (0.156) | (0.166) | (0.322) | (0.161) | (0.15) | (0.154) | (0.079) | (0.189) | |
| 4 | −0.682 *** | −0.133 | 0.698 ** | −0.09 | −0.077 | −0.621 *** | 0.178 ** | 0.158 |
| (0.155) | (0.158) | (0.312) | (0.154) | (0.147) | (0.145) | (0.078) | (0.183) | |
| 5 | 0.323 ** | 0.038 | −0.097 | −0.06 | 0.329 ** | 0.102 | 0.036 | −0.103 |
| (0.161) | (0.159) | (0.313) | (0.155) | (0.148) | (0.151) | (0.08) | (0.187) | |
| 6 | 0.216 | 0.038 | 0.194 | −0.245 | −0.049 | −0.043 | 0.059 | 0.193 |
| (0.164) | (0.073) | (0.311) | (0.158) | (0.149) | (0.151) | (0.081) | (0.19) | |
| 7 | 0.28 * | 0.169 | −0.495 | 0.273 * | 0.04 | −0.123 | −0.004 | 0.014 |
| (0.164) | (0.159) | (0.311) | (0.159) | (0.149) | (0.15) | (0.08) | (0.189) | |
| 8 | 0.175 | −0.019 | 0.835 *** | −0.119 | 0.01 | −0.306 ** | 0.107 | 0.16 |
| (0.163) | (0.155) | (0.308) | (0.156) | (0.146) | (0.147) | (0.079) | (0.186) | |
| 9 | −0.256 | −0.43 *** | −0.664 ** | −0.062 | −0.556 *** | 0.085 | −0.223 *** | −0.159 |
| ACT | NSW | NT | QLD | SA | TAS | VIC | WA | |
| (0.163) | (0.154) | (0.307) | (0.154) | (0.144) | (0.148) | (0.078) | (0.181) | |
| 10 | 0.257 | 0.105 | 0.529 * | 0.177 | −0.227 | 0.094 | 0.12 | 0.203 |
| (0.163) | (0.164) | (0.306) | (0.159) | (0.15) | (0.154) | (0.081) | (0.186) | |
| 11 | −0.315 * | −0.174 | −0.541 * | 0.132 | 0.303 ** | 0.406 *** | 0.038 | −0.259 |
| (0.162) | (0.161) | (0.306) | (0.156) | (0.15) | (0.153) | (0.08) | (0.184) | |
| 12 | −0.366 ** | 0.069 | −0.178 | −0.358 *** | −0.179 | 0.061 | −0.22 *** | −0.159 |
| (0.143) | (0.141) | (0.251) | (0.136) | (0.136) | (0.141) | (0.068) | (0.158) | |
| 0.136 ** | 0.224 *** | 0.344 *** | −0.089 | −0.11 | −0.151 * | −0.15 ** | −0.129 * | −0.125 ** |
| (0.056) | (0.056) | (0.067) | (0.07) | (0.074) | (0.084) | (0.059) | (0.074) | (0.049) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ip, R.H.L.; Demskoi, D.; Rahman, A.; Zheng, L. Evaluation of COVID-19 Mitigation Policies in Australia Using Generalised Space-Time Autoregressive Intervention Models. Int. J. Environ. Res. Public Health 2021, 18, 7474. https://doi.org/10.3390/ijerph18147474
Ip RHL, Demskoi D, Rahman A, Zheng L. Evaluation of COVID-19 Mitigation Policies in Australia Using Generalised Space-Time Autoregressive Intervention Models. International Journal of Environmental Research and Public Health. 2021; 18(14):7474. https://doi.org/10.3390/ijerph18147474
Chicago/Turabian StyleIp, Ryan H. L., Dmitry Demskoi, Azizur Rahman, and Lihong Zheng. 2021. "Evaluation of COVID-19 Mitigation Policies in Australia Using Generalised Space-Time Autoregressive Intervention Models" International Journal of Environmental Research and Public Health 18, no. 14: 7474. https://doi.org/10.3390/ijerph18147474
APA StyleIp, R. H. L., Demskoi, D., Rahman, A., & Zheng, L. (2021). Evaluation of COVID-19 Mitigation Policies in Australia Using Generalised Space-Time Autoregressive Intervention Models. International Journal of Environmental Research and Public Health, 18(14), 7474. https://doi.org/10.3390/ijerph18147474








