A Simplified Population-Level Landscape Model Identifying Ecological Risk Drivers of Pesticide Applications, Part One: Case Study for Large Herbivorous Mammals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Description
2.1.1. Model Conceptualization
2.1.2. Model Parameterization
- Change in acute mortality rate
- Change in chronic mortality rate
- Change in reproduction rate
2.1.3. Computer Implementation
- replicability assessment through a number of iterations (within nest replications) selected by the user and expression of results as mean with 95th confidence intervals or maximum/minimum,
- landscape with field areas defined by the user,
- inner and outer adjustable bands for each field, and
- selection of crops, crop rotation and pesticide applications at time dates defined by the user,
- selection of the lagomorph species and location and all ecological model parameters of each nest defined by the user.
2.2. Case Study with Lagomorphs
3. Results
3.1. Model Calibration and Validation for Context of Use Qualification
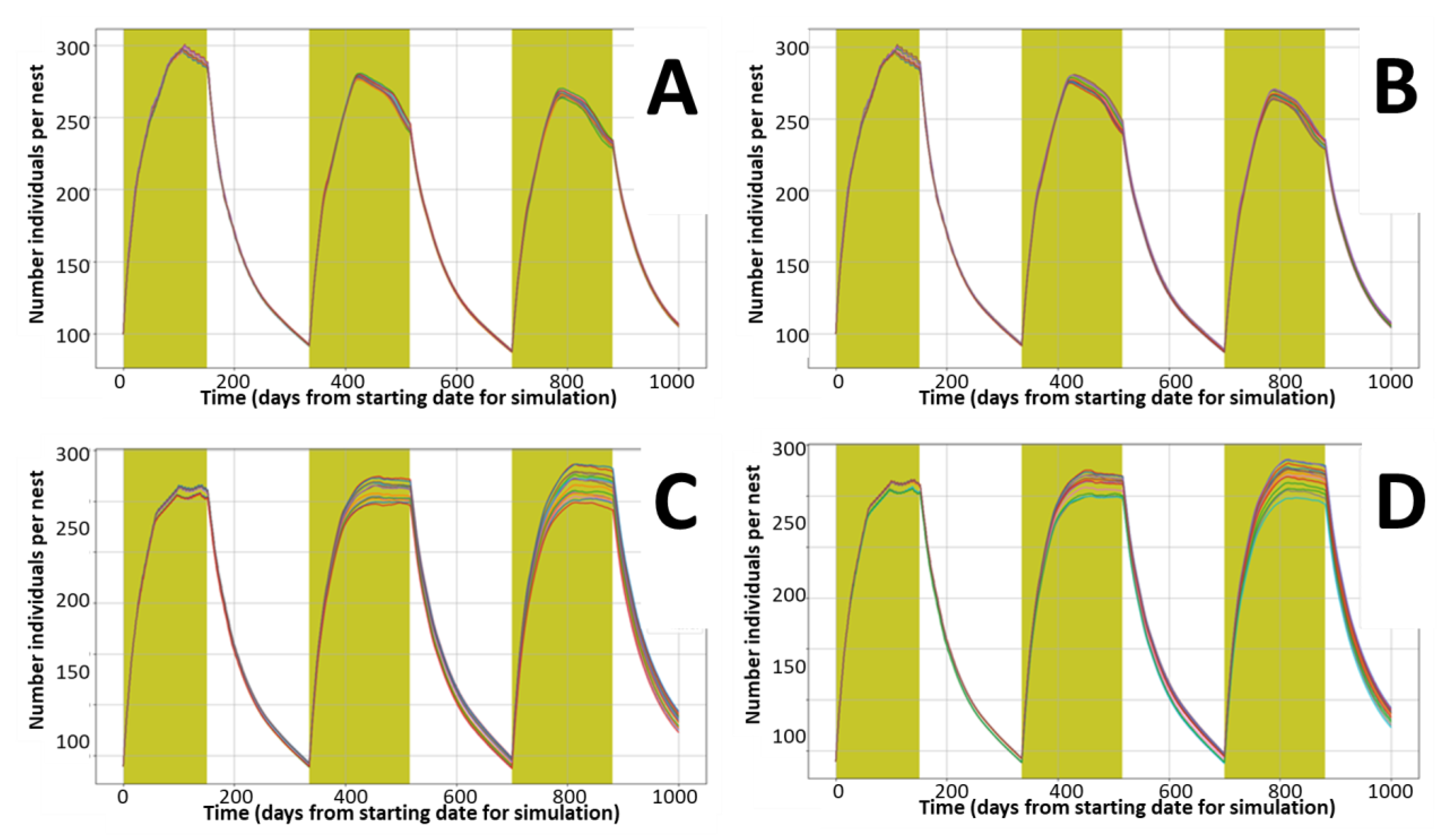
3.2. Model Replicability and Flexibility
3.3. Case Study with Lagomorphs
3.3.1. Glyphosate
3.3.2. Bromoxynil
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Problem Definition
Appendix A.2. Supporting Data
Appendix A.3. Conceptual Model

Appendix A.4. Formal Model
- Location and form (polygons) are defined by setting coordinates for the vertices.
- Associated crop, or a different land use (e.g., grassland, bare soil, forest), defined by the user, which can be changed to represent crop rotation.
- Associated inner and outer edge. The inner edge allows setting in-field risk mitigation options, such as uncropped or unsprayed buffer zones. The outer edge is used for estimating pesticide contamination due to spry drift in adjacent areas. The edges can be selected for each land sector.
- Residual concentration of pesticides at time zero, allowing the consideration of residues from previous exposures
- Pesticide applications, the number is defined by the user and each application is defined by:
- ○
- Pesticide
- ○
- Date of application
- ○
- Dose
- ○
- Interception, to estimate the dose that reaches the feeding items for the species
- ○
- Dose ratio for the inner edge, to account for unsprayed
- ○
- Dose ratio for the outer edge
- Species
- Location, defined by coordinates
- Initial population, defined by a number of individuals, average age, and age standard deviation
- Breeding months
- Four age groups, with defined age thresholds and food commodities, and the following associated variables that can be modified by the user:
- ○
- Initial male/female ratio
- ○
- Age range
- ○
- Average mobility range
- ○
- Maximum mobility range
- ○
- Background mortality rate for males
- ○
- Background mortality rate for females
- ○
- Background reproduction rate
- ○
- Attractiveness factor for the associated food commodities.
- Time variables: Use of actual or time-weighted averages for the pesticide exposure, and the averaging period when relevant.
- The exposure-response curves, for acute mortality, chronic mortality, and reproduction
- The time-scheme for updating the chronic mortality and reproduction rates
Appendix A.5. Computer Model
Appendix A.6. Regulatory Model—The Environmental Scenario
Appendix A.7. Regulatory Model—Parameter Estimation
Appendix A.8. Regulatory Model—Sensitivity and Uncertainty Analysis
Appendix A.9. Regulatory Model—Comparison with Measurements
Appendix A.10. Reality/Problem—MODEL Use
Appendix A.11. Reality/Problem—Conclusion
References
- Boivin, A.; Poulsen, V. Environmental risk assessment of pesticides: State of the art and prospective improvement from science. Environ. Sci. Pollut. Res. 2016, 24, 6889–6894. [Google Scholar] [CrossRef]
- EFSA Scientific Committee Guidance to develop specific protection goals options for environmental risk assessment at EFSA, in relation to biodiversity and ecosystem services. EFSA J. 2016, 14, 04499. [CrossRef] [Green Version]
- Risk Assessment for Birds and Mammals. EFSA J. 2009, 7, 1438. [CrossRef]
- Forbes, V.E.; Hommen, U.; Thorbek, P.; Heimbach, F.; Brink, P.V.D.; Wogram, J.; Thulke, H.-H.; Grimm, V. Ecological Models in Support of Regulatory Risk Assessments of Pesticides: Developing a Strategy for the Future. Integr. Environ. Assess. Manag. 2009, 5, 167–172. [Google Scholar] [CrossRef]
- EFSA Panel on Plant Protection Products and their Residues (PPR); Ockleford, C.; Adriaanse, P.; Berny, P.; Brock, T.; Duquesne, S.; Grilli, S.; Hernandez-Jerez, A.F.; Bennekou, S.H.; Klein, M.; et al. Scientific Opinion on the state of the art of Toxicokinetic/Toxicodynamic (TKTD) effect models for regulatory risk assessment of pesticides for aquatic organisms. EFSA J. 2018, 16, e05377. [Google Scholar] [CrossRef] [Green Version]
- Martin, T.; Thompson, H.; Thorbek, P.; Ashauer, R. Toxicokinetic–Toxicodynamic Modeling of the Effects of Pesticides on Growth of Rattus norvegicus. Chem. Res. Toxicol. 2019, 32, 2281–2294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topping, C.J.; Hansen, T.S.; Jensen, T.S.; Jepsen, J.U.; Nikolajsen, F.; Odderskær, P.; Topping, C. ALMaSS, an agent-based model for animals in temperate European landscapes. Ecol. Model. 2003, 167, 65–82. [Google Scholar] [CrossRef]
- Topping, C.J.; Sibly, R.M.; Akçakaya, H.R.; Smith, G.C.; Crocker, D.R. Risk Assessment of UK Skylark Populations Using Life-History and Individual-Based Landscape Models. Ecotoxicology 2005, 14, 925–936. [Google Scholar] [CrossRef]
- Topping, C.J.; Weyman, G.S. Rabbit Population Landscape-Scale Simulation to Investigate the Relevance of Using Rabbits in Regulatory Environmental Risk Assessment. Environ. Model. Assess. 2017, 23, 415–457. [Google Scholar] [CrossRef] [Green Version]
- Mayer, M.; Duan, X.; Sunde, P.; Topping, C.J. European hares do not avoid newly pesticide-sprayed fields: Overspray as unnoticed pathway of pesticide exposure. Sci. Total Environ. 2020, 715, 136977. [Google Scholar] [CrossRef] [PubMed]
- EFSA Panel on Plant Protection Products and their Residues (PPR). Scientific Opinion on good modelling practice in the context of mechanistic effect models for risk assessment of plant protection products. EFSA J. 2014, 12, 3589. [Google Scholar] [CrossRef]
- Raimondo, S.; Etterson, M.; Pollesch, N.; Garber, K.; Kanarek, A.; Lehmann, W.; Awkerman, J. A framework for linking population model development with ecological risk assessment objectives. Integr. Environ. Assess. Manag. 2017, 14, 369–380. [Google Scholar] [CrossRef]
- Devos, Y.; Craig, W.; Devlin, R.H.; Ippolito, A.; Leggatt, R.A.; Romeis, J.; Shaw, R.; Svendsen, C.; Topping, C.J. Using problem formulation for fit-for-purpose pre-market environmental risk assessments of regulated stressors. EFSA J. 2019, 17, 170708. [Google Scholar] [CrossRef]
- Streissl, F.; Egsmose, M.; Tarazona, J.V. Linking pesticide marketing authorisations with environmental impact assessments through realistic landscape risk assessment paradigms. Ecotoxicology 2018, 27, 980–991. [Google Scholar] [CrossRef] [PubMed]
- Brink, P.J.V.D.; Boxall, A.B.; Maltby, L.; Brooks, B.W.; Rudd, M.; Backhaus, T.; Spurgeon, D.; Verougstraete, V.; Ajao, C.; Ankley, G.T.; et al. Toward sustainable environmental quality: Priority research questions for Europe. Environ. Toxicol. Chem. 2018, 37, 2281–2295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raimondo, S.; Schmolke, A.; Pollesch, N.; Accolla, C.; Galic, N.; Moore, A.; Vaugeois, M.; Rueda-Cediel, P.; Kanarek, A.; Awkerman, J.; et al. Pop-guide: Population modeling guidance, use, interpretation, and development for ecological risk assessment. Integr. Environ. Assess. Manag. 2021, 17, 767–784. [Google Scholar] [CrossRef] [PubMed]
- Jones, H.F.; Özkundakci, D.; Hunt, S.; Giles, H.; Jenkins, B. Bridging the gap: A strategic framework for implementing best practice guidelines in environmental modelling. Environ. Sci. Policy 2020, 114, 533–541. [Google Scholar] [CrossRef]
- Schuwirth, N.; Borgwardt, F.; Domisch, S.; Friedrichs, M.; Kattwinkel, M.; Kneis, D.; Kuemmerlen, M.; Langhans, S.D.; Martínez-López, J.; Vermeiren, P. How to make ecological models useful for environmental management. Ecol. Model. 2019, 411, 108784. [Google Scholar] [CrossRef]
- Risk Assessment for Birds and Mammals—Revision of Guidance Document under Council Directive 91/414/EEC (SANCO/4145/2000—final of 25 September 2002)—Scientific Opinion of the Panel on Plant protection products and their Residues (PPR) on the Science behind the Guidance Document on Risk Assessment for birds and mammals. EFSA J. 2008, 6, 734. [CrossRef] [Green Version]
- EFSA Scientific Committee; Hardy, A.; Benford, D.; Halldorsson, T.; Jeger, M.J.; Knutsen, K.H.; More, S.; Mortensen, A.; Naegeli, H.; Noteborn, H.; et al. Update: Use of the benchmark dose approach in risk assessment. EFSA J. 2017, 15, e04658. [Google Scholar] [CrossRef]
- Tablado, Z.; Revilla, E. Contrasting Effects of Climate Change on Rabbit Populations through Reproduction. PLoS ONE 2012, 7, e48988. [Google Scholar] [CrossRef] [Green Version]
- Tablado, Z.; Revilla, E.; Palomares, F. Breeding like rabbits: Global patterns of variability and determinants of European wild rabbit reproduction. Ecography 2009, 32, 310–320. [Google Scholar] [CrossRef]
- Tablado, Z.; Revilla, E.; Palomares, F. Dying like rabbits: General determinants of spatiotemporal variability in survival. J. Anim. Ecol. 2011, 81, 150–161. [Google Scholar] [CrossRef] [PubMed]
- Marboutin, E.; Bray, Y.; Peroux, R.; Mauvy, B.; Lartiges, A. Population dynamics in European hare: Breeding parameters and sustainable harvest rates. J. Appl. Ecol. 2003, 40, 580–591. [Google Scholar] [CrossRef]
- Schai-Braun, S.C.; Kowalczyk, C.; Klansek, E.; Hackländer, K. Estimating Sustainable Harvest Rates for European Hare (Lepus Europaeus) Populations. Sustainability 2019, 11, 2837. [Google Scholar] [CrossRef] [Green Version]
- Voigt, U.; Siebert, U. Survival rates on pre-weaning European hares (Lepus europaeus) in an intensively used agricultural area. Eur. J. Wildl. Res. 2020, 66, 1–12. [Google Scholar] [CrossRef]
- Antoniou, A.; Kotoulas, G.; Magoulas, A.; Alves, P.C. Evidence of autumn reproduction in female European hares (Lepus europaeus) from southern Europe. Eur. J. Wildl. Res. 2008, 54, 581–587. [Google Scholar] [CrossRef]
- EFSA. Conclusion on the peer review of the pesticide risk assessment of the active substance glyphosate. EFSA J. 2015, 13, 107. [Google Scholar] [CrossRef]
- Arena, M.; Auteri, D.; Barmaz, S.; Bellisai, G.; Brancato, A.; Brocca, D.; Bura, L.; Byers, H.; Chiusolo, A.; Marques, D.C.; et al. Peer review of the pesticide risk assessment of the active substance bromoxynil (variant evaluated bromoxynil octanoate). EFSA J. 2017, 15. [Google Scholar] [CrossRef] [Green Version]
- Topping, C.J.; Aldrich, A.; Berny, P. Overhaul environmental risk assessment for pesticides. Science 2020, 367, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Mayfield, D.B.; Skall, D.G. Benchmark dose analysis framework for developing wildlife toxicity reference values. Environ. Toxicol. Chem. 2018, 37, 1496–1508. [Google Scholar] [CrossRef]
- Guidance on Expert Knowledge Elicitation in Food and Feed Safety Risk Assessment. EFSA J. 2014, 12, 3734. [CrossRef]
- EFSA Panel on Plant Protection Products and their Residues (PPR). Scientific Opinion on the development of specific protection goal options for environmental risk assessment of pesticides, in particular in relation to the revision of the Guidance Documents on Aquatic and Terrestrial Ecotoxicology (SANCO/3268/2001 and SA. EFSA J. 2010, 8, 1821. [Google Scholar] [CrossRef] [Green Version]
- Brock, T.; Bigler, F.; Frampton, G.; Hogstrand, C.; Luttik, R.; Martin-Laurent, F.; Topping, C.J.; Van Der Werf, W.; Rortais, A. Ecological Recovery and Resilience in Environmental Risk Assessments at the European Food Safety Authority. Integr. Environ. Assess. Manag. 2018, 14, 586–591. [Google Scholar] [CrossRef] [PubMed]
- EFSA. Scientific Committee Recovery in environmental risk assessments at EFSA. EFSA J. 2016, 14, 4313. [Google Scholar] [CrossRef]
- EFSA Panel on Plant Protection Products and their Residues (PPR). Guidance on tiered risk assessment for plant protection products for aquatic organisms in edge-of-field surface waters. EFSA J. 2013, 11, 3290. [Google Scholar] [CrossRef]
- Tanner, J.T. Effects of Population Density on Growth Rates of Animal Populations. Ecology 1966, 47, 733–745. [Google Scholar] [CrossRef] [Green Version]
- Panizzi, S.; Suciu, N.A.; Trevisan, M. Combined ecotoxicological risk assessment in the frame of European authorization of pesticides. Sci. Total Environ. 2017, 580, 136–146. [Google Scholar] [CrossRef]
- Bopp, S.K.; Barouki, R.; Brack, W.; Costa, S.D.; Dorne, J.-L.C.; Drakvik, P.E.; Faust, M.; Karjalainen, T.K.; Kephalopoulos, S.; van Klaveren, J.; et al. Current EU research activities on combined exposure to multiple chemicals. Environ. Int. 2018, 120, 544–562. [Google Scholar] [CrossRef] [PubMed]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.H.; Weiner, J.; Wiegand, T.; DeAngelis, D.L. Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 2005, 210, 987–991. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thursby, G.; Sappington, K.; Etterson, M.; Etterson, M. Coupling toxicokinetic-toxicodynamic and population models for assessing aquatic ecological risks to time-varying pesticide exposures. Environ. Toxicol. Chem. 2018, 37, 2633–2644. [Google Scholar] [CrossRef] [PubMed]
- Levine, S.L.; Giddings, J.; Valenti, T.; Cobb, G.P.; Carley, D.S.; McConnell, L.L. Overcoming Challenges of Incorporating Higher Tier Data in Ecological Risk Assessments and Risk Management of Pesticides in the United States: Findings and Recommendations from the 2017 Workshop on Regulation and Innovation in Agriculture. Integr. Environ. Assess. Manag. 2019, 15, 714–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimm, V.; Johnston, A.S.A.; Thulke, H.-H.; Forbes, V.E.; Thorbek, P. Three questions to ask before using model outputs for decision support. Nat. Commun. 2020, 11, 1–3. [Google Scholar] [CrossRef] [PubMed]







| Parameter | Rabbit | Brown Hare |
|---|---|---|
| Number of age groups number | 4 (0,1,2,3) | 4 (0,1,2,3) |
| Background monthly mortality rate (groups 0/1/2/3) | 0.77/0.38/0.11/0.11 | 0.87/0.30/0.08/0.08 |
| Background monthly reproduction rate (groups 0/1/2/3) | 0/0/0/4 | 0/0/0.6/1.75 |
| Reproductive season | December to May | January to August |
| Initial number of individuals per nest | 140 | 100 |
| Initial male/female rate | 1:1 | 1:1 |
| Parameters for exposure estimation | As by EFSA guidance (EFSA, 2009) | |
| TWAexposure-effect relationships | Equations developed for this study following the review of available information in the EFSA Conclusions | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarazona, D.; Tarazona, G.; Tarazona, J.V. A Simplified Population-Level Landscape Model Identifying Ecological Risk Drivers of Pesticide Applications, Part One: Case Study for Large Herbivorous Mammals. Int. J. Environ. Res. Public Health 2021, 18, 7720. https://doi.org/10.3390/ijerph18157720
Tarazona D, Tarazona G, Tarazona JV. A Simplified Population-Level Landscape Model Identifying Ecological Risk Drivers of Pesticide Applications, Part One: Case Study for Large Herbivorous Mammals. International Journal of Environmental Research and Public Health. 2021; 18(15):7720. https://doi.org/10.3390/ijerph18157720
Chicago/Turabian StyleTarazona, David, Guillermo Tarazona, and Jose V. Tarazona. 2021. "A Simplified Population-Level Landscape Model Identifying Ecological Risk Drivers of Pesticide Applications, Part One: Case Study for Large Herbivorous Mammals" International Journal of Environmental Research and Public Health 18, no. 15: 7720. https://doi.org/10.3390/ijerph18157720
APA StyleTarazona, D., Tarazona, G., & Tarazona, J. V. (2021). A Simplified Population-Level Landscape Model Identifying Ecological Risk Drivers of Pesticide Applications, Part One: Case Study for Large Herbivorous Mammals. International Journal of Environmental Research and Public Health, 18(15), 7720. https://doi.org/10.3390/ijerph18157720







