Modeling SF-6D Health Utilities: Is Bayesian Approach Appropriate?
Abstract
:1. Introduction
2. Materials and Methods
2.1. The SF-6D
2.2. The Valuation Survey and Data Set
2.2.1. UK
2.2.2. Lebanon
2.3. Modelling
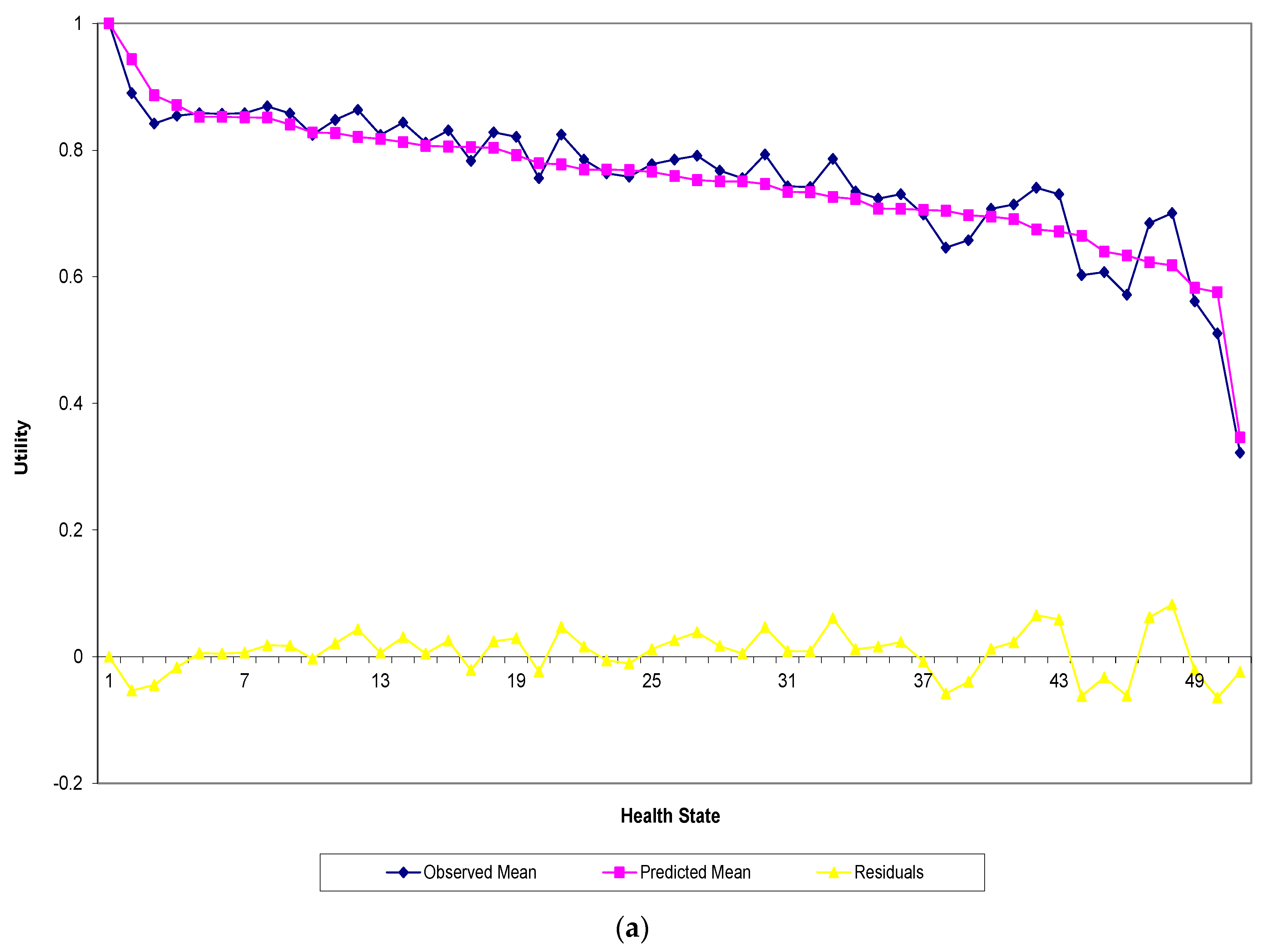
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brooks, R. EuroQol: The current state of play. Health Policy 1996, 37, 53–72. [Google Scholar] [CrossRef]
- Torrance, G.W.; Feeny, D.H.; Furlong, W.J.; Barr, R.D.; Zhang, Y.; Wang, Q.A. Multi-attribute utility function for a comprehensive health status classification system: Health Utilities Index Mark 2. Med. Care 1996, 34, 702–722. [Google Scholar] [CrossRef]
- Feeny, D.H.; Furlong, W.J.; Torrance, G.W.; Goldsmith, C.H.; Zenglong, Z.; Depauw, S.; Denton, M.; Boyle, M. Multi-attribute and sin-gle-attribute utility function for the Health Utility Index Mark 3 system. Med. Care 2002, 40, 113–128. [Google Scholar] [CrossRef] [PubMed]
- Hawthorne, G.; Richardson, J.; Day, N.A. A comparison of the Assessment of Quality of Life (AQoL) with four other generic utility instruments. Ann. Med. 2001, 33, 358–370. [Google Scholar] [CrossRef]
- Kaplan, R.M.; Anderson, J.P. A general health policy model: Update and applications. Health Serv. Res. 1988, 23, 203–235. [Google Scholar]
- Brazier, J.; Roberts, J.; Deverill, M. The estimation of a preference-based measure of health from the SF-36. J. Health Econ. 2002, 21, 271–292. [Google Scholar] [CrossRef] [Green Version]
- Revicki, D.A.; Leidy, N.K.; Brennan-Diemer, F.; Sorenson, S.; Togias, A. Integrating patients’ preferences into health outcomes assessment: The multiattribute asthma symptom utility index. Chest 1998, 114, 998–1007. [Google Scholar] [CrossRef] [PubMed]
- Brazier, J.; Murray, C.C.; Roberts, J.; Brown, M.; Symonds, T.; Kelleher, C. Estimation of a Preference-Based Index from a Condition-Specific Measure: The King’s Health Questionnaire. Med. Decis. Mak. 2007, 28, 113–126. [Google Scholar] [CrossRef] [PubMed]
- Drummond, M.F.; Sculpher, M.; O’Brien, B.; Stoddart, G.L.; Torrance, G.W. Methods for the Economic Evaluation of Health Care Programmes; Oxford Medical Publications: Oxford, UK, 2005. [Google Scholar]
- Lam, C.L.; Brazier, J.; McGhee, S.M. Valuation of the SF-6D health states is feasible, acceptable, reliable, and valid in a Chi-nese population. Value Health 2008, 11, 295–303. [Google Scholar] [CrossRef] [Green Version]
- Brazier, J.E.; Fukuhara, S.; Roberts, J.; Kharroubi, S.; Yamamoto, Y.; Ikeda, S.; Doherty, J.; Kurokawa, K. Estimating a preference-based index from the Japanese SF-36. J. Clin. Epidemiol. 2009, 62, 1323–1331. [Google Scholar] [CrossRef] [Green Version]
- McGhee, S.M.; Brazier, J.; Lam, C.L.K.; Wong, L.C.; Chau, J.; Cheung, A.; Ho, A. Quality-adjusted life years: Population-specific measurement of the quality component. Hong Kong Med. J. 2011, 17, 17–21. [Google Scholar]
- Cruz, L.C.; Camey, S.A.; Hoffman, J.F.; Rowen, D.; Brazier, J.E.; Fleck, M.P.; Polanczyk, C.A. Estimating the SF-6D value set for a Southern Brazilian population. Value Health 2011, 14, S108–S114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferreira, L.N.; Ferreira, P.; Pereira, L.; Brazier, J.; Rowen, D. A Portuguese Value Set for the SF-6D. Value Health 2010, 13, 624–630. [Google Scholar] [CrossRef] [Green Version]
- Norman, R.; Viney, R.; Brazier, J.; Burgess, L.; Cronin, P.; King, M.; Ratcliffe, J.; Street, D. Valuing SF-6D Health States Using a Discrete Choice Experiment. Med. Decis. Mak. 2013, 34, 773–786. [Google Scholar] [CrossRef] [PubMed]
- Ware, J.E.; Snow, K.K.; Kolinski, M.; Gandeck, B. SF-36 Health Survey Manual and Interpretation Guide; The Health Institute, New England Medical Centre: Boston, MA, USA, 1993. [Google Scholar]
- Kharroubi, S.A.; Beyh, Y.; El Harake, M.D.; Dawoud, D.; Rowen, D.; Brazier, J. Examining the Feasibility and Acceptability of Valuing the Arabic Version of SF-6D in a Lebanese Population. Int. J. Environ. Res. Public Health 2020, 17, 1037. [Google Scholar] [CrossRef] [Green Version]
- Kharroubi, S.A.; O’Hagan, A.; Brazier, J.E. Estimating utilities from individual health preference data: A nonparametric Bayesian method. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 879–895. [Google Scholar] [CrossRef]
- Kharroubi, S.A.; Rowen, D. Valuation of preference-based measures: Can existing preference data be used to select a smaller sample of health states? Eur. J. Health Econ. 2019, 20, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Kharroubi, S.A. Valuations of EQ-5D health states: Could United Kingdom results be used as informative priors for the United States. J. Appl. Stat. 2017, 45, 1579–1594. [Google Scholar] [CrossRef]
- Kharroubi, S.A. Bayesian nonparametric estimation of EQ-5D utilities for United States using the existing United Kingdom data. Health Qual. Life Outcomes 2017, 15, 195. [Google Scholar] [CrossRef] [Green Version]
- Kharroubi, S.A. Valuation of preference-based measures: Can existing preference data be used to generate better estimates? Health Qual. Life Outcomes 2018, 45, 1579–1594. [Google Scholar] [CrossRef]
- Kharroubi, S.A.; Beyh, Y. Bayesian modeling of health state preferences: Could borrowing strength from existing countries’ valuations produce better estimates. Eur. J. Health Econ. 2021, 22, 773–788. [Google Scholar] [CrossRef] [PubMed]
- Patrick, D.L.; Starks, H.E.; Cain, K.C.; Uhlmann, R.F.; Pearlman, R.A. Measuring Preferences for Health States Worse than Death. Med. Decis. Mak. 1994, 14, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A. Prior Distributions for Variance Parameters in Hierarchical Models. Bayesian Anal. 2006, 1, 515–533. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Chan, K.K.W.; Xie, F.; Willan, A.R.; Pullenayegum, E.M. Conducting EQ-5D Valuation Studies in Resource-Constrained Countries: The Potential Use of Shrinkage Estimators to Reduce Sample Size. Med. Decis. Mak. 2018, 38, 26–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Health State | Observed Mean | UK | Crude Model | Model (1) | |||
|---|---|---|---|---|---|---|---|
| Posterior Mean | Posterior SD | Posterior Mean | Posterior SD | Posterior Mean | Posterior SD | ||
| 111,111 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 111,621 | 0.8244 | 0.7482 | 0.0345 | 0.8276 | 0.0264 | 0.8218 | 0.0269 |
| 113,411 | 0.8544 | 0.7284 | 0.031 | 0.8713 | 0.0207 | 0.8637 | 0.022 |
| 115,653 | 0.7306 | 0.5652 | 0.0561 | 0.7073 | 0.0272 | 0.7116 | 0.0277 |
| 121,212 | 0.8422 | 0.8275 | 0.0261 | 0.8867 | 0.0194 | 0.8741 | 0.0209 |
| 122,233 | 0.8694 | 0.7475 | 0.034 | 0.8512 | 0.0235 | 0.8562 | 0.0259 |
| 122,425 | 0.7582 | 0.6784 | 0.0353 | 0.7686 | 0.0234 | 0.7652 | 0.0241 |
| 124,125 | 0.8478 | 0.7292 | 0.0475 | 0.8269 | 0.0245 | 0.835 | 0.0258 |
| 131,542 | 0.8283 | 0.6181 | 0.0304 | 0.8038 | 0.0236 | 0.7953 | 0.0257 |
| 132,524 | 0.7633 | 0.6574 | 0.037 | 0.7692 | 0.022 | 0.775 | 0.0232 |
| 133,132 | 0.8583 | 0.6942 | 0.0343 | 0.8517 | 0.0227 | 0.8467 | 0.0244 |
| 135,312 | 0.7556 | 0.6992 | 0.0488 | 0.7795 | 0.0221 | 0.7757 | 0.0229 |
| 142,154 | 0.7912 | 0.6844 | 0.0373 | 0.7527 | 0.0287 | 0.7569 | 0.0294 |
| 144,341 | 0.7418 | 0.72 | 0.0279 | 0.7335 | 0.0249 | 0.7425 | 0.0255 |
| 211,111 | 0.89 | 0.9197 | 0.0215 | 0.9434 | 0.0169 | 0.9176 | 0.0248 |
| 212,145 | 0.785 | 0.6927 | 0.0446 | 0.7693 | 0.0266 | 0.7591 | 0.0278 |
| 213,323 | 0.7833 | 0.7761 | 0.0296 | 0.8048 | 0.0208 | 0.8093 | 0.0215 |
| 221,452 | 0.8239 | 0.6237 | 0.0459 | 0.8178 | 0.0234 | 0.8148 | 0.0254 |
| 224,612 | 0.6461 | 0.6256 | 0.0392 | 0.7043 | 0.0238 | 0.6897 | 0.0244 |
| 232,111 | 0.8576 | 0.6987 | 0.0377 | 0.8525 | 0.0251 | 0.8336 | 0.0273 |
| 235,224 | 0.7676 | 0.6486 | 0.0335 | 0.7505 | 0.0241 | 0.7541 | 0.025 |
| 241,531 | 0.785 | 0.702 | 0.0352 | 0.7592 | 0.0251 | 0.7646 | 0.0266 |
| 312,332 | 0.8639 | 0.7472 | 0.0285 | 0.8207 | 0.0227 | 0.8348 | 0.0252 |
| 315,515 | 0.6983 | 0.6642 | 0.0363 | 0.7058 | 0.0247 | 0.7152 | 0.0247 |
| 321,122 | 0.8583 | 0.7638 | 0.0266 | 0.8527 | 0.0218 | 0.8542 | 0.0234 |
| 323,644 | 0.5717 | 0.5362 | 0.0287 | 0.6335 | 0.0256 | 0.6201 | 0.0257 |
| 332,411 | 0.8435 | 0.7217 | 0.0376 | 0.8125 | 0.0247 | 0.8289 | 0.0265 |
| 334,251 | 0.7347 | 0.6761 | 0.0532 | 0.7229 | 0.0251 | 0.7344 | 0.0258 |
| 341,123 | 0.8311 | 0.7009 | 0.0393 | 0.8055 | 0.0248 | 0.8085 | 0.0259 |
| 412,152 | 0.7933 | 0.6558 | 0.0371 | 0.7466 | 0.0251 | 0.7454 | 0.0277 |
| 414,522 | 0.7556 | 0.6612 | 0.0301 | 0.7505 | 0.023 | 0.7597 | 0.0235 |
| 421,314 | 0.8117 | 0.6689 | 0.0368 | 0.8067 | 0.0236 | 0.8066 | 0.025 |
| 425,131 | 0.6578 | 0.6771 | 0.0551 | 0.6973 | 0.0236 | 0.6935 | 0.0247 |
| 431,443 | 0.8247 | 0.638 | 0.0339 | 0.7775 | 0.027 | 0.7935 | 0.0274 |
| 432,621 | 0.7429 | 0.6468 | 0.0487 | 0.734 | 0.0237 | 0.7428 | 0.0254 |
| 443,215 | 0.7306 | 0.6548 | 0.0352 | 0.6718 | 0.0274 | 0.6746 | 0.0283 |
| 511,114 | 0.8578 | 0.6993 | 0.0379 | 0.8406 | 0.0247 | 0.8387 | 0.0267 |
| 512,242 | 0.6028 | 0.6906 | 0.0324 | 0.6647 | 0.0244 | 0.6573 | 0.0244 |
| 522,321 | 0.7778 | 0.6846 | 0.0324 | 0.7658 | 0.023 | 0.7654 | 0.0253 |
| 523,551 | 0.6072 | 0.6201 | 0.0471 | 0.6399 | 0.0257 | 0.6404 | 0.0261 |
| 531,635 | 0.7865 | 0.5323 | 0.0345 | 0.7258 | 0.0302 | 0.7438 | 0.0302 |
| 534,113 | 0.7235 | 0.7106 | 0.0437 | 0.7078 | 0.0249 | 0.7173 | 0.026 |
| 545,422 | 0.7006 | 0.6351 | 0.0322 | 0.6181 | 0.029 | 0.6365 | 0.0292 |
| 611,221 | 0.8211 | 0.6667 | 0.0521 | 0.7922 | 0.0253 | 0.7918 | 0.0275 |
| 614,434 | 0.5611 | 0.6497 | 0.0383 | 0.5826 | 0.0273 | 0.5922 | 0.0273 |
| 622,513 | 0.7072 | 0.5809 | 0.0392 | 0.6949 | 0.0259 | 0.6894 | 0.0275 |
| 625,141 | 0.5106 | 0.5561 | 0.0466 | 0.5755 | 0.0273 | 0.5582 | 0.028 |
| 631,355 | 0.7406 | 0.5823 | 0.0354 | 0.6749 | 0.0311 | 0.6948 | 0.0306 |
| 633,122 | 0.7141 | 0.6515 | 0.0338 | 0.6912 | 0.0249 | 0.6943 | 0.0261 |
| 642,612 | 0.685 | 0.5594 | 0.0336 | 0.6228 | 0.029 | 0.6633 | 0.0299 |
| 645,655 | 0.3222 | 0.3575 | 0.0186 | 0.3463 | 0.0252 | 0.3292 | 0.0237 |
| RMSE | 0.035 | 0.028 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kharroubi, S.A. Modeling SF-6D Health Utilities: Is Bayesian Approach Appropriate? Int. J. Environ. Res. Public Health 2021, 18, 8409. https://doi.org/10.3390/ijerph18168409
Kharroubi SA. Modeling SF-6D Health Utilities: Is Bayesian Approach Appropriate? International Journal of Environmental Research and Public Health. 2021; 18(16):8409. https://doi.org/10.3390/ijerph18168409
Chicago/Turabian StyleKharroubi, Samer A. 2021. "Modeling SF-6D Health Utilities: Is Bayesian Approach Appropriate?" International Journal of Environmental Research and Public Health 18, no. 16: 8409. https://doi.org/10.3390/ijerph18168409






