Integrated Assessment of Affinity to Chemical Fractions and Environmental Pollution with Heavy Metals: A New Approach Based on Sequential Extraction Results
Abstract
:1. Introduction
2. Assessment of Solid Components of the Environment Pollution with HMs’ Chemical Fractions
3. New Approach for a Comprehensive Assessment of HMs Fractionation and Solid Environmental Media Pollution
3.1. Modification of A index
- CAF < 0.4 corresponds to an extremely low chemical affinity of HM to this geochemical phase and contamination of studied solid environmental media with this HM fraction;
- 0.4 < CAF ≤ 0.8 amounts to a low chemical affinity and contamination;
- 0.8 < CAF ≤ 1.2 equals to a probable chemical affinity and contamination;
- 1.2 < CAF ≤ 2.4 points out the clear chemical affinity and contamination;
- CAF > 2.4 corresponds to an extremely strong chemical affinity of HM to this geochemical phase and contamination of studied solid environmental media with this HM fraction.
3.2. Assessment of Soil Contamination with Chemical Fractions of HMs
3.3. Assessment of Bottom Sediments Contamination with Chemical Fractions of HMs
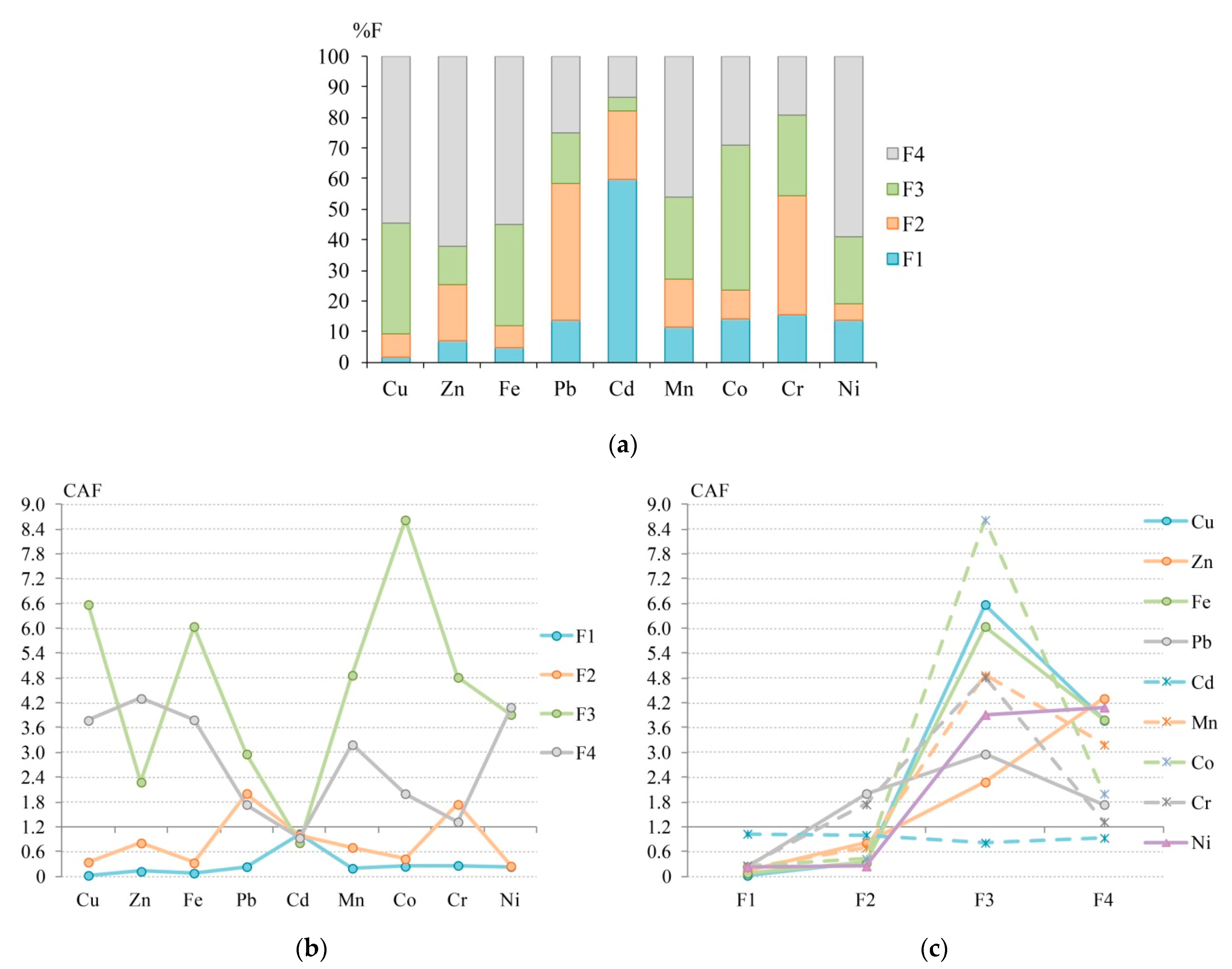
3.4. Assessment of Atmospheric Particulate Matter Contamination with Chemical Fractions of HMs
3.5. Pollution Assessment of Particle Size Fractions of Road Dust with Chemical Fractions of HMs (GF-Analysis)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhou, K.; Qin, W.; Tian, C.; Qi, M.; Yan, X.; Han, W. A Review on Heavy Metals Contamination in Soil: Effects, Sources, and Remediation Techniques. Soil Sediment Contam. Int. J. 2019, 28, 380–394. [Google Scholar] [CrossRef]
- Hodson, M.E. Heavy Metals—Geochemical Bogey Men? Environ. Pollut. 2004, 129, 341–343. [Google Scholar] [CrossRef]
- Minkina, T.M.; Motuzova, G.V.; Mandzhieva, S.S.; Nazarenko, O.G.; Burachevskaya, M.V.; Antonenko, E.M. Fractional and Group Composition of the Mn, Cr, Ni, and Cd Compounds in the Soils of Technogenic Landscapes in the Impact Zone of the Novocherkassk Power Station. Eurasian Soil Sci. 2013, 46, 375–385. [Google Scholar] [CrossRef]
- Semenkov, I.N.; Kasimov, N.S.; Terskaya, E.V. Lateral distribution of metal forms in tundra, taiga and forest steppe catenae of the East European plain. Vestn. Mosk. Univ. Seriya Geogr. 2016, 3, 29–39. [Google Scholar]
- Gabarrón, M.; Zornoza, R.; Martínez-Martínez, S.; Munoz, V.A.; Faz, A.; Acosta, J.A. Effect of Land Use and Soil Properties in the Feasibility of Two Sequential Extraction Procedures for Metals Fractionation. Chemosphere 2019, 218, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Cuvier, A.; Leleyter, L.; Probst, A.; Probst, J.-L.; Prunier, J.; Pourcelot, L.; Le Roux, G.; Lemoine, M.; Reinert, M.; Baraud, F. Why Comparison between Different Chemical Extraction Procedures Is Necessary to Better Assess the Metals Availability in Sediments. J. Geochem. Explor. 2021, 225, 106762. [Google Scholar] [CrossRef]
- Gatehouse, S.; Russell, D.W.; Van Moort, J.C. Sequential Soil Analysis in Exploration Geochemistry. J. Geochem. Explor. 1977, 8, 483–494. [Google Scholar] [CrossRef]
- Sungur, A.; Soylak, M.; Yilmaz, E.; Yilmaz, S.; Ozcan, H. Characterization of Heavy Metal Fractions in Agricultural Soils by Sequential Extraction Procedure: The Relationship Between Soil Properties and Heavy Metal Fractions. Soil Sediment Contam. Int. J. 2015, 24, 1–15. [Google Scholar] [CrossRef]
- Padoan, E.; Kath, A.H.; Vahl, L.C.; Ajmone-Marsan, F. Potential Release of Zinc and Cadmium From Mine-Affected Soils Under Flooding, a Mesocosm Study. Arch. Environm. Contam. Toxicol. 2020, 79, 421–434. [Google Scholar] [CrossRef]
- Tong, L.; He, J.; Wang, F.; Wang, Y.; Wang, L.; Tsang, D.C.W.; Hu, Q.; Hu, B.; Tang, Y. Evaluation of the BCR Sequential Extraction Scheme for Trace Metal Fractionation of Alkaline Municipal Solid Waste Incineration Fly Ash. Chemosphere 2020, 249, 126115. [Google Scholar] [CrossRef]
- Leermakers, M.; Mbachou, B.E.; Husson, A.; Lagneau, V.; Descostes, M. An Alternative Sequential Extraction Scheme for the Determination of Trace Elements in Ferrihydrite Rich Sediments. Talanta 2019, 199, 80–88. [Google Scholar] [CrossRef]
- Caraballo, M.A.; Serna, A.; Macías, F.; Pérez-López, R.; Ruiz-Cánovas, C.; Richter, P.; Becerra-Herrera, M. Uncertainty in the Measurement of Toxic Metals Mobility in Mining/Mineral Wastes by Standardized BCR®SEP. J. Hazard. Mater. 2018, 360, 587–593. [Google Scholar] [CrossRef]
- Fedotov, P.S. Rotating Coiled Columns in the Speciation Analysis of Natural Samples: Dynamic Fractionation of Element Forms in Soils, Sludges, and Bottom Sediments. J. Anal. Chem. 2012, 67, 399–413. [Google Scholar] [CrossRef]
- Zimmerman, A.J.; Weindorf, D.C. Heavy Metal and Trace Metal Analysis in Soil by Sequential Extraction: A Review of Procedures. Int. J. Anal. Chem. 2010, 2010, 387803. [Google Scholar] [CrossRef] [Green Version]
- Hass, A.; Fine, P. Sequential Selective Extraction Procedures for the Study of Heavy Metals in Soils, Sediments, and Waste Materials—a Critical Review. Crit. Rev. Environ. Sci. Technol. 2010, 40, 365–399. [Google Scholar] [CrossRef]
- Heltai, G.; Győri, Z.; Fekete, I.; Halász, G.; Kovács, K.; Takács, A.; Boros, N.; Horváth, M. Longterm Study of Transformation of Potentially Toxic Element Pollution in Soil/Water/Sediment System by Means of Fractionation with Sequential Extraction Procedures. Microchem. J. 2018, 136, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Abollino, O.; Malandrino, M.; Giacomino, A.; Mentasti, E. The Role of Chemometrics in Single and Sequential Extraction Assays: A Review. Anal. Chim. Acta 2011, 688, 104–121. [Google Scholar] [CrossRef]
- Davidson, C.M.; Duncan, A.L.; Littlejohn, D.; Ure, A.M.; Garden, L.M. A Critical Evaluation of the Three-Stage BCR Sequential Extraction Procedure to Assess the Potential Mobility and Toxicity of Heavy Metals in Industrially-Contaminated Land. Anal. Chim. Acta 1998, 363, 45–55. [Google Scholar] [CrossRef]
- Gleyzes, C.; Tellier, S.; Astruc, M. Fractionation Studies of Trace Elements in Contaminated Soils and Sediments: A Review of Sequential Extraction Procedures. Trends Anal. Chem. 2002, 21, 451–467. [Google Scholar] [CrossRef]
- Bacon, J.R.; Davidson, C.M. Is There a Future for Sequential Chemical Extraction? Analyst 2008, 133, 25–46. [Google Scholar] [CrossRef] [PubMed]
- Tessier, A.; Campbell, P.G.C.; Bisson, M. Sequential Extraction Procedure for the Speciation of Particulate Trace Metals. Anal. Chem. 1979, 51, 844–851. [Google Scholar] [CrossRef]
- Ure, A.M.; Quevauviller, Ph.; Muntau, H.; Griepink, B. Speciation of Heavy Metals in Soils and Sediments. An Account of the Improvement and Harmonization of Extraction Techniques Undertaken Under the Auspices of the BCR of the Commission of the European Communities. Int. J. Environ. Anal. Chem. 1993, 51, 135–151. [Google Scholar] [CrossRef]
- Rauret, G.; López-Sánchez, J.F.; Sahuquillo, A.; Rubio, R.; Davidson, C.; Ure, A.; Quevauviller, P. Improvement of the BCR Three Step Sequential Extraction Procedure Prior to the Certification of New Sediment and Soil Reference Materials. J. Environ. Monitor. 1999, 1, 57–61. [Google Scholar] [CrossRef]
- Kumkrong, P.; Mihai, O.; Mercier, P.H.J.; Pihilligawa, I.G.; Tyo, D.D.; Mester, Z. Tessier Sequential Extraction on 17 Elements from Three Marine Sediment Certified Reference Materials (HISS-1, MESS-4, and PACS-3). Anal. Bioanal. Chem. 2021, 413, 1047–1057. [Google Scholar] [CrossRef]
- Khan, W.R.; Zulkifli, S.Z.; bin Mohamad Kasim, M.R.; Zimmer, M.; Pazi, A.M.; Kamrudin, N.A.; Rasheed, F.; Zafar, Z.; Mostapa, R.; Nazre, M. Risk Assessment of Heavy Metal Concentrations in Sediments of Matang Mangrove Forest Reserve. Trop. Conserv. Sci. 2020, 13, 1–12. [Google Scholar] [CrossRef]
- Sofianska, E.; Michailidis, K. Chemical Assessment and Fractionation of Some Heavy Metals and Arsenic in Agricultural Soils of the Mining Affected Drama Plain, Macedonia, Northern Greece. Environ. Monit. Assess. 2015, 187, 101. [Google Scholar] [CrossRef]
- Woszczyk, M.; Spychalski, W.; Boluspaeva, L. Trace Metal (Cd, Cu, Pb, Zn) Fractionation in Urban-Industrial Soils of Ust-Kamenogorsk (Oskemen), Kazakhstan—Implications for the Assessment of Environmental Quality. Environ. Monit. Assess. 2018, 190, 362. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Geng, Y.; Sun, R.; Xie, M.; Feng, X.; Li, X.; Cui, Z. Distribution, Speciation and Ecological Risk Assessment of Heavy Metals in Jinan Iron & Steel Group Soils from China. J. Clean. Prod. 2021, 295, 126504. [Google Scholar] [CrossRef]
- Son, H.W.; Shim, S.H.; Oh, H.; Choi, J.H. An Assessment of Heavy Metal Contamination in the Nakdong River around the Weir. Water 2021, 13, 684. [Google Scholar] [CrossRef]
- Christophoridis, C.; Evgenakis, E.; Bourliva, A.; Papadopoulou, L.; Fytianos, K. Concentration, Fractionation, and Ecological Risk Assessment of Heavy Metals and Phosphorus in Surface Sediments from Lakes in N. Greece. Environ. Geochem. Health 2020, 42, 2747–2769. [Google Scholar] [CrossRef]
- Al-Mur, B.A. Geochemical Fractionation of Heavy Metals in Sediments of the Red Sea, Saudi Arabia. Oceanologia 2020, 62, 31–44. [Google Scholar] [CrossRef]
- Lee, P.-K.; Kang, M.-J.; Yu, S.; Ko, K.-S.; Ha, K.; Shin, S.-C.; Park, J.H. Enrichment and Geochemical Mobility of Heavy Metals in Bottom Sediment of the Hoedong Reservoir, Korea and Their Source Apportionment. Chemosphere 2017, 184, 74–85. [Google Scholar] [CrossRef]
- Camponelli, K.M.; Lev, S.M.; Snodgrass, J.W.; Landa, E.R.; Casey, R.E. Chemical Fractionation of Cu and Zn in Stormwater, Roadway Dust and Stormwater Pond Sediments. Environ. Pollut. 2010, 158, 2143–2149. [Google Scholar] [CrossRef] [PubMed]
- Haynes, H.M.; Taylor, K.G.; Rothwell, J.; Byrne, P. Characterisation of Road-Dust Sediment in Urban Systems: A Review of a Global Challenge. J. Soils Sediments 2020, 20, 4194–4217. [Google Scholar] [CrossRef]
- Bourliva, A.; Christophoridis, C.; Papadopoulou, L.; Giouri, K.; Papadopoulos, A.; Mitsika, E.; Fytianos, K. Characterization, Heavy Metal Content and Health Risk Assessment of Urban Road Dusts from the Historic Center of the City of Thessaloniki, Greece. Environ. Geochem. Health 2017, 39, 611–634. [Google Scholar] [CrossRef] [PubMed]
- Świetlik, R.; Trojanowska, M.; Strzelecka, M.; Bocho-Janiszewska, A. Fractionation and Mobility of Cu, Fe, Mn, Pb and Zn in the Road Dust Retained on Noise Barriers along Expressway—A Potential Tool for Determining the Effects of Driving Conditions on Speciation of Emitted Particulate Metals. Environ. Pollut. 2015, 196, 404–413. [Google Scholar] [CrossRef]
- Zhou, H.; Chun, X.; Lü, C.; He, J.; Du, D. Geochemical Characteristics of Rare Earth Elements in Windowsill Dust in Baotou, China: Influence of the Smelting Industry on Levels and Composition. Environ. Sci. Process. Impacts 2020, 22, 2398–2405. [Google Scholar] [CrossRef] [PubMed]
- Rajouriya, K.; Rohra, H.; Taneja, A. Levels of Fine Particulate Matter Bound Trace Metals in Air of Glass Industrial Area; Firozabad. Pollution 2020, 6. [Google Scholar] [CrossRef]
- Lee, P.-K.; Choi, B.-Y.; Kang, M.-J. Assessment of Mobility and Bio-Availability of Heavy Metals in Dry Depositions of Asian Dust and Implications for Environmental Risk. Chemosphere 2015, 119, 1411–1421. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhu, F.; Zhao, L.; Jiang, H.; Zhang, Z. Heavy Metal Speciation in Various Types of Fly Ash from Municipal Solid Waste Incinerator. J. Mater. Cycles Waste Manag. 2014, 16, 608–615. [Google Scholar] [CrossRef]
- Xia, F.; Zhang, C.; Qu, L.; Song, Q.; Ji, X.; Mei, K.; Dahlgren, R.A.; Zhang, M. A Comprehensive Analysis and Source Apportionment of Metals in Riverine Sediments of a Rural-Urban Watershed. J. Hazard. Mater. 2020, 381, 121230. [Google Scholar] [CrossRef] [PubMed]
- Sakan, S.; Frančišković-Bilinski, S.; Đorđević, D.; Popović, A.; Škrivanj, S.; Bilinski, H. Geochemical Fractionation and Risk Assessment of Potentially Toxic Elements in Sediments from Kupa River, Croatia. Water 2020, 12, 2024. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, E.; Lin, Q.; Zhang, E.; Yang, F.; Wei, C.; Shen, J. Comprehensive Assessment of Heavy Metal Pollution and Ecological Risk in Lake Sediment by Combining Total Concentration and Chemical Partitioning. Environ. Pollut. 2021, 269, 116212. [Google Scholar] [CrossRef]
- Passos, E.A.; Alves, J.C.; dos Santos, I.S.; Alves, J.P.H.; Garcia, C.A.B.; Spinola Costa, A.C. Assessment of Trace Metals Contamination in Estuarine Sediments Using a Sequential Extraction Technique and Principal Component Analysis. Microchem. J. 2010, 96, 50–57. [Google Scholar] [CrossRef]
- Baran, A.; Mierzwa-Hersztek, M.; Gondek, K.; Tarnawski, M.; Szara, M.; Gorczyca, O.; Koniarz, T. The Influence of the Quantity and Quality of Sediment Organic Matter on the Potential Mobility and Toxicity of Trace Elements in Bottom Sediment. Environ. Geochem. Health 2019, 41, 2893–2910. [Google Scholar] [CrossRef] [Green Version]
- Nelson, W. Fractionation of Trace Metals in Coastal Sediments from Trinidad and Tobago, West Indies. Mar. Pollut. Bull. 2020, 150, 110774. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Guo, P.; Su, H.; Deng, J.; Zheng, M.; Wang, J.; Wu, Y.; Jin, Y. Fraction Distribution and Bioavailability of Soil Heavy Metals under Different Planting Patterns in Mangrove Restoration Wetlands in Jinjiang, Fujian, China. Ecol. Eng. 2021, 166, 106242. [Google Scholar] [CrossRef]
- Naz, A.; Chowdhury, A.; Chandra, R.; Mishra, B.K. Potential Human Health Hazard Due to Bioavailable Heavy Metal Exposure via Consumption of Plants with Ethnobotanical Usage at the Largest Chromite Mine of India. Environ. Geochem. Health 2020, 42, 4213–4231. [Google Scholar] [CrossRef]
- Sungur, A.; Soylak, M.; Ozcan, H. Fractionation, Source Identification and Risk Assessments for Heavy Metals in Soils near a Small-Scale Industrial Area (Çanakkale-Turkey). Soil Sediment Contam. Int. J. 2019, 28, 213–227. [Google Scholar] [CrossRef]
- Cambier, P.; Michaud, A.; Paradelo, R.; Germain, M.; Mercier, V.; Guérin-Lebourg, A.; Revallier, A.; Houot, S. Trace Metal Availability in Soil Horizons Amended with Various Urban Waste Composts during 17 Years—Monitoring and Modelling. Sci. Total Environ. 2019, 651, 2961–2974. [Google Scholar] [CrossRef]
- Fernández-Calviño, D.; Cutillas-Barreiro, L.; Paradelo-Núñez, R.; Nóvoa-Muñoz, J.C.; Fernández-Sanjurjo, M.J.; Álvarez-Rodríguez, E.; Núñez-Delgado, A.; Arias-Estévez, M. Heavy Metals Fractionation and Desorption in Pine Bark Amended Mine Soils. J. Environ. Manag. 2017, 192, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Pandey, M.; Pandey, A.K.; Mishra, A.; Tripathi, B.D. Speciation of Carcinogenic and Non-Carcinogenic Metals in Respirable Suspended Particulate Matter (PM10) in Varanasi, India. Urban Clim. 2017, 19, 141–154. [Google Scholar] [CrossRef]
- Javed, M.B.; Shotyk, W. Estimating Bioaccessibility of Trace Elements in Particles Suspended in the Athabasca River Using Sequential Extraction. Environ. Pollut. 2018, 240, 466–474. [Google Scholar] [CrossRef]
- Kumar, M.; Furumai, H.; Kurisu, F.; Kasuga, I. Tracing Source and Distribution of Heavy Metals in Road Dust, Soil and Soakaway Sediment through Speciation and Isotopic Fingerprinting. Geoderma 2013, 211–212, 8–17. [Google Scholar] [CrossRef]
- Xiang, L.; Li, Y.; Yang, Z.; Shi, J. Seasonal Difference and Availability of Heavy Metals in Street Dust in Beijing. J. Environ. Sci. Health Part A 2010, 45, 1092–1100. [Google Scholar] [CrossRef] [PubMed]
- Adamiec, E. Chemical Fractionation and Mobility of Traffic-Related Elements in Road Environments. Environ. Geochem. Health 2017, 39, 1457–1468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yıldırım, G.; Tokalıoğlu, Ş. Heavy Metal Speciation in Various Grain Sizes of Industrially Contaminated Street Dust Using Multivariate Statistical Analysis. Ecotoxicol. Environ. Saf. 2016, 124, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Tytła, M. Assessment of Heavy Metal Pollution and Potential Ecological Risk in Sewage Sludge from Municipal Wastewater Treatment Plant Located in the Most Industrialized Region in Poland—Case Study. Int. J. Environ. Res. Public Health 2019, 16, 2430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jukić, M.; Ćurković, L.; Šabarić, J.; Kerolli-Mustafa, M. Fractionation of Heavy Metals in Fly Ash from Wood Biomass Using the BCR Sequential Extraction Procedure. Bull. Environ. Contam. Toxicol. 2017, 99, 524–529. [Google Scholar] [CrossRef]
- Khelifi, F.; Melki, A.; Hamed, Y.; Adamo, P.; Caporale, A.G. Environmental and Human Health Risk Assessment of Potentially Toxic Elements in Soil, Sediments, and Ore-Processing Wastes from a Mining Area of Southwestern Tunisia. Environ. Geochem. Health 2020, 42, 4125–4139. [Google Scholar] [CrossRef]
- Kersten, M.; Förstner, U. Chemical Fractionation of Heavy Metals in Anoxic Estuarine and Coastal Sediments. Water Sci. Technol. 1986, 18, 121–130. [Google Scholar] [CrossRef]
- Zeien, H.; Brümmer, G.W. Chemical extractions to determine heavy metal forms in soils. Mittlgn. Deutsch. Bodenkundl. Gesellsch. 1989, 59, 505–510. (In German) [Google Scholar]
- Leleyter, L.; Probst, J.-L. A New Sequential Extraction Procedure for the Speciation of Particulate Trace Elements in River Sediments. Int. J. Environ. Anal. Chem. 1999, 73, 109–128. [Google Scholar] [CrossRef]
- Obiols, J.; Devesa, R.; Sol, A. Speciation of Heavy Metals in Suspended Particulates in Urban Air†. Toxicol. Environ. Chem. 1986, 13, 121–128. [Google Scholar] [CrossRef]
- Chester, R.; Lin, F.J.; Murphy, K.J.T. A Three Stage Sequential Leaching Scheme for the Characterisation of the Sources and Environmental Mobility of Trace Metals in the Marine Aerosol. Environ. Technol. Lett. 1989, 10, 887–900. [Google Scholar] [CrossRef]
- Zatka, V.J.; Warner, J.S.; Maskery, D. Chemical Speciation of Nickel in Airborne Dusts: Analytical Method and Results of an Interlaboratory Test Program. Environ. Sci. Technol. 1992, 26, 138–144. [Google Scholar] [CrossRef]
- Fernández Espinosa, A.J.; Ternero Rodríguez, M.; Barragán de la Rosa, F.J.; Jiménez Sánchez, J.C. A Chemical Speciation of Trace Metals for Fine Urban Particles. Atmos. Environ. 2002, 36, 773–780. [Google Scholar] [CrossRef]
- Richter, P.; Griño, P.; Ahumada, I.; Giordano, A. Total Element Concentration and Chemical Fractionation in Airborne Particulate Matter from Santiago, Chile. Atmos. Environ. 2007, 41, 6729–6738. [Google Scholar] [CrossRef]
- Gong, Q.; Deng, J.; Xiang, Y.; Wang, Q.; Yang, L. Calculating Pollution Indices by Heavy Metals in Ecological Geochemistry Assessment and a Case Study in Parks of Beijing. J. China Univ. Geosci. 2008, 19, 230–241. [Google Scholar] [CrossRef]
- Zhao, S.; Feng, C.; Yang, Y.; Niu, J.; Shen, Z. Risk Assessment of Sedimentary Metals in the Yangtze Estuary: New Evidence of the Relationships between Two Typical Index Methods. J. Hazard. Mater. 2012, 241–242, 164–172. [Google Scholar] [CrossRef]
- Kumar, M.; Gogoi, A.; Kumari, D.; Borah, R.; Das, P.; Mazumder, P.; Tyagi, V.K. Review of Perspective, Problems, Challenges, and Future Scenario of Metal Contamination in the Urban Environment. J. Hazard. Toxic Radioact. Waste 2017, 21, 04017007. [Google Scholar] [CrossRef]
- Weissmannová, H.D.; Pavlovský, J. Indices of Soil Contamination by Heavy Metals—Methodology of Calculation for Pollution Assessment (Minireview). Environ. Monit. Assess. 2017, 189, 616. [Google Scholar] [CrossRef] [PubMed]
- Kowalska, J.B.; Mazurek, R.; Gąsiorek, M.; Zaleski, T. Pollution Indices as Useful Tools for the Comprehensive Evaluation of the Degree of Soil Contamination–A Review. Environ. Geochem. Health 2018, 40, 2395–2420. [Google Scholar] [CrossRef] [Green Version]
- Hakanson, L. An Ecological Risk Index for Aquatic Pollution Control.a Sedimentological Approach. Water Res. 1980, 14, 975–1001. [Google Scholar] [CrossRef]
- Vlasov, D.; Vasil’chuk, J.; Kosheleva, N.; Kasimov, N. Dissolved and Suspended Forms of Metals and Metalloids in Snow Cover of Megacity: Partitioning and Deposition Rates in Western Moscow. Atmosphere 2020, 11, 907. [Google Scholar] [CrossRef]
- Vlasov, D.; Kosheleva, N.; Kasimov, N. Spatial Distribution and Sources of Potentially Toxic Elements in Road Dust and Its PM10 Fraction of Moscow Megacity. Sci. Total Environ. 2021, 761, 143267. [Google Scholar] [CrossRef]
- Vlasov, D.; Kasimov, N.; Eremina, I.; Shinkareva, G.; Chubarova, N. Partitioning and Solubilities of Metals and Metalloids in Spring Rains in Moscow Megacity. Atmos. Pollut. Res. 2021, 12, 255–271. [Google Scholar] [CrossRef]
- Vlasov, D.V.; Shinkareva, G.L.; Kasimov, N.S. Metals and metalloids in bottom sediments of lakes and ponds of the eastern part of Moscow. Vestn. Mosk. Univ. Seriya Geogr. 2019, 4, 43–52. [Google Scholar]
- Müller, G. Index of Geoaccumulation in the Sediments of the Rhine River. Geojournal 1969, 2, 108–118. [Google Scholar]
- Saet, Yu.E.; Revich, B.A.; Yanin, E.P.; Smirnova, R.S.; Basharkevich, E.L.; Onischenko, T.L.; Pavlova, L.N.; Trefilova, N.Y.; Achkasov, A.I.; Sarkisyan, S.S. Geochemistry of the Environment; Nedra: Moscow, Russia, 1990; ISBN 5-247-01127-9. [Google Scholar]
- Buat-Menard, P.; Chesselet, R. Variable Influence of the Atmospheric Flux on the Trace Metal Chemistry of Oceanic Suspended Matter. Earth Planet. Sci. Lett. 1979, 42, 399–411. [Google Scholar] [CrossRef]
- Kasimov, N.S.; Vlasov, D.V.; Kosheleva, N.E.; Nikiforova, E.M. Geochemistry of Landscapes of Eastern Moscow; APR: Moscow, Russia, 2016; ISBN 978-5-904761-62-2. [Google Scholar]
- Ladonin, D.V. Fractionation of Heavy Metals in Technogenically Contaminated Soils. Habilitation Thesis, Lomonosov Moscow State University, Moscow, Russia, 2016. [Google Scholar]
- Sutherland, R.A.; Tack, F.M.G.; Ziegler, A.D. Road-Deposited Sediments in an Urban Environment: A First Look at Sequentially Extracted Element Loads in Grain Size Fractions. J. Hazard. Mater. 2012, 225–226, 54–62. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, J.; He, H. Assessment of the Tessier and BCR Sequential Extraction Procedures for Elemental Partitioning of Ca, Fe, Mn, Al, and Ti and Their Application to Surface Sediments from Chinese Continental Shelf. Acta Oceanol. Sin. 2018, 37, 22–28. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Nan, Z.; Zang, F.; Sun, H.; Zhang, Q.; Huang, W.; Bao, L. Accumulation, Fractionation and Health Risk Assessment of Fluoride and Heavy Metals in Soil-Crop Systems in Northwest China. Sci. Total Environ. 2019, 663, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Ikem, A.; Egiebor, N.O.; Nyavor, K. Trace Elements in Water, Fish and Sediment from Tuskegee Lake, Southeastern USA. Water Air Soil Pollut. 2003, 149, 51–75. [Google Scholar] [CrossRef]
- Ghrefat, H.A.; Yusuf, N.; Jamarh, A.; Nazzal, J. Fractionation and Risk Assessment of Heavy Metals in Soil Samples Collected along Zerqa River, Jordan. Environ. Earth Sci. 2012, 66, 199–208. [Google Scholar] [CrossRef]
- Kidd, P.S.; Domínguez-Rodríguez, M.J.; Díez, J.; Monterroso, C. Bioavailability and Plant Accumulation of Heavy Metals and Phosphorus in Agricultural Soils Amended by Long-Term Application of Sewage Sludge. Chemosphere 2007, 66, 1458–1467. [Google Scholar] [CrossRef]
- Mandzhieva, S.S.; Minkina, T.M.; Motuzova, G.V.; Golovatyi, S.E.; Miroshnichenko, N.N.; Lukashenko, N.K.; Fateev, A.I. Fractional and Group Composition of Zinc and Lead Compounds as an Indicator of the Environmental Status of Soils. Eurasian Soil Sci. 2014, 47, 511–518. [Google Scholar] [CrossRef]
- Karpukhin, A.I.; Bushuev, N.N. Effect of fertilization on the content of heavy metals in soils of long-term field experiments. Agrokhimia 2007, 5, 76–84. [Google Scholar]
- Sutherland, R.A.; Tack, F.M.G.; Ziegler, A.D.; Bussen, J.O. Metal Extraction from Road-Deposited Sediments Using Nine Partial Decomposition Procedures. Appl. Geochem. 2004, 19, 947–955. [Google Scholar] [CrossRef]
- Perin, G.; Craboledda, L.; Lucchese, M.; Cirillo, R.; Dotta, L.; Zanetta, M.L.; Oro, A.A. Heavy metal speciation in the sediments of northern Adriatic Sea. A new approach for environmental toxicity determination. In Heavy Metals in the Environment; Lakkas, T.D., Ed.; CEP Consultants: Edinburgh, UK, 1985; Volume 2, pp. 454–456. [Google Scholar]
- Rosado, D.; Usero, J.; Morillo, J. Assessment of Heavy Metals Bioavailability and Toxicity toward Vibrio Fischeri in Sediment of the Huelva Estuary. Chemosphere 2016, 153, 10–17. [Google Scholar] [CrossRef]
- Dong, S.; Zhang, S.; Wang, L.; Ma, G.; Lu, X.; Li, X. Concentrations, Speciation, and Bioavailability of Heavy Metals in Street Dust as Well as Relationships with Physiochemcal Properties: A Case Study of Jinan City in East China. Environ. Sci. Pollut. Res. 2020, 27, 35724–35737. [Google Scholar] [CrossRef]
- Rieuwerts, J.S. The Mobility and Bioavailability of Trace Metals in Tropical Soils: A Review. Chem. Speciat. Bioavailab. 2007, 19, 75–85. [Google Scholar] [CrossRef]
- Samonova, O.A.; Aseyeva, E.N. Particle Size Partitioning of Metals in Humus Horizons of Two Small Erosional Landforms in the Middle Protva Basin—A Comparative Study. Geogr. Environ. Sustain. 2020, 13, 260–271. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Luo, Y.; Makino, T.; Wu, L.; Nanzyo, M. The Heavy Metal Partition in Size-Fractions of the Fine Particles in Agricultural Soils Contaminated by Waste Water and Smelter Dust. J. Hazard. Mater. 2013, 248–249, 303–312. [Google Scholar] [CrossRef]
- Okunola, O. Geochemical Partitioning of Heavy Metals in Roadside Surface Soils of Different Grain Size along Major Roads in Kano Metropolis, Nigeria. Br. J. Appl. Sci. Technol. 2011, 1, 94–115. [Google Scholar] [CrossRef]
- Jayarathne, A.; Egodawatta, P.; Ayoko, G.A.; Goonetilleke, A. Assessment of Ecological and Human Health Risks of Metals in Urban Road Dust Based on Geochemical Fractionation and Potential Bioavailability. Sci. Total Environ. 2018, 635, 1609–1619. [Google Scholar] [CrossRef]
- Kang, X.; Song, J.; Yuan, H.; Duan, L.; Li, X.; Li, N.; Liang, X.; Qu, B. Speciation of Heavy Metals in Different Grain Sizes of Jiaozhou Bay Sediments_ Bioavailability, Ecological Risk Assessment and Source Analysis on a Centennial Timescale. Ecotoxicol. Environ. Saf. 2017, 143, 296–306. [Google Scholar] [CrossRef] [PubMed]
- Jan, R.; Roy, R.; Yadav, S.; Satsangi, P.G. Chemical Fractionation and Health Risk Assessment of Particulate Matter-Bound Metals in Pune, India. Environ. Geochem. Health 2018, 40, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Canepari, S.; Astolfi, M.L.; Catrambone, M.; Frasca, D.; Marcoccia, M.; Marcovecchio, F.; Massimi, L.; Rantica, E.; Perrino, C. A Combined Chemical/Size Fractionation Approach to Study Winter/Summer Variations, Ageing and Source Strength of Atmospheric Particles. Environ. Pollut. 2019, 253, 19–28. [Google Scholar] [CrossRef]
- Jayarathne, A.; Egodawatta, P.; Ayoko, G.A.; Goonetilleke, A. Geochemical Phase and Particle Size Relationships of Metals in Urban Road Dust. Environ. Pollut. 2017, 230, 218–226. [Google Scholar] [CrossRef]
- Zhang, J.; Hua, P.; Krebs, P. The Build-up Dynamic and Chemical Fractionation of Cu, Zn and Cd in Road-Deposited Sediment. Sci. Total Environ. 2015, 532, 723–732. [Google Scholar] [CrossRef]
- Vodyanitskii, Y.; Minkina, T.; Bauer, T. Methods to Determine the Affinity of Heavy Metals for the Chemically Extracted Carrier Phases in Soils. Environ. Geochem. Health 2021. [Google Scholar] [CrossRef]
- Kabata-Pendias, A. Trace Elements in Soils and Plants, 4th ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-1-4200-9368-1. [Google Scholar]
- Rudnick, R.L.; Gao, S. Composition of the Continental Crust. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–51. ISBN 978-0-08-098300-4. [Google Scholar]
- Kasimov, N.S.; Vlasov, D.V. Clarkes of chemical elements as comparison standards in ecogeochemistry. Vestn. Mosk. Univ. Seriya Geogr. 2015, 2, 7–17. [Google Scholar]
- Kasimov, N.S.; Vlasov, D.V.; Kosheleva, N.E. Enrichment of Road Dust Particles and Adjacent Environments with Metals and Metalloids in Eastern Moscow. Urban Clim. 2020, 32, 100638. [Google Scholar] [CrossRef]
- Gao, X.; Chen, C.-T.A.; Wang, G.; Xue, Q.; Tang, C.; Chen, S. Environmental Status of Daya Bay Surface Sediments Inferred from a Sequential Extraction Technique. Estuar. Coast. Shelf Sci. 2010, 86, 369–378. [Google Scholar] [CrossRef]
- Jain, C.K.; Gurunadha Rao, V.V.S.; Prakash, B.A.; Mahesh Kumar, K.; Yoshida, M. Metal Fractionation Study on Bed Sediments of Hussainsagar Lake, Hyderabad, India. Environ. Monit. Assess. 2010, 166, 57–67. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.-M.; Choi, K.-Y.; Chung, C.-S.; Kim, C.-J.; Kim, S.H. Fractionation and Risk Assessment of Metals in Sediments of an Ocean Dumping Site. Mar. Pollut. Bull. 2019, 141, 227–235. [Google Scholar] [CrossRef]
- Soliman, N.F.; El Zokm, G.M.; Okbah, M.A. Risk Assessment and Chemical Fractionation of Selected Elements in Surface Sediments from Lake Qarun, Egypt Using Modified BCR Technique. Chemosphere 2018, 191, 262–271. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Heavy Metals | ∑CAF | ||||||
|---|---|---|---|---|---|---|---|---|
| Cd | Ni | Pb | Zn | Cr | Cu | Mn | ||
| F1, mg/kg | 3.85 | 9.71 | 8.07 | 11.3 | 5.91 | 4.22 | 11.8 | n/a |
| F2, mg/kg | 4.17 | 16.2 | 60.5 | 108 | 1.16 | 40.0 | 85.6 | n/a |
| F3, mg/kg | 2.16 | 5.95 | 105 | 147 | 6.56 | 55.0 | 188 | n/a |
| F4, mg/kg | 0.28 | 5.94 | 48.8 | 60.9 | 5.79 | 123 | 37.2 | n/a |
| F5, mg/kg | 4.47 | 36.5 | 147 | 607 | 38.8 | 132 | 365 | n/a |
| ∑F, mg/kg | 14.9 | 74.3 | 369 | 934 | 58.2 | 354 | 688 | n/a |
| F1, % of ∑F | 26 | 13 | 2 | 1 | 10 | 1 | 2 | n/a |
| F2, % of ∑F | 28 | 22 | 16 | 12 | 2 | 11 | 12 | n/a |
| F3, % of ∑F | 14 | 8 | 28 | 16 | 11 | 16 | 27 | n/a |
| F4, % of ∑F | 2 | 8 | 13 | 7 | 10 | 35 | 5 | n/a |
| F5, % of ∑F | 30 | 49 | 40 | 65 | 67 | 37 | 53 | n/a |
| CAF(F1) | 1.28 | 0.65 | 0.11 | 0.06 | 0.50 | 0.06 | 0.09 | 2.74 |
| CAF (F2) | 1.14 | 0.89 | 0.67 | 0.47 | 0.08 | 0.46 | 0.51 | 4.21 |
| CAF (F3) | 0.90 | 0.50 | 1.78 | 0.99 | 0.70 | 0.97 | 1.71 | 7.55 |
| CAF (F4) | 0.35 | 1.51 | 2.49 | 1.23 | 1.88 | 6.55 | 1.02 | 15.0 |
| CAF (F5) | 0.88 | 1.45 | 1.17 | 1.91 | 1.96 | 1.10 | 1.56 | 10.0 |
| CAF (∑F) | 4.55 | 4.99 | 6.22 | 4.66 | 5.13 | 9.14 | 4.88 | 39.6 |
| Parameter | Heavy Metals | ∑CAF | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ba | Cd | Co | Cu | Mn | Mo | Ni | Pb | Sc | Sr | U | Zn | ||
| F1, mg/kg | 0.91 | 0.01 | 0.82 | 0.49 | 408 | 0.01 | 1.91 | 2.16 | 0.04 | 144 | 0.07 | 2.22 | n/a |
| F2, mg/kg | 1.91 | 0.01 | 1.67 | 1.68 | 125 | 0.01 | 1.80 | 14.7 | 0.02 | 13.3 | 0.07 | 10.9 | n/a |
| F3, mg/kg | 2.24 | 0.01 | 1.20 | 1.05 | 50.5 | 0.14 | 3.19 | 1.43 | 0.19 | 1.75 | 0.59 | 6.12 | n/a |
| F4, mg/kg | 356 | 0.02 | 9.01 | 17.5 | 253 | 1.67 | 24.3 | 27.5 | 11.8 | 50.5 | 2.81 | 93.5 | n/a |
| ∑F, mg/kg | 361 | 0.05 | 12.7 | 20.7 | 836 | 1.83 | 31.2 | 45.8 | 12.0 | 210 | 3.54 | 113 | n/a |
| F1, % of ∑F | 0 | 18 | 6 | 2 | 49 | 1 | 6 | 5 | 0 | 69 | 2 | 2 | n/a |
| F2, % of ∑F | 1 | 20 | 13 | 8 | 15 | 0 | 6 | 32 | 0 | 6 | 2 | 10 | n/a |
| F3, % of ∑F | 1 | 22 | 9 | 5 | 6 | 8 | 10 | 3 | 2 | 1 | 17 | 5 | n/a |
| F4, % of ∑F | 99 | 40 | 71 | 84 | 30 | 91 | 78 | 60 | 98 | 24 | 79 | 83 | n/a |
| CAF(F1) | 0.02 | 1.72 | 0.62 | 0.23 | 4.66 | 0.05 | 0.59 | 0.45 | 0.03 | 6.57 | 0.19 | 0.19 | 15.3 |
| CAF(F2) | 0.04 | 1.68 | 1.11 | 0.68 | 1.26 | 0.03 | 0.49 | 2.70 | 0.01 | 0.53 | 0.16 | 0.81 | 9.50 |
| CAF(F3) | 0.09 | 3.21 | 1.38 | 0.74 | 0.88 | 1.12 | 1.49 | 0.46 | 0.23 | 0.12 | 2.43 | 0.79 | 12.9 |
| CAF(F4) | 1.39 | 0.57 | 1.00 | 1.19 | 0.43 | 1.29 | 1.10 | 0.85 | 1.38 | 0.34 | 1.12 | 1.17 | 11.8 |
| CAF(∑F) | 1.55 | 7.18 | 4.10 | 2.84 | 7.23 | 2.49 | 3.66 | 4.45 | 1.66 | 7.56 | 3.90 | 2.96 | 49.6 |
| Parameter | Heavy Metals | ∑CAF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cu | Zn | Fe | Pb | Cd | Mn | Co | Cr | Ni | ||
| F1, ng/m3 | 3.0 | 23 | 233 | 20 | 53 | 45 | 31 | 37 | 17 | n/a |
| F2, ng/m3 | 16 | 59 | 375 | 66 | 20 | 62 | 21 | 94 | 7.0 | n/a |
| F3, ng/m3 | 75 | 41 | 1699 | 24 | 4.0 | 106 | 105 | 64 | 27 | n/a |
| F4, ng/m3 | 113 | 203 | 2795 | 37 | 12 | 182 | 64 | 46 | 74 | n/a |
| ∑F, ng/m3 | 207 | 326 | 5102 | 147 | 89 | 395 | 221 | 241 | 125 | n/a |
| F1, % of ∑F | 1 | 7 | 5 | 14 | 60 | 11 | 14 | 15 | 14 | n/a |
| F2, % of ∑F | 8 | 18 | 7 | 45 | 22 | 16 | 10 | 39 | 6 | n/a |
| F3, % of ∑F | 36 | 13 | 33 | 16 | 4 | 27 | 48 | 27 | 22 | n/a |
| F4, % of ∑F | 55 | 62 | 55 | 25 | 13 | 46 | 29 | 19 | 59 | n/a |
| CAF(F1) | 0.03 | 0.12 | 0.08 | 0.24 | 1.03 | 0.20 | 0.24 | 0.27 | 0.24 | 2.44 |
| CAF(F2) | 0.35 | 0.81 | 0.33 | 2.01 | 1.00 | 0.70 | 0.42 | 1.74 | 0.25 | 7.62 |
| CAF(F3) | 6.58 | 2.28 | 6.04 | 2.96 | 0.82 | 4.87 | 8.62 | 4.82 | 3.92 | 40.9 |
| CAF(F4) | 3.78 | 4.31 | 3.79 | 1.74 | 0.93 | 3.19 | 2.00 | 1.32 | 4.10 | 25.2 |
| CAF(∑F) | 10.7 | 7.52 | 10.2 | 6.95 | 3.79 | 8.96 | 11.3 | 8.15 | 8.50 | 76.1 |
| Parameter | Concentration, mg/kg of Road Dust | Parameter | Share in the Total Content, % | Parameter | CAF | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G4 | ∑G | %G1 | %G2 | %G3 | %G4 | ∑%G | G1 | G2 | G3 | G4 | ∑G | ||||
| Zn | F1 | 540 | 56 | 4.8 | 1.5 | 602 | %F1 | 52 | 5.4 | 0.47 | 0.15 | 58 | F1 | 1.49 | 1.40 | 1.18 | 0.81 | 4.88 |
| F2 | 313 | 22 | 1.2 | 0.69 | 337 | %F2 | 30 | 2.1 | 0.12 | 0.07 | 33 | F2 | 0.73 | 0.51 | 0.37 | 0.35 | 1.97 | |
| F3 | 87 | 7.6 | 0.41 | 0.38 | 95 | %F3 | 8.4 | 0.7 | 0.04 | 0.04 | 9 | F3 | 0.64 | 0.53 | 0.41 | 0.44 | 2.02 | |
| ∑F | 939 | 86 | 6.5 | 2.6 | ∑GF = 1034 | ∑%F | 91 | 8.3 | 0.63 | 0.25 | ∑%GF = 100 | ∑F | 2.87 | 2.44 | 1.97 | 1.61 | ∑GF = 8.88 | |
| Cd | F1 | 0.44 | 0.04 | 0.003 | 0.003 | 0.49 | %F1 | 59 | 6.0 | 0.37 | 0.41 | 66 | F1 | 1.69 | 1.54 | 0.93 | 2.27 | 6.42 |
| F2 | 0.19 | 0.02 | 0.0003 | 0.001 | 0.21 | %F2 | 26 | 2.2 | 0.04 | 0.08 | 28 | F2 | 0.62 | 0.52 | 0.12 | 0.40 | 1.66 | |
| F3 | 0.04 | 0.007 | 0.0003 | 0.0001 | 0.047 | %F3 | 5.4 | 0.9 | 0.04 | 0.01 | 6 | F3 | 0.41 | 0.66 | 0.38 | 0.15 | 1.60 | |
| ∑F | 0.67 | 0.07 | 0.003 | 0.004 | ∑GF = 0.75 | ∑%F | 90 | 9.1 | 0.44 | 0.50 | ∑%GF = 100 | ∑F | 2.72 | 2.73 | 1.42 | 2.82 | ∑GF = 9.68 | |
| Cu | F1 | 61 | 7.7 | 0.72 | 0.22 | 70 | %F1 | 22 | 2.8 | 0.26 | 0.08 | 25 | F1 | 0.64 | 0.72 | 0.66 | 0.44 | 2.46 |
| F2 | 144 | 21 | 1.8 | 0.83 | 167 | %F2 | 52 | 7.7 | 0.65 | 0.30 | 61 | F2 | 1.26 | 1.87 | 2.07 | 1.59 | 6.78 | |
| F3 | 33 | 4.3 | 0.61 | 0.67 | 39 | %F3 | 12 | 1.5 | 0.22 | 0.24 | 14 | F3 | 0.91 | 1.10 | 2.29 | 2.87 | 7.17 | |
| ∑F | 238 | 33 | 3.1 | 1.7 | ∑GF = 276 | ∑%F | 86 | 12.0 | 1.13 | 0.62 | ∑%GF = 100 | ∑F | 2.81 | 3.69 | 5.02 | 4.90 | ∑GF = 16.4 | |
| Pb | F1 | 23 | 3.7 | 0.99 | 0.36 | 28 | %F1 | 11 | 1.8 | 0.48 | 0.17 | 13 | F1 | 0.31 | 0.46 | 1.22 | 0.95 | 2.94 |
| F2 | 123 | 11 | 1.1 | 0.72 | 136 | %F2 | 60 | 5.4 | 0.51 | 0.35 | 66 | F2 | 1.44 | 1.31 | 1.62 | 1.85 | 6.23 | |
| F3 | 39 | 3.3 | 0.13 | 0.09 | 43 | %F3 | 19 | 1.6 | 0.06 | 0.04 | 21 | F3 | 1.44 | 1.15 | 0.66 | 0.51 | 3.76 | |
| ∑F | 185 | 18 | 2.2 | 1.2 | ∑GF = 207 | ∑%F | 90 | 8.8 | 1.06 | 0.56 | ∑%GF = 100 | ∑F | 3.20 | 2.93 | 3.50 | 3.30 | ∑GF = 12.9 | |
| Cr | F1 | 0.48 | 0.05 | 0.008 | 0.004 | 0.54 | %F1 | 0.7 | 0.1 | 0.01 | 0.01 | 1 | F1 | 0.02 | 0.02 | 0.03 | 0.03 | 0.10 |
| F2 | 11 | 0.87 | 0.058 | 0.027 | 12 | %F2 | 15 | 1.3 | 0.08 | 0.04 | 17 | F2 | 0.38 | 0.31 | 0.27 | 0.21 | 1.16 | |
| F3 | 50 | 6.4 | 0.34 | 0.20 | 57 | %F3 | 72 | 9.3 | 0.50 | 0.29 | 82 | F3 | 5.50 | 6.65 | 5.14 | 3.47 | 20.8 | |
| ∑F | 61 | 7.3 | 0.41 | 0.23 | ∑GF = 69 | ∑%F | 88 | 10.6 | 0.59 | 0.34 | ∑%GF = 100 | ∑F | 5.90 | 6.97 | 5.43 | 3.71 | ∑GF = 22.0 | |
| Ni | F1 | 3.1 | 0.48 | 0.025 | 0.008 | 3.6 | %F1 | 7.5 | 1.2 | 0.06 | 0.02 | 9 | F1 | 0.22 | 0.30 | 0.15 | 0.11 | 0.78 |
| F2 | 12 | 1.1 | 0.047 | 0.030 | 13 | %F2 | 30 | 2.6 | 0.11 | 0.07 | 32 | F2 | 0.72 | 0.62 | 0.36 | 0.38 | 2.08 | |
| F3 | 22 | 2.5 | 0.16 | 0.089 | 24 | %F3 | 52 | 6.1 | 0.38 | 0.21 | 59 | F3 | 3.97 | 4.39 | 3.95 | 2.56 | 14.9 | |
| ∑F | 37 | 4.1 | 0.23 | 0.13 | ∑GF = 42 | ∑%F | 89 | 9.9 | 0.56 | 0.31 | ∑%GF = 100 | ∑F | 4.91 | 5.31 | 4.46 | 3.05 | ∑GF = 17.7 | |
| Total | F1 | 4.37 | 4.44 | 4.16 | 4.61 | 17.6 | ||||||||||||
| F2 | 5.15 | 5.14 | 4.81 | 4.78 | 19.9 | |||||||||||||
| F3 | 12.9 | 14.5 | 12.8 | 10.0 | 50.2 | |||||||||||||
| ∑F | 22.4 | 24.1 | 21.8 | 19.4 | ∑GF = 87.6 | |||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vodyanitskii, Y.; Vlasov, D. Integrated Assessment of Affinity to Chemical Fractions and Environmental Pollution with Heavy Metals: A New Approach Based on Sequential Extraction Results. Int. J. Environ. Res. Public Health 2021, 18, 8458. https://doi.org/10.3390/ijerph18168458
Vodyanitskii Y, Vlasov D. Integrated Assessment of Affinity to Chemical Fractions and Environmental Pollution with Heavy Metals: A New Approach Based on Sequential Extraction Results. International Journal of Environmental Research and Public Health. 2021; 18(16):8458. https://doi.org/10.3390/ijerph18168458
Chicago/Turabian StyleVodyanitskii, Yuri, and Dmitry Vlasov. 2021. "Integrated Assessment of Affinity to Chemical Fractions and Environmental Pollution with Heavy Metals: A New Approach Based on Sequential Extraction Results" International Journal of Environmental Research and Public Health 18, no. 16: 8458. https://doi.org/10.3390/ijerph18168458
APA StyleVodyanitskii, Y., & Vlasov, D. (2021). Integrated Assessment of Affinity to Chemical Fractions and Environmental Pollution with Heavy Metals: A New Approach Based on Sequential Extraction Results. International Journal of Environmental Research and Public Health, 18(16), 8458. https://doi.org/10.3390/ijerph18168458







