A Comparison of Bayesian Spatial Models for HIV Mapping in South Africa
Abstract
1. Introduction
2. Methods and Data Source
2.1. Skew-t Spatial Random Effects Distribution
2.2. Methods for Comparing Competing Models
2.3. Implementation
2.4. Data
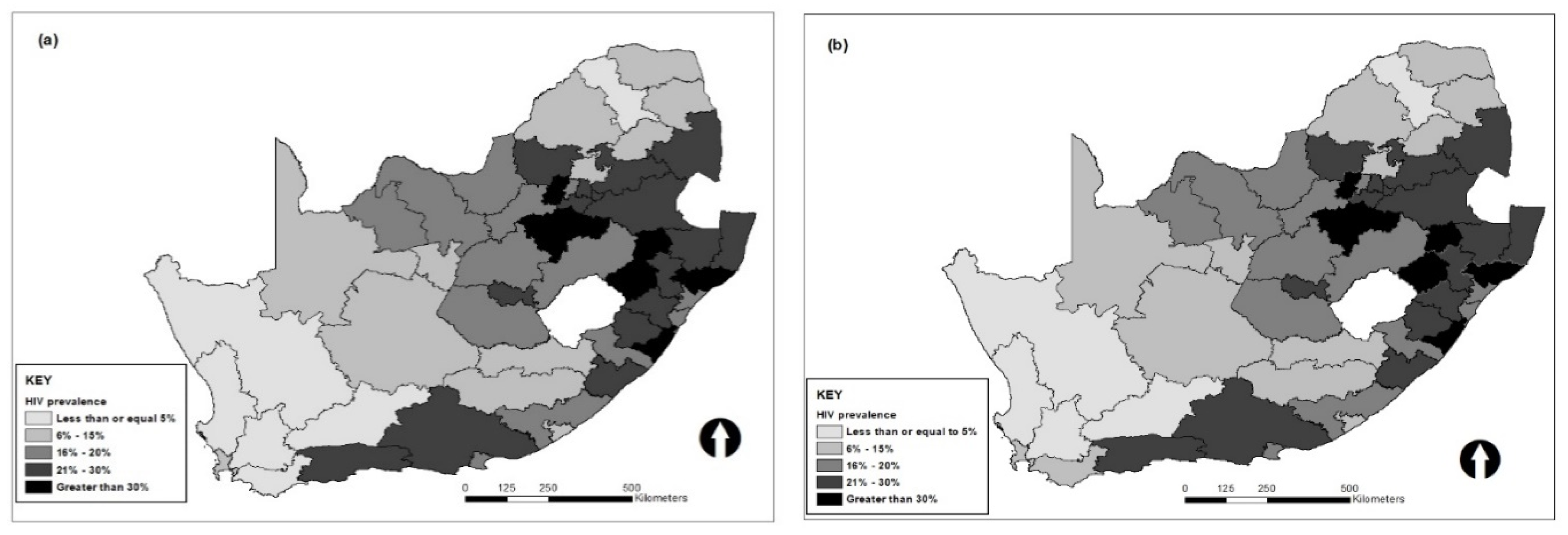
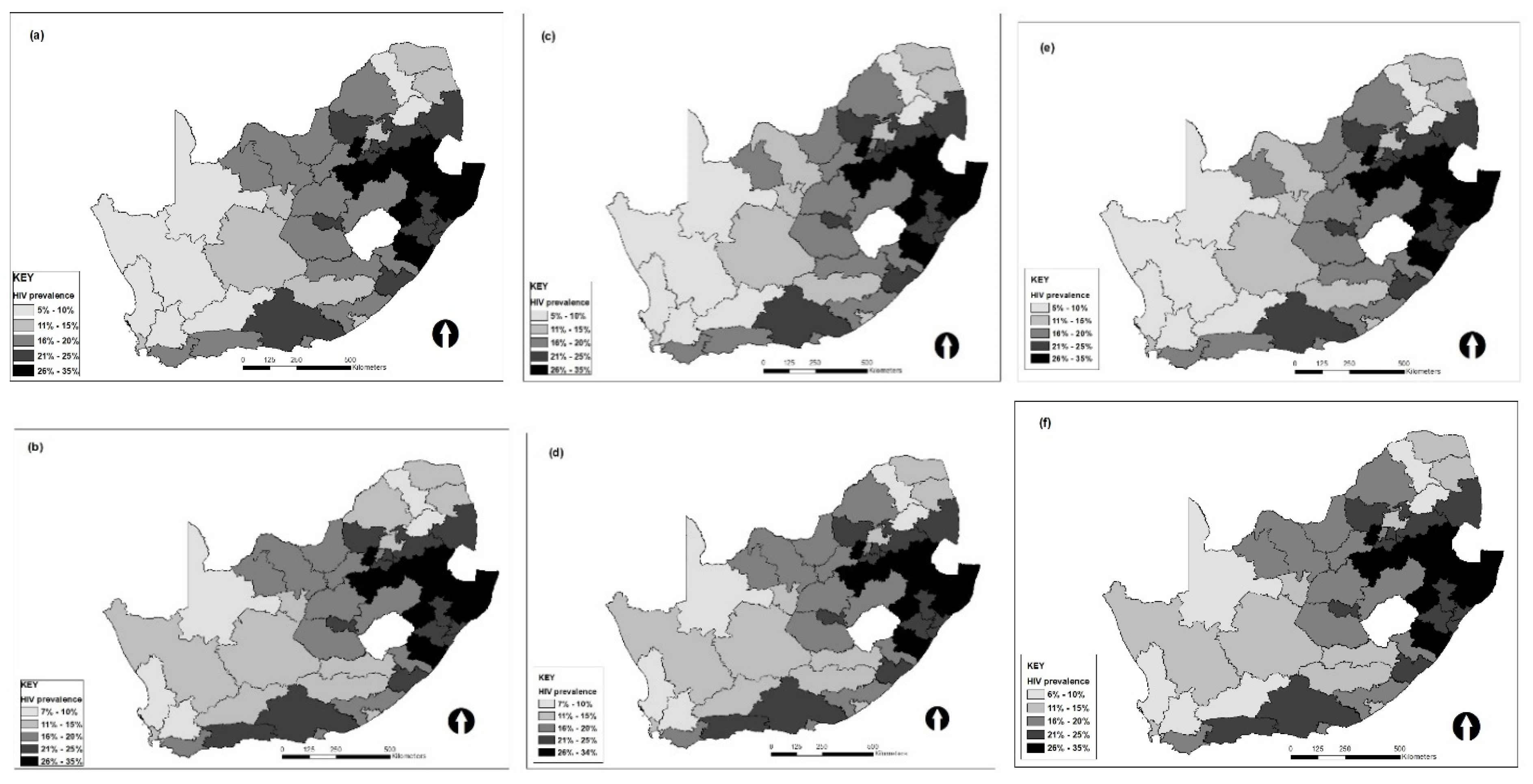
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- UNAIDS. 2016–2021 Strategy on the Fast-Track to end AIDS; UNAIDS: Geneva, Switzerland, 2015; Available online: https://www.unaids.org/sites/default/files/media_asset/20151027_UNAIDS_PCB37_15_18_EN_rev1.pdf (accessed on 1 August 2021).
- PEPFAR. PEPFAR 2021 Country and Regional Operational Plan (COP/ROP) Guidance for all PEPFAR Countries; PEPFAR: Washington, WA, USA, 2021. Available online: https://www.state.gov/wp-content/uploads/2020/12/PEPFAR-COP21-Guidance-Final.pdf (accessed on 1 August 2021).
- Manda, S.; Masenyetse, L.; Cai, B.; Meyer, R. Mapping HIV prevalence using population and antenatal sentinel-based HIV surveys: A multi-stage approach. Popul. Health Metrics. 2015, 13, 22. [Google Scholar] [CrossRef]
- Larmarange, J. Evaluation of geospatial methods to generate subnational HIV prevalence estimates for local level planning. AIDS 2016, 30, 1467–1474. [Google Scholar]
- Tanser, F.; Bärnighausen, T.; Cooke, G.; Newell, M.-L. Localized spatial clustering of HIV infections in a widely disseminated rural South African epidemic. Int. J. Epidemiol. 2009, 38, 1008–1016. [Google Scholar] [CrossRef] [PubMed]
- Niragire, F.; Achia, T.; Lyambabaje, A.; Ntaganira, J. Bayesian Mapping of HIV Infection among Women of Reproductive Age in Rwanda. PLoS ONE 2015, 10, e0119944. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chimoyi, L.A.; Musenge, E. Spatial analysis of factors associated with HIV infection among young people in Uganda, 2011. BMC Public Health 2014, 14, 555. [Google Scholar] [CrossRef] [PubMed]
- Houlihan, C.F.; Mutevedzi, P.C.; Lessells, R.J.; Cooke, G.S.; Tanser, F.C.; Newell, M.-L. The tuberculosis challenge in a rural South African HIV programme. BMC Infect. Dis. 2010, 10, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Johnson, G.D. Small area mapping of prostate cancer incidence in New York State (USA) using fully Bayesian hierarchical modelling. Int. J. Health Geogr. 2004, 3, 29. [Google Scholar] [CrossRef][Green Version]
- Leyland, A.H.; Langford, I.H.; Rasbash, J.; Goldstein, H. Multivariate spatial models for event data. Stat. Med. 2000, 19, 2469–2478. [Google Scholar] [CrossRef]
- Lawson, A.B.; Browne, W.J.; Rodeiro, C.L.V. Diease Mapping with WinBUGS and MLwiN; Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Knorr-Held, L.; Best, N.G. A shared component model for detecting joint and selective clustering of two diseases. J. R. Stat. Soc. Ser. A Stat. Soc. 2001, 164, 73–85. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Carlin, B.; Banerjee, S. Hierarchical Multivariate CAR Models for Spatio-Temporally Correlated Survival Data. Bayesian Stat. 2003, 7, 45–63. [Google Scholar]
- Arellano-Valle, R.; Bolfarine, H.; Lachos, V. Bayesian Inference for Skew-normal Linear Mixed Models. J. Appl. Stat. 2007, 34, 663–682. [Google Scholar] [CrossRef]
- Ghosh, P.; Branco, M.D.; Chakraborty, H. Bivariate random effect model using skew-normal distribution with application to HIV-RNA. Stat. Med. 2007, 26, 1255–1267. [Google Scholar] [CrossRef]
- Verbeke, G.; Lesaffre, E. A Linear Mixed-Effects Model with Heterogeneity in the Random-Effects Population. J. Am. Stat. Assoc. 1996, 91, 217–221. [Google Scholar] [CrossRef]
- Lunn, D.; Jackson, C.; Best, N.; Thomas, A.; Spiegelhalter, D. The BUGS Book: A Practical Introduction to Bayesian Analysis; CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Manda, S.O.M. Macro Determinants of Geographical Variation in Childhood Survival in South Africa Using Flexible Spatial Mixture Models. In Demographic Methods and Population Analysis; Kandala, N.-B., Ghilagaber, G., Eds.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Kim, H.-M.; Mallick, B.K. A Bayesian prediction using the skew Gaussian distribution. J. Stat. Plan. Inference 2004, 120, 85–101. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Genton, M.; Zhang, H. Identifiability problems in some non-Gaussian spatial random fields. Chil. J. Stat. 2012, 3, 171–179. [Google Scholar]
- Gelfand, A.E.; Sahu, S.K. Identifiability, Improper Priors, and Gibbs Sampling for Generalized Linear Models. J. Am. Stat. Assoc. 1999, 94, 247–253. [Google Scholar] [CrossRef]
- Zhang, H.; El-Shaarawi, A. On spatial ske—Gaussian processes and applications. Environmetrics 2009, 21, 33–47. [Google Scholar]
- Allard, D.; Naveau, P. A New Spatial Skew-Normal Random Field Model. Commun. Stat. Theory Methods 2007, 36, 1821–1834. [Google Scholar] [CrossRef]
- Zareifard, H.; Khaledi, M.J. Non-Gaussian modeling of spatial data using scale mixing of a unified skew Gaussian process. J. Multivar. Anal. 2013, 114, 16–28. [Google Scholar] [CrossRef]
- Domınguez-Molina, J.; González-Farıas, G.; Gupta, A. The Multivariate Closed Skew Normal Distribution; Technical Report; Department of Mathematics and Statistics, Bowling Green State University: Bowling Green, OH, USA, 2003. [Google Scholar]
- Palacios, M.B.; Steel, M.F.J. Non-Gaussian Bayesian Geostatistical Modeling. J. Am. Stat. Assoc. 2006, 101, 604–618. [Google Scholar] [CrossRef]
- Rantini, D.; Iriawan, N.; Irhamah, I. Fernandez–Steel Skew Normal Conditional Autoregressive (FSSN CAR) Model in Stan for Spatial Data. Symmetry 2021, 13, 545. [Google Scholar] [CrossRef]
- Fernández, C.; Steel, M.F.J. On Bayesian Modeling of Fat Tails and Skewness. J. Am. Stat. Assoc. 1998, 93, 359–371. [Google Scholar]
- Dwyer-Lindgren, L.; Cork, M.A.; Sligar, A.; Steuben, K.M.; Wilson, K.F.; Provost, N.R.; Mayala, B.K.; Vander Heide, J.D.; Collison, M.L.; Hall, J.B.; et al. Mapping HIV prevalence in sub-Saharan Africa between 2000 and 2017. Nat. Cell Biol. 2019, 570, 189–193. [Google Scholar] [CrossRef]
- Cuadros, D.F.; Abu-Raddad, L.J. Spatial variability in HIV prevalence declines in several countries in sub-Saharan Africa. Health Place 2014, 28, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Tanser, F.; Tomita, A.; Vandormael, A.; Cuadros, D.F. Beyond HIV prevalence: Identifying people living with HIV within underserved areas in South Africa. BMJ Glob. Health 2021, 6, e004089. [Google Scholar] [CrossRef]
- Gutreuter, S.; Igumbor, E.; Wabiri, N.; Desai, M.; Durand, L. Improving estimates of district HIV prevalence and burden in South Africa using small area estimation techniques. PLoS ONE 2019, 14, e0212445. [Google Scholar] [CrossRef]
- Nathoo, F.S.; Ghosh, P. Skew-elliptical spatial random effect modeling for areal data with application to mapping health utilization rates. Stat. Med. 2013, 32, 290–306. [Google Scholar] [CrossRef]
- Kish, L. Methods for Design Effects. J. Off. Stat. 1995, 11, 55–77. [Google Scholar]
- Chen, C.; Wakefield, J.; Lumely, T. The use of sampling weights in Bayesian hierarchical models for small area estimation. Spat. Spatio-Temporal Epidemiol. 2014, 11, 33–43. [Google Scholar] [CrossRef]
- Vandendijck, Y.; Faes, C.; Kirby, R.; Lawson, A.; Hens, N. Model-based inference for small area estimation with sampling weights. Spat. Stat. 2016, 18, 455–473. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.K.; Dey, D.K.; Branco, M.D. A new class of multivariate skew distributions with applications to bayesian regression models. Can. J. Stat. 2003, 31, 129–150. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit (with discussion). J. R. Stat. Soc. Ser. B 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Cai, B.; Lawson, A.B.; Hossain, M.; Choi, J.; Kirby, R.S.; Liu, J. Bayesian semiparametric model with spatially-temporally varying coefficients selection. Stat. Med. 2013, 32, 3670–3685. [Google Scholar] [CrossRef]
- Thomas, A.; Best, N.; Lunn, D. WinBUGS User Manual: Version 1.4. 2001. Available online: https://www.mrc-bsu.cam.ac.uk/wp-content/uploads/manual14.pdf (accessed on 1 August 2021).
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- National Department of Health. South Africa Demographic and Health Survey 2016. Available online: https://dhsprogram.com/pubs/pdf/FR337/FR337.pdf (accessed on 1 August 2021).
- Fransman, T.; Yu, D. Multidimensional poverty in South Africa in 2001–2016. Dev. S. Afr. 2019, 36, 50–79. [Google Scholar] [CrossRef]
- Woldesenbet, S.A.; Kufa, T.; Lombard, C.; Manda, S.; Ayalew, K.; Cheyip, M.; Puren, A. The 2017 National Antenatal Sentinel HIV Survey Key Findings; National Institute of Communicable Disease: Pretoria, South Africa, 2019.
- Massyn, N.; Padarath, A.; Peer, N.; Day, C. District Health Barometer 2016/17; Health System Trust: Durban, South Africa, 2017.
- Van Schalkwyk, C.; Dorrington, R.E.; Seatlhodi, T.; Velasquez, C.; Feizzadeh, A.; Johnson, L.F. Modelling of HIV prevention and treatment progress in five South African metropolitan districts. Sci. Rep. 2021, 11, 5652. [Google Scholar] [CrossRef]
- De la Cruz, R.; Branco, M.D. Bayesian analysis for nonlinear regression model under skewed errors, with application in growth curves. Biom. J. 2009, 51, 588–609. [Google Scholar] [CrossRef]
| Covariates | ICAR-Normal | ICAR-Laplace | ICAR-Skew-t |
|---|---|---|---|
| Intercept | 2.473 (−3.288, −1.65) | −2.542 (−3.321, −1.743) | −2.538 (−3.625, −1.469) |
| Population density | −0.0001 (−0.0003, 0.0002) | −0.0001 (−0.0003, 0.0002) | 0.0001 (−0.0003, 0.0002) |
| Male condom distribution | −0.0070 (−0.0183, 0.0069) | −0.0064 (−0.0178, 0.0039) | −0.0069 (−0.0177, 0.0032) |
| Multidimensional poverty index | 0.81056 (−2.826, 4.7939) | 0.593 (−3.139, 4.357) | 0.8934 (−2.915, 4.71) |
| ANC HIV prevalence | 3.778 (1.673, 5.7058) | 3.974 (2.074, 5.897) | 3.831 (1.7, 5.931) |
| 0.0061 (0.0006, 0.6596) | 0.0059 (0.0006, 0.9225) | 0.0088 (0.0009, 0.4719) | |
| 0.0066 (0.0007, 0.2281) | 0.0106 (0.0011, 0.2434) | 0.0031 (0.0004, 0.1688) | |
| 0.05 (−0.6, 0.62) | |||
| DIC | 291.3 | 315 | 348.1 |
| 172.4 | 174 | 170.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayalew, K.A.; Manda, S.; Cai, B. A Comparison of Bayesian Spatial Models for HIV Mapping in South Africa. Int. J. Environ. Res. Public Health 2021, 18, 11215. https://doi.org/10.3390/ijerph182111215
Ayalew KA, Manda S, Cai B. A Comparison of Bayesian Spatial Models for HIV Mapping in South Africa. International Journal of Environmental Research and Public Health. 2021; 18(21):11215. https://doi.org/10.3390/ijerph182111215
Chicago/Turabian StyleAyalew, Kassahun Abere, Samuel Manda, and Bo Cai. 2021. "A Comparison of Bayesian Spatial Models for HIV Mapping in South Africa" International Journal of Environmental Research and Public Health 18, no. 21: 11215. https://doi.org/10.3390/ijerph182111215
APA StyleAyalew, K. A., Manda, S., & Cai, B. (2021). A Comparison of Bayesian Spatial Models for HIV Mapping in South Africa. International Journal of Environmental Research and Public Health, 18(21), 11215. https://doi.org/10.3390/ijerph182111215







