How Does Air Pollution Influence Housing Prices in the Bay Area?
Abstract
:1. Introduction
2. Materials and Methods
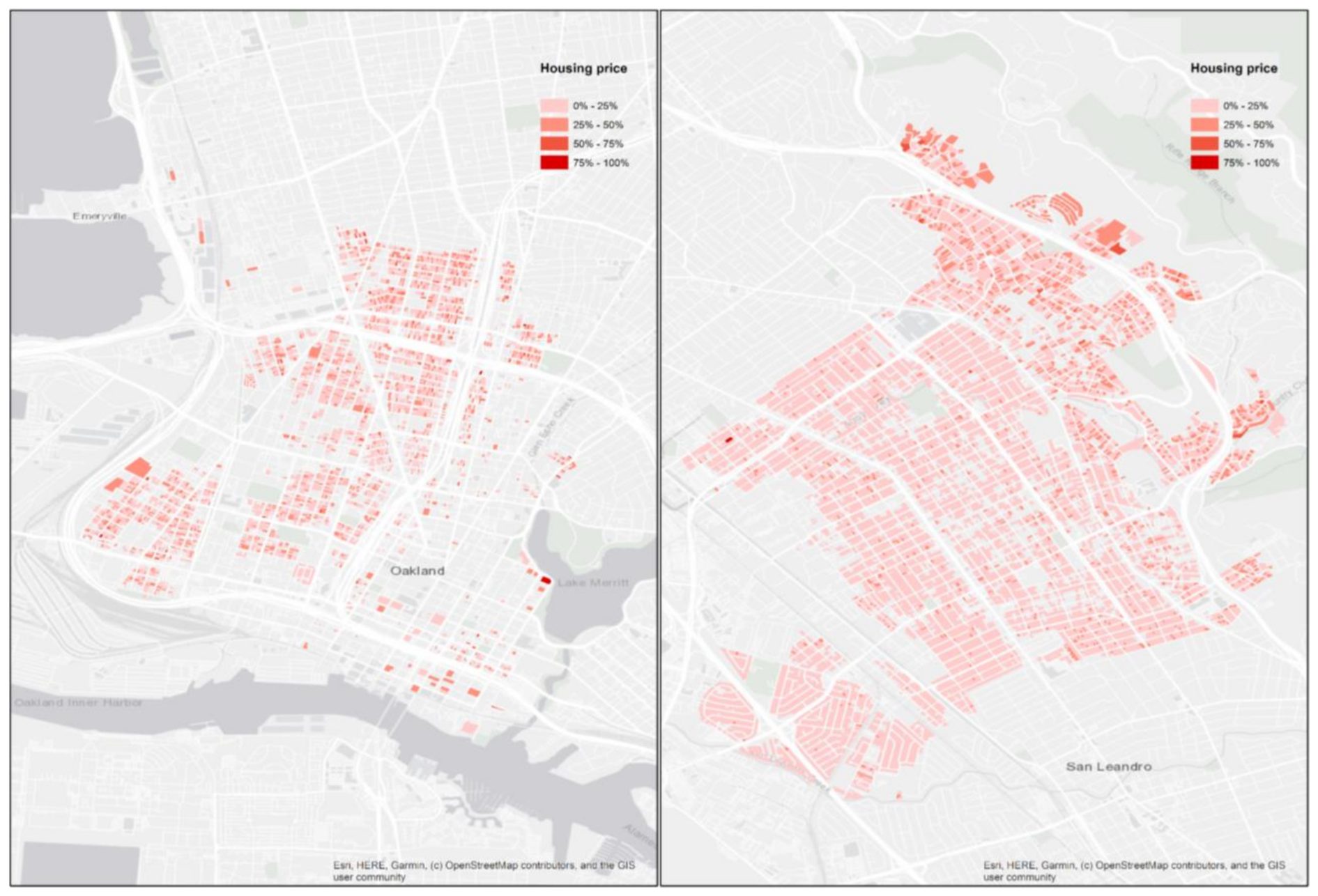
2.1. Study Area
2.2. Pollutant Concentration and Housing Valuation Data
2.3. Methods
3. Results and Discussion
3.1. Variable Distribution
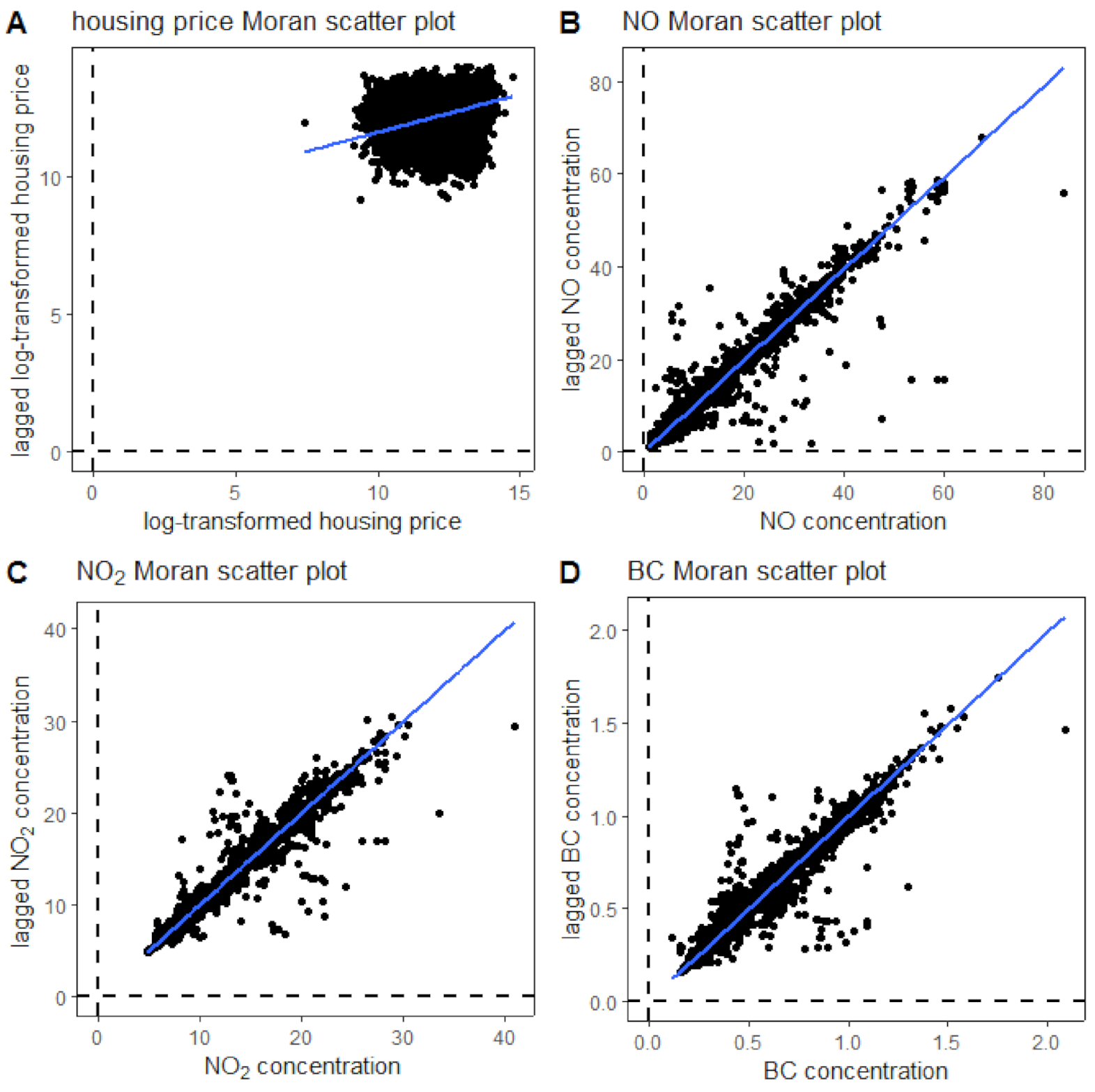
3.2. Spatial Autocorrelation
3.3. Spatial Lag Model Results
3.4. Discussion
4. Limitations and Conclusions
Author Contributions
Funding
Data Availability Statement:
Conflicts of Interest
References
- Apte, J.S.; Marshall, J.D.; Cohen, A.J.; Brauer, M. Addressing Global Mortality from Ambient PM2.5. Environ. Sci. Technol. 2015, 49, 8057–8066. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.S.; Vos, T.; Flaxman, A.D.; Danaei, G.; Shibuya, K.; Adair-Rohani, H.; AlMazroa, M.A.; Amann, M.; Anderson, H.R.; Andrews, K.G.; et al. A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990–2010: A systematic analysis for the Global Burden of Disease Study 2010. Lancet 2012, 380, 2224–2260. [Google Scholar] [CrossRef] [Green Version]
- Robinson, E. How Much Does Air Pollution Cost the U.S.? Available online: https://earth.stanford.edu/news/how-much-does-air-pollution-cost-us#gs.6njexm (accessed on 30 August 2020).
- Tschofen, P.; Azevedo, I.L.; Muller, N.Z. Fine particulate matter damages and value added in the US economy. Proc. Natl. Acad. Sci. USA 2019, 116, 19857–19862. [Google Scholar] [CrossRef] [Green Version]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Ekeland, I.; Heckman, J.J.; Nesheim, L. Identifying Hedonic Models. Am. Econ. Rev. 2002, 92, 304–309. [Google Scholar] [CrossRef] [Green Version]
- Raya, J.M.; Estévez, P.G.; Prado-Román, C.; Pruñonosa, J.T. Living in a Smart City Affects the Value of a Dwelling? In BT—Sustainable Smart Cities: Creating Spaces for Technological, Social and Business Development; Peris-Ortiz, M., Bennett, D.R., Pérez-Bustamante Yábar, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 193–198. ISBN 978-3-319-40895-8. [Google Scholar]
- Torres-Pruñonosa, J.; García-Estévez, P.; Prado-Román, C. Artificial Neural Network, Quantile and Semi-Log Regression Modelling of Mass Appraisal in Housing. Mathematics 2021, 9, 783. [Google Scholar] [CrossRef]
- Betz, T.; Cook, S.J.; Hollenbach, F.M. Spatial interdependence and instrumental variable models. Political Sci. Res. Methods 2020, 8, 646–661. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, F.; Leipnik, M.; Mazumder, D. How much are urban residents in Mexico willing to pay for cleaner air? Environ. Dev. Econ. 2013, 18, 354–379. [Google Scholar] [CrossRef]
- Ligus, M.; Peternek, P. Impacts of Urban Environmental Attributes on Residential Housing Prices in Warsaw (Poland): Spatial Hedonic Analysis of City Districts. In BT—Contemporary Trends and Challenges in Finance; Jajuga, K., Orlowski, L.T., Staehr, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 155–164. [Google Scholar]
- Kim, S.G.; Yoon, S. Measuring the value of airborne particulate matter reduction in Seoul. Air Qual. Atmos. Health 2019, 12, 549–560. [Google Scholar] [CrossRef]
- Montero, J.-M.; Mínguez, R.; Fernández-Avilés, G. Housing price prediction: Parametric versus semi-parametric spatial hedonic models. J. Geogr. Syst. 2018, 20, 27–55. [Google Scholar] [CrossRef]
- De, U.K.; Vupru, V. Location and neighbourhood conditions for housing choice and its rental value. Int. J. Hous. Mark. Anal. 2017, 10, 519–538. [Google Scholar] [CrossRef]
- Sun, B.; Yang, S. Asymmetric and Spatial Non-Stationary Effects of Particulate Air Pollution on Urban Housing Prices in Chinese Cities. Int. J. Environ. Res. Public Health 2020, 17, 7443. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.W.; Phipps, T.T.; Anselin, L. Measuring the benefits of air quality improvement: A spatial hedonic approach. J. Environ. Econ. Manag. 2003, 45, 24–39. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Jin, H. Pricing for the clean air: Evidence from Chinese housing market. J. Clean. Prod. 2019, 206, 297–306. [Google Scholar] [CrossRef]
- Bayer, P.; Keohane, N.; Timmins, C. Migration and hedonic valuation: The case of air quality. J. Environ. Econ. Manag. 2009, 58, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Mei, Y.; Gao, L.; Zhang, J.; Wang, J. Valuing urban air quality: A hedonic price analysis in Beijing, China. Environ. Sci. Pollut. Res. 2020, 27, 1373–1385. [Google Scholar] [CrossRef]
- Chay, K.Y.; Greenstone, M. Does Air Quality Matter? Evidence from the Housing Market. J. Political Econ. 2005, 113, 376–424. [Google Scholar] [CrossRef] [Green Version]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Yu, C.; Liu, C.; Jiang, J.; Xu, J. Impacts of Haze on Housing Prices: An Empirical Analysis Based on Data from Chengdu (China). Int. J. Environ. Res. Public Health 2018, 15, 1161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bae, C.-H.C.; Sandlin, G.; Bassok, A.; Kim, S. The exposure of disadvantaged populations in freeway air-pollution sheds: A case study of the Seattle and Portland regions. Environ. Plan. B Plan. Des. 2007, 34, 154–170. [Google Scholar] [CrossRef]
- Point2. Central East Demographics. Available online: https://www.point2homes.com/US/Neighborhood/CA/Oakland/Central-East-Demographics.html (accessed on 25 July 2021).
- Apte, J.S.; Messier, K.P.; Gani, S.; Brauer, M.; Kirchstetter, T.W.; Lunden, M.M.; Marshall, J.D.; Portier, C.J.; Vermeulen, R.C.H.; Hamburg, S.P. High-Resolution Air Pollution Mapping with Google Street View Cars: Exploiting Big Data. Environ. Sci. Technol. 2017, 51, 6999–7008. [Google Scholar] [CrossRef] [PubMed]
- Google. Oakland_201506-201605_GoogleAclimaAQ. Available online: https://www.edf.org/airqualitymaps/oakland/methodology-how-we-collected-data (accessed on 1 November 2017).
- Karner, A.A.; Eisinger, D.S.; Niemeier, D.A. Near-Roadway Air Quality: Synthesizing the Findings from Real-World Data. Environ. Sci. Technol. 2010, 44, 5334–5344. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Levy, J.I. Factors influencing the spatial extent of mobile source air pollution impacts: A meta-analysis. BMC Public Health 2007, 7, 89. [Google Scholar] [CrossRef] [Green Version]
- Arraiz, I.; Drukker, D.M.; Kelejian, H.H.; Prucha, I.R. A Spatial Cliff-Ord-Type Model with Heteroskedastic Innovations: Small and Large Sample Results. J. Reg. Sci. 2009, 50, 592–614. [Google Scholar] [CrossRef] [Green Version]
- Drukker, D.M.; Egger, P.; Prucha, I.R. On Two-Step Estimation of a Spatial Autoregressive Model with Autoregressive Disturbances and Endogenous Regressors. Econ. Rev. 2013, 32, 686–733. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. J. Econ. 2010, 157, 53–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kelejian, H.H.; Prucha, I.R. A Generalized Moments Estimator for the Autoregressive Parameter in a Spatial Model. Int. Econ. Rev. 1999, 40, 509–533. [Google Scholar] [CrossRef] [Green Version]
- Kelejian, H.H.; Prucha, I.R. A Generalized Spatial Two-Stage Least Squares Procedure for Estimating a Spatial Autoregressive Model with Autoregressive Disturbances. J. Real Estate Financ. Econ. 1998, 17, 99–121. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Piras, G. sphet: Spatial Models with Heteroskedastic Innovations in R. J. Stat. Softw. 2010, 35, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Bivand, R.; Piras, G. Comparing Implementations of Estimation Methods for Spatial Econometrics. J. Stat. Softw. 2015, 63, 1–36. [Google Scholar] [CrossRef] [Green Version]
- EPA. NAAQS Table. Available online: https://www.epa.gov/criteria-air-pollutants/naaqs-table (accessed on 2 August 2021).

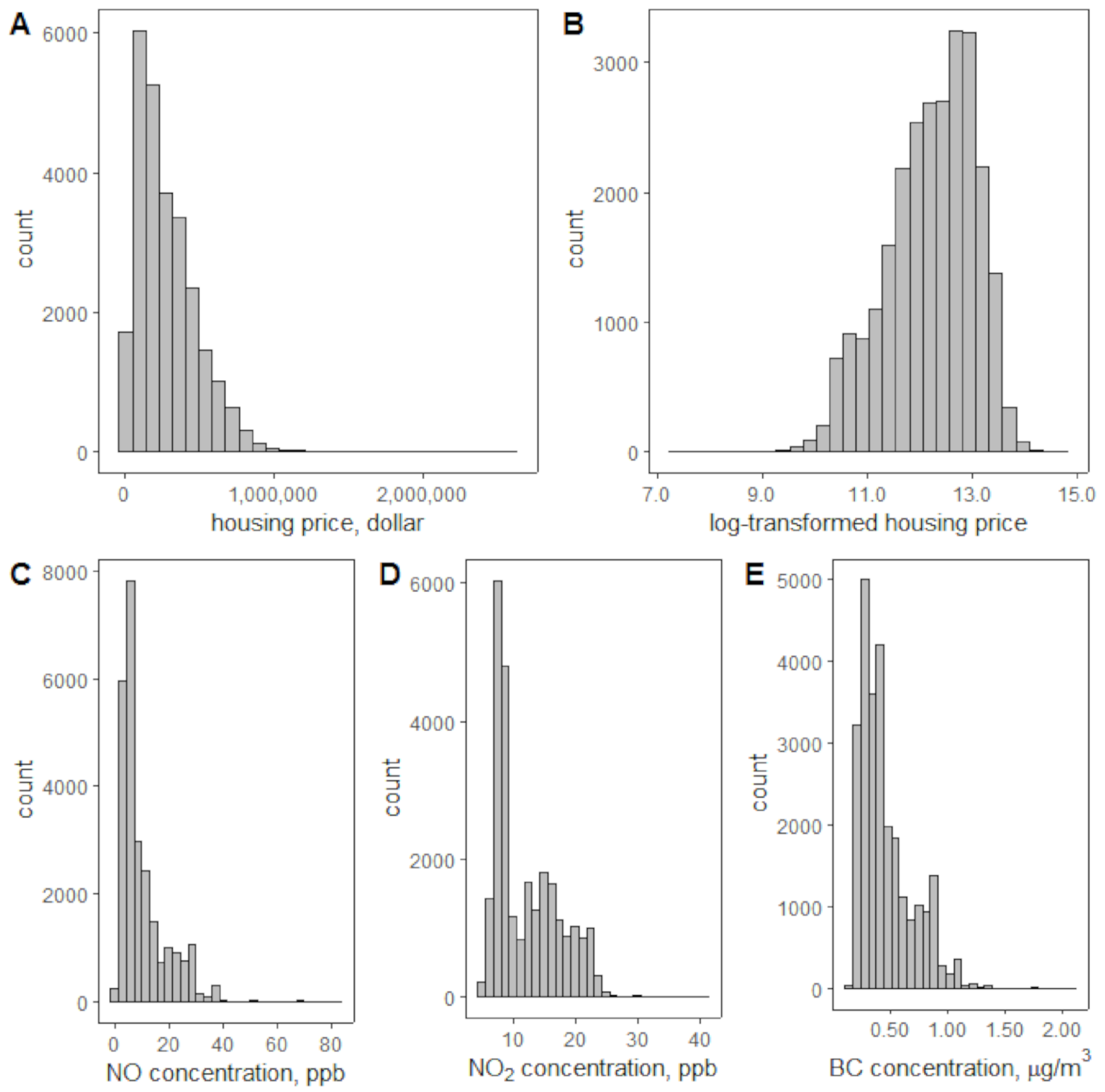

| Housing Price, USD | NO Concentration, ppb | NO2 Concentration, ppb | BC Concentration, µg/m3 | |
|---|---|---|---|---|
| Sample size | 26,386 a | 26,210 a | 26,210 a | 26,210 a |
| Mean | 275,664.1 | 10.293 | 12.121 | 0.457 |
| Median | 227,788.4 | 6.632 | 9.883 | 0.393 |
| Standard deviation | 200,586.2 | 8.68 | 5.07 | 0.23 |
| Housing Price | NO Concentration | NO2 Concentration | BC Concentration | |
|---|---|---|---|---|
| Moran’s I test statistic | 0.27643 | 0.98498 | 0.9927 | 0.99127 |
| Analytical method p-value | <0.001 | <0.001 | <0.001 | <0.001 |
| Monte-Carlo-based p-value | <0.001 | <0.001 | <0.001 | <0.001 |
| Variables | NO Concentration | NO2 Concentration | BC Concentration |
|---|---|---|---|
| Intercept | 2.9196 *** (0.4688) | 2.5027 *** (0.45954) | 2.8232 *** (0.46502) |
| Year Built | −0.0070745 *** (0.00033103) | −0.0068693 *** (0.00032984) | −0.0070433 *** (0.0003305) |
| Effective Year Built | 0.010137 *** (0.0003401) | 0.010268 *** (0.00033955) | 0.010166 *** (0.00033986) |
| Construction type: concrete | −0.014669 (0.061875) | −0.0076211 (0.061662) | −0.0041038 (0.061783) |
| Construction type: frame | −0.3531 *** (0.020988) | −0.32364 *** (0.021187) | −0.34251 *** (0.021) |
| Construction type: masonry | −0.36805 *** (0.075532) | −0.32321 *** (0.074869) | −0.35448 *** (0.075232) |
| Other rooms: gym | −0.10416 ** (0.043856) | −0.080572 * (0.04356) | −0.092731 ** (0.043693) |
| Other rooms: office | 0.17428 (0.40627) | 0.18374 (0.4051) | 0. 18428 (0.40593) |
| Parking type: Carport | −0.027576 (0.029369) | −0.016681 (0.029342) | −0.020942 (0.029382) |
| Parking type: garage | 0.051695 *** (0.010082) | 0.061715 *** (0.010229) | 0.055929 *** (0.010152) |
| Parking type: Mixed | −0.0064772 (0.041319) | 0.0046338 (0.041243) | −0.00011624 (0.04131) |
| Stories | 0.020611 *** (0.0021083) | 0.017629 *** (0.0021295) | 0.020372 *** (0.0021063) |
| Rooms | −0.0095808 ** (0.0040749) | −0.0096307 ** (0.0060424) | −0.094721 ** (0.0040706) |
| Beds | −0.010024 (0.0064244) | −0.0092185 (0.0064047) | −0.010209 (0.0064193) |
| Baths | 0.084969 *** (0.0086318) | 0.082202 *** (0.0086111) | 0.08463 *** (0.0086243) |
| Total area | 0.00027102 *** (0.000014127) | 0.00026972 *** (0.000014055) | 0.0002711 *** (0.000014107) |
| Population density | 0.000014708 *** ) | 0.00017308 *** ) | 0.000018455 *** ) |
| Median income | *** ) | *** ) | *** ) |
| Non-employment rate | 0.07601 (0.050197) | 0.031651 (0.050804) | 0.081003 (0.04948) |
| NO concentration | 0.0054361 *** (0.00082701) | - | - |
| NO2 concentration | - | 0.013246 *** (0.0016209) | - |
| BC concentration | - | - | 0.22871 *** (0.03212) |
| lambda | 0.21710 *** (0.019776) | 0.18774 *** (0.020526) | 0.20761 *** (0.020015) |
| R2 | 0.3183 | 0.3175 | 0.3178 |
| Location | Air Pollution Concentrations | Method | Air Pollution Impact on Housing Price | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CO, µg/m3 | NO2, µg/m3 | O3, µg/m3 | PM2.5, µg/m3 | PM10, µg/m3 | SO2, µg/m3 | TSP, µg/m3 | BC, µg/m3 | NO, µg/m3 | |||
| Seoul, Korea (Kim & Yoon, 2019) | 45.611 | SDM | insignificant | ||||||||
| Seoul, Korea (C.W. Kim, Phipps, & Anselin, 2003) | 45.57 a | SLM, SEM | insignificant | ||||||||
| 82.95 | negative | ||||||||||
| 18 districts in Warsaw, Poland (Ligus & Peternek, 2017) | __ | __ | Linear, Logarithm, SLM, SEM | insignificant b | |||||||
| Beijing, China (Mei, et al. 2020) | 1399.1 | Fixed effect | negative | ||||||||
| 60.34 | negative | ||||||||||
| 53.66 | positive | ||||||||||
| 88.24 | negative | ||||||||||
| 111.27 | negative | ||||||||||
| 20.5 | negative | ||||||||||
| 286 prefectural cities in China (Chen & Jin, 2019) | 64.81 | IV | negative | ||||||||
| 288 Chinese cities (Huang & Lanz, 2018) | 77.44 | IV and discontinuity regression | negative | ||||||||
| 3 largest cities in Mexico (Gonzalez, Leipnik & Mazumder, 2013) | 38.5, 51.7, 84 | IV | negative | ||||||||
| Metro areas US (Bayer et al., 2009) | 42.21 (1990), 33.87 (2000) | IV | negative | ||||||||
| All counties in USA (Chay & Greenstone, 2005) | 64.1 (1970), 56.3 (1980) | quasi-experimental discontinuity regression | negative | ||||||||
| Lebanon (Marrouch & Sayour, 2021) | 27.67 | Fixed effect | negative | ||||||||
| Oakland, CA, USA | 22.79 | 0.457 | 12.86 | IV and SLM | positive | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Niemeier, D. How Does Air Pollution Influence Housing Prices in the Bay Area? Int. J. Environ. Res. Public Health 2021, 18, 12195. https://doi.org/10.3390/ijerph182212195
Tang M, Niemeier D. How Does Air Pollution Influence Housing Prices in the Bay Area? International Journal of Environmental Research and Public Health. 2021; 18(22):12195. https://doi.org/10.3390/ijerph182212195
Chicago/Turabian StyleTang, Minmeng, and Deb Niemeier. 2021. "How Does Air Pollution Influence Housing Prices in the Bay Area?" International Journal of Environmental Research and Public Health 18, no. 22: 12195. https://doi.org/10.3390/ijerph182212195
APA StyleTang, M., & Niemeier, D. (2021). How Does Air Pollution Influence Housing Prices in the Bay Area? International Journal of Environmental Research and Public Health, 18(22), 12195. https://doi.org/10.3390/ijerph182212195







