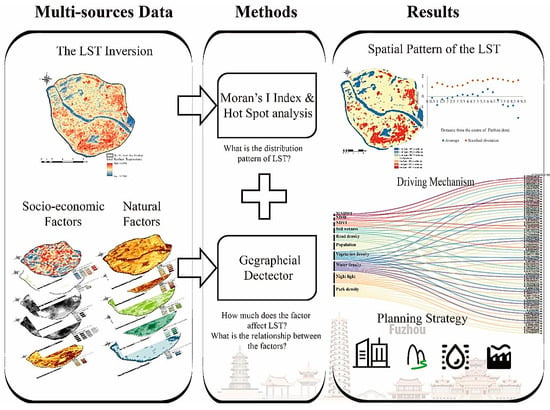
Quantitative Analysis of a Spatial Distribution and Driving Factors of the Urban Heat Island Effect: A Case Study of Fuzhou Central Area, China
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Scope: The Fuzhou Central Area, China
2.2. Data Preparation
2.3. Methodology
2.3.1. Retrieval of LST from Landsat Images
2.3.2. Spatial Analysis of the LST
2.3.3. Selection of UHI Drivers
2.3.4. Scale Section and Buffer Analysis
2.3.5. Geodetector Analysis
3. Results
3.1. Spatial Distribution Characteristics of the LST
3.2. Impact of a Single Influence Factor on LST
3.3. Interaction of Driving Factors on LST
4. Discussion and Prospect
4.1. The Spatial Pattern Analysis of LST
4.2. The Impact of a Single Factor on LST
4.3. Interaction of LST Drivers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Optimal Scale Pre-Experiment
| Net Size | Geographical Factor | Socio-Economic Factor | |||||
|---|---|---|---|---|---|---|---|
| NDBI X1 | MNDWI X2 | NDVI X3 | RDD X4 | PPD X5 | NL X6 | ||
| 100 m × 100 m | q-Value | 0.571 | 0.540 | 0.557 | 0.169 | 0.030 | 0.113 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 200 m × 200 m | q-Value | 0.571 | 0.584 | 0.596 | 0.173 | 0.032 | 0.123 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 300 m × 300 m | q-Value | 0.681 | 0.645 | 0.641 | 0.176 | 0.039 | 0.136 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 400 m × 400 m | q-Value | 0.653 | 0.615 | 0.634 | 0.179 | 0.041 | 0.135 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.000 | |
| 500 m × 500 m | q-Value | 0.728 | 0.658 | 0.642 | 0.185 | 0.057 | 0.137 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 | 0.041 | 0.000 | |
| Net Size | Geographical Factor | Socio-Economic Factor | |||||
|---|---|---|---|---|---|---|---|
| NDBI X1 | MNDWI X2 | NDVI X3 | RDD X4 | PPD X5 | NL X6 | ||
| 100 m × 100 m | X1 | 0.571 | |||||
| X2 | 0.683 | 0.540 | |||||
| X3 | 0.681 | 0.617 | 0.557 | ||||
| X4 | 0.650 | 0.682 | 0.630 | 0.169 | |||
| X5 | 0.624 | 0.681 | 0.601 | 0.358 | 0.030 | ||
| X6 | 0.617 | 0.678 | 0.605 | 0.384 | 0.105 | 0.113 | |
| 200 m × 200 m | X1 | 0.571 | |||||
| X2 | 0.671 | 0.584 | |||||
| X3 | 0.675 | 0.659 | 0.596 | ||||
| X4 | 0.640 | 0.617 | 0.716 | 0.173 | |||
| X5 | 0.626 | 0.605 | 0.664 | 0.348 | 0.032 | ||
| X6 | 0.622 | 0.609 | 0.683 | 0.378 | 0.108 | 0.123 | |
| 300 m × 300 m | X1 | 0.681 | |||||
| X2 | 0.775 | 0.645 | |||||
| X3 | 0.770 | 0.710 | 0.641 | ||||
| X4 | 0.744 | 0.654 | 0.728 | 0.176 | |||
| X5 | 0.696 | 0.665 | 0.670 | 0.345 | 0.039 | ||
| X6 | 0.704 | 0.660 | 0.698 | 0.381 | 0.116 | 0.136 | |
| 400 m × 400 m | X1 | 0.653 | |||||
| X2 | 0.747 | 0.615 | |||||
| X3 | 0.749 | 0.694 | 0.634 | ||||
| X4 | 0.704 | 0.621 | 0.717 | 0.179 | |||
| X5 | 0.681 | 0.625 | 0.654 | 0.358 | 0.041 | ||
| X6 | 0.682 | 0.620 | 0.686 | 0.380 | 0.110 | 0.135 | |
| 500 m × 500 m | X1 | 0.728 | |||||
| X2 | 0.815 | 0.658 | |||||
| X3 | 0.813 | 0.758 | 0.642 | ||||
| X4 | 0.778 | 0.664 | 0.736 | 0.185 | |||
| X5 | 0.732 | 0.667 | 0.674 | 0.354 | 0.057 | ||
| X6 | 0.731 | 0.658 | 0.706 | 0.388 | 0.117 | 0.137 | |
References
- Du, Y.; Xie, Z.; Zeng, Y.; Shi, Y.; Wu, J. Impact of urban expansion on regional temperature change in the Yangtze River Delta. J. Geogr. Sci. 2007, 17, 387–398. [Google Scholar] [CrossRef]
- Santarnouris, M.; Kolokotsa, D. On the impact of urban overheating and extreme climatic conditions on housing, energy, comfort and environmental quality of vulnerable population in Europe. Energy Build. 2015, 98, 125–133. [Google Scholar] [CrossRef]
- United Nations. World Urbanization Prospects: The 2018 Revision. Available online: https://population.un.org/wup/ (accessed on 1 April 2021).
- Edenhofer, O. Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, MA, USA, 2007; ISBN 978-1-107-05821-7. [Google Scholar]
- Grimmond, C.S.B.; Roth, M.; Oke, T.R.; Au, Y.C.; Best, M.; Betts, R.; Carmichael, G.; Cleugh, H.; Dabberdt, W.; Emmanuel, R.; et al. Climate and More Sustainable Cities: Climate Information for Improved Planning and Management of Cities (Producers/Capabilities Perspective). In Proceedings of the 3rd World Climate Conference (WCC) on Climate Prediction and Information for Decision-Making, Geneva, Switzerland, 31 August–4 September 2009; pp. 247–274. [Google Scholar]
- Roth, M. Urban Heat Islands. Handb. Environ. Fluid Dyn. 2012, 2, 143–160. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Reducing Urban Heat Islands: Compendium of Strategies. Available online: https://www.epa.gov/heatislands/heat-island-compendium (accessed on 1 April 2021).
- Oke, T.R. The energetic basic of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Min, M.; Lin, C.; Duan, X.; Jin, Z.; Zhang, L. Spatial distribution and driving force analysis of urban heat island effect based on raster data: A case study of the Nanjing metropolitan area, China. Sustain. Cities Soc. 2019, 50, 101637. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2016, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The distinction between canopy and boundary-layer urban heat islands. Atmosphere 1976, 14, 268–277. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.W.; Brown, R.D. Urban heat island (UHI) intensity and magnitude estimations: A systematic literature review. Sci. Total Environ. 2021, 779, 146389. [Google Scholar] [CrossRef]
- Hong, J.-W.; Hong, J.; Kwon, E.E.; Yoon, D.K. Temporal dynamics of urban heat island correlated with the socio-economic development over the past half-century in Seoul, Korea. Environ. Pollut. 2019, 254, 112934. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.; Mirzaei, P.A.; Zhang, J.; Zhao, Z. Urban heat island effect of a typical valley city in China: Responds to the global warming and rapid urbanization. Sustain. Cities Soc. 2018, 38, 736–745. [Google Scholar] [CrossRef]
- Ramamurthy, P.; Sangobanwo, M. Inter-annual variability in urban heat island intensity over 10 major cities in the United States. Sustain. Cities Soc. 2016, 26, 65–75. [Google Scholar] [CrossRef]
- Busato, F.; Lazzarin, R.M.; Noro, M. Three years of study of the Urban Heat Island in Padua: Experimental results. Sustain. Cities Soc. 2014, 10, 251–258. [Google Scholar] [CrossRef]
- Xu, H.; Lin, D.; Tang, F. The impact of impervious surface development on land surface temperature in a subtropical city: Xiamen, China. Int. J. Climatol. 2013, 33, 1873–1883. [Google Scholar] [CrossRef]
- Kumari, B.; Tayyab, M.; Shahfahad, S.; Mallick, J.; Khan, M.F.; Rahman, A. Satellite-Driven Land Surface Temperature (LST) Using Landsat 5, 7 (TM/ETM+ SLC) and Landsat 8 (OLI/TIRS) Data and Its Association with Built-Up and Green Cover Over Urban Delhi, India. Remote Sens. Earth Syst. Sci. 2018, 1, 63–78. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Masson, V. Urban surface modeling and the meso-scale impact of cities. Theor. Appl. Climatol. 2006, 84, 35–45. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-107-42953-6. [Google Scholar]
- Gomez-Martinez, F.; de Beurs, K.M.; Koch, J.; Widener, J. Multi-Temporal Land Surface Temperature and Vegetation Greenness in Urban Green Spaces of Puebla, Mexico. Land 2021, 10, 155. [Google Scholar] [CrossRef]
- Chi, X.; Li, R.; Cubasch, U.; Cao, W. The thermal comfort and its changes in the 31 provincial capital cities of mainland China in the past 30 years. Theor. Appl. Climatol. 2018, 132, 599–619. [Google Scholar] [CrossRef]
- Esau, I.; Miles, V.; Varentsov, M.; Konstantinov, P.; Melnikov, V. Spatial structure and temporal variability of a surface urban heat island in cold continental climate. Theor. Appl. Climatol. 2019, 137, 2513–2528. [Google Scholar] [CrossRef]
- Marzban, F.; Sodoudi, S.; Preusker, R. The influence of land-cover type on the relationship between NDVI-LST and LST-T-air. Int. J. Remote Sens. 2018, 39, 1377–1398. [Google Scholar] [CrossRef]
- Amani-Beni, M.; Zhang, B.; Xie, G.-D.; Shi, Y. Impacts of Urban Green Landscape Patterns on Land Surface Temperature: Evidence from the Adjacent Area of Olympic Forest Park of Beijing, China. Sustainability 2019, 11, 513. [Google Scholar] [CrossRef] [Green Version]
- Klimenko, V.V.; Ginzburg, A.S.; Demchenko, P.F.; Tereshin, A.G.; Belova, I.N.; Kasilova, E.V. Impact of urbanization and climate warming on energy consumption in large cities. Dokl. Phys. 2016, 61, 521–525. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R.; Krayenhoff, E.S. Evaluation of the ‘local climate zone’ scheme using temperature observations and model simulations. Int. J. Climatol. 2014, 34, 1062–1080. [Google Scholar] [CrossRef]
- Masoud, A.A. Predicting salt abundance in slightly saline soils from Landsat ETM plus imagery using Spectral Mixture Analysis and soil spectrometry. Geoderma 2014, 217, 45–56. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, S.; Wang, Y.; Wei, F.; Huang, J.; Shen, J.; Li, S. The relationship between urban form and heat island intensity along the urban development gradients. Sci. Total Environ. 2020, 708, 135011. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Berardi, U.; Akbari, H. Comparing the effects of urban heat island mitigation strategies for Toronto, Canada. Energy Build. 2016, 114, 2–19. [Google Scholar] [CrossRef]
- Son, J.M.; Eum, J.H.; Kim, D.P.; Kwon, J. Management Strategies of Thermal Environment in Urban Area Using the Cooling Function of the Mountains: A Case Study of the Honam Jeongmaek Areas in South Korea. Sustainability 2018, 10, 4691. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Lu, Y.; Yang, X.; Chen, L. Understanding the variability of urban heat islands from local background climate and urbanization. J. Clean. Prod. 2019, 208, 743–752. [Google Scholar] [CrossRef]
- Jin, C.; Bai, X.; Luo, T.; Zou, M. Effects of green Roofs’variations on the regional thermal environment using measurements and simulations in Chongqing, China. Urban For. Urban Green. 2018, 29, 223–237. [Google Scholar] [CrossRef]
- Chen, H.; Ooka, R.; Huang, H.; Tsuchiya, T. Study on mitigation measures for outdoor thermal environment on present urban blocks in Tokyo using coupled simulation. Build. Environ. 2009, 44, 2290–2299. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Wang, R.; Liu, J. Quantifying the Effects of Urban Form on Land Surface Temperature in Subtropical High-Density Urban Areas Using Machine Learning. Remote Sens. 2019, 11, 959. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhan, Q.; Guo, H.; Jin, Z. Characterizing the spatial dynamics of land surface temperature-impervious surface fraction relationship. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 55–65. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Miaomaio, X.; Wang, Y. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression. Environ. Model. Softw. 2010, 25, 1789–1800. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y. Monitoring surface urban heat island formation in a tropical mountain city using Landsat data (1987–2015). Isprs J. Photogramm. Remote Sens. 2017, 133, 18–29. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S. Impacts of urban landscape patterns on urban thermal variations in Guangzhou, China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 65–71. [Google Scholar] [CrossRef]
- Stewart, F.; Charlton, M.; Brunsdon, C. The Geography of Parameter Space: An Investigation of Spatial Non-stationarity. Int. J. Geogr. Inf. Syst. 1996, 10, 605–627. [Google Scholar] [CrossRef]
- Li, W.; Cao, Q.; Lang, K.; Wu, J. Linking potential heat source and sink to urban heat island: Heterogeneous effects of landscape pattern on land surface temperature. Sci. Total Environ. 2017, 586, 457–465. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yue, H.; Li, Z. Examining the influences of air quality in China’s cities using multi-scale geographically weighted regression. Trans. GIS 2019, 23, 1444–1464. [Google Scholar] [CrossRef]
- Wang, J.-F.; Li, X.-H.; Christakos, G.; Liao, Y.-L.; Zhang, T.; Gu, X.; Zheng, X.-Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, L.; Li, X.; Zhang, C.; Shi, T.; Wu, X.; Yang, C.; Gao, W.; Li, Q.; Wu, G. Exploring Annual Urban Expansions in the Guangdong-Hong Kong-Macau Greater Bay Area: Spatiotemporal Features and Driving Factors in 1986–2017. Remote Sens. 2020, 12, 2615. [Google Scholar] [CrossRef]
- Qu, Y.; Jiang, G.; Tian, Y.; Shang, R.; Wei, S.; Li, Y. Urban—Rural construction land Transition(URCLT) in Shandong Province of China: Features measurement and mechanism exploration. Habitat Int. 2019, 86, 101–115. [Google Scholar] [CrossRef]
- Liu, C.; Xu, Y.; Lu, X.; Han, J. Trade-offs and driving forces of land use functions in ecologically fragile areas of northern Hebei Province: Spatiotemporal analysis. Land Use Policy 2021, 104, 105387. [Google Scholar] [CrossRef]
- Fuzhou Climate Bulletin. Available online: http://www.fuzhou.gov.cn/tjxx/tjfx/202004/t20200416_3249675.htm (accessed on 1 April 2021).
- Hu, L.; Li, Z.; Ye, X. Delineating and modeling activity space using geotagged social media data. Cartogr. Geogr. Inf. Sci. 2020, 47, 277–288. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Bu, Y. Quantitative Analysis of Spatial Heterogeneity and Driving Forces of the Thermal Environment in Urban Built-up Areas: A Case Study in Xi’an, China. Sustainability 2021, 13, 1870. [Google Scholar] [CrossRef]
- Cui, Y.; Yan, D.; Hong, T.; Ma, J. Temporal and spatial characteristics of the urban heat island in Beijing and the impact on building design and energy performance. Energy 2017, 130, 286–297. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Wang, R.; Shen, C.; Da, L. Temporal and spatial characteristics of the urban heat island during rapid urbanization in Shanghai, China. Environ. Monit. Assess. 2010, 169, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, L.; Zhang, X.; Lu, C.; Zhang, L.; Chan, P.W. Analysis of the impact of geographic features, population distribution and power load on heat island effects in the metropolis of Shenzhen. Mausam 2014, 65, 569–574. [Google Scholar]
- Fujian Provincial Bureau of Statistics. 2018 Fujian Statistical Yearbook; China Statistics Press: Beijing, China, 2018; ISBN 9787503785153.
- Wang, K.; Tang, Y.; Chen, Y.; Shang, L.; Ji, X.; Yao, M.; Wang, P. The Coupling and Coordinated Development from Urban Land Using Benefits and Urbanization Level: Case Study from Fujian Province (China). Int. J. Environ. Res. Public Health 2020, 17, 5647. [Google Scholar] [CrossRef]
- China Meteorological Administration. National Climate Center Expert: More and More “Furnace” Cities. Available online: http://www.cma.gov.cn/2011xwzx/2011xqhbh/2011xdtxx/201208/t20120816_182112.html (accessed on 1 April 2021).
- Yu, Z.; Guo, X.; Jørgensen, G.; Vejre, H. How can urban green spaces be planned for climate adaptation in subtropical cities? Ecol. Indic. 2017, 82, 152–162. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 2016, 46, 234–240. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y. Impacts of urban surface characteristics on spatiotemporal pattern of land surface temperature in Kunming of China. Sustain. Cities Soc. 2017, 32, 87–99. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Peng, Y. Scale Effects of the Relationships between Urban Heat Islands and Impact Factors Based on a Geographically-Weighted Regression Model. Remote Sens. 2016, 8, 760. [Google Scholar] [CrossRef] [Green Version]
- Al-Gretawee, H.; Rayburg, S.; Neave, M. The cooling effect of a medium sized park on an urban environment. Int. J. Geomate 2016, 11, 2541–2546. [Google Scholar] [CrossRef]
- Voelker, S.; Kistemann, T. Developing the urban blue: Comparative health responses to blue and green urban open spaces in Germany. Health Place 2015, 35, 196–205. [Google Scholar] [CrossRef]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Tucker, C.J.; Townshend, J.R.; Goff, T.E. African land-cover classification using satellite data. Science 1985, 227, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a tasselled cap transformation based on Landsat 8 at-satellite reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, J.; He, C. A hierarchical analysis of the relationship between urban impervious surfaces and land surface temperatures: Spatial scale dependence, temporal variations, and bioclimatic modulation. Landsc. Ecol. 2016, 31, 1139–1153. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Folke, C.; Alberti, M.; Redman, C.L.; Schneider, S.H.; Ostrom, E.; Pell, A.N.; Lubchenco, J.; et al. Coupled human and natural systems. Ambio 2007, 36, 639–649. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Cai, X.; Yang, C.; Lu, X. Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sens. 2021, 13, 323. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, H.; Zheng, P.; Pan, W. Quantifying the Impact of Land use/Land Cover Changes on the Urban Heat Island: A Case Study of the Natural Wetlands Distribution Area of Fuzhou City, China. Wetlands 2016, 36, 285–298. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Cao, F.; Ge, Y.; Wang, J.F. Optimal discretization for geographical detectors-based risk assessment. GISci. Remote Sens. 2013, 50, 78–92. [Google Scholar] [CrossRef]
- Sussman, H.S.; Dai, A.; Roundy, P.E. The controlling factors of urban heat in Bengaluru, India. Urban Clim. 2021, 38, 100881. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Wu, J.; Wu, K. Demand prediction and regulation zoning of urban-industrial land: Evidence from Beijing-Tianjin-Hebei Urban Agglomeration, China. Environ. Monit. Assess. 2019, 191, 412. [Google Scholar] [CrossRef]
- Zhang, X.; Estoque, R.C.; Murayama, Y. An urban heat island study in Nanchang City, China based on land surface temperature and social-ecological variables. Sustain. Cities Soc. 2017, 32, 557–568. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Pengwang, C.; Gao, W. Evaluation of Urbanization Dynamics and its Impacts on Surface Heat Islands: A Case Study of Beijing, China. Remote Sens. 2017, 9, 453. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, C.; Klok, L.; Bruse, M.; Cortesão, J.; Lenzholzer, S.; Kluck, J. Are urban water bodies really cooling? Urban Clim. 2020, 32, 100607. [Google Scholar] [CrossRef]
- Rivera, E.; Antonio-Nemiga, X.; Origel-Gutierrez, G.; Sarricolea, P.; Adame-Martinez, S. Spatiotemporal analysis of the atmospheric and surface urban heat islands of the Metropolitan Area of Toluca, Mexico. Environ. Earth Sci. 2017, 76, 225. [Google Scholar] [CrossRef]
- Richard, Y.; Pohl, B.; Rega, M.; Pergaud, J.; Thevenin, T.; Emery, J.; Dudek, J.; Vairet, T.; Zito, S.; Chateau-Smith, C. Is Urban Heat Island intensity higher during hot spells and heat waves (Dijon, France, 2014–2019)? Urban Clim. 2021, 35, 100747. [Google Scholar] [CrossRef]
- Walker, J.; Rowntree, P.R. The effect of soil moisture on circulation and rainfall in a tropical model. Q. J. R. Meteorol. Soc. 1977, 103, 29–46. [Google Scholar] [CrossRef]
- Tan, M.; Li, X. Integrated assessment of the cool island intensity of green spaces in the mega city of Beijing. Int. J. Remote Sens. 2013, 34, 3028–3043. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, S.; Zhang, Y.; Jorgensen, G.; Vejre, H. Strong contributions of local background climate to the cooling effect of urban green vegetation. Sci. Rep. 2018, 8, 6798. [Google Scholar] [CrossRef]
- Yang, J.; Ren, J.; Sun, D.; Xiao, X.; Xia, J.; Jin, C.; Li, X. Understanding land surface temperature impact factors based on local climate zones. Sustain. Cities Soc. 2021, 69, 102818. [Google Scholar] [CrossRef]
- Ge, X.; Mauree, D.; Castello, R.; Scartezzini, J.L. Spatio-Temporal Relationship between Land Cover and Land Surface Temperature in Urban Areas: A Case Study in Geneva and Paris. Int. J. Geo-Inf. 2020, 9, 593. [Google Scholar] [CrossRef]
- Dai, Z.; Guldmann, J.M.; Hu, Y. Spatial regression models of park and land-use impacts on the urban heat island in central Beijing. Sci. Total Environ. 2018, 626, 1136–1147. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Li, J. Detecting the Cool Island Effect of Urban Parks in Wuhan: A City on Rivers. Int. J. Environ. Res. Public Health 2021, 18, 132. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wu, L.; Yuan, F.; Dou, J.; Miao, S. Mass human migration and Beijing’s urban heat island during the Chinese New Year holiday. Sci. Bull. 2015, 60, 1038–1041. [Google Scholar] [CrossRef]
- Kim, M.G.; Koh, J.H. Recent research trends for geospatial information explored by Twitter data. Spat. Inf. Res. 2016, 24, 65–73. [Google Scholar] [CrossRef]
- Zhou, X.; Okaze, T.; Ren, C.; Cai, M.; Ishida, Y.; Watanabe, H.; Mochida, A. Evaluation of urban heat islands using local climate zones and the influence of sea-land breeze. Sustain. Cities Soc. 2020, 55, 102060. [Google Scholar] [CrossRef]
- Kong, F.; Yin, H.; Wang, C.; Cavan, G.; James, P. A satellite image-based analysis of factors contributing to the green-space cool island intensity on a city scale. Urban For. Urban Green. 2014, 13, 846–853. [Google Scholar] [CrossRef] [Green Version]






| Type | Driving Factor | Abbreviation | Formulas | Sources |
|---|---|---|---|---|
| Socio-economic factor | Road Density | RDD | https://www.openstreetmap.org/ | |
| Population Density | PPD | - | https://www.worldpop.org/ | |
| Nighttime Light | NL | - | https://www.ngdc.noaa.gov/eog/viirs/ | |
| Park Density | PD | https://www.openstreetmap.org/ | ||
| Normalized Difference Built-up Index | NDBI | [64] | ||
| Geographical factor | Normalized Difference Vegetation Index | NDVI | [65] | |
| Modified Normalized Difference Water Index | MNDWI | [66] | ||
| Soil Brightness | SB | [67] | ||
| Soil Wetness | SW | |||
| Water Density | WD | http://www.gscloud.cn/ | ||
| Vegetation Density | VD | http://www.gscloud.cn/ |
| Driving Factors | Significance Level | Impact Ordering | ||
|---|---|---|---|---|
| Geographical factor | SW | 0.792 | 0.01 | 1 |
| NDBI | 0.732 | 0.01 | 2 | |
| MNDWI | 0.618 | 0.01 | 3 | |
| NDVI | 0.604 | 0.01 | 4 | |
| SB | 0.565 | 0.01 | 5 | |
| WD | 0.326 | 0.01 | 6 | |
| VD | 0.236 | 0.01 | 7 | |
| Socio-economic factor | RDD | 0.191 | 0.01 | 8 |
| NL | 0.144 | 0.01 | 9 | |
| PPD | 0.081 | 0.05 | 10 | |
| PD | 0.076 | 0.01 | 11 | |
| TCB | MNDWI | NDBI | NDVI | TCW | RDD | PPD | VD | WD | NL | PD | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TCB | 0.565 | ||||||||||
| MNDWI | b | 0.618 | |||||||||
| NDBI | 0.733 | ||||||||||
| NDVI | 0.604 | ||||||||||
| TCW | 0.792 | ||||||||||
| RDD | 0.191 | ||||||||||
| PPD | 0.081 | ||||||||||
| VD | 0.236 | ||||||||||
| WD | 0.327 | ||||||||||
| NL | 0.145 | ||||||||||
| PD | 0.076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, M.; Lai, R.; Lin, J.; Zhu, Z. Quantitative Analysis of a Spatial Distribution and Driving Factors of the Urban Heat Island Effect: A Case Study of Fuzhou Central Area, China. Int. J. Environ. Res. Public Health 2021, 18, 13088. https://doi.org/10.3390/ijerph182413088
You M, Lai R, Lin J, Zhu Z. Quantitative Analysis of a Spatial Distribution and Driving Factors of the Urban Heat Island Effect: A Case Study of Fuzhou Central Area, China. International Journal of Environmental Research and Public Health. 2021; 18(24):13088. https://doi.org/10.3390/ijerph182413088
Chicago/Turabian StyleYou, Meizi, Riwen Lai, Jiayuan Lin, and Zhesheng Zhu. 2021. "Quantitative Analysis of a Spatial Distribution and Driving Factors of the Urban Heat Island Effect: A Case Study of Fuzhou Central Area, China" International Journal of Environmental Research and Public Health 18, no. 24: 13088. https://doi.org/10.3390/ijerph182413088
APA StyleYou, M., Lai, R., Lin, J., & Zhu, Z. (2021). Quantitative Analysis of a Spatial Distribution and Driving Factors of the Urban Heat Island Effect: A Case Study of Fuzhou Central Area, China. International Journal of Environmental Research and Public Health, 18(24), 13088. https://doi.org/10.3390/ijerph182413088