SEAHIR: A Specialized Compartmental Model for COVID-19
Abstract
1. Introduction
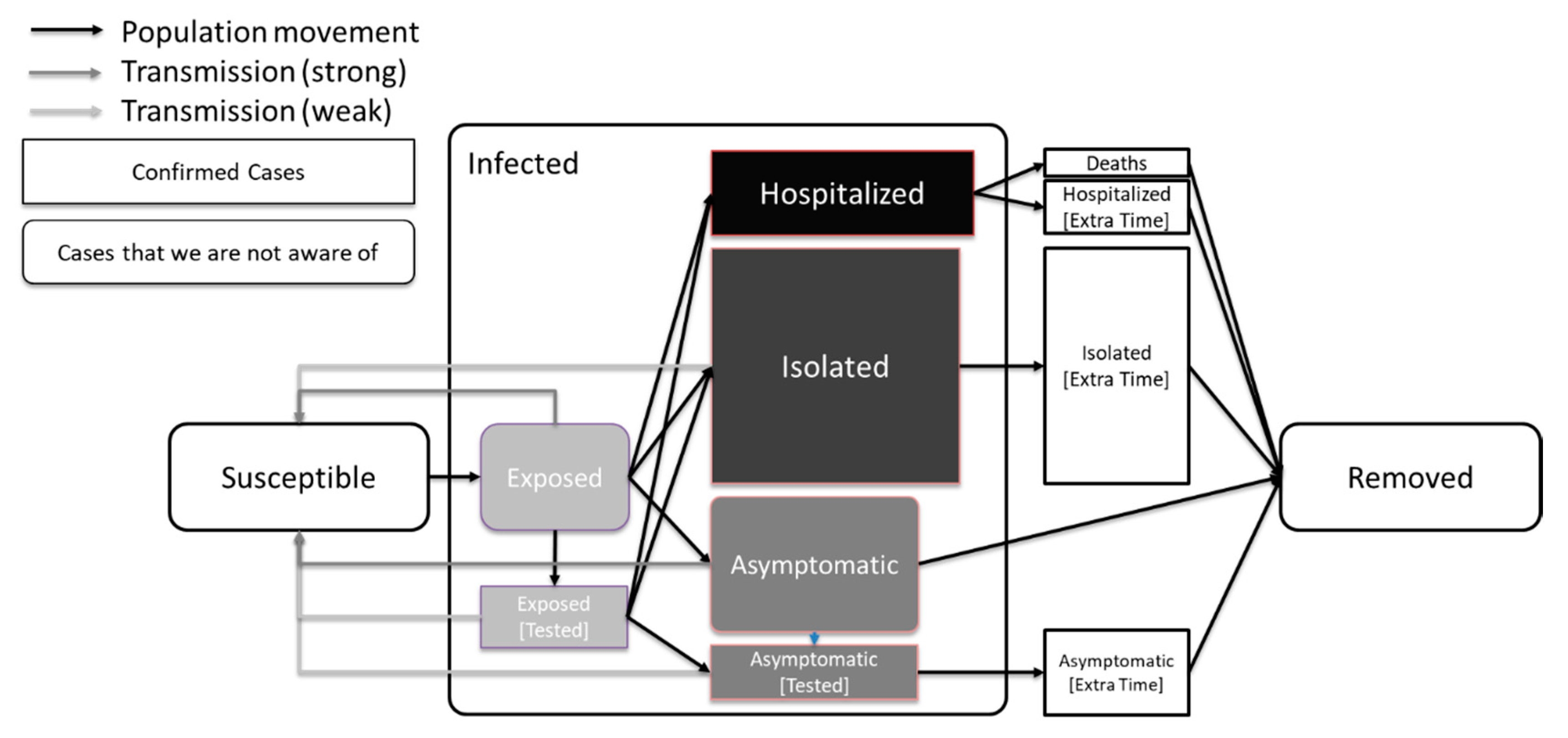
2. The SEAHIR Model Assumptions
- Six compartments: Susceptible-Exposed-Asymptomatic-Hospitalized-Isolated-Removed (SEAHIR).
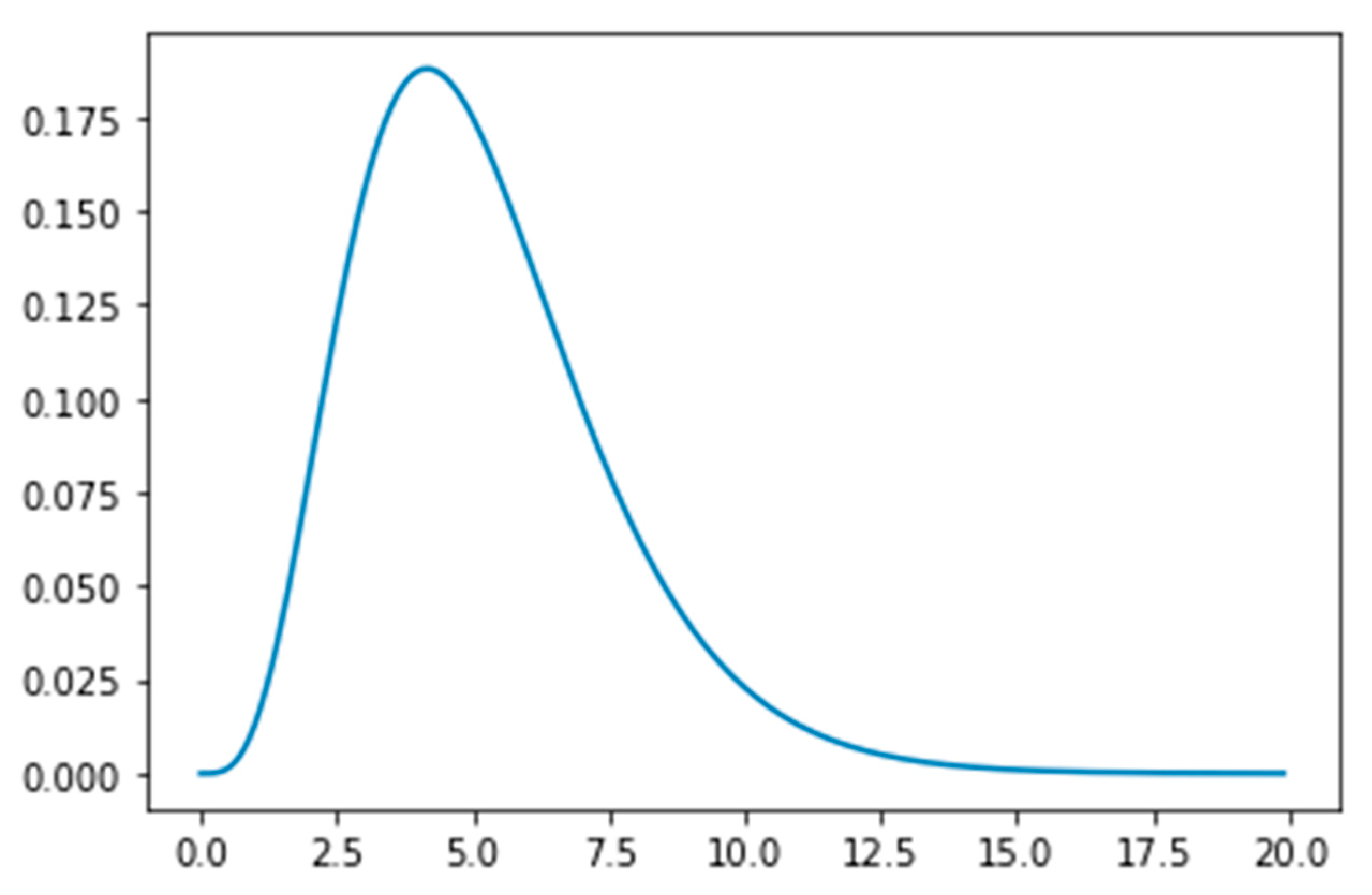
- The Susceptible (S) become Exposed (E) after their interaction with the Infected population. The virus is in the incubation period within the Exposed population, until the onset of symptoms. The Exposed population show no symptoms of the virus, although they can transmit the virus to the Susceptible population. The time period that a person remains in the Exposed compartment follows the Erlang distribution with parameters k = 5 and λ = 5/5.2 = 0.96. According to this distribution the mean is 5.2 days, the 95% confidence interval is between 1.24 days and 9.88 days, and the 99% confidence interval is between 0.71 days and 12.6 days, which is aligned with the estimated incubation period reported in the literature [9]. The transmission rate of the Exposed population is affected by public health measures.
- After the incubation period, a person should be classified as either an asymptomatic, mild case, or a moderate/severe case. We assumed that 30% of the infected population would be asymptomatic, 55% mild cases, and 15% moderate/severe cases according to Lauer et al. [9]. There are three distinct behaviors connected to this classification:
- -
- Asymptomatic carriers (A) are mainly undetected and able to transmit the virus at the normal transmission rate (β). The only way to detect the asymptomatic carriers is through testing. Also, the transmission rate of asymptomatic individuals is affected by measures such as physical distancing.
- -
- Mild cases are isolated at home or in designated isolation centers (I) for 14 days on average. Mild cases may be infectious, but with a lower transmission rate than normal (βI) due to isolation and their transmission rate is affected by the government’s intervention measures.
- -
- Moderate and severe cases are admitted to hospitals (H) for 18 days on average. Depending on severity, they are assigned to regular beds or intensive care unit beds. We assumed the hospitalized percentage as 5.5 × CFR (case fatality ratio) while we assumed that the hospitalized population is not able to transmit the virus due to stringent isolation.
- The Removed compartment (R) includes
- -
- Deaths: a percentage given by the CFR and the population age structure
- -
- Recovered patients: The remaining cases, who have cleared the infection and developed antibodies against the virus. In the context of our modelling, we consider the recovered patients immune to the virus thereafter.
2.1. Government Intervention: Public Health Measures
2.2. Government Intervention: Testing
2.3. Model Definition
2.4. Possible Challenges Caused by the Asymptomatic Patients
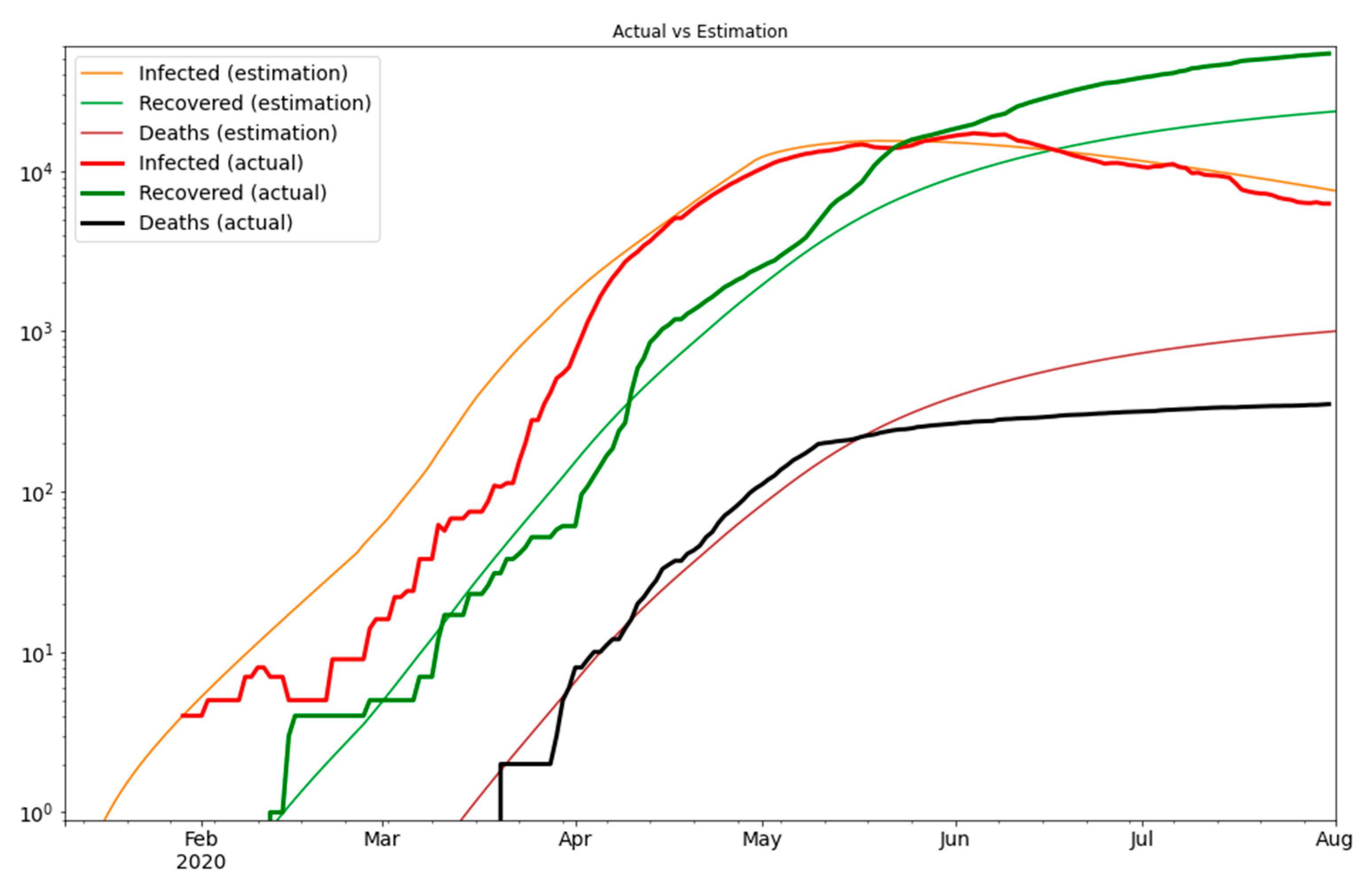
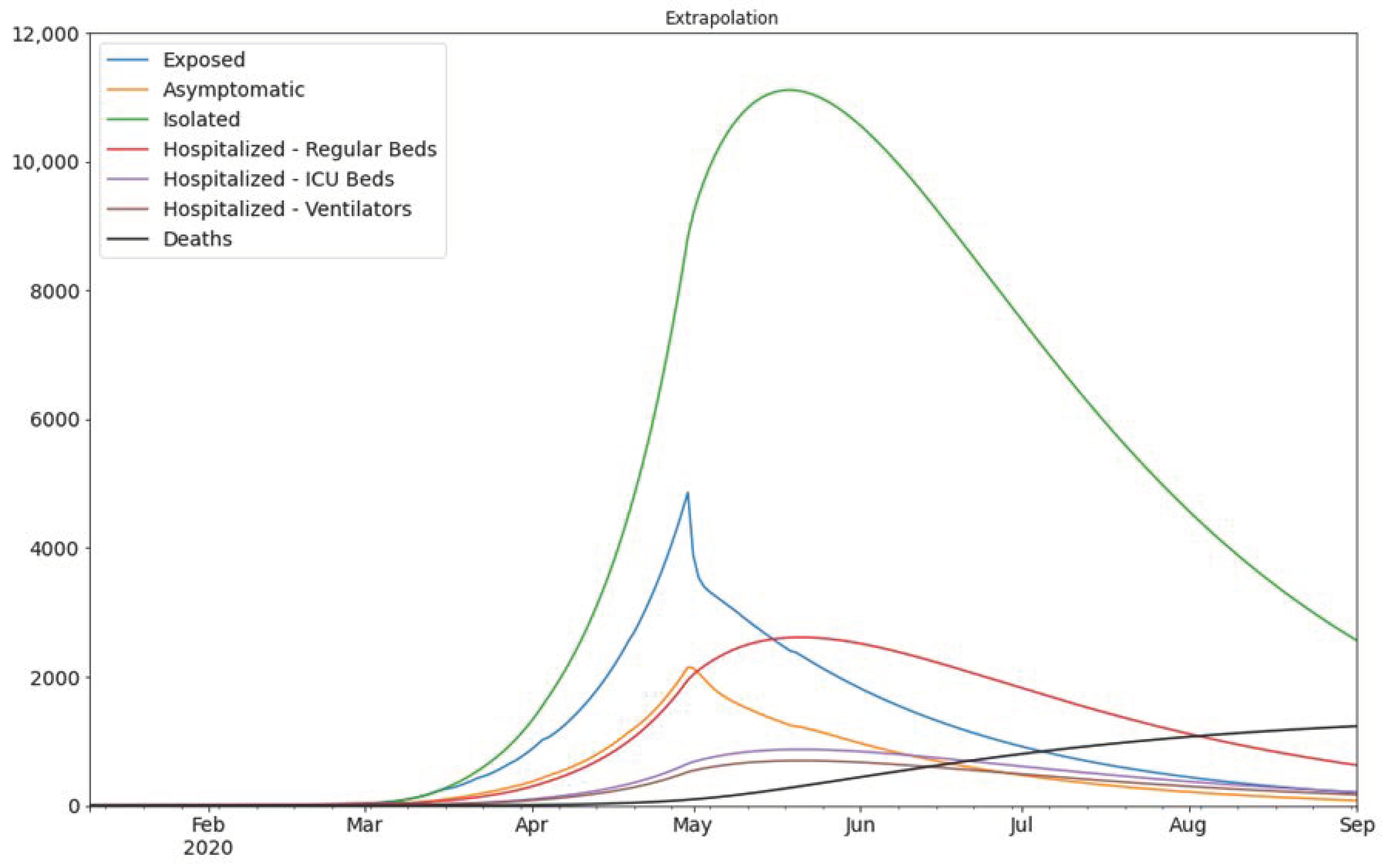
3. Results
4. Discussion
5. Future Work
- Estimating the public reaction on physical distancing. The more deaths announced, the more we expect people to take measures for personal hygiene and distancing. That said, population compliance with infection control and public health measures might reduce over time due to pandemic fatigue.
- Modelling the mortality and transmission rate of the virus, as it mutates over time, and embed the findings into the SEAHIR model. Over time we expect that the more prevalent viral strain in the population may be more transmissible but less pathogenic and lethal (virulent).
- Optimizing the parameters of government intervention on physical distancing. To date, the physical distancing modifiers imposed by the government were chosen arbitrarily. A focused study would be useful on how these measures can be quantified based on the available data.
- The viral load is not modelled in this work. Given that we have adequate evidence that in the future, we may assume that the viral load in a patient gradually increases during the incubation period, affecting the test results and the transmission rate. Our choice of Erlang distribution can easily model the viral load by assigning a gradually increasing percentage in each of the Ei phases the patient belongs to.
- The current version of our model does not account for re-infections. The available scientific literature on the duration of immunity following SARS-CoV-2 infection, risk of re-infection, and severity of disease following re-infection is sparse. Evidence on the duration of immunity will emerge and become more robust over the next 6–12 months and future models (or adaptations of the SEAHIR model) may be able to include parameters related to re-infection.
- Numerous countries, including the UAE, have initiated population-wide vaccination campaigns and future models may be able to quantify the effect of different vaccines on transmission dynamics when sufficient data are available.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alm, E.; Broberg, E.K.; Connor, T.; Hodcroft, E.B.; Komissarov, A.B.; Maurer-Stroh, S.; Melidou, A.; Neher, R.A.; O’Toole, Á.; Pereyaslov, D.; et al. Geographical and temporal distribution of SARS-CoV-2 clades in the WHO European Region, January to June 2020. Euro. Surveill. 2020, 25, 2001410. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.; Mustafa, F.; Rizvi, T.A.; Loney, T.; Suwaidi, H.A.; Al-Marzouqi, A.H.H.; Eldin, A.K.; Alsabeeha, N.; Adrian, T.E.; Stefanini, C.; et al. SARS-CoV-2/COVID-19: Viral Genomics, Epidemiology, Vaccines, and Therapeutic Interventions. Viruses 2020, 12, 526. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Director General’s Opening Remarks at the Media Briefing on COVID-19—11 March 2020. 2020. Available online: https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020 (accessed on 30 December 2020).
- Al-Omari, A.; Rabaan, A.A.; Salih, S.; Al-Tawfiq, J.A.; Memish, Z.A. MERS coronavirus outbreak: Implications for emerging viral infections. Diagn. Microbiol. Infect. Dis. 2019, 93, 265–285. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Xu, Y.; Bao, L.; Zhang, L.; Yu, P.; Qu, Y.; Zhu, H.; Zhao, W.; Han, Y.; Qin, C. From SARS to MERS, Thrusting Coronaviruses into the Spotlight. Viruses 2019, 11, 59. [Google Scholar] [CrossRef] [PubMed]
- Su, S.; Wong, G.; Shi, W.; Liu, J.; Lai, A.C.K.; Zhou, J.; Liu, W.; Bi, Y.; Gao, G.F. Epidemiology, Genetic Recombination, and Pathogenesis of Coronaviruses. Trends Microbiol. 2016, 24, 490–502. [Google Scholar] [CrossRef] [PubMed]
- Johns Hopkins Center for Systems Sciences and Engineering. COVID-19 Dashboard. Available online: https://www.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6 (accessed on 30 December 2020).
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet. Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- United Arab Emirates Federal Competitiveness and Statistics Authority. Latest United Arab Emirates COVID-19 Data. Available online: https://fcsa.gov.ae/en-us/Pages/Covid19/UAE-Covid-19-Updates.aspx. (accessed on 30 December 2020).
- Rocha Filho, T.M.; Ganem dos Santos, F.S.; Gomes, V.B.; Rocha, T.A.H.; Croda, J.H.R.; Ramalho, W.M.; Araujo, W.N. Expected impact of COVID-19 outbreak in a major metropolitan area in Brazil. medRxiv 2020. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- United Arab Emirates Federal Competitiveness and Statistics Authority. Key Statistics and Data for Global Competitiveness and Sustainable Development in the United Arab Emirates (Page 17). Available online: https://fcsa.gov.ae/en-us/Documents/UAE%20Numbers%20En%202019.pdf (accessed on 30 December 2020).
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.L.; Hui, D.S.C.; et al. China Medical Treatment Expert Group for Covid-19. Clinical Characteristics of Coronavirus Disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef] [PubMed]
- Harilal, D.; Ramaswamy, S.; Loney, T.; Al Suwaidi, H.; Khansaheb, H.; Alkhaja, A.; Varghese, R.; Deesi, Z.; Nowotny, N.; Alsheikh-Ali, A.; et al. SARS-CoV-2 Whole Genome Amplification and Sequencing for Effective Population-Based Surveillance and Control of Viral Transmission. Clin. Chem. 2020, 66, 1450–1458. [Google Scholar] [CrossRef] [PubMed]
- Tayoun, A.A.; Loney, T.; Khansaheb, H.; Ramaswamy, S.; Harilal, D.; Deesi, Z.O.; Varghese, R.M.; Al Suwaidi, H.; Alkhajeh, A.; AlDabal, L.M.; et al. Multiple early introductions of SARS-CoV-2 into a global travel hub in the Middle East. Sci. Rep. 2020, 10, 17720. [Google Scholar] [CrossRef] [PubMed]
- Loney, T.; Khansaheb, H.; Ramaswamy, S.; Harilal, D.; Deesi, Z.O.; Varghese, R.M.; Al Ali, A.B.; Khadeeja, A.; Al Suwaidi, H.; Alkhajeh, A.; et al. Genotype-phenotype correlation identified a novel SARS-CoV-2 variant possibly linked to severe disease. Transbound. Emerg. Dis. 2021. [Google Scholar] [CrossRef] [PubMed]
- Champredon, D.; Dushoff, J.; Earn, D.J.D. Equivalence of the Erlang SEIR epidemic model and the renewal equation. SIAM J. Appl. Math. 2018, 78, 3258–3278. [Google Scholar] [CrossRef]
| Date | G(t) | Description |
|---|---|---|
| 2020-03-01 | 0.95 | Nurseries closed 1 |
| 2020-03-08 | 0.90 | Schools and universities closed 2 |
| 2020-03-15 | 0.85 | Gyms, parks, cinemas, and pools closed 3 |
| 2020-03-16 | 0.80 | Mosques and other worship places closed 4 |
| 2020-03-17 | 0.75 | Suspension of issuing entry visas 5 |
| 2020-03-23 | 0.70 | Malls, shopping centers, restaurants closed 6 Passenger flights suspended 7 |
| 2020-04-04 | 0.65 | Restrictions on non-essential movement (extension of the disinfection program to 24 h a day in Dubai) 8 |
| 2020-05-01 | 0.40 | Physical distancing measures |
| Date | Positive |
|---|---|
| 2020-02-27 | 1 |
| 2020-03-03 | 2 |
| 2020-03-09 | 3 |
| 2020-03-10 | 5 |
| 2020-03-29 | 20 |
| 2020-04-20 | 60 |
| 2020-05-01 | 80 |
| 2020-05-10 | 90 |
| 2020-05-20 | 40 |
| Name | Notation | Value | Description |
|---|---|---|---|
| Initial population size | N | 9,366,829 | Given by the UAE Federal Competitiveness and Statistics Authority [14] |
| Transmission rate | β | 0.1466 ± 0.0004 * | Estimated in optimization based on publicly available data, see Section 3 below. This is the estimated base transmission rate for the UAE |
| Transmission rate in isolation | βI | 0.0623 ± 0.0011 * | Estimated in optimization based on publicly available data, see Section 3 below. This parameter is modelling the effects of (1) the nosocomial infections in the isolation facilities, (2) expected infected healthcare workers who might then move/live in the community and contribute to community-transmission, (3) infecting housemates, and (4) possible breaking the isolation rules |
| Base transmission rate multiplier | G(t) | See Table 1 (physical distancing). The values of G(t) vary over time due to the government measures implemented. Before 1 March 2020 we set G(t) = 1. From 1 March 2020 and up to 4 March 2020, we set G(t) = 0.95. From 5 March 2020 and up to 14 March 2020, we set G(t) = 0.90, and so on. From 1 March 2020 onwards, we set G(t) = 0.40. | |
| Positive tested cases | P(t) | See Table 2 (testing). The values of P(t) vary over time. For dates before 27 February 2020 we assume no positive people would be found if a member of the population was randomly selected and tested, so P(t) = 0. For the dates not shown we assume the number of the last date shown, up to the specific date we are interested in. For example, for the 25 March 2020 we consider P(t) = 5 positive people found, because the last date up to 25 March 2020 shown is 10 March 2020 that indicates 5 positive people found based on our assumption in Table 2. | |
| Mean incubation period (days) | α | 5.2 | Based on data from [9,15,16] |
| Average period the asymptomatic carriers are considered infectious (days) | ζ | 9.0 | Assumed based on data from [9] |
| Average period in isolation (days) | γI | 14.0 | Assumed based on data from [9,16] |
| Average period in hospital (days) | γH | 18.0 | Assumed based on data from [16] |
| Average extra time in hospital or isolation (days) | δ | 31.1 ± 8.0 * | Estimated in optimization based on publicly available data, see below. Some people stay in hospital or isolation for additional time, until they are finally discharged. During this period, they are not infectious anymore and are only recovering |
| Mortality rate | m | 2.4% | Given from the population age structure and the CFR table [15] |
| Hospitalization need | h | 5.5 | Assumed based on data from [16] |
| Percentage of the Exposed population requiring hospitalization | s | 13.2% | m·h |
| Asymptomatic percentage | p | 30% | Assumed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leontitsis, A.; Senok, A.; Alsheikh-Ali, A.; Al Nasser, Y.; Loney, T.; Alshamsi, A. SEAHIR: A Specialized Compartmental Model for COVID-19. Int. J. Environ. Res. Public Health 2021, 18, 2667. https://doi.org/10.3390/ijerph18052667
Leontitsis A, Senok A, Alsheikh-Ali A, Al Nasser Y, Loney T, Alshamsi A. SEAHIR: A Specialized Compartmental Model for COVID-19. International Journal of Environmental Research and Public Health. 2021; 18(5):2667. https://doi.org/10.3390/ijerph18052667
Chicago/Turabian StyleLeontitsis, Alexandros, Abiola Senok, Alawi Alsheikh-Ali, Younus Al Nasser, Tom Loney, and Aamena Alshamsi. 2021. "SEAHIR: A Specialized Compartmental Model for COVID-19" International Journal of Environmental Research and Public Health 18, no. 5: 2667. https://doi.org/10.3390/ijerph18052667
APA StyleLeontitsis, A., Senok, A., Alsheikh-Ali, A., Al Nasser, Y., Loney, T., & Alshamsi, A. (2021). SEAHIR: A Specialized Compartmental Model for COVID-19. International Journal of Environmental Research and Public Health, 18(5), 2667. https://doi.org/10.3390/ijerph18052667






