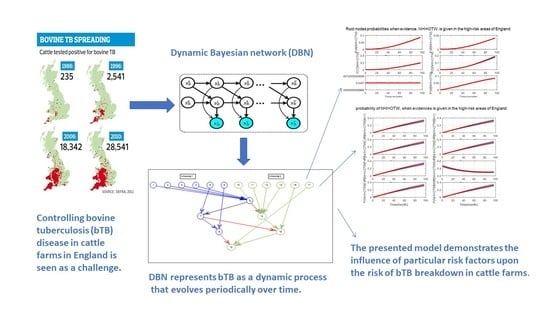
Evaluating the Bovine Tuberculosis Eradication Mechanism and Its Risk Factors in England’s Cattle Farms
Abstract
:1. Introduction
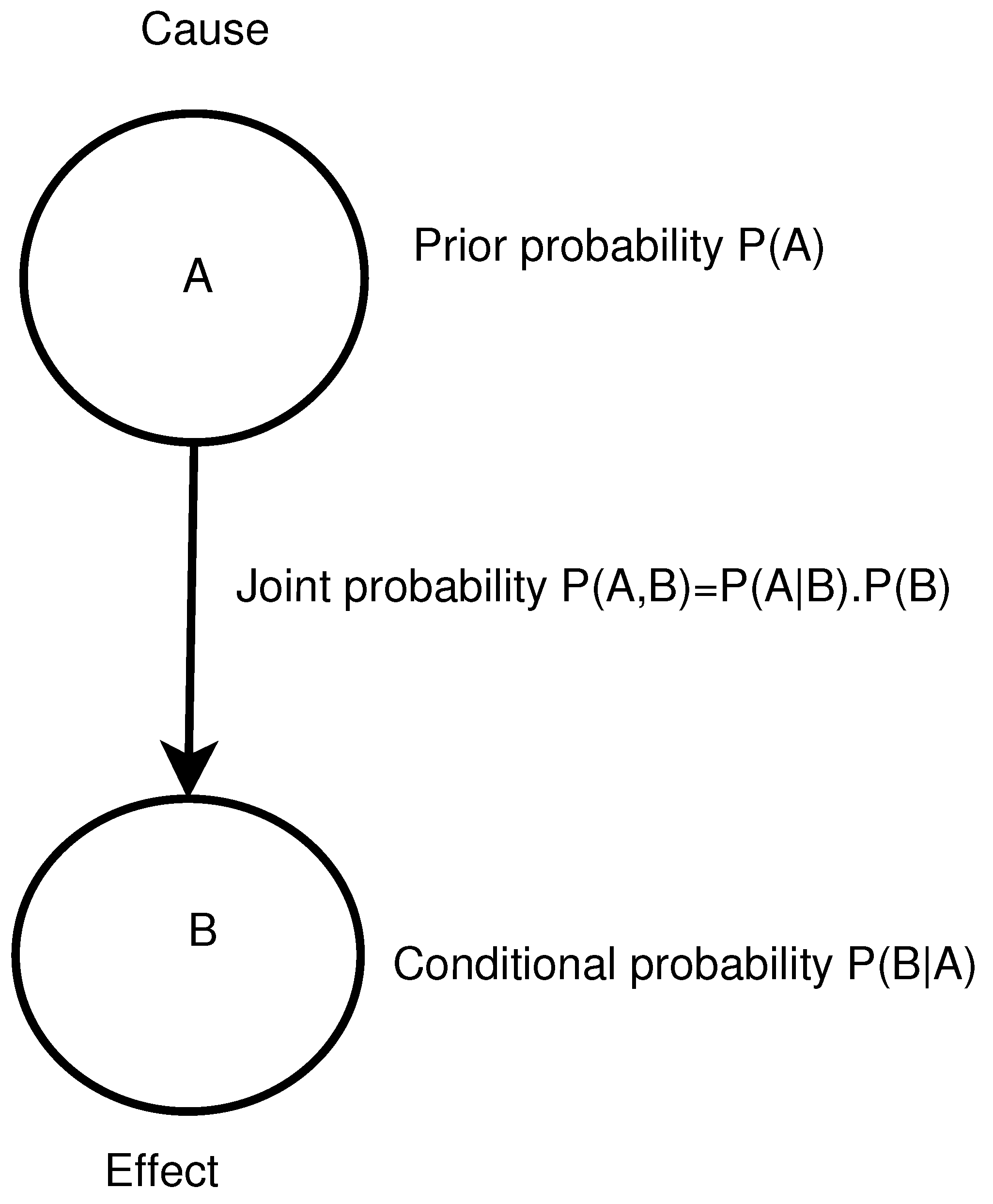
2. Bayesian Network
- Static BN (SBN): All variables are discrete.
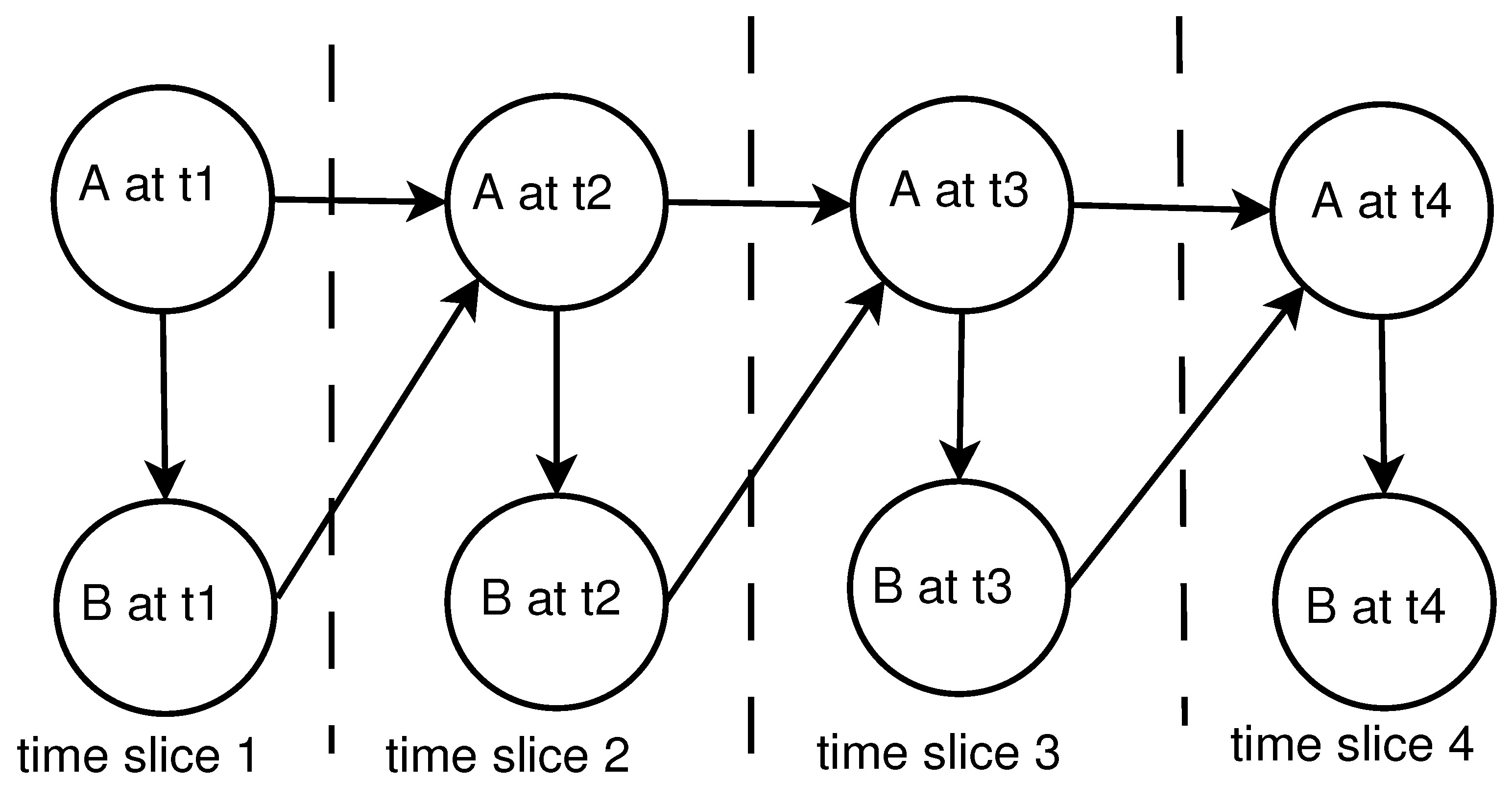
- Dynamic BN (DBN): It consists of a limited number of BNs, each of which corresponds to a particular time interval. The connections between adjacent BNs represent how the states of the system evolve over time. Figure 2 shows a simple two-node DBN with feedback over four time steps.In Figure 2, node A at affects node B at current time slice , but it is in turn affected by node B in the next time slice, . This amounts to a feedback loop, since A affects B and B affects A (at time ).DBN is a powerful algorithm that can be applied to various applications with the temporal dependencies in sequential data. Moreover, inference and learning with DBNs including temporal structural learning and prediction have been used routinely in several fields where the filtering and smoothing are performed in Kalman filter models [39].
- Hybrid dynamic BN (HDBN): Random variables can be discrete such as someone’s gender or continuous such as someone’s age. A BN which contains both discrete and continuous variables is called an HDBN.
3. Case Study: Dynamic Bayesian Network for bTB in the England’s Cattle Farms
3.1. Bovine Tuberculosis
- Failed test: At least one animal tests positive during any herd-level test (routine, whole-herd or follow up).
- Breakdown: A failed test occurs on an officially bTB free herd, not currently subject to movement restriction.
3.2. Dynamic Bayesian Network
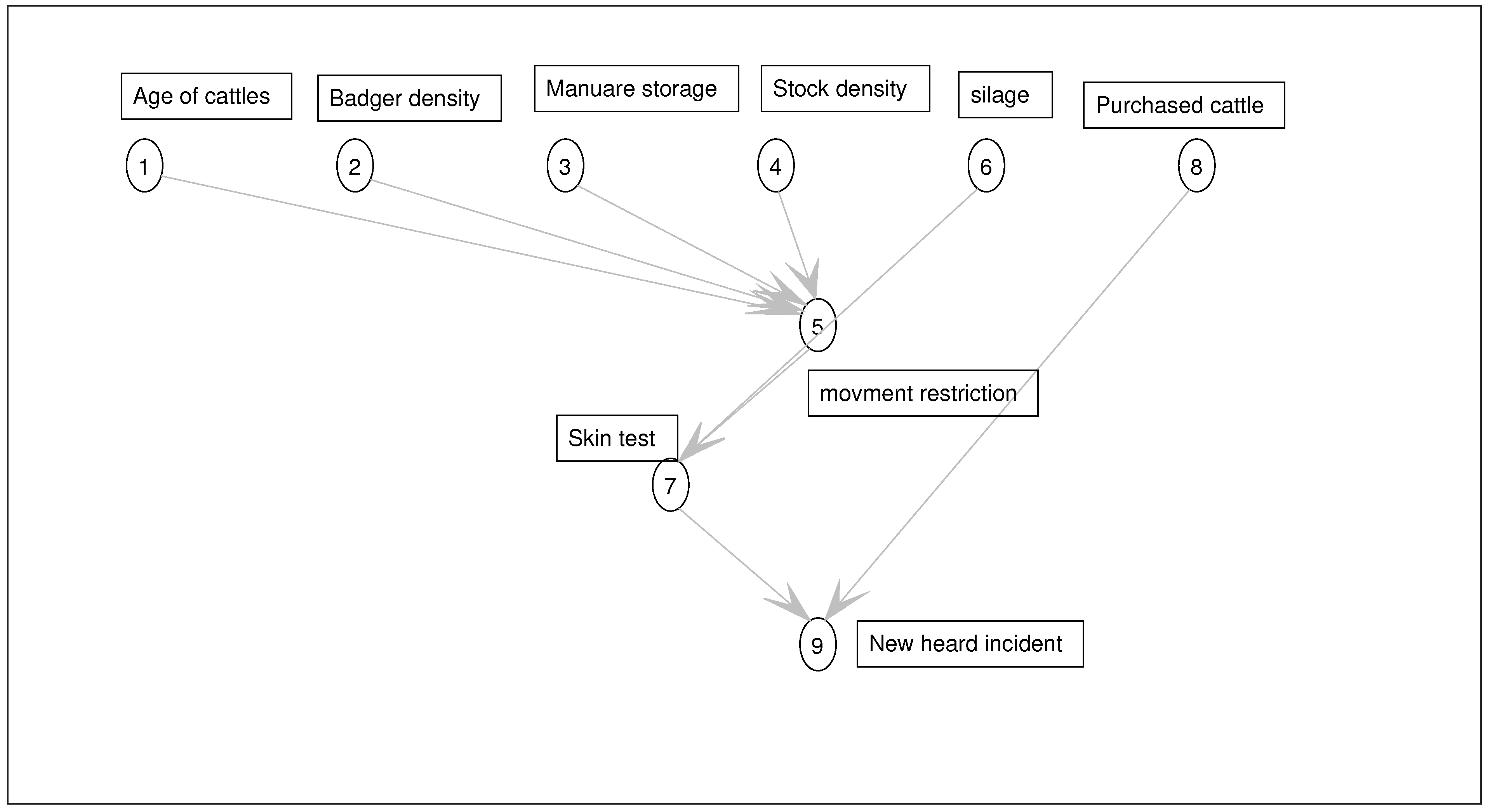
3.3. Method: Identification of Variables and Their States
Farm’s Risk Factors
- Farm food: There are different types of food and storage methods and storage periods. However, routes of transmission from badgers that are attracted to the cattle food are considered important. Studies show that farms that feed maize silage, grass silage or molasses to cattle are more attractive to badgers. In addition, studies show that 100% of farms with persistent breakdown fed grass silage to cattle, whereas feeding hay was effective against persistent breakdown.
- Badgers: Active badger sett density showed significant associations with herd incidents. In our model, active sett density was entered as a categorical variable as zero, medium (≤0–3 setts/km) or high (>3 setts/km). Based on available studies, a relatively high active sett density is associated with persistent breakdown, which shows that badgers play a part in spreading the disease, especially in hotspot areas.
- Age of the cattle: Based on available information, age of purchased animals was categorised as:
- –
- Calves: Stores or replacement breeding animal less than 12 months
- –
- Yearlings: Stores or replacement breeding animal between 12 and 24 months
- –
- Cows: Female breeding animals over 24 months
Based on available information, farms with more cattle older than 24 months are more likely to find bTB becomes persistent compared with farms with younger cattle. In other words, bTB prevalence tends to increase with age. - Stock density: Based on available data, farms with relatively low stocking densities (≤3 head of cattle/ha) were more protected from breakdown versus the farms with high densities (>3 head of cattle/ha).
- Purchased cattle: In control farms, the main reason of increasing the risk of infection is cattle movement onto farms from market or other farms. Since purchased cattle is responsible for the majority of newly infected farms, buying animals accelerates bTB incidents. Studies demonstrate that farms with the purchase of larger number of cattle (>50 heads compared to ≤50 heads) are at more risk of breakdown (short period is more likely than persistent).
- Manure storage: Based on available literature, manure storage for over six months is one of the significant factors for breakdown in the farms.
3.4. Data and Statistical Procedures
3.5. Dynamic Bayesian Network Model
3.5.1. Nodes and Edges
3.5.2. Prior Probabilities
3.5.3. Interslice Probabilities
3.5.4. Posterior Probabilities
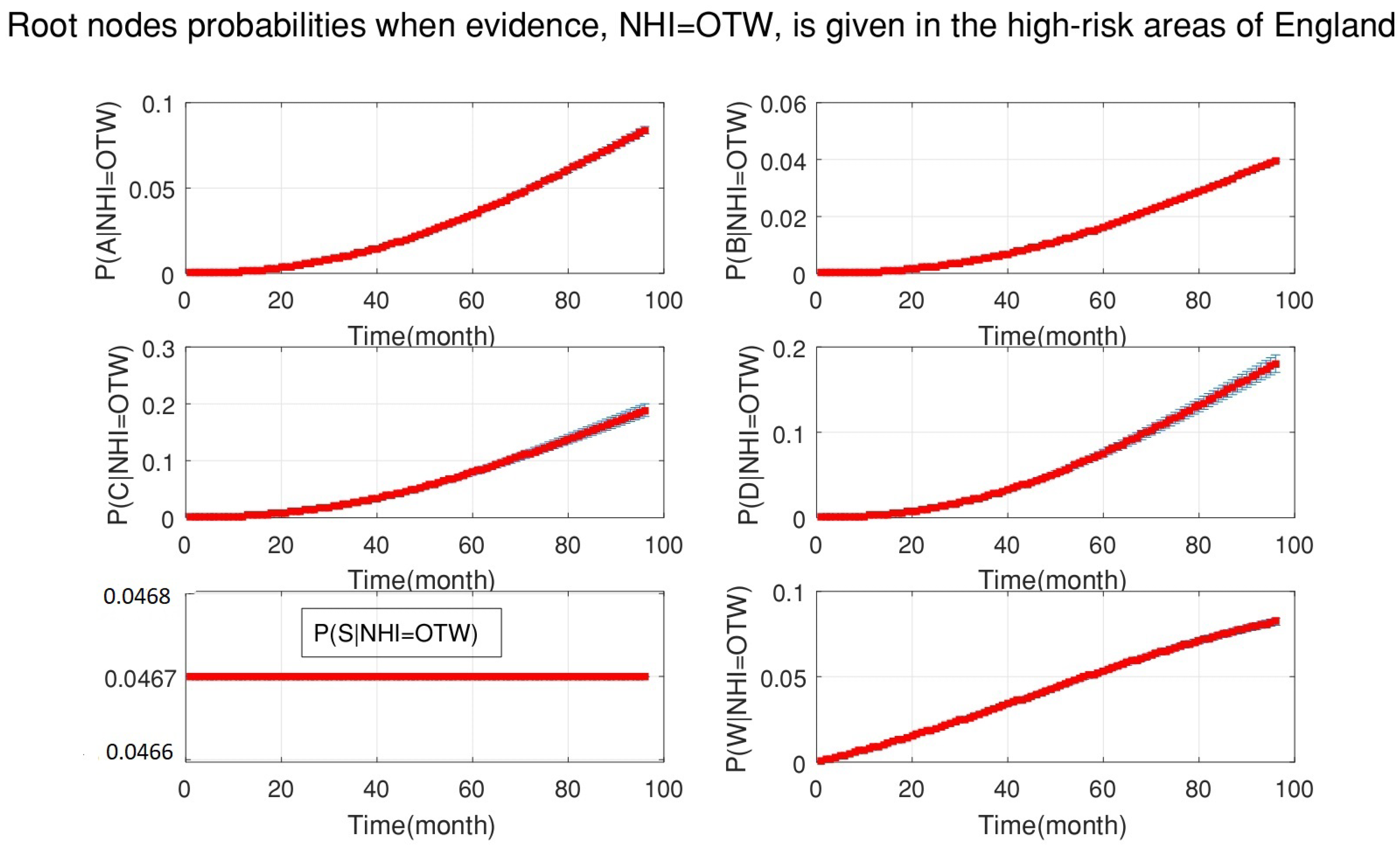
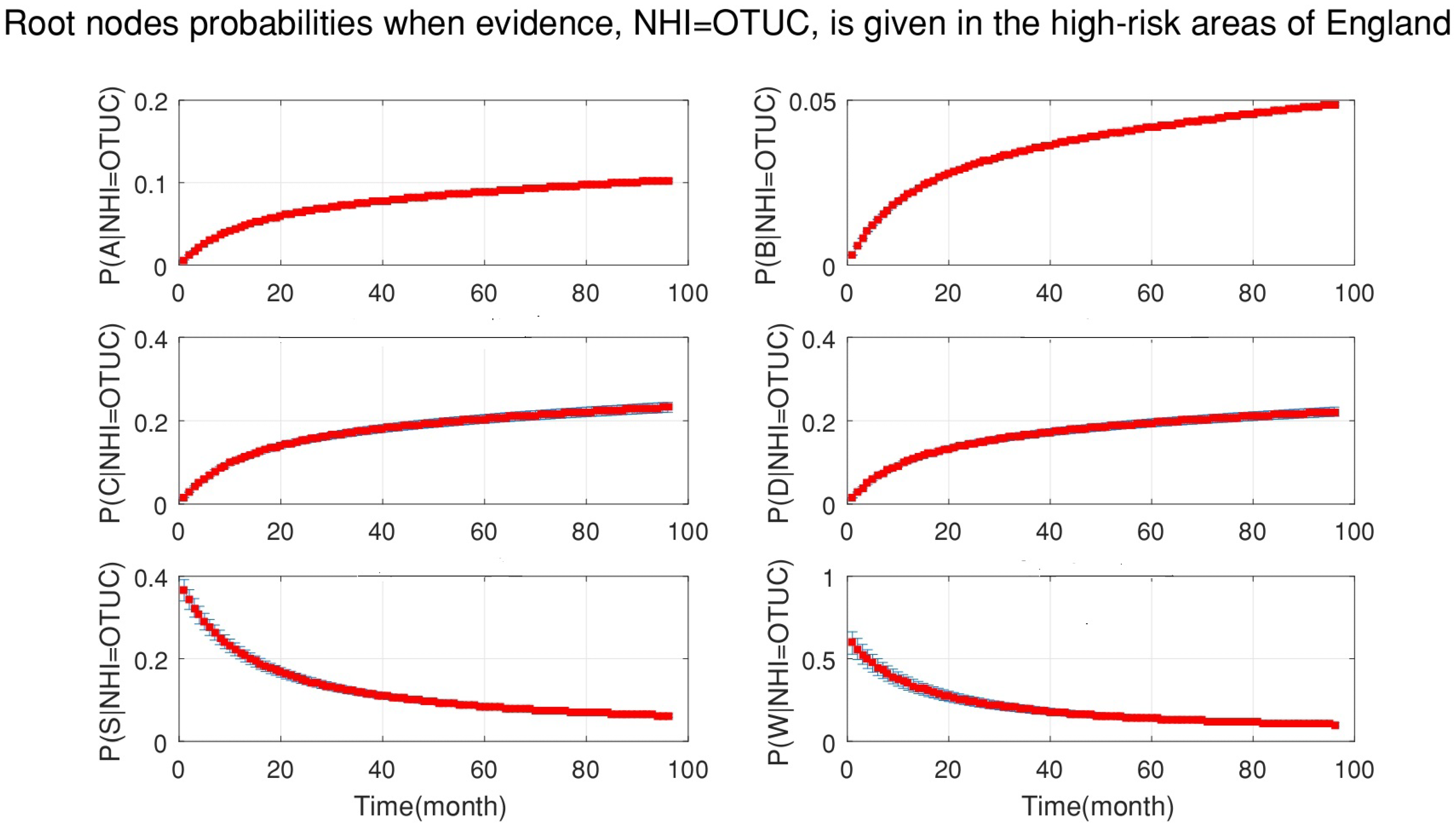
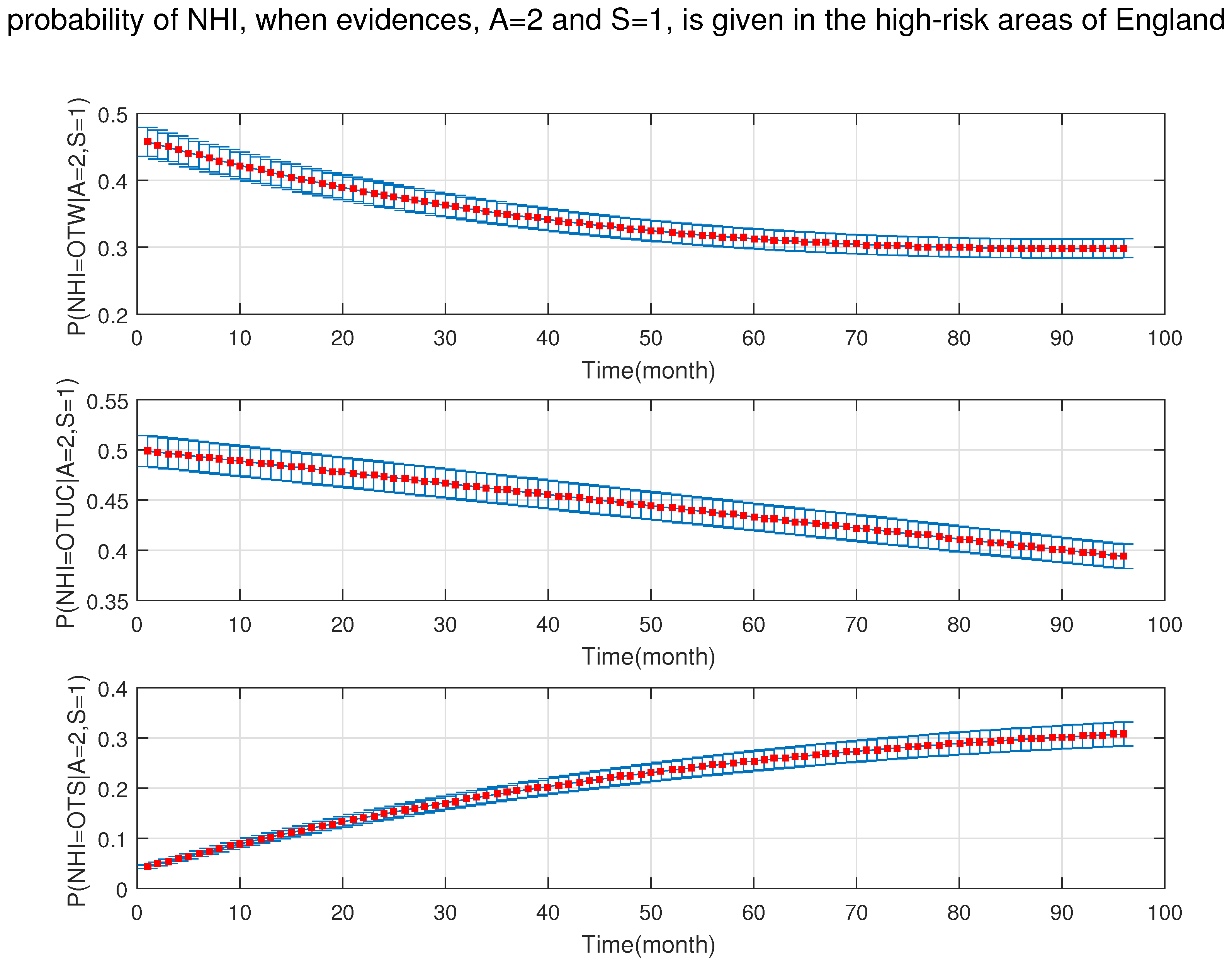
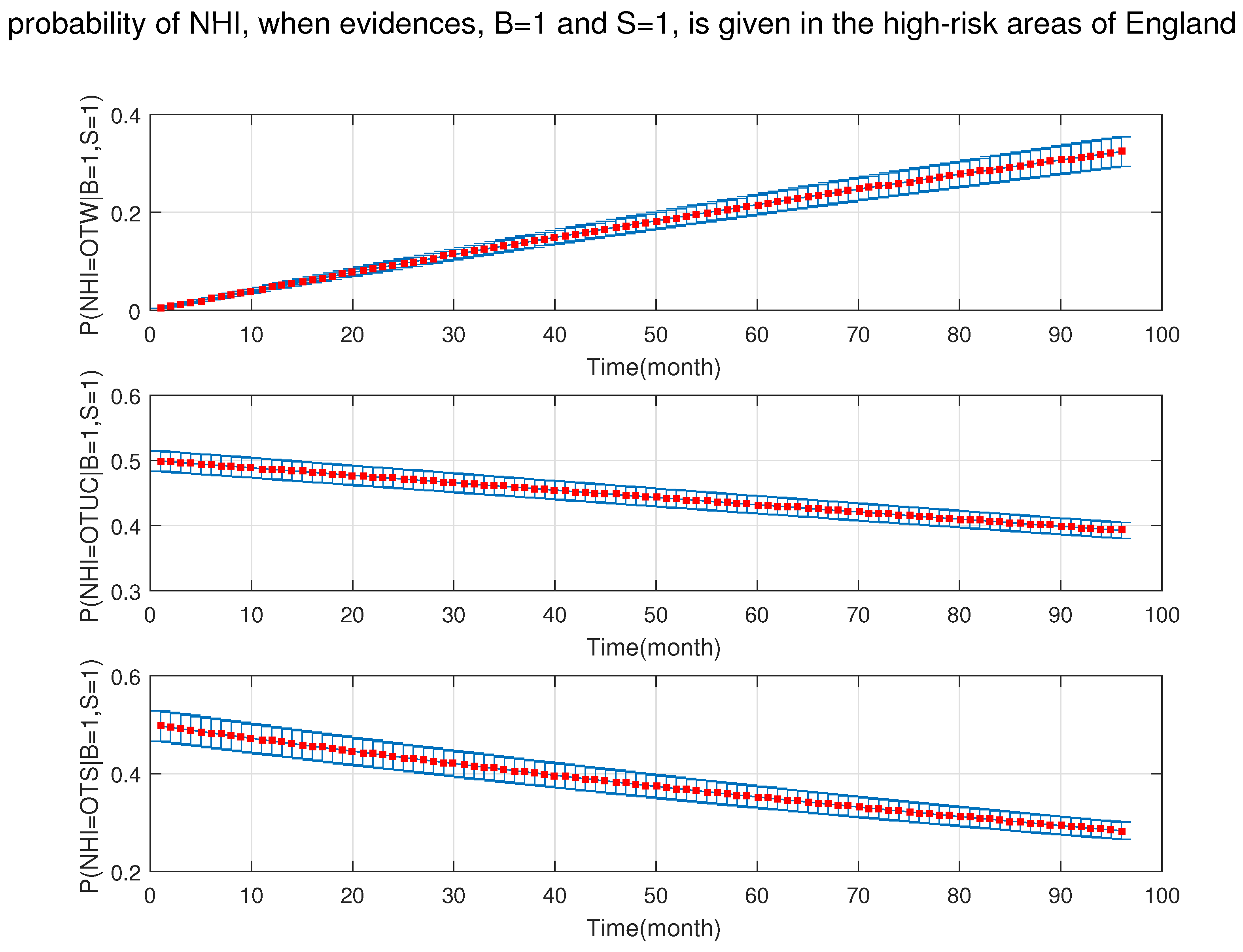
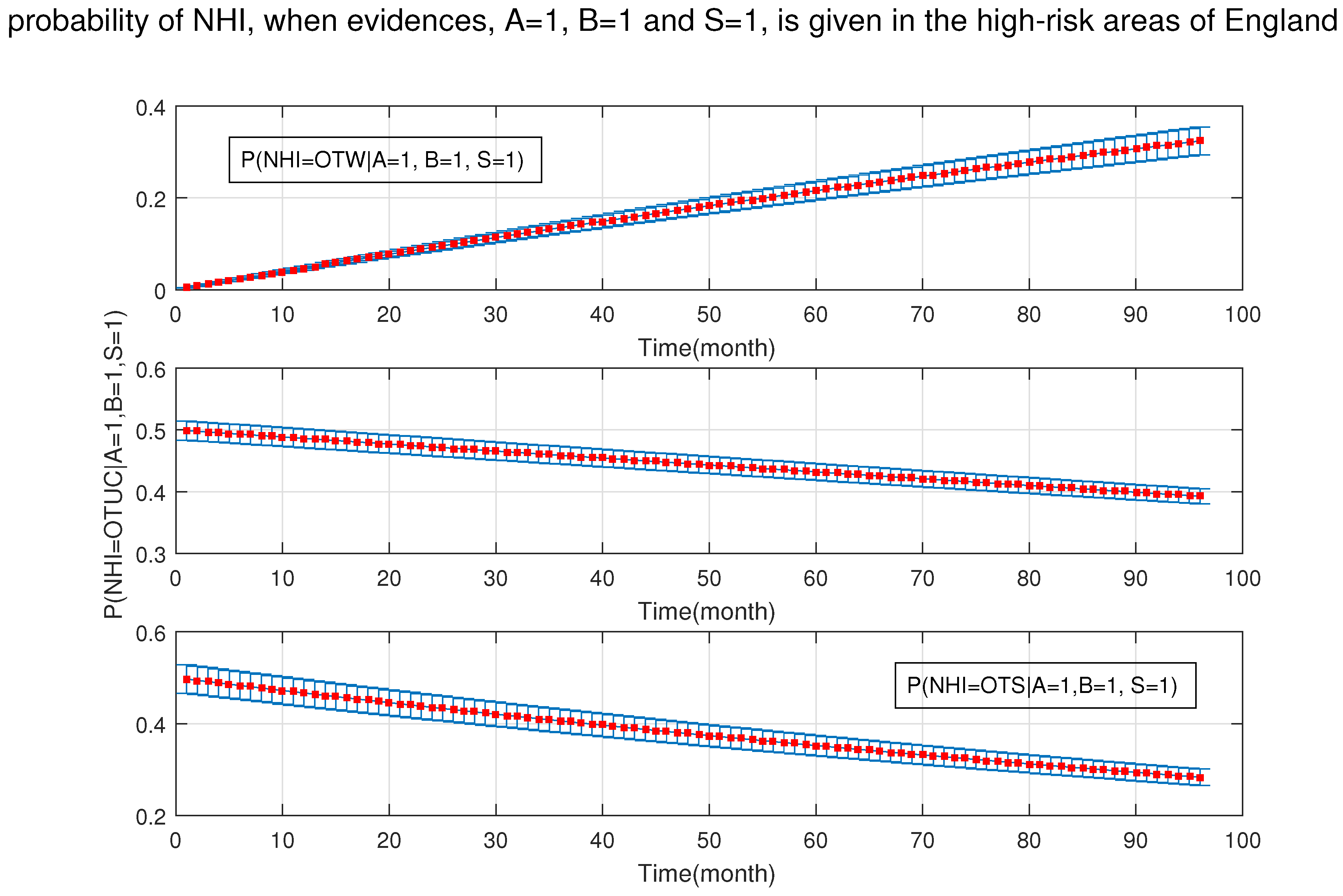
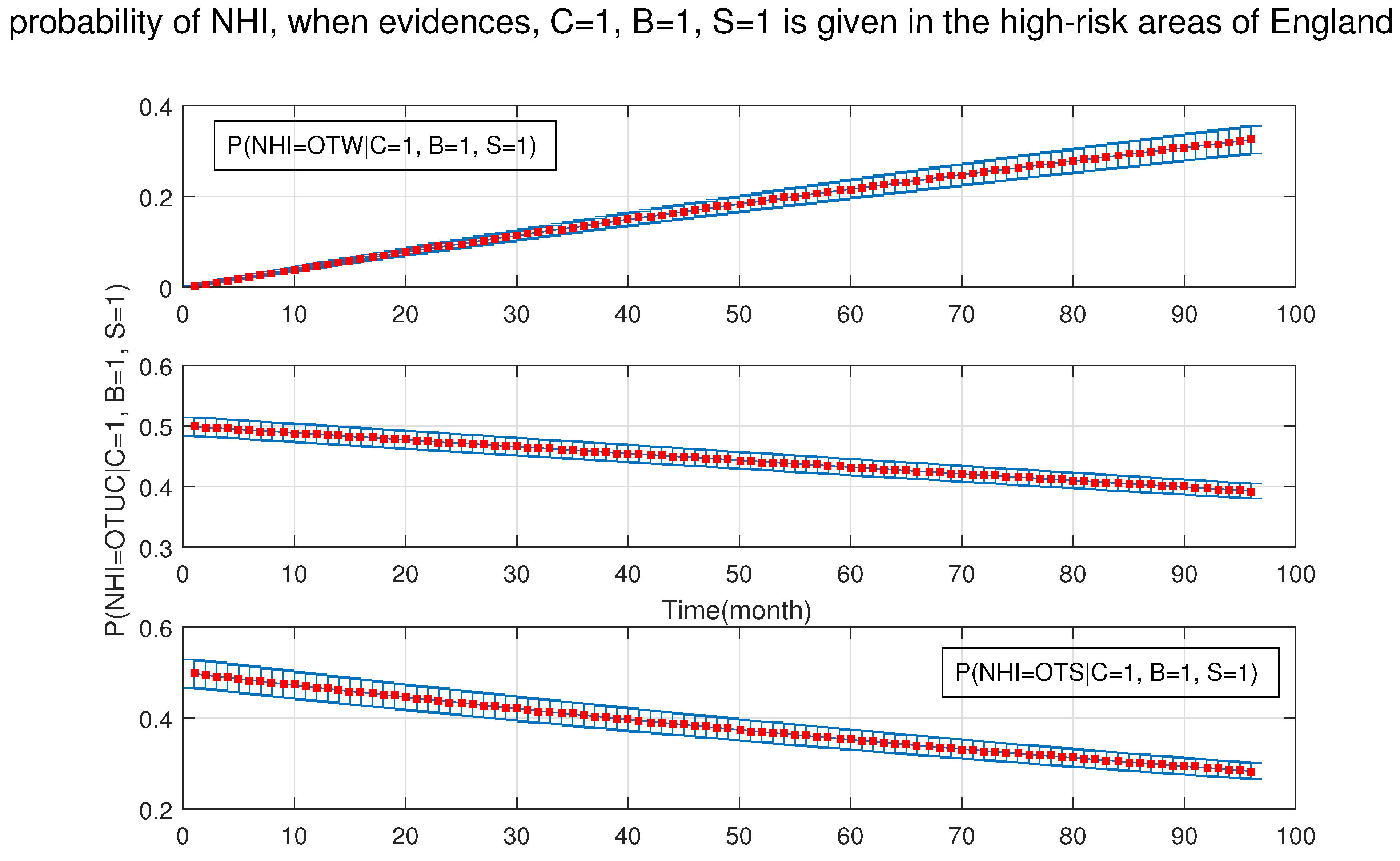
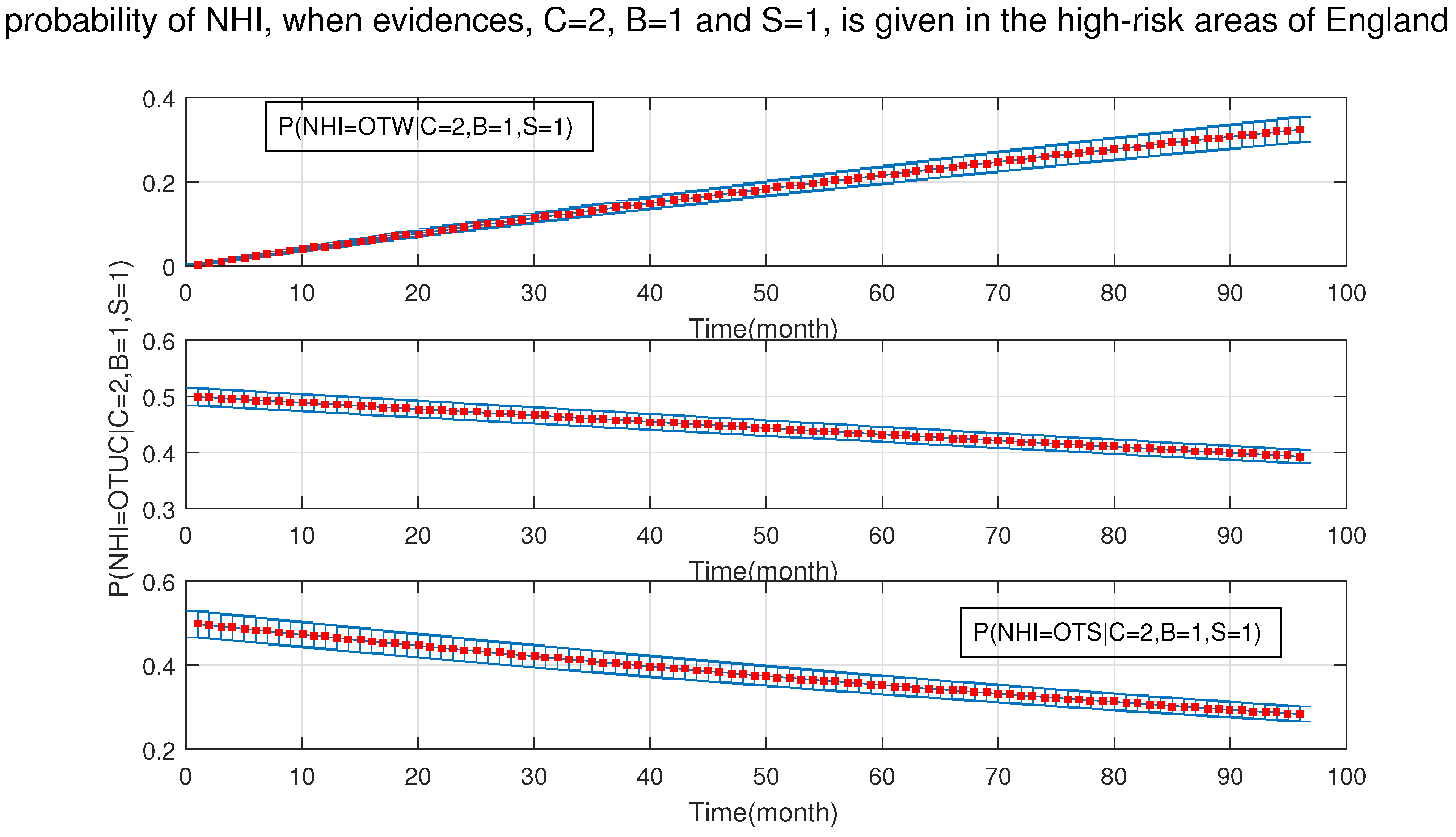
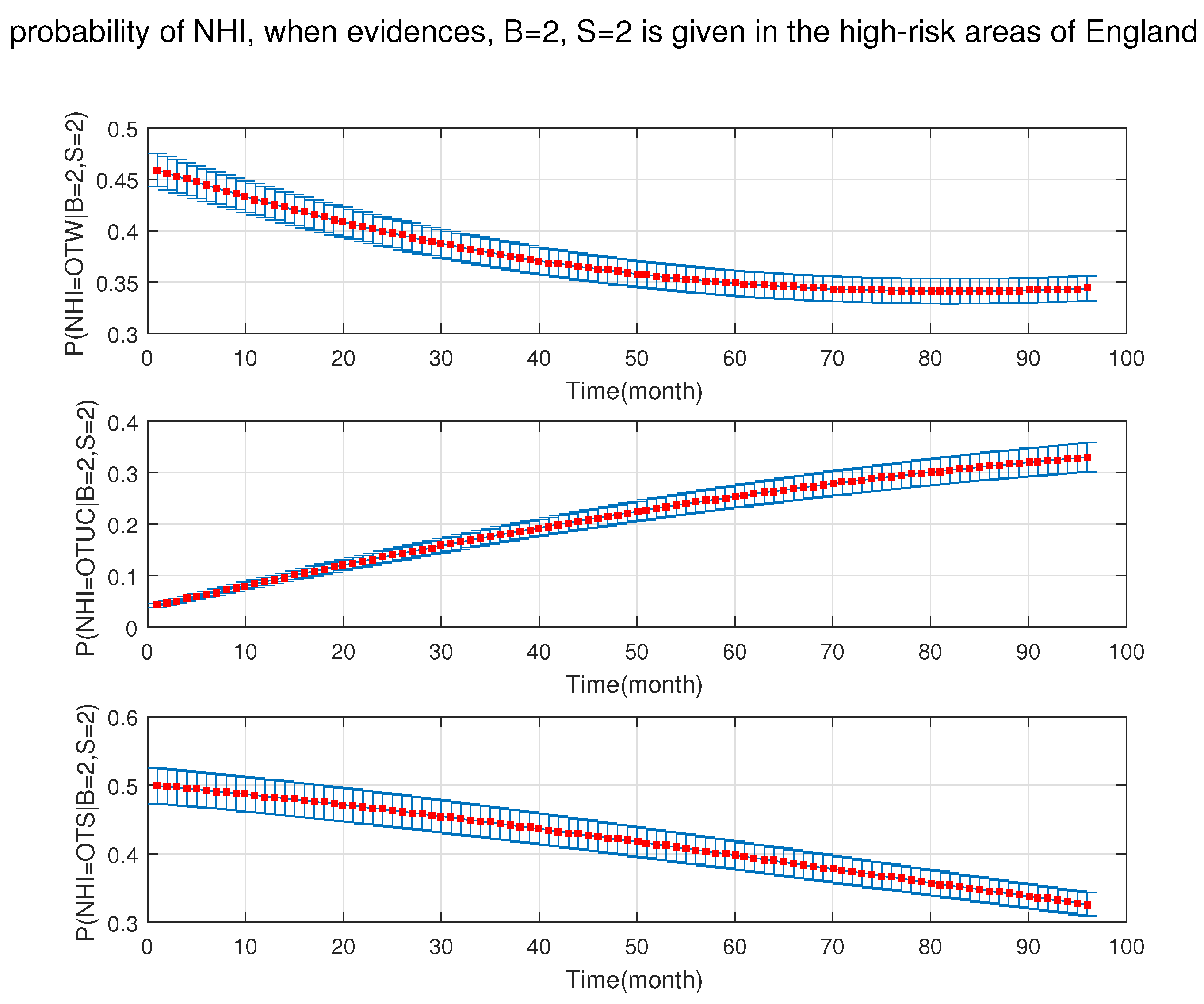
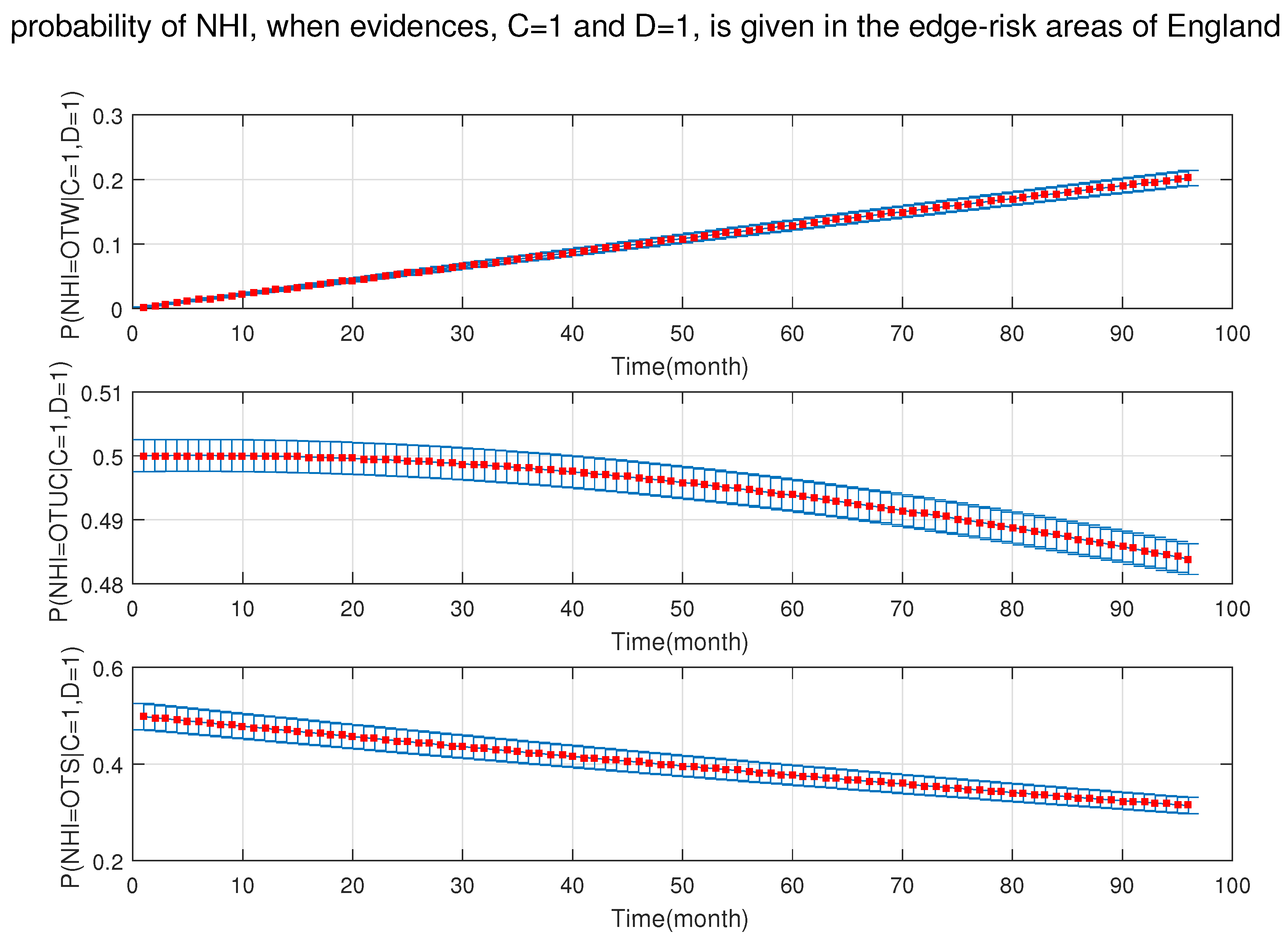
4. Simulation Results
- After the DBN graph was constructed and the prior probabilities were elicited from the available literature and data, the DBN updated the prior probabilities every time new information (evidence) was added to the network.
- Each node has upper, estimated and lower bounds. Thus, the proposed DBN was run several times to compute the posterior probabilities of the interested variables for all three bounds of each node and different node combinations (different scenarios). This computation allows us to handle the uncertainty due to the lack of information in selecting our priors (see Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11).
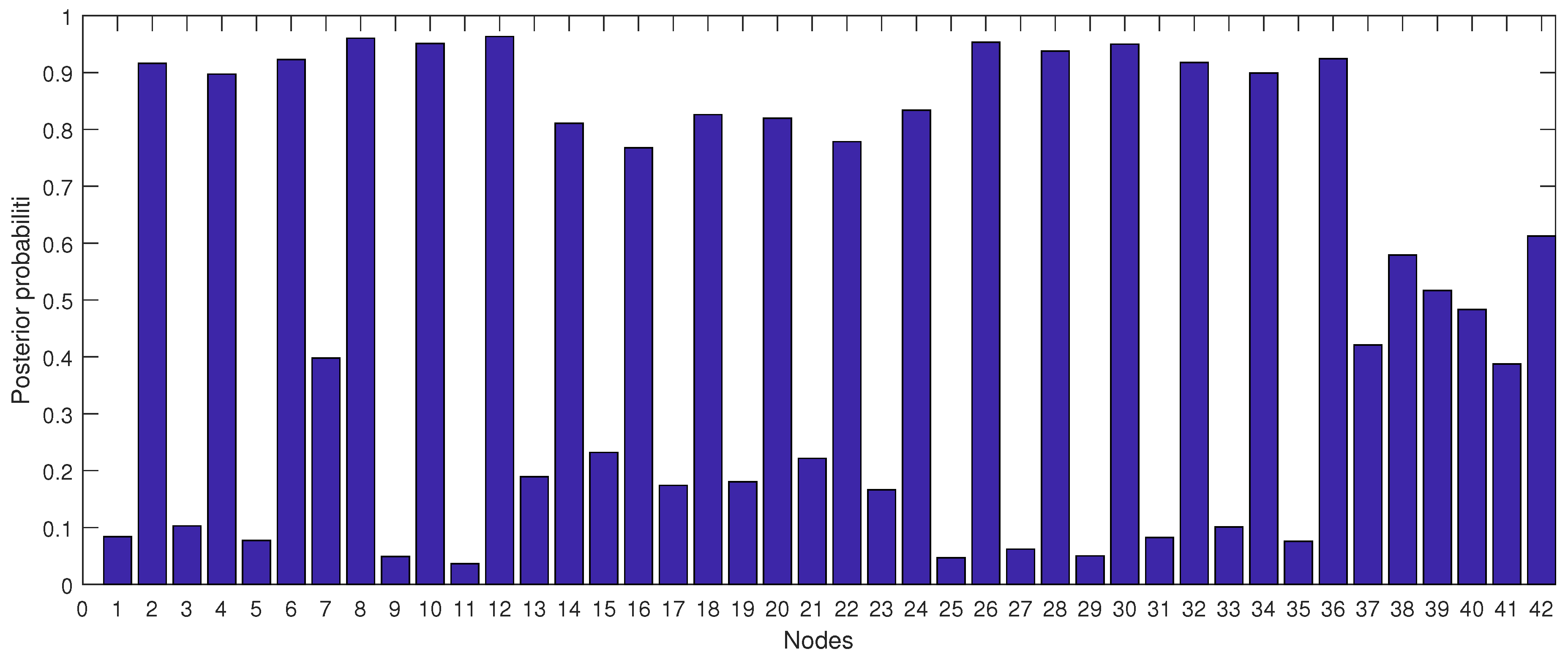
- The DBN ran 66 times for each risk area (198 times in total) to define the sensitivity sets for each area. The sensitivity sets are the risk factors which have the greatest influence on NHI.
- Finally, the DBN ran for different combinations of sensitivity sets to find out which risk factors may have grater effect if they are combined together.
- The probability of silage being the cause of OTUC decreased.
- The probability of the purchased cattle over 50 heads being the cause of OTUC decreased.
- Stock density and manure storage over six months had a greater chance to be the causes of OUTC.
- Silage had a greater chance to be the cause of OTS (in comparison with OTW and OTUC).
- The effect of purchased cattle over 50 heads was decreasing, although its effect was greater than the age of cattle.
- Stock density and manure storage had the greater chance to be the causes of OTS with some level of uncertainty by the end of the simulation.
5. Discussions and the Lessons Learned
- The sensitivity sets for different risk areas are different.
- The effect of one risk factor when it is integrated with other risk factors may change significantly. As the results show, in the high-risk areas, the age of cattle is not very concerning on its own; however, when it is associated with the types of feeding (e.g., silage), their joint probability increases the chance of NHI significantly. Furthermore, since the trade of live cattle between different areas is constantly increasing, the risk of moving infected cattle from an OTW region into an OTF area exists. The risk related to the movement of live animals must be emphasised mostly in the low-risk areas. It is thus necessary to remind the people involved in cattle trading of the importance of testing at purchase, especially if the animal introduced in an OTF area comes from a non-OTF-region. Besides, pre-movement testing is important. Thus, limiting movement of cattle onto the farm or purchasing from high-risk areas, along with follow up tests and longer isolation periods (more than 30 days) could reduce the risk of breakdowns. Based on available data, there are five categories from which farmers decide to isolate their newly purchased animals or milking equipment:
- –
- 7 day
- –
- 8–15 days
- –
- 16–21 days
- –
- 22–30 days
- –
- More than 30 days
Most farmers adopt 15 days of isolation because of lack of space. The level of infection in the environment is predicted to decay with a half-life of 34 days (credible intervals 20–71 days). Although decay is rapid, infection may arise months after infectious cattle are removed. Farmers who choose a longer period of isolation have less breakdown incidents. - The results are presented graphically and are easy to understand which is one of the strengths of BN.
- The presented results are not based on one dataset analysis. In fact, the model considered monthly data from 2008 to 2015. Therefore, the model is dynamic, rather than static and, anytime that new evidence is added to the model, the results are updated accordingly. Hence, it is possible to track the effect of risk factors on NHI for the whole period of study.
5.1. Advantages of BNs
- Initial beliefs about the values of each variable (prior probabilities) can be updated in the face of new evidence via Bayes’ theorem.
- A BN can perform three types of inference: deductive (top-down, forward and predictive), diagnostic (bottom-up, inverse and explanatory) and intercausal (bi-directional “explaining away”). This is useful since the same BNs can be used for both the assessment and the evaluation.
- Analysts can make probability judgments consistent with the direction of causality.
- Evidence can be entered into the model, and the effect on the other variables (nodes) can be observed (improving or worsening, and by what magnitude).
- BNs are able to work with data of different types and sources: they handle a mix of subjective and objective data and, hence, supplement traditional experimental and statistical methods.
5.2. Assumptions and Limitations
5.3. Software and Toolboxes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Defra. Government Strategic Framework for the Sustainable Control of Bovine Tuberculosis (bTB) in Great Britain; Department for Environment, Food and Rural Affairs (Defra): London, UK, 2005.
- Allen, A.; Minozzi, G.; Glass, E.; Skuce, R.; McDowell, S.; Woolliams, J.; Bishop, S. Bovine tuberculosis: The genetic basis of host susceptibility. Proc. R. Soc. Lond. B Biol. Sci. 2010, 277, 2737–2745. [Google Scholar] [CrossRef] [Green Version]
- Rossi, G.; De Leo, G.A.; Pongolini, S.; Natalini, S.; Vincenzi, S.; Bolzoni, L. Epidemiological modelling for the assessment of bovine tuberculosis surveillance in the dairy farm network in Emilia-Romagna (Italy). Epidemics 2015, 11, 62–70. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, D. A review of tuberculosis science and policy in Great Britain. Vet. Microbiol. 2006, 112, 119–126. [Google Scholar] [CrossRef]
- De la Rua-Domenech, R.; Goodchild, A.; Vordermeier, H.; Hewinson, R.; Christiansen, K.; Clifton-Hadley, R. Ante mortem diagnosis of tuberculosis in cattle: A review of the tuberculin tests, γ-interferon assay and other ancillary diagnostic techniques. Res. Vet. Sci. 2006, 81, 190–210. [Google Scholar] [CrossRef]
- Caffrey, J. Status of bovine tuberculosis eradication programmes in Europe. Vet. Microbiol. 1994, 40, 1–4. [Google Scholar] [CrossRef]
- Banos, G.; Winters, M.; Mrode, R.; Mitchell, A.; Bishop, S.; Woolliams, J.; Coffey, M. Genetic evaluation for bovine tuberculosis resistance in dairy cattle. J. Dairy Sci. 2017, 100, 1272–1281. [Google Scholar] [CrossRef]
- Donnelly, C.A.; Woodroffe, R.; Cox, D.; Bourne, J.; Gettinby, G.; Le Fevre, A.M.; McInerney, J.P.; Morrison, W.I. Impact of localized badger culling on tuberculosis incidence in British cattle. Nature 2003, 426, 834. [Google Scholar] [CrossRef] [PubMed]
- Küster, A.; Adler, N. Pharmaceuticals in the environment: Scientific evidence of risks and its regulation. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130587. [Google Scholar] [CrossRef] [Green Version]
- Skuce, R.A.; Allen, A.R.; McDowell, S.W. Herd-level risk factors for bovine tuberculosis: A literature review. Vet. Med. Int. 2012, 2012. [Google Scholar] [CrossRef]
- Krebs, J.R. Bovine tuberculosis in cattle and badgers. State Vet. J. 1998, 1, 1–191. [Google Scholar]
- O’Brien, D.J.; Schmitt, S.M.; Rudolph, B.A.; Nugent, G. Recent advances in the management of bovine tuberculosis in free-ranging wildlife. Vet. Microbiol. 2011, 151, 23–33. [Google Scholar] [CrossRef]
- Godfray, H.C.J.; Donnelly, C.A.; Kao, R.R.; Macdonald, D.W.; McDonald, R.A.; Petrokofsky, G.; Wood, J.L.; Woodroffe, R.; Young, D.B.; McLean, A.R. A restatement of the natural science evidence base relevant to the control of bovine tuberculosis in Great Britain. Proc. R. Soc. B Biol. Sci. 2013, 280, 20131634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, W.; Gettinby, G.; Cox, D.; Donnelly, C.; Bourne, J.; Clifton-Hadley, R.; Le Fevre, A.; McInerney, J.; Mitchell, A.; Morrison, W.; et al. Herd-level risk factors associated with tuberculosis breakdowns among cattle herds in England before the 2001 foot-and-mouth disease epidemic. Biol. Lett. 2005, 1, 53–56. [Google Scholar] [CrossRef] [Green Version]
- Reilly, L.; Courtenay, O. Husbandry practices, badger sett density and habitat composition as risk factors for transient and persistent bovine tuberculosis on UK cattle farms. Prev. Vet. Med. 2007, 80, 129–142. [Google Scholar] [CrossRef]
- Garnett, B.; Delahay, R.; Roper, T. Use of cattle farm resources by badgers (Meles meles) and risk of bovine tuberculosis (Mycobacterium bovis) transmission to cattle. Proc. R. Soc. Lond. B Biol. Sci. 2002, 269, 1487–1491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Courtenay, O.; Reilly, L.; Sweeney, F.; Hibberd, V.; Bryan, S.; Ul-Hassan, A.; Newman, C.; Macdonald, D.; Delahay, R.; Wilson, G.; et al. Is Mycobacterium bovis in the environment important for the persistence of bovine tuberculosis? Biol. Lett. 2006, 2, 460–462. [Google Scholar] [CrossRef] [Green Version]
- Gopal, R.; Goodchild, A.; Hewinson, G.; de la Rua Domenech, R.; Clifton-Hadley, R. Introduction of bovine tuberculosis to north-east England by. Proc. R. Soc. B Biol. Sci. 2006, 281, 8. [Google Scholar]
- Green, D.M.; Kiss, I.Z.; Mitchell, A.P.; Kao, R.R. Estimates for local and movement-based transmission of bovine tuberculosis in British cattle. Proc. R. Soc. Lond. B Biol. Sci. 2008, 275, 1001–1005. [Google Scholar] [CrossRef]
- Scantlebury, M.; Hutchings, M.; Allcroft, D.; Harris, S. Risk of disease from wildlife reservoirs: Badgers, cattle, and bovine tuberculosis. J. Dairy Sci. 2004, 87, 330–339. [Google Scholar] [CrossRef] [Green Version]
- Humblet, M.F.; Boschiroli, M.L.; Saegerman, C. Classification of worldwide bovine tuberculosis risk factors in cattle: A stratified approach. Vet. Res. 2009, 40, 1–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, F.; Brülisauer, F.; Gunn, G. Structure discovery in Bayesian networks: An analytical tool for analysing complex animal health data. Prev. Vet. Med. 2011, 100, 109–115. [Google Scholar] [CrossRef]
- Denholm, S.; Brand, W.; Mitchell, A.; Wells, A.; Krzyzelewski, T.; Smith, S.; Wall, E.; Coffey, M. Predicting bovine tuberculosis status of dairy cows from mid-infrared spectral data of milk using deep learning. J. Dairy Sci. 2020, 103, 9355–9367. [Google Scholar] [CrossRef]
- Pereira, L.; Ferraudo, A.; Panosso, A.; Carvalho, A.; Mathias, L.; Saches, A.; Hellwig, K.; Ancêncio, R. Machine Learning to predict tuberculosis in cattle from the state of Sao Paulo, Brazil. Eur. J. Public Health 2020, 30, ckaa166. [Google Scholar] [CrossRef]
- Poon, A.F.; Lewis, F.I.; Pond, S.L.K.; Frost, S.D. An evolutionary-network model reveals stratified interactions in the V3 loop of the HIV-1 envelope. PLoS Comput. Biol. 2007, 3, e231. [Google Scholar] [CrossRef]
- Malagrino, L.S.; Roman, N.T.; Monteiro, A.M. Forecasting stock market index daily direction: A Bayesian Network approach. Expert Syst. Appl. 2018, 105, 11–22. [Google Scholar] [CrossRef]
- Sousa, H.S.; Prieto-Castrillo, F.; Matos, J.C.; Branco, J.M.; Lourenço, P.B. Combination of expert decision and learned based Bayesian Networks for multi-scale mechanical analysis of timber elements. Expert Syst. Appl. 2018, 93, 156–168. [Google Scholar] [CrossRef]
- Azar, A.; Dolatabad, K.M. A method for modelling operational risk with fuzzy cognitive maps and Bayesian belief networks. Expert Syst. Appl. 2019, 115, 607–617. [Google Scholar] [CrossRef]
- Jiang, Y.; Liang, Z.; Gao, H.; Guo, Y.; Zhong, Z.; Yang, C.; Liu, J. An improved constraint-based Bayesian network learning method using Gaussian kernel probability density estimator. Expert Syst. Appl. 2018, 113, 544–554. [Google Scholar] [CrossRef]
- Onta nón, S.; Monta na, J.L.; Gonzalez, A.J. A Dynamic-Bayesian Network framework for modeling and evaluating learning from observation. Expert Syst. Appl. 2014, 41, 5212–5226. [Google Scholar] [CrossRef]
- Smith, R.; Dick, J.; Trench, H.; Oijen, M.V. Extending a Bayesian Belief Network for ecosystem evaluation. In Proceedings of the Berlin Conference on Human Dimensions of Global Environmental Change 2012, Berlin, Germany, 5–6 October 2012. [Google Scholar]
- Arsene, O.; Dumitrache, I.; Mihu, I. Medicine expert system dynamic Bayesian Network and ontology based. Expert Syst. Appl. 2011, 38, 15253–15261. [Google Scholar] [CrossRef]
- Carriger, J.F.; Barron, M.G.; Newman, M.C. Bayesian networks improve causal environmental assessments for evidence-based policy. Environ. Sci. Technol. 2016, 50, 13195–13205. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Bouvry, P. Challenges on Probabilistic Modeling for Evolving Networks. In EVOLVE-A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation III; Springer: New York, NY, USA, 2014; pp. 77–93. [Google Scholar]
- Chatrabgoun, O.; Hosseinian-Far, A.; Chang, V.; Stocks, N.G.; Daneshkhah, A. Approximating non-Gaussian Bayesian networks using minimum information vine model with applications in financial modelling. J. Comput. Sci. 2018, 24, 266–276. [Google Scholar] [CrossRef] [Green Version]
- Daneshkhah, A.; Smith, J.Q. Multicausal Prior Families, Randomisation and Essential Graphs. In Proceedings of the Probabilistic Graphical Models, Cuenca, Spain, 6–8 November 2002. [Google Scholar]
- Bolstad, W.M.; Curran, J.M. Introduction to Bayesian Statistics; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Daneshkhah, A.; Parham, G.; Chatrabgoun, O.; Jokar, M. Approximation multivariate distribution with pair copula using the orthonormal polynomial and Legendre multiwavelets basis functions. Commun. Stat. Simul. Comput. 2016, 45, 389–419. [Google Scholar] [CrossRef]
- Valentin, S.; Bramley, N.R.; Lucas, C.G. Learning Hidden Causal Structure from Temporal Data. Cogn. Sci. Soc. 2020, 4, 1906–1912. [Google Scholar]
- Sedighi, T. Using Dynamic Bayesian Network (DBN) for Evaluation. 2019. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/69698-using-dynamic-bayesian-network-dbn-for-evaluation (accessed on 9 January 2019).
- Wang, G.; Xu, T.; Tang, T.; Yuan, T.; Wang, H. A Bayesian network model for prediction of weather-related failures in railway turnout systems. Expert Syst. Appl. 2017, 69, 247–256. [Google Scholar] [CrossRef]
- Daneshkhah, A.; Hosseinian-Far, A.; Sedighi, T.; Farsi, M. Prior elicitation and evaluation of imprecise judgements for Bayesian analysis of system reliability. In Strategic Engineering for Cloud Computing and Big Data Analytics; Springer: New York, NY, USA, 2017; pp. 63–79. [Google Scholar]
- O’Hagan, A.; Buck, C.E.; Daneshkhah, A.; Eiser, J.R.; Garthwaite, P.H.; Jenkinson, D.J.; Oakley, J.E.; Rakow, T. Uncertain Judgements: Eliciting Experts’ Probabilities; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]





| Nodes | State 1 | State 2 |
|---|---|---|
| A: Age of Cattle | >24 months | ≤24 months |
| B: Badgers density | >3 setts/km | ≤3 setts/km |
| C: Manure storage | >6 months | ≤6 months |
| D: Stock density | >3 heads/ha | ≤3 heads/ha |
| S: Silage | True | False |
| W: Purchased cattle | >50 heads | ≤50 heads |
| F: Movement restriction | True | False |
| Nodes | State 1 | State 2 | State 3 |
|---|---|---|---|
| E: Skin test results | Positive | Inconclusive | Negative |
| NHI | OTW | OTUC | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| m | OTW | ||||||
| m | 1 | 1 | 1 | 1 | 0.916 | 0.98 | OTW |
| m | 0.0066 | 0.0016 | 0.1029 | 0.0080 | OTUS | ||
| m | 1 | 0.9934 | 0.9992 | 0.9984 | 0.8971 | 0.9920 | OTUS |
| m | 0.0772 | 0.0023 | OTS | ||||
| m | 1 | 0.9991 | 0.999 | 0.9996 | 0.9228 | 0.9977 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| setts/km | 0.398 | 0.1533 | OTW | ||||
| setts/km | 1 | 1 | 1 | 0.9994 | 0.9602 | 0.8467 | OTW |
| setts/km | 0.0031 | 0.0068 | 0.0382 | 0.0488 | 0.0691 | OTUS | |
| setts/km | 0.9992 | 0.9969 | 0.9932 | 0.9618 | 0.9512 | 0.9309 | OTUS |
| setts/km | 4.0727 | 0.0098 | 0.0366 | 0.0202 | OTS | ||
| setts/km | 0.9999 | 0.9996 | 0.9991 | 0.9902 | 0.9634 | 0.9798 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| months | 0.1891 | 0.0526 | OTW | ||||
| months | 1 | 1 | 1 | 0.9997 | 0.8109 | 0.9474 | OTW |
| months | 0.0157 | 0.0023 | 0.0201 | 0.2321 | 0.0237 | OTUC | |
| months | 0.9996 | 0.9843 | 0.9977 | 0.9799 | 0.7679 | 0.9763 | OTUC |
| months | 0.0021 | 0.0052 | 0.1741 | 0.0069 | OTS | ||
| months | 0.99997 | 0.9979 | 0.9997 | 0.9948 | 0.8259 | 0.9931 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| heads/ha | 0.0027 | 0.1804 | 0.5857 | OTW | |||
| heads/ha | 1 | 1 | 0.9999 | 0.9973 | 0.8196 | 0.4094 | OTW |
| heads/ha | 0.0044 | 0.0149 | 0.0303 | 0.1894 | 0.2216 | 0.2663 | OTUC |
| heads/ha | 0.9959 | 0.9851 | 0.9697 | 0.8106 | 0.7784 | 0.7337 | OTUC |
| heads/ha | 0.0020 | 0.0042 | 0.0487 | 0.1661 | 0.0778 | OTS | |
| heads/ha | 0.9995 | 0.9980 | 0.9958 | 0.9513 | 0.8339 | 0.9222 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| S:True | 0.0467 | 0.0467 | 0.0467 | 0.0467 | 0.0467 | 0.0467 | OTW |
| S:False | 0.9533 | 0.9533 | 0.9533 | 0.9533 | 0.9533 | 0.9533 | OTW |
| S:True | 0.3875 | 0.3660 | 0.3545 | 0.1887 | 0.0621 | 0.0390 | OTUC |
| S:False | 0.6125 | 0.6340 | 0.6455 | 0.8113 | 0.9379 | 0.9610 | OTUC |
| S:True | 0.0038 | 0.0043 | 0.0062 | 0.0091 | 0.0501 | 0.7675 | OTS |
| S:False | 0.9962 | 0.9957 | 0.9938 | 0.9909 | 0.9499 | 0.2325 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| heads | 0.0017 | 0.0044 | 0.0822 | 0.1408 | OTW | ||
| heads | 1 | 0.9993 | 0.9983 | 0.9956 | 0.9178 | 0.8592 | OTW |
| heads | 0.6306 | 0.5956 | 0.5769 | 0.3071 | 0.1010 | 0.0635 | OTUC |
| heads | 0.3694 | 0.4044 | 0.4231 | 0.6929 | 0.8990 | 0.9365 | OTUC |
| heads | 0.0794 | 0.0794 | 0.0792 | 0.0790 | 0.0757 | 0.0185 | OTS |
| heads | 0.9206 | 0.9206 | 0.9208 | 0.9210 | 0.9243 | 0.9815 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| F: True | 0.0036 | 0.4209 | 0.7386 | OTW | |||
| F: False | 1 | 1 | 0.9999 | 0.9964 | 0.5791 | 0.2614 | OTW |
| F: True | 0.0054 | 0.0401 | 0.0401 | 0.2463 | 0.5168 | 0.3331 | OTUC |
| F: False | 0.9946 | 0.9599 | 0.9599 | 0.7537 | 0.4832 | 0.6669 | OTUC |
| F: True | 0.0053 | 0.0055 | 0.0633 | 0.3875 | 0.0973 | OTS | |
| F: False | 0.9993 | 0.9947 | 0.9945 | 0.9367 | 0.6125 | 0.9027 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) | Evidence: New Herd Incidents (NHI) |
|---|---|---|---|---|---|---|---|
| E: Positive | 0.0036 | 0.4209 | 0.7386 | OTW | |||
| E: Inconclusive | 0.9533 | 0.9533 | 0.9532 | 0.9499 | 0.5521 | 0.2492 | OTW |
| E: Negative | 0.0467 | 0.0467 | 0.0467 | 0.0465 | 0.0270 | 0.0122 | OTW |
| E: Positive | 0.0054 | 0.0401 | 0.0401 | 0.2463 | 0.5153 | 0.3331 | OTUC |
| E: Inconclusive | 0.6073 | 0.5958 | 0.6072 | 0.5765 | 0.4459 | 0.6435 | OTUC |
| E: Negative | 0.3872 | 0.3641 | 0.3526 | 0.1772 | 0.0388 | 0.0234 | OTUC |
| E: Positive | 0.0053 | 0.0055 | 0.0633 | 0.3875 | 0.0973 | OTS | |
| E: Inconclusive | 0.9956 | 0.9906 | 0.9885 | 0.9305 | 0.5805 | 0.1398 | OTS |
| E: Negative | 0.0037 | 0.0040 | 0.0060 | 0.0062 | 0.0320 | 0.7630 | OTS |
| Nodes | Prior Probability (Lower Bound) | Prior Probability (Estimated) | Prior Probability (Higher Bound) | Posterior Probability (Lower Bound) | Posterior Probability (Estimated) | Posterior Probability (Higher Bound) |
|---|---|---|---|---|---|---|
| OTW | 0.1197 | 0.1237 | 0.1238 | 0.1728 | 0.4617 | 0.4704 |
| OTUC | 0.8803 | 0.8763 | 0.8762 | 0.8272 | 0.5383 | 0.5296 |
| OTS | 0.0431 | 0.0429 | 0.0429 | 0.0405 | 0.0264 | 0.0259 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sedighi, T.; Varga, L. Evaluating the Bovine Tuberculosis Eradication Mechanism and Its Risk Factors in England’s Cattle Farms. Int. J. Environ. Res. Public Health 2021, 18, 3451. https://doi.org/10.3390/ijerph18073451
Sedighi T, Varga L. Evaluating the Bovine Tuberculosis Eradication Mechanism and Its Risk Factors in England’s Cattle Farms. International Journal of Environmental Research and Public Health. 2021; 18(7):3451. https://doi.org/10.3390/ijerph18073451
Chicago/Turabian StyleSedighi, Tabassom, and Liz Varga. 2021. "Evaluating the Bovine Tuberculosis Eradication Mechanism and Its Risk Factors in England’s Cattle Farms" International Journal of Environmental Research and Public Health 18, no. 7: 3451. https://doi.org/10.3390/ijerph18073451