Analysis of Taiwan’s Mask Collection and Plan Evasion during the COVID-19 Pandemic
Abstract
:1. Introduction
2. Literature Review
3. The NMT’s Output and the Plan under Perfect Information
3.1. Assumptions of the Model
3.2. The NMT’s Output Decision
3.3. The Planner’s Decisions for the Planned Output and Price
4. The NMT’s Plan Evasion under Imperfect Information
4.1. The Model
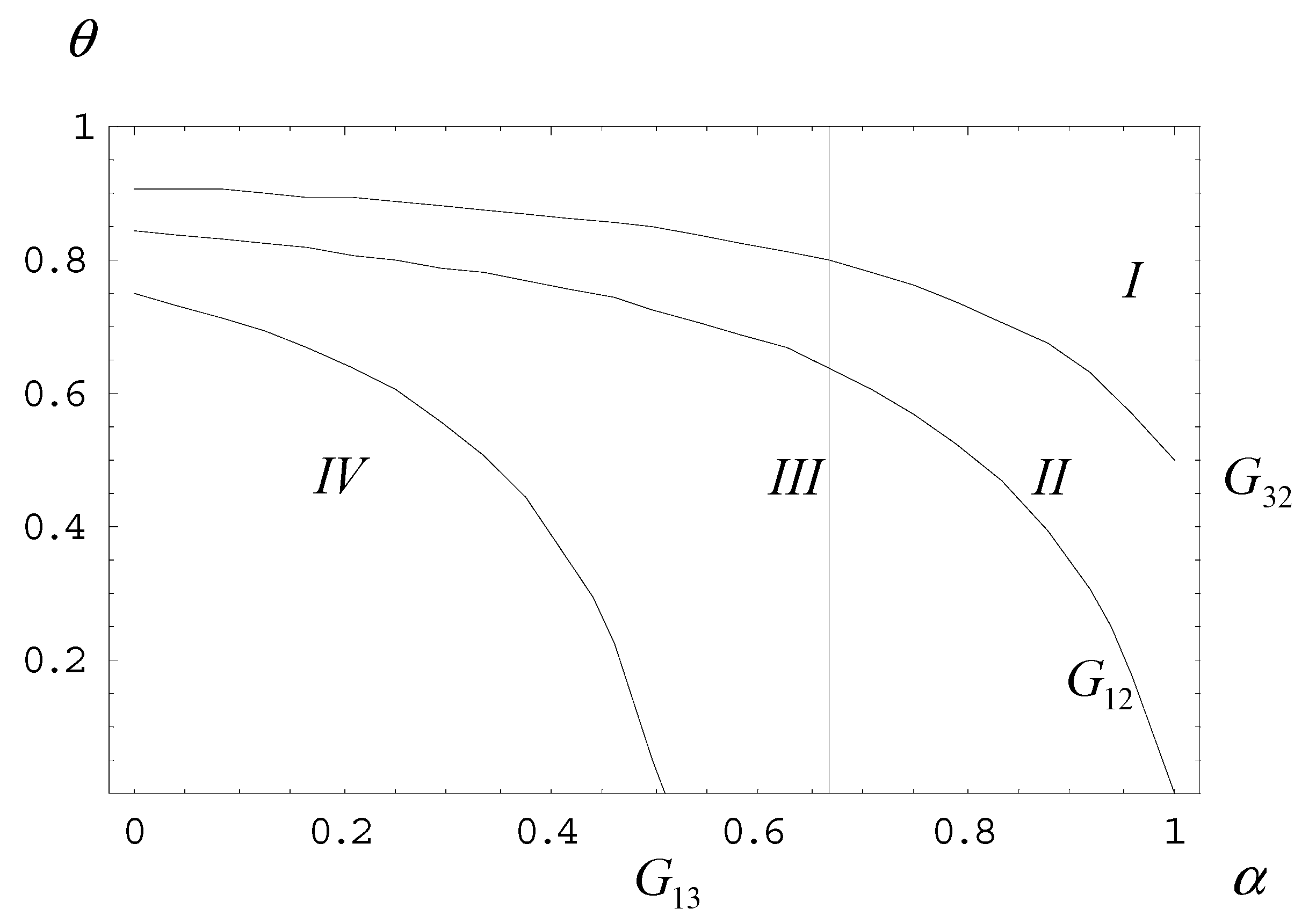
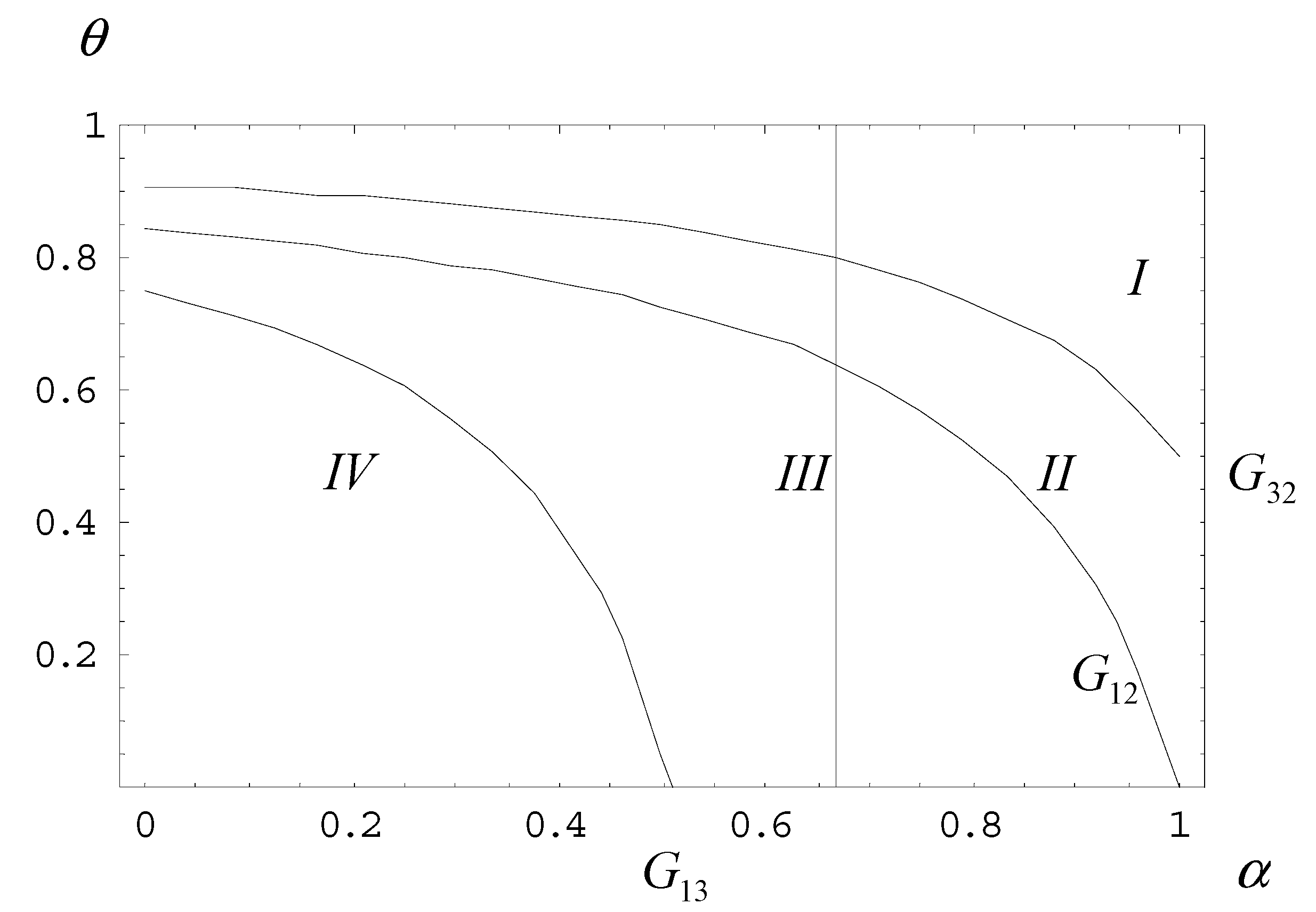
4.2. Impact of the Planned Quota on the NMT’s Excess Output Decision
4.3. Determination of the Planned Quota and Price by the Planner
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Ranking of the Planner’s Expected Return among the Three Scenarios
References
- Karaivanov, A.; Lu, S.E.; Shigeoka, H.; Chen, C.; Pamplona, S. Face Masks, Public Policies and Slowing the Spread of COVID-19: Evidence from Canada; NBER working paper no.27891; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar] [CrossRef]
- Mitze, T.; Kosfeld, R.; Rode, J.; Wälde, K. Face masks considerably reduce COVID-19 cases in Germany. Proc. Natl. Acad. Sci. USA 2020, 117, 32293–32301. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.; Chi, H.; Chiu, N.; Tseng, C.; Huang, Y.; Lin, C. The Effect of a Name-Based Mask Rationing Plan in Taiwan on Public Anxiety Regarding a Mask Shortage during the COVID-19 Pandemic: Observational Study. JMIR Form. Res. 2021, 5, e21409. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. Coronavirus Disease 2019 (COVID-19). 2020. Available online: https://www.cdc.gov.tw/En (accessed on 12 September 2020).
- Chiu, N.; Chi, H.; Tai, Y.; Peng, C.; Tseng, C.; Chen, C. Impact of Wearing Masks, Hand Hygiene, and Social Distancing on Influenza, Enterovirus, and All-Cause Pneumonia during the Coronavirus Pandemic: Retrospective National Epidemiological Surveillance Study. J. Med. Internet. Res. 2020, 22, e21257. [Google Scholar] [CrossRef]
- Chen, C.; Tseng, C.; Choi, W.; Lee, Y.; Su, T.; Hsieh, C. Taiwan Government-Guided Strategies Contributed to Combating and Controlling COVID-19 Pandemic. Front. Public Health 2020, 8, 547423. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Coronavirus Disease (COVID-19) Outbreak Situation. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 12 September 2020).
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J. COVID-19 Systematic Urgent Review Group Effort (SURGE) study authors. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- The Ministry of Economic Affairs, Taiwan. The Ministry of Economic Affairs Fights for Epidemic Prevention to Build a Mask Production Line, and the Domestic Daily Production Capacity is Expected to Reach 10 Million Pieces. 2020. Available online: https://www.moea.gov.tw/Mns/populace/news/News.aspx?kind=1&menu_id=40&news_id=88573 (accessed on 10 March 2021).
- The Ministry of Economic Affairs, Taiwan. Taiwan to Lift Ban on Mask Exports on June 1. 2020. Available online: https://www.trade.gov.tw/English/Pages/Detail.aspx?nodeID=855&pid-696005 (accessed on 10 March 2021).
- The Ministry of Justice, Taiwan. Deer Masks Technology Co. Ltd. Privately Set up Mask Production Lines to Produce Masks. Due to Violation of Pharmaceutical Affairs Act, the Owner was Remanded on Bail of NT$ 300000 by Taiwan Ciaotou District Prosecutors, Ministry of Justice. 2020. Available online: https://qtc.moj.gov.tw/midea/228140/1090924 (accessed on 10 March 2021).
- WHO. Shortage of PPE Endangering Health Workers Worldwide. 2020. Available online: https://www.who.int/news/item/03-03-2020-shortage-of-personal-protective-equipment-endangering-health-workers-worldwide (accessed on 12 September 2020).
- Missoni, E.; Armocida, B.; Formenti, B. Face Masks for All and All for Face Masks in the COVID-19 Pandemic: Community Level Production to Face the Global Shortage and Shorten the Epidemic. Disaster Med. Public Health Prep. 2020, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Howard, J.; Huang, A.; Li, Z.; Tufekci, Z.; Zdimal, V.; van der Westhuized, H.; von Delft, A.; Price, A.; Fridman, L.; Tang, L.; et al. An evidence review of face masks against COVID-19. Proc. Natl. Acad. Sci. USA 2020, 118, e2014564118. [Google Scholar] [CrossRef]
- Flanagan, S.T.; Ballard, D.J. 3D Printed Face Shields: A Community Response to the COVID-19 Global Pandemic. Acad Radiol. 2020, 27, 905–906. [Google Scholar] [CrossRef] [PubMed]
- Manero, A.; Smith, P.; Koontz, A.; Dombrowski, M.; Sparkman, J.; Courbin, D.; Chi, A. Leveraging 3D Printing Capacity in Times of Crisis: Recommendations for COVID-19 Distributed Manufacturing for Medical Equipment Rapid Response. Int. J. Environ. Res. Public Health 2020, 17, 4634. [Google Scholar] [CrossRef] [PubMed]
- François, P.-M.; Bonnet, X.; Kosior, J.; Adam, J.; Khonsari, R. 3D-printed contact-free devices designed and dispatched against the COVID-19 pandemic: The 3D COVID initiative. J. Stomatol. Oral Maxillofac. Surg. 2020. [Google Scholar] [CrossRef] [PubMed]
- Ma, Q.; Shan, H.; Zhang, C.; Zhang, H.; Li, G.; Yang, R.; Chen, J. Decontamination of face masks with steam for mask reuse in fighting the pandemic COVID-19: Experimental supports. J. Med Virol. 2020, 92, 1971–1974. [Google Scholar] [CrossRef]
- WHO. Rational Use of Personal Protective Equipment for Coronavirus Disease 2019 (COVID-19). 2020. Available online: https://apps.who.int/iris/bitstream/handle/10665/331215/WHO-2019-nCov-IPCPPE_use-2020.1-eng.pdf (accessed on 12 September 2020).
- Kirubarajan, A.; Khan, S.; Got, T. Mask shortage during epidemics and pandemics: A scoping review of interventions to overcome limited supply. BMJ Open 2020, 10, e040547. [Google Scholar] [CrossRef] [PubMed]
- Fisher, E.M.; Williams, J.L.; Shaffer, R.E. Evaluation of microwave steam bags for the decontamination of filtering facepiece respirators. PLoS ONE 2011, 6, e18585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mills, D.; Harnish, D.A.; Lawrence, C. Ultraviolet germicidal irradiation of influenza-contaminated N95 filtering facepiece respirators. Am. J. Infect. Control 2018, 46, e49–e55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nemeth, C.; Laufersweiler, D.; Polander, E. Preparing for an influenza pandemic: Hospital acceptance study of filtering Facepiece respirator decontamination using ultraviolet germicidal irradiation. J. Patient Saf. 2020, 16, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Fisher, E.; Shaffer, R. Survival of Bacteriophage MS2 on Filtering Facepiece Respirator Coupons. Appl. Biosaf. 2010, 15, 71–76. [Google Scholar] [CrossRef]
- Fisher, E.M.; Richardson, A.W.; Harpest, S.D. Reaerosolization of MS2 bacteriophage from an N95 filtering facepiece respirator by simulated coughing. Ann. Occup. Hyg. 2012, 56, 315–325. [Google Scholar] [CrossRef]
- Coulliette, A.D.; Perry, K.A.; Edwards, J.R.; Noble-Wang, J.A. Persistence of the 2009 Pandemic Influenza A (H1N1) Virus on N95 Respirators. Appl. Environ. Microbiol. 2013, 79, 2148–2155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vuma, C.D.; Manganyi, J.; Wilson, K.; Rees, D. The Effect on Fit of Multiple Consecutive Donning and Doffing of N95 Filtering Facepiece Respirators. Ann. Work. Expo. Health 2019, 63, 930–936. [Google Scholar] [CrossRef]
- Shenal, B.V.; Radonovich, L.J.R., Jr.; Cheng, J.; Hodgson, M.; Bender, B.S. Discomfort and Exertion Associated with Prolonged Wear of Respiratory Protection in a Health Care Setting. J. Occup. Environ. Hyg. 2012, 9, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Rebmann, T.; Carrico, R.; Wang, J. Physiologic and other effects and compliance with long-term respirator use among medical intensive care unit nurses. Am. J. Infect. Control. 2013, 41, 1218–1223. [Google Scholar] [CrossRef] [PubMed]
- Derrick, J.; Gomersall, C. Protecting healthcare staff from severe acute respiratory syndrome: Filtration capacity of multiple surgical masks. J. Hosp. Infect. 2005, 59, 365–368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Au, S.; Gomersall, C.; Leung, P.; Li, P. A randomised controlled pilot study to compare filtration factor of a novel non-fit-tested high-efficiency particulate air (HEPA) filtering facemask with a fit-tested N95 mask. J. Hosp. Infect. 2010, 76, 23–25. [Google Scholar] [CrossRef] [PubMed]
- Quan, F.-S.; Rubino, I.; Lee, S.-H.; Koch, B.; Choi, H.-J. Universal and reusable virus deactivation system for respiratory protection. Sci. Rep. 2017, 7, 39956. [Google Scholar] [CrossRef] [Green Version]
- Bergman, M.; Zhuang, Z.; Brochu, E.; Palmiero, A. Fit Assessment of N95 Filtering-Facepiece Respirators in the U.S. Centers for Disease Control and Prevention Strategic National Stockpile. J. Int. Soc. Respir. Prot. 2016, 32, 50–64. [Google Scholar]
- Rottach, D.R.; Lei, Z. Stockpiled N95 Filtering Facepiece Respirator Polyisoprene Strap Performance. J. Int. Soc. Respir. Prot. 2017, 34, 69–80. [Google Scholar] [PubMed]
- Greenawald, L.; Moore, S.; Yorio, P. Inhalation and Exhalation Resistance and Filtration Performance of Stockpiled Air-Purifying Respirators: Overall Performance of Nearly 4000 Respirators Sampled from Ten Stockpile Facilities. Available online: https://www.cdc.gov/niosh/npptl/ppecase/pdfs/PPE-CASE-Aggregated-Stockpile-Study-03252020-508.pdf (accessed on 10 March 2021).
- Yu, S.; Kim, S.; Kang, J. Face Mask Policies in South Korea in Response to COVID-19. Asia Pac. J. Public Health 2020, 32, 497–499. [Google Scholar] [CrossRef]
- Shleifer, A.; Vishny, R. Pervasive Shortages under Socialism. RAND J. Econ. 1992, 23, 237. [Google Scholar] [CrossRef]
- Zhou, H. Partial reform and full price liberalization in the short and the long run. China Econ. Rev. 1997, 8, 53–66. [Google Scholar] [CrossRef]
- Huang, C.S.; Lee, J.Y. The Output Determination of State-Owned Enterprise under Gradual Price Reform of Chinese Economy. Asia Pac. Econ. Manag. Rev. 2000, 3, 117–144. [Google Scholar]
- Koo, A.Y.C.; Obst, N.P. Dual-Track and Mandatory Quota in China’s Price Reform. Comp. Econ. Stud. 1995, 37, 1–17. [Google Scholar] [CrossRef]
- Jing, H.H. Plan, Market and the Supply Behaviour of Foodgrain of Chinese Peasants. In Jingji Yanjiu (Economic Research Journal); Chinese Academy of Social Sciences: Beijing, China, 1990; pp. 62–68. [Google Scholar]
- Sicular, T. Plan and Market in China’s Agricultural Commerce. J. Political Econ. 1988, 96, 283–307. [Google Scholar] [CrossRef]
- Tsang, S.K.; Cheng, Y.S. Plan Evasion and Supply Instability in a Double-Track System. Econ. Plan. 1997, 30, 1–16. [Google Scholar]
- WHO. Considerations for Implementing a Risk-Based Approach to International Travel in the Context of COVID-19. 2020. Available online: https://www.who.int/publications/i/item/WHO-2019-nCoV-Risk-based-international-travel-2020.1 (accessed on 10 March 2021).
- WHO. Advice on the Use of Masks in the Context of COVID-19: Interim Guidance. 2020. Available online: https://apps.who.int/iris/handle/10665/332293 (accessed on 10 March 2021).
- Wang, J.; Pan, L.; Tang, S.; Ji, J.S.; Shi, X. Mask use during COVID-19: A risk adjusted strategy. Environ. Pollut. 2020, 266, 115099. [Google Scholar] [CrossRef] [PubMed]
- WHO. Coronavirus Disease (COVID-19) Advice for the Public: When and How to Use Masks. 2020. Available online: https://www.who.int/emergencies/diseases/novelcoronavirus-2019/advice-for-public/when-and-how-to-use-masks (accessed on 10 March 2021).
- State Council, China. Guidelines for the Selection and Use of Different Types of Masks for Preventing New Coronavirus Infection in Different Populations. 2020 (in Chinese). Available online: http://www.gov.cn/xinwen/2020-02/05/content_5474774.htm (accessed on 10 March 2021).
- Feng, S.; Shen, C.; Xia, N.; Song, W.; Fan, M.; Cowling, B.J. Rational use of face masks in the COVID-19 pandemic. Lancet Respir. Med. 2020, 8, 434–436. [Google Scholar] [CrossRef]
- Lee, E.; Chen, Y.-Y.; McDonald, M.; O’Neill, E. Dynamic Response Systems of Healthcare Mask Production to COVID-19: A Case Study of Korea. Systems 2020, 8, 18. [Google Scholar] [CrossRef]
- CDC, USA, Requirement for Face Masks on Public Transportation Conveyances and at Transportation Hubs. 2021. Available online: https://www.cdc.gov/coronavirus/2019-ncov/travelers/face-masks-public-transportation.html (accessed on 11 March 2021).
- Shan, X.; Zhang, H.; Liu, C.; Yu, L.; Di, Y.; Zhang, X.; Dong, L.; Gan, Z. Reusable Self-Sterilization Masks Based on Electrothermal Graphene Filters. ACS Appl. Mater. Interfaces 2020, 12, 56579–56586. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.-L.; Huang, J.; Zhang, C.J.; He, Z.; Ming, W.-K. Facemask shortage and the novel coronavirus disease (COVID-19) outbreak: Reflections on public health measures. EClinicalMedicine 2020, 21, 100329. [Google Scholar] [CrossRef]

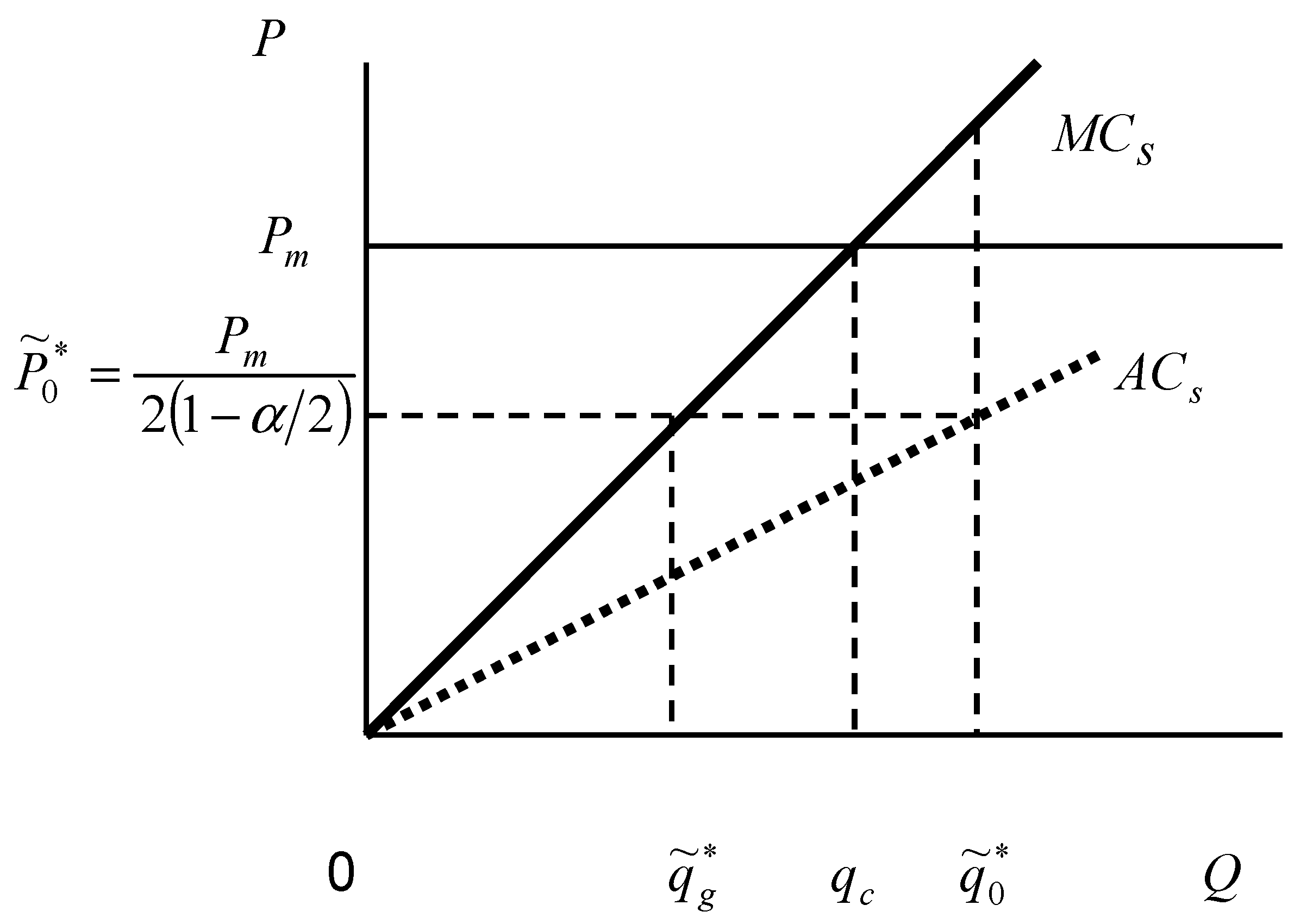

| Planner * | NMT | |
|---|---|---|
| The planned quota and price in scenario (1): , | , | , |
| The planned quota and price in scenario (2): , | , | , |
| The planned quota and price in scenario (3): , | , | , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, P.-S.; Lee, J.-Y. Analysis of Taiwan’s Mask Collection and Plan Evasion during the COVID-19 Pandemic. Int. J. Environ. Res. Public Health 2021, 18, 4137. https://doi.org/10.3390/ijerph18084137
Ko P-S, Lee J-Y. Analysis of Taiwan’s Mask Collection and Plan Evasion during the COVID-19 Pandemic. International Journal of Environmental Research and Public Health. 2021; 18(8):4137. https://doi.org/10.3390/ijerph18084137
Chicago/Turabian StyleKo, Po-Sheng, and Jen-Yao Lee. 2021. "Analysis of Taiwan’s Mask Collection and Plan Evasion during the COVID-19 Pandemic" International Journal of Environmental Research and Public Health 18, no. 8: 4137. https://doi.org/10.3390/ijerph18084137
APA StyleKo, P.-S., & Lee, J.-Y. (2021). Analysis of Taiwan’s Mask Collection and Plan Evasion during the COVID-19 Pandemic. International Journal of Environmental Research and Public Health, 18(8), 4137. https://doi.org/10.3390/ijerph18084137





