Next Article in Journal
Effective Elements for Workplace Responses to Critical Incidents and Suicide: A Rapid Review
Previous Article in Journal
Hospitalizations and Treatment Outcomes in Patients with Urogenital Tuberculosis in Tashkent, Uzbekistan, 2016–2018
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJERPH
Volume 18
Issue 9
10.3390/ijerph18094820
ijerph-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Optimization Strategy of the Existing Urban Green Space Soil Monitoring System in Shanghai, China

by
Weiwei Zhang
1,2,
Jigang Han
1,2,*,
Abiot Molla
3,4,*,
Shudi Zuo
3 and
Yin Ren
3
1
Key Laboratory of National Forestry and Grassland Administration on Ecological Landscaping of Challenging Urban Sites, Shanghai Academy of Landscape Architecture Science and Planning, Shanghai 200232, China
2
Shanghai Engineering Research Center of Landscaping on Challenging Urban Sites, Shanghai 200232, China
3
Key Laboratory of Urban Environment and Health, Institute of Urban Environment, Chinese Academy of Sciences, Xiamen 361021, China
4
University of Chinese Academy of Sciences, Beijing 100049, China
*
Authors to whom correspondence should be addressed.
Int. J. Environ. Res. Public Health 2021, 18(9), 4820; https://doi.org/10.3390/ijerph18094820
Submission received: 8 February 2021 / Revised: 18 April 2021 / Accepted: 20 April 2021 / Published: 30 April 2021
Browse Figures
Versions Notes

Abstract

:
High concentrations of potentially toxic elements (PTE) create global environmental stress due to the crucial threat of their impacts on the environment and human health. Therefore, determining the concentration levels of PTE and improving their prediction accuracy by sampling optimization strategy is necessary for making sustainable environmental decisions. The concentrations of five PTEs (Pb, Cd, Cr, Cu, and Zn) were compared with reference values for Shanghai and China. The prediction of PTE in soil was undertaken using a geostatistical and spatial simulated annealing algorithm. Compared to Shanghai’s background values, the five PTE mean concentrations are much higher, except for Cd and Cr. However, all measured values exceeded the reference values for China. Pb, Cu, and Zn levels were 1.45, 1.20, and 1.56 times the background value of Shanghai, respectively, and 1.57, 1.66, 1.91 times the background values in China, respectively. The optimization approach resulted in an increased prediction accuracy (22.4% higher) for non-sampled locations compared to the initial sampling design. The higher concentration of PTE compared to background values indicates a soil pollution issue in the study area. The optimization approach allows a soil pollution map to be generated without deleting or adding additional monitoring points. This approach is also crucial for filling the sampling strategy gap.

1. Introduction

The quality of the urban ecosystem depends on the green space soil quality. Soil quality refers to the soil’s ability to ensure biological productivity, maintain environmental quality, and promote organism health functions within the limit of ecosystems [1]. Rapid urbanization, industrialization [2] and greenery development will affect the soil quality in urban areas [3]. Therefore, urban areas become the sources of various pollutant elements that can be accumulated for an extended period of time in the soil [4,5,6]. Studies on the concentrations of potentially toxic elements (PTE) in urban soils, previously known as heavy metals, started in the 1960s and identified massive heavy metals sources of urban soil pollution [4,5]. The origins of PTE in urban soils are natural and anthropogenic. The pedogenesis processes are considered the natural source of PTE in the soil [7]. The anthropogenic factors are the crucial sources of PTE in soils and predominantly result from urban development and urbanization [8], the distribution of vehicles and the types of fuels [9], emission from industries and transportation [10], smelting, manufacturing, mining, and coal-burning [11]. Based on these factors, urban soils are enriched with a high level of PTE compared to threshold values [12,13,14].
Numerous studies about PTE in urban soils have been conducted in many cities around the world, including Glasgow [15], London [16], Hong Kong [17], New Orleans [18], and Oslo [19]. To date, studies on urban areas in North Pakistan [2], Brazilian Amazon [20], South-central Poland [21], Southwest Iran [22], Eastern China [23], Istanbul Turkey [24], Xiangtan Central China [25], and Krakow Poland [26]. These studies showed increased concentrations of PTE in urban soils. High concentrations of PTE, especially in green space soils, create global environmental stress due to the crucial threat to the environment and human health [27]. High concentrations of PTE in the environment are a concern due to their toxicity, persistence, and bioaccumulation, which threaten the health of all living systems [28]. For example, PTE in soil affects the key microbial processes, decreases soil microorganism diversity and activity [29], and impacts the food chain systems in the environment [30]. Health issues associated with PTE are associated with respiration, hand-mouth ingestion, and direct skin contact [31]. Excessive intake can lead to digestive disorders, respiratory diseases, abdominal pain, vomiting, anorexia, burnout, hemolysis, liver, and gallbladder damage [30]. Since urban green spaces are places where local populations can rest, play, and socialize, they often serve as family gathering sites after work [32]. These may favor contact with soil contaminants. Many previous studies focused on industrial areas and zones. Recently, the evaluation of PTE has become a high priority in urban greening space soils [33]. Furthermore, many authors are concerned about analyzing the total contents of PTE compared with background values to evaluate the environmental quality [31,34]. Nevertheless, the analysis of the total concentrations of PTE, compared with threshold values in the soil, may not always be a sufficient strategy for assessment [35,36,37], and in identifying appropriate remediation strategies [38].
Monitoring PTE concentrations with improved prediction accuracy through an optimization strategy is necessary for obtaining reliable results in surveying soil pollution and making sustainable environmental decisions on urban green spaces. Optimization is the process of selecting the optimal sample points and layouts based on the distance between the observation points and the interpolation grid [39]. One useful method using geostatistical tools for sampling design and predicting concentrations of soil pollution is kriging. Kriging not only provides an interpolated concentration map, but it is also useful in linking the prediction variance [40]. Minimizing the mean kriging variance as the objective function is used to optimize the sampling scheme and produce a space-filling distribution over the area of interest [41,42]. This optimization ensures the prediction of soil pollution and fills the sampling strategy gap by perpetuating limited sampling points, without deleting and adding monitoring points using spatial simulated annealing (SSA) algorithm. Such optimization and improved sampling design [39,41,43] are very useful, since no standardized approaches exist for choosing sample size and locations for soil and air pollution [44].
The main objectives of this work were as follows: (i) Evaluate the concentration levels of five PTE (copper (Cu), zinc (Zn), cadmium (Cd), chromium (Cr), and lead (Pb)) in green space soil; (ii) improve the prediction accuracy of the initial sampling design using an optimization strategy, and showing methodological approaches how to generate of soil pollution map without the extra expense. Since the pre-survey launched before found that the urban green soils were mainly dominated by these five elements. The Shanghai municipality started to focused on: (1) Investigating the contamination situation and sources differentiation of the five PTE on greens spaces soils, (2) managing and reducing soil pollution risks on urban parks [45].

2. Materials and Methods

2.1. Study Area

The study is conducted in Shanghai, one of China’s most highly developed and densely populated cities. It is located at 31.14° N and 121.29° E (Figure 1). Shanghai is one of the most extensive coastal cities in eastern China, which plays a crucial role in its main economic, financial, trade, and shipping center, with the most important industrial centers in China. The town covers about 6340.5 km2, of which 6218.65 km2 is the land, and the rest is water, and it covers 0.06% of China’s total territory [46]. The soil types mainly include paddy soil, fluvial-aquic soil, and coastal saline soil [46]. The entire green spaces in 2015 were about 3593.5 km2 [47]. The city has characterized the subtropical monsoon climate, with an annual mean temperature of 16 °C and yearly average precipitation is approximately 1200 mm.

2.2. Soil Sampling and Chemical Analysis

A total of 460 surface soil (0–20 cm) samples were collected from different green spaces in 2018. The locations were recorded using a global positioning system (GPS) and displayed in Figure 1. Five random soil samples were collected using a soil corer (2.5 cm diameter) and then pooled into one composite sample. The composite samples were air-dried, cleared of visible plant roots and residues. In order to ensure the complete digestion of soil samples, the air-dried soils were ground and passed through a 0.15 mm nylon mesh sieve. For each sample, 0.5 g of soil was digested with a concentrated mixture of HNO3, HF, and HClO4 as stated in the EPA 3052 method [48]. Mixed acid digestion makes the soil digestion more complete. Therefore, compared with the aqua regia digestion, the result of mixed acid digestion becomes higher, which is closer to the actual concentrations of PTE in the soil. The five PTE, including Cu, Zn, Cd, Cr, and Pb contents, were measured using Inductively Coupled Plasma Mass Spectrometry (ICP-MS, NexION 300X, Spectralab Scientific Inc. Markham, ON L3R 3V6, Canada). The limit of detection (LOD) and limit of quantification (LOQ) for the different metals were determined. The LOD for analysis of Cr, Cu, Zn, Cd, and Pb were 0.47 mg kg−1, 0.25 mg kg−1, 0.70 mg kg−1, 0.01 mg kg−1, and 0.30 mg kg−1, respectively. The LOQ of the above five PTE was four times their respective LOD. Certified soils (GSS series, China) were used as standard reference materials to verify the accuracy of the method, and the recovery rate of all measured PTE was 95–105%. All tested glass and blanks were soaked in HNO3, rinsed, and Milli-Q water to prevent contamination of the testing instrument.

2.3. Geostatistical Methods

Geostatistics is an extension tool in GIS that describes the spatial variation and carries out spatial interpolations [49]. The semivariance function and the kriging interpolations were used to produce the initial interpolation map on green spaces soil [50].
Semivariogram is equal to one-half of the expected value of the squared differences between values of X at locations (i) and (i + h) [51],
γ ( h ) = 1 2 m ( h ) ∑ i = 1 m ( h ) [ Z ( x i ) − Z ( x i + h ) ] 2
where m(h) is the number of pairs of observations separated by distance h, Z(xi) is the sample value of the variable Z at location xi, and Z(xi + h) is the sample value of the variable Z at location xi + h.
The ordinary Kriging interpolation is one of the most frequently used geostatistics tools to estimate unknown values using the sample data [52],
z ^ ( x 0 ) = ∑ i = 0 n y i z ( x i )
where z ^ (x0) is the value to be estimated at the location of x0; and z(xi) is the known value at the sampling site xi; yi represents constant values of each local neighborhood. While, n represents the number of sites or sampling points within the search neighborhoods used for the estimation.
The existing monitoring points were visualized and analyzed using exploratory spatial data analysis (ESDA) tools. ESDA was used to assess the degree of spatial association and examine how the data are normally distributed [53,54]. The spatial clusters and outliers of existing data sets were identified using Local Moran’s I [55] and Global Moran’s I statistic [56].

2.4. Prediction Accuracy Improvement Procedures

The prediction accuracy improvements can normally be achieved by optimizing sample locations over the geographical areas [57]. Optimization usually consists of adding, removing, and moving stations or sampling points [58]. One of the optimization algorithms used to add, remove, and transfer stations to generate optimized sampling sizes and designs is called SSA [42]. The SSA algorithm uses the mean kriging variance (MKV) as the objective function to obtain an optimal sample layout. In this case, the initial design was optimized by moving existing spatial points to the given study surface areas using soil Pb data as an example. Sample optimization by SSA also considers the kriging prediction and fitting variogram models [59]. Then, data were log-transformed before spatial optimization analysis was undertaken. The detailed optimization and evaluation techniques were explained as follows.

Perturb Initial Sampling Design by SSA and Evaluations

A 100 m × 100 m grid size overlaid on the study greens spaces areas, and an initial (before optimized) kriging soil Pb predictions and MKV were produced. Then, 50 to 200 random existing sample points were perturbed using 10,000 times iterations by the SSA algorithm. A new combination is generated, and the MKV values are compared with the initial sampling layout’s value. The combination is accepted if the change has improved the MKV values. The maximum perturbed sampling points were decided based on the improved MKV values. The process continued until the prediction variance became constant or higher. The best-improved MKV combination was chosen, and a kriging prediction map and sampling distributions were generated. Finally, to evaluate prediction accuracy improvement, cross-validations were performed.

2.5. Statistical Analysis Software and Tools

Spatial sampling optimization and descriptive statistics were performed using the R Statistical Software (version 4.0.2) [60,61]. The spatial clusters and outliers of existing data sets were analyzed using the software GeoDa (version 1.14.0) [62]. Arc GIS (10.4 version) is also used to produce the kriging prediction maps.

3. Results and Discussion

3.1. Mean Concentrations and Summary Statistics of Potentially Toxic Elements

The summary statistics and mean concentration of the five PTE in urban green space soils are indicated in Table 1. The highest and lowest mean concentrations were found for Zn, and Cd, respectively. The soil mean background values in Shanghai [63] and China [64] are used as reference values to compare the present study’s values. Compared to Shanghai’s background values, the mean concentrations of PTE in urban green spaces soil are much higher, except for Cd and Cr. All measured mean values exceed China’s reference values (Table 1). Pb, Cu, and Zn concentrations were 1.45, 1.20, 1.56 times the background value of Shanghai, respectively, and 1.57, 1.66, 1.91 times the mean background values in China. The higher values of PTE in the soil in comparison to background values indicate there is a soil pollution issue in the study areas.
Similarly, the coefficients of variation (CV, %) for Pb, Cu, Zn, and Cd were higher, meaning more significant variations among the urban green spaces soils (Table 1). The high CV of Pb, Cu, Zn, and Cd suggests soil pollution sources in urban green spaces are from anthropogenic sources [65]. On the contrary, the Cr CV is low, which means both natural and anthropogenic factors govern its spatial distribution. The lower CV value of Cr is consistent with many other studies [66,67,68].
The present study is consistent with the previous findings on the park and roadside green spaces in Shanghai [69], but inconsistent with results found on road-greenbelts, except for Pb [70]. The average values of Zn and Cr were significantly higher than the values reported in the western city of Urumqi in China [71]. The mean concentrations of the majority of the five pollutants considered in our study were lower than those found in studies that reported about ten years ago in roadside soil, dust, and sediment in eastern cities in China, including Shanghai [46], Guangzhou [72], and Hangzhou [73] (Table 2).
Compared to the average concentrations in worldwide studies, Pb, Cu, and Zn values of our study were much lower than reported values from Spain, Mexico, Turkey, Sweden, and Cuba, but Cr concentration was much higher than the study from Turkey and Sweden (Table 2). In this study, the Cr concentration value was 2.7 and 5.2 times higher than the concentrations values found from Sweden, and Turkey, respectively (Table 2). For all investigated pollutants, the mean concentration values were higher than those observed in the City of Pensacola, USA (Table 2). The differences in results between this study and other studies could be due to the test method, level of urbanization in the city, the management strategies on urban green space soils [8], and the sources for variation of PTE [7], such as emissions from industry and transportation [10], smelting, manufacturing, mining, and coal-burning [11].

3.2. Optimization Strategy and Evaluation of Existing Monitoring Points

The spatial interpolation in kriging is undertaken by accounting for the following assumptions [49]: (1) Data with a normal distribution, (2) data are stationary, and (3) data fit a variogram and spatial autocorrelation. Prior to carrying out the optimization strategy and the evaluation of prediction accuracy, these assumptions should be assessed and evaluated.

3.2.1. Spatial Patterns of Existing Monitoring Points

The spatial patterns and distribution of each PTE are shown in Table 3. All variables revealed a clustered spatial distribution with a statistical significance (p value < 0.01) and a positive spatial autocorrelation in the existing data sets. The most clustered positive spatial autocorrelation pattern was observed for Pb and Cd (Table 3). Global Moran’s I Index values confirmed that the spatial points are clustered and non-randomness. Similarly, the kurtosis and skewness values for all pollutants, except Cr, were higher, which means the data are not normally distributed (Table 3). The higher Kurtosis values showed many outlier data sets, and the majority of them are clustered at relatively low values. However, it does not state which spatial location features are spatial clustering [80]. Spatial outliers or local outliers are neighboring values that are spatially located at a certain distance [81]. Local Indicators of Spatial Association (LISA), known as Anselin’s Local Moran’s I, were used to visualize and identify the degree of spatial instability and outliers of the given data set [55].
The results of univariate Local Moran’s I scatter plots of the four PTE in the soil at 12905 m threshold distance divided into four association neighborhood layouts are indicated in the supporting data files, Figure 1. The upper right quadrant (high values above the mean surrounded by high values, HH), the lower left (low values surrounded by low values, LL); the upper left (low values surrounded by high Values, LH); and the lower right (high values surrounded by low values, HL). Spatial outlier values that include HL and LH values and spatial clusters that include HH and LL values are also indicated. For example, for soil Pb data sets, a 45 feature has neighboring features with values above the mean surrounded by HH values, and one features surrounded by LL values, which is the part of a cluster or pattern data set (Figure 2). In contrast, 19 data points have nearby features with different values (low high and high low), and this feature is a spatial outlier. Spatial outliers are the values that are different from the values recorded in their surrounding location, while spatial patterns often exhibit spatial continuity and autocorrelation with nearby samples [81]. These spatial outliers influence the spatial structure modeling and prediction of soil pollutant concentrations in urban green spaces. Therefore, the outliers were excluded, and data were transformed before the optimization strategy was undertaken.

3.2.2. Spatial Structures and Dependency

The theoretical Semivariogram models are used to kriging interpolation and optimizing the existing points. The best-fitting Semivariogram models were selected based on root mean square error (RMSE), average standard error (ASE), and root mean square standardized error (RMSSE) values, indicated in Table 4. The best-fitted model is considered to be the one with the smallest value of RMSE, the absolute values of mean errors near to zero, the mean square error (MSE) near zero, and the RMSSE closest to 1 [82]. Based on these criteria, the fitted semivariograms models for each soil element are summarized in Table 5. The best-fit spatial model of Pb and Cr was spherical, whereas Zn and Cu were best-fitted using the Gaussian model. The Cd was fitted with the exponential model. In the semivariograms, the nugget values represent the variability of the measured variables at a certain distance. The spatial dependence and variation of soil properties can be categorized based on the Nugget/Sill ratio values. Suppose the Nugget/Sill ratio is less than 25%, between 25% and 75%, and greater than 75%, the variable has strong, moderate, and weak spatial dependence [83], respectively. All studied elements had a moderate-to-strong spatial dependency, and fit the assumptions around spatial autocorrelation (Table 5). The Nugget/Sill ratio also indicated predominant sources or soil PTE factors, either natural or anthropogenic factors. Strong spatial dependence can be attributed to intrinsic factors, and weak spatial dependence can be attributed to extrinsic factors [83].

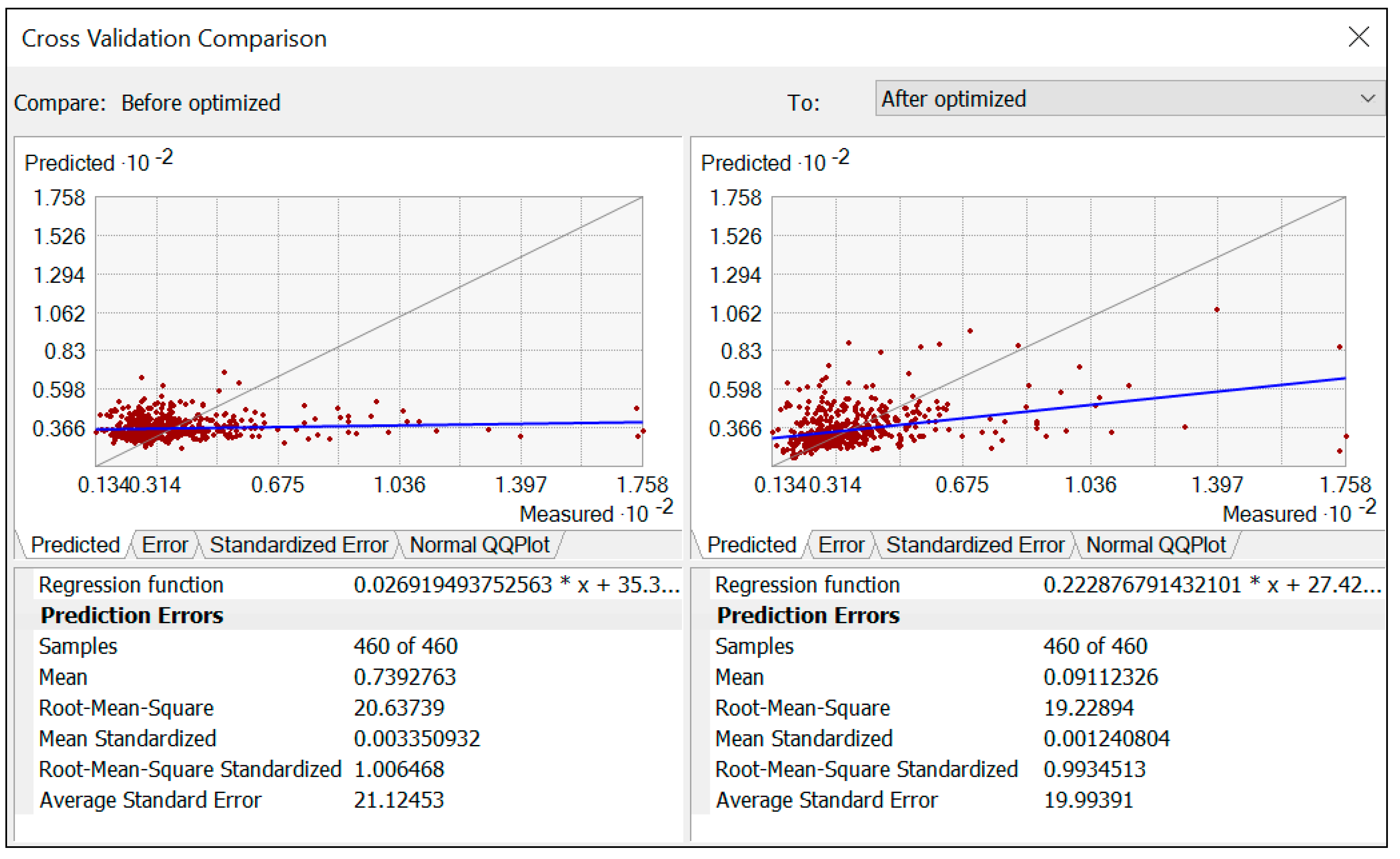
3.2.3. Prediction Accuracy Improvement by Optimization Strategy

A kriging interpolation surface of the study green spaces soil before optimized hereafter refers to the initial sampling design shows a predicted Pb MKV of 131.74 mg kg−1. The kriging concentration of Pb in the initial sampling design displays spatial heterogeneity with a high prediction hotspot, which is located in the high clustered sampling points and low concentration at the edge segment, since these are the sparse and lacking in sampled areas (Figure 3a). It is also clearly noted that there are many non-sampled green spaces areas at the initial sampling design, which leads to high spatial prediction variance (131.74 mg kg−1). In this study, the MKV as the objective function was used in the SSA algorithm to optimize the initial sampling design [84,85]. Each SSA iteration step only involves moving one random sampling point, and the row and column of the covariance matrix are changed. As Figure 3b shows, after optimization, soil Pb sampling points were placed with a better uniformity over the study area than the initial sampling design.
The MKV values also were calculated after the initial sampling design is perturbed by SSA (10,000 iterations). The initial soil Pb MKV (131.7 mg kg−1) decreased to 128.9 mg kg−1 under 50 random spatial samplings perturbed and 102.3 mg kg−1 by 200 random spatial samples perturbed (Table 6). This means the existing soil Pb sampling points captured 22.4% of the total kriged variance improvement and increased the accuracy of un-sampled green spaces without extra sampling points.
To evaluate the prediction accuracy and improvements in the initial sampling design, we performed a cross-validation comparison based on prediction RMSE, RMSSE, and ASE (Figure 4). The values identified for RMSE, RMSSE, and ASE of 20.63, 1.006, and 21.12, respectively, before the initial sampling design was optimized; the values were 19.22, 0.99, 19.99, respectively, after the initial sampling design optimized by SSA. The better prediction accuracy could be found in the smaller values of RMSE, the closer values of RMSE with ASE, and the values of RMSSE approximate to one (Figure 4). In contrast, the value of RMSSE is higher than one for the initial sampling design, which explains the underestimation of the variability of soil Pb predictions on green spaces soil. Figure 3a also shows a higher variability of soil Pb predication concentration in the study areas by comparing the optimized sampling configuration. Many studies confirmed that the initials sampling design samples, optimized by SSA methods, provided closer prediction results to the actual value and the lowest value of mean-variance of spatial prediction [84,86,87,88,89,90].

4. Conclusions

The current work has been carried out to investigate the five potentially toxic element concentrations and identify a method to improve prediction accuracy in the non-sampled locations in urban green space soils. The mean concentrations of five pollutants in urban green areas are much higher than Shanghai’s background values, except for Cd and Cr. However, all measured values exceed the mean reference values in China. The concentrations of Pb, Cu, and Zn were 1.45, 1.2, 1.56 times the background value of Shanghai, respectively, and 1.57, 1.66, 1.91 times the background values of China, respectively. The higher values, in comparison to the background values, may indicate the presence of soil pollution in the study areas. Similarly, the higher CV means more significant variation exists among urban green spaces soils.
The second objective was to improve the prediction values of non-sampled locations by optimized limited sampling points in the SSA algorism. As a result, an improvement in prediction accuracy by 22.4% was found for spatial prediction in non-sampled locations. Similarly, the lower mean-variance values of spatial prediction were comparable to those the initial sampling design. Therefore, this optimization approach ensures good quality of soil pollution predictions without deleting or adding monitoring points.

Author Contributions

Conceptualization, A.M. and S.Z.; formal analysis, S.Z.; investigation, Y.R.; methodology, A.M. and S.Z.; project administration, W.Z. and J.H.; visualization, Y.R.; writing—original draft, A.M. and S.Z.; writing—review and editing, W.Z. and J.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Shanghai Finance Special Project (Soil quality monitoring system for typical urban green spaces in Shanghai) and the Scientific Research Foundation of Shanghai Landscaping & City Appearance Administrative Bureau, grant number (G200201) and the APC covered by authors.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

We thank Shanghai Finance Special Project (Soil quality monitoring system for typical urban green spaces in Shanghai) and the Scientific Research Foundation of Shanghai Landscaping & City Appearance Administrative Bureau for the financial support. We also immensely thank the CAS_TWAS presidential fellowship for the international doctoral student program. We thank the anonymous reviewers, editor for their constructive comments on the manuscript, and Manuel J. Rodriguez-Pinzon for editing the English grammar and spelling.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Tan, C.S. Optimal soil physical quality inferred through structural regression and parameter interactions. Geoderma 2008, 146, 466–474. [Google Scholar] [CrossRef]
  2. Jadoon, S.; Muhammad, S.; Hilal, Z.; Ali, M.; Khan, S.; Khattak, N.U. Spatial distribution of potentially toxic elements in urban soils of Abbottabad city, (N Pakistan): Evaluation for potential risk. Microchem. J. 2020, 153, 104489. [Google Scholar] [CrossRef]
  3. Lan, T.; Guo, S.-W.; Han, J.-W.; Yang, Y.-L.; Zhang, K.; Zhang, Q.; Yang, W.; Li, P.-F. Evaluation of physical properties of typical urban green space soils in Binhai Area, Tianjin, China. Urban For. Urban Green. 2019, 44, 126430. [Google Scholar] [CrossRef]
  4. Purves, D. Contamination of urban garden soils with copper and boron. Nat. Cell Biol. 1966, 210, 1077–1078. [Google Scholar] [CrossRef]
  5. Wilkins, C. The distribution of lead in the soils and herbage of West Pembrokeshire. Environ. Pollut. 1978, 15, 23–30. [Google Scholar] [CrossRef]
  6. Cai, Q.-Y.; Mo, C.-H.; Li, H.-Q.; Lü, H.; Zeng, Q.-Y.; Li, Y.-W.; Wu, X.-L. Heavy metal contamination of urban soils and dusts in Guangzhou, South China. Environ. Monit. Assess. 2012, 185, 1095–1106. [Google Scholar] [CrossRef]
  7. Huang, S.; Shao, G.; Wang, L.; Tang, L. Spatial distribution and potential sources of five heavy metals and one metalloid in the soils of Xiamen city, China. Bull. Environ. Contam. Toxicol. 2019, 103, 308–315. [Google Scholar] [CrossRef]
  8. Rodríguez-Seijo, A.; Andrade, M.L.; Vega, F.A. Origin and spatial distribution of metals in urban soils. J. Soils Sediments 2017, 17, 1514–1526. [Google Scholar] [CrossRef]
  9. Minguillón, M.C.; Cirach, M.; Hoek, G.; Brunekreef, B.; Tsai, M.; De Hoogh, K.; Jedynska, A.; Kooter, I.M.; Nieuwenhuijsen, M.J.; Querol, X. Spatial variability of trace elements and sources for improved exposure assessment in Barcelona. Atmos. Environ. 2014, 89, 268–281. [Google Scholar] [CrossRef]
  10. Dao, L.; Morrison, L.; Zhang, H.; Zhang, C. Influences of traffic on Pb, Cu and Zn concentrations in roadside soils of an urban park in Dublin, Ireland. Environ. Geochem. Health 2013, 36, 333–343. [Google Scholar] [CrossRef]
  11. Zhang, C. Using multivariate analyses and GIS to identify pollutants and their spatial patterns in urban soils in Galway, Ireland. Environ. Pollut. 2006, 142, 501–511. [Google Scholar] [CrossRef] [PubMed]
  12. Liu, X.; Wu, J.; Xu, J. Characterizing the risk assessment of heavy metals and sampling uncertainty analysis in paddy field by geostatistics and GIS. Environ. Pollut. 2006, 141, 257–264. [Google Scholar] [CrossRef] [PubMed]
  13. Miao, L.; Xu, R.; Ma, Y.; Zhu, Z.; Wang, J.; Cai, R.; Chen, Y. Geochemistry and biogeochemistry of rare earth elements in a surface environment (soil and plant) in South China. Environ. Earth Sci. 2008, 56, 225–235. [Google Scholar] [CrossRef]
  14. Adedeji, O.H.; Olayinka, O.O.; Tope-Ajayi, O.O. Spatial distribution and health risk assessment of soil pollution by heavy metals in Ijebu-Ode, Nigeria. J. Health Pollut. 2019, 9, 190601. [Google Scholar] [CrossRef]
  15. Farmer, J.G.; Lyon, T.D.B. Lead in glasgow street dirt and soul. Sci. Total Environ. 1977, 8, 89–93. [Google Scholar] [CrossRef]
  16. Kelly, J.; Thornton, I.; Simpson, P.R. Urban geochemistry: A study of the influence of anthropogenic activity on the heavy metal content of soils in traditionally industrial and non-industrial areas of Britain. Appl. Geochem. 1996, 11, 363–370. [Google Scholar] [CrossRef]
  17. Li, X.; Chi-sun, P.; Pui Sum, L. Heavy metal contamination of urban soils and street dusts in Hong Kong. Appl. Geochem. 2001, 16, 1361–1368. [Google Scholar] [CrossRef]
  18. Mielke, H.W.; Gonzales, C.R.; Smith, M.K.; Mielke, P.W. Quantities and associations of lead, zinc, cadmium, manganese, chromium, nickel, vanadium, and copper in fresh Mississippi delta alluvium and New Orleans alluvial soils. Sci. Total Environ. 2000, 246, 249–259. [Google Scholar] [CrossRef]
  19. Tijhuis, L.; Brattli, B.; Sæther, O.M. A geochemical survey of topsoil in the city of Oslo, Norway. Environ. Geochem. Health 2002, 24, 67–94. [Google Scholar] [CrossRef]
  20. Sahoo, P.K.; Dall’Agnol, R.; Salomão, G.N.; Junior, J.D.S.F.; Da Silva, M.S.; Martins, G.C.; Filho, P.W.M.E.S.; Powell, M.A.; Maurity, C.W.; Angelica, R.S.; et al. Source and background threshold values of potentially toxic elements in soils by multivariate statistics and GIS-based mapping: A high density sampling survey in the Parauapebas basin, Brazilian Amazon. Environ. Geochem. Health 2019, 42, 255–282. [Google Scholar] [CrossRef] [PubMed]
  21. Ciupa, T.; Suligowski, R.; Kozłowski, R. Trace metals in surface soils under different land uses in Kielce city, south-central Poland. Environ. Earth Sci. 2020, 79, 14. [Google Scholar] [CrossRef]
  22. Nazarpour, A.; Watts, M.J.; Madhani, A.; Elahi, S. Source, spatial distribution and pollution assessment of Pb, Zn, Cu, and Pb, Isotopes in urban soils of Ahvaz city, a semi-arid metropolis in southwest Iran. Sci. Rep. 2019, 9, 5349. [Google Scholar] [CrossRef] [PubMed]
  23. Li, S.; Yang, L.; Chen, L.; Zhao, F.; Sun, L. Spatial distribution of heavy metal concentrations in peri-urban soils in eastern China. Environ. Sci. Pollut. Res. 2018, 26, 1615–1627. [Google Scholar] [CrossRef] [PubMed]
  24. Balkaya, N.; Guneysu, S. Recycling and Reuse Approaches for Better Sustainability; Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; p. 297. [Google Scholar]
  25. Zhang, Y.; Chen, Q. Contents of heavy metals in urban parks and university campuses. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 42060. [Google Scholar] [CrossRef]
  26. Gąsiorek, M.; Kowalska, J.; Mazurek, R.; Pająk, M. Comprehensive assessment of heavy metal pollution in topsoil of historical urban park on an example of the Planty Park in Krakow (Poland). Chemosphere 2017, 179, 148–158. [Google Scholar] [CrossRef] [PubMed]
  27. Praveena, S.M.; Yuswir, N.S.; Aris, A.Z.; Hashim, Z. Contamination assessment and potential human health risks of heavy metals in Klang urban soils: A preliminary study. Environ. Earth Sci. 2015, 73, 8155–8165. [Google Scholar] [CrossRef]
  28. Amari, T.; Ghnaya, T.; Abdelly, C. Nickel, cadmium and lead phytotoxicity and potential of halophytic plants in heavy metal extraction. S. Afr. J. Bot. 2017, 111, 99–110. [Google Scholar] [CrossRef]
  29. Jiwan, S.; Ajay, K. Effects of heavy metals on soil, plants, human health and aquatic life. Int. J. Res. Chem. Environ. 2011, 1, 15–21. [Google Scholar]
  30. Khelifi, F.; Melki, A.; Hamed, Y.; Adamo, P.; Caporale, A.G. Environmental and human health risk assessment of potentially toxic elements in soil, sediments, and ore-processing wastes from a mining area of southwestern Tunisia. Environ. Geochem. Health 2020, 42, 4125–4139. [Google Scholar] [CrossRef] [PubMed]
  31. Wei, B.; Yang, L. A review of heavy metal contaminations in urban soils, urban road dusts and agricultural soils from China. Microchem. J. 2010, 94, 99–107. [Google Scholar] [CrossRef]
  32. Manta, D.S.; Angelone, M.; Bellanca, A.; Neri, R.; Sprovieri, M. Heavy metals in urban soils: A case study from the city of Palermo (Sicily), Italy. Sci. Total Environ. 2002, 300, 229–243. [Google Scholar] [CrossRef]
  33. Cao, S.; Duan, X.; Zhao, X.; Chen, Y.; Wang, B.; Sun, C.; Zheng, B.; Wei, F. Health risks of children’s cumulative and aggregative exposure to metals and metalloids in a typical urban environment in China. Chemosphere 2016, 147, 404–411. [Google Scholar] [CrossRef]
  34. Martín, J.R.; Ramos-Miras, J.; Boluda, R.; Gil, C. Spatial relations of heavy metals in arable and greenhouse soils of a mediterranean environment region (Spain). Geoderma 2013, 200–201, 180–188. [Google Scholar] [CrossRef]
  35. Caeiro, S.; Costa, M.; Ramos, T.; Fernandes, F.; Silveira, N.; Coimbra, A.; Medeiros, G.; Painho, M. Assessing heavy metal contamination in Sado Estuary sediment: An index analysis approach. Ecol. Indic. 2005, 5, 151–169. [Google Scholar] [CrossRef]
  36. Hong-Gui, D.; Teng-Feng, G.; Ming-Hui, L.; Xu, D. Comprehensive assessment model on heavy metal pollution in soil. Int. J. Electrochem. Sci. 2012, 7, 5286–5296. [Google Scholar]
  37. Kowalska, J.B.; Mazurek, R.; Gąsiorek, M.; Zaleski, T. Pollution indices as useful tools for the comprehensive evaluation of the degree of soil contamination—A review. Environ. Geochem. Health 2018, 40, 2395–2420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Liao, Y.; Li, D.; Zhang, N. Comparison of interpolation models for estimating heavy metals in soils under various spatial characteristics and sampling methods. Trans. GIS 2018, 22, 409–434. [Google Scholar] [CrossRef]
  39. Brus, D.J.; Heuvelink, G.B. Optimization of sample patterns for universal kriging of environmental variables. Geoderma 2007, 138, 86–95. [Google Scholar] [CrossRef]
  40. Berman, J.D.; Jin, L.; Bell, M.L.; Curriero, F.C. Developing a geostatistical simulation method to inform the quantity and placement of new monitors for a follow-up air sampling campaign. J. Expo. Sci. Environ. Epidemiol. 2019, 29, 248–257. [Google Scholar] [CrossRef]
  41. Wadoux, A.M.; Marchant, B.P.; Lark, R.M. Efficient sampling for geostatistical surveys. Eur. J. Soil Sci. 2019. [Google Scholar] [CrossRef]
  42. Van Groenigen, J.W.; Stein, A. Constrained optimization of spatial sampling using continuous simulated annealing. J. Environ. Qual. 1998, 27, 1078–1086. [Google Scholar] [CrossRef]
  43. Gonçalves, M.; Jimenez-Guerrero, P.; Baldasano, J.M. Air quality management strategies in large cities: Effects of changing the vehicle fleet composition in Barcelona and Madrid Greater Areas (Spain) by introducing natural gas vehicles. In Air Pollution Modeling and Its Application XIX; Springer: Dordrecht, The Netherlands, 2008; pp. 54–62. [Google Scholar] [CrossRef]
  44. Matte, T.D.; Ross, Z.; Kheirbek, I.; Eisl, H.; Johnson, S.E.; Gorczynski, J.; Kass, D.; Markowitz, S.; Pezeshki, G.E.; Clougherty, J. Monitoring intraurban spatial patterns of multiple combustion air pollutants in New York City: Design and implementation. J. Expo. Sci. Environ. Epidemiol. 2013, 23, 223–231. [Google Scholar] [CrossRef] [PubMed]
  45. Shanghai Municipal Government (SMG). Shanghai Master Plan 2017–2035; Shanghai Municipal Government (SMG): Shanghai, China, 2018; pp. 1–80. Available online: https://doi.org/http://www.shanghai.gov.cn/newshanghai/xxgkfj/2035004.pdf (accessed on 20 December 2020).
  46. Shi, G.; Chen, Z.; Xu, S.; Zhang, J.; Wang, L.; Bi, C.; Teng, J. Potentially toxic metal contamination of urban soils and roadside dust in Shanghai, China. Environ. Pollut. 2008, 156, 251–260. [Google Scholar] [CrossRef] [PubMed]
  47. Wu, Z.; Chen, R.; Meadows, M.E.; Sengupta, D.; Xu, D. Changing urban green spaces in Shanghai: Trends, drivers and policy implications. Land Use Policy 2019, 87, 104080. [Google Scholar] [CrossRef]
  48. Environmental Protection Agency (EPA). Environmental Protection Agency (EPA), “Method 3052: Microwave Assisted Acid Digestion of Siliceous and Organically Based Matrices; Environmental Protection Agency (EPA): Washington, DC, USA, 1996; pp. 1–20.
  49. Zhang, C.; McGrath, D. Geostatistical and GIS analyses on soil organic carbon concentrations in grassland of southeastern Ireland from two different periods. Geoderma 2004, 119, 261–275. [Google Scholar] [CrossRef]
  50. Yang, Y.; Zhang, S. Approach of developing spatial. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Wuyishan, China, 18–20 August 2007. [Google Scholar]
  51. Campbell, J.B. Divisions-5—Soil genesis, morphology, Spatial variation of sand content and pH within single contiguousdelineations of two. Soil Sci. Soc. Am. J. 1978, 42, 460–464. [Google Scholar] [CrossRef]
  52. Goovaerts, P. Geostatistics in soil science: State-of-the-art and perspectives. Geoderma 1999, 89, 1–45. [Google Scholar] [CrossRef]
  53. Haining, R.; Wise, S.; Ma, J. Exploratory spatial data analysis in a geographic information system environment. J. R. Stat. Soc. 1998, 457–469. [Google Scholar] [CrossRef]
  54. Haining, R.; Wise, S. Unit 128—Exploratory spatial data analysis. J. R. Stat. Soc. 2002. [Google Scholar] [CrossRef]
  55. Anselin, L. Local indicators of spatial Association—LISA. Geogr. Anal. 1995, 27, 1–25. [Google Scholar] [CrossRef]
  56. Moran, B.Y.P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
  57. Wang, J.; Haining, R.; Cao, Z. Sample surveying to estimate the mean of a heterogeneous surface: Reducing the error variance through zoning. Int. J. Geogr. Inf. Sci. 2010, 24, 523–543. [Google Scholar] [CrossRef]
  58. Barca, E.; Passarella, G.; Uricchio, V. Optimal extension of the rain gauge monitoring network of the apulian regional consortium for crop protection. Environ. Monit. Assess. 2007, 145, 375–386. [Google Scholar] [CrossRef] [PubMed]
  59. Lark, R.M. Kriging a soil variable with a simple nonstationary variance model. J. Agric. Biol. Environ. Stat. 2009, 14, 301–321. [Google Scholar] [CrossRef]
  60. Samuel-rosa, A.; Heuvelink, G.; Vasques, G.; Anjos, L. Spsann—Optimization of Sample Patterns Using Spatial Simulated Annealing. 2015. Available online: https://cran.r-project.org/web/packages/spsann/vignettes/spsann.pdf (accessed on 5 January 2021).
  61. Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R.; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
  62. Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An introduction to spatial data analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
  63. Wang, Y.; Luo, H. The Backgrounds of Soil Environment in Shanghai; China Environmental Science Press: Beijing, China, 1992. [Google Scholar]
  64. CNEMC. The Backgrounds of Soil Environment in China, Beijing; Environmental Science Press of China: Beijing, China, 1990. (In Chinese) [Google Scholar]
  65. Chen, T.; Liu, X.; Li, X.; Zhao, K.; Zhang, J.; Xu, J.; Shi, J.; Dahlgren, R.A. Heavy metal sources identification and sampling uncertainty analysis in a field-scale vegetable soil of Hangzhou, China. Environ. Pollut. 2009, 157, 1003–1010. [Google Scholar] [CrossRef] [PubMed]
  66. Adimalla, N.; Chen, J.; Qian, H. Spatial characteristics of heavy metal contamination and potential human health risk assessment of urban soils: A case study from an urban region of South India. Ecotoxicol. Environ. Saf. 2020, 194, 110406. [Google Scholar] [CrossRef]
  67. Wang, Y.; Duan, X.; Wang, L. Spatial distribution and source analysis of heavy metals in soils influenced by industrial enterprise distribution: Case study in Jiangsu Province. Sci. Total Environ. 2020, 710, 134953. [Google Scholar] [CrossRef]
  68. Said, I.; Salman, S.A.E.-R.; Samy, Y.; Awad, S.A.; Melegy, A.; Hursthouse, A.S. Environmental factors controlling potentially toxic element behaviour in urban soils, El Tebbin, Egypt. Environ. Monit. Assess. 2019, 191, 267. [Google Scholar] [CrossRef] [Green Version]
  69. Liang, J.; Wu, H.B.; Wang, X.X. Distribution characteristics and health risk assessment of heavy metals and PAHs in the soils of green spaces in Shanghai, China. Environ. Monit. Assess. 2019, 191, 345. [Google Scholar] [CrossRef] [PubMed]
  70. Fang, H.L.; Dong, Y.; Gu, B.; Hao, G.J.; Lv, Z.W.; Liang, J.; Chen, L. Distribution of heavy metals and arsenic in greenbelt roadside soils of Pudong new district in Shanghai. Soil Sediment Contam. Int. J. 2009, 18, 702–714. [Google Scholar] [CrossRef]
  71. Zhaoyong, Z.; Xiaodong, Y.; Simay, Z.; Mohammed, A. Health risk evaluation of heavy metals in green land soils from urban parks in Urumqi, northwest China. Environ. Sci. Pollut. Res. 2018, 25, 4459–4473. [Google Scholar] [CrossRef]
  72. Duzgoren-Aydin, N.; Wong, C.; Aydin, A.; Song, Z.; You, M.; Li, X. Heavy metal contamination and distribution in the urban environment of Guangzhou, SE China. Environ. Geochem. Health 2006, 28, 375–391. [Google Scholar] [CrossRef]
  73. Zhang, M.; Wang, H. Concentrations and chemical forms of potentially toxic metals in road-deposited sediments from different zones of Hangzhou, China. J. Environ. Sci. 2009, 21, 625–631. [Google Scholar] [CrossRef]
  74. Madrid, L.; Díaz-Barrientos, E.; Madrid, F. Distribution of heavy metal contents of urban soils in parks of Seville. Chemosphere 2002, 49, 1301–1308. [Google Scholar] [CrossRef]
  75. Morton-Bermea, O.; Hernández-Álvarez, E.; González-Hernández, G.; Romero, F.; Lozano, R.; Beramendi-Orosco, L. Assessment of heavy metal pollution in urban topsoils from the metropolitan area of Mexico City. J. Geochem. Explor. 2009, 101, 218–224. [Google Scholar] [CrossRef]
  76. Onder, S.; Dursun, S.; Gezgin, S.; Demirbas, A. Determination of heavy metal pollution in grass and soil of city centre green areas (Konya, Turkey). Pol. J. Environ. Stud. 2007, 16, 145–154. [Google Scholar]
  77. Linde, M.; Bengtsson, H.; Öborn, I. Concentrations and pools of heavy metals in urban soils in Stockholm, Sweden. Water Air Soil Pollut. Focus 2001, 1, 83–101. [Google Scholar] [CrossRef]
  78. Rizo, O.D.; Morell, D.F.; López, J.O.A.; Muñoz, J.L.B.; Rodríguez, K.D.; Pino, N.L. Spatial distribution and contamination assessment of heavy metals in urban Topsoils from Las Tunas City, Cuba. Bull. Environ. Contam. Toxicol. 2013, 91, 29–35. [Google Scholar] [CrossRef]
  79. Liebens, J.; Mohrherr, C.J.; Rao, K.R. Trace metal assessment in soils in a small city and its rural surroundings, Pensacola, FL, USA. Environ. Earth Sci. 2011, 65, 1781–1793. [Google Scholar] [CrossRef]
  80. Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 2010, 24, 189–206. [Google Scholar] [CrossRef]
  81. Zhang, C.; Tang, Y.; Luo, L.; Xu, W. Outlier identification and visualization for Pb concentrations in urban soils and its implications for identification of potential contaminated land. Environ. Pollut. 2009, 157, 3083–3090. [Google Scholar] [CrossRef] [PubMed]
  82. Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; GIS by ESRI: California, CA, USA, 2001. [Google Scholar]
  83. Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
  84. Chen, R.; Liu, S.; Yang, Y.; Huang, W.; Han, Z.; Fu, P. Optimization of soil sampling design based on road networks—A simulated annealing/neural network algorithm. Earth Sci. 2019, 8, 335. [Google Scholar] [CrossRef]
  85. van Groenigen, J.W.; Siderius, W.; Stein, A. Constrained optimisation of soil sampling for minimisation of the kriging variance. Geoderma 1999, 87, 239–259. [Google Scholar] [CrossRef]
  86. Pagliosa, L.; Justiniano, P.; Maria, S.A.M. Optimization of spatial sample configurations using hybrid genetic algorithm and simulated annealing. Chil. J. Stat. 2011, 2, 39–50. [Google Scholar]
  87. Gao, B.; Lu, A.; Pan, Y.; Huo, L.; Gao, Y.; Li, X.; Li, S.; Chen, Z. Additional sampling layout optimization method for environmental quality grade classifications of farmland Soil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5350–5358. [Google Scholar] [CrossRef]
  88. Szatmári, G.; Barta, K.; Pásztor, L. An application of a spatial simulated annealing sampling optimization algorithm to support digital soil mapping. Hung. Geogr. Bull. 2015, 64, 35–48. [Google Scholar] [CrossRef] [Green Version]
  89. Wadoux, A.M.-C.; Brus, D.J.; Rico-Ramirez, M.A.; Heuvelink, G.B. Sampling design optimisation for rainfall prediction using a non-stationary geostatistical model. Adv. Water Resour. 2017, 107, 126–138. [Google Scholar] [CrossRef]
  90. Pang, S.; Li, T.-X.; Wang, Y.-D.; Yu, H.-Y.; Li, X. Spatial interpolation and sample size optimization for soil copper (Cu) investigation in cropland soil at county scale using Cokriging. Agric. Sci. China 2009, 8, 1369–1377. [Google Scholar] [CrossRef]
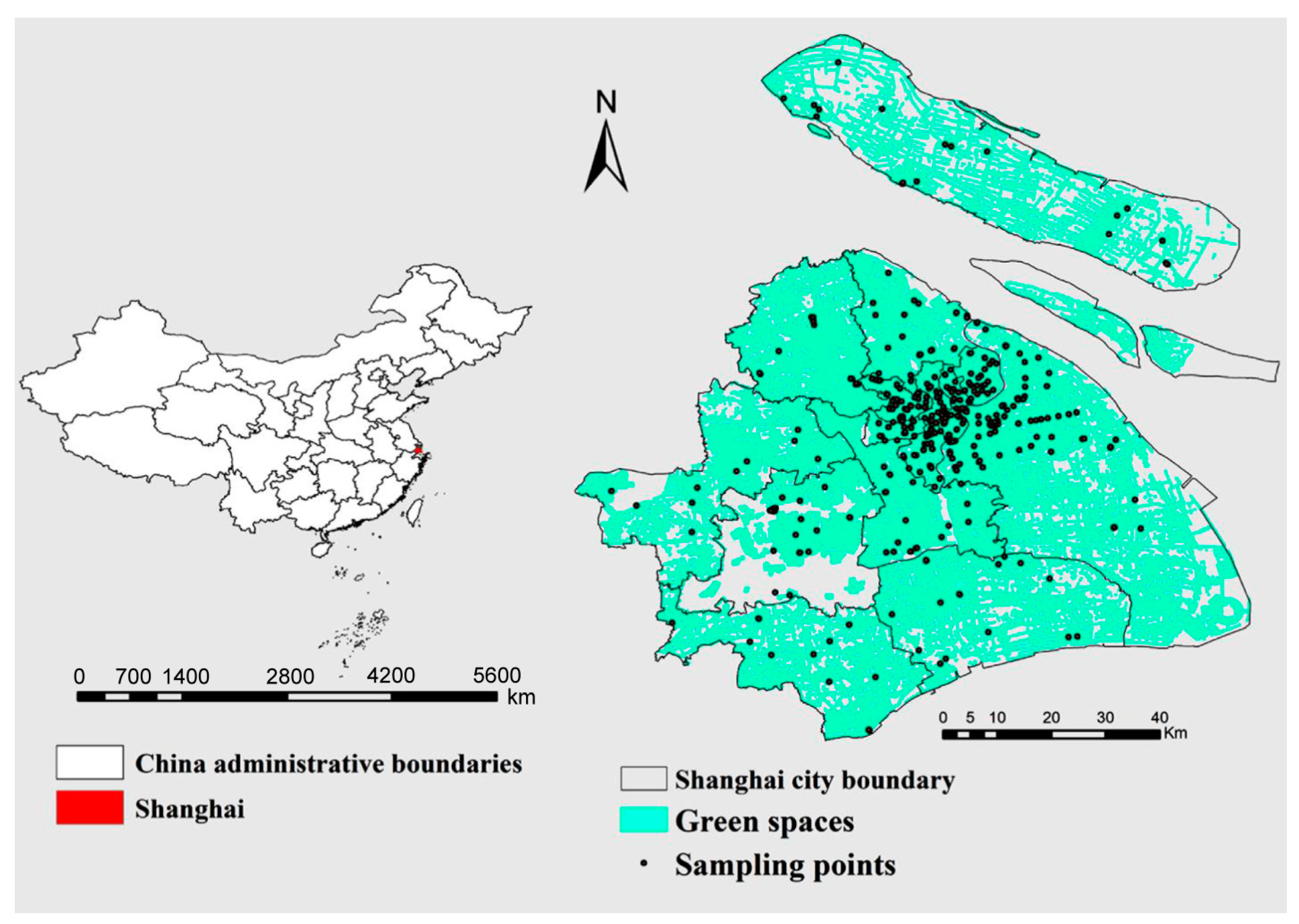
Ijerph 18 04820 g001 550
Figure 1. Location of study areas and sampling point’s distribution on urban green spaces.
Figure 1. Location of study areas and sampling point’s distribution on urban green spaces.
Ijerph 18 04820 g001
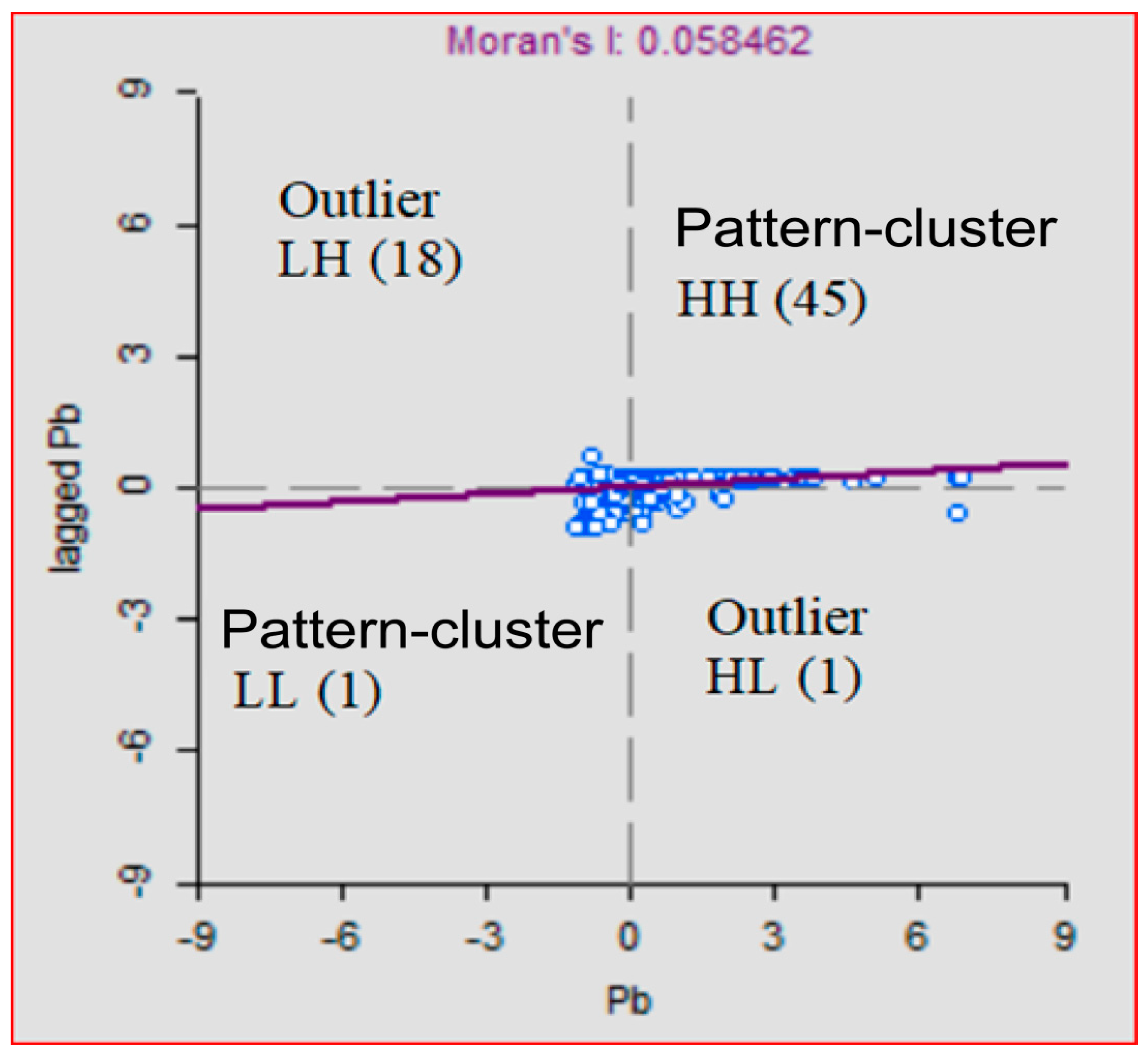
Ijerph 18 04820 g002 550
Figure 2. Univariate Local Moran’s I scatter plots at 12,905 m threshold distance of soil Pb.
Figure 2. Univariate Local Moran’s I scatter plots at 12,905 m threshold distance of soil Pb.
Ijerph 18 04820 g002
Ijerph 18 04820 g003 550
Figure 3. The initial sampling (A) and optimized (B) design Soil Pb concentration mapping on urban green spaces.
Figure 3. The initial sampling (A) and optimized (B) design Soil Pb concentration mapping on urban green spaces.
Ijerph 18 04820 g003
Ijerph 18 04820 g004 550
Figure 4. Prediction error cross-validation comparison before and after the original sampling configuration optimized by using SSA.
Figure 4. Prediction error cross-validation comparison before and after the original sampling configuration optimized by using SSA.
Ijerph 18 04820 g004
Table
Table 1. Description statistics of PTE in urban green spaces soil (mg kg−1).
Table 1. Description statistics of PTE in urban green spaces soil (mg kg−1).
PTEMeanMedian Range Values SD CV (%)Background Values of Shanghai *Background Values of China **
Pb36.9631.7013.41–175.820.2054.6625.4723.50
Cu34.4130.2710.09–225.419.0455.3228.5920.70
Zn130.3113.649.15–109884.8365.1083.6868.00
Cr73.0973.2038.24–143.210.7614.7375.0057.30
Cd0.210.170.06–3.680.21100.500.130.08
* [63], ** [64], CV = Coefficients of variation, SD = Standard Deviation. PTE = potentially toxic elements.
Table
Table 2. PTE mean concentrations level (mg kg−1) of sampling of global urban green space areas.
Table 2. PTE mean concentrations level (mg kg−1) of sampling of global urban green space areas.
Study AreasPbCuZnCrCdReference
Parks of Seville, Spain161.072.00210.075.00-[74]
Mexico City, Mexico82.0054.00219.0-116.0[75]
Konya Park, Turkey289.4427.4289.814.021.0[76]
Stockholm, Sweden104.047.0157.027.00.43[77]
Tunas City, Cuba42.094.0199.097.0-[78]
Pensacola, USA23.986.2633.229.010.13[79]
Urumqi, China 43.2242.5494.7930.970.71[71]
Guangzhou, China240.0176.0586.078.82.41[72]
Hangzhou, China202.1116.0321.451.251.59[73]
Shanghai, China70.6959.25301.4107.90.52[46]
Shanghai, China 36.9634.40130.373.090.21This study
Note: - = not data available. PTE = potentially toxic elements.
Table
Table 3. Global Moran’s I Summary of statics for an existing data set of PTE in green space areas.
Table 3. Global Moran’s I Summary of statics for an existing data set of PTE in green space areas.
Variables Moran’s IVarianceZ-Scorep-ValueDistribution SkewnessKurtosis
Pb0.1599680.0003129.1786940.000000Clustered 3.3114.97
Cu0.1348030.0004036.8246770.0000005.0135.06
Zn0.1342430.000288.1436430.0000006.7755.94
Cr0.1966360.0004289.6142800.0000001.438.41
Cd0.0575020.0002863.5302630.00041510.01130.23
PTE = potentially toxic elements.
Table
Table 4. Kriging prediction errors of interpolation by the ordinary kriging method.
Table 4. Kriging prediction errors of interpolation by the ordinary kriging method.
PTE Mean ErrorRMSEMSEASE RMSSE
Pb0.09119.220.00119.990.993
CU0.29518.520.00918.931.120
Zn0.42281.350.002104.430.828
Cr0.0049.89−0.00211.060.898
Cd0.0000.210.0010.220.994
RMSE = root mean square error, RMSSE= root mean square standardized error, MSE = mean standardized error, ASE = average standard error, PTE = potentially toxic elements.
Table
Table 5. Theoretical fitting semivariograms models and spatial dependency.
Table 5. Theoretical fitting semivariograms models and spatial dependency.
PTE ModelNugget (C0)Partial Sill (C)Sill
(C0 + C)		Range (m)Nugget Ratio %
C0/(C0 + C)		Spatial Dependency
PbSpherical0.0470.1330.182263.3026.11Moderate
CuGaussian0.0530.1280.1812597.0029.28Moderate
ZnGaussian0.0000.1410.141213.980.00Strong
CrSpherical0.0000.0150.015120.480.00strong
CdExponential 0.0000.2380.238140.930.00Strong
PTE = potentially toxic elements.
Table
Table 6. The improvement MKV after the initial sampling design was perturbed by SSA.
Table 6. The improvement MKV after the initial sampling design was perturbed by SSA.
Numbers of Points PerturbedSoil Pb MKV (mg kg−1)Improvement MKV (%)
50128.92.16
100118.210.25
150109.117.16
200102.322.36
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhang, W.; Han, J.; Molla, A.; Zuo, S.; Ren, Y. The Optimization Strategy of the Existing Urban Green Space Soil Monitoring System in Shanghai, China. Int. J. Environ. Res. Public Health 2021, 18, 4820. https://doi.org/10.3390/ijerph18094820

AMA Style

Zhang W, Han J, Molla A, Zuo S, Ren Y. The Optimization Strategy of the Existing Urban Green Space Soil Monitoring System in Shanghai, China. International Journal of Environmental Research and Public Health. 2021; 18(9):4820. https://doi.org/10.3390/ijerph18094820

Chicago/Turabian Style

Zhang, Weiwei, Jigang Han, Abiot Molla, Shudi Zuo, and Yin Ren. 2021. "The Optimization Strategy of the Existing Urban Green Space Soil Monitoring System in Shanghai, China" International Journal of Environmental Research and Public Health 18, no. 9: 4820. https://doi.org/10.3390/ijerph18094820

APA Style

Zhang, W., Han, J., Molla, A., Zuo, S., & Ren, Y. (2021). The Optimization Strategy of the Existing Urban Green Space Soil Monitoring System in Shanghai, China. International Journal of Environmental Research and Public Health, 18(9), 4820. https://doi.org/10.3390/ijerph18094820

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop