Distribution Levels of Particulate Matter Fractions (<2.5 µm, 2.5–10 µm and >10 µm) at Seven Primary Schools in a European Ceramic Cluster
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Analysis of Differences Depending on the Type of Location
3.1.1. Fraction Smaller Than 2.5 µm
3.1.2. Fraction between 2.5 and 10 µm
3.1.3. Fraction Greater Than 10 µm
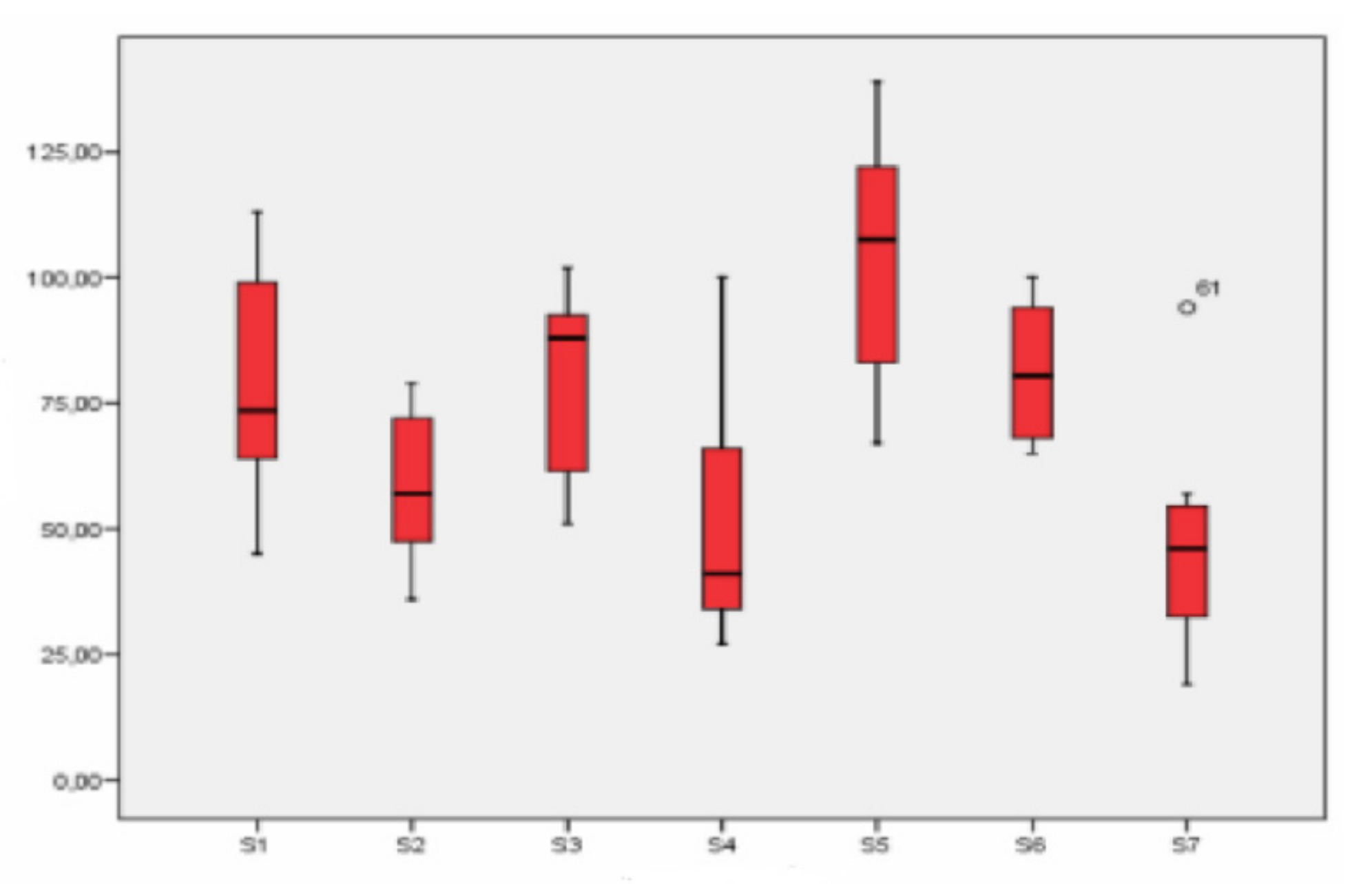
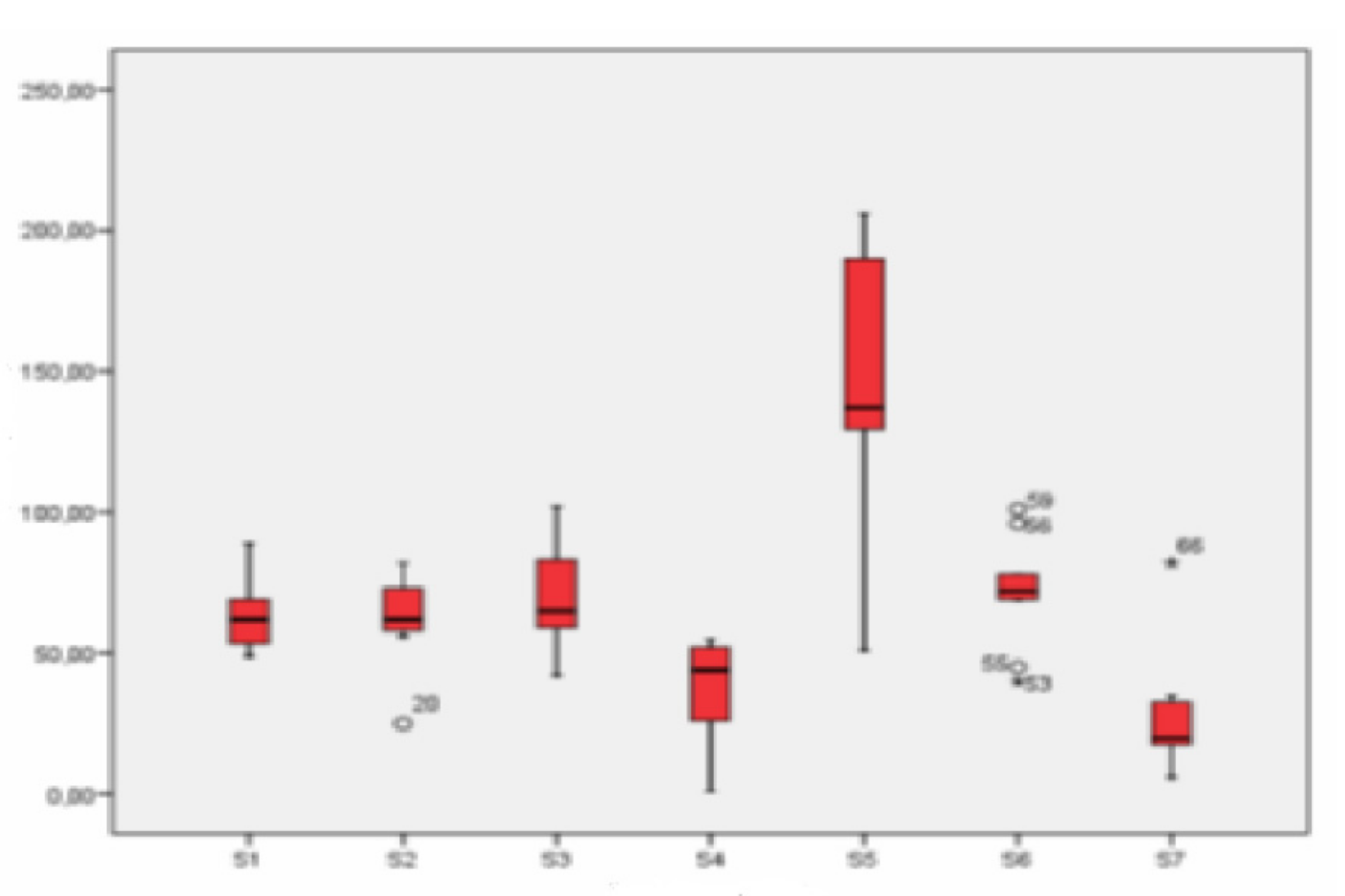
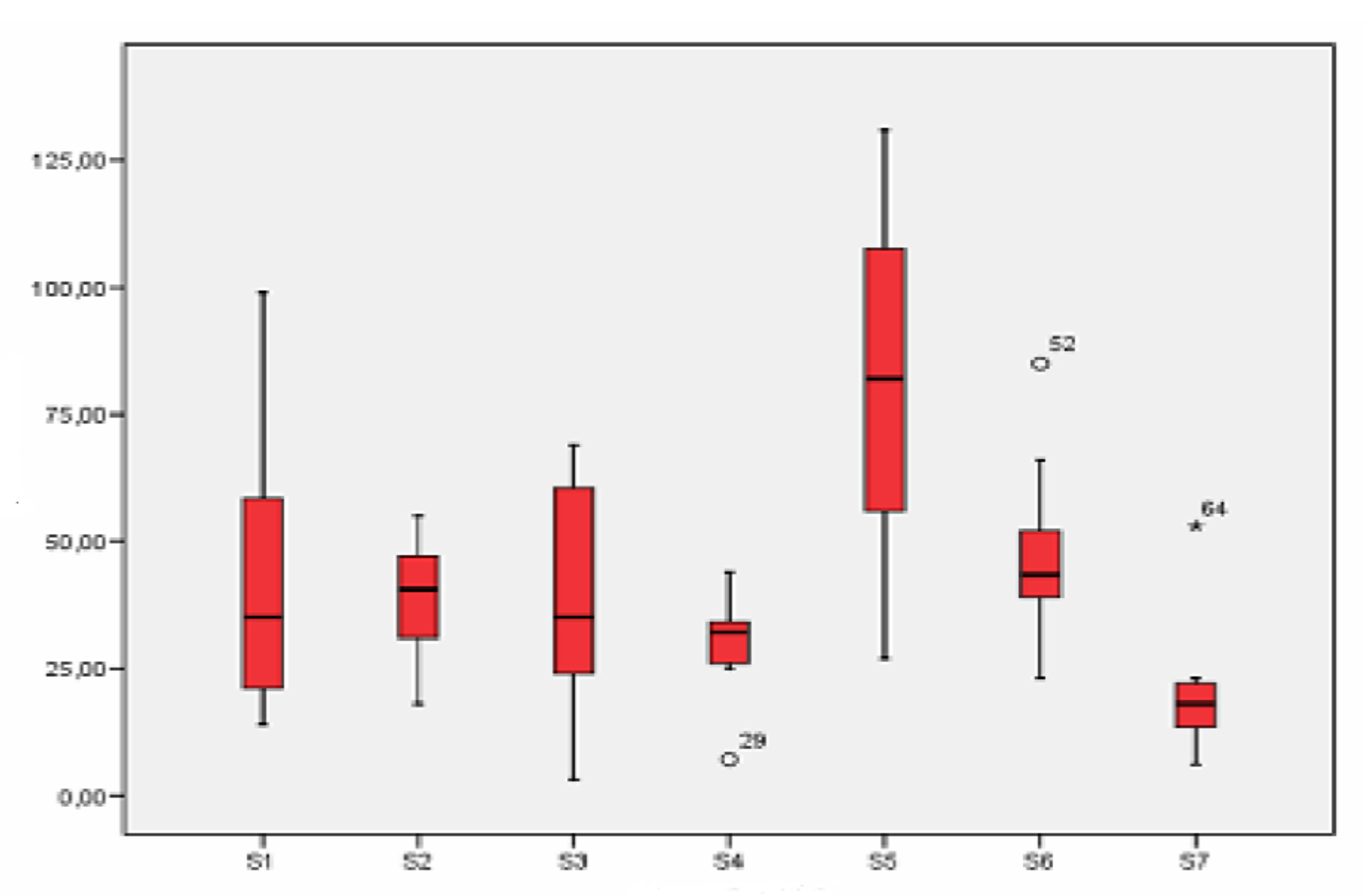
3.2. Study of the Differences Depending on the Sampling Point
3.2.1. Fraction Smaller Than 2.5 µm
3.2.2. Fraction between 2.5 and 10 µm
3.2.3. Fraction Larger Than 10 µm
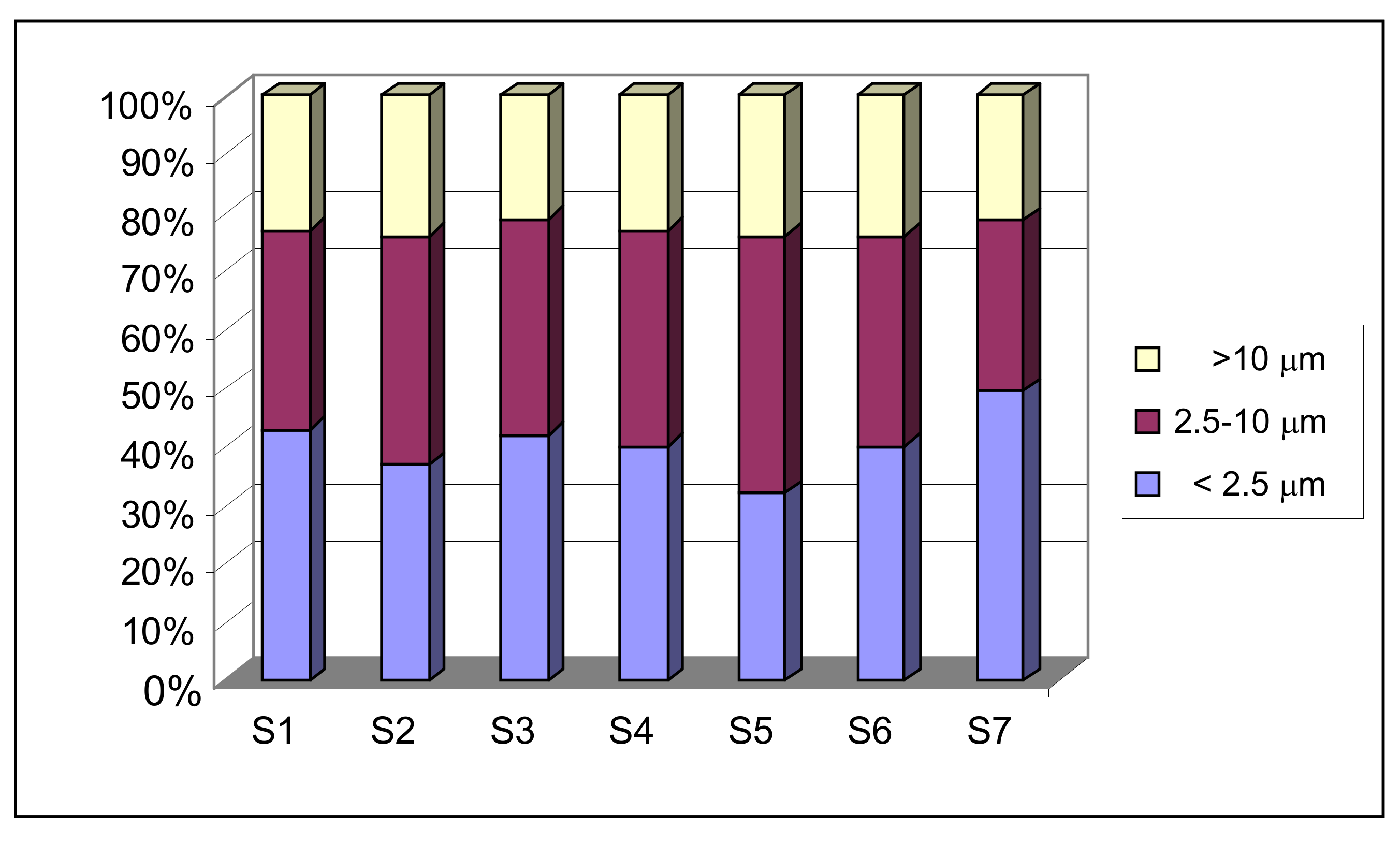
3.3. Relationship between the Different Granulometric Fractions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamens, R.; Lee, C.-T.; Weiner, R.; Leith, D. A study to characterize indoor particles in three non-smoking homes. Atmos. Environ. 1991, 25, 939–948. [Google Scholar] [CrossRef]
- Thatcher, T.; Layton, D. Deposition, resuspension and penetration of particles within a residence. Atmos. Environ. 1995, 29, 1487–1497. [Google Scholar] [CrossRef]
- Pallarés, S.; Gómez, E.T.; Jordán, M.M. Typological characterisation of mineral and combustion airborne particles indoors in primary schools. Atmosphere 2019, 10, 209. [Google Scholar] [CrossRef] [Green Version]
- Kingham, S.; Durand, M.; Harrison, J.; Cavanagh, J.; Epton, M.J. Temporal variations in particulate exposure to wood smoke in a residential school environment. Atmos. Environ. 2008, 42, 4619–4631. [Google Scholar] [CrossRef]
- Pallarés, S.; Gómez, E.; Martínez, A.; Vidal, M.M.J. The relationship between indoor and outdoor levels of PM10 and its chemical composition at schools in a coastal region in Spain. Heliyon 2019, 5, e02270. [Google Scholar] [CrossRef] [Green Version]
- Migallon, M.C.; Monfort, E.; Querol, X.; Alastuey, A.; Celades, I.; Miró, J.V. Effect of ceramic industrial particulate emission control on key components of ambient PM10. J. Environ. Manag. 2009, 90, 2558–2567. [Google Scholar]
- Vicente, A.B.; Juan, P.; Meseguer, S.; Díaz-Avalos, C.; Serra, L. Variablility of PM10 in industrialized-urban áreas. New coefficients to establish significante differences between samplin points. Environ. Pollut. 2018, 234, 969–978. [Google Scholar] [CrossRef]
- Abu-Allaban, M.; Lowenthal, D.H.; Gertler, A.; Labib, M. Sources of PM10 and PM2.5 in Cairo’s ambient air. Environ. Monit. Assess. 2007, 133, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Slezakovaa, K.; de Oliveira Fernandes, E.; Pereira, M.C. Assessment of ultrafine particles in primary schools: Emphasis on different indoor microenvironments. Environ. Pollut. 2019, 246, 885–895. [Google Scholar] [CrossRef]
- Querol, X.; Alastuey, A.; Viana, M.M.; Rodríguez, S.; Artiñano, B.; Salvador, P.; Mantilla, E.; Santos, S.G.D.; Fernández-Patier, R.; de la Rosa, J.; et al. Levels of particulate matter in rural, urban and industrial sites in Spain. Sci. Total Environ. 2004, 334–335, 359–376. [Google Scholar] [CrossRef]
- Branis, M.; Rezacova, P.; Domasova, M. The effect of outdoor air and indoor human activity on mass concentrations of PM10, PM2.5 and PM1 in a classroom. Environ. Res. 2005, 99, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, C.; Jordán, M.M.; Boix, A.; Gómez, E.T.; Sanfeliu, T. Air Pollution; Power, H., Moussiopoulos, N., Brebbia, C.A., Eds.; Wessex Institute of Technology; Computational Mechanics Publications: Ashurst, Southampton, UK, 1999; Volume 7, pp. 385–393. [Google Scholar]
- Giechaskiel, B.; Ntziachristos, L.; Samaras, Z.; Scheer, V.; Casati, R.; Vogt, R. Formation potencial of vehicle exhaust mode particles on-road and in the laboratory. Atmos. Environ. 2005, 39, 3191–3198. [Google Scholar] [CrossRef]
- Luoma, M.; Batterman, S.A. Characterization of particulate emissions from occupant activities in offices. Indoor Air 2001, 11, 35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Janssen, N.; Hoek, G.; Harssema, H.; Brunekreef, B. Personal exposure to fine particles in children correlates closely with ambient fine particles. Arch. Environ. Health 1999, 54, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Marr, L.C.; Dunlea, E.J.; Herndon, S.C.; Jayne, J.T.; Kolb, C.E.; Knighton, W.B.; Rogers, T.M.; Zvala, M.; Molina, M.J. Vehicle fleet emissions of black carbon, polycyclic aromatic hidrocarbons and other pollutants measured by a mobile laboratory in Mexico City. Atm. Chem. Physics. 2005, 5, 3377–3387. [Google Scholar] [CrossRef] [Green Version]
- Artiñano, B.; Slavador, P.; Alonso, D.G.; Querl, X.; Alastuey, A. Influence of traffic on the PM10 and PM2.5 urban aerosol fraction in Madrid (Spain). Sci. Total Environ. 2004, 334, 111–123. [Google Scholar] [CrossRef]
- Rasmussen, P.E.; Subramanian, K.S.; Jessiman, B.J. A multi-element profile of housedust in relation to exterior dust and soils in the city of Ottawa, Canada. Sci. Total Environ. 2001, 267, 125–140. [Google Scholar] [CrossRef]
- Ruwin, B.; Finn, P.; Ole, H.; Elisabetta, V. Using measurements of air pollution in street for evaluation of urban air quality-meteorological analysis and model calculations. Sci. Total Environ. 1996, 189–190, 259–265. [Google Scholar]
- Samara, C.; Kouimitzis, T.; Tsitouridou, R.; Kanias, G.; Simeonov, V. Chemical mass balance source apportionment of PM10 in an industrialized area of Northern Greece. Atmos. Environ. 2003, 37, 41–54. [Google Scholar]
- Querol, X.; Alastuey, A.; Lopez-Soler, A.; Plana, F.; Mantilla, E.; Ruiz, C.R.; La Orden, A. Characterisation of atmospheric particulates around a coal-fired power station. Int. J. Coal Geol. 1999, 40, 175–188. [Google Scholar] [CrossRef]
- Parker, J.L.; Larson, R.R.; Eskelson, E.; Wood, E.M.; Veranth, J.M. Particle size distribution and composition in a mechanically ventilated school building during air pollution episodes. Indoor Air 2008, 18, 386–393. [Google Scholar] [CrossRef] [PubMed]
- Poupard, O.; Blondeau, P.; Iordache, V.; Allard, I. Statistical analysis of parameters influencing the relationship between outdoor and indoor air quality in schools. Atmos. Environ. 2005, 39, 2071–2080. [Google Scholar] [CrossRef]
- Raunemaa, T.; Kulmala, M.; Saari, H.; Olin, M.; Kulmala, M.M. Indoor air aerosol model: Transport indoors and deposition of fine and coarse particles. Aerosol Sci. Technol. 1989, 11, 11–25. [Google Scholar] [CrossRef]
- Alastuey, A.; Mantilla, E.; Querol, X.; Rodriguez, S. Study and evaluation of atmospheric pollution in Spain: Necessary measures arising from the EC Directive on PM10 and PM2.5 in the ceramic industry. Bol. Soc. Esp. Cerám. Vidr. 2000, 39, 141–148. [Google Scholar]
- Monfort, E.; Celades, I.; Sanfelix, V.; Gomar, S.; López, J.C. Estimación de las emisiones difusas de PM10 y rendimiento de MTS’s en el sector cerámico. Bol. Soc. Esp. de Ceram. Vidr. 2009, 48, 15–25. [Google Scholar]




| School | Site | Town Location | Traffic Density | Classroom Volume (m3) | Window Orientation |
|---|---|---|---|---|---|
| S1 | Urban | E | High | 268.03 | WNW |
| S2 | Urban | NW | Medium | 159.56 | SSE |
| S3 | Urban | W | High | 173.49 | ESE |
| S4 | Industrial | SE | Medium | 36.17 | WNW |
| S5 | Industrial | E | Medium | 109.09 | ENE |
| S6 | Industrial | SW | Low-Medium | 97.67 | SSE |
| S7 | Rural | SE | Low | 182.60 | SE |
| Comparations | Sum of Squares | Df | Root Mean Square | F | Sig. |
|---|---|---|---|---|---|
| Inter-group | 5946.22 | 2 | 2973.11 | 4.42 | 0.016 |
| Intra-group | 40,349.71 | 60 | 672.50 | ||
| Total | 46,295.94 | 62 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Upper Limit | Lower Limit | |||||
| Urban | Industrial Rural | −7.33 25.09 | 6.93 11.00 | 0.884 0.078 | −24.41 −1.99 | 9.75 52.18 |
| Industrial | Urban Rural | 7.33 32.43 * | 6.93 10.92 | 0.884 0.013 | −9.75 5.53 | 24.41 59.33 |
| Rural | Urban Industrial | −25.09 −32.43 * | 11.00 10.92 | 0.078 0.013 | −52.18 −59.33 | 1.99 −5.53 |
| Test Statistics a,b | |
|---|---|
| Chi-squared | 12.458 |
| Df | 2 |
| Asymp. sig. | 0.002 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| Urban | Industrial Rural | −22.95 37.14 * | 10.71 8.74 | 0.112 0.006 | −49.81 11.82 | 3.90 62.47 |
| Industrial | Urban Rural | 22.95 60.10 * | 10.71 13.20 | 0.112 0.000 | −3.90 26.73 | 49.81 93.47 |
| Rural | Urban Industrial | −37.14 * −60.10 * | 8.74 13.20 | 0.006 0.000 | −62.47 −93.47 | −11.82 −26.73 |
| Test Statistics a,b | |
|---|---|
| Chi-squared | 12.500 |
| Df | 2 |
| Asymp. sig. | 0.002 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| Urban | Industrial Rural | −13.94 19.51 * | 6.98 6.42 | 0.144 0.021 | −31.15 2.64 | 3.26 36.38 |
| Industrial | Urban Rural | 13.94 33.45 * | 6.98 7.55 | 0.144 0.000 | −3.26 14.26 | 31.15 52.64 |
| Rural | Urban Industrial | −19.51 * −33.45 * | 6.42 7.55 | 0.021 0.000 | −36.38 −52.64 | −2.64 −14.26 |
| Comparations | Sum of Squares | Df | Mean Square | F | Sig. |
|---|---|---|---|---|---|
| Inter-groups | 22,764.52 | 6 | 3794.09 | 9.03 | 0.000 |
| Intra-groups | 23,531.42 | 56 | 420.20 | ||
| Total | 46,295.94 | 62 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| S1 | S2 S3 S4 S5 S6 S7 | 20.37 0.42 28.54 −26.82 2.12 31.30 | 10.25 9.52 9.96 9.72 9.72 10.61 | 1.000 1.000 0.123 0.164 1.000 0.097 | −12.25 −29.90 −3.16 −57.77 −33.07 −2.46 | 53.00 30.74 60.24 4.12 28.82 65.07 |
| S2 | S1 S3 S4 S5 S6 S7 | −20.35 −19.95 8.17 −47.20 * −22.50 10.93 | 10.25 9.52 9.96 9.72 9.72 10.61 | 1.000 0.855 1.000 0.000 0.512 1.000 | −53.00 −50.27 −23.54 −78.15 −53.45 −22.84 | 12.25 10.36 39.87 −16.25 8.44 44.70 |
| S3 | S1 S2 S4 S5 S6 S7 | −0.42 19.95 28.12 −27.24 −2.54 30.88 | 9.52 9.52 9.21 8.96 8.96 9.91 | 1.000 0.855 0.073 0.075 1.000 0.061 | −30.74 −10.36 −1.20 −55.75 −31.05 −0.66 | 29.90 50.27 57.45 1.26 25.96 62.43 |
| S4 | S1 S2 S3 S5 S6 S7 | −28.54 −8.17 −28.12 −55.37 * −30.67 * 2.76 | 9.96 9.96 9.21 9.42 9.42 10.33 | 0.123 1.000 0.073 0.000 0.040 1.000 | −60.24 −39.87 −57.45 −85.34 −60.64 −30.12 | 3.16 23.54 1.20 −25.39 −0.069 35.64 |
| S5 | S1 S2 S3 S4 S6 S7 | 26.82 47.20 * 27.24 55.37 * 24.70 58.13 * | 9.72 9.72 8.96 9.42 9.17 10.10 | 0.164 0.000 0.075 0.000 0.195 0.000 | −4.12 16.25 −1.26 25.39 −4.75 25.98 | 57.77 78.15 55.75 85.34 53.88 90.28 |
| S6 | S1 S2 S3 S4 S5 S7 | 2.12 22.50 2.54 30.67 * −24.70 33.43 * | 9.72 9.72 8.96 9.42 9.17 10.10 | 1.000 0.512 1.000 0.040 0.195 0.034 | −28.82 −8.44 −25.96 0.69 −53.88 1.28 | 33.07 53.45 31.05 60.64 4.48 65.58 |
| S7 | S1 S2 S3 S4 S5 S6 | −31.30 −10.92 −30.88 −2.76 −58.13 * −33.43 * | 10.61 10.61 9.91 10.33 10.10 10.10 | 0.097 1.000 0.061 1.000 0.000 0.034 | −65.07 −44.70 −62.43 −35.64 −90.28 −65.58 | 2.46 22.84 0.66 30.12 −25.98 −1.28 |
| Test Statistics a,b | |
|---|---|
| Chi-squared | 38.743 |
| Df | 6 |
| Asymp. sig. | 0.000 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| S1 | S2 S3 S4 S5 S6 S7 | 0.97 −6.45 27.08 −83.00 * −7.96 35.14 * | 6.96 6.77 8.26 14.42 7.18 9.15 | 1.000 0.999 0.098 0.002 0.994 0.049 | −23.87 −29.89 −3.19 −136.74 −33.29 −0.12 | 25.81 16.98 57.35 −29.26 17.36 70.16 |
| S2 | S1 S3 S4 S5 S6 S7 | −0.97 −7.42 26.11 −83.97 * −8.93 34.17 | 6.96 7.94 9.24 15.01 8.29 10.04 | 1.000 0.999 0.191 0.002 0.996 0.078 | −25.81 −35.02 −6.68 −138.52 −37.88 −2.54 | 23.87 20.17 58.91 −29.42 20.01 70.88 |
| S3 | S1 S2 S4 S5 S6 S7 | 6.45 7.42 33.54 * −76.55 * −1.51 41.59 * | 6.77 7.94 9.10 14.92 8.13 9.91 | 0.999 0.999 0.037 0.004 1.000 0.019 | −16.98 −20.17 1.41 −130.89 −29.54 5.38 | 29.89 35.03 65.66 −22.20 26.52 77.80 |
| S4 | S1 S2 S3 S5 S6 S7 | −27.08 −26.11 −33.54 * −110.08 * −35.04 * 8.06 | 8.26 9.24 9.10 15.65 9.40 10.98 | 0.098 0.191 0.037 0.000 0.033 1.000 | −57.35 −58.91 −65.66 −165.87 −68.15 −31.23 | 3.19 6.68 −1.41 −54.29 −1.94 47.34 |
| S5 | S1 S2 S3 S4 S6 S7 | 83.00 * 83.97 * 76.54 * 110.08 * 75.04 * 118.14 * | 14.42 15.01 14.92 15.65 15.11 16.14 | 0.002 0.002 0.004 0.000 0.004 0.000 | 29.26 29.42 22.20 54.29 20.36 61.03 | 136.74 138.52 130.89 165.87 29.71 75.24 |
| S6 | S1 S2 S3 S4 S5 S7 | 7.96 8.93 1.51 35.04 * −75.04 * 43.10 * | 7.18 8.29 8.13 9.40 15.11 10.19 | 0.994 0.996 1.000 0.033 0.004 0.017 | −17.36 −20.01 −26.53 1.94 −129.71 6.17 | 33.27 37.88 29.54 68.15 −20.36 80.03 |
| S7 | S1 S2 S3 S4 S5 S6 | −35.14 * −34.17 −41.59 * −8.06 −118.14 * −43.10 * | 9.15 10.04 9.91 10.98 16.14 10.19 | 0.049 0.078 0.019 1.000 0.000 0.017 | −70.16 −70.88 −77.80 −47.34 −175.24 −80.03 | −0.12 2.54 −5.39 31.23 −61.03 −6.17 |
| Test Statistics a,b | |
|---|---|
| Chi-squared | 25.614 |
| Df | 6 |
| Asymp. sig. | 0.000 |
| (I) Location | (J) Location | Mean Difference (I–J) | Standard Error | Sig. | 95% Confidence Interval | |
|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | |||||
| S1 | S2 S3 S4 S5 S6 S7 | 4.00 3.20 13.19 −37.61 −4.85 22.00 | 10.90 12.05 10.67 14.22 11.44 11.24 | 1.000 1.000 0.972 0.254 1.000 0.662 | −38.66 −40.92 −29.33 −87.52 −48.00 −21.01 | 46.66 47.33 55.71 12.29 38.30 65.01 |
| S2 | S1 S3 S4 S5 S6 S7 | −4.00 −0.80 9.19 −41.61 * −8.85 18.00 | 10.90 7.83 5.46 10.88 6.84 6.49 | 1.000 1.000 0.829 0.036 0.973 0.219 | −46.66 −28.38 −10.39 −81.16 −33.00 −5.48 | 38.66 26.79 28.78 −2.07 15.30 41.48 |
| S3 | S1 S2 S4 S5 S6 S7 | −3.20 0.80 9.99 −40.82 −8.05 18.80 | 12.05 7.83 7.50 12.03 8.55 8.28 | 1.000 1.000 0.965 0.060 0.999 0.452 | −47.33 −26.79 −16.69 −82.72 −37.56 −10.16 | 40.92 28.38 36.67 1.09 21.45 47.75 |
| S4 | S1 S2 S3 S5 S6 S7 | −13.19 −9.19 −9.99 −50.81 * −18.04 * 8.80 | 10.67 5.46 7.50 10.64 6.46 6.09 | 0.972 0.829 0.965 0.008 0.202 0.931 | −55.71 −28.78 −36.67 −89.96 −40.98 −13.42 | 29.33 10.39 16.69 −11.65 4.89 31.03 |
| S5 | S1 S2 S3 S4 S6 S7 | 37.61 41.61 * 40.82 50.81 * 32.76 59.61 * | 14.23 10.88 12.03 10.64 11.41 11.21 | 0.254 0.036 0.060 0.008 0.177 0.002 | −12.29 2.07 −1.08 11.65 −7.74 19.41 | 87.52 81.16 82.72 89.96 73.27 99.81 |
| S6 | S1 S2 S3 S4 S5 S7 | 4.85 8.85 8.05 18.04 −32.76 26.85 * | 11.44 6.84 8.55 6.46 11.41 7.35 | 1.000 0.973 0.999 0.202 0.177 0.039 | −38.30 −15.30 −21.45 −4.89 −73.27 0.94 | 48.00 33.00 37.56 40.98 7.74 52.76 |
| S7 | S1 S2 S3 S4 S5 S6 | −22.00 −18.00 −18.80 −8.80 −59.61 * −26.85 * | 11.24 6.49 8.28 6.09 11.21 7.35 | 0.662 0.219 0.452 0.931 0.002 0.039 | −65.01 −41.48 −47.75 −31.03 −99.81 −52.76 | 21.01 5.48 10.16 13.42 −19.42 −0.94 |
| School | Indoor PM10 Conc. Calcul.—μg m−3—(min–max) | Outdoor PM10 Conc.—μg m−3—(min–max) | I/O Ratio |
|---|---|---|---|
| S1 | 132 (95–160) | 53 (30–73) | 2.6 |
| S2 | 114 (63–138) | 54 (36–81) | 2.3 |
| S3 | 141 (92–185) | 59 (29–98) | 2.6 |
| S4 | 69 (19–92) | 53 (35–76) | 1.3 |
| S5 | 261 (201–309) | 36 (17–49) | 7.8 |
| S6 | 145 (98–181) | 45 (33–68) | 3.5 |
| S7 | 71 (15–159) | 36 (16–52) | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pallarés, S.; Gómez, E.T.; Martínez-Poveda, Á.; Jordán, M.M. Distribution Levels of Particulate Matter Fractions (<2.5 µm, 2.5–10 µm and >10 µm) at Seven Primary Schools in a European Ceramic Cluster. Int. J. Environ. Res. Public Health 2021, 18, 4922. https://doi.org/10.3390/ijerph18094922
Pallarés S, Gómez ET, Martínez-Poveda Á, Jordán MM. Distribution Levels of Particulate Matter Fractions (<2.5 µm, 2.5–10 µm and >10 µm) at Seven Primary Schools in a European Ceramic Cluster. International Journal of Environmental Research and Public Health. 2021; 18(9):4922. https://doi.org/10.3390/ijerph18094922
Chicago/Turabian StylePallarés, Susana, Eva Trinidad Gómez, África Martínez-Poveda, and Manuel Miguel Jordán. 2021. "Distribution Levels of Particulate Matter Fractions (<2.5 µm, 2.5–10 µm and >10 µm) at Seven Primary Schools in a European Ceramic Cluster" International Journal of Environmental Research and Public Health 18, no. 9: 4922. https://doi.org/10.3390/ijerph18094922





