Influence of the In-Stream Structure on Solute Transport in the Hyporheic Zone
Abstract
:1. Introduction
2. Methods
2.1. Laboratory Experiments
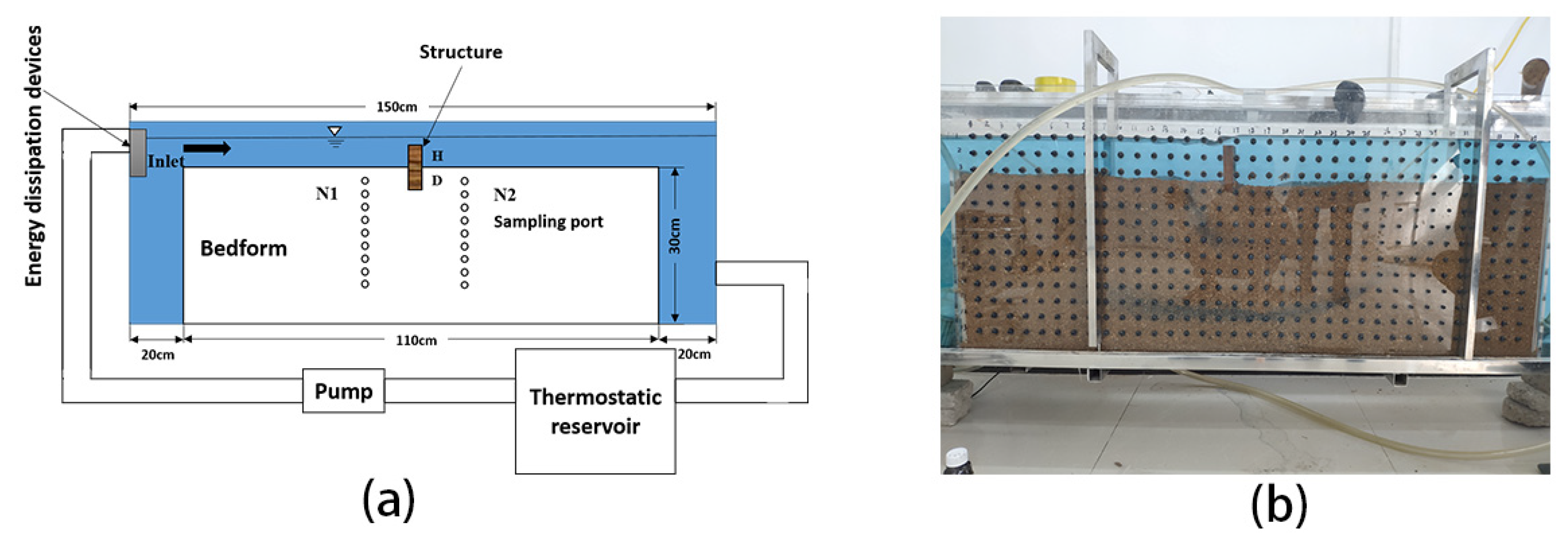
2.1.1. Flume Setup
2.1.2. Bed Sand Properties and Preparation
2.1.3. Experimental Conditions and Measurements
2.2. Numerical Simulations
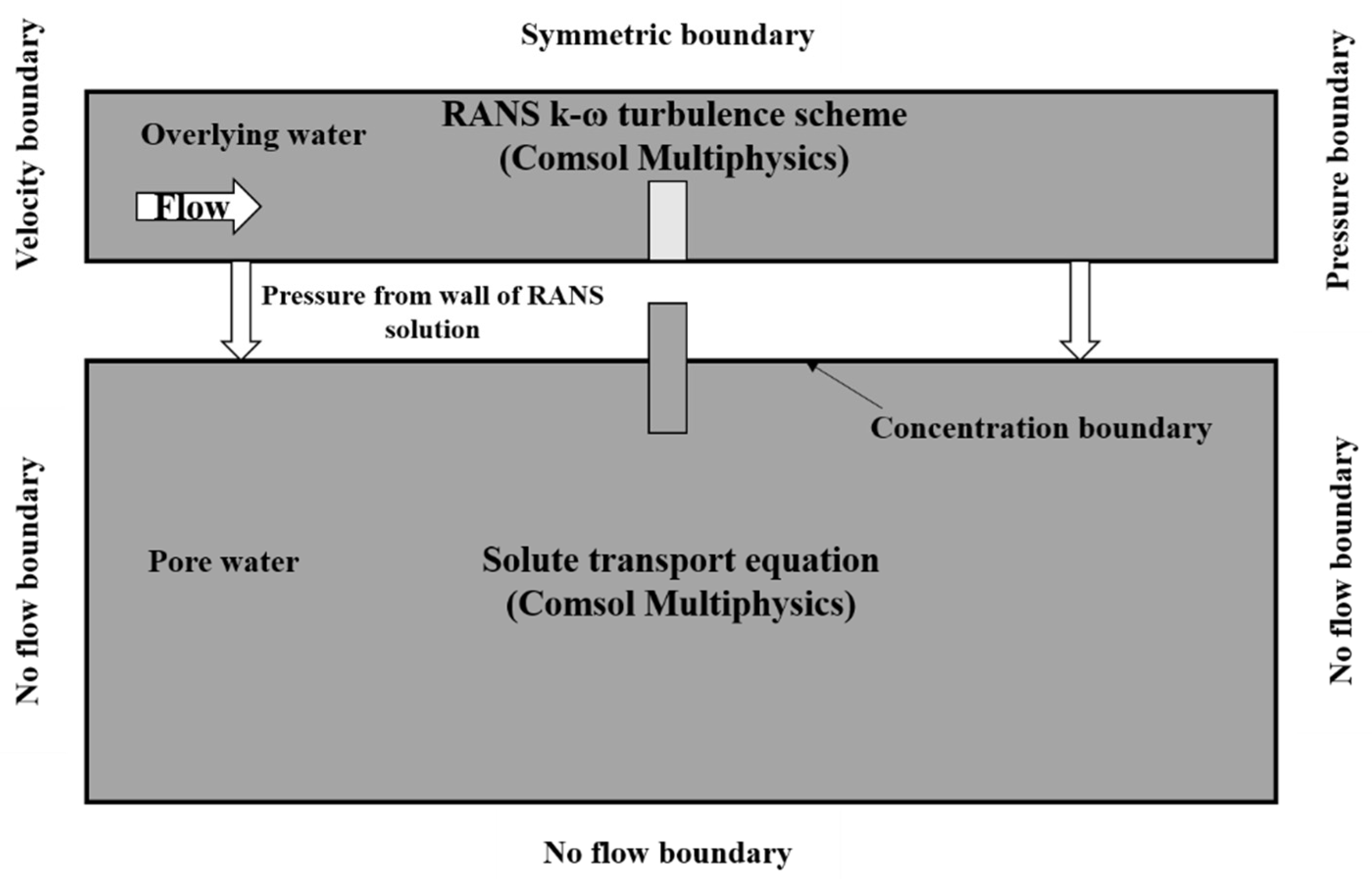
2.2.1. Mathematical Model and Boundary Conditions for Overlying Water
2.2.2. Mathematical Model and Boundary Conditions for Pore Water
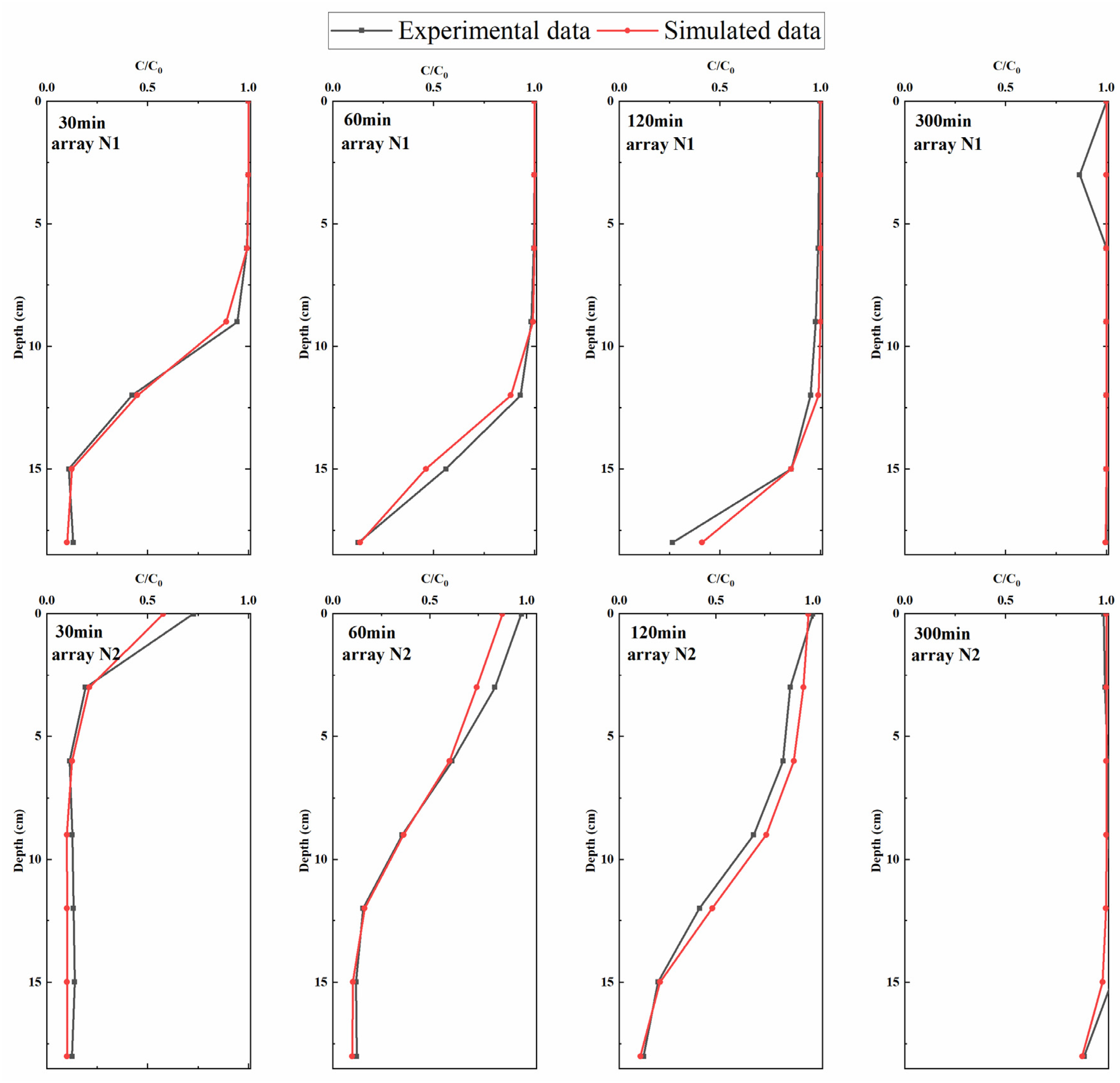
2.3. Model Evaluation
3. Results
3.1. Model Valuation
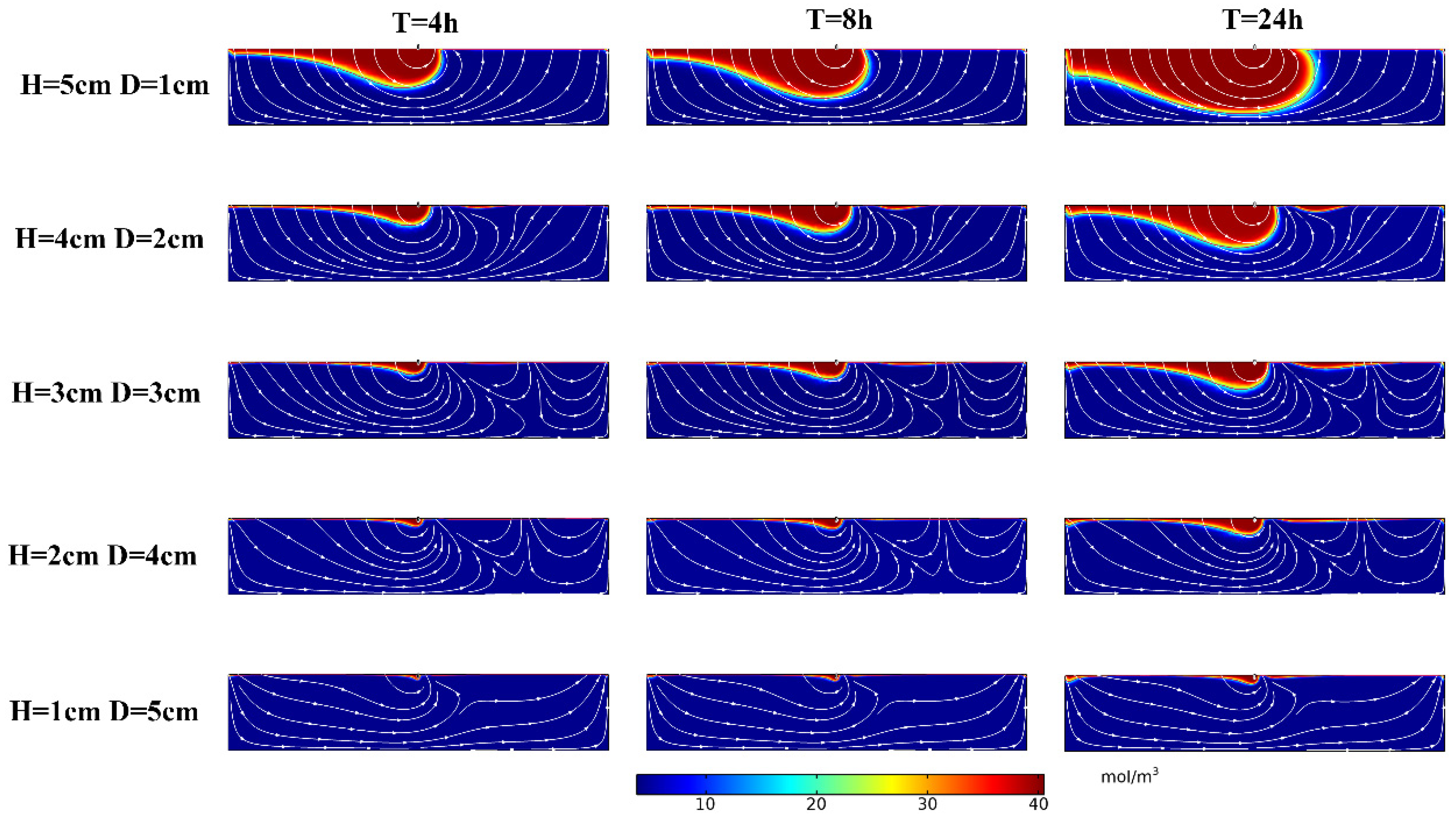
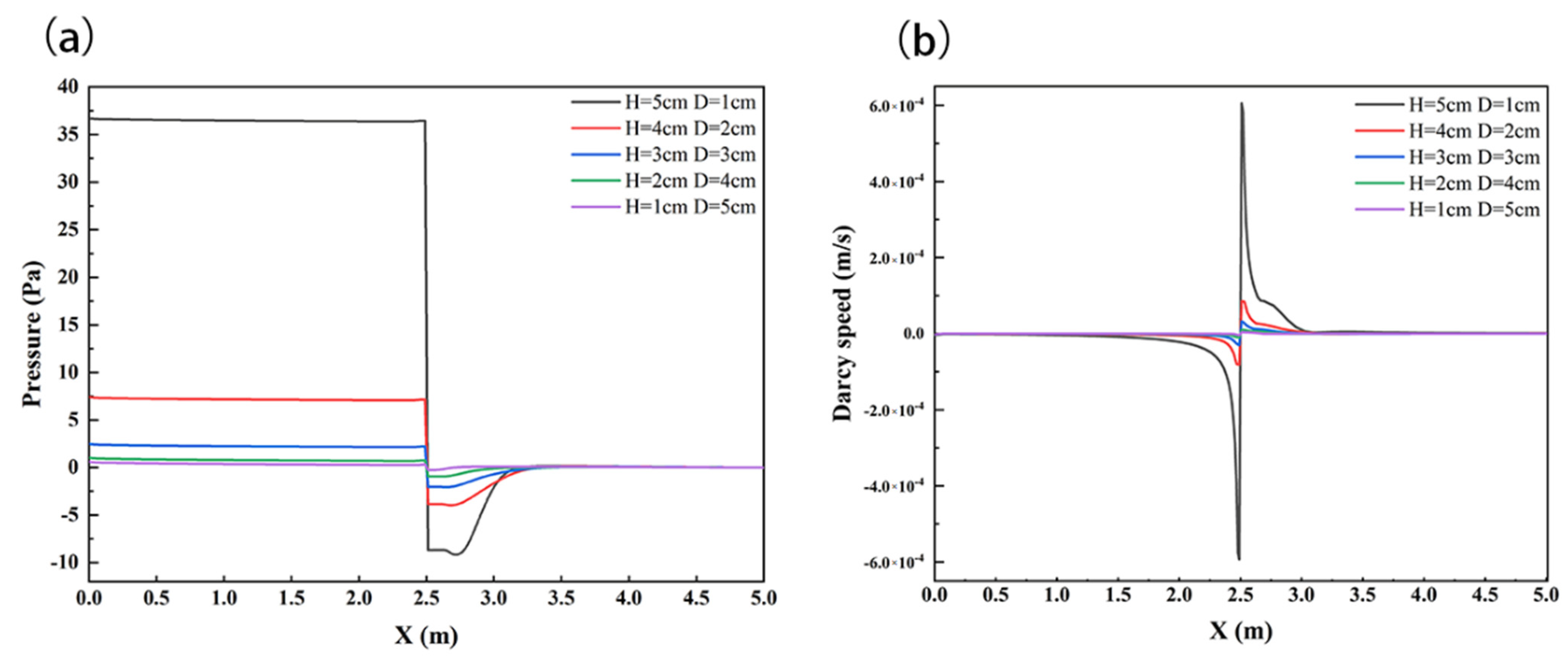
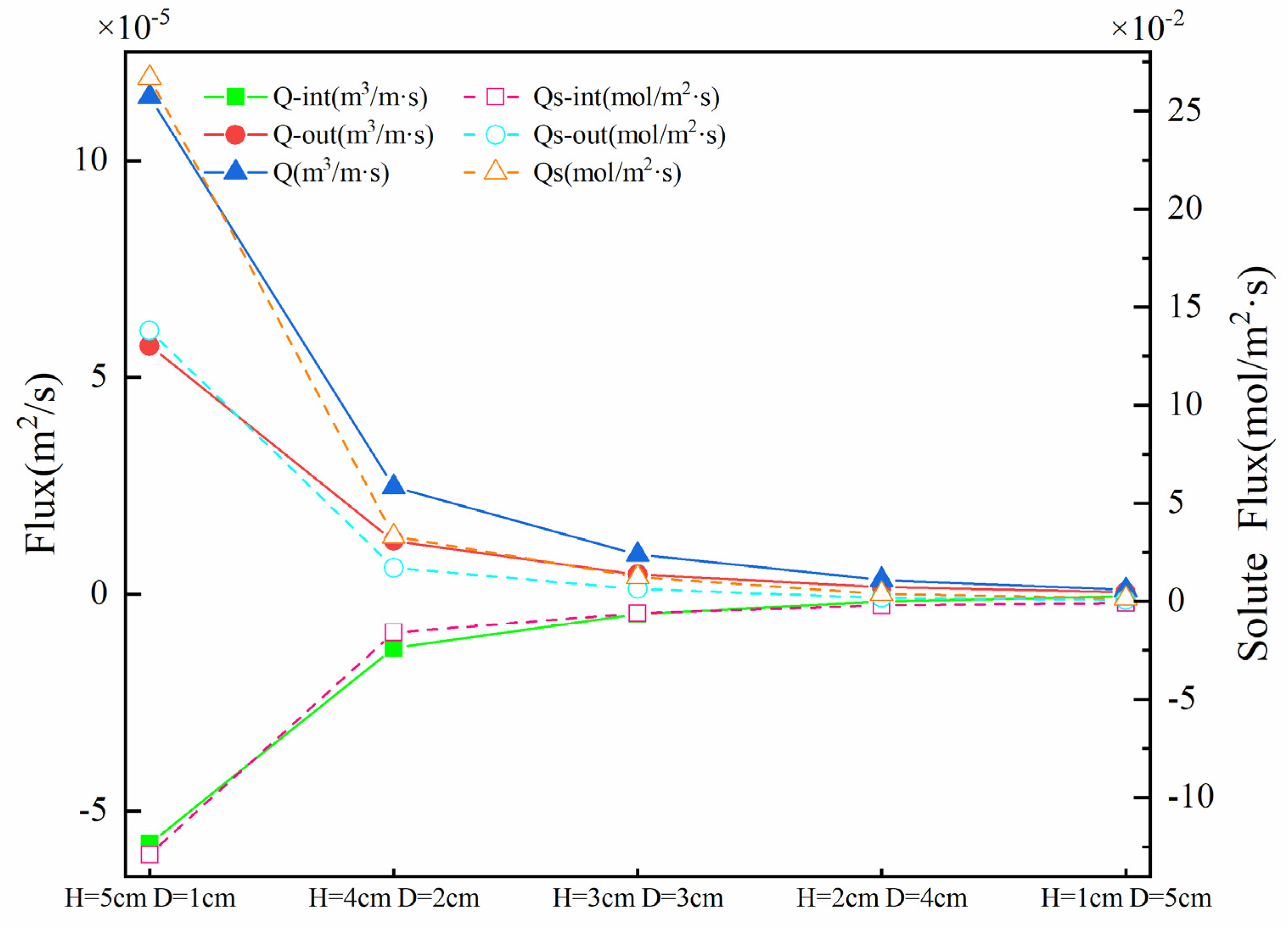
3.2. Influence of Structural Proportion
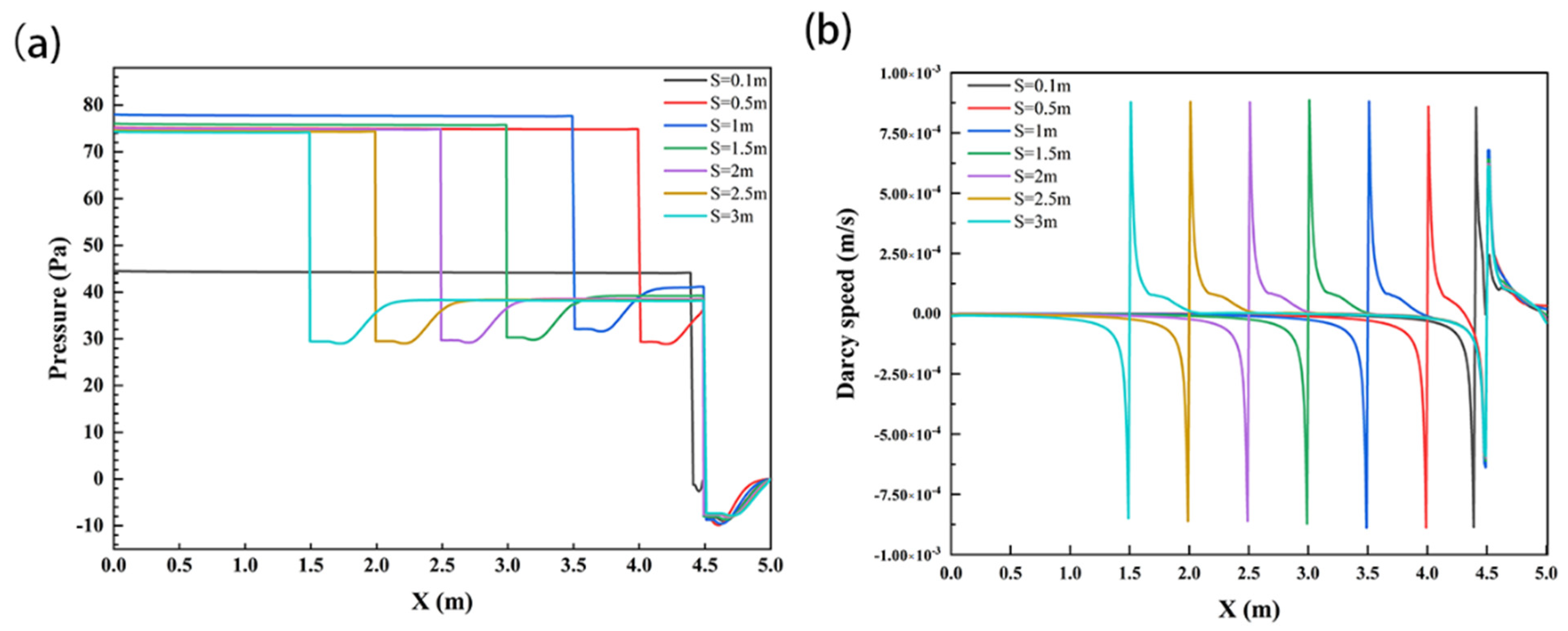
3.3. Influence of Structural Spacing
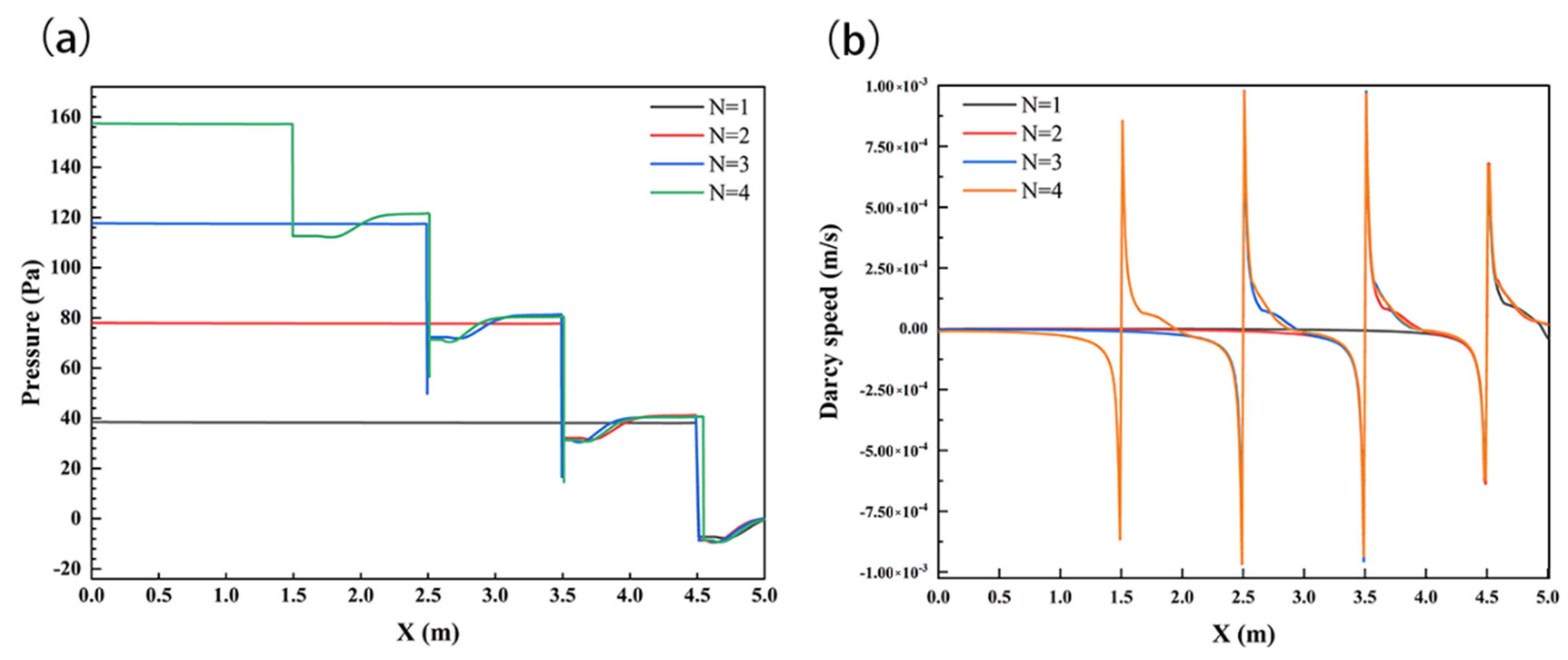
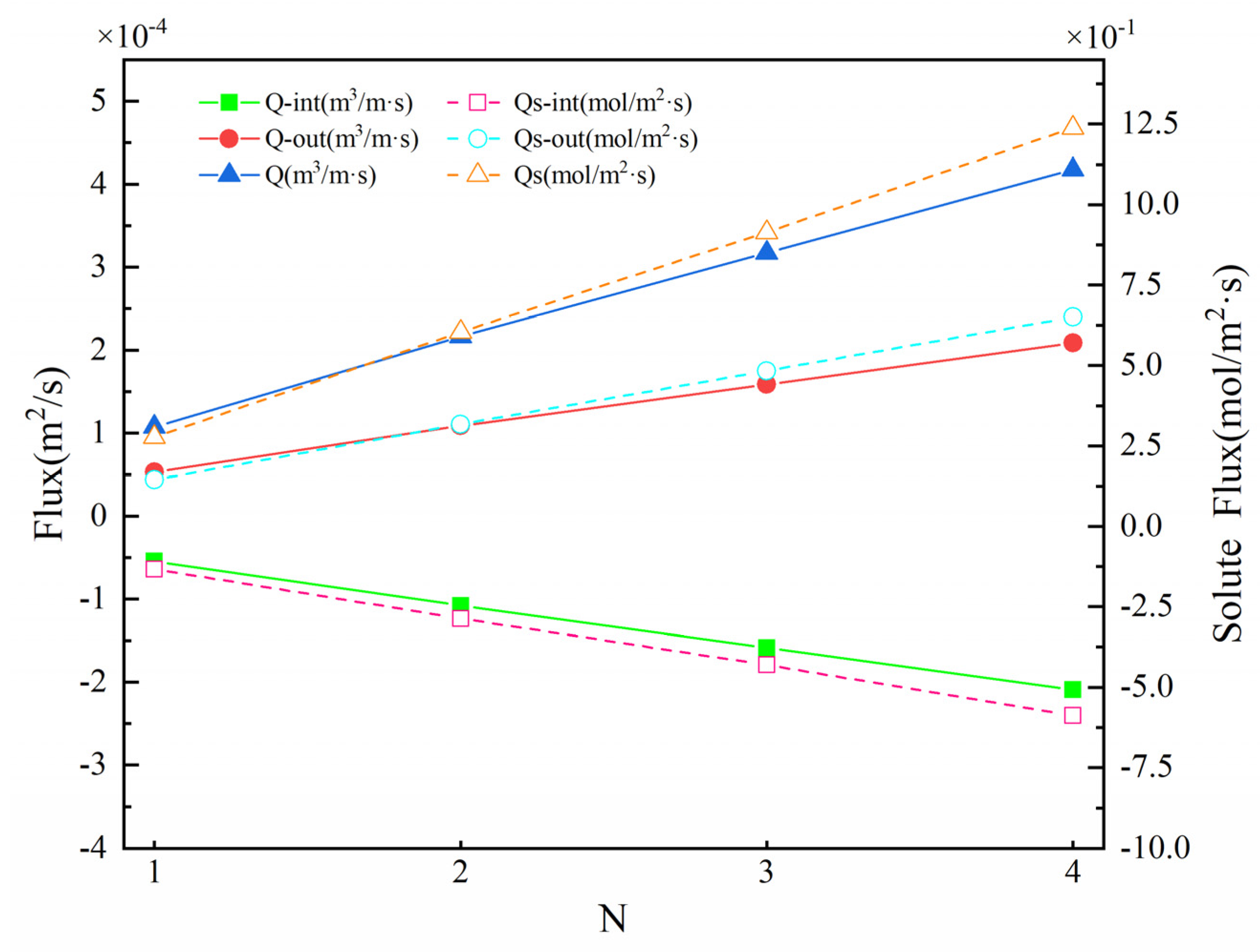
3.4. Influence of Structural Number
4. Discussion
4.1. Influence of Structural Design Parameters
4.2. Implications for River Restoration Design
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hester, E.T.; Gooseff, M.N. Moving Beyond the Banks: Hyporheic Restoration Is Fundamental to Restoring Ecological Services and Functions of Streams. Environ. Sci. Technol. 2010, 44, 1521–1525. [Google Scholar] [CrossRef] [PubMed]
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The Functional Significance of the Hyporheic Zone in Streams and Rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Chui, T.F.M. Impacts of Streambed Heterogeneity and Anisotropy on Residence Time of Hyporheic Zone. Groundwater 2017, 56, 425–436. [Google Scholar] [CrossRef] [PubMed]
- Peterson, E.W.; Sickbert, T.B.; Moore, S.L. High frequency stream bed mobility of a low-gradient agricultural stream with implications on the hyporheic zone. Hydrol. Process. 2008, 22, 4239–4248. [Google Scholar] [CrossRef]
- Peralta-Maraver, I.; Reiss, J.; Robertson, A.L. Interplay of hydrology, community ecology and pollutant attenuation in the hyporheic zone. Sci. Total Environ. 2018, 610–611, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Chui, T.F.M. Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone. Water 2020, 12, 1399. [Google Scholar] [CrossRef]
- Krause, S.; Hannah, D.M.; Fleckenstein, J.H. Hyporheic hydrology: Interactions at the groundwater-surface water interface. Hydrol. Process. 2009, 23, 2103–2107. [Google Scholar] [CrossRef]
- Huettel, M.; Ziebis, W.; Forster, S. Flow-Induced Uptake of Particulate Matter in Permeable Sediments. Limnol. Oceanogr. 1996, 41, 309–322. [Google Scholar] [CrossRef]
- Hester, E.T.; Cardenas, M.B.; Haggerty, R.; Apte, S.V. The importance and challenge of hyporheic mixing. Water Resour. Res. 2017, 53, 3565–3575. [Google Scholar] [CrossRef] [Green Version]
- Swanson, E.T.; Cardenas, M.B. Diel Heat Transport within the Hyporheic Zone of a Pool-Riffle-Pool Sequence of a Losing Stream and Evaluation of Models for Fluid Flux Estimation Using Heat. Limnol. Oceanogr. 2010, 55, 1741–1754. [Google Scholar] [CrossRef]
- Norman, F.A.; Cardenas, M.B. Heat transport in hyporheic zones due to bedforms: An experimental study. Water Resour. Res. 2014, 50, 3568–3582. [Google Scholar] [CrossRef]
- Packman, A.I.; Salehin, M.; Zaramella, M. Hyporheic Exchange with Gravel Beds: Basic Hydrodynamic Interactions and Bedform-Induced Advective Flows. J. Hydraul. Eng. 2004, 130, 647–656. [Google Scholar] [CrossRef]
- Packman, A.I.; Brooks, N.H.; Morgan, J.J. A physicochemical model for colloid exchange between a stream and a sand streambed with bed forms. Water Resour. Res. 2000, 36, 2351–2361. [Google Scholar] [CrossRef]
- Roche, K.R.; Li, A.; Bolster, D.; Wagner, G.J.; Packman, A.I. Effects of Turbulent Hyporheic Mixing on Reach-Scale Transport. Water Resour. Res. 2019, 55, 3780–3795. [Google Scholar] [CrossRef] [Green Version]
- Soulsby, C.; Malcolm, I.; Youngson, A. Hydrochemistry of the hyporheic zone in salmon spawning gravels: A preliminary assessment in a degraded agricultural stream. Regul. Rivers Res. Manag. 2001, 17, 651–665. [Google Scholar] [CrossRef]
- Groffman, P.M.; Dorsey, A.M.; Mayer, P.M. N processing within geomorphic structures in urban streams. J. N. Am. Benthol. Soc. 2005, 24, 613–625. [Google Scholar] [CrossRef]
- Harvey, J.; Gooseff, M. River corridor science: Hydrologic exchange and ecological consequences from bedforms to basins. Water Resour. Res. 2015, 51, 6893–6922. [Google Scholar] [CrossRef] [Green Version]
- Lewandowski, J.; Arnon, S.; Banks, E.; Batelaan, O.; Betterle, A.; Broecker, T.; Coll, C.; Drummond, J.D.; Garcia, J.G.; Galloway, J. Is the Hyporheic Zone Relevant Beyond the Scientific Community? Water 2019, 11, 2230. [Google Scholar] [CrossRef] [Green Version]
- Hancock, P.J.; Boulton, A.J.; Humphreys, W. Aquifers and hyporheic zones: Towards an ecological understanding of groundwater. Appl. Hydrogeol. 2005, 13, 98–111. [Google Scholar] [CrossRef]
- Boulton, A.J. Hyporheic rehabilitation in rivers: Restoring vertical connectivity. Freshw. Biol. 2007, 52, 632–650. [Google Scholar] [CrossRef]
- Boulton, A.J.; Datry, T.; Kasahara, T.; Mutz, M.; Stanford, J.A. Ecology and management of the hyporheic zone: Stream–groundwater interactions of running waters and their floodplains. J. N. Am. Benthol. Soc. 2010, 29, 26–40. [Google Scholar] [CrossRef] [Green Version]
- Hester, E.T.; Brooks, K.E.; Scott, D.T. Comparing reach scale hyporheic exchange and denitrification induced by instream restoration structures and natural streambed morphology. Ecol. Eng. 2018, 115, 105–121. [Google Scholar] [CrossRef]
- Kasahara, T.; Wondzell, S.M. Geomorphic controls on hyporheic exchange flow in mountain streams. Water Resour. Res. 2003, 39, SBH-3. [Google Scholar] [CrossRef] [Green Version]
- Mutz, M.; Kalbus, E.; Meinecke, S. Effect of instream wood on vertical water flux in low-energy sand bed flume experiments. Water Resour. Res. 2007, 43, W10424. [Google Scholar] [CrossRef]
- Smidt, S.; Cullin, J.A.; Ward, A.S.; Robinson, J.; Zimmer, M.A.; Lautz, L.K.; Endreny, T.A. A Comparison of Hyporheic Transport at a Cross-Vane Structure and Natural Riffle. Groundwater 2014, 53, 859–871. [Google Scholar] [CrossRef]
- Dudunake, T.; Tonina, D.; Reeder, W.J.; Monsalve, A. Local and Reach-Scale Hyporheic Flow Response from Boulder-Induced Geomorphic Changes. Water Resour. Res. 2020, 56, e2020WR027719. [Google Scholar] [CrossRef]
- Rana, S.M.; Scott, D.T.; Hester, E.T. Effects of in-stream structures and channel flow rate variation on transient storage. J. Hydrol. 2017, 548, 157–169. [Google Scholar] [CrossRef] [Green Version]
- Hester, E.T.; Hammond, B.; Scott, D.T. Effects of inset floodplains and hyporheic exchange induced by in-stream structures on nitrate removal in a headwater stream. Ecol. Eng. 2016, 97, 452–464. [Google Scholar] [CrossRef] [Green Version]
- Wade, J.; Lautz, L.; Kelleher, C.; Vidon, P.; Davis, J.; Beltran, J.; Pearce, C. Beaver dam analogues drive heterogeneous groundwater–surface water interactions. Hydrol. Process. 2020, 34, 5340–5353. [Google Scholar] [CrossRef]
- Hester, E.T.; Doyle, M.W. In-stream geomorphic structures as drivers of hyporheic exchange. Water Resour. Res. 2008, 44, W03417. [Google Scholar] [CrossRef]
- Ward, A.S.; Gooseff, M.N.; Johnson, P.A. How Can Subsurface Modifications to Hydraulic Conductivity Be Designed as Stream Restoration Structures? Analysis of Vaux’s Conceptual Models to Enhance Hyporheic Exchange. Water Resour. Res. 2011, 47, W08512. [Google Scholar] [CrossRef]
- Jin, G.; Tang, H.; Gibbes, B.; Li, L.; Barry, D. Transport of nonsorbing solutes in a streambed with periodic bedforms. Adv. Water Resour. 2010, 33, 1402–1416. [Google Scholar] [CrossRef] [Green Version]
- Cardenas, M.B.; Wilson, J. Hydrodynamics of coupled flow above and below a sediment–water interface with triangular bedforms. Adv. Water Resour. 2007, 30, 301–313. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
- Ren, J.; Wang, X.; Zhou, Y.; Chen, B.; Men, L. An Analysis of the Factors Affecting Hyporheic Exchange based on Numerical Modeling. Water 2019, 11, 665. [Google Scholar] [CrossRef] [Green Version]
- Quinino, R.C.; Reis, E.A.; Bessegato, L.F. Using the Coefficient of Determination R2 to Test the Significance of Multiple Linear Regression. Teach. Stat. 2013, 35, 84–88. [Google Scholar] [CrossRef]
- Suñé, V.; Carrasco, J.A. Efficient implementations of the randomization method with control of the relative error. Comput. Oper. Res. 2005, 32, 1089–1114. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Liu, D.; Liu, Y.; Li, Y.; Li, H.; Chen, L.; Xiao, J.; Liu, J.; Dong, J. Hyporheic exchange due to in-stream geomorphic structures. J. Freshw. Ecol. 2022, 37, 221–241. [Google Scholar] [CrossRef]
- Ward, B.B.; Devol, A.H.; Rich, J.J.; Chang, B.X.; Bulow, S.E.; Naik, H.; Pratihary, A.; Jayakumar, A. Denitrification as the dominant nitrogen loss process in the Arabian Sea. Nature 2009, 461, 78–81. [Google Scholar] [CrossRef]



| Surface Water Velocity (m/s) | Porosity Ratio n | Permeability k (m2) | Fluid Viscosity μ (Pa·s) | Molecular Diffusion Coefficient Dm (m2/s) |
|---|---|---|---|---|
| 0.04 | 0.4 | 1 × 10−9 | 0.0011 | 5 × 10−10 |
| Array N1 | Array N2 | |||||
|---|---|---|---|---|---|---|
| Time | RMSE | R2 | Re% | RMSE | R2 | Re% |
| 30 min | 0.0263 | 0.9955 | 7.10% | 0.0617 | 0.9119 | 19.03% |
| 60 min | 0.0417 | 0.9822 | 4.42% | 0.0527 | 0.9745 | 9.16% |
| 120 min | 0.0583 | 0.9444 | 9.22% | 0.1291 | 0.8392 | 8.45% |
| 300 min | 0.0527 | 0.8987 | 3.48% | 0.0218 | 0.7522 | 1.72% |
| Case | u0 | Water Depth | Width | Depth (D) | Height (H) | H/D |
| 1 | 4 cm/s | 6 cm | 10 cm | 5 cm | 1 cm | 1/5 |
| 2 | 4 cm/s | 6 cm | 10 cm | 4 cm | 2 cm | 2/4 |
| 3 | 4 cm/s | 6 cm | 10 cm | 3 cm | 3 cm | 3/3 |
| 4 | 4 cm/s | 6 cm | 10 cm | 2 cm | 4 cm | 4/2 |
| 5 | 4 cm/s | 6 cm | 10 cm | 1 cm | 5 cm | 5/1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, Y.; Feng, J.; Liu, D.; Li, Y.; Chen, L.; Xiao, J. Influence of the In-Stream Structure on Solute Transport in the Hyporheic Zone. Int. J. Environ. Res. Public Health 2022, 19, 5856. https://doi.org/10.3390/ijerph19105856
Li H, Liu Y, Feng J, Liu D, Li Y, Chen L, Xiao J. Influence of the In-Stream Structure on Solute Transport in the Hyporheic Zone. International Journal of Environmental Research and Public Health. 2022; 19(10):5856. https://doi.org/10.3390/ijerph19105856
Chicago/Turabian StyleLi, Han, Ying Liu, Jinghong Feng, Defu Liu, Yi Li, Lihui Chen, and Jingwen Xiao. 2022. "Influence of the In-Stream Structure on Solute Transport in the Hyporheic Zone" International Journal of Environmental Research and Public Health 19, no. 10: 5856. https://doi.org/10.3390/ijerph19105856
APA StyleLi, H., Liu, Y., Feng, J., Liu, D., Li, Y., Chen, L., & Xiao, J. (2022). Influence of the In-Stream Structure on Solute Transport in the Hyporheic Zone. International Journal of Environmental Research and Public Health, 19(10), 5856. https://doi.org/10.3390/ijerph19105856





