A Time-Varying Model for Predicting Formaldehyde Emission Rates in Homes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection Overview
2.2. Time-Resolved Formaldehyde Emission Rate Calculation
2.3. Predictors for Formaldehyde Emission Rate
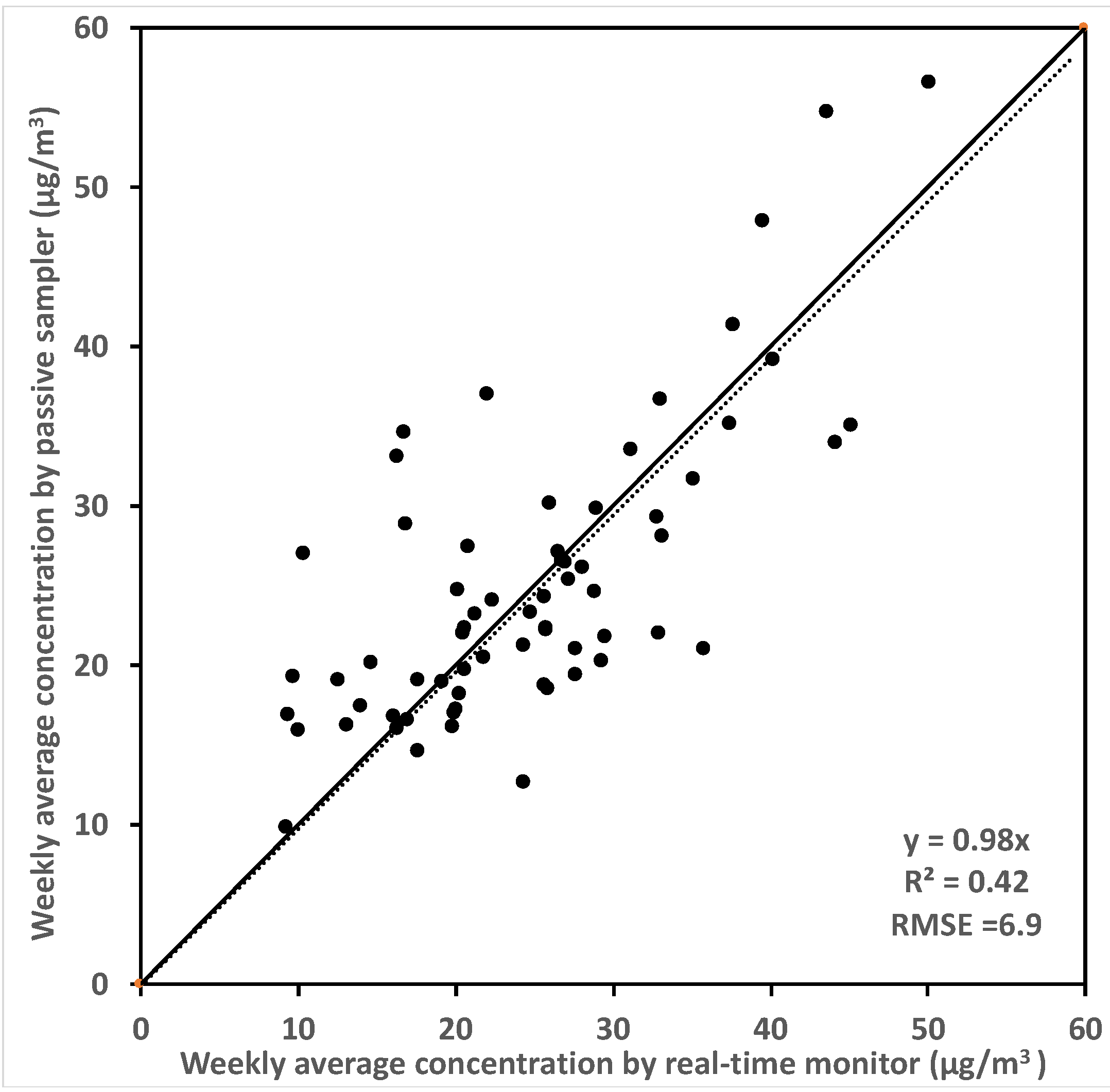
- The degree of correlation and the remaining errors from the empirical multi-parameter model for predicting the emission rate, which were identified by calculating the r-squared and root mean square error (RMSE) for each regression;
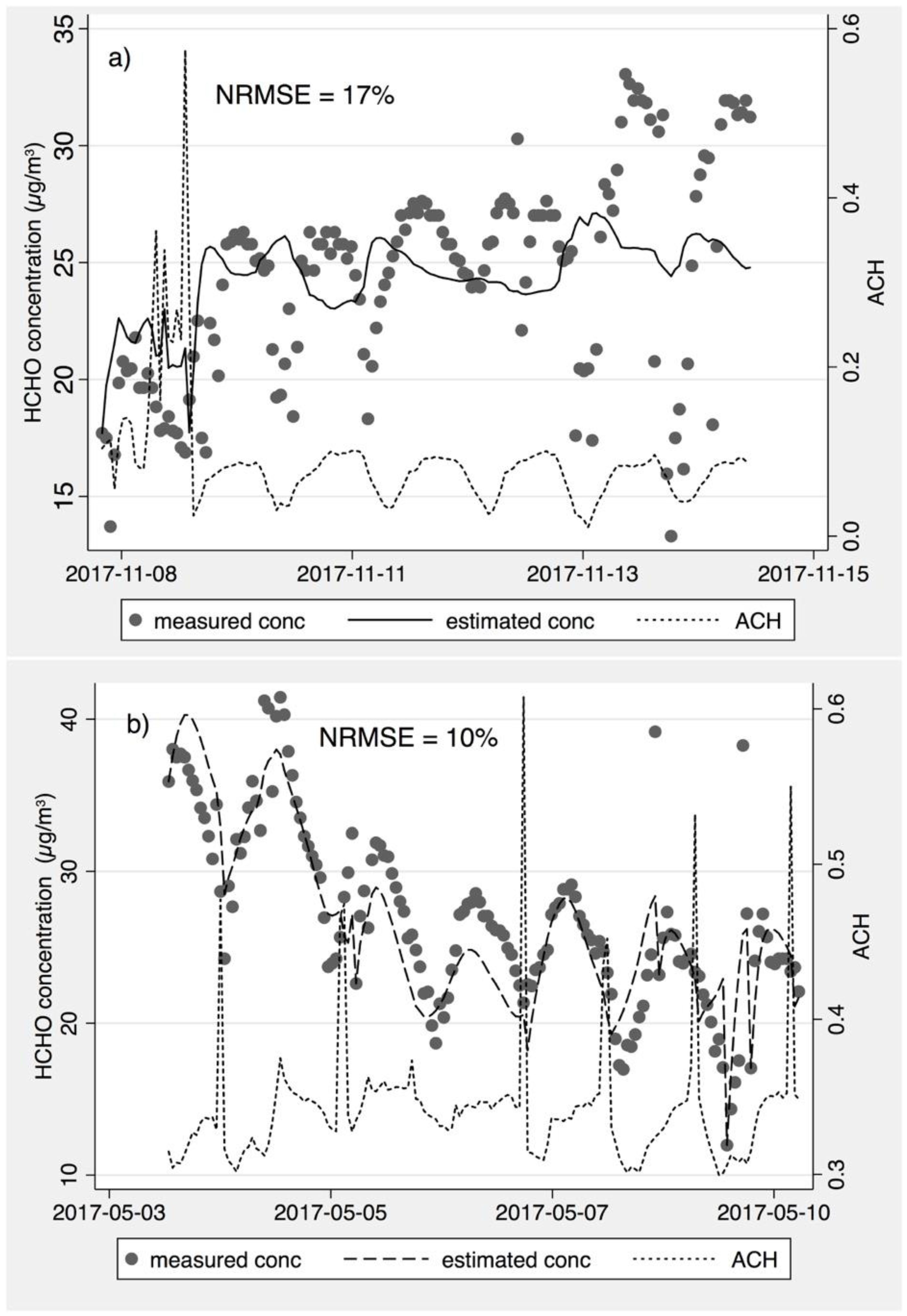
- The accuracy and consistency of the predicted emission rate for estimating indoor formaldehyde concentration, which was evaluated by comparing the measured time-resolved formaldehyde concentrations (Cin) in each home versus the estimated concentration (Cinest) calculated using the regression model’s time-varying emission rate predicted by temperature, relative humidity, and air change rates at the corresponding time step, as shown in Equation (10).
3. Results and Discussion
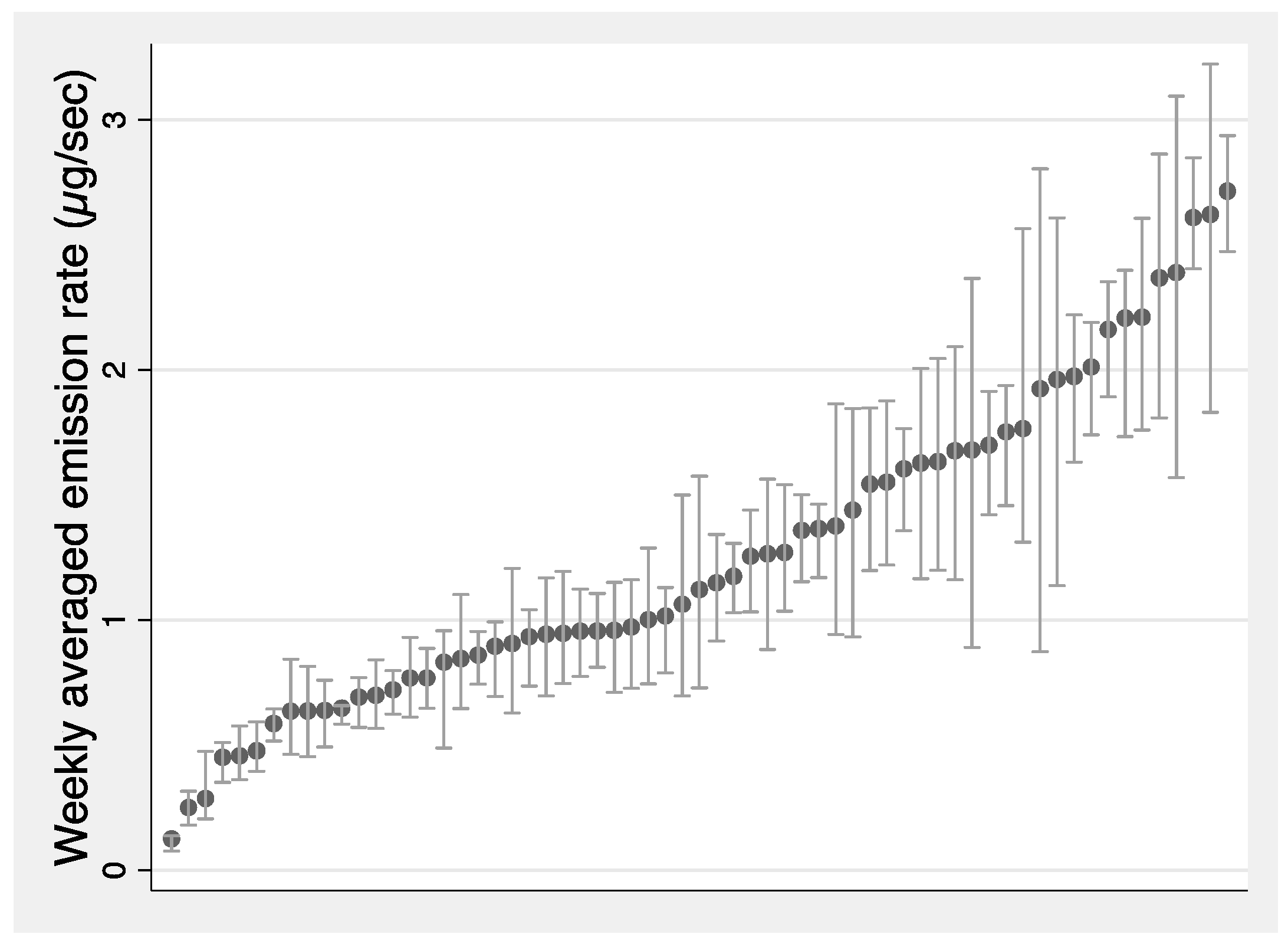
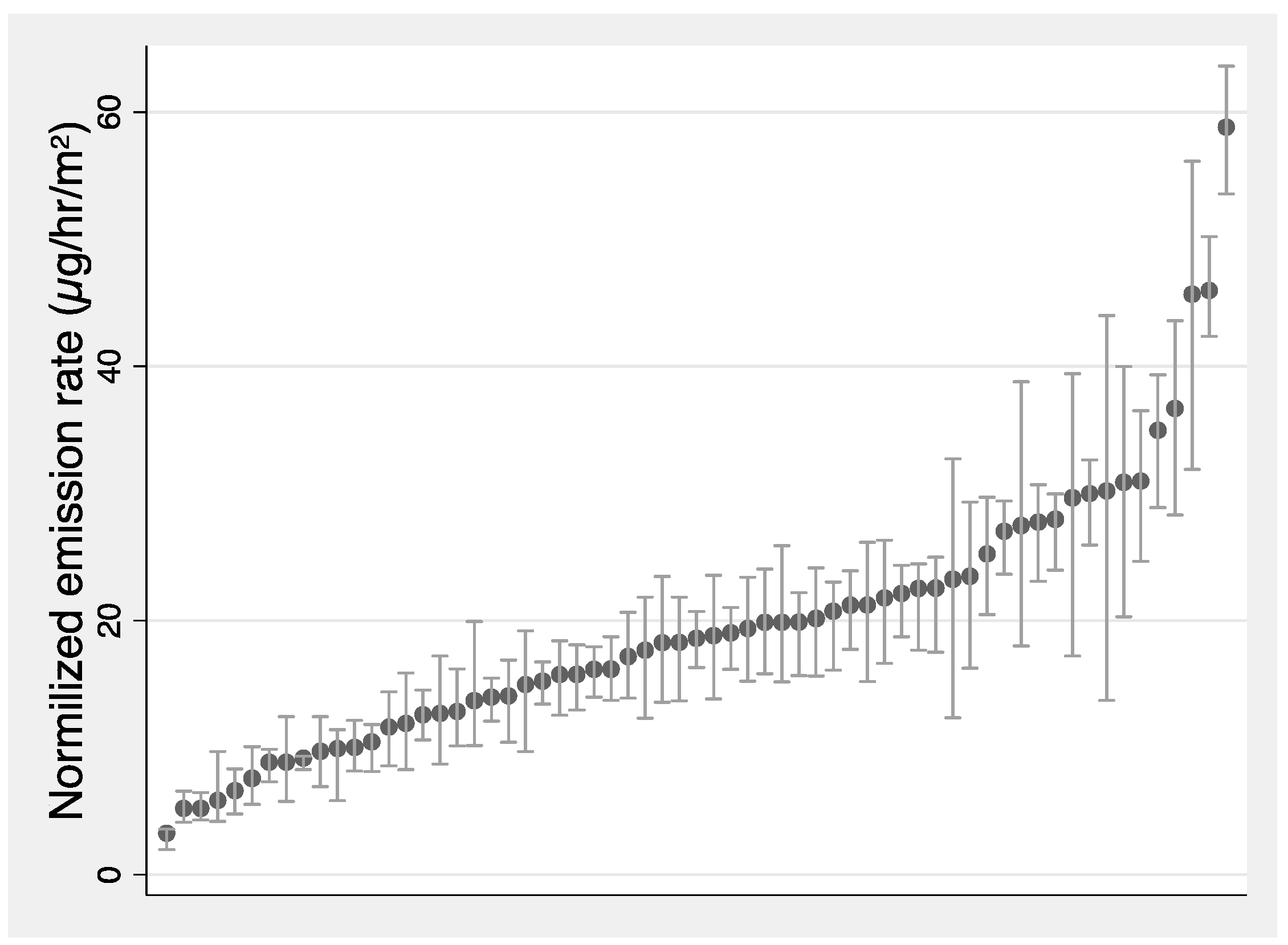
3.1. Emission Rate Estimation
3.2. Formaldehyde Emission Rate Model and Concentration Prediction
4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Salthammer, T.; Mentese, S.; Marutzky, R. Formaldehyde in the Indoor Environment. Chem. Rev. 2010, 110, 2536–2572. [Google Scholar] [CrossRef] [PubMed]
- Kelly, T.J.; Smith, D.L.; Satola, J. Emission Rates of Formaldehyde from Materials and Consumer Products Found in California Homes. Environ. Sci. Technol. 1999, 33, 81–88. [Google Scholar] [CrossRef]
- Logue, J.M.; Price, P.N.; Sherman, M.H.; Singer, B.C. A Method to Estimate the Chronic Health Impact of Air Pollutants in US Residences. Environ. Health Perspect. 2012, 120, 216–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- WHO. Who Guidelines for Indoor Air Quality: Selected Pollutants; World Health Organization: Copenhagen, Denmark, 2010; ISBN 978-92-890-0213-4. [Google Scholar]
- Lang, I.; Bruckner, T.; Triebig, G. Formaldehyde and Chemosensory Irritation in Humans: A Controlled Human Exposure Study. Regul. Toxicol. Pharmacol. 2008, 50, 23–36. [Google Scholar] [CrossRef]
- McGwin, G.; Lienert, J.; Kennedy, J.I. Formaldehyde Exposure and Asthma in Children: A Systematic Review. Environ. Health Perspect. 2010, 118, 313–317. [Google Scholar] [CrossRef] [Green Version]
- IARC Formaldehyde, 2-Butoxyethanol and 1-Tert-Butoxypropan-2-Ol. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; International Agency for Research on Cancer: Lyon, France, 2006; ISBN 978-92-832-1288-1.
- Offermann, F.J. Ventilation and Indoor Air Quality in New Homes; California Energy Commission and California Air Resources Board: Sacramento, CA, USA, 2009. [Google Scholar]
- OEHHA OEHHA Acute, 8-Hour and Chronic Reference Exposure Level (REL) Summary. Available online: https://oehha.ca.gov/air/general-info/oehha-acute-8-hour-and-chronic-reference-exposure-level-rel-summary (accessed on 26 January 2021).
- Singer, B.C.; Chan, W.R.; Kim, Y.; Offermann, F.J.; Walker, I.S. Indoor Air Quality in California Homes with Code-required Mechanical Ventilation. Indoor Air 2020, 30, 885–899. [Google Scholar] [CrossRef]
- Mullen, N.A.; Li, J.; Russell, M.L.; Spears, M.; Less, B.D.; Singer, B.C. Results of the California Healthy Homes Indoor Air Quality Study of 2011-2013: Impact of Natural Gas Appliances on Air Pollutant Concentrations. Indoor Air 2016, 26, 231–245. [Google Scholar] [CrossRef] [Green Version]
- Weisel, C.P.; Zhang, J.; Turpin, B.J.; Morandi, M.T.; Colome, S.; Stock, T.H.; Spektor, D.M.; Korn, L.; Winer, A.M.; Kwon, J.; et al. Relationships of Indoor, Outdoor, and Personal Air (RIOPA). Part I. Collection Methods and Descriptive Analyses. Res. Rep. Health Eff. Inst. 2005, 1–107; discussion 109–127. [Google Scholar]
- Health Canada Residential Indoor Air Quality Guideline: Formaldehyde. Available online: https://www.canada.ca/en/health-canada/services/publications/healthy-living/residential-indoor-air-quality-guideline-formaldehyde.html (accessed on 26 January 2021).
- Gilbert, N.L.; Gauvin, D.; Guay, M.; Heroux, M.E.; Dupuis, G.; Legris, M.; Chan, C.C.; Dietz, R.N.; Levesque, B. Housing Characteristics and Indoor Concentrations of Nitrogen Dioxide and Formaldehyde in Quebec City, Canada. Environ. Res. 2006, 102, 1–8. [Google Scholar] [CrossRef]
- Gilbert, N.L.; Guay, M.; Gauvin, D.; Dietz, R.N.; Chan, C.C.; Lévesque, B. Air Change Rate and Concentration of Formaldehyde in Residential Indoor Air. Atmos. Environ. 2008, 42, 2424–2428. [Google Scholar] [CrossRef]
- 15 U.S.C. 2697(d). 40 CFR 770 - Formaldehyde Standards for Composite Wood Products. 2018. Available online: https://www.ecfr.gov/current/title-40/chapter-I/subchapter-R/part-770 (accessed on 29 March 2022).
- Hult, E.L.; Willem, H.; Price, P.N.; Hotchi, T.; Russell, M.L.; Singer, B.C. Formaldehyde and Acetaldehyde Exposure Mitigation in US Residences: In-Home Measurements of Ventilation Control and Source Control. Indoor Air 2015, 25, 523–535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burman, E.; Stamp, S. Trade-Offs between Ventilation Rates and Formaldehyde Concentrations in New-Build Dwellings in the UK. In Proceedings of the 40th AIVC–8th TightVent & 6th Venticool Conference, AIVC (Air Infiltration and Ventilation Centre), Ghent, Belgium, 15 October 2019; Volume 40. [Google Scholar]
- Salthammer, T.; Fuhrmann, F.; Kaufhold, S.; Meyer, B.; Schwarz, A. Effects of Climatic Parameters on Formaldehyde Concentrations in Indoor Air. Indoor Air 1995, 5, 120–128. [Google Scholar] [CrossRef]
- Van der Wal, J.F. Formaldehyde Measurements in Dutch Houses, Schools and Offices in the Years 1977–1980. Atmos. Environ. (1967) 1982, 16, 2471–2478. [Google Scholar] [CrossRef]
- Sherman, M.H.; Hodgson, A.T. Formaldehyde as a Basis for Residential Ventilation Rates: Formaldehyde as a Basis for Residential Ventilation Rates. Indoor Air 2004, 14, 2–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poppendieck, D.G.; Ng, L.C.; Persily, A.K.; Hodgson, A.T. Long Term Air Quality Monitoring in a Net-Zero Energy Residence Designed with Low Emitting Interior Products. Build. Environ. 2015, 94, 33–42. [Google Scholar] [CrossRef]
- Huangfu, Y.; Lima, N.M.; O’Keeffe, P.T.; Kirk, W.M.; Lamb, B.K.; Walden, V.P.; Jobson, B.T. Whole-House Emission Rates and Loss Coefficients of Formaldehyde and Other Volatile Organic Compounds as a Function of the Air Change Rate. Environ. Sci. Technol. 2020, 54, 2143–2151. [Google Scholar] [CrossRef]
- Willem, H.; Hult, E.L.; Hotchi, T.; Russell, M.L.; Maddalena, R.L.; Singer, B.C. Ventilation Control of Volatile Organic Compounds in New US Homes: Results of a Controlled Field Study in Nine Residential Units; Lawrence Berkeely National Laboratory: Berkeley, CA, USA, 2013. [Google Scholar]
- Liu, Y.; Misztal, P.K.; Xiong, J.; Tian, Y.; Arata, C.; Weber, R.J.; Nazaroff, W.W.; Goldstein, A.H. Characterizing Sources and Emissions of Volatile Organic Compounds in a Northern California Residence Using Space- and Time-Resolved Measurements. Indoor Air 2019, 29, 630–644. [Google Scholar] [CrossRef] [Green Version]
- Offermann, F.J.; Hodgson, A.T. Emission Rates of Volatile Organic Compounds in New Homes. In Proceedings of the Indoor Air: Proceedings of the 12th International Conference on Indoor Air Quality and Climate, Austin, TX, USA, 5–10 June 2011; pp. 5–10.
- Andersen, I.B.; Lundqvist, G.R.; Mølhave, L. Indoor Air Pollution Due to Chipboard Used as a Construction Material. Atmos. Environ. (1967) 1975, 9, 1121–1127. [Google Scholar] [CrossRef]
- Liang, W.; Yang, S.; Yang, X. Long-Term Formaldehyde Emissions from Medium-Density Fiberboard in a Full-Scale Experimental Room: Emission Characteristics and the Effects of Temperature and Humidity. Environ. Sci. Technol. 2015, 49, 10349–10356. [Google Scholar] [CrossRef]
- Little, J.C.; Hodgson, A.T.; Gadgil, A.J. Modeling Emissions of Volatile Organic Compounds from New Carpets. Atmos. Environ. 1994, 28, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Cox, S.S.; Little, J.C.; Hodgson, A.T. Predicting the Emission Rate of Volatile Organic Compounds from Vinyl Flooring. Environ. Sci. Technol. 2002, 36, 709–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, H.; Haghighat, F. Modelling of Volatile Organic Compounds Emission from Dry Building Materials. Build. Environ. 2002, 37, 1127–1138. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, X.; Wang, X.; Qian, K.; Zhao, R. Influence of Temperature on Formaldehyde Emission Parameters of Dry Building Materials. Atmos. Environ. 2007, 41, 3203–3216. [Google Scholar] [CrossRef]
- Deng, Q.; Yang, X.; Zhang, J. Study on a New Correlation between Diffusion Coefficient and Temperature in Porous Building Materials. Atmos. Environ. 2009, 43, 2080–2083. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Tan, Y.; Liu, J.; Wang, K.; Ji, W.; Sun, L.; Yu, X.; Zhao, J.; Xu, B.; et al. Measurement of the Key Parameters of VOC Emissions from Wooden Furniture, and the Impact of Temperature. Atmos. Environ. 2021, 259, 118510. [Google Scholar] [CrossRef]
- Liang, W.; Lv, M.; Yang, X. The Combined Effects of Temperature and Humidity on Initial Emittable Formaldehyde Concentration of a Medium-Density Fiberboard. Build. Environ. 2016, 98, 80–88. [Google Scholar] [CrossRef]
- Jonge, K.D.; Laverge, J. Modeling Dynamic Behavior of Volatile Organic Compounds in a Zero Energy Building. Int. J. Vent. 2020, 20, 193–203. [Google Scholar] [CrossRef]
- Bourdin, D.; Mocho, P.; Desauziers, V.; Plaisance, H. Formaldehyde Emission Behavior of Building Materials: On-Site Measurements and Modeling Approach to Predict Indoor Air Pollution. J. Hazard. Mater. 2014, 280, 164–173. [Google Scholar] [CrossRef]
- Wei, W.; Ramalho, O.; Malingre, L.; Sivanantham, S.; Little, J.C.; Mandin, C. Machine Learning and Statistical Models for Predicting Indoor Air Quality. Indoor Air 2019, 29, 704–726. [Google Scholar] [CrossRef]
- Akyüz, İ.; Özşahin, Ş.; Tiryaki, S.; Aydın, A. An Application of Artificial Neural Networks for Modeling Formaldehyde Emission Based on Process Parameters in Particleboard Manufacturing Process. Clean Technol. Environ. Policy 2017, 19, 1449–1458. [Google Scholar] [CrossRef]
- Ouaret, R.; Ionescu, A.; Petrehus, V.; Candau, Y.; Ramalho, O. Spectral Band Decomposition Combined with Nonlinear Models: Application to Indoor Formaldehyde Concentration Forecasting. Stoch. Environ. Res. Risk Assess. 2018, 32, 985–997. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, H.; Tan, Y.; Zhang, M.; Zhang, X.; Wang, K.; Ji, W.; Sun, L.; Yu, X.; Zhao, J.; et al. Using a Machine Learning Approach to Predict the Emission Characteristics of VOCs from Furniture. Build. Environ. 2021, 196, 107786. [Google Scholar] [CrossRef]
- Zhang, R.; Tan, Y.; Wang, Y.; Wang, H.; Zhang, M.; Liu, J.; Xiong, J. Predicting the Concentrations of VOCs in a Controlled Chamber and an Occupied Classroom via a Deep Learning Approach. Build. Environ. 2022, 207, 108525. [Google Scholar] [CrossRef]
- Mohammadshirazi, A.; Kalkhorani, V.A.; Humes, J.; Speno, B.; Rike, J.; Ramnath, R.; Clark, J.D. Predicting Airborne Pollutant Concentrations and Events in a Commercial Building Using Low-Cost Pollutant Sensors and Machine Learning: A Case Study. Build. Environ. 2022, 213, 108833. [Google Scholar] [CrossRef]
- Sparks, L.E.; Tichenor, B.A.; Chang, J.; Guo, Z. Gas-Phase Mass Transfer Model for Predicting Volatile Organic Compound (Voc) Emission Rates from Indoor Pollutant Sources. Indoor Air 1996, 6, 31–40. [Google Scholar] [CrossRef]
- Myers, G.E. Effect of Ventilation Rate and Board Loading on Formaldehyde Concentration: A Critical Review of the Literature. For. Prod. Research 1984, 34, 59–68. [Google Scholar]
- Sherman, M.H.; Hult, E.L. Impacts of Contaminant Storage on Indoor Air Quality: Model Development. Atmos. Environ. 2013, 72, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Silberstein, S.; Grot, R.A.; Ishiguro, K.; Mulligan, J.L. Validation of Models for Predicting Formaldehyde Concentrations in Residences Due to Pressed-Wood Products. JAPCA 1988, 38, 1403–1411. [Google Scholar] [CrossRef] [Green Version]
- Myers, G.E. The Effects of Temperature and Humidity on Formaldehyde Emission from UF-Bonded Boards: A Literature Critique. For. Prod. J. 1985, 35, 20–31. [Google Scholar]
- Chan, W.R.; Kim, Y.-S.; Less, B.D.; Singer, B.C.; Walker, I.S. Ventilation and Indoor Air Quality in New California Homes with Gas Appliances and Mechanical Ventilation; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2019. [Google Scholar]
- ASHRAE. ASHRAE Handbook of Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2017; ISBN 978-1-939200-58-7. [Google Scholar]
- Walker, I.S.; Wilson, D.J. Field Validation of Equations for Stack and Wind Driven Air Infiltration Calculations. ASHRAE HVACR Res. J. 1998, 4, 119–140. [Google Scholar] [CrossRef]
- Hurel, N.; Sherman, M.H.; Walker, I.S. Sub-Additivity in Combining Infiltration with Mechanical Ventilation for Single Zone Buildings. Build. Environ. 2016, 98, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Walker, I.S.; Wray, C.P.; Dickerhoff, D.J.; Sherman, M.H. Evaluation of Flow Hood Measurements for Residential Register Flows; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2001. [Google Scholar]
- Mendez, M.; Blond, N.; Blondeau, P.; Schoemaecker, C.; Hauglustaine, D.A. Assessment of the Impact of Oxidation Processes on Indoor Air Pollution Using the New Time-Resolved INCA-Indoor Model. Atmos. Environ. 2015, 122, 521–530. [Google Scholar] [CrossRef]
- Marchand, C.; Le Calvé, S.; Mirabel, P.; Glasser, N.; Casset, A.; Schneider, N.; de Blay, F. Concentrations and Determinants of Gaseous Aldehydes in 162 Homes in Strasbourg (France). Atmos. Environ. 2008, 42, 505–516. [Google Scholar] [CrossRef]
- Hodgson, A.T.; Ming, K.Y.; Singer, B.C. Quantifying Object and Material Surface Areas in Residences; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005. [Google Scholar]
- Kadiyala, A.; Kumar, A. Evaluation of Indoor Air Quality Models with the Ranked Statistical Performance Measures Using Available Software. Environ. Prog. Sustain. Energy 2012, 31, 170–175. [Google Scholar] [CrossRef]
- Kadiyala, A.; Kumar, A. Guidelines for Operational Evaluation of Air Quality Models; Lambert Academic Publishing GmbH & Co.: Saarbrücken, Germany, 2012. [Google Scholar]
- Hodgson, A.T.; Rudd, A.F.; Beal, D.; Chandra, S. Volatile Organic Compound Concentrations and Emission Rates in New Manufactured and Site-Built Houses: VOC Concentrations and Emission Rates in New Manufactured and Site-Built Houses. Indoor Air 2000, 10, 178–192. [Google Scholar] [CrossRef] [Green Version]



| Evaluation Criteria | 1-h Average | 8-h Moving Window Running Average | Use Hourly Emission Rate within 5th to 95th Percentile | |
|---|---|---|---|---|
| Number of homes with valid coefficients | 39 | 41 | 41 | |
| For predicting emission rates | R-square [Mean Median (Min–Max)] | 0.88 0.91 (0.40–0.98) | 0.97 0.98 (0.89–0.99) | 0.94 0.96 (0.66–0.99) |
| RMSE (%) [Mean Median (Min–Max)] | 29% 27% (12%–81%) | 15% 12% (6%–43%) | 20% 19% (8%–44%) | |
| For estimating indoor concentrations using predicted emission rates | NRMSE % [Mean Median (Min–Max)] | 13% 13% (6%–24%) | 11% 9% (5%–22%) 1 13% 12% (6%–26%) 2 | 13% 13% (6%–25%) |
| Method | 1-Hour Average | 8-Hour Running Average | Use Hourly Emission Rate within 5th to 95th Percentile | Reference Range from Previous Studies | |
|---|---|---|---|---|---|
| Coefficient estimates [Mean Median (Min-Max)] | A (1/°C) | 0.088 0.085 (0.015–0.253) | 0.086 0.080 (0.005–0.230) | 0.089 0.072 (0.007–0.203) | 0.080 [27] 0.05–0.15 [48] |
| B (1/RH%) | 0.036 0.031 (0.009–0.076) | 0.047 0.042 (0.014–0.100) | 0.033 0.029 (0.006–0.078) | 0.005–0.038 [48] | |
| Cst (µg/m3) | 72.9 74.8 (24.1–117.8) | 70.8 70.7 (39.6–111.1) | 64.1 66.1 (37.2–90.4) | 41–118 [17] 23–985 [46] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Walker, I.S.; Sohn, M.D.; Less, B. A Time-Varying Model for Predicting Formaldehyde Emission Rates in Homes. Int. J. Environ. Res. Public Health 2022, 19, 6603. https://doi.org/10.3390/ijerph19116603
Zhao H, Walker IS, Sohn MD, Less B. A Time-Varying Model for Predicting Formaldehyde Emission Rates in Homes. International Journal of Environmental Research and Public Health. 2022; 19(11):6603. https://doi.org/10.3390/ijerph19116603
Chicago/Turabian StyleZhao, Haoran, Iain S. Walker, Michael D. Sohn, and Brennan Less. 2022. "A Time-Varying Model for Predicting Formaldehyde Emission Rates in Homes" International Journal of Environmental Research and Public Health 19, no. 11: 6603. https://doi.org/10.3390/ijerph19116603
APA StyleZhao, H., Walker, I. S., Sohn, M. D., & Less, B. (2022). A Time-Varying Model for Predicting Formaldehyde Emission Rates in Homes. International Journal of Environmental Research and Public Health, 19(11), 6603. https://doi.org/10.3390/ijerph19116603






