Temporal Instability of Factors Affecting Injury Severity in Helmet-Wearing and Non-Helmet-Wearing Motorcycle Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances
Abstract
:1. Introduction
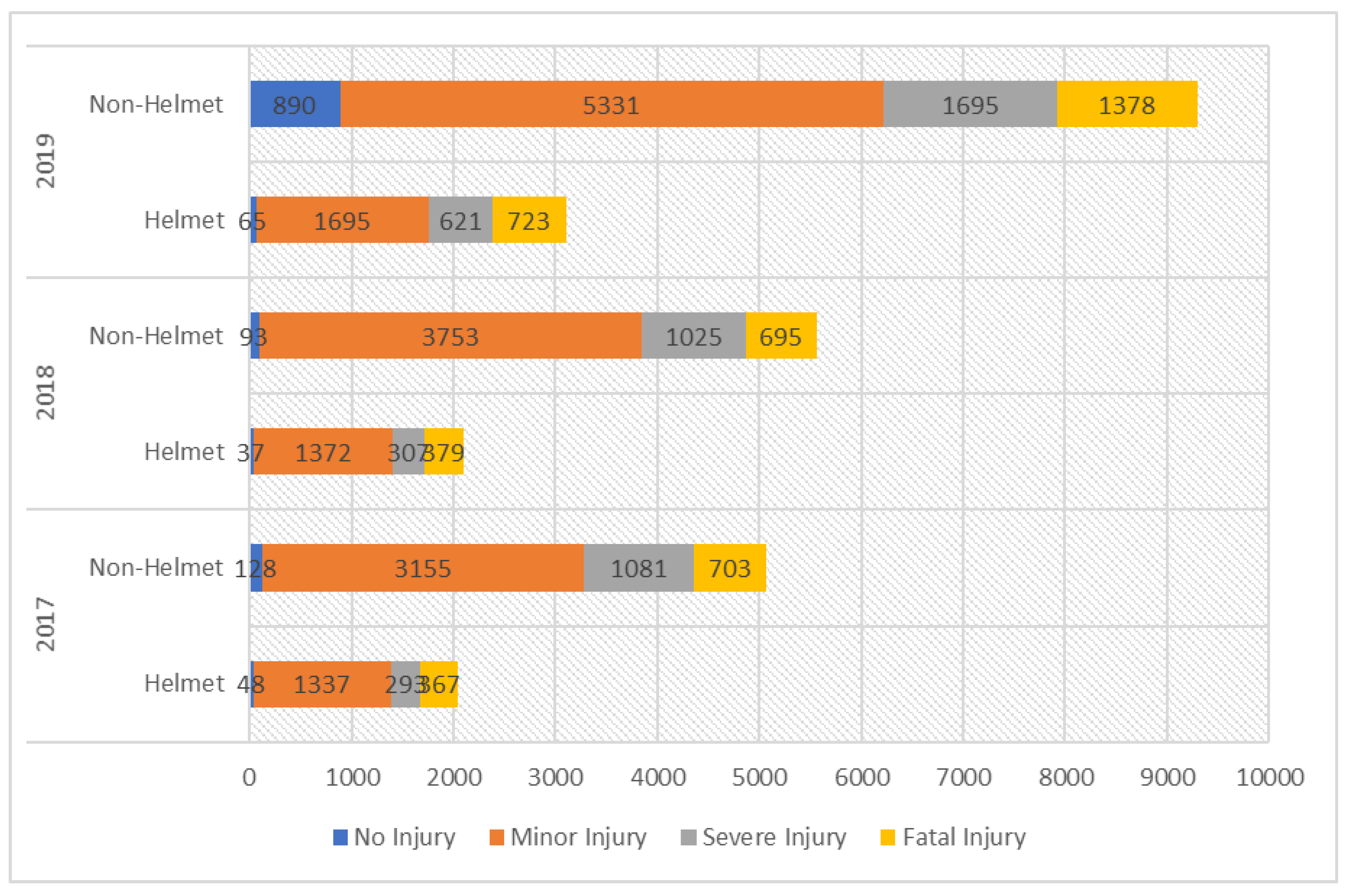
2. Data Description
3. Methodology
3.1. Modeling Approach
3.2. Temporal Instability
4. Results and Discussion
4.1. Helmet Users
4.2. Non-Helmet Users
4.3. Effect of Explanatory Variables
4.3.1. Roadway Attributes
4.3.2. Rider Attributes
4.3.3. Crash Characteristics
4.3.4. Violation Attributes
4.3.5. Temporal Attributes
| Variables | No Injury | Minor Injury | Severe Injury | Fatal Injury | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2017 | 2018 | 2019 | 2017 | 2018 | 2019 | 2017 | 2018 | 2019 | 2017 | 2018 | 2019 | |
| Roadway attributes | ||||||||||||
| Lane 2 indicator | −0.0017 -- | -- (−0.0010) | -- -- | 0.0009 -- | -- (0.0003) | -- -- | 0.0005 -- | -- (0.0005) | -- -- | 0.0003 -- | -- (0.0002) | -- -- |
| Lane 3 indicator | −0.0007 -- | -- -- | -- -- | −0.0123 -- | -- -- | -- -- | 0.0149 -- | -- -- | -- -- | −0.0019 -- | -- -- | -- -- |
| Collector road indicator | 0.0007 -- | -- -- | -- (0.0027) | 0.0041 -- | -- -- | -- (−0.0082) | −0.0065 -- | -- -- | -- (0.0029) | 0.0017 -- | -- -- | -- (0.0026) |
| Rider Attributes | ||||||||||||
| Below 20 years indicator | −0.0006 -- | −0.0004 (−0.0010) | (−0.0020) | −0.0159 -- | −0.0078 (−0.0102) | (-0.0131) | 0.0208 -- | 0.0116 (−0.0085) | (0.0177) | −0.0043 -- | −0.0033 (0.0193) | (-0.0026) |
| Between 20–30 indicator | 0.0016 (−0.0030) | -- | -- | 0.0118 (0.0328) | -- | -- | 0.0080 (−0.0190) | -- | -- | −0.0214 (−0.0108) | -- | -- |
| Between 40–50 indicator | -- (−0.0002) | -- -- | -- -- | -- (−0.0029) | -- -- | -- -- | -- (−0.0011) | -- -- | -- -- | -- (0.0042) | -- -- | -- -- |
| Above 50 Years indicator | -- -- | −0.0006 (−0.0006) | −0.0005 (−0.0010) | -- -- | −0.0131 (−0.0102) | −0.0114 (−0.0124) | -- -- | −0.0038 (−0.0085) | −0.0050 (−0.0049) | -- -- | 0.0175 (0.0193) | 0.0169 (0.0184) |
| Female Indicator | -- -- | −0.0008 -- | −0.0020 -- | -- -- | −0.0342 -- | −0.0586 -- | -- -- | 0.0520 -- | 0.0858 -- | -- -- | −0.0170 -- | −0.0252 -- |
| Male indicator | −0.0529 (−0.0175) | -- -- | -- -- | 0.5925 (−0.3261) | -- -- | -- -- | −0.3533 (0.3686) | -- -- | -- -- | −0.1863 (−0.0250) | -- -- | -- -- |
| Crash attributes | ||||||||||||
| Passenger car indicator | −0.0001 | 0.0006 (0.0002) | 0.0006 (0.0003) | −0.0014 | 0.0028 (0.0007) | 0.0048 (0.0016) | −0.0008 | 0.0004 (0.0011) | 0.0008 (0.0003) | 0.0024 | −0.0038 (−0.0019) | −0.0062 (−0.0022) |
| Motorcycle indicator | −0.0012 -- | 0.0092 (0.0270) | -- | 0.0080 -- | −0.0722 (−0.0870) | -- | −0.0030 -- | 0.0267 (0.0308) | -- | −0.0038 -- | 0.0363 (0.0292) | |
| Large truck | −0.0003 (−0.0001) | -- (0.0001) | 0.0001 -- | −0.0040 (−0.0016) | -- (0.0001) | 0.0011 -- | 0.0047 (0.0017) | -- (0.0004) | 0.0002 -- | −0.0003 (−0.0001) | -- (−0.0006) | −0.0014 -- |
| Auto-rickshaw indicator | -- (0.0021) | -- -- | -- -- | -- (−0.0016) | -- -- | -- -- | -- (−0.0004) | -- -- | -- -- | -- (−0.0001) | -- -- | -- -- |
| Violation Attributes | ||||||||||||
| Wrong-way indicator | -- (0.0018) | -- -- | -- -- | -- (−0.0052) | -- -- | -- -- | -- -- | -- (0.0025) | -- -- | -- (0.0009) | -- -- | -- -- |
| Distraction indicator | 0.0025 (−0.0061) | −0.0055 (−0.0038) | −0.0055 (−0.0105) | −0.0555 (−0.2093) | 0.0015 (0.0012) | 0.0016 (0.0039) | 0.0147 (−0.0507) | 0.0006 (0.0014) | 0.0010 (0.0017) | 0.0382 (0.2661) | 0.0034 (0.0012) | 0.0029 (0.0049) |
| U-turn indicator | 0.0002 (.0054) | -- (0.0001) | −0.0016 (0.0003) | 0.0010 (−0.0173) | -- (0.0003) | 0.0056 (0.0002) | 0.0007 (0.0088) | -- (0.0004) | −0.0014 (0.0001) | −0.0019 (0.0031) | -- (−0.0007) | −0.0026 (−0.0006) |
| Over-speeding indicator | 0.0027 (−0.0029) | −0.0402 -- | −0.0384 (−0.1287) | 0.0274 (−0.0910) | 0.2110 -- | 0.2490 (0.3260) | 0.0144 (0.0953) | −0.0815 -- | −0.1077 (−0.1361) | −0.0445 (−0.0015) | −0.0894 -- | −0.1029 (−0.0611) |
| Temporal attributes | ||||||||||||
| Off-peak hour indicator | -- (0.0003) | -- -- | -- -- | -- (0.0075) | -- -- | -- -- | -- (0.0020) | -- -- | -- -- | -- (−0.0098) | -- -- | -- -- |
| Weekday indicator | -- (−0.0007) | -- (0.0020) | -- -- | -- (−0.0167) | -- (0.0160) | -- -- | -- (−0.0043) | -- (−0.0293) | -- -- | -- (0.0218) | -- (0.0112) | -- -- |
| Spring indicator | -- -- | -- -- | -- (0.0101) | -- -- | -- -- | -- (−0.0081) | -- -- | -- -- | -- (−0.0014) | -- -- | -- -- | -- (−0.0006) |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global Status Report on Road Safety. World Health Organization. Available online: https://www.who.int/violence_injury_prevention/road_safety_status/2018/en/ (accessed on 28 October 2020).
- Farooq, D.; Moslem, S.; Jamal, A.; Butt, F.M.; Almarhabi, Y.; Faisal Tufail, R.; Almoshaogeh, M. Assessment of Significant Factors Affecting Frequent Lane-Changing Related to Road Safety: An Integrated Approach of the AHP–BWM Model. Int. J. Environ. Res. Public Health 2021, 18, 10628. [Google Scholar] [CrossRef] [PubMed]
- Jamal, A.; Rahman, M.T.; Al-Ahmadi, H.M.; Mansoor, U. The Dilemma of Road Safety in the Eastern Province of Saudi Arabia: Consequences and Prevention Strategies. Int. J. Environ. Res. Public Health 2020, 17, 157. [Google Scholar] [CrossRef] [Green Version]
- Jamal, A.; Zahid, M.; Tauhidur Rahman, M.; Al-Ahmadi, H.M.; Almoshaogeh, M.; Farooq, D.; Ahmad, M. Injury Severity Prediction of Traffic Crashes with Ensemble Machine Learning Techniques: A Comparative Study. Int. J. Inj. Control Saf. Promot. 2021, 28, 408–427. [Google Scholar] [CrossRef] [PubMed]
- Zahid, M.; Chen, Y.; Jamal, A.; Al-Ahmadi, H.M.; Al-Ofi, A.K. Adopting Machine Learning and Spatial Analysis Techniques for Driver Risk Assessment: Insights from a Case Study. Int. J. Environ. Res. Public Health 2020, 17, 5193. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.-R.; Kraus, J.F. A Review of Risk Factors and Patterns of Motorcycle Injuries. Accid. Anal. Prev. 2009, 41, 710–722. [Google Scholar] [CrossRef] [PubMed]
- Ijaz, M.; Lan, L.; Usman, S.M.; Zahid, M.; Jamal, A. Investigation of Factors Influencing Motorcyclist Injury Severity Using Random Parameters Logit Model with Heterogeneity in Means and Variances. Int. J. Crashworthiness 2021, 1–11. [Google Scholar] [CrossRef]
- Ijaz, M.; Lan, L.; Zahid, M.; Jamal, A. A Comparative Study of Machine Learning Classifiers for Injury Severity Prediction of Crashes Involving Three-Wheeled Motorized Rickshaw. Accid. Anal. Prev. 2021, 154, 106094. [Google Scholar] [CrossRef]
- Liu, B.C.; Ivers, R.; Norton, R.; Boufous, S.; Blows, S.; Lo, S.K. Helmets for Preventing Injury in Motorcycle Riders. Cochrane Database Syst. Rev. 2008. [Google Scholar] [CrossRef]
- MacLeod, J.B.; DiGiacomo, J.C.; Tinkoff, G. An Evidence-Based Review: Helmet Efficacy to Reduce Head Injury and Mortality in Motorcycle Crashes: EAST Practice Management Guidelines. J. Trauma Acute Care Surg. 2010, 69, 1101–1111. [Google Scholar] [CrossRef]
- Peek-Asa, C.; McArthur, D.L.; Kraus, J.F. The Prevalence of Non-Standard Helmet Use and Head Injuries among Motorcycle Riders. Accid. Anal. Prev. 1999, 31, 229–233. [Google Scholar] [CrossRef]
- Li, L.-P.; Li, G.-L.; Cai, Q.-E.; Zhang, A.L.; Lo, S.K. Improper Motorcycle Helmet Use in Provincial Areas of a Developing Country. Accid. Anal. Prev. 2008, 40, 1937–1942. [Google Scholar] [CrossRef] [PubMed]
- Conrad, P.; Bradshaw, Y.S.; Lamsudin, R.; Kasniyah, N.; Costello, C. Helmets, Injuries and Cultural Definitions: Motorcycle Injury in Urban Indonesia. Accid. Anal. Prev. 1996, 28, 193–200. [Google Scholar] [CrossRef]
- Jamal, A.; Umer, W. Exploring the Injury Severity Risk Factors in Fatal Crashes with Neural Network. Int. J. Environ. Res. Public Health 2020, 17, 7466. [Google Scholar] [CrossRef]
- Tauhidur Rahman, M.; Jamal, A.; Al-Ahmadi, H.M. Examining Hotspots of Traffic Collisions and Their Spatial Relationships with Land Use: A GIS-Based GeographicallyWeighted Regression Approach for Dammam, Saudi Arabia. ISPRS Int. J. Geo-Inf. 2020, 9, 540. [Google Scholar] [CrossRef]
- Zahid, M.; Chen, Y.; Khan, S.; Jamal, A.; Ijaz, M.; Ahmed, T. Predicting Risky and Aggressive Driving Behavior among Taxi Drivers: Do Spatio-Temporal Attributes Matter? Int. J. Environ. Res. Public Health 2020, 17, 3937. [Google Scholar] [CrossRef]
- Almoshaogeh, M.; Abdulrehman, R.; Haider, H.; Alharbi, F.; Jamal, A.; Alarifi, S.; Shafiquzzaman, M. Traffic Accident Risk Assessment Framework for Qassim, Saudi Arabia: Evaluating the Impact of Speed Cameras. Appl. Sci. 2021, 11, 6682. [Google Scholar] [CrossRef]
- Almadi, A.I.M.; Al Mamlook, R.E.; Almarhabi, Y.; Ullah, I.; Jamal, A.; Bandara, N. A Fuzzy-Logic Approach Based on Driver Decision-Making Behavior Modeling and Simulation. Sustainability 2022, 14, 8874. [Google Scholar] [CrossRef]
- Moslem, S.; Farooq, D.; Jamal, A.; Almarhabi, Y.; Almoshaogeh, M.; Butt, F.M.; Tufail, R.F. An Integrated Fuzzy Analytic Hierarchy Process (AHP) Model for Studying Significant Factors Associated with Frequent Lane Changing. Entropy 2022, 24, 367. [Google Scholar] [CrossRef]
- Jamal, A.; Mahmood, T.; Riaz, M.; Al-Ahmadi, H.M. GLM-Based Flexible Monitoring Methods: An Application to Real-Time Highway Safety Surveillance. Symmetry 2021, 13, 362. [Google Scholar] [CrossRef]
- Al-Ahmadi, H.M.; Jamal, A.; Ahmed, T.; Rahman, M.T.; Reza, I.; Farooq, D. Calibrating the Highway Safety Manual Predictive Models for Multilane Rural Highway Segments in Saudi Arabia. Arab. J. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Ahmed, T.; Moeinaddini, M.; Almoshaogeh, M.; Jamal, A.; Nawaz, I.; Alharbi, F. A New Pedestrian Crossing Level of Service (PCLOS) Method for Promoting Safe Pedestrian Crossing in Urban Areas. Int. J. Environ. Res. Public Health 2021, 18, 8813. [Google Scholar] [CrossRef] [PubMed]
- Ichikawa, M.; Chadbunchachai, W.; Marui, E. Effect of the Helmet Act for Motorcyclists in Thailand. Accid. Anal. Prev. 2003, 35, 183–189. [Google Scholar] [CrossRef]
- Lee, J.M. Mandatory Helmet Legislation as a Policy Tool for Reducing Motorcycle Fatalities: Pinpointing the Efficacy of Universal Helmet Laws. Accid. Anal. Prev. 2018, 111, 173–183. [Google Scholar] [CrossRef] [PubMed]
- Barron, S.; Falank, C.; Ontengco, J.; Chung, B.; Carter, D.W. Severity and Patterns of Injury in Helmeted vs. Non-Helmeted Motorcyclists in a Rural State. J. Saf. Res. 2021, 77, 212–216. [Google Scholar] [CrossRef]
- Alfrey, E.J.; Tracy, M.; Alfrey, J.R.; Carroll, M.; Aranda-Wikman, E.D.; Arora, T.; Maa, J.; Minnis, J. Helmet Usage Reduces Serious Head Injury without Decreasing Concussion after Bicycle Riders Crash. J. Surg. Res. 2021, 257, 593–596. [Google Scholar] [CrossRef]
- Christian, J.M.; Thomas, R.F.; Scarbecz, M. The Incidence and Pattern of Maxillofacial Injuries in Helmeted versus Non-Helmeted Motorcycle Accident Patients. J. Oral Maxillofac. Surg. 2014, 72, 2503–2506. [Google Scholar] [CrossRef]
- Perumal, V.; Gupta, S. Modeling Helmet Usage Behavior of Motorized Two-Wheeler Riders in Developing Countries. Transp. Res. Procedia 2020, 48, 3121–3131. [Google Scholar]
- O’Connor, P.J. Motorcycle Helmets and Spinal Cord Injury: Helmet Usage and Type. Traffic Inj. Prev. 2005, 6, 60–66. [Google Scholar] [CrossRef]
- Jung, S.; Xiao, Q.; Yoon, Y. Evaluation of Motorcycle Safety Strategies Using the Severity of Injuries. Accid. Anal. Prev. 2013, 59, 357–364. [Google Scholar] [CrossRef]
- Ackaah, W.; Afukaar, F.; Agyemang, W.; Anh, T.T.; Hejar, A.R.; Abdul, G.; Gururaj, G.; Elisa, H.-S.; Martha, H.; Hyder, A.A. The Use of Non-Standard Motorcycle Helmets in Low-and Middle-Income Countries: A Multicentre Study. Inj. Prev. 2013, 19, 158–163. [Google Scholar]
- Chalya, P.L.; Ngayomela, I.H.; Mabula, J.B.; Mbelenge, N.; Dass, R.M.; Chandika, A.B.; Gilyoma, J.M.; Ngallaba, S.E.; Kapesa, A. Injury Outcome among Helmeted and Non-Helmeted Motorcycle Riders and Passengers at a Tertiary Care Hospital in North-Western Tanzania. Tanzan. J. Health Res. 2014, 16, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peltzer, K.; Pengpid, S. Helmet Use and Associated Factors among Motorcyclists in the Association of Southeast Asian Nations: Prevalence and Effect of Interventions. Afr. Saf. Promot. A J. Inj. Violence Prev. 2014, 12, 72–86. [Google Scholar]
- Turner, P.A.; Hagelin, C. Motorcycle Helmet Use and Trends before and after Florida’s Helmet Law Change in 2000. Transp. Res. Rec. 2005, 1922, 183–187. [Google Scholar] [CrossRef]
- Blanco, M.; Cabrera, J.; Carozzi, F.; Cid, A. Mandatory Helmet Use and the Severity of Motorcycle Accidents: No Brainer? SSRN 2020, 3753900. [Google Scholar]
- Forbes, A.E.; Schutzer-Weissmann, J.; Menassa, D.A.; Wilson, M.H. Head Injury Patterns in Helmeted and Non-Helmeted Cyclists Admitted to a London Major Trauma Centre with Serious Head Injury. PLoS ONE 2017, 12, e0185367. [Google Scholar] [CrossRef] [Green Version]
- Hundley, J.C.; Kilgo, P.D.; Miller, P.R.; Chang, M.C.; Hensberry, R.A.; Meredith, J.W.; Hoth, J.J. Non-Helmeted Motorcyclists: A Burden to Society? A Study Using the National Trauma Data Bank. J. Trauma Acute Care Surg. 2004, 57, 944–949. [Google Scholar] [CrossRef]
- Frumento, R.J. Motorcycle Trauma: Helmet Use and Effects on Injury Severity; Southern Connecticut State University: New Haven, CT, USA, 1994. [Google Scholar]
- Fong, M.C.; Measelle, J.R.; Dwyer, J.L.; Taylor, Y.K.; Mobasser, A.; Strong, T.M.; Werner, S.; Ouansavanh, S.; Mounmingkham, A.; Kasuavang, M. Rates of Motorcycle Helmet Use and Reasons for Non-Use among Adults and Children in Luang Prabang, Lao People’s Democratic Republic. BMC Public Health 2015, 15, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Olsen, C.S.; Thomas, A.M.; Singleton, M.; Gaichas, A.M.; Smith, T.J.; Smith, G.A.; Peng, J.; Bauer, M.J.; Qu, M.; Yeager, D. Motorcycle Helmet Effectiveness in Reducing Head, Face and Brain Injuries by State and Helmet Law. Inj. Epidemiol. 2016, 3, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ding, C.; Rizzi, M.; Strandroth, J.; Sander, U.; Lubbe, N. Motorcyclist Injury Risk as a Function of Real-Life Crash Speed and Other Contributing Factors. Accid. Anal. Prev. 2019, 123, 374–386. [Google Scholar] [CrossRef]
- Chen, P.-L.; Pai, C.-W. Evaluation of Injuries Sustained by Motorcyclists in Approach-Turn Crashes in Taiwan. Accid. Anal. Prev. 2019, 124, 33–39. [Google Scholar] [CrossRef]
- Wiratama, B.S.; Chen, P.-L.; Ma, S.-T.; Chen, Y.-H.; Saleh, W.; Lin, H.-A.; Pai, C.-W. Evaluating the Combined Effect of Alcohol-Involved and Un-Helmeted Riding on Motorcyclist Fatalities in Taiwan. Accid. Anal. Prev. 2020, 143, 105594. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.; Cernicchi, A.; Kleiven, S.; Halldin, P. High-Speed Helmeted Head Impacts in Motorcycling: A Computational Study. Accid. Anal. Prev. 2020, 134, 105297. [Google Scholar] [CrossRef] [PubMed]
- Khor, D.; Inaba, K.; Aiolfi, A.; Delapena, S.; Benjamin, E.; Matsushima, K.; Strumwasser, A.M.; Demetriades, D. The Impact of Helmet Use on Outcomes after a Motorcycle Crash. Injury 2017, 48, 1093–1097. [Google Scholar] [CrossRef]
- Chang, F.; Xu, P.; Zhou, H.; Chan, A.H.S.; Huang, H. Investigating Injury Severities of Motorcycle Riders: A Two-Step Method Integrating Latent Class Cluster Analysis and Random Parameters Logit Model. Accid. Anal. Prev. 2019, 131, 316–326. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y. An Application of In-Vehicle Recording Technologies to Analyze Injury Severity in Crashes between Taxis and Two-Wheelers. Accid. Anal. Prev. 2022, 166, 106541. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Ro, Y.S.; Shin, S.D.; Song, K.J.; Hong, K.J.; Jeong, J. Preventive Effects of Motorcycle Helmets on Intracranial Injury and Mortality from Severe Road Traffic Injuries. Am. J. Emerg. Med. 2018, 36, 173–178. [Google Scholar] [CrossRef]
- Ramli, R.; Oxley, J.; Noor, F.M.; Abdullah, N.K.; Mahmood, M.S.; Tajuddin, A.K.; McClure, R. Fatal Injuries among Motorcyclists in Klang Valley, Malaysia. J. Forensic Leg. Med. 2014, 26, 39–45. [Google Scholar] [CrossRef]
- Brown, C.V.R.; Hejl, K.; Bui, E.; Tips, G.; Coopwood, B. Risk Factors for Riding and Crashing a Motorcycle Unhelmeted. J. Emerg. Med. 2011, 41, 441–446. [Google Scholar] [CrossRef]
- Houston, D.J.; Richardson, L.E. Motorcyclist Fatality Rates and Mandatory Helmet-Use Laws. Accid. Anal. Prev. 2008, 40, 200–208. [Google Scholar] [CrossRef]
- Milton, J.C.; Shankar, V.N.; Mannering, F.L. Highway Accident Severities and the Mixed Logit Model: An Exploratory Empirical Analysis. Accid. Anal. Prev. 2008, 40, 260–266. [Google Scholar] [CrossRef]
- Eluru, N.; Bhat, C.R.; Hensher, D.A. A Mixed Generalized Ordered Response Model for Examining Pedestrian and Bicyclist Injury Severity Level in Traffic Crashes. Accid. Anal. Prev. 2008, 40, 1033–1054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morgan, A.; Mannering, F.L. The Effects of Road-Surface Conditions, Age, and Gender on Driver-Injury Severities. Accid. Anal. Prev. 2011, 43, 1852–1863. [Google Scholar] [CrossRef]
- Anastasopoulos, P.C.; Mannering, F.L. An Empirical Assessment of Fixed and Random Parameter Logit Models Using Crash-and Non-Crash-Specific Injury Data. Accid. Anal. Prev. 2011, 43, 1140–1147. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-K.; Ulfarsson, G.F.; Kim, S.; Shankar, V.N. Driver-Injury Severity in Single-Vehicle Crashes in California: A Mixed Logit Analysis of Heterogeneity Due to Age and Gender. Accid. Anal. Prev. 2013, 50, 1073–1081. [Google Scholar] [CrossRef] [PubMed]
- Venkataraman, N.; Ulfarsson, G.F.; Shankar, V.N. Random Parameter Models of Interstate Crash Frequencies by Severity, Number of Vehicles Involved, Collision and Location Type. Accid. Anal. Prev. 2013, 59, 309–318. [Google Scholar] [CrossRef]
- Islam, M.; Mannering, F. A Temporal Analysis of Driver-Injury Severities in Crashes Involving Aggressive and Non-Aggressive Driving. Anal. Methods Accid. Res. 2020, 27, 100128. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F.L. The Temporal Stability of Factors Affecting Driver-Injury Severities in Single-Vehicle Crashes: Some Empirical Evidence. Anal. Methods Accid. Res. 2015, 8, 7–32. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. Determinants of Bicyclist Injury Severities in Bicycle-Vehicle Crashes: A Random Parameters Approach with Heterogeneity in Means and Variances. Anal. Methods Accid. Res. 2017, 16, 35–47. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. The Effect of Passengers on Driver-Injury Severities in Single-Vehicle Crashes: A Random Parameters Heterogeneity-in-Means Approach. Anal. Methods Accid. Res. 2017, 14, 41–53. [Google Scholar] [CrossRef]
- Alnawmasi, N.; Mannering, F. A Statistical Assessment of Temporal Instability in the Factors Determining Motorcyclist Injury Severities. Anal. Methods Accid. Res. 2019, 22, 100090. [Google Scholar] [CrossRef]
- Seraneeprakarn, P.; Huang, S.; Shankar, V.; Mannering, F.; Venkataraman, N.; Milton, J. Occupant Injury Severities in Hybrid-Vehicle Involved Crashes: A Random Parameters Approach with Heterogeneity in Means and Variances. Anal. Methods Accid. Res. 2017, 15, 41–55. [Google Scholar] [CrossRef]
- Waseem, M.; Ahmed, A.; Saeed, T.U. Factors Affecting Motorcyclists’ Injury Severities: An Empirical Assessment Using Random Parameters Logit Model with Heterogeneity in Means and Variances. Accid. Anal. Prev. 2019, 123, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Washington, S.; Karlaftis, M.G.; Mannering, F.; Anastasopoulos, P. Statistical and Econometric Methods for Transportation Data Analysis; CRC Press: Boca Raton, FL, USA, 2020; ISBN 0429534221. [Google Scholar]
- McFadden, D. Econometric Models of Probabilistic Choice. Struct. Anal. Discret. Data Econom. Appl. 1981, 198272. [Google Scholar]
- Bhat, C.R. Simulation Estimation of Mixed Discrete Choice Models Using Randomized and Scrambled Halton Sequences. Transp. Res. Part B Methodol. 2003, 37, 837–855. [Google Scholar] [CrossRef] [Green Version]
- Train, K. Halton Sequences for Mixed Logit; University of California: Berkeley, CA, USA, 2000. [Google Scholar]
- Anastasopoulos, P.C.; Mannering, F.L. A Note on Modeling Vehicle Accident Frequencies with Random-Parameters Count Models. Accid. Anal. Prev. 2009, 41, 153–159. [Google Scholar] [CrossRef]
- Savolainen, P.T. Examining Driver Behavior at the Onset of Yellow in a Traffic Simulator Environment: Comparisons between Random Parameters and Latent Class Logit Models. Accid. Anal. Prev. 2016, 96, 300–307. [Google Scholar] [CrossRef]
- Shaheed, M.S.B.; Gkritza, K.; Zhang, W.; Hans, Z. A Mixed Logit Analysis of Two-Vehicle Crash Severities Involving a Motorcycle. Accid. Anal. Prev. 2013, 61, 119–128. [Google Scholar] [CrossRef]
- Siddiqui, A.W.; Raza, S.A.; Elahi, M.A.; Minhas, K.S.; Butt, F.M. Temporal Impacts of Road Safety Interventions: A Structural-Shifts-Based Method for Road Accident Mortality Analysis. Accid. Anal. Prev. 2022, 174, 106767. [Google Scholar] [CrossRef]
- Mannering, F. Temporal Instability and the Analysis of Highway Accident Data. Anal. Methods Accid. Res. 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. Time-of-Day Variations and Temporal Instability of Factors Affecting Injury Severities in Large-Truck Crashes. Anal. Methods Accid. Res. 2019, 23, 100102. [Google Scholar] [CrossRef]
- Islam, M.; Alnawmasi, N.; Mannering, F. Unobserved Heterogeneity and Temporal Instability in the Analysis of Work-Zone Crash-Injury Severities. Anal. Methods Accid. Res. 2020, 28, 100130. [Google Scholar] [CrossRef]
- Mannering, F.L.; Grodsky, L.L. Statistical Analysis of Motorcyclists’ Perceived Accident Risk. Accid. Anal. Prev. 1995, 27, 21–31. [Google Scholar] [CrossRef]
- Talving, P.; Teixeira, P.G.; Barmparas, G.; DuBose, J.; Preston, C.; Inaba, K.; Demetriades, D. Motorcycle-Related Injuries: Effect of Age on Type and Severity of Injuries and Mortality. J. Trauma Acute Care Surg. 2010, 68, 441–446. [Google Scholar] [CrossRef] [PubMed]
- Geedipally, S.R.; Turner, P.A.; Patil, S. Analysis of Motorcycle Crashes in Texas with Multinomial Logit Model. Transp. Res. Rec. 2011, 2265, 62–69. [Google Scholar] [CrossRef]
- Savolainen, P.; Mannering, F. Probabilistic Models of Motorcyclists’ Injury Severities in Single-and Multi-Vehicle Crashes. Accid. Anal. Prev. 2007, 39, 955–963. [Google Scholar] [CrossRef]
- Pervez, A.; Lee, J.; Huang, H.; Zhai, X. What Factors Would Make Single-Vehicle Motorcycle Crashes Fatal? Empirical Evidence from Pakistan. Int. J. Environ. Res. Public Health 2022, 19, 5813. [Google Scholar] [CrossRef]
- Khan, U.; Zia, N.; Awan, S.; Khan, A. SP5-27 Perception of Pakistani Women Pillion Riders about Helmet Use: A Qualitative Study. J. Epidemiol. Community Health 2011, 65, A452. [Google Scholar] [CrossRef] [Green Version]
- Siddiqui, A.A.; Shamim, M.S.; Jooma, R.; Enam, A. Long Scarf Injuries. J. Coll. Physicians Surg.-Pak. JCPSP 2006, 16, 152–153. [Google Scholar]
- Evans, L. Traffic Safety and the Driver; Science Serving Society: Bloomfield Hills, MI, USA, 1991. [Google Scholar]
- Ahmad, N.; Ahmed, A.; Wali, B.; Saeed, T.U. Exploring Factors Associated with Crash Severity on Motorways in Pakistan. In Proceedings of the Institution of Civil Engineers-Transport; Thomas Telford Ltd.: London, UK, 2022; Volume 175, pp. 189–198. [Google Scholar]
- Traffic Safety Facts National Highway Traffic Safety Adminastration Traffic Safety Facts 2019. Available online: https://www.nhtsa.gov/risky-driving/distracted-driving (accessed on 15 June 2021).
- Se, C.; Champahom, T.; Jomnonkwao, S.; Chaimuang, P.; Ratanavaraha, V. Empirical Comparison of the Effects of Urban and Rural Crashes on Motorcyclist Injury Severities: A Correlated Random Parameters Ordered Probit Approach with Heterogeneity in Means. Accid. Anal. Prev. 2021, 161, 106352. [Google Scholar] [CrossRef]
| Methodology Adopted | Previous Research |
|---|---|
| Logistic regression | [41,42,43] |
| Finite element head model | [44] |
| Univariate analysis and multiple logistic regression | [45] |
| Latent class cluster and random parameters logit model | [46] |
| Student’s t-test and Pearson’s χ2 p-value | [25] |
| Partial proportional odds model | [47] |
| Cross-sectional observational study | [48,49] |
| Retrospective study | [25,50] |
| Fixed effects regression models | [51] |
| Variable | 2017 | 2018 | 2019 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Helmet | No Helmet | Helmet | No Helmet | Helmet | No Helmet | |||||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | |
| Roadway Attributes | ||||||||||||
| Major arterial indicator (1 if crash occurred on major arterial, 0 otherwise) | 0.597 | 0.490 | 0.640 | 0.479 | 0.590 | 0.496 | 0.607 | 0.488 | 0.209 | 0.497 | 0.523 | 0.499 |
| Lane 2 indicator (1 if crash occurred on two lanes each side road, 0 otherwise) | 0.212 | 0.409 | 0.166 | 0.372 | 0.166 | 0.372 | 0.158 | 0.365 | 0.152 | 0.359 | 0.143 | 0.350 |
| Local road indicator (1 if crash occurred on local road, 0 otherwise) | 0.054 | 0.226 | 0.059 | 0.236 | 0.044 | 0.205 | 0.046 | 0.249 | 0.046 | 0.241 | 0.046 | 0.210 |
| Collector road indicator (1 if crash occurred on collector road, 0 otherwise) | 0.142 | 0.349 | 0.119 | 0.324 | 0.154 | 0.361 | 0.144 | 0.353 | 0.195 | 0.396 | 0.219 | 0.414 |
| Speed: 60 kmph indicator (1 if crash occurred at a road with speed limit 60 kmph, 0 otherwise) | 0.645 | 0.478 | 0.674 | 0.468 | 0.697 | 0.459 | 0.690 | 0.462 | 0.747 | 0.434 | 0.722 | 0.447 |
| Violation Attributes | ||||||||||||
| Wrong-way indicator (1 if crash occurred while riding the wrong way, 0 otherwise) | 0.005 | 0.076 | 0.009 | 0.095 | 0.010 | 0.101 | 0.012 | 0.109 | 0.019 | 0.139 | 0.010 | 0.100 |
| Distraction indicator (1 if crash occurred due to distraction, 0 otherwise) | 0.272 | 0.445 | 0.269 | 0.448 | 0.245 | 0.430 | 0.231 | 0.421 | 0.236 | 0.425 | 0.215 | 0.410 |
| U-turn indicator (1 if crash occurred on U-turn, 0 otherwise) | 0.030 | 0.172 | 0.032 | 0.176 | 0.027 | 0.162 | 0.032 | 0.176 | 0.033 | 0.179 | 0.046 | 0.211 |
| Over-speeding indicator (1 if crash occurred due to over-speeding, 0 otherwise) | 0.690 | 0.462 | 0.688 | 0.430 | 0.716 | 0.450 | 0.724 | 0.446 | 0.709 | 0.453 | 0.727 | 0.445 |
| Rider attributes | ||||||||||||
| Between 20–30 years indicator (1 if motorcyclist’s age lies between 20 and 30 years, 0 otherwise) | 0.354 | 0.478 | 0.397 | 0.489 | 0.377 | 0.484 | 0.395 | 0.485 | 0.361 | 0.480 | 0.350 | 0.477 |
| Male indicator (1 if motorcyclist was male, 0 otherwise) | 0.877 | 0.328 | 0.865 | 0.341 | 0.822 | 0.322 | 0.832 | 0.343 | 0.867 | 0.331 | 0.878 | 0.324 |
| Below 20 years indicator (1 if motorcyclist’s age is below 20 years, 0 otherwise) | 0.208 | 0.411 | - | - | 0.185 | 0.388 | 0.210 | 0.407 | 0.203 | 0.402 | 0.263 | 0.440 |
| Between 40–50 indicator (1 if motorcyclist’s age lies between 40–50 years, 0 otherwise) | 0.226 | 0.418 | 0.103 | 0.304 | 0.118 | 0.323 | 0.107 | 0.310 | 0.118 | 0.322 | 0.101 | 0.302 |
| Crash Attributes | ||||||||||||
| Large truck indicator (1 if crash occurred with truck, 0 otherwise) | 0.059 | 0.236 | 0.019 | 0.143 | 0.060 | 0.238 | 0.022 | 0.147 | 0.815 | 0.387 | 0.013 | 0.118 |
| Motorcycle indicator (1 if two motorcycles collided with each other, 0 otherwise) | 0.132 | 0.339 | 0.142 | 0.349 | 0.141 | 0.348 | 0.157 | 0.364 | 0.056 | 0.230 | 0.832 | 0.378 |
| Passenger car indicator (1 if crash occurred with passenger car, 0 otherwise) | 0.165 | 0.371 | 0.169 | 0.375 | 0.162 | 0.368 | 0.166 | 0.372 | 0.164 | 0.370 | 0.177 | 0.382 |
| Auto-rickshaw indicator (1 if crash occurred with auto-rickshaw, 0 otherwise) | 0.724 | 0.236 | 0.041 | 0.198 | 0.040 | 0.197 | 0.049 | 0.217 | 0.041 | 0.199 | 0.052 | 0.223 |
| Temporal Attributes | ||||||||||||
| Weekday indicator (1 if crash occurred on weekday, 0 otherwise) | 0.711 | 0.452 | 0.718 | 0.449 | 0.708 | 0.454 | 0.709 | 0.451 | 0.717 | 0.450 | 0.720 | 0.448 |
| Weekend indicator (1 if crash occurred on weekend, 0 otherwise) | 0.288 | 0.452 | 0.281 | 0.449 | 0.291 | 0.454 | 0.209 | 0.454 | 0.282 | 0.450 | 0.279 | 0.448 |
| Off-peak hour indicator (1 if crash occurred in off-peak hours, 0 otherwise) | 0.494 | 0.499 | 0.500 | 0.500 | 0.501 | 0.500 | 0.512 | 0.499 | 0.508 | 0.499 | 0.504 | 0.499 |
| Spring indicator (1 if crash occurred in spring season, 0 otherwise) | 0.158 | 0.365 | 0.171 | 0.376 | 0.170 | 0.376 | 0.157 | 0.363 | 0.152 | 0.359 | 0.164 | 0.371 |
| Model Goodness of Fit Values | Model for Motorcyclists Wearing Helmet | Model for Motorcyclists Not Wearing Helmet |
|---|---|---|
| Log-likelihood at convergence of overall model LL(β2017–2019) | −4025.185 | −13,641.844 |
| Log-likelihood at convergence of 2017 model LL(β2017) | −1199.931 | −3477.439 |
| Log-likelihood at convergence of 2018 model LL(β2018) | −1258.448 | −4151.247 |
| Log-likelihood at convergence of 2019 model LL(β2019) | −1477.467 | −5942.630 |
| χ2 Value | 178.68 | 141.06 |
| Degrees of Freedom | 22 | 26 |
| Level of Confidence | 99% | 99% |
| Critical χ2 value | 40.29 | 45.64 |
| Conclusion | Temporally unstable | Temporally unstable |
| t1 | t2 | ||
|---|---|---|---|
| 2017 | 2018 | 2019 | |
| 2017 | - | 1583.938 (12) [>99%] | 728.024 (14) [>99%] |
| 2018 | 198.152 (17) [>99%] | - | 83.33 (14) [>99%] |
| 2019 | 305.584 (17) [>99%] | 25.402 (12) [>99%] | - |
| t1 | t2 | ||
|---|---|---|---|
| 2017 | 2018 | 2019 | |
| 2017 | - | 1738.202 (15) [>99%] | 1446.054 (14) [>99%] |
| 2018 | 1859.062 (19) [>99%] | - | 121.158 (14) [>99%] |
| 2019 | 9360.034 (19) [>99%] | 4870.566 (15) [>99%] | - |
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [MI] | −1.536 | −2.84 | ||||
| Constant [SI] | 1.526 | 8.81 | ||||
| Constant [FI] | 3.267 | 14.71 | ||||
| Random parameter (normally distributed) | ||||||
| Major arterial [FI] | 0.367 | 1.87 | −0.0009 | −0.0167 | −0.0046 | 0.0222 |
| Heterogeneity in the mean of the random parameter | ||||||
| Large truck (1 if a crash occurred with a truck, 0 otherwise) [SI] | −1.783 | −2.37 | ||||
| Heterogeneity in variance of the random parameter | ||||||
| Between 20–30 years (1 if motorcyclist’s age lies between 20 and 30 years, 0 otherwise) [SI] | 0.581 | 1.91 | ||||
| Roadway Attributes | ||||||
| Lane 2 indicator (1 if a crash occurred on two-lane each side road, 0 otherwise) [NI] | −1.736 | −2.38 | −0.0017 | 0.0009 | 0.0005 | 0.0003 |
| Collector road (1 if an accident happened on a collector road, 0 in any case) [SI] | −0.672 | −2.47 | 0.0007 | 0.0041 | −0.0065 | 0.0017 |
| Rider Attributes | ||||||
| Between 20–30 years indicator ( 1 if motorcyclists age is between 20 and 30, 0 otherwise) [FI] | −1.292 | −5.62 | 0.0016 | 0.0118 | 0.0008 | −0.0214 |
| Below 20 years indicator (1 if that motorcyclist’s age is under 20 years, 0 in any case) [SI] | 0.75 | 4.38 | −0.0006 | −0.0159 | 0.0208 | −0.0043 |
| Male rider (1 if a male rider was involved in crash only, 0 otherwise) [MI] | 5.487 | 10.44 | −0.0529 | 0.5925 | −0.3533 | −0.1863 |
| Crash Attributes | ||||||
| Passenger car indicator (1 if an accident happened with a Passenger car, 0 otherwise) [FI] | −1.851 | −2.96 | −0.0001 | −0.0014 | −0.0008 | 0.0024 |
| Large Truck indicator (1 if an accident happened with a truck, 0 in any case) [SI] | 0.584 | 2.09 | −0.0003 | −0.0004 | 0.0047 | −0.0003 |
| Violation Attributes | ||||||
| Distraction indicator (1 if an accident happened due to distraction, 0 otherwise) [MI] | −1.481 | −8.03 | 0.0025 | −0.0555 | 0.0147 | 0.0382 |
| U-Turn indicator (1 if an accident happened at U-turn, 0 otherwise) [FI] | −4.147 | −4.01 | 0.0002 | 0.0001 | 0.0007 | −0.0019 |
| Over-speeding indicator (1 if an accident happened due to over-speeding, 0 otherwise) [FI] | −3.685 | −9.67 | 0.0027 | 0.0274 | 0.0144 | −0.0445 |
| Number of observations | 2045 | |||||
| Number of parameters | 17 | |||||
| Log-likelihood at zero | −2834.971 | |||||
| Log-likelihood at convergence | −1199.931 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.576 | |||||
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [FI] | 0.886 | 8.41 | ||||
| Random parameter (normally distributed) | ||||||
| Weekday indicator [SI] | −3.72 | −6.94 | −0.0005 | −0.0263 | 0.0204 | 0.0064 |
| Heterogeneity in the mean of the random parameter | ||||||
| Above 50 years indicator (1 if motorcyclist’s age is above 50 years, 0 otherwise) [FI] | −1.353 | −1.71 | ||||
| Heterogeneity in the variance of random parameter | ||||||
| Passenger car indicator (1 if an accident happened with a passenger car, 0 otherwise) [FI] | 0.201 | 1.78 | ||||
| Rider Attributes | ||||||
| Female indicator (1 if pillion rider involved was female, 0 otherwise) [SI] | 5.539 | 22.37 | −0.0008 | −0.0342 | 0.0052 | −0.017 |
| Below 20 years indicator (1 if motorcyclist’s age is under 20 years, 0 otherwise) [SI] | 1.13 | 4.71 | −0.0004 | −0.0078 | 0.0116 | −0.0033 |
| Above 50 years indicator (1 if motorcyclist’s age is above 50 years, 0 otherwise) [FI] | 1.505 | 5.33 | −0.0006 | −0.0131 | −0.0038 | 0.0175 |
| Crash Attributes | ||||||
| Motorcycle indicator (1 if two motorcyclists collide with each other, 0 otherwise) [MI] | 0.952 | 2.99 | −0.0012 | 0.0008 | −0.0003 | −0.0038 |
| Passenger car indicator (1 if an accident happened with a passenger car, 0 otherwise) [FI] | −3.057 | −5.33 | 0.0006 | 0.0028 | 0.0004 | −0.0038 |
| Violation Attributes | ||||||
| Distraction indicator (1 if an accident happened due to distraction, 0 otherwise) [NI] | −3.198 | −6.3 | −0.0055 | 0.0015 | 0.0006 | 0.0034 |
| Over-speeding indicator (1 if an accident happened due to over-speeding, 0 otherwise) [MI] | 3.825 | 25.48 | −0.0402 | 0.211 | −0.0815 | −0.0894 |
| Number of observations | 2095 | |||||
| Number of parameters | 12 | |||||
| Log-probability at zero | −2904.287 | |||||
| Log-probability at union | −1258.448 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.567 | |||||
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [MI] | 1.262 | 5.71 | ||||
| Constant [FI] | 1.248 | 9.29 | ||||
| Random parameter (normally distributed) | ||||||
| Below 20-year indicator [SI] | −1.861 | −3.17 | −0.0009 | −0.0326 | 0.0345 | −0.0011 |
| Heterogeneity in the mean of the random parameter | ||||||
| Over-speeding indicator (1 if a crash occurred due to over-speeding, 0 otherwise) [MI] | 3.439 | 6.45 | ||||
| Heterogeneity in the variance of the random parameter | ||||||
| Distraction indicator (1 if a crash occurred due to distraction, 0 otherwise) [NI] | 0.883 | 1.78 | ||||
| Rider Attributes | ||||||
| Female (1 on the off chance that pillion rider included was female, 0 otherwise) [SI] | 3.63 | 23.94 | −0.002 | −0.0586 | 0.0858 | −0.0252 |
| Above 50 years indicator (1 if motorcyclist’s age is above 50 years, 0 otherwise) [FI] | 0.929 | 5.14 | −0.0005 | −0.0114 | −0.005 | 0.0169 |
| Crash Attributes | ||||||
| Motorcycle indicator (1 if two motorcycles collide with each other, 0 otherwise) [MI] | −0.617 | −3.49 | 0.0092 | −0.0722 | 0.0267 | 0.0363 |
| Passenger car (1 if a crash occurred with a passenger car, 0 otherwise) [FI] | −2.44 | −5.82 | 0.0006 | 0.0048 | 0.0008 | −0.0062 |
| Large truck (1 if a crash occurred with a truck, 0 otherwise) [MI] | −3.259 | −3.28 | 0.0001 | 0.0011 | 0.0002 | −0.0014 |
| Violation Attributes | ||||||
| U-turn indicator (1 if crash occurred at U-turn, 0 otherwise) [MI] | 0.738 | 2.61 | −0.0016 | 0.0056 | −0.0014 | −0.0026 |
| Over-speeding indicator (1 if a crash occurred due to over-speeding, 0 otherwise) [MI] | 2.801 | 17.89 | −0.0384 | 0.0249 | −0.1077 | −0.1029 |
| Distraction indicator (1 if a crash occurred due to distraction, 0 otherwise) [NI] | −2.516 | −5.4 | −0.0055 | 0.0016 | 0.0001 | 0.0029 |
| Number of perceptions | 2262 | |||||
| Number of parameters | 14 | |||||
| Log-likelihood at zero | −3135.797 | |||||
| Log-likelihood at convergence | −1477.467 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.528 | |||||
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [MI] | 3.369 | 24.73 | ||||
| Constant [SI] | 4.769 | 23.9 | ||||
| Constant [FI] | −0.831 | −3.9 | ||||
| Random parameter (normally distributed) | ||||||
| Peak hour indicator [SI] | −0.659 | −3.92 | 0.0000 | −0.0016 | 0.0045 | −0.003 |
| Heterogeneity in the mean of the random parameter | ||||||
| Between 20–30 years indicator (1 if motorcyclist’s age is between 20 and 30 years, 0 otherwise) [MI] | 0.533 | 3.33 | ||||
| Heterogeneity in the variance of the random parameter | ||||||
| Over-speeding indicator (1 if a crash occurred due to over-speeding, 0 otherwise] [SI] | −0.726 | −2.59 | ||||
| Rider Attributes | ||||||
| Between 20–30 years indicator (1 if motorcyclist’s age lies b/w 20 and 30 years, 0 otherwise) [MI] | 0.534 | 6.14 | −0.0003 | 0.0328 | −0.019 | −0.0108 |
| Between 40–50 years indicator (1 if motorcyclist’s age lies b/w 40 and 50 years, 0 in any case) [FI] | 0.518 | 3.08 | −0.0002 | −0.0029 | −0.0011 | 0.0042 |
| Male indicator (1 if a male rider was involved in crash, 0 otherwise) | −4.097 | −24.31 | 0.0175 | 0.3261 | 0.3686 | 0.025 |
| Roadway attributes | ||||||
| Lane 3 indicator (1 if a crash happened on 3 lane road, 0 otherwise) [SI] | 0.196 | 2.04 | −0.0007 | −0.0123 | 0.0149 | −0.0019 |
| Crash Attributes | ||||||
| Auto-rickshaw indicator (1 if a crash happened with auto-cart, 0 otherwise) [NI] | 0.936 | 2.79 | 0.0021 | −0.0016 | −0.0004 | −0.0001 |
| Large truck indicator (1 if an accident happened with a truck, 0 otherwise) [SI] | 0.571 | 2.22 | −0.0001 | −0.0016 | 0.0017 | −0.0001 |
| Violation Attributes | ||||||
| Wrong-way indicator (1 if an accident happened the wrong way, 0 otherwise) [MI] | −3.346 | −9.32 | 0.0018 | −0.0052 | 0.0025 | 0.0009 |
| Distraction indicator (1 if an accident happened due to distraction, 0 otherwise) [FI] | 4.48 | 30.68 | −0.0061 | −0.2093 | −0.0507 | 0.2661 |
| U-turn indicator (1 if an accident happened at U-turn, 0 otherwise) [MI] | −2.596 | −12.88 | 0.0054 | −0.0173 | 0.0088 | 0.0031 |
| Over-speeding indicator (1 if an accident happened due to over-speeding, 0 otherwise) [SI] | 1.163 | 8.32 | −0.0029 | −0.091 | 0.0953 | −0.0015 |
| Temporal Attributes | ||||||
| Off-peak hour indicator (1 if an accident happened in off-peak hours, 0 otherwise) [FI] | −0.29 | −2.61 | 0.0003 | 0.0075 | 0.0002 | −0.0098 |
| Weekday indicator (1 if an accident happened on a weekday, 0 otherwise) [FI] | 0.418 | 3.59 | −0.0007 | −0.0167 | −0.0043 | 0.0218 |
| Number of observations | 5067 | |||||
| Number of parameters | 19 | |||||
| Log-likelihood at zero | −7024.353 | |||||
| Log-likelihood at convergence | −3477.439 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.504 | |||||
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [MI] | 1.663 | 13.01 | ||||
| Constant [SI] | 1.981 | 13.5 | ||||
| Constant [FI] | 1.509 | 11.27 | ||||
| Random parameter (normally distributed) | ||||||
| Over-speeding indicator [MI] | 5.085 | 3.64 | −0.0044 | 0.0581 | −0.0325 | −0.0212 |
| Heterogeneity in the mean of the random parameter | ||||||
| Below-20 years indicator (1 if motorcyclist’s age lies below 20 years, 0 otherwise) [SI] | −1.184 | −2.14 | ||||
| Heterogeneity in the variance of the random parameter | ||||||
| Large truck indicator (1 if a truck was involved in a crash, 0 otherwise) [FI] | 0.527 | 2.28 | ||||
| Roadway attributes | ||||||
| Lane 2 indicator (1 if a crash occurred on 2 lane road, 0 otherwise) [NI] | −1.412 | −2.71 | −0.0010 | 0.0003 | 0.0005 | 0.0002 |
| Rider Attributes | ||||||
| Below-20 years indicator (1 if motorcyclist’s age lies below 20 years, 0 otherwise) [SI] | 0.585 | 4.69 | −0.0010 | −0.0087 | 0.0153 | −0.0056 |
| Above 50 years indicator (1 if motorcyclist’s age is above 50 years, 0 otherwise) [FI] | 1.538 | 10.23 | −0.0006 | −0.0102 | −0.0085 | 0.0193 |
| Crash Attributes | ||||||
| Passenger car indicator (1 if an accident happened with a passenger car, 0 otherwise) [FI] | −3.824 | −6.57 | 0.0002 | 0.0007 | 0.0011 | −0.0019 |
| Large truck indicator (1 if a large truck is involved in a crash, 0 otherwise) [FI] | −3.419 | −3.25 | 0.0001 | 0.0001 | 0.0004 | −0.0006 |
| Violation Attributes | ||||||
| Distraction indicator (1 if a crash occurred due to distraction, 0 otherwise) [NI] | −1.516 | −5.11 | −0.0038 | 0.0012 | 0.0014 | 0.0012 |
| U-turn indicator (1 if crash occurred at U-turn, 0 otherwise) [FI] | −4.151 | −4.14 | 0.0001 | 0.0003 | 0.0004 | −0.0007 |
| Temporal Attributes | ||||||
| Weekday indicator (1 if an accident happened during non-weekend days, 0 otherwise) [SI] | 0.399 | 4.24 | 0.002 | 0.016 | −0.0293 | 0.0112 |
| Number of observations | 5566 | |||||
| Number of parameters | 15 | |||||
| Log-likelihood at zero | −7716.114 | |||||
| Log-likelihood at convergence | −4151.247 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.458 | |||||
| Variables | Parameter Estimates | t-Stats | Marginal Effects | |||
|---|---|---|---|---|---|---|
| No Injury | Minor Injury | Severe Injury | Fatal Injury | |||
| Constant [FI] | −0.542 | −7.54 | ||||
| Random parameter (normally distributed) | ||||||
| Weekday indicator [SI] | −3.211 | −5 | −0.0034 | −0.0396 | 0.0397 | 0.0033 |
| Heterogeneity in the mean of the random parameter | ||||||
| Over-speeding indicator (1 if a crash happened due to over-speeding, 0 otherwise) [MI] | 2.096 | 10.82 | ||||
| Heterogeneity in the variance of the random parameter | ||||||
| U-turn indicator (1 if a crash occurred at U-turn, 0 otherwise) [FI] | 0.314 | 2.08 | ||||
| Roadway attributes | ||||||
| Collector road indicator ( 1 if a crash occurred on collector road, 0 otherwise) [MI] | −0.23 | −3.1 | 0.0027 | −0.0082 | 0.0029 | 0.0026 |
| Rider Attributes | ||||||
| Below 20 years indicator (1 if motorcyclist’s age is below 20 years, 0 otherwise) [SI] | 0.705 | 7.44 | −0.002 | −0.0131 | 0.0177 | −0.0026 |
| Above 50 years indicator (1 if motorcyclist’s age is above 50 years, 0 otherwise) [FI] | 1.385 | 9.79 | −0.001 | −0.0124 | −0.0049 | 0.0184 |
| Crash Attributes | ||||||
| Passenger car indicator (1 if an accident happened with a passenger car, 0 otherwise) [FI] | −2.404 | −6.21 | 0.0003 | 0.0016 | 0.0003 | −0.0022 |
| Motorcycle indicator (1 if two motorcyclists collide with each other, 0 otherwise) [MI] | −0.639 | −10.05 | 0.027 | −0.087 | 0.0308 | 0.0292 |
| Violation Attributes | ||||||
| U-turn indicator (1 if crash occurred at U-turn, 0 otherwise) [FI] | −4.389 | −4.39 | 0.0003 | 0.0002 | 0.0001 | −0.0006 |
| Over-speeding indicator (1 if a crash occurred due to over-speeding, 0 otherwise) [MI] | 3.094 | 46.33 | −0.1287 | 0.326 | −0.1361 | −0.0611 |
| Distraction indicator (1 if a crash occurred due to distraction, 0 otherwise) [NI] | −4.041 | −16.97 | −0.0105 | 0.0039 | 0.0017 | 0.0049 |
| Temporal Attributes | ||||||
| Spring indicator (1 if a crash happened in the spring season, 0 otherwise ) [NI] | 0.675 | 6.51 | 0.0101 | −0.0081 | −0.0014 | −0.006 |
| Number of observations | 7202 | |||||
| Number of parameters | 14 | |||||
| Log-likelihood at zero | −9984.092 | |||||
| Log-likelihood at convergence | −5942.63 | |||||
| ρ2 = 1 − LL(β)/LL(0) | 0.405 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ijaz, M.; Liu, L.; Almarhabi, Y.; Jamal, A.; Usman, S.M.; Zahid, M. Temporal Instability of Factors Affecting Injury Severity in Helmet-Wearing and Non-Helmet-Wearing Motorcycle Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances. Int. J. Environ. Res. Public Health 2022, 19, 10526. https://doi.org/10.3390/ijerph191710526
Ijaz M, Liu L, Almarhabi Y, Jamal A, Usman SM, Zahid M. Temporal Instability of Factors Affecting Injury Severity in Helmet-Wearing and Non-Helmet-Wearing Motorcycle Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances. International Journal of Environmental Research and Public Health. 2022; 19(17):10526. https://doi.org/10.3390/ijerph191710526
Chicago/Turabian StyleIjaz, Muhammad, Lan Liu, Yahya Almarhabi, Arshad Jamal, Sheikh Muhammad Usman, and Muhammad Zahid. 2022. "Temporal Instability of Factors Affecting Injury Severity in Helmet-Wearing and Non-Helmet-Wearing Motorcycle Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances" International Journal of Environmental Research and Public Health 19, no. 17: 10526. https://doi.org/10.3390/ijerph191710526
APA StyleIjaz, M., Liu, L., Almarhabi, Y., Jamal, A., Usman, S. M., & Zahid, M. (2022). Temporal Instability of Factors Affecting Injury Severity in Helmet-Wearing and Non-Helmet-Wearing Motorcycle Crashes: A Random Parameter Approach with Heterogeneity in Means and Variances. International Journal of Environmental Research and Public Health, 19(17), 10526. https://doi.org/10.3390/ijerph191710526







