Numerical Analysis Method That Considers Weathering and Water-Softening Effects for the Slope Stability of Carbonaceous Mudstone
Abstract
1. Introduction
2. Methodology
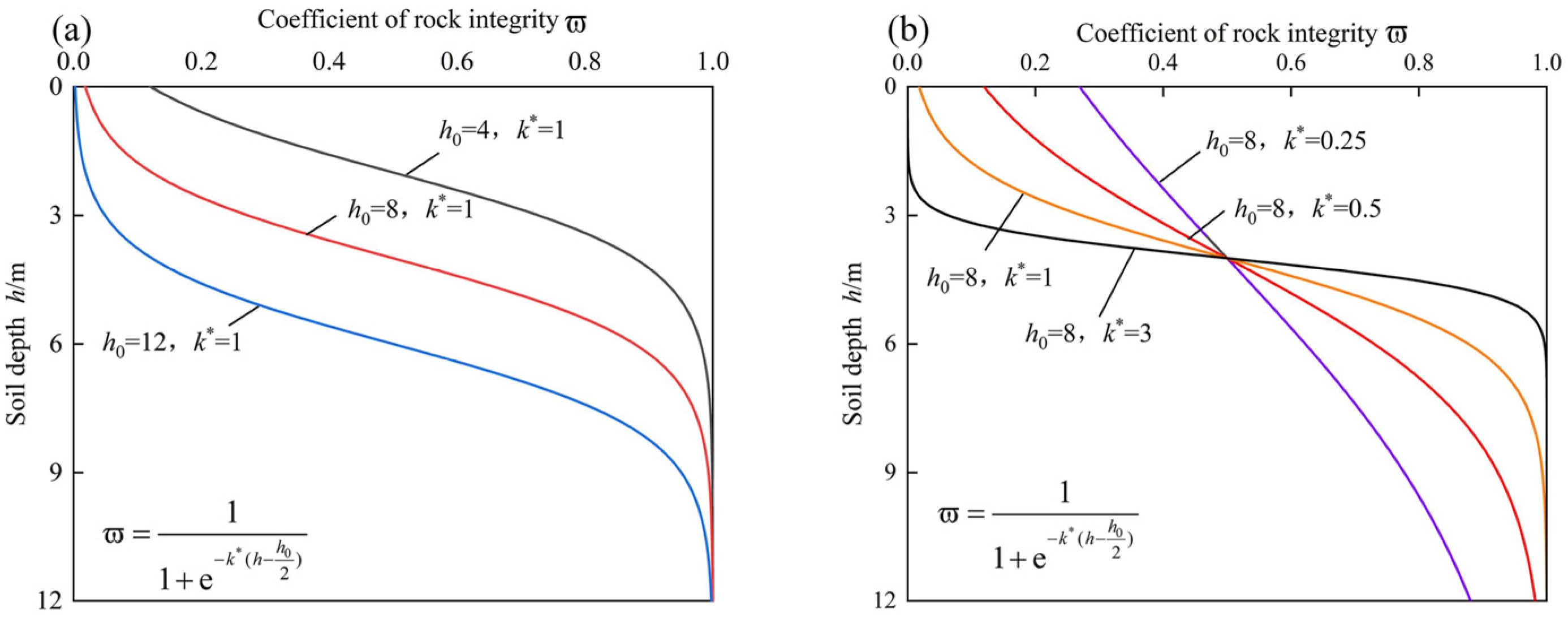
2.1. Weathering Effect
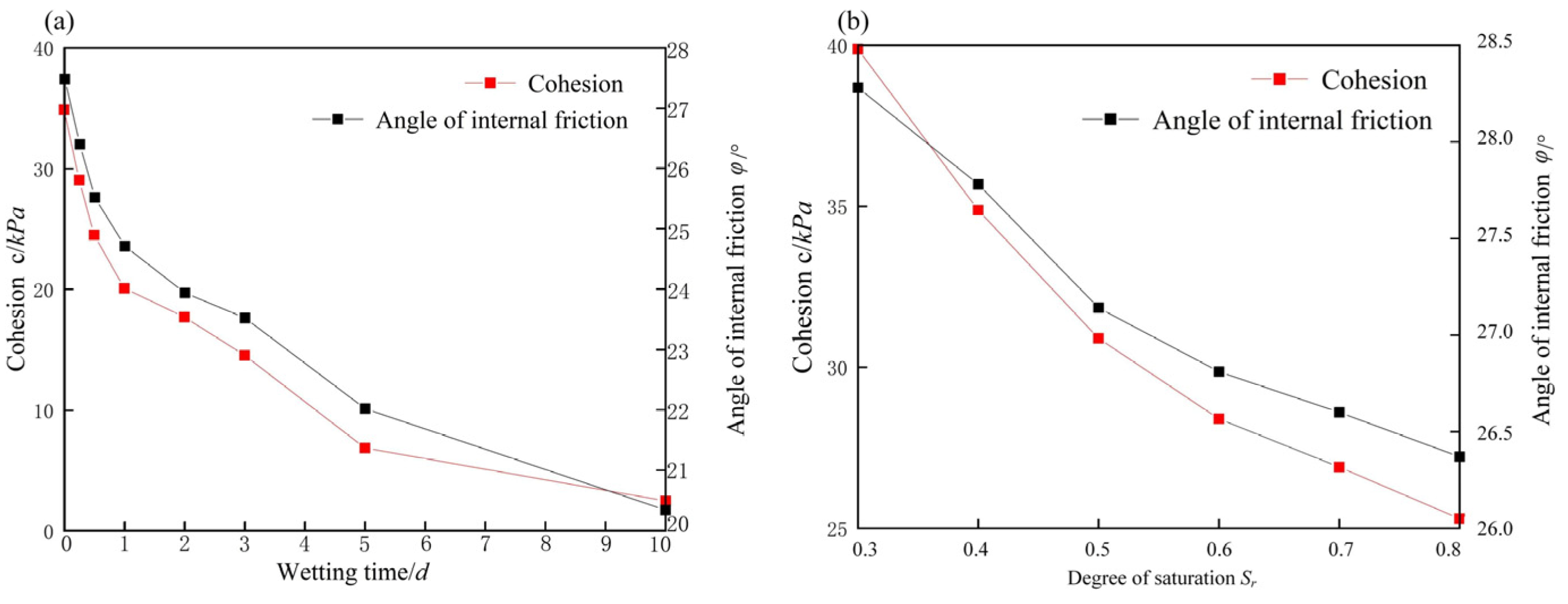
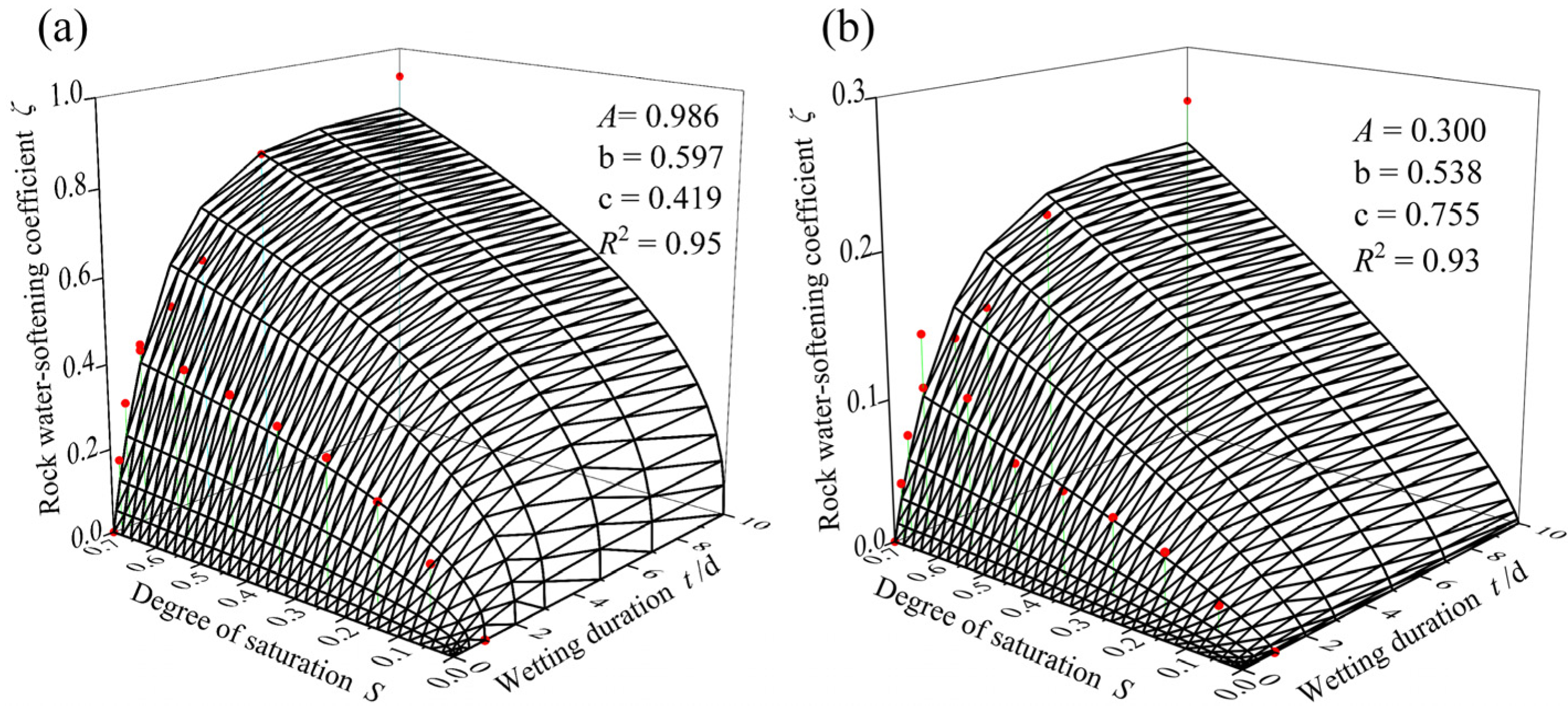
2.2. Water-Softening Effect
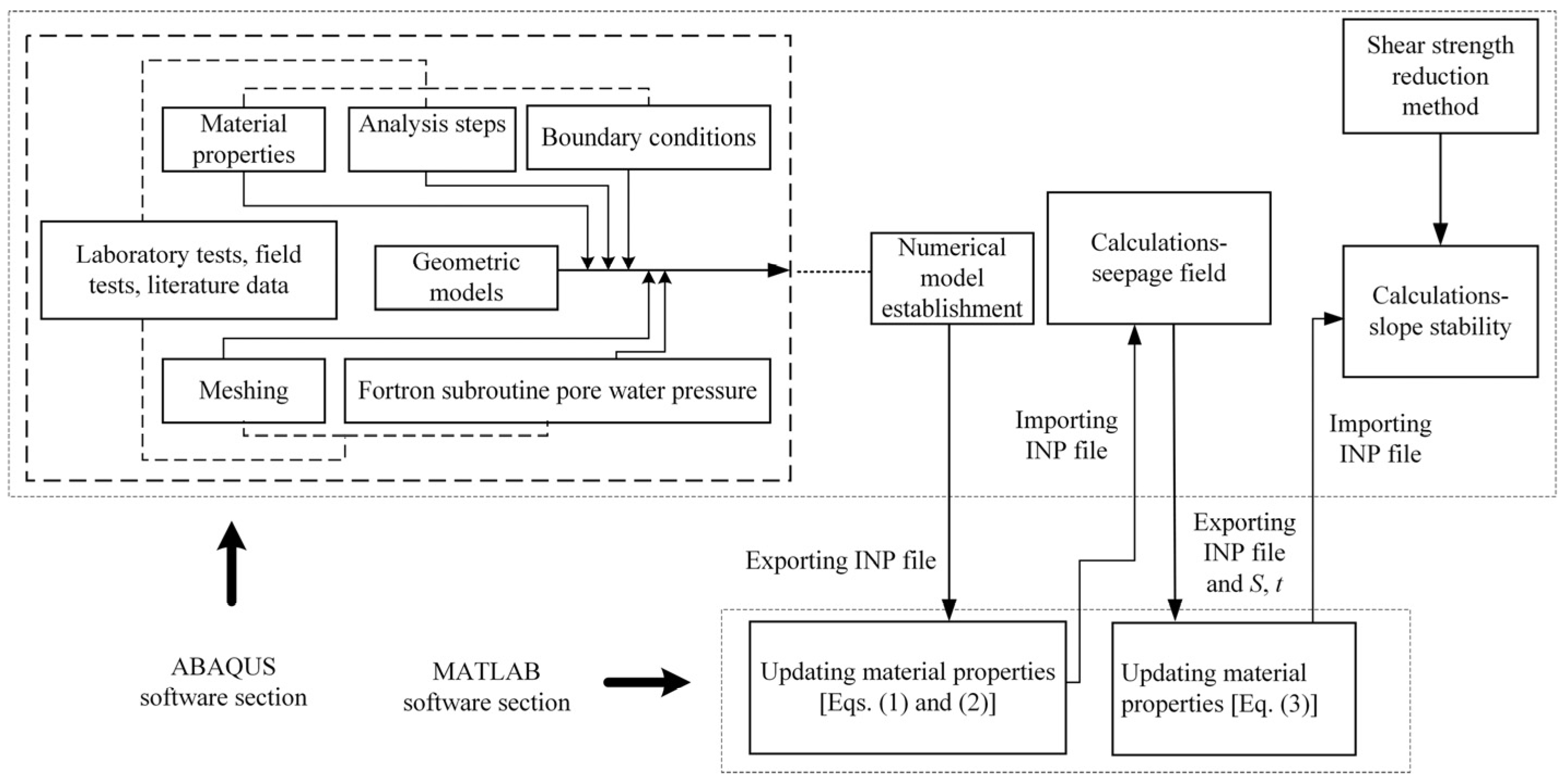
2.3. Numerical Realization
- (1)
- The numerical model that considers rainfall infiltration is established. A geometric model of a carbonaceous mudstone slope is created in the ABAQUS software. Then, the material properties without considering the weathering and water-softening effects are assigned. After setting the proper meshes, analysis steps, and boundary conditions (e.g., gravity, rainfall boundary, and initial profile of pore water pressure), the numerical model is established.
- (2)
- The ABAQUS Input (INP) file is modified to simulate the weathering effect. The depth of each element relative to the original ground surface in the slope is determined by MATLAB programming after the INP file is exported from the ABAQUS software. Then, the material properties of carbonaceous mudstone at various depths after weathering are calculated by Equations (1) and (2), and the weathering effect is taken into account by updating the material properties of every element in the INP file.
- (3)
- The seepage field of the slope under rainfall infiltration is calculated. Numerical calculation is conducted in the ABAQUS software using the modified INP file. After the finite element analysis, the seepage data of the slope, including the degree of saturation and wetting duration of every element, are determined.
- (4)
- The INP file is again modified to consider the water-softening effect. Based on the degree of saturation and the wetting duration of each element in the slope, MATLAB programming is employed to calculate the shear strength parameters of carbonaceous mudstone after water-softening following Equation (3). The material properties of every carbonaceous mudstone element in the INP file are updated for the second time to simulate the water-softening effect.
- (5)
- The stability of the carbonaceous mudstone slope is calculated. The modified INP file is imported into the ABAQUS software, and then the stability of the carbonaceous mudstone slope is analyzed using the shear strength reduction method. Finally, the safety factor and the failure mode of the slope are determined.
2.4. Case Application
2.5. Numerical Model
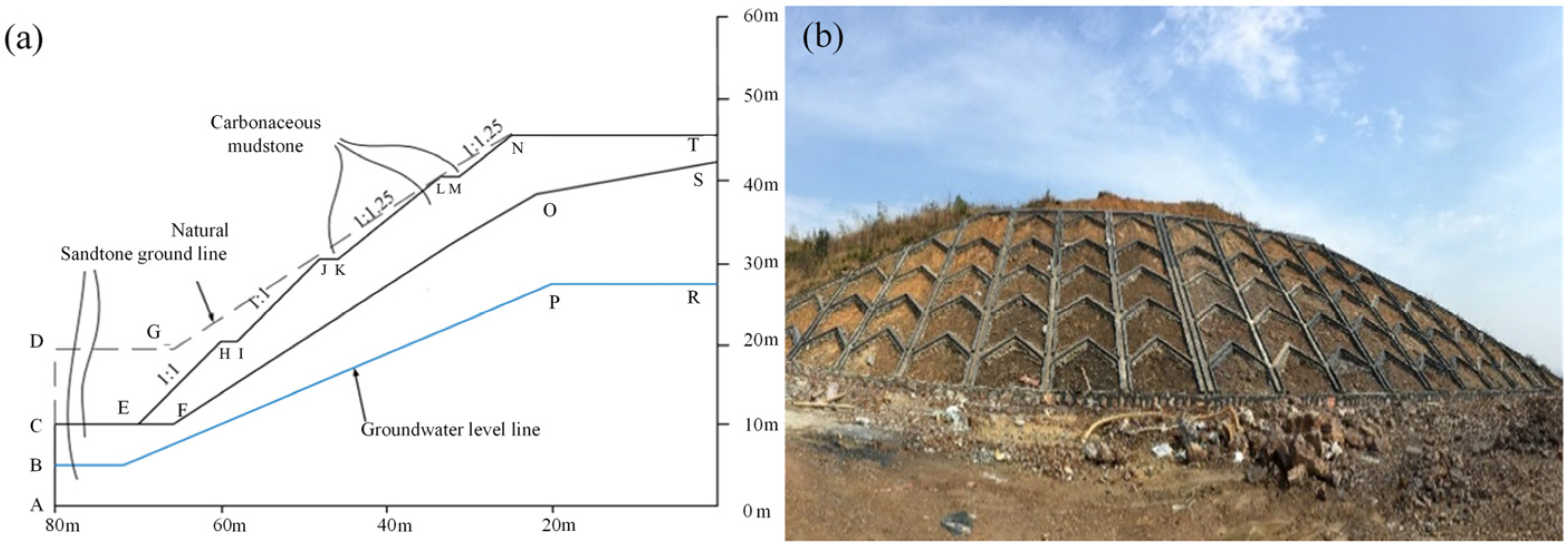
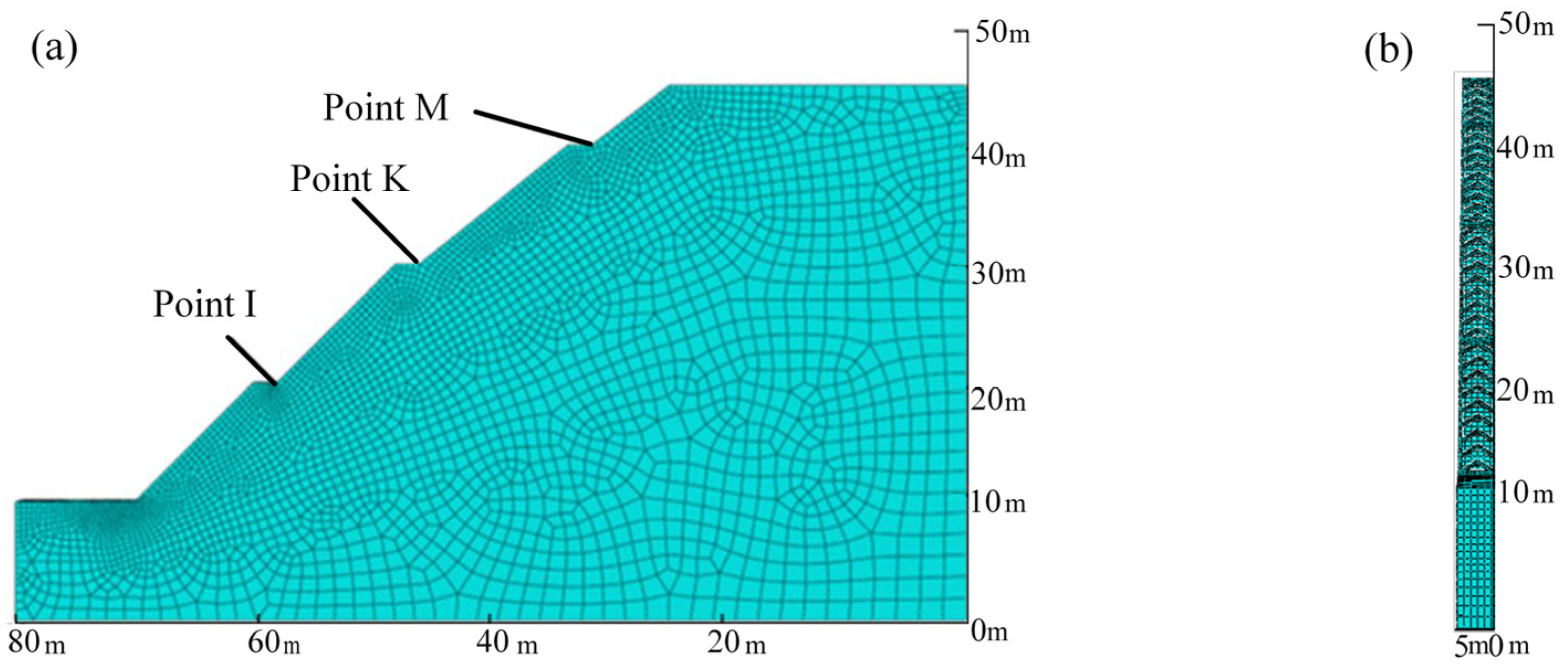
2.5.1. Geometric Model and Meshing
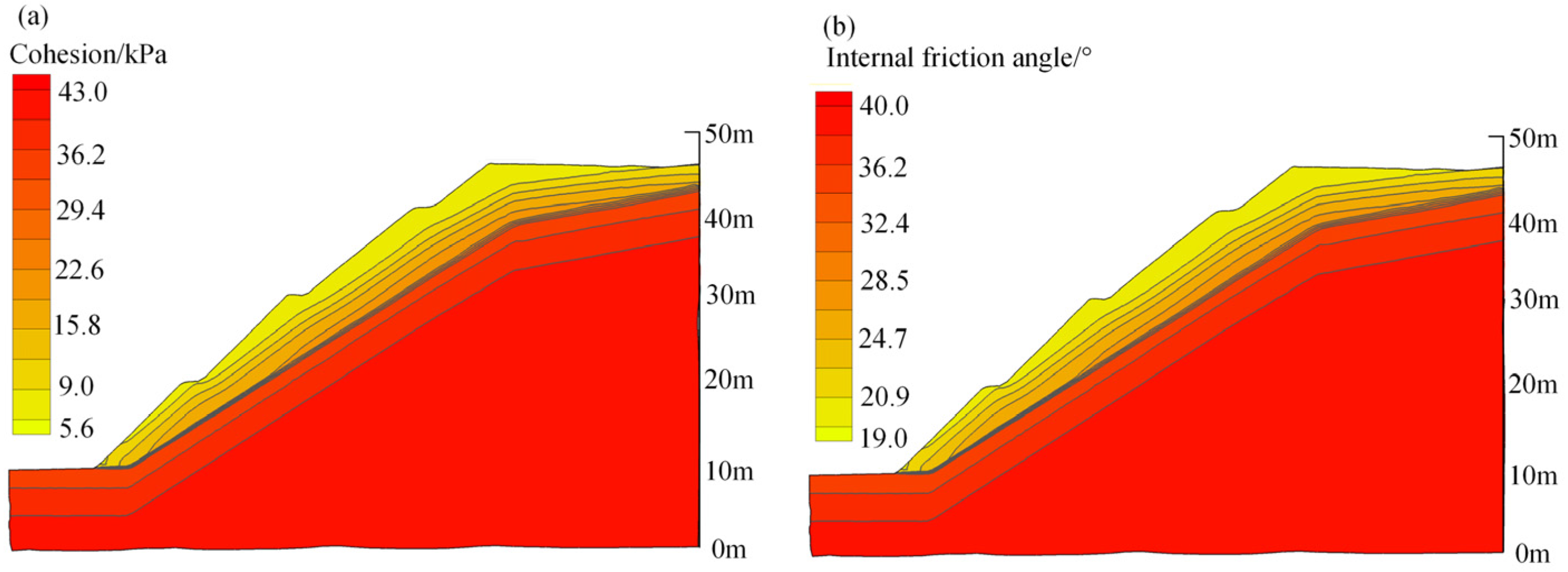
2.5.2. Material Properties
2.5.3. Boundary Conditions
3. Results and Discussion
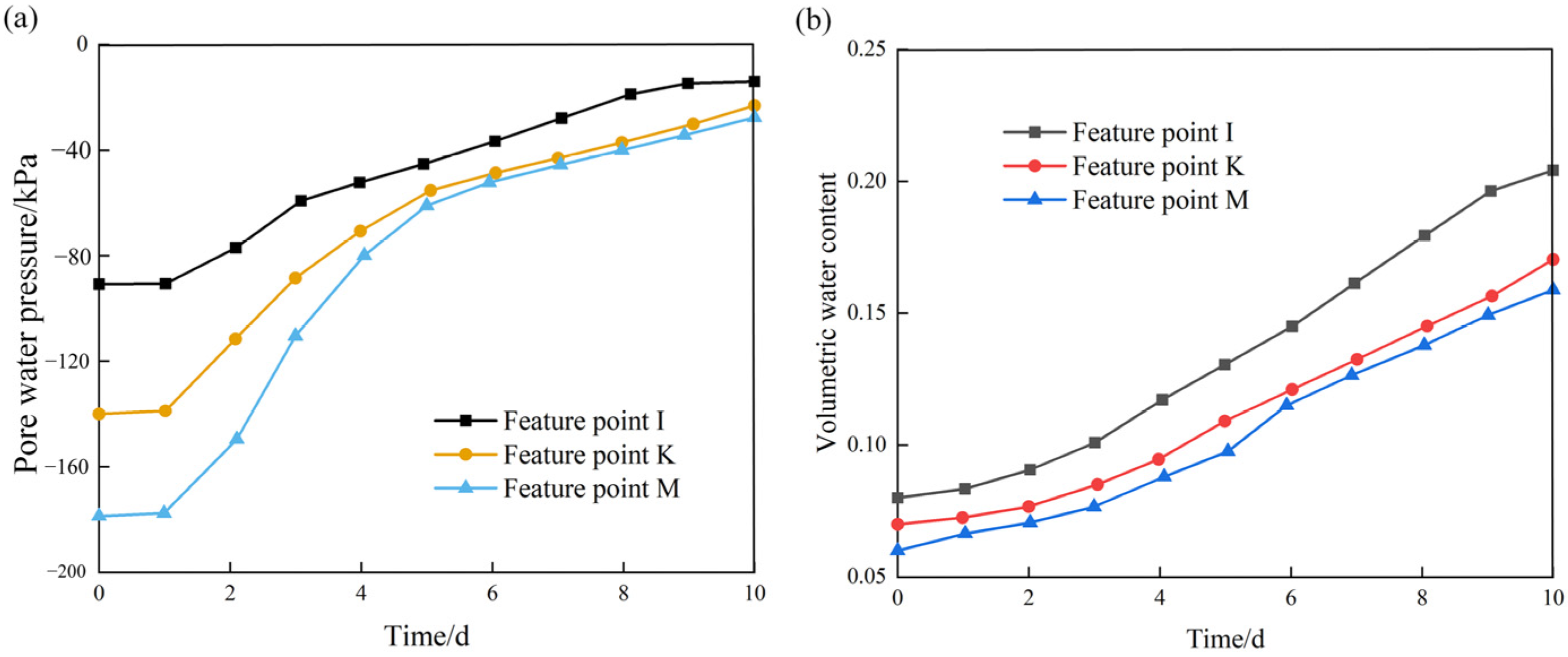
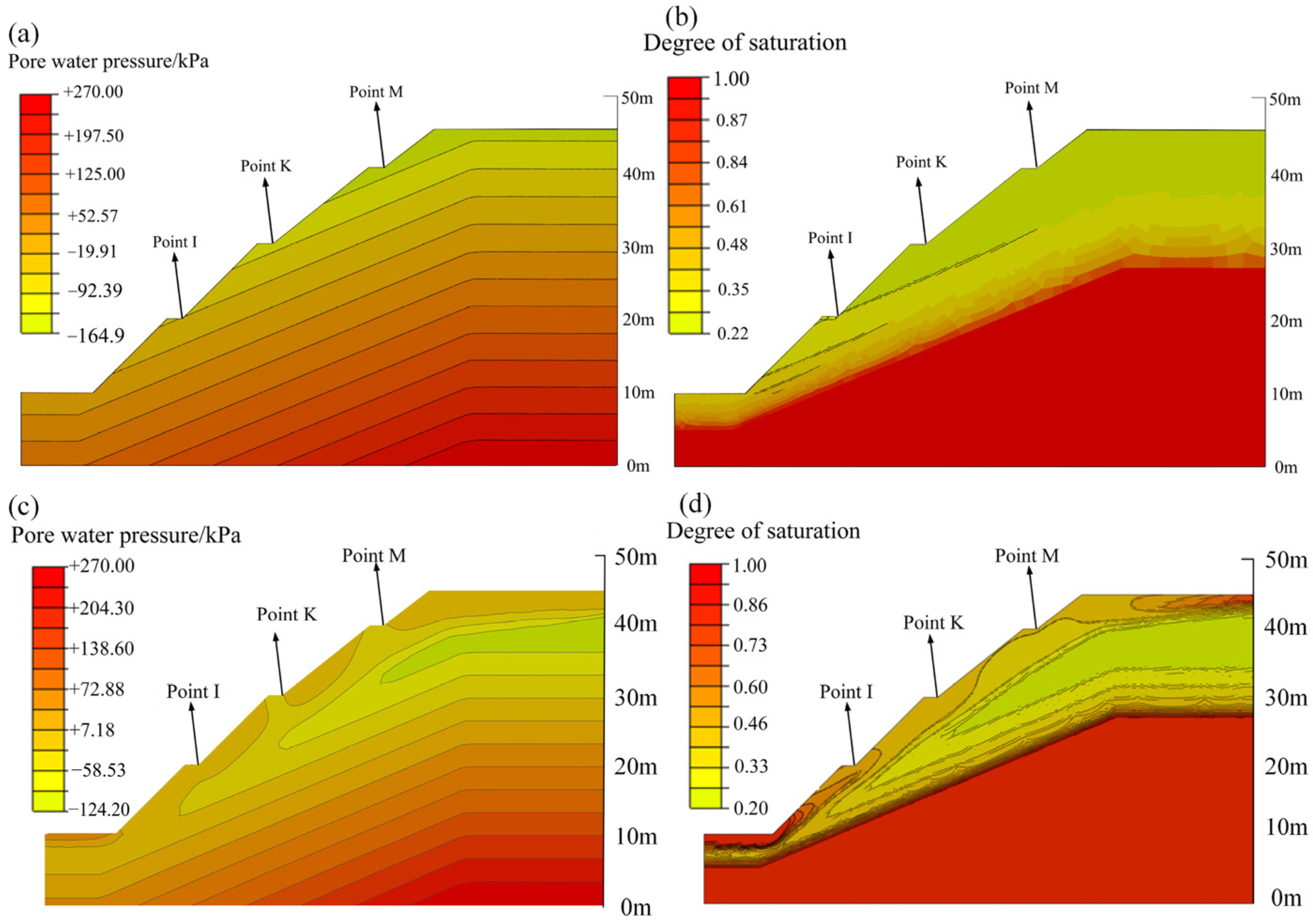
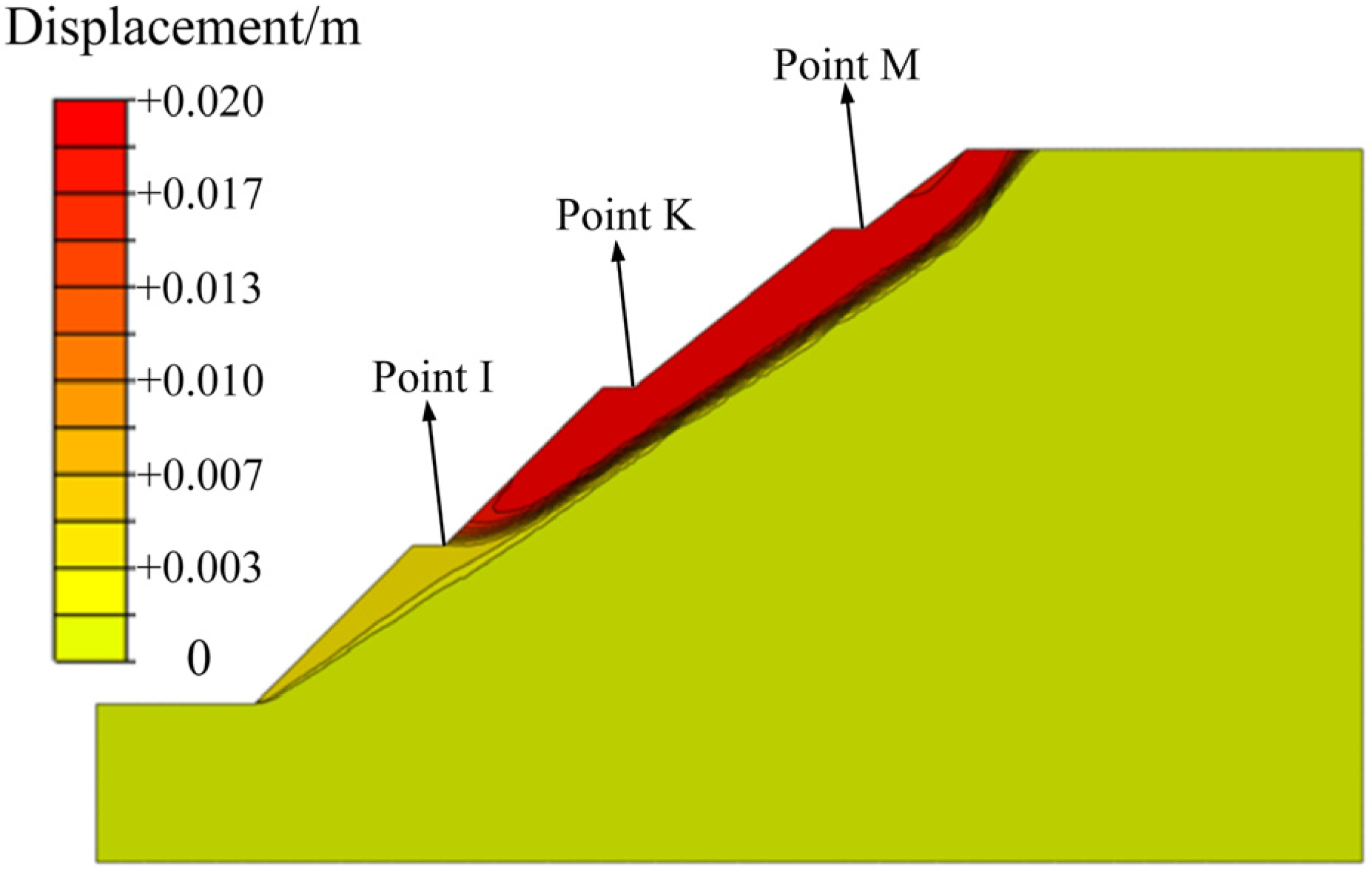
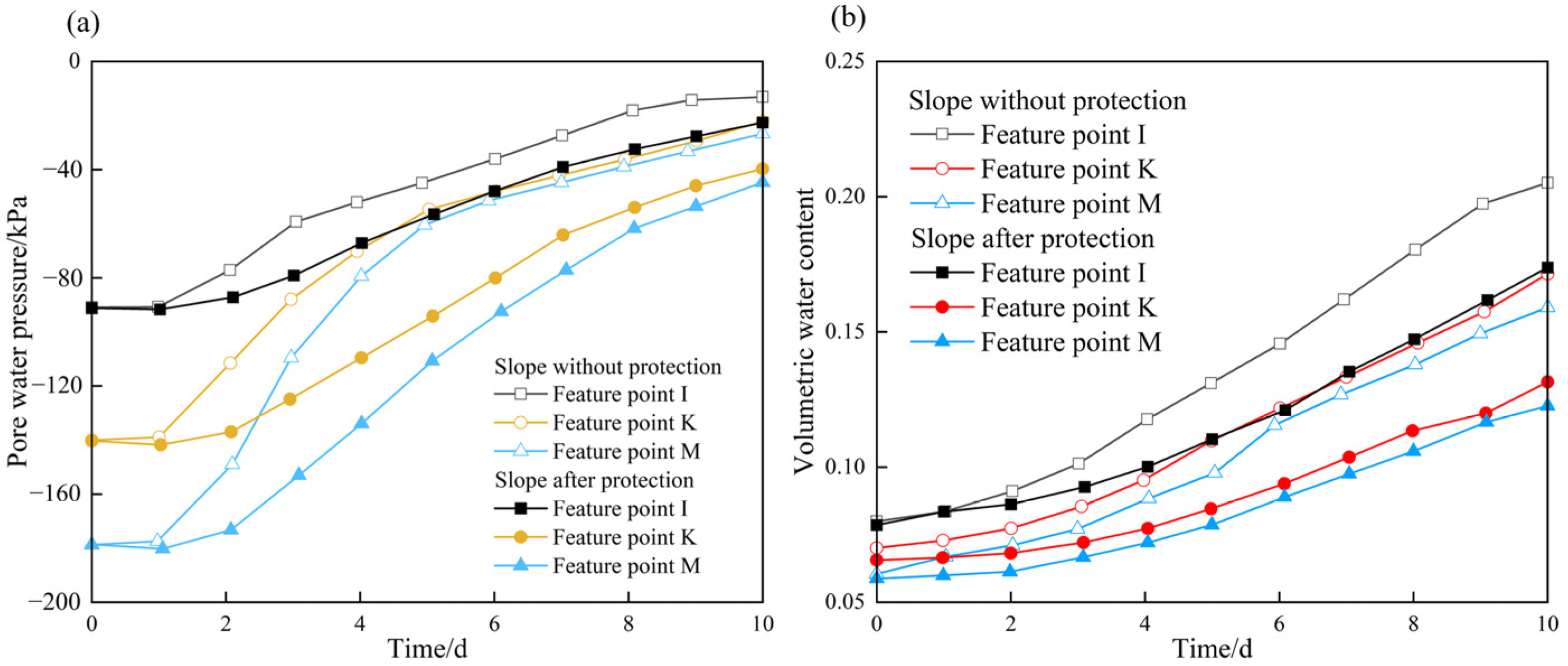
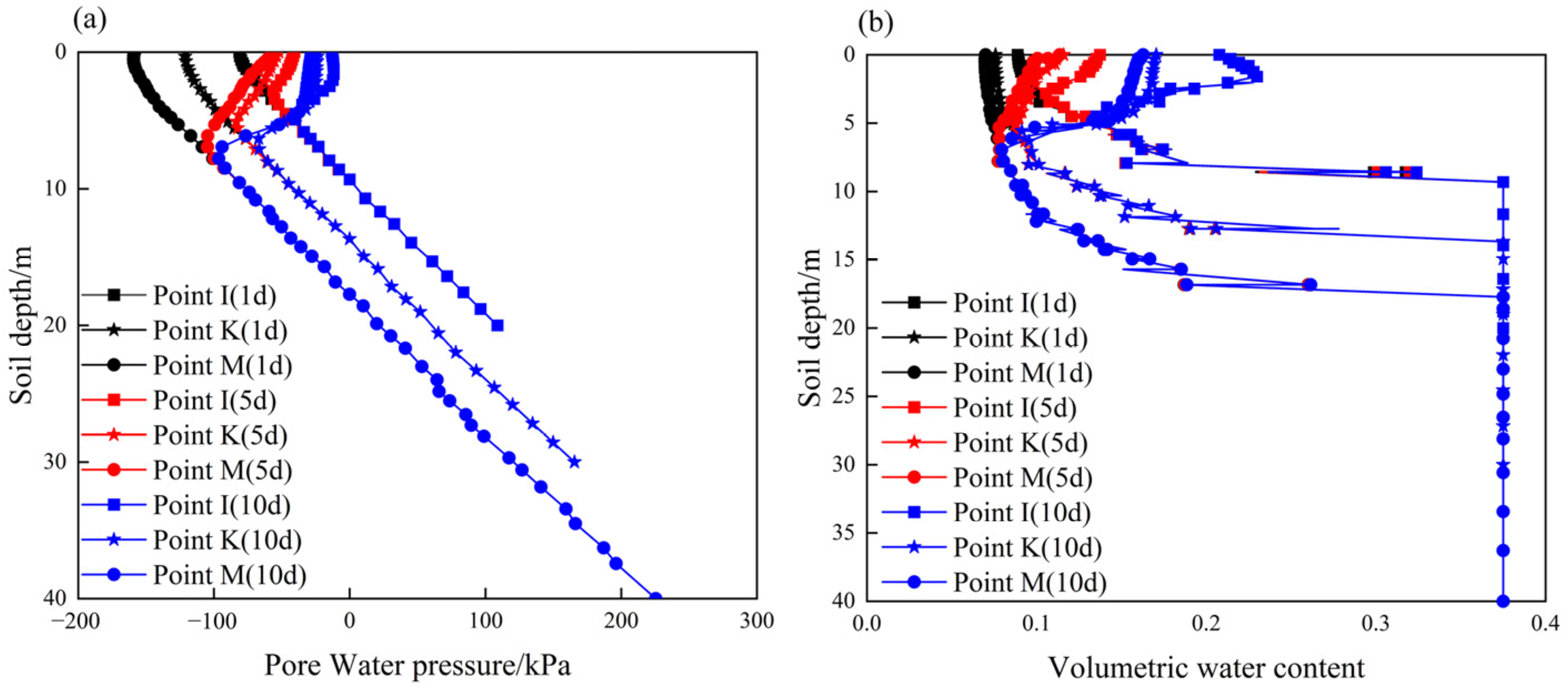
3.1. Slope Behavior before Protection Structures
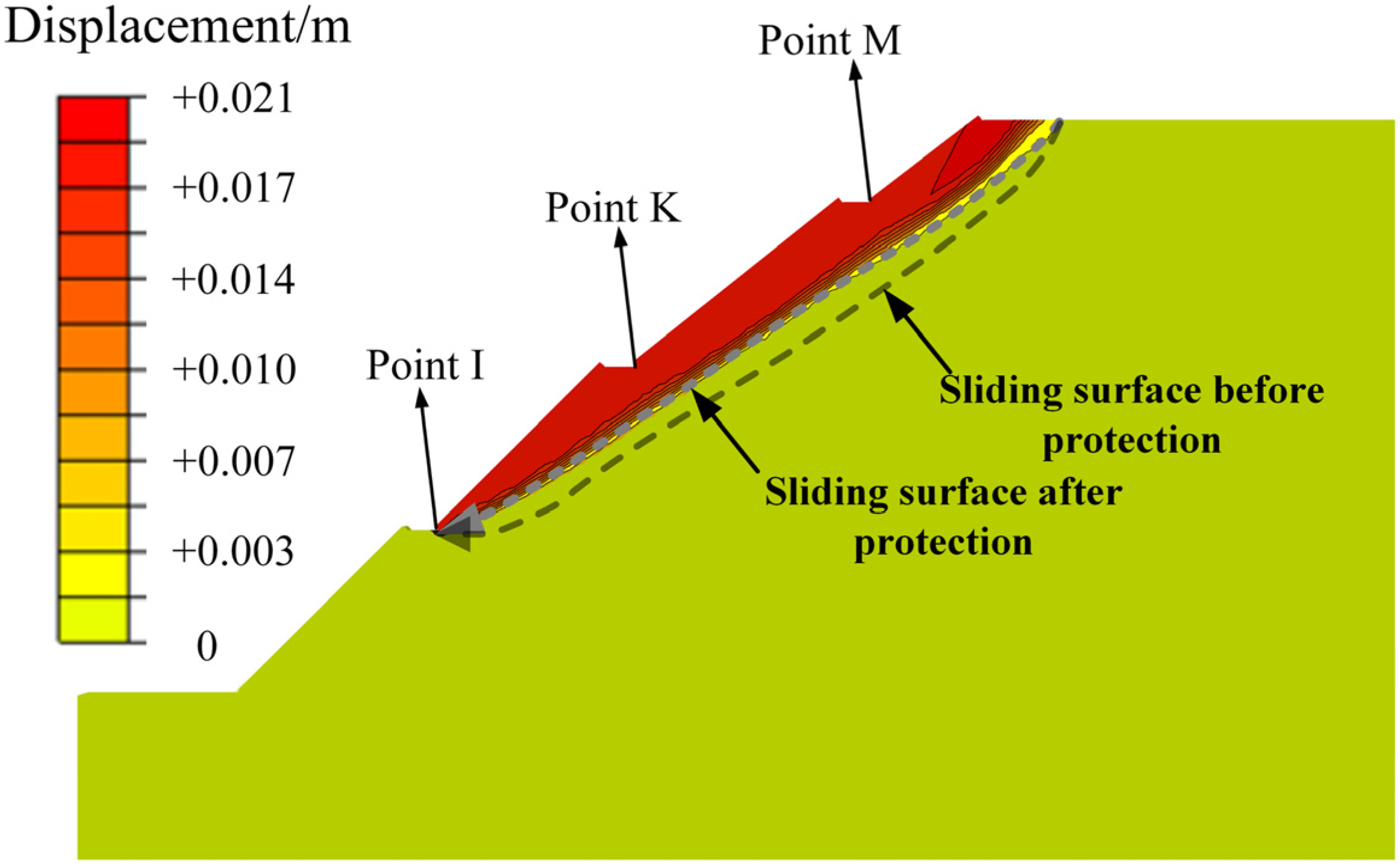
3.2. Slope Behavior with Herringbone Concrete Skeleton Protection
4. Conclusions
- (1)
- The relationship between the mechanical and hydraulic properties of carbonaceous mudstone and the depth on a slope is assumed to be a logistic function. On this basis, a mathematical equation was established to consider the effect of weathering on carbonaceous mudstone slopes.
- (2)
- Laboratory tests showed that the shear strength parameters were reduced, following an exponential form, as the wetting duration increased; at the same time, they showed a decreasing trend as the degree of saturation increased. Therefore, the rock water-softening coefficient that was a function of wetting duration and degree of saturation was introduced, which could characterize the effect of water-softening on carbonaceous mudstone.
- (3)
- The consideration of the effects of weathering and water-softening on carbonaceous mudstone in the ABAQUS finite element software was realized by updating the INP file. The material properties in the INP file were modified by MATLAB programming based on the mathematical equations of weathering and water-softening.
- (4)
- The above proposed numerical analysis method was used to analyze the seepage field and stability of a highway cut slope with and without herringbone concrete skeletons being subjected to rainfall. The results indicated that the use of herringbone concrete skeletons can retard rainfall infiltration and enhance the stability of carbonaceous mudstone slopes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, L.; Yu, H.C.; Liu, J.; Gao, Q.F.; Bian, H.-B. Mechanical behaviour of disintegrated carbonaceous mudstone under stress and cyclic drying wetting. Constr. Build. Mater. 2021, 282, 122656. [Google Scholar] [CrossRef]
- Zeng, L.; Luo, J.T.; Liu, J.; Gao, Q.-F.; Bian, H.-B. Disintegration characteristics and mechanisms of carbonaceous mudstone subjected to load and cyclic drying-wetting. J. Mater. Civ. Eng. 2021, 33, 04021195. [Google Scholar] [CrossRef]
- Zeng, L.; Qiu, X.; Fu, H.Y.; Tang, H.L.; Li, G.Y. Stability analysis of disintegrated pretreated carbonaceous mudstone embankment during water level rise and fall. Chin. J. Highw. Tranport 2017, 30, 10–19. (In Chinese) [Google Scholar]
- Luo, J.Y.; Xu, Z.M.; Ren, Z.; Wang, K.; Gao, H.-Y.; Yang, K.; Tang, Y.-J.; Tian, L. Quantitative assessment of weathering degree of the Touzhai rock-avalanche deposit in Southwest China. Geomorphology 2020, 359, 107162. [Google Scholar] [CrossRef]
- Borrelli, L.; Gulla, G. Tectonic constraints on a deep-seated rock slide in weathered crystalline rocks. Geomorphology 2017, 290, 288–316. [Google Scholar] [CrossRef]
- Dagdelenler, G.; Sezer, E.A.; Gokceoglu, C. Some non-linear models to predict the weathering degrees of a granitic rock from physical and mechanical parameters. Expert Syst. Appl. 2011, 38, 7476–7485. [Google Scholar] [CrossRef]
- Yu, L.; Zheng, X.; Liu, Z.; Zhou, C.; Zhang, L. Multiscale modelling of the seepage-induced failure of a soft rock slope. Acta Geotech. 2022, 17, 4717–4738. [Google Scholar] [CrossRef]
- Bhattarai, P.; Marui, H.; Tiwari, B.; Watanabe, N. Influence of weathering on physical and mechanical properties of mudstone. Phys. Rev. 2006, B80, 308–310. [Google Scholar]
- Nong, X.; Towhata, I. Investigation of mechanical properties of soft rock due to laboratory reproduction of physical weathering process. Soils Found. 2017, 57, 267–276. [Google Scholar] [CrossRef]
- Qureshi, M.U.; Towhata, I.; Yamada, S. An experimental relation between shear strength under low pressure and S-wave velocity of rock subjected to mechanical weathering. Soils Found. 2019, 59, 1468–1480. [Google Scholar] [CrossRef]
- Hachinohe, S.; Hiraki, N.; Suzuki, T. Rates of weathering and temporal changes in strength of bedrock of marine terraces in Boso Peninsula, Japan. Eng. Geol. 2000, 84, 171–185. [Google Scholar] [CrossRef]
- Lee, J.S.; Yoon, H.K. Characterization of rock weathering using elastic waves: A Laboratory-scale experimental study. J. Appl. Geophys. 2017, 140, 24–33. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.S.; Bo, Y.; Liu, B.; Ding, Z.-W.; Zhang, Q.-T. An elasto-plastic and viscoplastic damage constitutive model for dilatancy and fracturing behavior of soft rock squeezing deformation. J. Mt. Sci. 2022, 19, 826–848. [Google Scholar] [CrossRef]
- Zhou, M.; Li, J.; Luo, Z.; Sun, J.; Xu, F.; Jiang, Q.; Deng, H. Impact of water-rock interaction on the pore structures of red-bed soft rock. Sci. Rep. 2021, 11, 7398. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, M.; Davoodi, P.Y.; Najmoddini, I. Studying the correlation of rock properties with P-wave velocity index in dry and saturated conditions. J. Appl. Geophys. 2019, 169, 49–57. [Google Scholar] [CrossRef]
- Shakoor, A.; Barefield, E.H. Relationship between unconfined compressive strength and degree of saturation for selected sandstones. Environ. Eng. Geosci. 2009, 15, 29–40. [Google Scholar] [CrossRef]
- Fu, H.Y.; Chen, J.C.; Zeng, L.; Qiu, X. Experiments on the effect of temperature and humidity on the uniaxial mechanical properties of siltstone. China Civ. Eng. J. 2019, 52, 89–98. (In Chinese) [Google Scholar] [CrossRef]
- Johari, A.; Talebi, A. Stochastic Analysis of Rainfall-Induced Slope Instability and Steady-State Seepage Flow Using Random Finite-Element Method. Int. J. Geomech. 2019, 19, 04019085. [Google Scholar] [CrossRef]
- Showkati, A.; Salari-rad, H.; Aghchai, M.H. Predicting long-term stability of tunnels considering rock mass weathering and deterioration of primary support. Tunn. Undergr. Space Technol. 2021, 107, 103670. [Google Scholar] [CrossRef]
- Fu, H.Y.; Chen, J.C.; Zeng, L.; Qiu, X. Model experiments test on the effects of rainfall on seepage and deformation of charcoal mudstone-soil layered embankment. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 2852–2860. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, Z.M.; Xiong, X.H.; Zeng, L. Unsaturated rainfall infiltration analysis of slopes based on FLAC3D. Rock Soil Mech. 2014, 35, 855–861. (In Chinese) [Google Scholar] [CrossRef]
- Ma, J.Q.; Fu, H.Y.; Wang, G.Y.; Zeng, L. Seepage characteristics of layered soil slope under rainfall conditions. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 464–471. (In Chinese) [Google Scholar] [CrossRef]
- Miscevic, P.; Vlastelica, G. Impact of weathering on slope stability in soft rock mass. J. Rock Mech. Geotech. Eng. 2014, 6, 240–250. [Google Scholar] [CrossRef]
- Admassu, Y.; Shakoor, A.; Wells, N.A. Evaluating selected factors affecting the depth of undercutting in rocks subject to differential weathering. Eng. Geol. 2012, 124, 1–11. [Google Scholar] [CrossRef]
- Li, S.J.; Gao, H.; Xu, D.M.; Meng, F. Comprehensive determination of reinforcement parameters for high cut slope based on intelligent optimization and numerical analysis. J. Earth Sci. 2012, 23, 233–242. [Google Scholar] [CrossRef]
- Lin, C.N.; Li, T.C.; Zhao, L.H.; Zhang, Z.; Lin, C.; Liu, X.; Niu, Z. Reinforcement effects and safety monitoring index for high steep slopes: A case study in China. Eng. Geol. 2020, 279, 105861. [Google Scholar] [CrossRef]
- Bai, H.L.; Feng, W.-K.; Li, S.-Q.; Ye, L.-Z.; Wu, Z.-T.; Hu, R.; Dai, H.-C.; Hu, Y.-P.; Yi, X.-Y.; Deng, P.-C. Flow-slide characteristics and failure mechanism of shallow landslides in granite residual soil under heavy rainfall. J. Mt. Sci. 2022, 19, 1541–1557. [Google Scholar] [CrossRef]
- Xu, J.S.; Zhao, X.; Li, P.F.; Zhang, M. Stability of a 3D unsaturated vertical cut slope subjected to variable rainfall infiltration. Comput. Geotech. 2021, 134, 104–110. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Three-dimensional stability assessment of slopes in intact rock governed by the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2020, 137, 104522. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Wang, B.; Tung, Y.K. Three-dimensional numerical investigations of groundwater responses in an unsaturated slope subjected to various rainfall patterns. Can. Geotech. J. 2001, 38, 1049–1062. [Google Scholar] [CrossRef]
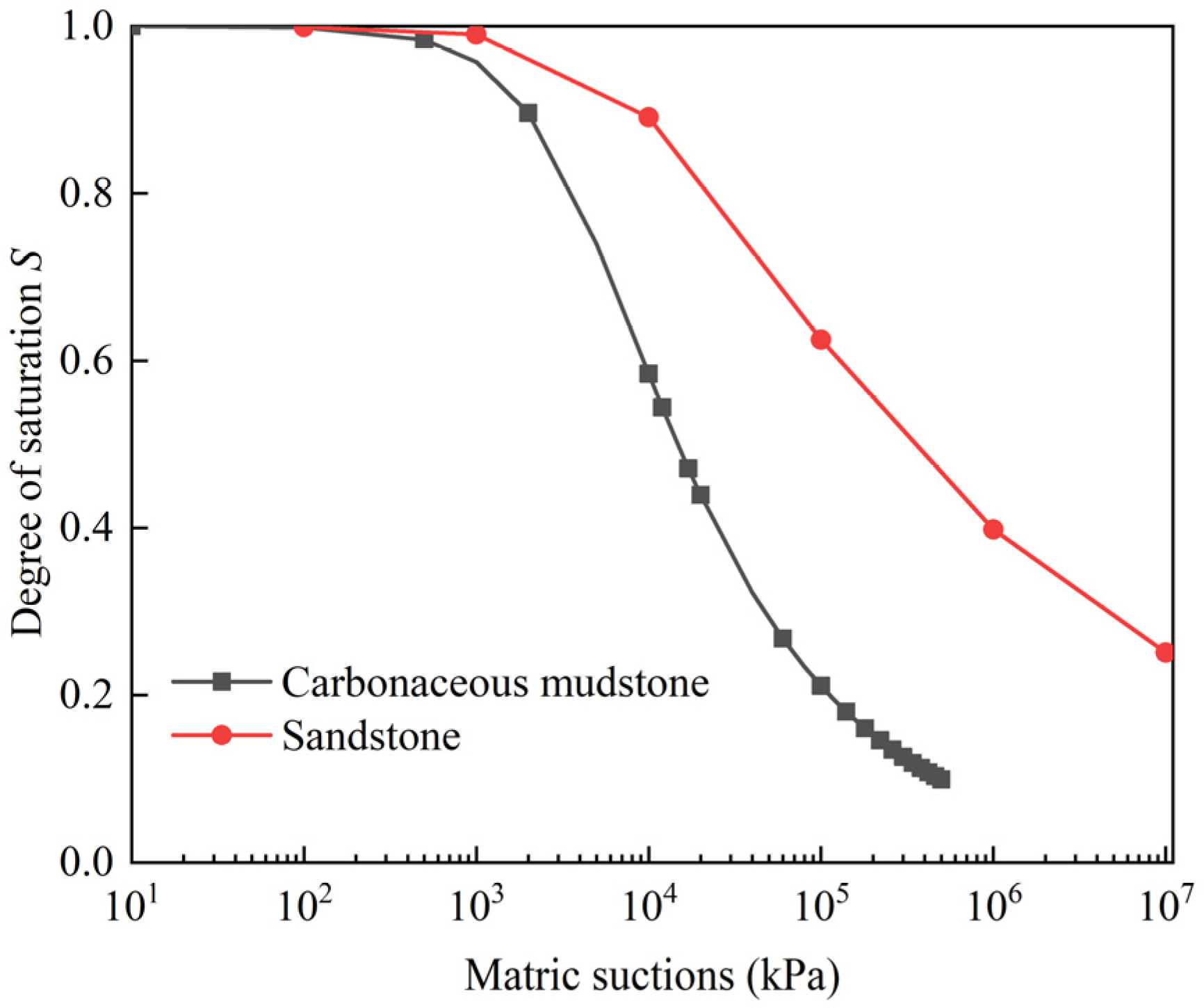
- Zeng, L.; Li, F.; Liu, J.; Gao, Q.; Bian, H. Effect of initial gravimetric water content and cyclic wetting-drying on soil-water characteristic curves of disintegrated carbonaceous mudstone. Transp. Saf. Environ. 2019, 1, 230–240. [Google Scholar] [CrossRef]


| Material | Density (kg/m3) | Cohesion (kPa) | Angle of Internal Friction (°) | Elastic Modulus (MPa) | Poisson’s Ratio | Void Ratio | Permeability Coefficient (m/d) |
|---|---|---|---|---|---|---|---|
| Carbonaceous mudstone | 2000 | 22.5–42.57 | 21.4–28.24 | 120–750 | 0.33 | 0.6 | 0.864–0.0864 |
| Sandstone | 2250 | 41.5–43.0 | 27.6–40.0 | 800–1150 | 0.23 | 0.6 | 0.02592–0.0002592 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Liu, Z.; Zeng, L.; Gao, Q.; Luo, J.; Xiao, X. Numerical Analysis Method That Considers Weathering and Water-Softening Effects for the Slope Stability of Carbonaceous Mudstone. Int. J. Environ. Res. Public Health 2022, 19, 14308. https://doi.org/10.3390/ijerph192114308
Fu Y, Liu Z, Zeng L, Gao Q, Luo J, Xiao X. Numerical Analysis Method That Considers Weathering and Water-Softening Effects for the Slope Stability of Carbonaceous Mudstone. International Journal of Environmental Research and Public Health. 2022; 19(21):14308. https://doi.org/10.3390/ijerph192114308
Chicago/Turabian StyleFu, Yeyang, Zhaohui Liu, Ling Zeng, Qianfeng Gao, Jintao Luo, and Xinhui Xiao. 2022. "Numerical Analysis Method That Considers Weathering and Water-Softening Effects for the Slope Stability of Carbonaceous Mudstone" International Journal of Environmental Research and Public Health 19, no. 21: 14308. https://doi.org/10.3390/ijerph192114308
APA StyleFu, Y., Liu, Z., Zeng, L., Gao, Q., Luo, J., & Xiao, X. (2022). Numerical Analysis Method That Considers Weathering and Water-Softening Effects for the Slope Stability of Carbonaceous Mudstone. International Journal of Environmental Research and Public Health, 19(21), 14308. https://doi.org/10.3390/ijerph192114308







