Combined Effects of CO2 Adsorption-Induced Swelling and Dehydration-Induced Shrinkage on Caprock Sealing Efficiency
Abstract
1. Introduction
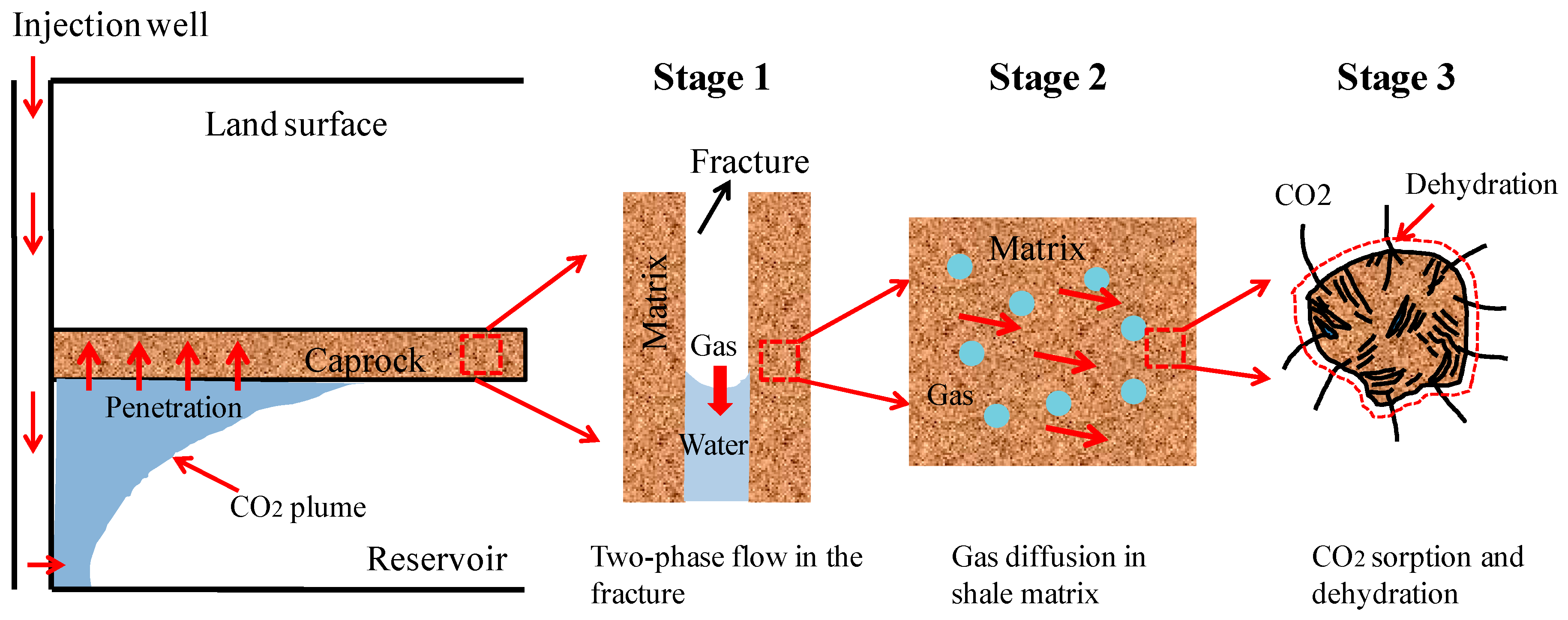
2. Multi-Physical Interaction Model for a Fractured Caprock Layer
2.1. Multi-Physical Interactions in a Fractured Caprock
2.2. Dehydration and Shrinkage of Shale Matrix
2.2.1. Water Content, Saturation, and Porosity of Shale Matrix
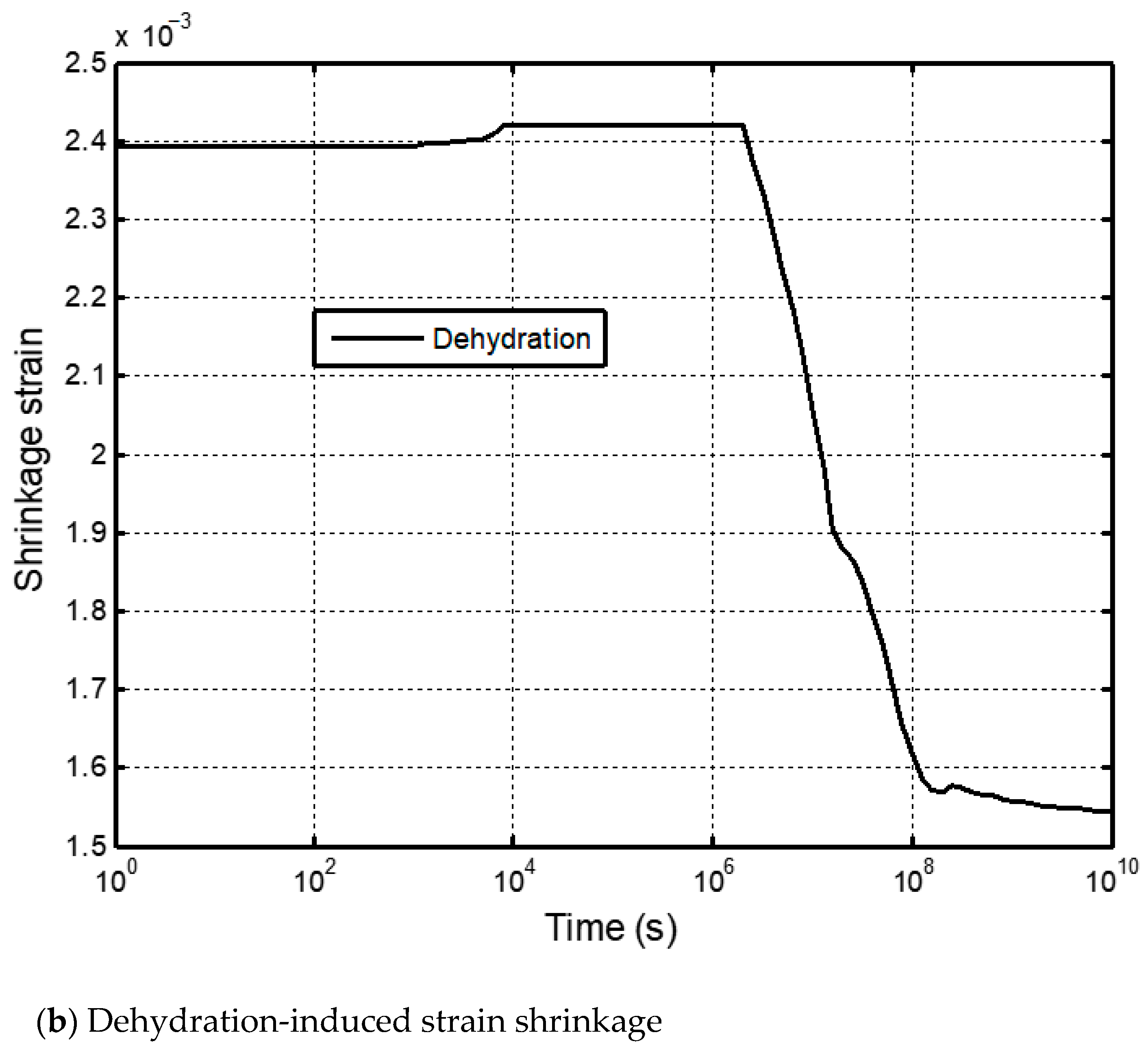
2.2.2. Dehydration-Induced Volumetric Strain of Shale Matrix
2.3. Dehydration-Induced Modifications for Porosity and Permeability Models
2.3.1. Porosity Evolution in Homogeneous Shale Matrix
2.3.2. Local Fracture Strain
2.3.3. Evolution of Permeability
2.4. Change in Entry Capillary Pressure with Fracture Deformation
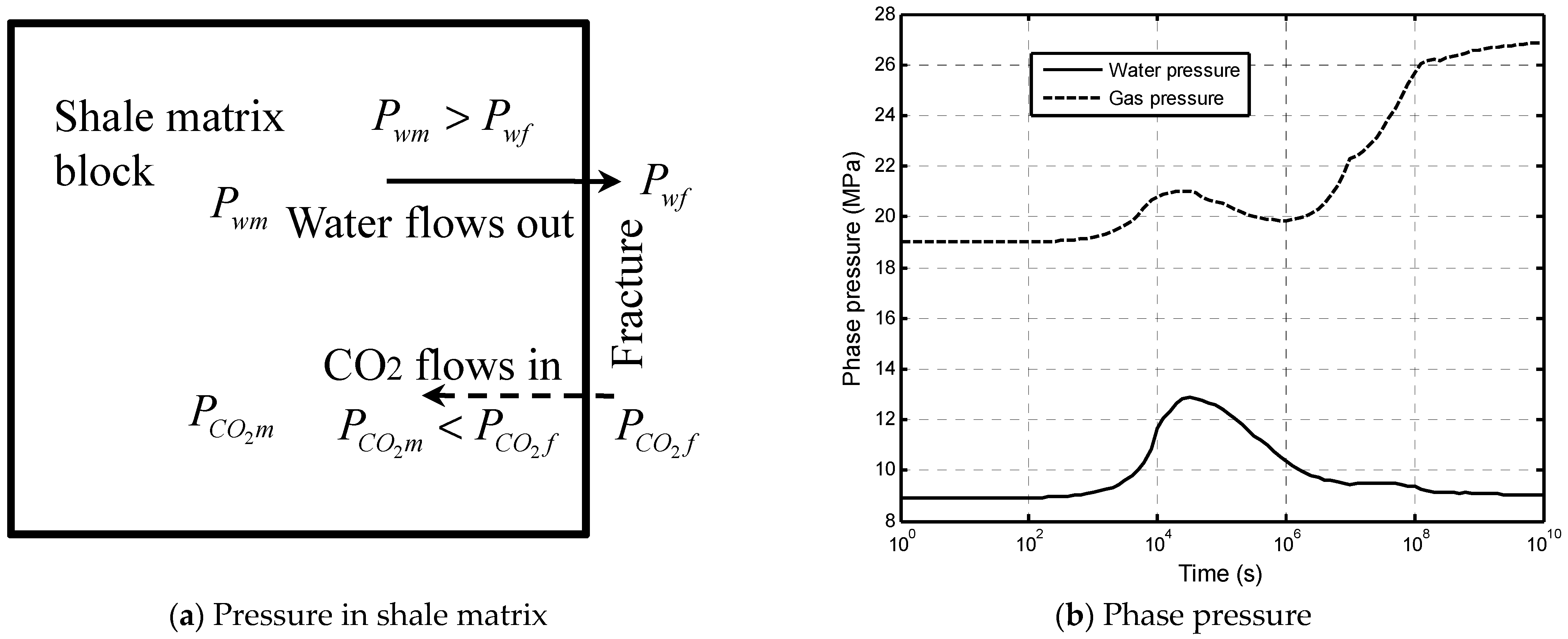
3. Mass Transfer of Two-Phase Flow between Fractures and Shale Matrix
3.1. Mass Transfer of CO2 between Fractures and Shale Matrix
3.2. Dehydration due to Water Transfer between Fractures and Shale Matrix
4. Mathematical Descriptions of Multi-Physical Processes
4.1. Mass Conservation Laws for CO2–Brine Water Two-Phase Flow in Fractures
4.2. Navier Equation for Shale Deformation
5. Numerical Modelling for the Assessment of Caprock Sealing Efficiency
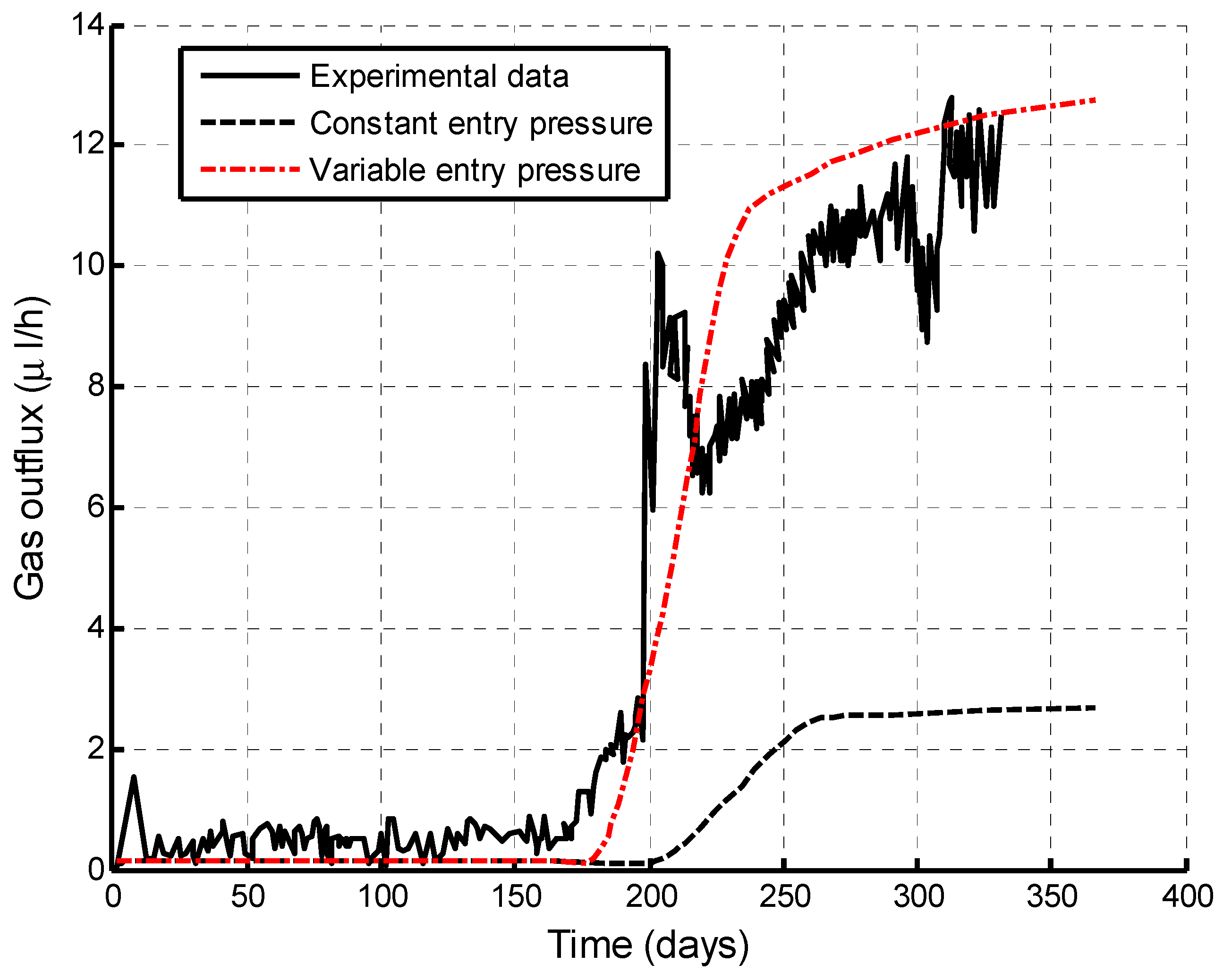
5.1. Verification of This fully Coupled Multi-Physical Model
5.2. Impacts of Shale Matrix Dehydration on CO2 Penetration
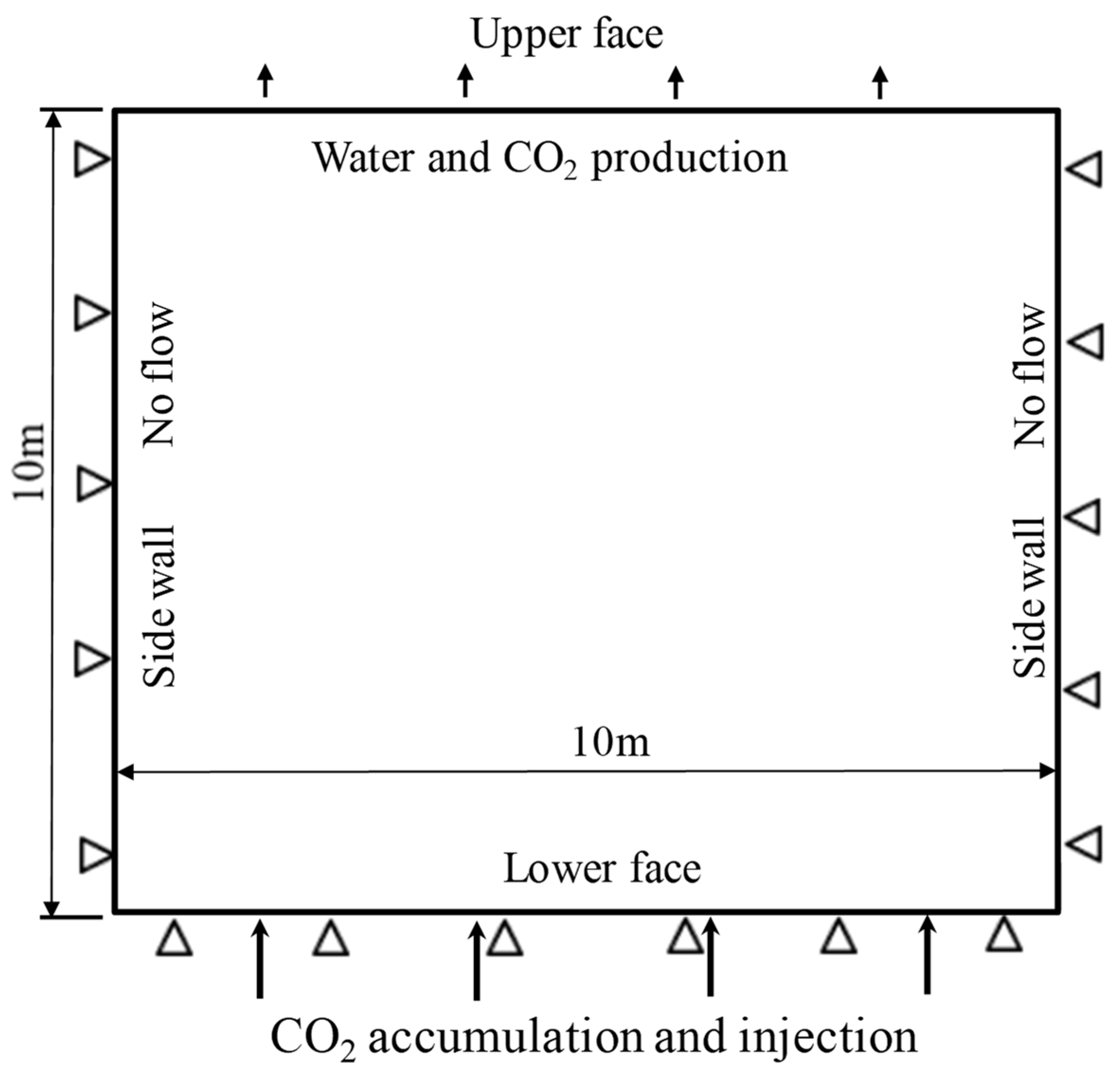
5.2.1. Model and Parameters
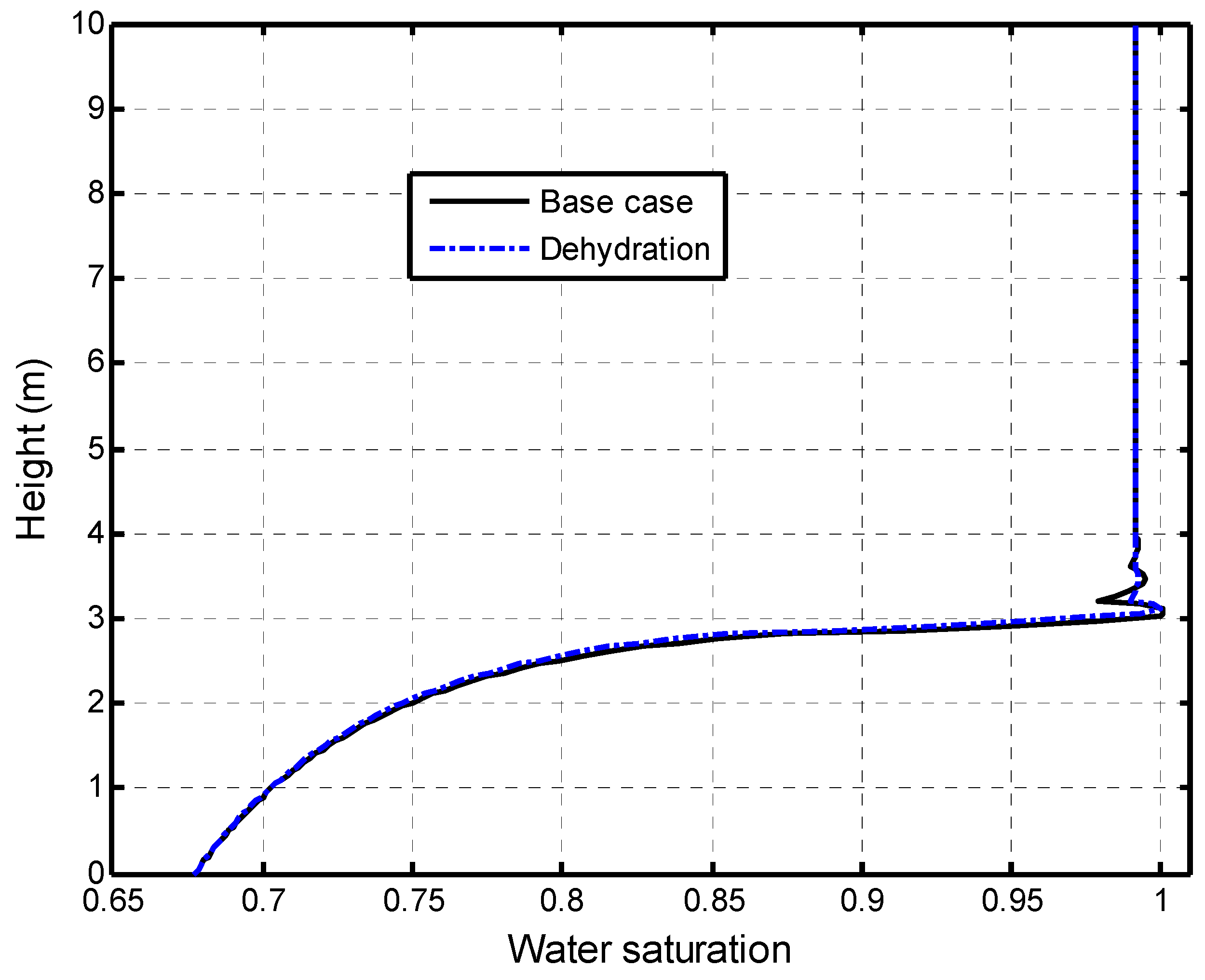
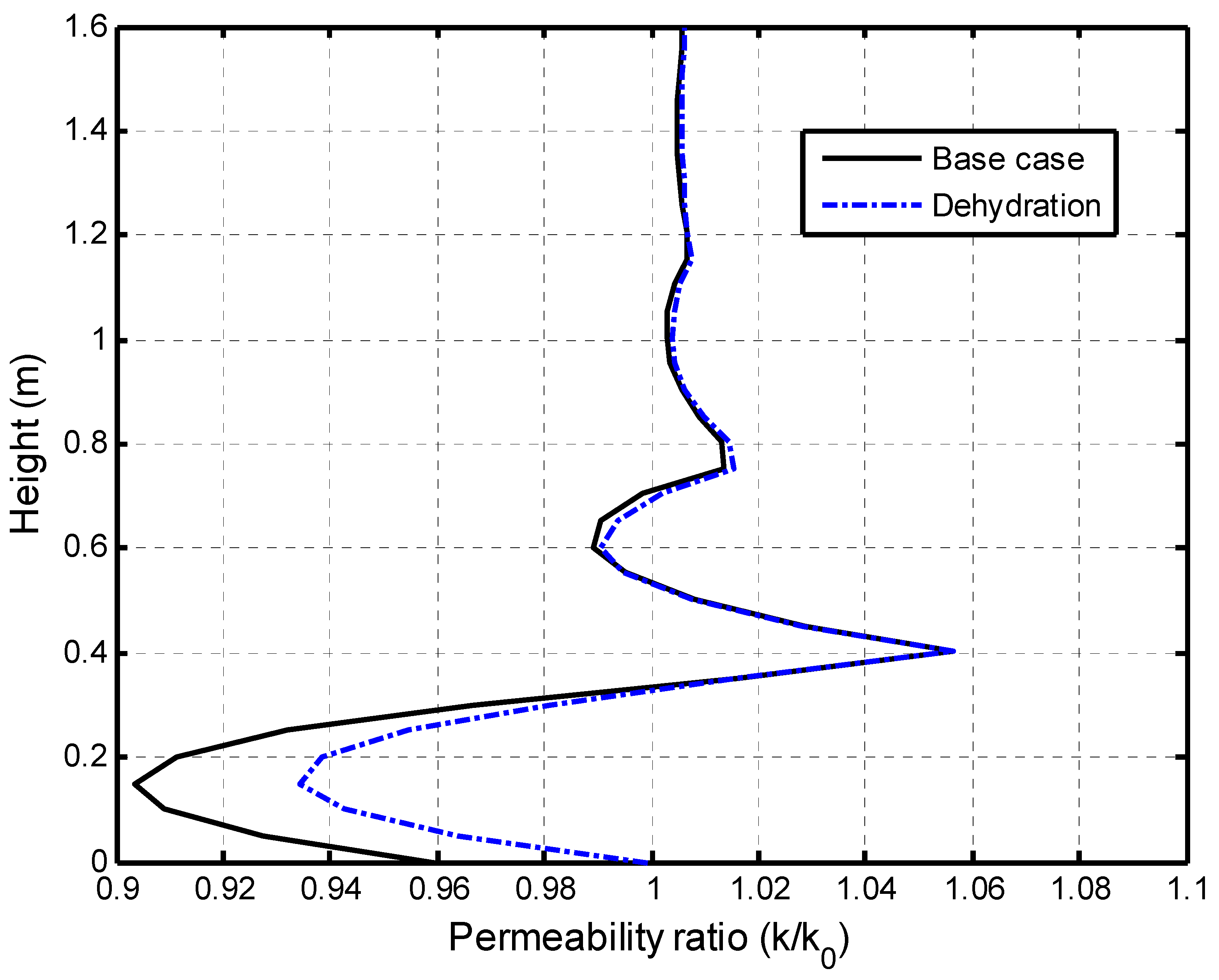
5.2.2. Impacts of Matrix Dehydration on CO2–Brine Displacement Process
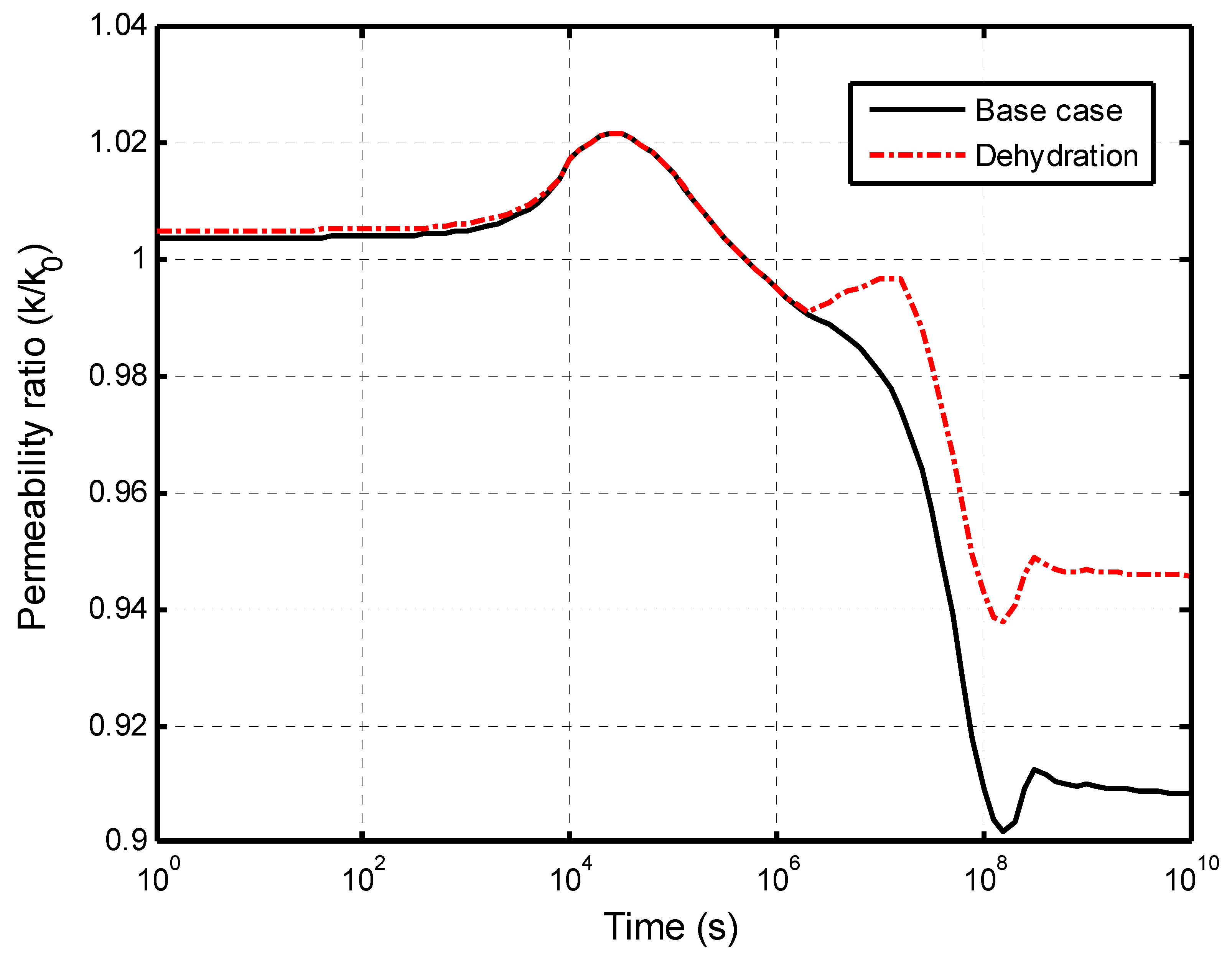
5.2.3. Self-Limiting Mechanism Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Capillary Pressure
Appendix B. Relative Permeability Model in Fracture Network
Appendix C. Gas Absorption and Sorption-Induced Swelling in Matrix
References
- Vialle, S.; Druhan, J.L.; Maher, K. Multi-phase flow simulation of CO2, leakage through a fractured caprock in response to mitigation strategies. Int. J. Greenh. Gas Control 2016, 44, 11–25. [Google Scholar] [CrossRef]
- Hardisty, P.E.; Sivapalan, M.; Brooks, P. The Environmental and Economic Sustainability of Carbon Capture and Storage. Int. J. Environ. Res. Public Health 2011, 8, 1460–1477. [Google Scholar] [CrossRef] [PubMed]
- Dalkhaa, C.; Shevalier, M.; Nightingale, M.; Mayer, B. 2-D reactive transport modeling of the fate of CO2 injected into a saline aquifer in the Wabamun Lake Area, Alberta, Canada. Appl. Geochem. 2013, 38, 10–23. [Google Scholar] [CrossRef]
- Zhou, Q.; Birkholzer, J.T. On scale and magnitude of pressure build-up induced by large-scale geologic storage of CO2. Greenh. Gases. 2015, 1, 11–20. [Google Scholar] [CrossRef]
- MacMinn, C.W.; Juanes, R. Post-injection spreading and trapping of CO2 in saline aquifers: Impact of the plume shape at the end of injection. Comput. Geosci. 2009, 13, 483–491. [Google Scholar] [CrossRef]
- Hou, L.H.; Yu, Z.C.; Luo, X.; Wu, S.T. Self-sealing of caprocks during CO2 geological sequestration. Energy 2022, 252, 124064. [Google Scholar] [CrossRef]
- Matter, J.M.; Kelemen, P.B. Permanent storage of carbon dioxide in geological reservoirs by mineral carbonation. Nat. Geosci. 2009, 2, 837–841. [Google Scholar] [CrossRef]
- Lee, S.; Fischer, T.B.; Stokes, M.R.; Klingler, R.J.; Ilavsky, J.; McCarty, D.K.; Wigand, M.O.; Derkowski, A.; Winans, R.E. Dehydration effect on the pore size, porosity, and fractal parameters of shale rocks: Ultrasmall-angle X-ray scattering study. Energy Fuels 2014, 28, 6772–6779. [Google Scholar] [CrossRef]
- Iglauer, S.; Al-Yaseri, A.Z.; Rezaee, R.; Lebedev, M. CO2 wettability of caprocks: Implications for structural storage capacity and containment security. Geophys. Res. Lett. 2016, 42, 9279–9284. [Google Scholar] [CrossRef]
- Boait, F.C.; White, N.J.; Bickle, M.J.; Chadwick, R.A.; Neufeld, J.A.; Huppert, H.E. Spatial and temporal evolution of injected CO2 at the Sleipner feld, North Sea. J. Geophys. Res. 2012, 117, B03309. [Google Scholar]
- Abdelouahab, A.; Abdelhakim, B. CO2-storage assessment and effective capacity in Algeria. Springerplus 2016, 5, 1038. [Google Scholar]
- Kivi, I.R.; Makhnenko, R.Y.; Vilarrasa, V. Two-Phase Flow Mechanisms Controlling CO2 Intrusion into Shaly Caprock. Transp. Porous Med. 2022, 141, 771–798. [Google Scholar] [CrossRef]
- Bickle, M.; Chadwick, A.; Huppert, H.E.; Hallworth, M.; Lyle, S. Modelling carbon dioxide accumulation at Sleipner: Implications for underground carbon storage. Earth Planet. Sc. Lett. 2007, 255, 164–176. [Google Scholar] [CrossRef]
- Heath, J.E.; Dewers, T.A.; McPherson, B.J.O.L.; Nemer, M.B.; Kotula, P.G. Pore-lining phases and capillary breakthrough pressure of mudstone caprocks: Sealing efficiency of geologic CO2 storage sites. Int. J. Greenh. Gas Control 2012, 11, 204–220. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, M.L. A critical review of breakthrough pressure for tight rocks and relevant factors. J. Nat. Gas Sci. Eng. 2022, 100, 104456. [Google Scholar] [CrossRef]
- Wang, J.G.; Peng, Y. Numerical modeling for the combined effects of two-phase flow, deformation, gas diffusion and CO2 sorption on caprock sealing efficiency. J. Geochem. Explor. 2014, 144, 154–167. [Google Scholar] [CrossRef]
- Espinoza, D.N.; Santamarina, J.C. CO2 breakthrough—Caprock sealing efficiency and integrity for carbon geological storage. Int. J. Greenh. Gas Control 2017, 66, 218–229. [Google Scholar] [CrossRef]
- Roshan, H.; Ehsani, S.; Marjo, C.E.; Andersen, M.S.; Acworth, R.I. Mechanisms of water adsorption into partially saturated fractured shales: An experimental study. Fuel 2015, 159, 628–637. [Google Scholar] [CrossRef]
- Ewy, R.T. Shale swelling/shrinkage and water content change due to imposed suction and due to direct brine contact. Acta Geotech. 2014, 9, 869–886. [Google Scholar] [CrossRef]
- Shang, X.J.; Wang, J.G.; Zhang, Z.Z.; Gao, F. A three-parameter permeability model for the cracking process of fractured rocks under temperature change and external loading. Int. J. Rock Mech. Min. 2019, 123, 104106. [Google Scholar] [CrossRef]
- Vega, B.; Dutta, A.; Kovscek, A.R. CT imaging of low-permeability, dual-porosity systems using high X-ray contrast gas. Transp. Porous Med. 2014, 101, 81–97. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.G.; Gao, F.; Ju, Y.; Tang, F. Impact of micro- and macro-scale consistent flows on well performance in fractured shale gas reservoirs. J. Nat. Gas Sci. Eng. 2016, 36, 1239–1252. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Jin, Z.J.; Li, S.Y. Coupled miscible carbon utilization-storage processes in fractured shales. Chem. Eng. J. 2022, 441, 135987. [Google Scholar] [CrossRef]
- Wang, J.G.; Ju, Y.; Gao, F.; Peng, Y.; Gao, Y. Effect of CO2 anisotropic sorption and swelling on caprock sealing efficiency. J. Clean. Prod. 2015, 103, 685–695. [Google Scholar] [CrossRef]
- Lyu, Q.; Ranjith, P.G.; Long, X.; Kang, Y.; Huang, M. A review of shale swelling by water adsorption. J. Nat. Gas Sci. Eng. 2015, 27, 1421–1431. [Google Scholar] [CrossRef]
- War, K.; Raveendran, G.; Arnepalli, D.N. Coupled hydromechanical model for evaluating the volume change and fluid permeation behavior of expansive clay smear in a fault upon interaction with CO2. Int. J. Greenh. Gas Control 2022, 119, 103696. [Google Scholar] [CrossRef]
- Ougier-Simonin, A.; Renard, F.; Boehm, C.; Vidal-Gilbert, S. Microfracturing and microporosity in shales. Earth-Sci. Rev. 2016, 162, 198–226. [Google Scholar] [CrossRef]
- Rohmer, J.; Tremosa, J.; Marty, N.C.M.; Audigane, P. Modelling of the CO2-induced degradation of a fractured caprock during leakage: Potential for a mechanical self-limiting process. Rock Mech. Rock Eng. 2017, 50, 2763–2783. [Google Scholar] [CrossRef]
- Liu, C.; Hoang, S.K.; Tran, M.H.; Abousleiman, Y.N.; Ewy, R.T. Poroelastic dual-porosity dual-permeability simulation of pressure transmission test on chemically active shale. J. Eng. Mech. 2017, 143, 04017016. [Google Scholar] [CrossRef]
- Kassa, A.M.; Gasda, S.E.; Landa-Marb’an, D.; Sandve, T.H.; Kumar, K. Field-scale impacts of long-term wettability alteration in geological CO2 storage. Int. J. Greenh. Gas Control 2022, 114, 103556. [Google Scholar] [CrossRef]
- Wang, K.; Xu, T.; Wang, F.; Tian, H. Experimental study of CO2 –brine–rock interaction during CO2, sequestration in deep coal seams. Int. J. Coal Geol. 2016, 154–155, 265–274. [Google Scholar] [CrossRef]
- Gao, F.; Liu, J.; Wang, J.G.; Ju, Y. Impact of micro-scale heterogeneity on gas diffusivity of organic-rich shale matrix. J. Nat. Gas Sci. Eng. 2017, 45, 75–87. [Google Scholar] [CrossRef]
- Chareonsuppanimit, P.; Mohammad, S.A.; Robinson, R.L.; Gasem, K.A.M. High-pressure adsorption of gases on shales: Measurements and modelling. Int. J. Coal Geol. 2012, 95, 34–46. [Google Scholar] [CrossRef]
- Bai, G.; Zhou, Z.J.; Li, X.M.; Cheng, Y.T.; Hu, K.; Chen, Y.; Zhou, X.H. Quantitative analysis of carbon dioxide replacement of adsorbed methane in different coal ranks using low-field NMR technique. Fuel 2022, 326, 124980. [Google Scholar] [CrossRef]
- Wang, J.G.; Ju, Y.; Gao, F.; Liu, J. A simple approach for the estimation of CO2 penetration depth into a caprock layer. J. Rock Mech. Geotech. 2016, 8, 75–86. [Google Scholar] [CrossRef]
- Broseta, D.; Tonnet, N.; Shah, V. Are rocks still water-wet in the presence of dense CO2 or H2S? Geofluids 2012, 12, 280–294. [Google Scholar] [CrossRef]
- Edvardsen, L.; Bhuiyan, M.H.; Cerasi, P.R.; Bjorge, R. Fast evaluation of caprock strength sensitivity to different CO2 solutions using small sample techniques. Rock Mech. Rock Eng. 2021, 54, 6123–6133. [Google Scholar] [CrossRef]
- Mouzakis, K.M.; Navarre-Sitchler, A.K.; Rother, G.; Banuelos, J.L.; Wang, X.Y.; Kaszuba, J.P.; Heath, J.E.; Miller, Q.R.S.; Alvarado, V.; McCray, J.E. Experimental study of porosity changes in shale caprocks exposed to CO2-saturated brines I: Evolution of mineralogy, pore connectivity, pore size distribution, and surface Area. Environ. Eng. Sci. 2016, 33, 725–735. [Google Scholar] [CrossRef]
- Fatah, A.; Bennour, Z.; Ben Mahmud, H.; Gholami, R.; Hossain, M.M. A review on the influence of CO2/shale interaction on shale properties: Implications of CCS in shales. Energies 2020, 13, 3200. [Google Scholar] [CrossRef]
- Liu, J.Y.; Wang, S.; Javadpour, F.; Feng, Q.H.; Cha, L.M. Hydrogen diffusion in clay slit: Implications for the geological storage. Energy Fuels 2022, 36, 7651–7660. [Google Scholar] [CrossRef]
- Brown, K.M.; Ransom, B. Porosity corrections for smectite-rich sediments: Impact on studied of compaction, fluid generation, and tectonic history. Geology 1996, 24, 843–846. [Google Scholar] [CrossRef]
- Yew, C.H.; Chenevert, M.E.; Wang, C.L.; Osisanya, S.O. Wellbore stress distribution produced by moisture adsorption. SPE Drill. Eng. 1990, 5, 311–316. [Google Scholar] [CrossRef]
- Rabbani, H.S.; Joekarniasar, V.; Shokri, N. Effects of intermediate wettability on entry capillary pressure in angular pores. J. Colloid Interf. Sci. 2016, 473, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Oostrom, M.; Grate, J.W.; Wietsma, T.W.; Warner, M. Liquid CO2 displacement of water in a dual-permeability pore network micromodel. Environ. Sci. Technol. 2011, 45, 7581–7588. [Google Scholar] [CrossRef] [PubMed]
- Gholami, M.; Talaie, M.R.; Roodpeyma, S. Mathematical modeling of gas dehydration using adsorption process. Chem. Eng. Sci. 2010, 65, 5942–5949. [Google Scholar] [CrossRef]
- Gerard, P.; Harrington, J.; Charlier, R.; Collin, F. Hydro-mechanical modeling of the development of preferential gas pathways in claystone. In Unsaturated Soils: Research and Applications; Springer Press: Berlin, Germany, 2012; pp. 175–180. [Google Scholar]
- Yang, K.; Zhou, J.P.; Xian, X.F.; Zhou, L.; Zhang, C.P.; Tian, S.F.; Lu, Z.H.; Zhang, F.S. Chemical-mechanical coupling effects on the permeability of shale subjected to supercritical CO2-water exposure. Energy 2022, 248, 123591. [Google Scholar] [CrossRef]
- Wang, J.S.; Samara, H.; Jaeger, P.; Ko, V.; Rodgers, D.; Ryan, D. Investigation for CO2 adsorption and wettability of reservoir rocks. Energy Fuels 2022, 36, 1626–1634. [Google Scholar] [CrossRef]
- Sang, G.J.; Liu, S.M. Carbonate caprock-brine-carbon dioxide interaction: Alteration of hydromechanical properties and implications on carbon dioxide leakage. SPE J. 2021, 26, 2780–2792. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO2-brine systems. Environ. Geol. 2008, 54, 1707–1722. [Google Scholar] [CrossRef]






| Relative Constant | Directions to the Bedding | ||
|---|---|---|---|
| Paralleling | Perpendicular | Average | |
| (MPa) | 6.5 | 6.2 | 6.0 |
| 1.5 | 3.7 | 2.7 | |
| Parameter | Unit | Value | Physical Meanings |
|---|---|---|---|
| 0.05 | Helium residual saturation | ||
| 0.6 | Water residual saturation | ||
| MPa | 2.1 | Initial entry capillary pressure | |
| Pa*s | 0.00085 | Water viscosity | |
| Pa*s | Helium viscosity | ||
| 3 | Water’s Corey parameter | ||
| 3 | Helium’s Corey parameter | ||
| 1.1 | Pore size distribution index | ||
| T | K | 300 | Experimental temperature |
| MPa | 4.5 | Initial pressure of water | |
| MPa | 6.66 | Initial pressure of helium | |
| 0.18 | Initial porosity | ||
| m2 | Initial shale permeability | ||
| MPa | 6 | Langmuir pressure of helium | |
| GPa | 3.8 | Overall Young’s modulus of shale | |
| GPa | 9.5 | Matrix Young’s modulus of shale | |
| 0.3 | Poisson’s ratio | ||
| kg/m3 | 2300 | Density of shale | |
| 0.005 | Helium’s relative permeability at end point | ||
| MPa | 6.62 | Outlet pressure of helium | |
| MPa | 4.5 | Outlet pressure of water |
| Parameter | Unit | Value | Physical Meanings |
|---|---|---|---|
| 0.15 | CO2 residual saturation | ||
| 0.6 | Brine water residual saturation | ||
| MPa | 10 | Capillary entry pressure at initial state | |
| T | K | 353.15 | Temperature taken from CO2 storage reservoirs |
| Pa*s | Viscosity of brine water | ||
| Pa*s | Viscosity of CO2 | ||
| 6.5 | Brine Water’s Corey parameter | ||
| 2.6 | CO2’s Corey parameter | ||
| 2.0 | Distribution index of pore size | ||
| MPa | 8.95 | Pressure at the top boundary | |
| MPa | 8.95 | Water pressure at initial state | |
| MPa | 19 | CO2 pressure at initial state | |
| 0.04 | Initial porosity | ||
| m2 | Initial permeability | ||
| MPa | 6 | CO2 Langmuir pressure | |
| m3/kg | 0.03 | Shale Langmuir sorption capacity | |
| GPa | 8 | Overall Young’s modulus of shale | |
| GPa | 20 | Matrix Young’s modulus of shale | |
| 0.30 | Poisson’s ratio | ||
| kg/m3 | 2300 | Density of shale | |
| MPa | 19 | Outlet pressure of CO2 | |
| MPa | 8.95 | Outlet pressure of brine water | |
| m2/s | Coefficient of diffusion in shale | ||
| 1.0 | Brine water relative permeability at end point | ||
| 0.015 | CO2 relative permeability at end point |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, X.; Wang, J.; Wang, H.; Wang, X. Combined Effects of CO2 Adsorption-Induced Swelling and Dehydration-Induced Shrinkage on Caprock Sealing Efficiency. Int. J. Environ. Res. Public Health 2022, 19, 14574. https://doi.org/10.3390/ijerph192114574
Shang X, Wang J, Wang H, Wang X. Combined Effects of CO2 Adsorption-Induced Swelling and Dehydration-Induced Shrinkage on Caprock Sealing Efficiency. International Journal of Environmental Research and Public Health. 2022; 19(21):14574. https://doi.org/10.3390/ijerph192114574
Chicago/Turabian StyleShang, Xiaoji, Jianguo Wang, Huimin Wang, and Xiaolin Wang. 2022. "Combined Effects of CO2 Adsorption-Induced Swelling and Dehydration-Induced Shrinkage on Caprock Sealing Efficiency" International Journal of Environmental Research and Public Health 19, no. 21: 14574. https://doi.org/10.3390/ijerph192114574
APA StyleShang, X., Wang, J., Wang, H., & Wang, X. (2022). Combined Effects of CO2 Adsorption-Induced Swelling and Dehydration-Induced Shrinkage on Caprock Sealing Efficiency. International Journal of Environmental Research and Public Health, 19(21), 14574. https://doi.org/10.3390/ijerph192114574









