Impact of Artificial Intelligence on Regional Green Development under China’s Environmental Decentralization System—Based on Spatial Durbin Model and Threshold Effect
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Equation Setting
3.2. Variable Selection
3.3. Data Source
4. Empirical Results
4.1. Baseline Regression Analysis
4.2. Analysis of Moderating Effects
4.3. Regional Heterogeneity Analysis
4.4. Analysis of Spatial Effects
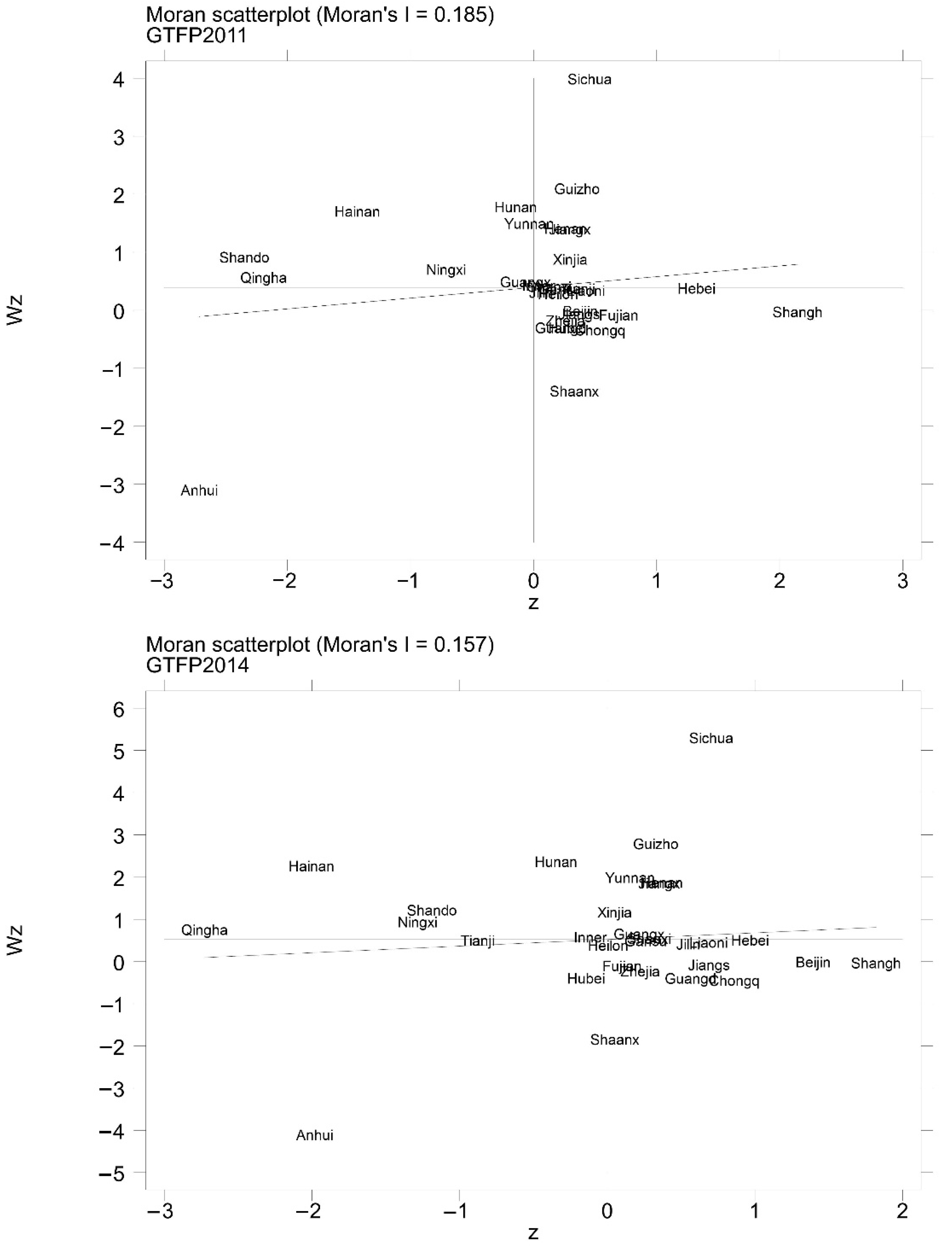
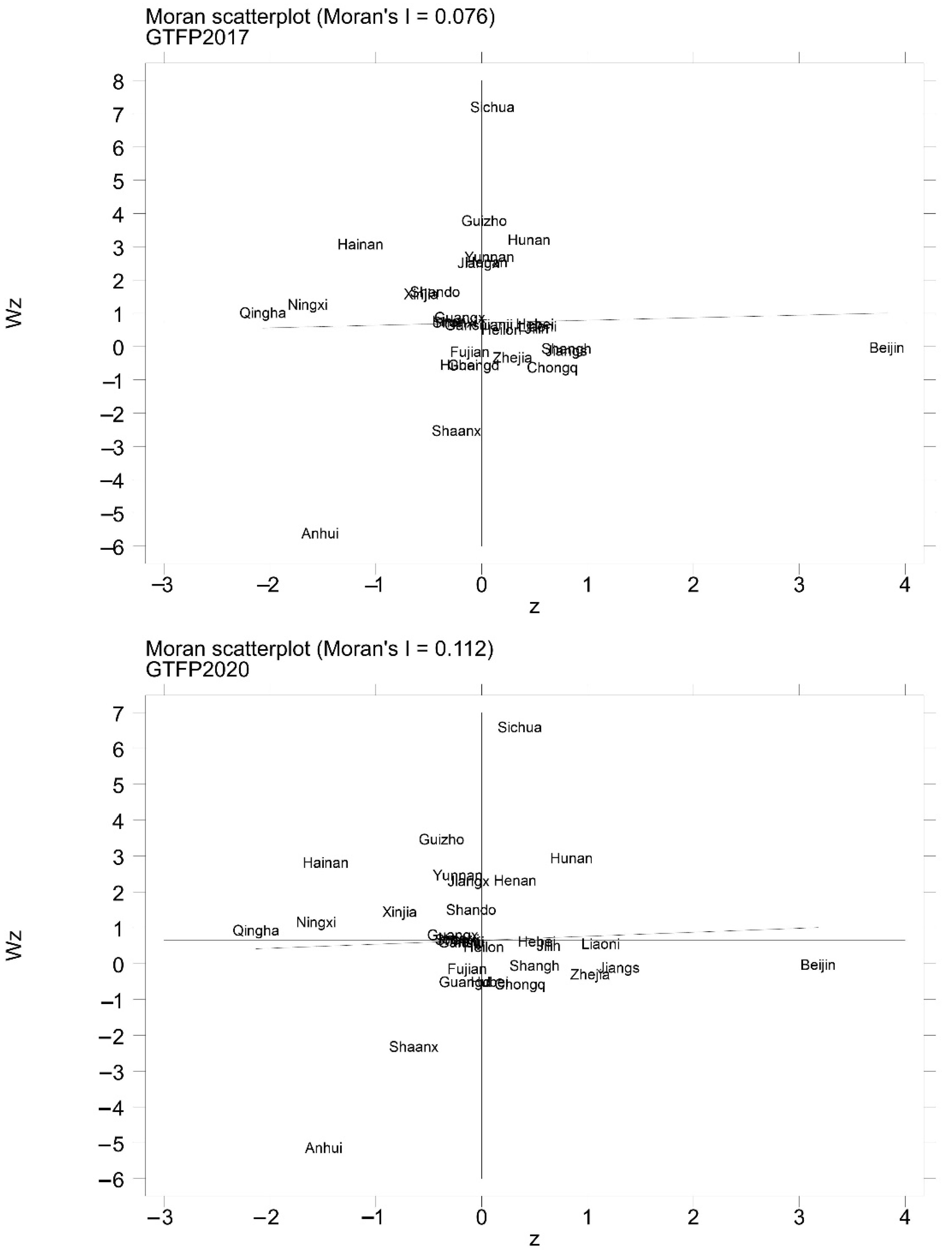
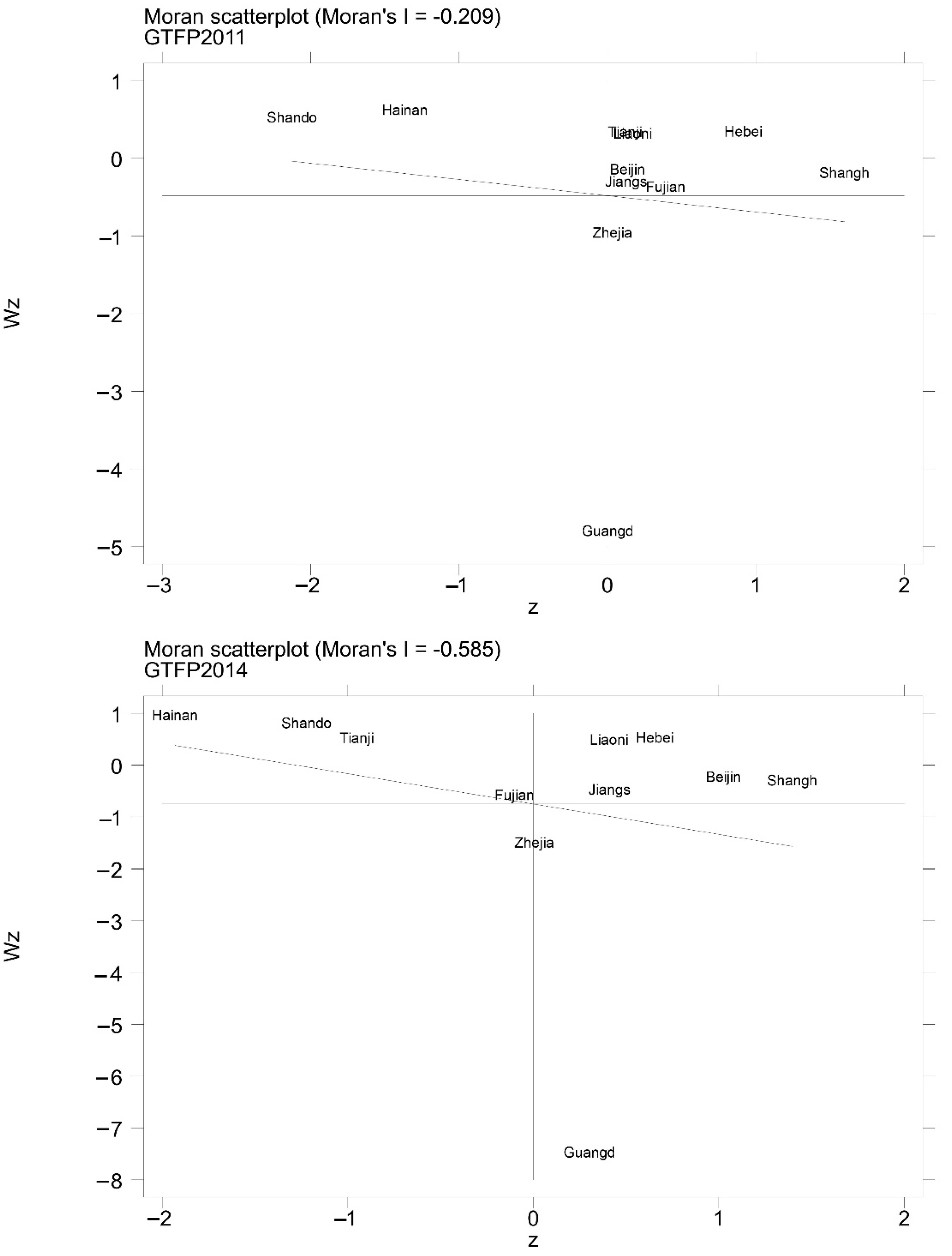
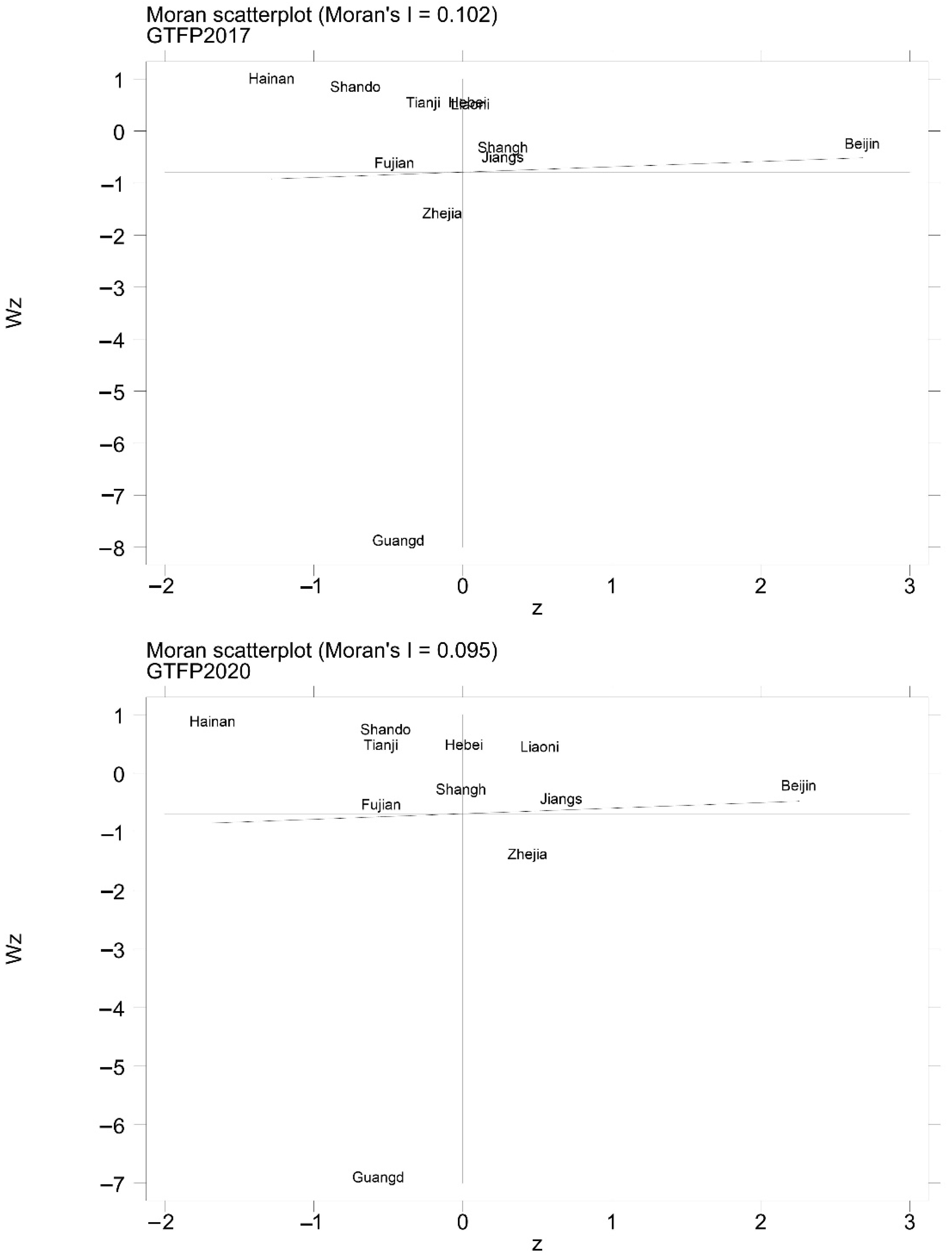
4.4.1. Analysis of Spatial Correlation
4.4.2. Spatial Econometric Analysis
4.4.3. MAUP Test
4.5. Robustness Test
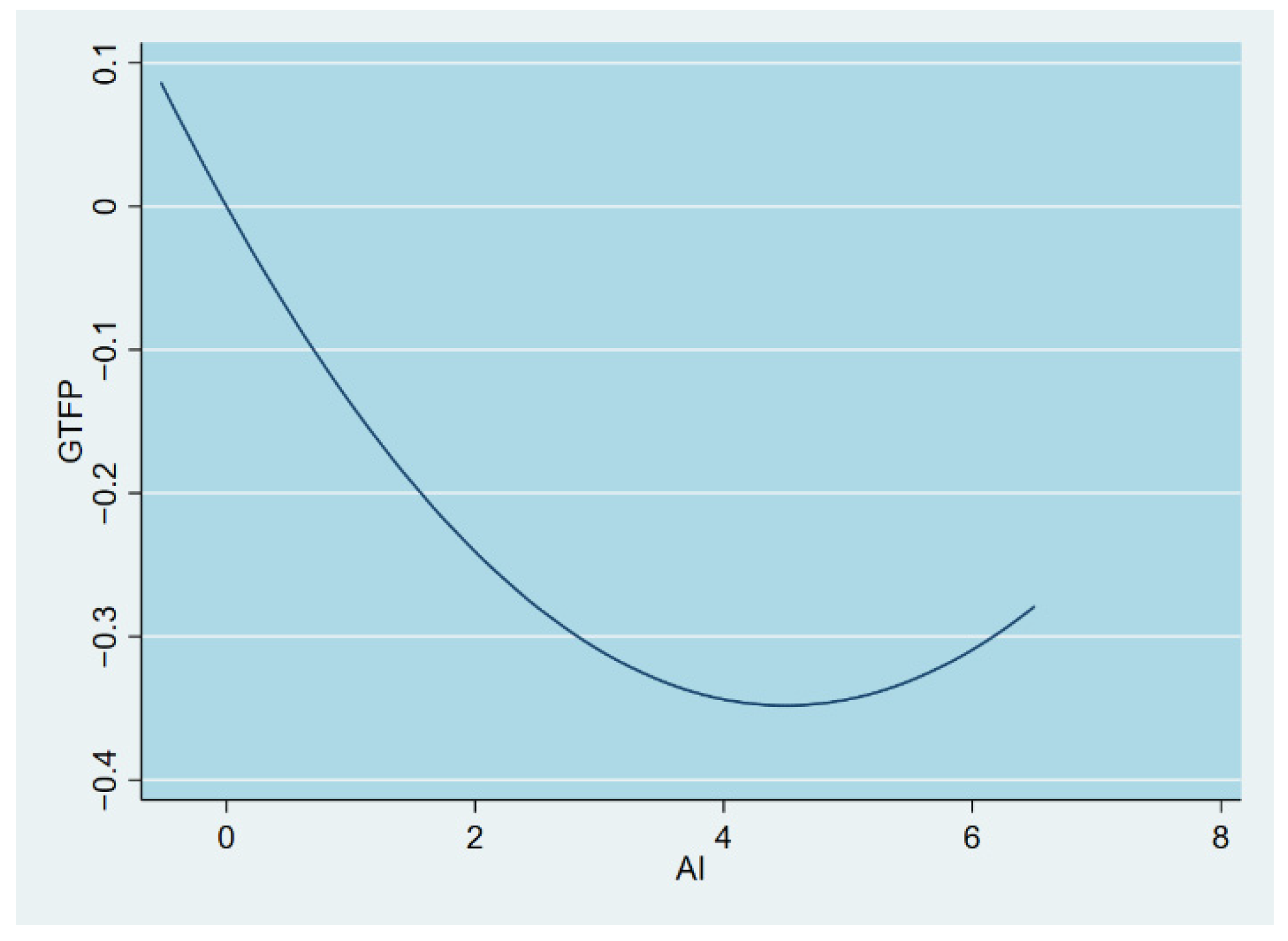
4.6. Threshold Regression Analysis
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GTFP | Green Total Factor Productivity |
| SBM | Slacks-based Measure |
| SDM | Spatial Durbin model |
| AI | Artificial Intelligence |
| ED | Environmental Decentralization |
| W-DDF | Weak Directional Distance Function |
| S-DDF | Strong Directional Distance Function |
| DMU | Decision Making Unit |
| IT | Information Technology |
| TI | Technological Innovation |
| RAC | Regional Absorptive Capacity |
| R&D | Research and Development |
| IS | Industrial Structure |
| FDI | Foreign Direct Investment |
| GOV | Government Intervention |
| ECS | Energy Consumption Structure |
| POP | Population Density |
| SEM | Spatial Error Model |
| SAR | Spatial Lag Model |
| MAUP | Modifiable Areal Unit Problem |
| OFDI | Outward Foreign Direct Investment |
References
- Chung, Y.H.; Fare, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Han, D.; Ding, Y.; Shi, Z. How does the development of the internet affect green total factor productivity? Evidence from China. IEEE Access 2020, 8, 216477–216490. [Google Scholar] [CrossRef]
- Chen, C.; Lan, Q.; Gao, M.; Sun, Y. Green total factor productivity growth and its determinants in China’s industrial economy. Sustainability 2018, 10, 1052. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.X.; Lu, G.Y.; Skitmore, M.; Ballesteros-Perez, P. A critical review of the current research mainstreams and the influencing factors of green total factor productivity. Environ. Sci. Pollut. Res. 2021, 28, 35392–35405. [Google Scholar] [CrossRef] [PubMed]
- Haenlein, M.; Kaplan, A. A brief history of artificial intelligence: On the past, present, and future of artificial intelligence. Calif. Manag. Rev. 2019, 61, 5–14. [Google Scholar] [CrossRef]
- Garg, V.; Srivastav, S.; Gupta, A. Application of Artificial Intelligence for Sustaining Green Human Resource Management. In Proceedings of the International Conference on Automation and Computational Engineering (ICACE), Greater Noida, India, 3–4 October 2018; pp. 113–116. [Google Scholar]
- Lyu, Y.; Wang, W.; Wu, Y.; Zhang, J. How does digital economy affect green total factor productivity? Evidence from China. Sci. Total Environ. 2022, 857, 159428. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, G.-H.; Huang, J.-C.; Hu, I.H.; Chiu, Y.-C. Performance of sustainable development and technological innovation based on green manufacturing technology of artificial intelligence and block chain. Math. Probl. Eng. 2021, 2021, 5527489. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, Z.G. Impact and threshold effect of Internet technology upgrade on forestry green total factor productivity: Evidence from China. J. Clean. Prod. 2020, 271, 122657. [Google Scholar] [CrossRef]
- Xiao, C.; Sun, J. Institutional governance influence mechanism and model of regional green development in China. Sci. Program. 2022, 2022, 2169684. [Google Scholar] [CrossRef]
- Fu, J.; Geng, Y. Public participation, regulatory compliance and green development in China based on provincial panel data. J. Clean. Prod. 2019, 230, 1344–1353. [Google Scholar] [CrossRef]
- Zhang, W.; Li, G.X. Environmental decentralization, environmental protection investment, and green technology innovation. Environ. Sci. Pollut. Res. 2022, 29, 12740–12755. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yang, X. Impact of China’s environmental decentralization on carbon emissions from energy consumption: An empirical study based on the dynamic spatial econometric model. Environ. Sci. Pollut. Res. Int. 2022, 29, 72140–72158. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Sui, B.; Liu, H.; Li, G. Environmental decentralization and innovation in China. Econ. Model. 2020, 93, 660–674. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, J.; Shi, L.; Forrest, J.Y.-L.; Yang, Z. Can artificial intelligence improve green economic growth? Evidence from China. Environ. Sci. Pollut. Res. Int. 2022. [Google Scholar] [CrossRef]
- Su, H.; Qu, X.; Tian, S.; Ma, Q.; Li, L.; Chen, Y. Artificial intelligence empowerment: The impact of research and development investment on green radical innovation in high-tech enterprises. Syst. Res. Behav. Sci. 2022, 39, 489–502. [Google Scholar] [CrossRef]
- Hemanand, D.; Mishra, N.; Premalatha, G.; Mavaluru, D.; Vajpayee, A.; Kushwaha, S.; Sahile, K. Applications of intelligent model to analyze the green finance for environmental development in the context of artificial intelligence. Comput. Intell. Neurosci. 2022, 2022, 2977824. [Google Scholar] [CrossRef]
- Zhao, P.Y.; Gao, Y.; Sun, X. How does artificial intelligence affect green economic growth?-Evidence from China. Sci. Total Environ. 2022, 834, 155306. [Google Scholar] [CrossRef]
- Alsamhi, S.H.; Almalki, F.A.; Afghah, F.; Hawbani, A.; Shvetsov, A.V.; Lee, B.; Song, H. Drones’ edge intelligence over smart environments in B5G: Blockchain and federated learning synergy. IEEE Trans. Green Commun. Netw. 2022, 6, 295–312. [Google Scholar] [CrossRef]
- Cicerone, G.; Faggian, A.; Montresor, S.; Rentocchini, F. Regional artificial intelligence and the geography of environmental technologies: Does local AI knowledge help regional green-tech specialization? Reg. Stud. 2022. [Google Scholar] [CrossRef]
- Papagiannis, F.; Gazzola, P.; Burak, O.; Pokutsa, I. An intelligent environmental plan for sustainable regionalisation policies: The case of Ukraine. Environ. Sci. Policy 2020, 108, 77–84. [Google Scholar] [CrossRef]
- Madhavan, R.; Kerr, J.A.; Corcos, A.R.; Isaacoff, B.P. Toward trustworthy and responsible artificial intelligence policy development. IEEE Intell. Syst. 2020, 35, 103–108. [Google Scholar] [CrossRef]
- Xiao, H.; You, J.L. The heterogeneous impacts of human capital on green total factor productivity: Regional diversity perspective. Front. Environ. Sci. 2021, 9, 713562. [Google Scholar] [CrossRef]
- Meng, F.S.; Zhao, Y. How does digital economy affect green total factor productivity at the industry level in China: From a perspective of global value chain. Environ. Sci. Pollut. Res. 2022, 29, 79497–79515. [Google Scholar] [CrossRef] [PubMed]
- Hailu, A.; Veeman, T.S. Non-parametric productivity analysis with undesirable outputs: An application to the Canadian pulp and paper industry. Am. J. Agric. Econ. 2001, 83, 605–616. [Google Scholar] [CrossRef]
- Li, L.; Tao, F. The choice of the optimal environmental regulation intensity in China’s manufacturing industry—Based on the perspective of green total factor productivity. China Ind. Econ. 2012, 5, 70–82. [Google Scholar]
- Chen, S.; Golley, J. ‘Green’ productivity growth in China’s industrial economy. Energy Econ. 2014, 44, 89–98. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Li, H.; Zhong, K. Digital economy development, industrial structure upgrading and green total factor productivity: Empirical evidence from China’s cities. Int. J. Environ. Res. Public Health 2022, 19, 2414. [Google Scholar] [CrossRef]
- Lee, C.C.; Lee, C.C. How does green finance affect green total factor productivity? Evidence from China. Energy Econ. 2022, 107, 105863. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, Z.; Geng, S. How do environmental regulation and foreign investment behavior affect green productivity growth in the industrial sector? An empirical test based on Chinese provincial panel data. J. Environ. Manag. 2021, 287, 112282. [Google Scholar] [CrossRef]
- Wang, H.; Cui, H.; Zhao, Q. Effect of green technology innovation on green total factor productivity in China: Evidence from spatial durbin model analysis. J. Clean. Prod. 2021, 288, 125624. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, J. Natural resource abundance, resource industry dependence and economic green growth in China. Resour. Policy 2020, 68, 101734. [Google Scholar] [CrossRef]
- Yan, Z.; Zou, B.; Du, K.; Li, K. Do renewable energy technology innovations promote China’s green productivity growth? Fresh evidence from partially linear functional-coefficient models. Energy Econ. 2020, 90, 104842. [Google Scholar] [CrossRef]
- Cui, X.; Wang, P.; Sensoy, A.; Duc Khuong, N.; Pan, Y. Green credit policy and corporate productivity: Evidence from a quasi-natural experiment in China. Technol. Forecast. Soc. Chang. 2022, 177, 121516. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. Impact of energy conservation policies on the green productivity in China’s manufacturing sector: Evidence from a three-stage DEA model. Appl. Energy 2016, 168, 351–363. [Google Scholar] [CrossRef]
- Zhang, D. Green credit regulation, induced R&D and green productivity: Revisiting the Porter Hypothesis. Int. Rev. Financ. Anal. 2021, 75, 101723. [Google Scholar]
- Gu, B.; Liu, J.; Ji, Q. The effect of social sphere digitalization on green total factor productivity in China: Evidence from a dynamic spatial Durbin model. J. Environ. Manag. 2022, 320, 115946. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y. Artificial intelligence: A survey on evolution, models, applications and future trends. J. Manag. Anal. 2019, 6, 1–29. [Google Scholar] [CrossRef]
- Song, M.L.; Peng, L.C.; Shang, Y.P.; Zhao, X. Green technology progress and total factor productivity of resource-based enterprises: A perspective of technical compensation of environmental regulation. Technol. Forecast. Soc. Chang. 2022, 174, 121276. [Google Scholar] [CrossRef]
- Balaprakash, P.; Dunn, J.B. Chapter 1—Overview of Data Science and Sustainability Analysis. In Data Science Applied to Sustainability Analysis; Dunn, J., Balaprakash, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–14. [Google Scholar]
- Wang, L.; Chen, Y.Y.; Ramsey, T.S.; Hewings, G.J.D. Will researching digital technology really empower green development? Technol. Soc. 2021, 66, 101638. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Wu, Z. Intelligence and green total factor productivity based on China’s province-level manufacturing data. Sustainability 2021, 13, 4989. [Google Scholar] [CrossRef]
- Han, J.; Chen, X.; Sun, Y.W. Technology or institutions: Which is the source of green economic growth in Chinese cities? Sustainability 2021, 13, 10934. [Google Scholar] [CrossRef]
- Bai, X.; Sun, X. Impact of internet development on total factor carbon productivity: Induced by cost, innovation, or demand? China Popul. Resour. Environ. 2021, 31, 105–117. [Google Scholar]
- Zhou, R. Measurement and spatial-temporal characteristics of inclusive green growth in China. Land 2022, 11, 1131. [Google Scholar] [CrossRef]
- Li, C.; Song, L.R. Regional differences and spatial convergence of green development in China. Sustainability 2022, 14, 8511. [Google Scholar] [CrossRef]
- Song, M.; Du, J.; Tan, K.H. Impact of fiscal decentralization on green total factor productivity. Int. J. Prod. Econ. 2018, 205, 359–367. [Google Scholar] [CrossRef]
- Wang, K.-L.; He, S.; Zhang, F.-Q. Relationship between FDI, fiscal expenditure and green total-factor productivity in China: From the perspective of spatial spillover. PLoS ONE 2021, 16, e0250798. [Google Scholar] [CrossRef]
- Song, K.; Bian, Y.; Zhu, C.; Nan, Y. Impacts of dual decentralization on green total factor productivity: Evidence from China’s economic transition. Environ. Sci. Pollut. Res. 2020, 27, 14070–14084. [Google Scholar] [CrossRef]
- Li, B.; Wu, S.S. Effects of local and civil environmental regulation on green total factor productivity in China: A spatial Durbin econometric analysis. J. Clean. Prod. 2017, 153, 342–353. [Google Scholar] [CrossRef]
- Hao, Y.; Xu, L.; Guo, Y.X.; Wu, H.T. The inducing factors of environmental emergencies: Do environmental decentralization and regional corruption matter? J. Environ. Manag. 2022, 302, 114098. [Google Scholar] [CrossRef]
- Qin, T.; Peng, J.; Deng, Z.; Wang, J. Environmental decentralization, environmental regulation and agricultural non-point source pollution. China Popul. Resour. Environ. 2021, 31, 61–70. [Google Scholar]
- Millimet, D.L. Environmental federalism: A survey of the empirical literature. Case W. Res. L. Rev. 2013, 64, 1669. [Google Scholar] [CrossRef]
- Xia, S.; You, D.; Tang, Z.; Yang, B. Analysis of the spatial effect of fiscal decentralization and environmental decentralization on carbon emissions under the pressure of officials’ promotion. Energies 2021, 14, 1878. [Google Scholar] [CrossRef]
- Hansen, B.E. Threshold effects in non-dynamic panels: Estimation, testing, and inference. J. Econom. 1999, 93, 345–368. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, S. The measurement of China’s provincial green total factor productivity based on DEA method: Does the choice of DEA model make difference. Acta Sci. Nat. Univ. Pekin. 2017, 53, 151–159. [Google Scholar]
- Ding, L.L.; Wu, M.L.; Jiao, Z.; Nie, Y.Y. The positive role of trade openness in industrial green total factor productivity-provincial evidence from China. Environ. Sci. Pollut. Res. 2022, 29, 6538–6551. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhu, X.; Wang, Y. China’s agricultural green total factor productivity based on carbon emission: An analysis of evolution trend and influencing factors. J. Clean. Prod. 2021, 278, 123692. [Google Scholar] [CrossRef]
- Teng, Z. Spatial differentiation and driving factors of green total factor productivity in China’s service industry. Quant. Tech. Econ. 2020, 37, 23–41. [Google Scholar]
- Li, Y.; Chen, Y.Y. Development of an SBM-ML model for the measurement of green total factor productivity: The case of pearl river delta urban agglomeration. Renew. Sustain. Energy Rev. 2021, 145, 111131. [Google Scholar] [CrossRef]
- Ren, Y. Research on the green total factor productivity and its influencing factors based on system GMM model. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 3497–3508. [Google Scholar] [CrossRef]
- Shan, H. Reestimating the capital stock of China: 1952~2006. Quant. Tech. Econ. 2008, 25, 17–31. [Google Scholar]
- Borland, J.; Coelli, M. Are robots taking our jobs? Aust. Econ. Rev. 2017, 50, 377–397. [Google Scholar] [CrossRef]
- Wang, R.; Qi, Z.; Shu, Y. Multiple relationships between fixed-asset investment and industrial structure evolution in China—Based on Directed Acyclic Graph (DAG) analysis and VAR model. Struct. Chang. Econ. Dyn. 2020, 55, 222–231. [Google Scholar] [CrossRef]
- Sigman, H. Decentralization and environmental quality: An international analysis of water pollution levels and variation. Land Econ. 2014, 90, 114–130. [Google Scholar] [CrossRef]
- Ran, Q.; Zhang, J.; Hao, Y. Does environmental decentralization exacerbate China’s carbon emissions? Evidence based on dynamic threshold effect analysis. Sci. Total Environ. 2020, 721, 137656. [Google Scholar] [CrossRef] [PubMed]
- Ganda, F. The impact of innovation and technology investments on carbon emissions in selected organisation for economic co-operation and development countries. J. Clean. Prod. 2019, 217, 469–483. [Google Scholar] [CrossRef]
- Wang, M.L.; Pang, S.L.; Hmani, I.; Hmani, I.; Li, C.F.; He, Z.X. Towards sustainable development: How does technological innovation drive the increase in green total factor productivity? Sustain. Dev. 2021, 29, 217–227. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, S.; Abbas, A. Relationship between R&D grants, R&D investment, and innovation performance: The moderating effect of absorptive capacity. J. Public Aff. 2020, 20, e1973. [Google Scholar]
- Schillaci, C.E.; Romano, M.; Nicotra, M. Territory’s absorptive capacity. Entrep. Res. J. 2013, 3, 109–126. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Lin, B. Economic growth model, structural transformation, and green productivity in China. Appl. Energy 2017, 187, 489–500. [Google Scholar] [CrossRef]
- Dong, B.; Xu, Y.; Fan, X. How to achieve a win-win situation between economic growth and carbon emission reduction: Empirical evidence from the perspective of industrial structure upgrading. Environ. Sci. Pollut. Res. 2020, 27, 43829–43844. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.X.; Shao, S.; Zhang, Y. Does FDI have energy-saving spillover effect in China? A perspective of energy-biased technical change. J. Clean. Prod. 2019, 234, 436–450. [Google Scholar] [CrossRef]
- You, D.; Zhang, Y.; Yuan, B. Environmental regulation and firm eco-innovation: Evidence of moderating effects of fiscal decentralization and political competition from listed Chinese industrial companies. J. Clean. Prod. 2019, 207, 1072–1083. [Google Scholar] [CrossRef]
- Wang, K.-L.; Pang, S.-Q.; Ding, L.-L.; Miao, Z. Combining the biennial Malmquist-Luenberger index and panel quantile regression to analyze the green total factor productivity of the industrial sector in China. Sci. Total Environ. 2020, 739, 140280. [Google Scholar] [CrossRef] [PubMed]
- Sarkodie, S.A.; Ozturk, I. Investigating the Environmental Kuznets Curve hypothesis in Kenya: A multivariate analysis. Renew. Sustain. Energy Rev. 2020, 117, 109481. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, Y.J. Does environmental regulatory system drive the green development of China’s pollution-intensive industries? J. Clean. Prod. 2022, 330, 129832. [Google Scholar] [CrossRef]
- Haans, R.F.J.; Pieters, C.; He, Z.-L. Thinking about U: Theorizing and testing u- and inverted u-shaped relationships in strategy research. Strateg. Manag. J. 2016, 37, 1177–1195. [Google Scholar] [CrossRef]
- Contreras, S.A.; Greenlee, A.J. Evaluating the effectiveness of ChileCompra’s Entrepreneurship Centers policy. Reg. Sci. Policy Pract. 2021, 13, 1262–1282. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, Y. Study on artificial intelligence: The state of the art and future prospects. J. Ind. Inf. Integr. 2021, 23, 100224. [Google Scholar] [CrossRef]
- Zhao, S.K.; Cao, Y.Q.; Feng, C.; Guo, K.; Zhang, J.N. How do heterogeneous R&D investments affect China’s green productivity: Revisiting the Porter hypothesis. Sci. Total Environ. 2022, 825, 154090. [Google Scholar]
- Kelejian, H.H.; Prucha, I.R. On the asymptotic distribution of the Moran I test statistic with applications. J. Econom. 2001, 104, 219–257. [Google Scholar] [CrossRef] [Green Version]
- Anselin, L. Spatial externalities, spatial multipliers, and spatial econometrics. Int. Reg. Sci. Rev. 2003, 26, 153–166. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Yu, D.; Li, X.; Yu, J.; Li, H. The impact of the spatial agglomeration of foreign direct investment on green total factor productivity of Chinese cities. J. Environ. Manag. 2021, 290, 112666. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L.; Bera, A.K.; Florax, R.; Yoon, M.J. Simple diagnostic tests for spatial dependence. Reg. Sci. Urban Econ. 1996, 26, 77–104. [Google Scholar] [CrossRef]
- Hennerdal, P.; Nielsen, M.M. A multiscalar approach for identifying clusters and segregation patterns that avoids the modifiable areal unit problem. Ann. Am. Assoc. Geogr. 2017, 107, 555–574. [Google Scholar] [CrossRef]
- Chung, S.; Hewings, G.J. A Short Exercise to Assess the Effects of Temporal and Spatial Aggregation on the Amounts of Spatial Spillovers. In Population, Place, and Spatial Interaction; Springer: Berlin/Heidelberg, Germany, 2019; pp. 35–56. [Google Scholar]
- Contreras, S.A. One size does not fit all: Evaluating the impact of microenterprise measurement on policy evaluation. Ann. Reg. Sci. 2022, 68, 587–613. [Google Scholar] [CrossRef]
- Rey, S.J.; Gallo, J.L. Spatial Analysis of Economic Convergence. In Palgrave Handbook of Econometrics; Spatial Analysis Research Center (SPARC): Tempe, AZ, USA, 2009; pp. 1251–1290. [Google Scholar]
- Hu, D.; Jiao, J.; Tang, Y.; Han, X.; Sun, H. The effect of global value chain position on green technology innovation efficiency: From the perspective of environmental regulation. Ecol. Indic. 2021, 121, 107195. [Google Scholar] [CrossRef]
- Hao, X.; Wang, X.; Wu, H.; Hao, Y. Path to sustainable development: Does digital economy matter in manufacturing green total factor productivity? Sustain. Dev. 2022. Online Version of Record before inclusion in an issue. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, X.; Hu, S. Effects of FDI and OFDI on green total factor productivity in China: An analysis based on spatial econometric models. Chin. J. Manag. Sci. 2021, 29, 81–91. [Google Scholar]
- Zhang, W.; Ge, Y. The spatial effect analysis of OFDI on green total factor productivity. Chin. J. Manag. Sci. 2021, 29, 26–35. [Google Scholar]
- Twum, F.A.; Long, X.; Salman, M.; Mensah, C.N.; Kankam, W.A.; Tachie, A.K. The influence of technological innovation and human capital on environmental efficiency among different regions in Asia-Pacific. Environ. Sci. Pollut. Res. 2021, 28, 17119–17131. [Google Scholar] [CrossRef] [PubMed]
- Arbia, G. Statistics, New Empiricism and Society in the Era of Big Data; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]

| Indicator Type | Indicator Designation | Indicator Meaning | Measurement Approach |
|---|---|---|---|
| Output | Expected output | Real GDP per year by region | Deflated by the regional GDP index and converted to GDP in constant 2000 prices |
| Non-desired output | Annual environmental pollution composite index by region | Entropy method [62] | |
| Input | Labor input | Annual year-end figures for all employed persons by province | Total amount of employed persons in urban entities, private enterprises, and self-employment in all provinces at annual year-end |
| Capital input | Actual physical capital stock per year by province | Perpetual Inventory Method [63] | |
| Energy input | Total annual energy consumption by region | Direct access to the China Statistical Yearbook |
| Variable Type | Variable Symbol | Variable Meaning | Mean | Standard Deviation | Min. | Max. |
|---|---|---|---|---|---|---|
| Explained Variable | GTFP | Green Total Factor Productivity | 0.95 | 0.23 | 0.33 | 2.12 |
| Core Explanatory Variable | AI | Artificial Intelligence | 4.76 | 0.99 | −0.52 | 6.50 |
| Adjustment Variable | ED | Environmental Decentralization | 1.13 | 0.47 | 0.50 | 3.20 |
| Threshold Variable | TI | Technology Innovation | 2.33 | 1.08 | 0.07 | 4.65 |
| RAC | Regional Absorptive Capacity | 10.84 | 1.00 | 7.56 | 13.29 | |
| Control Variable | IS | Industry Structure | 1.14 | 0.66 | 0.50 | 5.17 |
| FDI | Foreign Direct Investment | 5.49 | 1.66 | −1.22 | 7.72 | |
| GOV | Government Intervention | 0.11 | 0.03 | 0.06 | 0.23 | |
| ECS | Energy Consumption Structure | 0.16 | 0.04 | 0.08 | 0.26 | |
| POP | Population Density | 463.50 | 690.50 | 7.80 | 3829.00 |
| Variables | Model 1 GTFP | Model 2 GTFP | Model 3 GTFP |
|---|---|---|---|
| AI | −0.03 ** | −0.016 *** | 0.48 *** |
| (−2.51) | (−4.56) | (3.49) | |
| AI_sq | 0.02 *** | −0.05 *** | |
| (3.94) | (−3.54) | ||
| ED | 1.28 *** | ||
| (4.14) | |||
| AI*ED | −0.63 *** | ||
| (−4.76) | |||
| AI_sq*ED | 0.07 *** | ||
| (4.91) | |||
| IS | 0.22 *** | 0.21 *** | 0.21 *** |
| (6.40) | (6.36) | (6.42) | |
| FDI | 0.03 *** | 0.02 *** | 0.02 *** |
| (2.36) | (1.20) | (1.35) | |
| GOV | −2.93 *** | −2.87 *** | −2.21 *** |
| (−5.06) | (−5.08) | (−3.87) | |
| ECS | 0.56 | −0.26 | −0.49 |
| (1.16) | (−0.50) | (−0.98) | |
| POP | 0.00 ** | 0.00 *** | 0.00 ** |
| (2.80) | (2.71) | (2.24) | |
| _cons | 0.46 *** | 0.89 *** | −0.37 |
| (2.88) | (4.68) | (−1.04) | |
| N | 300 | 300 | 300 |
| R2 | 0.34 | 0.38 | 0.43 |
| R2_a | 0.25 | 0.29 | 0.35 |
| Variables | Model 4 GTFP East | Model 5 GTFP East | Model 6 GTFP Central | Model 7 GTFP Central | Model 8 GTFP West | Model 9 GTFP West |
|---|---|---|---|---|---|---|
| AI | −0.67 *** | 1.17 *** | −0.40 ** | −1.19 ** | −0.05 * | 0.08 *** |
| (−3.68) | (2.01) | (−2.65) | (−2.21) | (−1.84) | (3.59) | |
| AI_sq | 0.06 *** | −0.13 *** | 0.05 *** | 0.14 ** | 0.00 | |
| (3.31) | (−2.27) | (3.30) | (2.56) | (0.24) | ||
| ED | 2.91 *** | −1.87 | 0.52 *** | |||
| (2.72) | (−1.53) | (5.06) | ||||
| AI*ED | −1.38 *** | 0.86 | −0.12 *** | |||
| (−3.29) | (1.60) | (−5.8) | ||||
| AI_sq*ED | 0.15 *** | −0.10 * | ||||
| (3.61) | (−1.76) | |||||
| IS | 0.35 *** | 0.35 * | 0.05 | 0.07 | 0.12 ** | 0.12 *** |
| (6.10) | (5.58) | (1.04) | (1.49) | (2.69) | (3.39) | |
| FDI | 0.12 ** | 0.11 * | 0.01 | −0.00 | 0.02 | 0.02 |
| (3.45) | (2.99) | (0.32) | (−0.18) | (1.44) | (1.33) | |
| GOV | −4.61 *** | −3.95 *** | −3.61 *** | −4.25 *** | −2.98 *** | −1.90 *** |
| (−4.14) | (−3.51) | (−3.39) | (−4.06) | (−5.34) | (−3.69) | |
| ECS | 2.04 | 2.51 ** | 0.76 | 1.45 | −0.61 | −0.68 |
| (1.66) | (2.28) | (0.67) | (1.19) | (−1.35) | (−1.81) | |
| POP | 0.00 | −0.00 | −0.01* | −0.01** | 0.00 | 0.00 |
| (0.79) | (−0.33) | (−1.91) | (−0.47) | (0.40) | (1.04) | |
| _cons | 1.40 ** | −2.34 | 3.43 *** | 6.62 *** | 1.17 *** | 0.41 |
| (2.26) | (−1.53) | (3.89) | (3.90) | (3.91) | (1.41) | |
| N | 110 | 110 | 80 | 80 | 110 | 110 |
| R2 | 0.63 | 0.73 | 0.51 | 0.58 | 0.41 | 0.58 |
| R2_a | 0.55 | 0.67 | 0.41 | 0.46 | 0.31 | 0.49 |
| Variables | I | E(I) | sd(I) | z | p-Value * |
|---|---|---|---|---|---|
| GTFP2011 | 0.60 | −0.03 | 0.04 | 15.95 | 0.00 *** |
| GTFP2012 | −0.72 | −0.03 | 0.04 | −15.49 | 0.00 *** |
| GTFP2013 | 3.09 | −0.03 | 0.05 | 69.55 | 0.00 *** |
| GTFP2014 | 1.04 | −0.03 | 0.04 | 25.05 | 0.00 *** |
| GTFP2015 | 0.27 | −0.03 | 0.04 | 7.01 | 0.00 *** |
| GTFP2016 | −2.62 | −0.03 | 0.04 | −59.03 | 0.00 *** |
| GTFP2017 | 2.42 | −0.03 | 0.02 | 111.34 | 0.00 *** |
| GTFP2018 | 1.85 | −0.03 | 0.04 | 45.87 | 0.00 *** |
| GTFP2019 | −1.94 | −0.03 | 0.04 | −45.79 | 0.00 *** |
| GTFP2020 | −2.05 | −0.03 | 0.04 | −52.13 | 0.00 *** |
| Test | Statistic | p-Value | |
|---|---|---|---|
| LM test | LM-SEM | 11.99 | 0.00 *** |
| Robust LM-SEM | 6.44 | 0.02 ** | |
| LM-SAR | 6.98 | 0.01 ** | |
| Robust LM-SAR | 1.43 | 0.29 | |
| Hausman test | 0.05 * | ||
| LR test | SEM nested in SDM | 15.64 | 0.03 ** |
| SAR nested in SDM | 17.81 | 0.01 ** | |
| Wald test | SDM-Error | 32.21 | 0.00 *** |
| SDM-Lag | 27.64 | 0.00 *** | |
| LR test | Ind nested in both | 8.54 | 0.58 |
| Time nested in both | 360.48 | 0.00 *** | |
| Variables | Model 11 SDM | Model 12 SDM Direct | Model 13 SDM Indirect | Model 14 SDM Total | Model 15 SDM Moderating |
|---|---|---|---|---|---|
| AI | −0.07 | −0.07 | 0.00 | −0.07 | 0.31 |
| (0.05) | (0.05) | (0.23) | (0.23) | (0.20) | |
| AI_sq | 0.01 ** | 0.01 ** | 0.00 | 0.01 | −0.04 ** |
| (0.01) | (0.01) | (0.04) | (0.04) | (0.02) | |
| ED | 0.51 | ||||
| (0.43) | |||||
| AI*ED | −0.38 ** | ||||
| (0.19) | |||||
| AI_sq*ED | 0.06 *** | ||||
| (0.02) | |||||
| IS | 0.15 *** | 0.15 *** | 0.09 | 0.25 | 0.09 *** |
| (0.02) | (0.02) | (0.25) | (0.25) | (0.03) | |
| FDI | 0.04 *** | 0.04 *** | −0.01 | 0.03 | 0.04 *** |
| (0.01) | (0.01) | (0.09) | (0.09) | (0.01) | |
| GOV | −1.03 * | −1.07 ** | 1.47 | 0.40 | −0.33 |
| (0.55) | (0.53) | (4.07) | (4.11) | (0.56) | |
| ECS | −1.18 *** | −1.14 *** | 0.75 | −0.39 | −1.08 *** |
| (0.33) | (0.35) | (8.27) | (8.31) | (0.33) | |
| POP | 0.00 * | 0.00 | −0.00 | −0.00 | 0.00 |
| (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | |
| W*AI | 0.02 | 0.42 | |||
| (0.22) | (2.00) | ||||
| W*AI_sq | −0.00 | 0.06 | |||
| (0.04) | (0.31) | ||||
| W*ED | 4.97 | ||||
| (23.35) | |||||
| W*(AI*ED) | −1.02 | ||||
| (4.89) | |||||
| W*(AI_sq*ED) | 0.04 | ||||
| (0.19) | |||||
| W*IS | 0.06 | 0.88 | |||
| (0.22) | (4.06) | ||||
| W*FDI | −0.02 | 0.32 | |||
| (0.09) | (1.69) | ||||
| W*GOV | 1.04 | −9.35 | |||
| (3.60) | (44.87) | ||||
| W*ECS | 1.34 | −23.53 | |||
| (7.56) | (118.70) | ||||
| W*POP | −0.00 | 0.00 | |||
| (0.00) | (0.02) | ||||
| sigma2_e | 0.03 *** | 0.03 *** | |||
| (0.00) | (0.00) | ||||
| Log-likelihood | 111.82 | 125.09 | |||
| R2 | 0.44 | 0.36 |
| Variables | Model 16 SDM | Model 17 SDM Direct | Model 18 SDM Indirect | Model 19 SDM Total | Model 20 SDM Moderating |
|---|---|---|---|---|---|
| AI | −0.68 *** | −0.69 *** | 0.39 | −0.31 | 1.37 *** |
| (0.16) | (0.17) | (0.66) | (0.65) | (0.52) | |
| AI_sq | 0.06 *** | 0.06 *** | −0.04 | 0.02 | −0.15 *** |
| (0.02) | (0.02) | (0.08) | (0.08) | (0.05) | |
| ED | 3.09 *** | ||||
| (0.92) | |||||
| AI*ED | −1.46 *** | ||||
| (0.37) | |||||
| AI_sq*ED | 0.15 *** | ||||
| (0.04) | |||||
| IS | 0.32 *** | 0.32 *** | 0.07 | 0.39 | 0.31 *** |
| (0.07) | (0.07) | (0.27) | (0.26) | (0.08) | |
| FDI | 0.22 *** | 0.22 *** | 0.08 | 0.29 ** | 0.16 *** |
| (0.04) | (0.04) | (0.12) | (0.12) | (0.04) | |
| GOV | −5.32 *** | −5.34 ** | 2.46 | −2.88 | −4.45 *** |
| (1.26) | (1.23) | (4.14) | (4.24) | (1.24) | |
| ECS | 3.12 ** | 3.39 *** | −2.74 | −0.65 | 3.93 *** |
| (1.52) | (1.56) | (10.49) | (10.41) | (1.37) | |
| POP | −0.00 | −0.00 | 0.00 | 0.00 | 0.00 |
| (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | |
| W*AI | 0.38 | 13.97 *** | |||
| (0.74) | (4.74) | ||||
| W*AI_sq | −0.05 | −1.40 *** | |||
| (0.09) | (0.50) | ||||
| W*ED | 31.44 *** | ||||
| (8.90) | |||||
| W*(AI*ED) | −13.93 *** | ||||
| (3.86) | |||||
| W*(AI_sq*ED) | 1.51 *** | ||||
| (0.40) | |||||
| W*IS | 0.13 | −4.48 *** | |||
| (0.31) | (1.03) | ||||
| W*FDI | 0.12 | −3.01 *** | |||
| (0.14) | (0.61) | ||||
| W*GOV | 1.49 | 40.64 *** | |||
| (4.55) | (0) | ||||
| W*ECS | −3.82 | 2.81 | |||
| (11.35) | (22.56) | ||||
| W*POP | 0.00 | −0.07 ** | |||
| (0.00) | (0.03) | ||||
| sigma2_e | 0.01 *** | 0.03 *** | |||
| (0.00) | (0.00) | ||||
| Log-likelihood | 107.27 | 124.86 | |||
| R2 | 0.01 | 0.00 |
| Variables | Model 21 GTFP | Model 22 GTFP | Model 23 SDM Direct | Model 24 SDM Indirect | Model 25 SDM Total |
|---|---|---|---|---|---|
| AI | −0.26 *** | 0.37 *** | −0.13 *** | 0.03 | −0.11 |
| (−6.32) | (2.88) | (0.06) | (0.28) | (0.29) | |
| AI_sq | 0.03 *** | −0.04 *** | 0.02 *** | −0.00 | 0.02 |
| (5.96) | (−2.85) | (0.01) | (0.04) | (0.04) | |
| ED | 1.29 *** | ||||
| (4.50) | |||||
| AI*ED | −0.63 *** | ||||
| (−5.17) | |||||
| AI_sq*ED | 0.07 *** | ||||
| (5.35) | |||||
| IS | 0.17 *** | 0.18 *** | 0.13 *** | 0.14 | 0.27 |
| (5.20) | (5.73) | (0.02) | (0.39) | (0.39) | |
| FDI | 0.01 | 0.01 | 0.04 *** | −0.02 | 0.02 |
| (0.62) | (0.84) | (0.01) | (0.08) | (0.08) | |
| GOV | −2.86 *** | −2.19 *** | −0.89 * | 0.79 | −0.10 |
| (−5.48) | (−4.20) | (0.51) | (5.07) | (5.12) | |
| ECS | −0.41 | −0.69 | −1.37 ** | 0.09 | −1.28 |
| (−0.85) | (−1.49) | (0.34) | (8.32) | (8.36) | |
| POP | 0.00 *** | 0.00 ** | 0.00 | −0.00 | −0.00 |
| (3.13) | (2.49) | (0.00) | (0.00) | (0.00) | |
| _cons | 1.17 *** | −0.07 | |||
| (6.17) | (−0.20) | ||||
| N | 300 | 300 | 300 | 300 | 300 |
| R2 | 0.39 | 0.45 | 0.43 | 0.43 | 0.43 |
| R2_a | 0.30 | 0.37 |
| Variables | Model 26 GTFP | Model 27 GTFP | Model 28 SDM Direct | Model 29 SDM Indirect | Model 30 SDM Total |
|---|---|---|---|---|---|
| AI | −0.15 *** | 0.44 *** | −0.07 | 0.10 | 0.031 |
| (−4.39) | (3.21) | (0.05) | (0.32) | (0.32) | |
| AI_sq | 0.016 *** | −0.05 *** | 0.01 ** | −0.02 | −0.01 |
| (3.72) | (−3.23) | (0.01) | (0.06) | (0.06) | |
| ED | 1.18 *** | ||||
| (3.84) | |||||
| AI*ED | −0.58 *** | ||||
| (−4.41) | |||||
| AI_sq*ED | 0.06 *** | ||||
| (4.48) | |||||
| IS | 0.19 *** | 0.20 *** | 0.15 *** | 0.02 | 0.18 |
| (5.56) | (5.94) | (0.02) | (0.31) | (0.32) | |
| FDI | 0.01 | 0.02 | 0.04 *** | −0.03 | 0.01 |
| (1.01) | (1.32) | (0.01) | (0.10) | (0.10) | |
| GOV | −3.14 *** | −2.52 *** | −1.07 ** | −0.31 | −1.38 |
| (−5.59) | (−4.38) | (0.54) | (5.17) | (5.25) | |
| ECS | −0.11 | −0.38 | −1.09 *** | 4.97 | 3.87 |
| (−0.22) | (−0.77) | (0.41) | (11.82) | (11.86) | |
| POP | 0.00 | 0.00 | 0.00 | −0.00 | −0.00 |
| (1.55) | (1.30) | (0.00) | (0.00) | (0.00) | |
| OFDI | −0.21 *** | −0.18 *** | −0.01 | 0.12 | |
| (−3.10) | (−2.67) | (0.07) | (0.37) | ||
| _cons | 1.15 *** | −0.06 | |||
| (5.62) | (−0.16) | ||||
| N | 300 | 300 | 300 | 300 | 300 |
| R2 | 0.40 | 0.45 | 0.46 | 0.46 | 0.46 |
| R2_a | 0.31 | 0.36 |
| Threshold Variables | Number of Thresholds | F-Statistic | p-Value | Threshold Value | ||
|---|---|---|---|---|---|---|
| 1% | 5% | 10% | ||||
| TI | 1 | 107.12 *** | 0.00 | 35.30 | 27.53 | 22.56 |
| 2 | 15.98 | 0.25 | 226.22 | 171.77 | 124.45 | |
| RAC | 1 | 47.40 ** | 0.01 | 47.53 | 33.12 | 27.86 |
| 2 | 23.93 | 0.15 | 54.73 | 36.35 | 27.64 | |
| Threshold Variables | Number of Thresholds | Estimated Values | Confidence Intervals |
|---|---|---|---|
| TI | Single Threshold | 4.27 | [4.25, 4.31] |
| RAC | Single Threshold | 12.15 | [12.08, 12.22] |
| Threshold Variables | Model 28 TI | Model 29 RAC |
|---|---|---|
| IFI (TI ≤ 4.27) | −0.02 ** | |
| (−2.21) | ||
| IFI (TI > 4.27) | 0.05 *** | |
| (3.74) | ||
| IFI (RAC ≤ 12.15) | −0.03 ** | |
| (0.02) | ||
| IFI (RAC > 12.15) | 0.01 | |
| (0.62) | ||
| IS | 0.17 *** | 0.20 *** |
| (5.92) | (6.37) | |
| FDI | 0.02 * | 0.03 ** |
| (1.74) | (2.17) | |
| GOV | −2.57 *** | −2.64 *** |
| (−5.17) | (−4.85) | |
| ECS | 0.26 | −0.02 |
| (0.62) | (−0.05) | |
| POP | 0.00 * | 0.00 * |
| (1.96) | (1.91) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Cao, H.; Sun, J. Impact of Artificial Intelligence on Regional Green Development under China’s Environmental Decentralization System—Based on Spatial Durbin Model and Threshold Effect. Int. J. Environ. Res. Public Health 2022, 19, 14776. https://doi.org/10.3390/ijerph192214776
Fang Y, Cao H, Sun J. Impact of Artificial Intelligence on Regional Green Development under China’s Environmental Decentralization System—Based on Spatial Durbin Model and Threshold Effect. International Journal of Environmental Research and Public Health. 2022; 19(22):14776. https://doi.org/10.3390/ijerph192214776
Chicago/Turabian StyleFang, Yuxin, Hongjun Cao, and Jihui Sun. 2022. "Impact of Artificial Intelligence on Regional Green Development under China’s Environmental Decentralization System—Based on Spatial Durbin Model and Threshold Effect" International Journal of Environmental Research and Public Health 19, no. 22: 14776. https://doi.org/10.3390/ijerph192214776
APA StyleFang, Y., Cao, H., & Sun, J. (2022). Impact of Artificial Intelligence on Regional Green Development under China’s Environmental Decentralization System—Based on Spatial Durbin Model and Threshold Effect. International Journal of Environmental Research and Public Health, 19(22), 14776. https://doi.org/10.3390/ijerph192214776






