How Do Environmental Regulations and Outward Foreign Direct Investment Impact the Green Total Factor Productivity in China? A Mediating Effect Test Based on Provincial Panel Data
Abstract
1. Introduction
2. Literature Review
2.1. The Measurement of Green Total Factor Productivity
2.2. Environmental Regulation and Its Impacts on GTFP and OFDI
2.3. OFDI and Its Impact on Green Economy Development
3. Theoretical Framework and Research Hypotheses
3.1. Environmental Regulations in China
3.1.1. Command-and-Control Regulation
3.1.2. Market-Based Regulation
3.1.3. Informal Regulation
3.2. The Theoretical Mechanism of ERs on OFDI and GTFP
3.2.1. The Crowding-Out and Technology Seeking Effects of ERs on OFDI
3.2.2. The Promoting and Preventing Effects of ERs on GTFP through OFDI
3.3. The Theoretical Mechanism of OFDI on GTFP
The Green Spillover Effect of OFDI on GTFP
4. Research Design
4.1. The GTFP Measurement
4.1.1. Non-Radial Directional Distance Function (NDDF) with Undesirable Outputs
4.1.2. GML Index and Its Decomposition
4.2. Model, Variables, and Data Sources
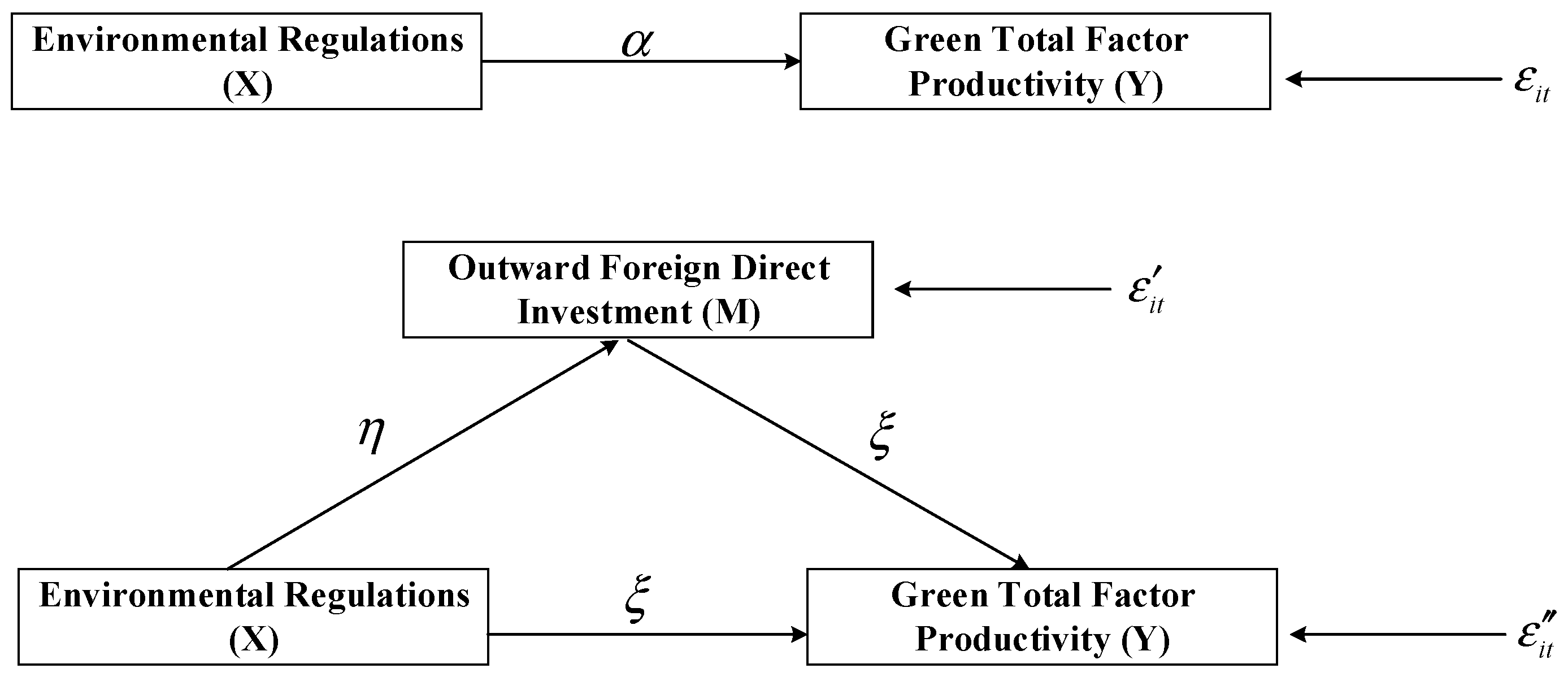
4.2.1. The Econometric Model
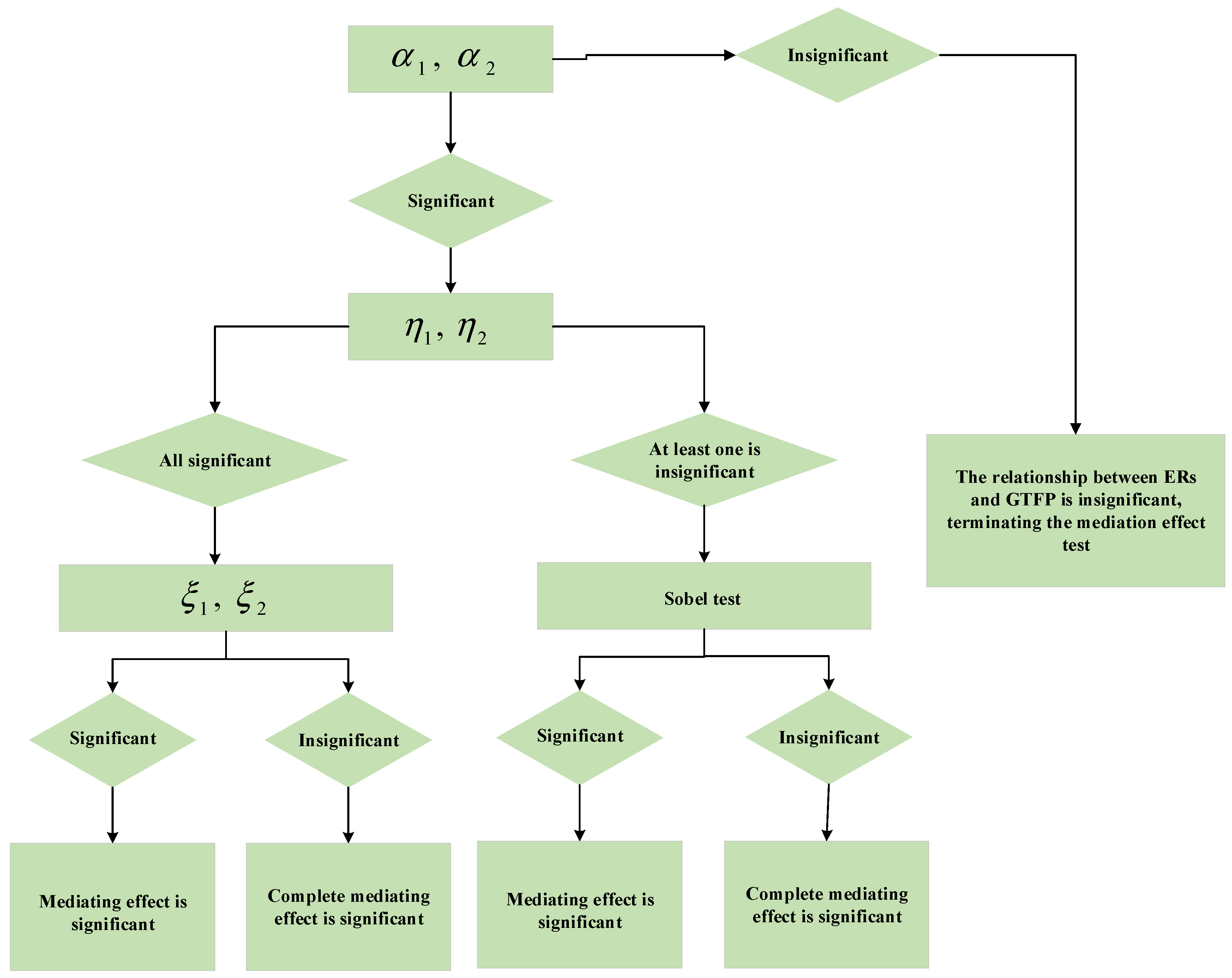
4.2.2. The Non-Linear Mediating Effect Model
4.2.3. Variables and Data Processing
Dependent Variable
Core Independent Variable
Control Variables
4.2.4. Data Sources
5. Results and Discussions
5.1. Results and Analysis of GTFP and Its Decomposition
5.2. Estimated Results of the Two-Step Econometric Model
5.2.1. The Effect of ERs on OFDI
5.2.2. The Effects of ERs and OFDI on GTFP
5.3. Endogenous and GMM Estimation
5.4. Heterogeneity Analysis
5.4.1. The Effect of ERs on OFDI across Regions
5.4.2. The Effect of ERs and OFDI on GTFP across Regions
5.4.3. Analysis of the Mediating Effect across Regions
5.5. Analysis of the Mediating Effect
6. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Coefficients | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Full sample | POOL | 0.587 | 0.002 | 0.026 | 0 | 0.043 | 1.781 | 0.006 | −0.05 | 0 | 11.85 | 29.21 | 0.976 | 59.41 |
| FE | −1.276 | 0.004 | 0.057 | 0 | 0.039 | 1.431 | 0.004 | −0.042 | 0 | |||||
| Reference | Table 8 | Table 7 | Table 4 | |||||||||||
| Eastern area | POOL | −0.460 | 0.008 | 0.019 | −0.001 | −0.013 | 2.061 | −0.040 | −0.058 | 0.001 | 12.08 | 5.41 | 1.201 | 4.540 |
| FE | −1.151 | 0.007 | 0.052 | −0.001 | 0.003 | 1.292 | −0.007 | −0.050 | 0 | |||||
| Reference | Table A5 and Table A6 | Table A3 and Table A4 | Regional descriptive statistics | |||||||||||
| Central area | POOL | −3.287 | −0.024 | 0.132 | 0.002 | 0.037 | −2.304 | −0.012 | 0.089 | 0.001 | 11.94 | 6.873 | 0.717 | 5.019 |
| FE | −4.511 | −0.020 | 0.189 | 0.001 | 0.086 | −0.535 | −0.067 | 0.034 | 0003 | |||||
| Reference | Table A5 and Table A6 | Table A3 and Table A4 | Regional descriptive statistics | |||||||||||
| Western area | POOL | −1.671 | 0.003 | 0.077 | 0 | 0.007 | 1.725 | 0.013 | −0.034 | 0 | 11.55 | 69.25 | 0.802 | 84.13 |
| FE | −1.289 | 0.004 | 0.060 | 0 | 0.058 | 2.019 | 0.006 | −0.059 | 0 | |||||
| Reference | Table A5 and Table A6 | Table A3 and Table A4 | Regional descriptive statistics | |||||||||||
| Quantified Value | ||||||||
|---|---|---|---|---|---|---|---|---|
| Calculation formula | ||||||||
| Reference | Model (14) | Model (15) | Model (16) | Model (17) | Model (18) | Model (18) | Model (19) | Model (19) |
Appendix C
| Eastern | Central | Western | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CACER | 2.061 *** | 0.746 *** | 2.095 *** | −2.304 | −0.188 | −2.260 | 1.725 | 0.962 *** | 1.430 |
| (3.51) | (11.92) | (3.58) | (−0.65) | (−1.34) | (−0.64) | (0.87) | (7.43) | (0.69) | |
| MIER | −0.040 | −0.045 | −0.017 | −0.012 | −0.011 | −0.002 | 0.013 *** | 0.013 *** | 0.004 *** |
| (−1.42) | (−1.57) | (−1.55) | (−0.21) | (−0.18) | (−0.10) | (4.61) | (4.62) | (3.92) | |
| CACER2 | −0.058 ** | −0.060 ** | 0.089 | 0.087 | −0.034 | −0.025 | |||
| (−2.25) | (−2.32) | (0.60) | (0.59) | (−0.38) | (−0.27) | ||||
| MIER2 | 0.001 | 0.001 | 0.001 | 0.000 | −0.000 *** | −0.000 *** | |||
| (0.90) | (1.03) | (0.19) | (0.15) | (−3.35) | (−3.35) | ||||
| R&D | −42.467 *** | −39.910 *** | −42.456 *** | −17.857 | −18.883 | −18.015 | −15.635 | −16.605 | −5.998 |
| (−9.35) | (−8.95) | (−9.35) | (−0.91) | (−0.97) | (−0.93) | (−0.85) | (−0.92) | (−0.32) | |
| ISTR | 2.721 *** | 2.568 *** | 2.720 *** | 2.662 *** | 2.660 *** | 2.656 *** | 1.784 *** | 1.827 *** | 1.883 *** |
| (12.97) | (12.76) | (12.97) | (8.97) | (8.99) | (9.05) | (4.92) | (5.32) | (5.04) | |
| ESTR | −1.458 *** | −1.815 *** | −1.466 *** | 0.340 | 0.377 | 0.342 | −0.757 *** | −0.776 *** | −0.643 *** |
| (−3.18) | (−4.16) | (−3.20) | (1.33) | (1.52) | (1.34) | (−3.32) | (−3.49) | (−2.76) | |
| FDI | 0.114 | 0.082 | 0.099 | −1.195 *** | −1.174 *** | −1.197 *** | 0.655 *** | 0.663 *** | 0.472 ** |
| (1.13) | (0.81) | (1.00) | (−4.57) | (−4.55) | (−4.60) | (3.15) | (3.22) | (2.28) | |
| HU | 0.197 | 0.439 | 0.182 | −3.028 *** | −3.017 *** | −3.016 *** | −2.663 | −2.489 | −2.789 |
| (0.27) | (0.61) | (0.25) | (−4.75) | (−4.75) | (−4.78) | (−1.63) | (−1.59) | (−1.65) | |
| Constant | −18.410 *** | −10.891 *** | −18.654 *** | 8.703 | −3.859 *** | 8.427 | −18.260 | −13.954 *** | −16.350 |
| (−5.38) | (−14.56) | (−5.47) | (0.41) | (−2.72) | (0.40) | (−1.61) | (−10.20) | (−1.40) | |
| Observations | 154 | 154 | 154 | 112 | 112 | 112 | 154 | 154 | 154 |
| R-squared | 0.771 | 0.763 | 0.770 | 0.475 | 0.473 | 0.474 | 0.468 | 0.467 | 0.426 |
| Inflection point | 17.7672 | ||||||||
| Eastern | Central | Western | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CACER | 1.292 *** | 0.173 * | 1.297 *** | −0.535 | 0.265 | −0.252 | 2.019 | 0.674 *** | 1.672 |
| (3.61) | (1.90) | (3.65) | (−0.22) | (0.83) | (−0.11) | (1.26) | (4.00) | (1.09) | |
| MIER | −0.007 | −0.009 | 0.000 | −0.067 | −0.067 | −0.010 | 0.006 * | 0.006 | 0.002 * |
| (−0.47) | (−0.57) | (0.05) | (−0.90) | (−0.90) | (−0.45) | (1.86) | (1.80) | (2.06) | |
| CACER2 | −0.050 ** | −0.050 ** | 0.034 | 0.021 | −0.059 | −0.044 | |||
| (−3.01) | (−3.08) | (0.33) | (0.21) | (−0.83) | (−0.64) | ||||
| MIER2 | 0.000 | 0.000 | 0.003 | 0.003 | −0.000 | −0.000 | |||
| (0.69) | (0.83) | (0.96) | (0.96) | (−1.61) | (−1.53) | ||||
| R&D | 1.320 | −0.033 | 1.446 | −0.116 | −0.020 | −0.972 | −94.457 *** | −96.866 *** | −93.941 *** |
| (0.11) | (−0.00) | (0.12) | (−0.00) | (−0.00) | (−0.03) | (−5.23) | (−5.62) | (−4.88) | |
| ISTR | 3.787 *** | 3.794 *** | 3.790 *** | 2.387 *** | 2.390 *** | 2.367 *** | 2.697 *** | 2.709 *** | 2.641 *** |
| (6.34) | (6.30) | (6.30) | (5.59) | (5.74) | (5.43) | (7.20) | (7.07) | (6.71) | |
| ESTR | −1.733 | −1.465 | −1.741 | −2.101 | −2.113 | −2.033 | −0.339 | −0.455 | −0.461 |
| (−0.96) | (−0.81) | (−0.97) | (−1.77) | (−1.77) | (−1.70) | (−0.68) | (−0.84) | (−0.98) | |
| FDI | −0.629 *** | −0.701 *** | −0.633 *** | −1.029 * | −1.016 * | −1.028 * | 0.354 | 0.383 | 0.383 |
| (−3.33) | (−3.87) | (−3.41) | (−2.33) | (−2.21) | (−2.31) | (0.74) | (0.82) | (0.77) | |
| HU | −0.929 | −1.406 | −0.925 | −3.076 ** | −3.085 ** | −3.012 ** | −3.531 | −3.290 | −4.038 |
| (−0.40) | (−0.64) | (−0.41) | (−2.50) | (−2.56) | (−2.46) | (−1.17) | (−1.13) | (−1.29) | |
| Constant | −11.745 *** | −5.651 ** | −11.775 *** | −1.554 | −6.234 | −3.318 | −17.871 * | −10.097 *** | −15.520 |
| (−7.23) | (−3.11) | (−7.24) | (−0.11) | (−1.57) | (−0.23) | (−1.95) | (−5.08) | (−1.81) | |
| Number of id | 11 | 11 | 11 | 8 | 8 | 8 | 11 | 11 | 11 |
| R-squared | 0.861 | 0.856 | 0.860 | 0.583 | 0.583 | 0.577 | 0.649 | 0.647 | 0.643 |
| Inflection point | 9.3635 | 13.0165 | |||||||
| Eastern | Central | Western | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CACER | −0.460 | −0.033 | −0.431 | −0.014 | −3.287 | −0.130 | −3.231 | −0.122 | −1.671 * | 0.066 | −1.683 * | 0.062 |
| (−1.11) | (−0.76) | (−0.99) | (−0.22) | (−1.02) | (−1.00) | (−1.00) | (−0.93) | (−1.70) | (1.01) | (−1.70) | (0.80) | |
| MIER | 0.008 | 0.009 | 0.007 | 0.008 | −0.024 | −0.022 | −0.024 | −0.021 | 0.003 ** | 0.003 ** | 0.003 * | 0.003 * |
| (0.39) | (0.45) | (0.36) | (0.40) | (−0.46) | (−0.42) | (−0.45) | (−0.41) | (2.14) | (2.14) | (1.93) | (1.95) | |
| CACER2 | 0.019 | 0.018 | 0.132 | 0.130 | 0.077 * | 0.077 * | ||||||
| (1.04) | (0.97) | (0.99) | (0.96) | (1.77) | (1.77) | |||||||
| MIER2 | −0.001 | −0.001 | −0.001 | −0.001 | 0.002 | 0.002 | 0.002 | 0.001 | −0.000 * | −0.000 * | −0.000 * | −0.000 * |
| (−0.91) | (−0.98) | (−0.90) | (−0.94) | (0.62) | (0.56) | (0.61) | (0.55) | (−1.90) | (−1.94) | (−1.77) | (−1.83) | |
| OFDI | −0.013 | −0.026 | 0.037 | 0.041 | 0.007 * | 0.005 * | ||||||
| (−0.21) | (−0.43) | (0.42) | (0.46) | (2.16) | (2.11) | |||||||
| R&D | −0.008 | −0.843 | −0.560 | −1.855 | 16.207 | 14.408 | 16.923 | 15.215 | 10.785 | 13.730 | 10.807 | 13.750 |
| (−0.00) | (−0.25) | (−0.13) | (−0.45) | (0.93) | (0.83) | (0.96) | (0.87) | (1.12) | (1.43) | (1.12) | (1.43) | |
| ISTR | −0.147 | −0.097 | −0.111 | −0.031 | 0.364 | 0.358 | 0.265 | 0.251 | 0.236 | 0.149 | 0.224 | 0.141 |
| (−0.97) | (−0.68) | (−0.48) | (−0.14) | (1.37) | (1.35) | (0.75) | (0.71) | (1.35) | (0.88) | (1.17) | (0.76) | |
| ESTR | −0.600 * | −0.487 | −0.617 * | −0.530 | −0.089 | −0.035 | −0.102 | −0.050 | −0.102 | −0.063 | −0.097 | −0.059 |
| (−1.78) | (−1.52) | (−1.77) | (−1.57) | (−0.39) | (−0.16) | (−0.44) | (−0.22) | (−0.93) | (−0.58) | (−0.84) | (−0.52) | |
| FDI | −0.087 | −0.077 | −0.085 | −0.074 | −0.541 ** | −0.505 ** | −0.497 * | −0.458 * | −0.122 | −0.150 | −0.126 | −0.152 |
| (−1.17) | (−1.04) | (−1.14) | (−1.00) | (−2.29) | (−2.17) | (−1.91) | (−1.78) | (−1.17) | (−1.44) | (−1.17) | (−1.42) | |
| HU | −0.449 | −0.521 | −0.444 | −0.506 | −0.836 | −0.814 | −0.722 | −0.691 | −0.430 | −0.861 | −0.412 | −0.850 |
| (−0.87) | (−1.02) | (−0.85) | (−0.98) | (−1.48) | (−1.44) | (−1.15) | (−1.10) | (−0.53) | (−1.10) | (−0.50) | (−1.08) | |
| Constant | 3.236 | 0.802 | 2.984 | 0.519 | 19.509 | 0.755 | 19.356 | 0.910 | 8.747 | −1.107 | 8.871 | −1.042 |
| (1.35) | (1.56) | (1.11) | (0.62) | (1.02) | (0.58) | (1.01) | (0.67) | (1.56) | (−1.57) | (1.56) | (−1.13) | |
| R-squared | 0.069 | 0.061 | 0.069 | 0.063 | 0.077 | 0.068 | 0.078 | 0.070 | 0.101 | 0.079 | 0.101 | 0.079 |
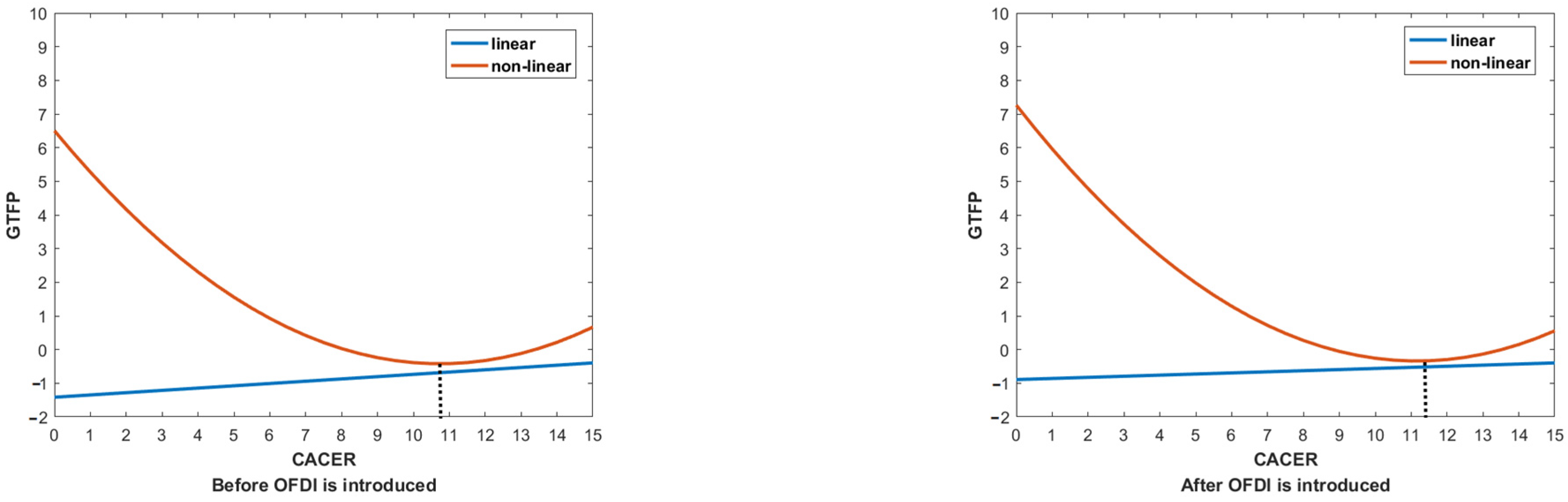
| Inflection point | 12.1053 | 11.9722 | 10.8506 | 10.9286 | ||||||||
| VARIABLES | Eastern | Central | Western | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CACER | −1.151 ** | 0.023 | −1.154 * | 0.028 | −4.511 | −0.030 | −4.459 | −0.055 | −1.289 ** | 0.068 | −1.362 ** | 0.033 |
| (−2.35) | (0.41) | (−2.21) | (0.49) | (−1.19) | (−0.39) | (−1.16) | (−0.52) | (−2.95) | (0.96) | (−3.16) | (0.35) | |
| MIER | 0.007 | 0.008 | 0.007 | 0.008 | −0.020 | −0.015 | −0.013 | −0.009 | 0.004 ** | 0.004 ** | 0.004 ** | 0.004 ** |
| (0.36) | (0.39) | (0.36) | (0.39) | (−0.91) | (−0.84) | (−0.55) | (−0.46) | (2.48) | (2.66) | (2.24) | (2.40) | |
| CACER2 | 0.052 ** | 0.052 ** | 0.189 | 0.186 | 0.060 ** | 0.061 ** | ||||||
| (2.41) | (2.30) | (1.18) | (1.14) | (2.85) | (2.97) | |||||||
| MIER2 | −0.001 | −0.001 | −0.001 | −0.001 | 0.001 | 0.001 | 0.001 | 0.001 | −0.000 ** | −0.000 ** | −0.000 * | −0.000 ** |
| (−0.62) | (−0.63) | (−0.62) | (−0.62) | (1.10) | (1.16) | (0.72) | (0.66) | (−2.36) | (−2.52) | (−2.18) | (−2.34) | |
| OFDI | 0.003 ** | −0.022 ** | 0.086 | 0.090 | 0.058 ** | 0.056 ** | ||||||
| (2.03) | (−2.29) | (0.71) | (0.79) | (3.91) | (3.87) | |||||||
| R&D | 4.326 | 5.582 | 4.328 | 5.549 | 22.004 | 21.640 | 22.493 | 22.160 | −8.818 | −4.812 | −3.088 | 0.810 |
| (0.71) | (0.88) | (0.70) | (0.88) | (0.79) | (0.81) | (0.92) | (0.95) | (−0.73) | (−0.41) | (−0.21) | (0.06) | |
| ISTR | −0.205 | −0.216 | −0.217 | −0.132 | 0.540 | 0.552 | 0.338 | 0.341 | 0.338 *** | 0.332 *** | 0.185 * | 0.184 |
| (−1.04) | (−0.99) | (−0.51) | (−0.32) | (1.41) | (1.53) | (0.55) | (0.58) | (3.37) | (3.20) | (1.92) | (1.68) | |
| ESTR | −0.075 | −0.386 | −0.070 | −0.417 | 1.399 *** | 1.348 *** | 1.579 *** | 1.537 *** | 0.175 | 0.303 | 0.198 | 0.329 |
| (−0.11) | (−0.61) | (−0.10) | (−0.67) | (4.59) | (3.83) | (6.20) | (6.42) | (0.55) | (1.05) | (0.64) | (1.19) | |
| FDI | −0.111 | −0.033 | −0.109 | −0.049 | −0.675 * | −0.594 * | −0.592 | −0.508 | −0.151 | −0.186 | −0.173 | −0.208 |
| (−0.73) | (−0.26) | (−0.76) | (−0.43) | (−2.04) | (−2.35) | (−1.43) | (−1.54) | (−1.22) | (−1.51) | (−1.33) | (−1.66) | |
| HU | −1.728 | −1.109 | −1.725 | −1.140 | −0.884 | −0.910 | −0.621 | −0.634 | −0.684 | −0.902 | −0.478 | −0.710 |
| (−1.62) | (−0.98) | (−1.64) | (−1.02) | (−1.65) | (−1.69) | (−0.84) | (−0.86) | (−0.95) | (−1.21) | (−0.74) | (−1.06) | |
| Constant | 6.367 ** | 0.016 | 6.401 * | −0.120 | 23.999 | −2.224 | 24.085 | −1.660 | 6.501 ** | −1.417 | 7.262 ** | −0.892 |
| (2.36) | (0.02) | (2.05) | (−0.11) | (1.10) | (−1.31) | (1.10) | (−0.77) | (2.59) | (−1.73) | (2.86) | (−0.79) | |
| R-squared | 0.069 | 0.034 | 0.069 | 0.035 | 0.099 | 0.082 | 0.104 | 0.088 | 0.100 | 0.092 | 0.106 | 0.097 |
| Inflection point | 8.9874 | 13.5895 | 9.4242 | 13.3065 | 10.7417 | 11.1640 | ||||||
References
- World Bank. World Development Indicators. 2020. Available online: https://data.worldbank.org/ (accessed on 14 April 2022).
- Mi, Z.; Wei, Y.-M.; Wang, B.; Meng, J.; Liu, Z.; Shan, Y.; Liu, J.; Guan, D. Socioeconomic impact assessment of China’s CO2 emissions peak prior to 2030. J. Clean. Prod. 2017, 142, 2227–2236. [Google Scholar] [CrossRef]
- Chen, Z.M.; Ohshita, S.; Lenzen, M.; Wiedmann, T.; Jiborn, M.; Chen, B.; Lester, L.; Guan, D.; Meng, J.; Xu, S.; et al. Consumption-based greenhouse gas emissions accounting with capital stock change highlights dynamics of fast-developing countries. Nat. Commun. 2018, 9, 3581. [Google Scholar] [CrossRef]
- Cheng, Z.; Kong, S. The effect of environmental regulation on green total-factor productivity in China’s industry. Environ. Impact Assess. Rev. 2022, 94, 106757. [Google Scholar] [CrossRef]
- Tang, D.; Tang, J.; Xiao, Z.; Ma, T.; Bethel, B.J. Environmental regulation efficiency and total factor productivity—Effect analysis based on Chinese data from 2003 to 2013. Ecol. Indic. 2016, 73, 312–318. [Google Scholar] [CrossRef]
- Sun, J.; Tang, D.; Kong, H.; Boamah, V. Impact of Industrial Structure Upgrading on Green Total Factor Productivity in the Yangtze River Economic Belt. Int. J. Environ. Res. Public Health 2022, 19, 3718. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Tang, D. Research on Green Total Factor Productivity of Yangtze River Economic Belt Based on Environmental Regulation. Int. J. Environ. Res. Public Health 2021, 18, 12242. [Google Scholar] [CrossRef]
- Xia, F.; Xu, J. Green total factor productivity: A re-examination of quality of growth for provinces in China. China Econ. Rev. 2020, 62, 101454. [Google Scholar] [CrossRef]
- The 13th Five-Year Plan for Economic and Social Development of the People’s Republic of China. Available online: http://www.gov.cn/ (accessed on 14 April 2022).
- Tang, K.; Kragt, M.E.; Hailu, A.; Ma, C. Carbon farming economics: What have we learned? J. Environ. Manag. 2016, 172, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.; Qiu, Y.; Zhou, D. Does command-and-control regulation promote green innovation performance? Evidence from China’s industrial enterprises. Sci. Total Environ. 2020, 712, 136362. [Google Scholar] [CrossRef] [PubMed]
- Cozza, C.; Rabellotti, R.; Sanfilippo, M. The impact of outward FDI on the performance of Chinese firms. China Econ. Rev. 2015, 36, 42–57. [Google Scholar] [CrossRef]
- Dong, Y.; Tian, J.; Ye, J. Environmental regulation and foreign direct investment: Evidence from China’s outward FDI. Financ. Res. Lett. 2021, 39, 101611. [Google Scholar] [CrossRef]
- Wang, H.; Hu, X.Y. China’s “going-out” strategy and corporate social responsibility: Preliminary evidence of a “boomerang effect”. J. Contemp. China 2017, 26, 820–833. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Z.; Su, B.; Ng, T.S.; Zhang, M.; Qi, L. Structural breakpoints in the relationship between outward foreign direct investment and green innovation: An empirical study in China. Energy Econ. 2021, 103, 105578. [Google Scholar] [CrossRef]
- Eskeland, G.S.; Harrison, A.E. Moving to greener pastures? Multinationals and the pollution haven hypothesis. J. Dev. Econ. 2003, 70, 1–23. [Google Scholar] [CrossRef]
- Cole, M.A. Trade, the pollution haven hypothesis and the environmental Kuznets curve: Examining the linkages. Ecol. Econ. 2004, 48, 71–81. [Google Scholar] [CrossRef]
- Hoffmann, R.; Lee, C.G.; Ramasamy, B.; Yeung, M. FDI and pollution: A granger causality test using panel data. J. Int. Dev. J. Dev. Stud. Assoc. 2005, 17, 311–317. [Google Scholar] [CrossRef]
- Levinson, A.; Taylor, M.S. Unmasking the pollution haven effect. Int. Econ. Rev. 2008, 49, 223–254. [Google Scholar] [CrossRef]
- Kearsley, A.; Riddel, M. A further inquiry into the pollution haven hypothesis and the environmental Kuznets curve. Ecol. Econ. 2010, 69, 905–919. [Google Scholar] [CrossRef]
- Wang, H.; Dong, C.; Liu, Y. Beijing direct investment to its neighbors: A pollution haven or pollution halo effect? J. Clean. Prod. 2019, 239, 118062. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, W.; Zhang, M.; Cheng, B. Pollution haven or halo? The role of the energy transition in the impact of FDI on SO2 emissions. Sci. Total Environ. 2021, 763, 143002. [Google Scholar] [CrossRef]
- Abid, M.; Sekrafi, H. Pollution haven or halo effect? A comparative analysis of developing and developed countries. Energy Rep. 2021, 7, 4862–4871. [Google Scholar]
- Jefferson, G.H.; Rawski, T.G.; Zhang, Y. Productivity growth and convergence across China’s industrial economy. J. Chin. Econ. Bus. Stud. 2008, 6, 121–140. [Google Scholar] [CrossRef]
- Chen, P.C.; Ming-Miin, Y.U.; Chang, C.C.; Hsu, S.-H. Total factor productivity growth in China’s agricultural sector. China Econ. Rev. 2008, 19, 580–593. [Google Scholar] [CrossRef]
- Michaelides, P.; Milios, J. TFP change, output gap and inflation in the Russian Federation (1994–2006). J. Econ. Bus. 2009, 61, 339–352. [Google Scholar] [CrossRef]
- Cepeda, L.E.T.; Ramos, L.F.C. Patterns of TFP growth in Mexico: 1991–2011. N. Am. J. Econ. Financ. 2015, 34, 398–420. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, J. Decomposition of environmental total factor productivity growth using hyperbolic distance functions: A panel data analysis for China. Energy Econ. 2015, 47, 87–97. [Google Scholar] [CrossRef]
- Wu, H.; Ren, S.; Yan, G.; Hao, Y. Does China’s outward direct investment improve green total factor productivity in the “Belt and Road” countries? Evidence from dynamic threshold panel model analysis. J. Environ. Manag. 2020, 275, 111295. [Google Scholar] [CrossRef]
- Cheng, Z.; Liu, J.; Li, L.; Gu, X. Research on meta-frontier total-factor energy efficiency and its spatial convergence in Chinese provinces. Energy Econ. 2020, 86, 104702. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A survey of data envelopment analysis in energy and environmental studies. Eur. J. Oper. Res. 2008, 189, 1–18. [Google Scholar] [CrossRef]
- Cai, W.; Ye, P. How does environmental regulation influence enterprises’ total factor productivity? A quasi-natural experiment based on China’s new environmental protection law. J. Clean. Prod. 2020, 276, 124105. [Google Scholar] [CrossRef]
- Porter, M.E.; Van der Linde, C. Toward a new conception of the environment-competitiveness relationship. J. Econ. Perspect. 1995, 9, 97–118. [Google Scholar] [CrossRef]
- Mi, Z.; Zang, G.; Xin, X.; Shang, Y.; Hai, J. The extension of the Porter hypothesis: Can the role of environmental regulation on economic development be affected by other dimensional regulations? J. Clean. Prod. 2018, 203, 933–942. [Google Scholar]
- Wang, Y.; Sun, X.; Guo, X. Environmental regulation and green productivity growth: Empirical evidence on the Porter Hypothesis from OECD industrial sectors. Energy Policy 2019, 132, 611–619. [Google Scholar] [CrossRef]
- Zhang, D. Green credit regulation, induced R&D and green productivity: Revisiting the Porter Hypothesis. Int. Rev. Financ. Anal. 2021, 75, 101723. [Google Scholar]
- Zhang, C.; Liu, H.; Bressers, H.T.A.; Buchanan, K.S. Productivity growth and environmental regulations-accounting for undesirable outputs: Analysis of China’s thirty provincial regions using the Malmquist–Luenberger index. Ecol. Econ. 2011, 70, 2369–2379. [Google Scholar] [CrossRef]
- Peng, J.; Xie, R.; Ma, C.; Fu, Y. Market-based environmental regulation and total factor productivity: Evidence from Chinese enterprises. Econ. Model. 2021, 95, 394–407. [Google Scholar] [CrossRef]
- Li, J.; Tang, D.; Tenkorang, A.P.; Shi, Z. Research on environmental regulation and green total factor productivity in Yangtze River Delta: From the perspective of financial development. Int. J. Environ. Res. Public Health 2021, 18, 12453. [Google Scholar] [CrossRef]
- Wu, R.; Lin, B. Environmental regulation and its influence on energy-environmental performance: Evidence on the porter hypothesis from China’s iron and steel industry. Resour. Conserv. Recycl. 2022, 176, 105954. [Google Scholar] [CrossRef]
- Guo, R.; Yuan, Y. Different types of environmental regulations and heterogeneous influence on energy efficiency in the industrial sector: Evidence from Chinese provincial data. Energy Policy 2020, 145, 111747. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, J.; Ye, B.; Hou, B. Green spillovers of outward foreign direct investment on home countries: Evidence from China’s province-level data. J. Clean. Prod. 2019, 215, 829–844. [Google Scholar] [CrossRef]
- Yu, P.; Cai, Z.; Sun, Y. Does the emissions trading system in developing countries accelerate carbon leakage through OFDI? Evidence from China. Energy Econ. 2021, 101, 105397. [Google Scholar] [CrossRef]
- Pan, X.; Chu, J.; Tian, M.; Li, M. Non-linear effects of outward foreign direct investment on total factor energy efficiency in China. Energy 2022, 239, 122293. [Google Scholar] [CrossRef]
- Hao, Y.; Guo, Y.; Guo, Y.; Wu, H. Does outward foreign direct investment (OFDI) affect the home country’s environmental quality? The case of China. Struct. Chang. Econ. Dyn. 2020, 52, 109–119. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Z.; Zhang, M.; Zhou, C.; Zhou, D. The effects of environmental regulation on outward foreign direct investment’s reverse green technology spillover: Crowding out or facilitation? J. Clean. Prod. 2021, 284, 124689. [Google Scholar] [CrossRef]
- Choi, C.; Yi, M.H. The Internet, R&D expenditure and economic growth. Appl. Econ. Lett. 2018, 25, 264–267. [Google Scholar]
- Kogut, B.; Chang, S.J. Technological capabilities and Japanese foreign direct investment in the United States. Rev. Econ. Stat. 1991, 73, 401–413. [Google Scholar] [CrossRef]
- Potterie, B.P.; Lichtenberg, F. Does foreign direct investment transfer technology across borders? Rev. Econ. Stat. 2001, 83, 490–497. [Google Scholar] [CrossRef]
- Pradhan, R.P.; Arvin, M.B.; Nair, M.; Bennett, S.E. The dynamics among entrepreneurship, innovation, and economic growth in the Eurozone countries. J. Policy Model. 2020, 42, 1106–1122. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Wang, B. Do cross-border acquisitions create value? Evidence from overseas acquisitions by Chinese firms. Int. Bus. Rev. 2016, 25, 471–483. [Google Scholar] [CrossRef]
- Nugent, J.B.; Lu, J. China’s outward foreign direct investment in the Belt and Road Initiative: What are the motives for Chinese firms to invest? China Econ. Rev. 2021, 68, 101628. [Google Scholar] [CrossRef]
- Chen, L.; Guo, S.; Lu, J.; Gerschewski, S. Outward FDI and efficiency in within-firm resource allocation–Evidence from firm-level data of China. J. Asian Econ. 2021, 74, 101298. [Google Scholar] [CrossRef]
- Zhang, D.; Kong, Q. How does energy policy affect firms’ outward foreign direct investment: An explanation based on investment motivation and firms’ performance. Energy Policy 2021, 158, 112548. [Google Scholar] [CrossRef]
- Valacchi, G.; Doytch, N.; Yonzan, N. Impact of outward foreign direct investments on patent activity of Greenfield multinationals. Technol. Forecast. Soc. Chang. 2021, 173, 121168. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Hou, J. Research on the impact of OFDI on the home country’s global value chain upgrading. Int. Rev. Financ. Anal. 2021, 77, 101862. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, D.; Bethel, B.J. Analyzing the Characteristics and Evolution of Chinese Enterprises’ Outward Forward Direct Investment Host Country Network. Sustainability 2021, 13, 9824. [Google Scholar] [CrossRef]
- Tang, D.; Yi, R.; Kong, H.; Da, D.; Boamah, V. Foreign direct investment entry mode and China’s carbon productivity based on spatial econometric model. Front. Environ. Sci. 2022, 10, 922151. [Google Scholar] [CrossRef]
- Luo, Y.; Salman, M.; Lu, Z. Heterogeneous impacts of environmental regulations and foreign direct investment on green innovation across different regions in China. Sci. Total Environ. 2021, 759, 143744. [Google Scholar] [CrossRef]
- Herzer, D. Outward FDI, total factor productivity and domestic output: Evidence from Germany. Int. Econ. J. 2012, 26, 155–174. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, L.; Zhao, T. The contribution of outward direct investment to productivity changes within China 1991–2007. J. Int. Manag. 2010, 16, 121–130. [Google Scholar] [CrossRef]
- Driffield, N.; Pereira, V.; Temouri, Y. Does offshore outsourcing impact home employment? Evidence from service multinationals. J. Bus. Res. 2019, 103, 448–459. [Google Scholar] [CrossRef]
- Bitzer, J.; Kerekes, M. Does foreign direct investment transfer technology across borders? New evidence. Econ. Lett. 2008, 100, 355–358. [Google Scholar] [CrossRef]
- Li, J.; Strange, R.; Ning, L.; Sutherland, D. Outward foreign direct investment and domestic innovation performance: Evidence from China. Int. Bus. Rev. 2016, 25, 1010–1019. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y. How does outward foreign direct investment enhance firm productivity? A heterogeneous empirical analysis from Chinese manufacturing. China Econ. Rev. 2017, 44, 1–15. [Google Scholar] [CrossRef]
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Chen, S.; Golley, J. ‘Green’productivity growth in China’s industrial economy. Energy Econ. 2014, 44, 89–98. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Wang, H. Energy and CO2 emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. Oper. Res. 2012, 221, 625–635. [Google Scholar] [CrossRef]
- Wang, D.; Du, K.; Zhang, N. Measuring technical efficiency and total factor productivity change with undesirable outputs in Stata. Stata J. 2022, 22, 103–124. [Google Scholar] [CrossRef]
- Oh, D. A global Malmquist-Luenberger productivity index. J. Product. Anal. 2010, 34, 183–197. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Baron, R.M.; Kenny, D.A. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. J. Personal. Soc. Psychol. 1986, 51, 1173–1182. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Zha, D.; Wang, X.; Chen, Q. Exploring the nonlinear association between environmental regulation and carbon intensity in China: The mediating effect of green technology. Ecol. Indic. 2020, 114, 106309. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, Z.; Geng, S. How do environmental regulation and foreign investment behavior affect green productivity growth in the industrial sector? An empirical test based on Chinese provincial panel data. J. Environ. Manag. 2021, 287, 112282. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.C.; Lee, C.C. How does green finance affect green total factor productivity? Evidence from China. Energy Econ. 2022, 107, 105863. [Google Scholar] [CrossRef]
- Hamamoto, M. Environmental regulation and the productivity of Japanese manufacturing industries. Resour. Energy Econ. 2006, 28, 299–312. [Google Scholar] [CrossRef]
- Xie, R.; Yuan, Y.; Huang, J. Different types of environmental regulations and heterogeneous influence on “green” productivity: Evidence from China. Ecol. Econ. 2017, 132, 104–112. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.J. Does environmental regulation policy help improve green production performance? Evidence from China’s industry. Corp. Soc. Responsib. Environ. Manag. 2020, 27, 937–951. [Google Scholar] [CrossRef]
- Zhang, M.; Bai, C.; Zhou, M. Decomposition analysis for assessing the progress in decoupling relationship between coal consumption and economic growth in China. Resour. Conserv. Recycl. 2018, 129, 454–462. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, L.; Zhang, Y.; Shuai, C.; Yan, H.; Lou, Y.; Ye, G. A new panel for analyzing the impact factors on carbon emission: A regional perspective in China. Ecol. Indic. 2019, 97, 260–268. [Google Scholar] [CrossRef]
- Feng, C.; Huang, J.B.; Wang, M. Analysis of green total-factor productivity in China’s regional metal industry: A meta-frontier approach. Resour. Policy 2018, 58, 219–229. [Google Scholar] [CrossRef]
- Guo, W.; Chen, Y. Assessing the efficiency of China’s environmental regulation on carbon emissions based on Tapio decoupling models and GMM models. Energy Rep. 2018, 4, 713–723. [Google Scholar]



| Category | Strategy | Specific Policy |
|---|---|---|
| Command-and-control regulation | Permits | Pollution permit system (2016) |
| Restricted use | Measures for the Administration of the Restricted Use of the Hazardous (2016) | |
| Emission standards | Pharmaceutical industry air emission standards (2019) | |
| Quotas | A quota system for electricity consumption from renewable sources (2019) | |
| Market-incentive regulation | Pollution discharge fees | Collection Pay for Pollution Regulation (1982) |
| Environmental tax | Environmental Protection Tax Law (2016) | |
| Producer Responsibility | Extended Producer Responsibility System Implementation Plan (2017) | |
| Emission trading | Carbon Emissions Trading Management Approach (2021) |
| Category | Variable | Measurement | Unit | Reference |
|---|---|---|---|---|
| Input Indicators | Labor | Annual average number of industrial employees | 10,000 people | Qiu et al. [74] |
| Capital | Total fixed assets investments | CNY 100M | Lee and Lee [75] | |
| Energy | Total industrial energy consumption | 104 tons | Cheng and Kong [4] | |
| Desirable output | Desirable output | Real gross domestic product | CNY 100M | Qiu et al. [74] |
| Undesirable output | Industrial waste water emissions | 104 tons | Lee and Lee [75] | |
| Industrial waste gas emissions | 104 tons | |||
| Industrial solid waste emissions | 104 tons |
| Variable | Definition |
|---|---|
| R&D | A country’s scientific and technological strength |
| ISTR | Secondary industry output to total GDP |
| ESTR | The ratio of coal consumption to total energy consumption |
| FDI | Foreign direct investment |
| HU | Reflects the education level of employees in a region |
| Variable | Obs | P50 | Mean | Sta. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| GTFP | 420 | 1.010 | 0.922 | 0.880 | −7.857 | 8.870 |
| CACER | 420 | 11.91 | 11.85 | 0.976 | 8.178 | 14.16 |
| MIER | 420 | 5.620 | 29.21 | 59.41 | 0.180 | 420.5 |
| OFDI | 420 | 0.0108 | 0.0217 | 0.0363 | 0.0001 | 0.247 |
| R&D | 420 | 0.0137 | 0.0166 | 0.0119 | 0.0022 | 0.0908 |
| ISTR | 420 | 0.891 | 1.067 | 0.609 | 0.500 | 5.169 |
| ESTR | 420 | 0.876 | 0.944 | 0.408 | 0.0248 | 2.461 |
| FDI | 420 | 0.141 | 0.163 | 0.110 | 0.0263 | 1.087 |
| HU | 420 | 0.215 | 0.404 | 0.511 | 0.0473 | 5.705 |
| VIF | GTFP | CACER | MIER | OFDI | R&D | ISTR | ESTR | FDI | HU | |
|---|---|---|---|---|---|---|---|---|---|---|
| GTFP | 1 | |||||||||
| CACER | 1.46 | −0.04 | 1 | |||||||
| MIER | 1.19 | 0.05 | −0.15 | 1 | ||||||
| OFDI | 2.11 | 0.06 | −0.02 | −0.04 | 1 | |||||
| R&D | 1.82 | 0.05 | 0.06 | −0.18 | 0.38 | 1 | ||||
| ISTR | 2.50 | 0.09 | −0.27 | −0.04 | 0.65 | 0.53 | 1 | |||
| ESTR | 1.63 | −0.09 | 0.33 | 0.15 | −0.37 | −0.38 | −0.42 | 1 | ||
| FDI | 2.04 | 0.01 | −0.14 | −0.27 | 0.50 | 0.53 | 0.48 | −0.49 | 1 | |
| HU | 1.21 | −0.07 | −0.01 | −0.04 | −0.24 | −0.17 | −0.13 | 0.27 | −0.33 | 1 |
| Region | Province | GML | GMLTC | GMLEC | GMLSC |
|---|---|---|---|---|---|
| Eastern China | Beijing | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Tianjin | 0.8441 | 1.0000 | 0.9002 | 0.9439 | |
| Hebei | 0.9976 | 1.0670 | 0.9136 | 1.0170 | |
| Liaoning | 0.9119 | 0.9914 | 0.8171 | 1.0587 | |
| Shanghai | 1.0727 | 1.1857 | 0.8839 | 1.0031 | |
| Jiangsu | 0.8686 | 1.0000 | 1.0000 | 0.8686 | |
| Zhejiang | 0.9842 | 1.1059 | 0.8683 | 1.0100 | |
| Fujian | 0.9308 | 1.0741 | 0.8587 | 0.9981 | |
| Shandong | 0.8674 | 0.9943 | 0.8734 | 0.9997 | |
| Guangdong | 0.8421 | 0.9437 | 0.8883 | 1.0043 | |
| Hainan | 1.1509 | 1.0000 | 0.9566 | 1.1943 | |
| Mean | 0.9518 | 1.0329 | 0.9055 | 1.0089 | |
| Central China | Shanxi | 0.9276 | 1.0000 | 0.9294 | 0.9982 |
| Jilin | 0.9129 | 1.0865 | 0.8281 | 0.9983 | |
| Heilongjiang | 0.9192 | 1.0000 | 0.9308 | 0.9884 | |
| Anhui | 0.9697 | 1.0753 | 0.8946 | 0.9998 | |
| Jiangxi | 0.9512 | 1.0341 | 0.9158 | 1.0012 | |
| Henan | 1.0489 | 1.1173 | 0.9175 | 1.0141 | |
| Hubei | 0.9750 | 1.0828 | 0.9094 | 0.9828 | |
| Hunan | 0.9530 | 0.9701 | 0.8945 | 1.0885 | |
| Mean | 0.9572 | 1.0457 | 0.9025 | 1.0089 | |
| Western China | Inner Mongolia | 0.9717 | 1.0774 | 0.8174 | 1.0769 |
| Guangxi | 0.8991 | 0.9587 | 0.9254 | 1.0150 | |
| Chongqing | 1.0287 | 1.1455 | 0.8787 | 1.0045 | |
| Sichuan | 0.8910 | 0.9907 | 0.8773 | 1.0230 | |
| Guizhou | 0.9170 | 1.0521 | 0.8711 | 0.9937 | |
| Yunnan | 0.9562 | 1.0145 | 0.9377 | 1.0040 | |
| Shaanxi | 0.9557 | 0.9814 | 0.9665 | 1.0078 | |
| Gansu | 0.8676 | 1.0000 | 0.8879 | 0.9797 | |
| Qinghai | 0.8620 | 1.0000 | 0.8939 | 0.9681 | |
| Ningxia | 0.9758 | 1.0000 | 0.9488 | 1.0270 | |
| Xinjiang | 0.8414 | 1.0000 | 0.8539 | 0.9875 | |
| Mean | 0.9242 | 1.0200 | 0.8963 | 1.0079 | |
| Full sample mean | 0.9444 | 1.0329 | 0.9014 | 1.0086 |
| POOL | FE | |||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| CACER | 1.781 *** | 0.636 *** | 1.748 ** | 1.431 * | 0.471 *** | 1.398 * |
| (2.61) | (11.71) | (2.56) | (1.92) | (4.57) | (1.93) | |
| MIER | 0.006 *** | 0.006 *** | 0.003 *** | 0.004 | 0.004 | 0.002 |
| (2.82) | (2.84) | (3.04) | (0.85) | (0.80) | (1.08) | |
| CACER2 | −0.050 * | −0.049 * | −0.042 | −0.040 | ||
| (−1.68) | (−1.66) | (−1.34) | (−1.33) | |||
| MIER2 | −0.000 * | −0.000 * | −0.000 | −0.000 | ||
| (−1.77) | (−1.75) | (−0.68) | (−0.63) | |||
| R&D | −27.970 *** | −26.721 *** | −27.457 *** | −36.175 ** | −36.608 ** | −36.132 ** |
| (−5.44) | (−5.24) | (−5.34) | (−2.64) | (−2.66) | (−2.62) | |
| ISTR | 2.344 *** | 2.325 *** | 2.346 *** | 2.956 *** | 2.950 *** | 2.948 *** |
| (16.45) | (16.33) | (16.42) | (11.58) | (11.26) | (11.57) | |
| ESTR | −0.532 *** | −0.552 *** | −0.516 *** | −0.942 * | −0.935 * | −0.978 * |
| (−3.79) | (−3.93) | (−3.67) | (−1.77) | (−1.75) | (−1.89) | |
| FDI | 0.380 *** | 0.351 *** | 0.348 *** | −0.270 | −0.296 | −0.264 |
| (4.96) | (4.69) | (4.66) | (−1.04) | (−1.13) | (−0.98) | |
| HU | −0.787 * | −0.684 | −0.874 * | −3.814 *** | −3.800 *** | −3.870 *** |
| (−1.74) | (−1.52) | (−1.94) | (−4.66) | (−4.68) | (−4.53) | |
| Constant | −17.200 *** | −10.726 *** | −16.923 *** | −13.956 *** | −8.531 *** | −13.671 *** |
| (−4.42) | (−17.61) | (−4.34) | (−3.26) | (−7.07) | (−3.32) | |
| Observations | 420 | 420 | 420 | 420 | 420 | 420 |
| R-squared | 0.560 | 0.557 | 0.556 | 0.642 | 0.640 | 0.640 |
| Province | No | No | No | Yes | Yes | Yes |
| Year | No | No | No | Yes | Yes | Yes |
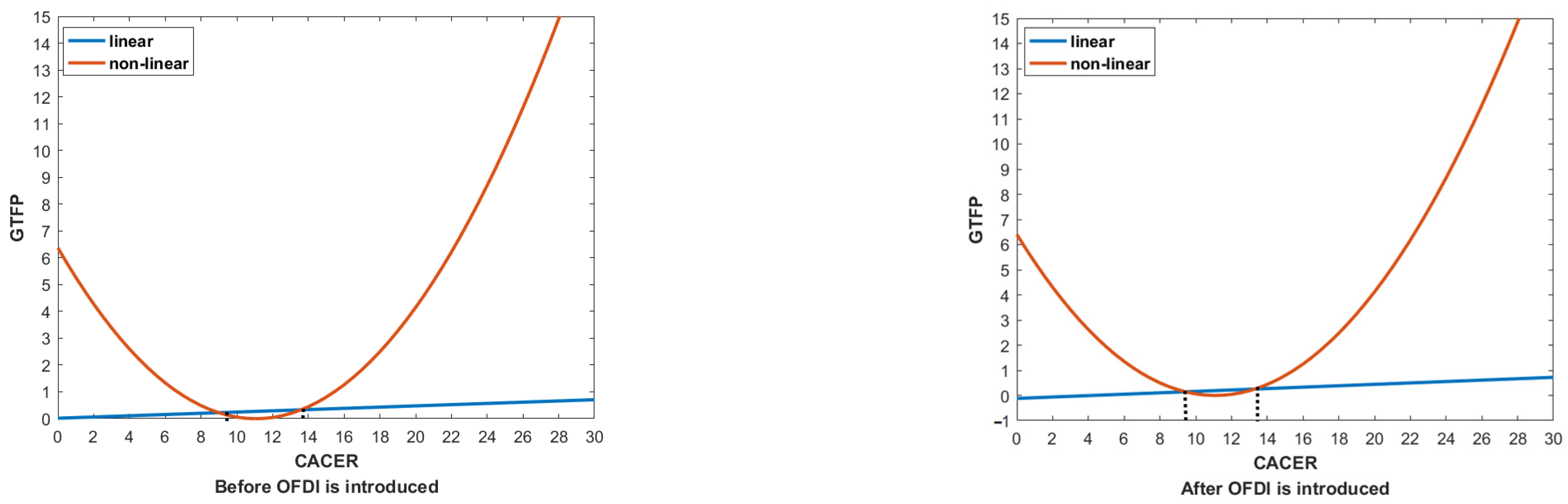
| Inflection point | 10.1762 | 12.7238 | 10.2262 | 12.6309 | ||
| POOL | FE | |||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| CACER | −0.587 ** | 0.007 | −0.662 ** | −0.018 | −1.276 *** | 0.027 | −1.326 *** | 0.011 |
| (−2.27) | (0.27) | (−2.35) | (−0.49) | (−3.77) | (0.69) | (−4.14) | (0.22) | |
| MIER | 0.002 * | 0.002 | 0.002 | 0.002 | 0.004 ** | 0.004 ** | 0.003 ** | 0.004 ** |
| (1.72) | (1.67) | (1.42) | (1.40) | (2.31) | (2.61) | (2.16) | (2.44) | |
| CACER2 | 0.026 ** | 0.028 ** | 0.057 *** | 0.058 *** | ||||
| (2.23) | (2.27) | (3.82) | (4.10) | |||||
| MIER2 | −0.000 | −0.000 | −0.000 | −0.000 | −0.000 ** | −0.000 ** | −0.000 ** | −0.000 ** |
| (−1.67) | (−1.66) | (−1.45) | (−1.46) | (−2.21) | (−2.47) | (−2.10) | (−2.36) | |
| OFDI | 0.043 ** | 0.039 ** | 0.039 *** | 0.033 ** | ||||
| (1.23) | (1.13) | (3.83) | (2.67) | |||||
| RD | 1.193 | 0.506 | 2.299 | 1.462 | −0.713 | −0.187 | 0.558 | 0.885 |
| (0.59) | (0.24) | (0.90) | (0.57) | (−0.12) | (−0.03) | (0.10) | (0.15) | |
| ISTR | 0.098 | 0.110 | −0.002 | 0.021 | 0.228 * | 0.232 | 0.114 | 0.138 |
| (1.24) | (1.38) | (−0.01) | (0.16) | (1.77) | (1.67) | (0.53) | (0.63) | |
| ESTR | −0.123 | −0.112 | −0.100 | −0.090 | 0.568 ** | 0.564 * | 0.604 ** | 0.594 ** |
| (−1.60) | (−1.53) | (−1.17) | (−1.10) | (2.05) | (2.00) | (2.26) | (2.20) | |
| FDI | −0.056 | −0.040 | −0.072 * | −0.054 | −0.170 * | −0.134 | −0.160 * | −0.124 |
| (−1.41) | (−1.01) | (−1.72) | (−1.24) | (−1.93) | (−1.33) | (−1.81) | (−1.25) | |
| HU | −0.196 | −0.247 | −0.164 | −0.222 | −0.776 * | −0.788 * | −0.634 | −0.669 |
| (−0.99) | (−1.20) | (−0.83) | (−1.08) | (−1.97) | (−1.95) | (−1.40) | (−1.44) | |
| Constant | 3.304 ** | −0.060 | 4.039 ** | 0.363 | 6.373 *** | −0.985 | 6.894 *** | −0.694 |
| (2.35) | (−0.18) | (2.46) | (0.79) | (3.61) | (−1.58) | (4.12) | (−0.83) | |
| Observations | 420 | 420 | 420 | 420 | 420 | 420 | 420 | 420 |
| R-squared | 0.032 | 0.027 | 0.037 | 0.031 | 0.055 | 0.040 | 0.057 | 0.042 |
| Province | No | No | No | No | Yes | Yes | Yes | Yes |
| Year | No | No | No | No | Yes | Yes | Yes | Yes |
| Inflection Point | 10.3733 12.4729 | 11.8214 | 10.1806 12.6761 | 10.1053 12.9464 | ||||
| Sys-GMM | Diff-GMM | Sys-GMM | Diff-GMM | |
|---|---|---|---|---|
| L.OFDI | 0.664 *** | 0.647 *** | ||
| (15.85) | (15.29) | |||
| L.GTFP | −0.111 *** | −0.171 *** | ||
| (−3.13) | (−4.67) | |||
| CACER | 0.481 * | 0.682 *** | −0.940 *** | −1.792 *** |
| (1.77) | (2.64) | (−3.05) | (−4.11) | |
| MIER | 0.001 | 0.001 | 0.001 | 0.004 *** |
| (1.37) | (0.86) | (1.24) | (2.68) | |
| CACER2 | −0.013 | −0.023 ** | 0.040 *** | 0.078 *** |
| (−1.21) | (−2.19) | (2.99) | (4.07) | |
| MIER2 | −0.000 | −0.000 | −0.000 | −0.000 *** |
| (−0.88) | (−0.32) | (−1.37) | (−2.81) | |
| OFDI | 0.062 *** | 0.064 *** | ||
| (1.59) | (1.07) | |||
| RD | −6.313 * | 1.805 | 2.241 | 4.524 |
| (−1.82) | (0.42) | (0.77) | (0.64) | |
| ISTR | 0.678 *** | 0.927 *** | 0.154 | 0.325 |
| (3.78) | (5.46) | (0.96) | (1.21) | |
| ESTR | −0.199 ** | −0.180 | −0.042 | 0.732 ** |
| (−2.06) | (−0.73) | (−0.52) | (2.39) | |
| FDI | 0.084 * | −0.122 | −0.121 ** | −0.223 ** |
| (1.69) | (−1.35) | (−2.39) | (−2.03) | |
| HU | −0.347 | −0.853 *** | −0.330 | −0.621 |
| (−1.36) | (−3.18) | (−1.41) | (−1.39) | |
| Constant | −4.750 *** | 5.575 *** | ||
| (−2.75) | (3.15) | |||
| AR(1) | [0.000] | [0.000] | [0.028] | [0.061] |
| AR(2) | [0.663] | [0.636] | [0.484] | [0.404] |
| Hansen | [0.729] | [0.846] | [0.887] | [0.636] |
| Full Sample | Eastern Area | Central Area | Western Area | |
|---|---|---|---|---|
| [0.0749, 1.2032] | [−0.0010, 0.1053] | [−0.1348, 0.0023] | [0.097, 0.1077] | |
| [0.0020, 0.0040] | [−0.0038, −0.0028] | [−0.0063, 0.0035] | [0.003, 0.004] | |
| [0.0170, 0.0256] | [−0.0086, 0.0003] | (−0.0066, 0.0238) | [0.0066, 0.0381] | |
| [0.0002, 0.0003] | (0, 0.0004) | (−0.0022, 0.0001) | [0.0001, 0.0004] | |
| [2.13%, 7.41%] | [22.29%,23.93%] | (4.90%, 29.50%) | [6.11%, 39.23%] | |
| [1.39%, 22.68%] | [−144.62%, 893.37%] | (−3.47%, 1026.51%) | [−39.19%, 4284.86%] | |
| [12.9%, 2564.10%] | (−4.03%, −0.55%) | (1.85%) | [30.33%] | |
| [12.9%, 2564.10%] | (−13.45%, 9.89%) | (−29.50%, 35.43%) | [30.33%] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, D.; Shan, Z.; He, J.; Zhao, Z. How Do Environmental Regulations and Outward Foreign Direct Investment Impact the Green Total Factor Productivity in China? A Mediating Effect Test Based on Provincial Panel Data. Int. J. Environ. Res. Public Health 2022, 19, 15717. https://doi.org/10.3390/ijerph192315717
Tang D, Shan Z, He J, Zhao Z. How Do Environmental Regulations and Outward Foreign Direct Investment Impact the Green Total Factor Productivity in China? A Mediating Effect Test Based on Provincial Panel Data. International Journal of Environmental Research and Public Health. 2022; 19(23):15717. https://doi.org/10.3390/ijerph192315717
Chicago/Turabian StyleTang, Decai, Zhangming Shan, Junxia He, and Ziqian Zhao. 2022. "How Do Environmental Regulations and Outward Foreign Direct Investment Impact the Green Total Factor Productivity in China? A Mediating Effect Test Based on Provincial Panel Data" International Journal of Environmental Research and Public Health 19, no. 23: 15717. https://doi.org/10.3390/ijerph192315717
APA StyleTang, D., Shan, Z., He, J., & Zhao, Z. (2022). How Do Environmental Regulations and Outward Foreign Direct Investment Impact the Green Total Factor Productivity in China? A Mediating Effect Test Based on Provincial Panel Data. International Journal of Environmental Research and Public Health, 19(23), 15717. https://doi.org/10.3390/ijerph192315717






