Critical Periods, Critical Time Points and Day-of-the-Week Effects in COVID-19 Surveillance Data: An Example in Middlesex County, Massachusetts, USA
Abstract
:1. Introduction
2. Methods
2.1. Data Extraction and Management
2.2. Inspection of Data Reliability
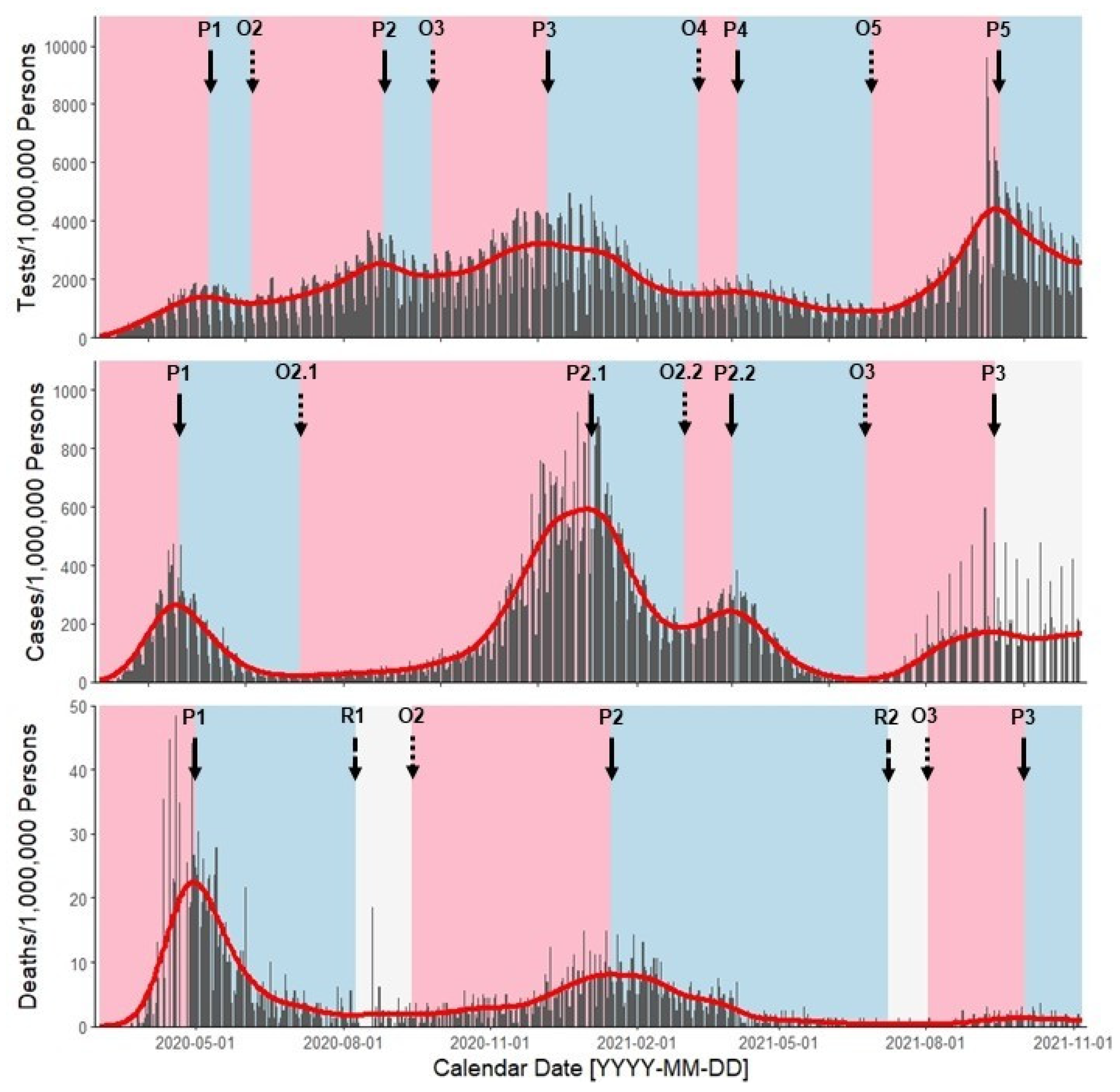
2.3. Defining Outbreak Signatures
2.4. Defining Intervention Stringency Phases
2.5. Modeling DoW Effects
3. Results
3.1. JHU and MDPH Data Cross-Referensing
3.2. Outbreak Signatures and Their Features
3.3. Day-of-the-Week Effects
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holtgrave, D.R.; Vermund, S.H.; Wen, L.S. Potential Benefits of Expanded COVID-19 Surveillance in the US. JAMA 2021, 326, 381–382. [Google Scholar] [CrossRef]
- World Health Organization. Public Health Surveillance for COVID-19: Interim Guidance. 16 December 2020. Available online: https://apps.who.int/iris/bitstream/handle/10665/337897/WHO-2019-nCoV-SurveillanceGuidance-2020.8-eng.pdf (accessed on 20 December 2021).
- Ibrahim, N.K. Epidemiologic surveillance for controlling COVID-19 pandemic: Challenges and implications. J. Infect. Public Health 2020, 13, 1630–1638. [Google Scholar] [CrossRef]
- Bernardo, T.; Sobkowich, K.E.; Forrest, R.O.; Stewart, L.S.; D’Agostino, M.; Gutierrez, E.P.; Gillis, D. Collaborating in the time of COVID-19: The scope and scale of innovative responses to a global pandemic. JMIR Public Health Surveill. 2021, 7, e25935. [Google Scholar] [CrossRef] [PubMed]
- United States White House. National Strategy for the COVID-19 Response and Pandemic Preparedness: January 2021. Available online: https://www.whitehouse.gov/wp-content/uploads/2021/01/National-Strategy-for-the-COVID-19-Response-and-Pandemic-Preparedness.pdf (accessed on 20 December 2021).
- Perski, O.; Herbeć, A.; Shahab, L.; Brown, J. Influence of the SARS-CoV-2 outbreak on the uptake of a popular smoking cessation app in UK smokers: Interrupted time series analysis. JMIR mHealth uHealth 2020, 8, e19494. [Google Scholar] [CrossRef] [PubMed]
- Karaca-Mandic, P.; Sen, S.; Georgiou, A.; Zhu, Y.; Basu, A. Association of COVID-19-related hospital use and overall COVID-19 mortality in the USA. J. Gen. Intern. Med. 2020, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.J.; Brown, P.E.; Rosenthal, J.S. Forecasting subnational COVID-19 mortality using a day-of-the-week adjusted Bayesian hierarchical model. Stat 2021, 10, e328. [Google Scholar] [CrossRef]
- Bo, Y.; Guo, C.; Lin, C.; Zeng, Y.; Li, H.B.; Zhang, Y.; Hossain, M.S.; Chan, J.W.; Yeung, D.W.; Kwok, K.O.; et al. Effectiveness of non-pharmaceutical interventions on COVID-19 transmission in 190 countries from 23 January to 13 April 2020. Int. J. Infect. Dis. 2021, 102, 247–253. [Google Scholar] [CrossRef]
- Nam, S. St. Lucie County Offering COVID-19 Testing Every Day of the Week. 25 WPBF News, 24 August 2021. Available online: https://www.wpbf.com/article/st-lucie-county-covid-19-tests-vaccine-cases/37385079# (accessed on 20 December 2021).
- Moraes, M.M.; Badea, A.; Reddy, A.; Bosch, M.; Salcedo, N.; Gomez, A.R. Validating and Modeling the Impact of High-Frequency Rapid Antigen Screening on COVID-19 Spread and Outcomes. J. Clin. Trials 2021, 11, 483. [Google Scholar]
- Wingerter, M. State Pushes COVID Testing, but It’s Hard to Find Some Parts of Colorado. The Denver Post, 3 September 2021. Available online: https://www.denverpost.com/2021/09/03/colorado-covid-testing-denver-rural/ (accessed on 20 December 2021).
- Alltucker, K. The Demand for COVID-19 Testing Is Up, Stressing Labs and Delaying Results. USA Today, 26 November 2020. Available online: https://www.usatoday.com/story/news/health/2020/11/26/covid-19-testing-delays-record-demand-thanksgiving/6417506002/ (accessed on 20 December 2021).
- Cunningham, K. RDU Prepares for Crowds This Week as Doctors Share Travel Concerns. WRAL.COM, 20 December 2021. Available online: https://www.wral.com/coronavirus/rdu-prepares-for-crowds-this-week-as-doctors-share-travel-concerns/20043724/ (accessed on 20 December 2021).
- Moran, J. COVID-19 Testing Demand in New Hampshire Expected to Remain High after Holiday Season. WMUR9, 20 December 2021. Available online: https://www.wmur.com/article/new-hampshire-covid-testing-demand-12-20-2021/38573850# (accessed on 20 December 2021).
- Buckley, M.; Schencker, L.; Petrella, D. COVID-19 Testing Demand Is Up as Holiday Looms and Illinois Sees Most Single-Day Cases Since 1 December 2020. Chicago Tribune, 20 December 2021. Available online: https://www.chicagotribune.com/coronavirus/ct-covid-testing-demand-20211221-oqjwdnk2n5gq3iebooqovnhc2m-story.html (accessed on 20 December 2021).
- Keithley, J. COVID-19 Testing Demand Skyrockets Ahead of the Christmas Holiday. WMTW8, 20 December 2021. Available online: https://www.wmtw.com/article/covid-19-testing-demand-skyrockets-ahead-of-the-christmas-holiday/38571687 (accessed on 20 December 2021).
- Jiang, L.; Lee, V.J.; Lim, W.Y.; Chen, M.I.; Chen, Y.; Tan, L.; Lin, R.T.; Leo, Y.S.; Barr, I.; Cook, A.R. Performance of case definitions for influenza surveillance. Eurosurveillance 2015, 20, 21145. [Google Scholar] [CrossRef]
- De Luca, G.; Van Kerckhove, K.; Coletti, P.; Poletto, C.; Bossuyt, N.; Hens, N.; Colizza, V. The impact of regular school closure on seasonal influenza epidemics: A data-driven spatial transmission model for Belgium. BMC Infect. Dis. 2018, 18, 29. [Google Scholar]
- Simpson, R.B.; Falconi, T.M.A.; Venkat, A.; Chui, K.H.; Navidad, J.; Naumov, Y.N.; Gorski, J.; Bhattacharyya, S.; Naumova, E.N. Incorporating calendar effects to predict influenza seasonality in Milwaukee, Wisconsin. Epidemiol. Infect. 2019, 147, e268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sugisaki, K.; Seki, N.; Tanabe, N.; Saito, R.; Sasaki, A.; Sasaki, S.; Suzuki, H. Effective School Actions for Mitigating Seasonal Influenza Outbreaks in Niigata, Japan. PLoS ONE 2013, 8, e74716. [Google Scholar] [CrossRef] [PubMed]
- Breitner, S.; Stölzel, M.; Cyrys, J.; Pitz, M.; Wölke, G.; Kreyling, W.; Küchenhoff, H.; Heinrich, J.; Wichmann, H.E.; Peters, A. Short-term mortality rates during a decade of improved air quality in Erfurt, Germany. Environ. Health Perspect. 2009, 117, 448–454. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.D.; Naumova, E.N.; Munasinghe, R.L. Ambient air pollution and hospitalization for congestive heart failure among elderly people in seven large US cities. Am. J. Public Health 1995, 85, 1361–1365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- United States Government Accountability Office. Technology Assessment, COVID-19: Data Quality and Considerations for Modeling and Analysis. Available online: https://www.gao.gov/assets/gao-20-635sp.pdf (accessed on 20 December 2021).
- Morgan, O.W.; Aguilera, X.; Ammon, A.; Amuasi, J.; Fall, I.S.; Frieden, T.; Heymann, D.; Ihekweazu, C.; Jeong, E.K.; Leung, G.M.; et al. Disease Surveillance for the COVID-19 era: Time for bold changes. Lancet 2021, 397, 2317–2319. [Google Scholar] [CrossRef]
- Pearce, N.; Vandenbroucke, J.P.; VanderWeele, T.J.; Greenland, S. Accurate Statistics on COVID-19 Are Essential for Policy Guidance and Decisions. Am. J. Public Health 2020, 110, 949–951. [Google Scholar] [CrossRef]
- Arvisais-Anhalt, S.; Lehmann, C.U.; Park, J.Y.; Araj, E.; Holcomb, M.; Jamieson, A.R.; McDonald, S.; Medford, R.J.; Perl, T.M.; Toomay, S.M.; et al. What the Coronavirus Disease 2019 (COVID-19) Pandemic Has Reinforced: The Need for Accurate Data. Clin. Infect. Dis. Off. Publ. Infect. Dis. Soc. Am. 2021, 72, 920–923. [Google Scholar] [CrossRef]
- Yiannakoulias, N.; Slavik, C.E.; Sturrock, S.L.; Darlington, J.C. Open government data, uncertainty and coronavirus: An infodemiological case study. Soc. Sci. Med. 2020, 265, 113549. [Google Scholar] [CrossRef]
- Cavataio, J.; Schnell, S. Interpreting SARS-CoV-2 seroprevalence, deaths, and fatality rate—Making a case for standardized reporting to improve communication. Math. Biosci. 2021, 333, 108545. [Google Scholar] [CrossRef]
- Rosenbaum, J.E.; Stillo, M.; Graves, N.; Rivera, R. Timeliness of provisional United States mortality data releases during the COVID-19 pandemic: Delays associated with electronic death registration system and weekly mortality. J. Public Health Policy 2021, 42, 536–549. [Google Scholar] [CrossRef]
- Galaitsi, S.E.; Cegan, J.C.; Volk, K.; Joyner, M.; Trump, B.D.; Linkov, I. The challenges of data usage for the United States’ COVID-19 response. Int. J. Inf. Manag. 2021, 59, 102352. [Google Scholar] [CrossRef] [PubMed]
- Costa-Santos, C.; Neves, A.L.; Correia, R.; Santos, P.; Monteiro-Soares, M.; Freitas, A.; Ribeiro-Vaz, I.; Henriques, T.S.; Rodrigues, P.P.; Costa-Pereira, A.; et al. COVID-19 surveillance data quality issues: A national consecutive case series. BMJ Open 2021, 11, e047623. [Google Scholar] [PubMed]
- Clare, T.; Twohig, K.A.; O’Connell, A.M.; Dabrera, G. Timeliness and completeness of laboratory-based surveillance of COVID-19 cases in England. Public Health 2021, 194, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Rogers, K. John Hopkins’ Dashboard: The People behind the Pandemic’s Most Visited Site. CNN Health, 11 July 2020. Available online: https://www.cnn.com/2020/07/11/health/johns-hopkins-covid-19-map-team-wellness-trnd/index.html (accessed on 20 December 2021).
- Swenson, K. Millions Track the Pandemic on John Hopkin’s Dashboard. Those Who Built It Say Some Miss the Real Story. The Washington Post, 29 June 2020. Available online: https://www.washingtonpost.com/local/johns-hopkins-tracker/2020/06/29/daea7eea-a03f-11ea-9590-1858a893bd59_story.html (accessed on 20 December 2021).
- Johns Hopkins University. Time Series Summary (Csse_COVID_19_Time_Series). Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series (accessed on 9 November 2020).
- Ziegler, B. Health Care Rankings: Measuring How Well States Are Meeting Citizens’ Healthcare Needs. U.S. News. 2021. Available online: https://www.usnews.com/news/best-states/rankings/health-care (accessed on 9 November 2021).
- United States Census Bureau. Middlesex County, Massachusetts. Available online: https://data.census.gov/cedsci/profile?g=0500000US25017 (accessed on 9 November 2021).
- John Hopkins University. JHU CSSE COVID-19 Dataset. Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data (accessed on 9 November 2021).
- John Hopkins University. U.S. Testing Data. Available online: https://github.com/govex/COVID-19/tree/master/data_tables/testing_data (accessed on 9 November 2021).
- Massachusetts Department of Public Health. COVID-19 Response Reporting. Available online: https://www.mass.gov/info-details/covid-19-response-reporting#covid-19-interactive-data-dashboard (accessed on 9 November 2021).
- Massachusetts Department of Public Health. Archive of COVID-19 Cases in Massachusetts. Available online: https://www.mass.gov/info-details/archive-of-covid-19-cases-in-massachusetts (accessed on 9 November 2021).
- Simpson, R.B.; Gottlieb, J.; Zhou, B.; Hartwick, M.A.; Naumova, E.N. Completeness of open access FluNet influenza surveillance data for Pan-America in 2005–2019. Sci. Rep. 2021, 11, 795. [Google Scholar] [CrossRef] [PubMed]
- Fefferman, N.H.; Naumova, E.N. Combinatorial decomposition of an outbreak signature. Math. Biosci. 2006, 202, 269–287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naumova, E.N.; O’Neil, E.; MacNeill, I. INFERNO: A system for early outbreak detection and signature forecasting. MMWR Morb. Mortal. Wkly. Rep. 2005, 54, 77–83. [Google Scholar]
- Naumova, E.N.; MacNeill, I.B. Signature-forecasting and early outbreak detection system. Environmetrics 2005, 16, 749–766. [Google Scholar] [CrossRef] [Green Version]
- Tukey, J.W. Thinking about Non-Linear Smoothers; Report # ARO-23360.4-MA; Princeton University Department of Statistics: Princeton, NJ, USA; United States Army Research Office: Durham, NC, USA, 1986. [Google Scholar]
- Yang, W.; Zurbenko, I. Kolmogorov–Zurbenko Filters. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 340–351. [Google Scholar] [CrossRef]
- Zurbenko, I.G.; Sun, M. Applying Kolmogorov-Zurbenko Adaptive R-Software. Int. J. Probab. Stat. 2017, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- Zurbenko, I.G.; Smith, D. Kolmogorov–Zurbenko Filters in Spatiotemporal Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2018, 10, e1419. [Google Scholar] [CrossRef]
- Massachusetts Department of Public Health. COVID-19 State of Emergency. Available online: https://www.mass.gov/info-details/covid-19-state-of-emergency (accessed on 9 November 2021).
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B. Stat. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Massachusetts Lab to Be Among First to Use New Pooled Testing Method for COVID-19. WCVB5, 20 June 2020. Available online: https://www.wcvb.com/article/massachusetts-lab-to-be-among-first-to-use-new-pooled-testing-method-for-covid-19/33365999 (accessed on 19 December 2021).
- Loncich, J. Coronavirus Concerns Growing in Massachusetts Due to Delayed Test Results. WCVB5, 3 August 2020. Available online: https://www.wcvb.com/article/coronavirus-concerns-growing-in-massachusetts-due-to-delayed-covid-19-test-results/33503683# (accessed on 19 December 2021).
- Chen, A. If a Second COVID-19 Wave Is on the Horizon in Mass., Experts Say There’s a Good chance We’ll See it Coming. Wbur, 5 August 2020. Available online: https://www.wbur.org/news/2020/08/05/second-wave-covid-coming (accessed on 19 December 2021).
- Kashinsky, L. 20 Massachusetts Cities and Towns at High Risk for Coronavirus, First Increase in Weeks. Boston Herald, 19 March 2021. Available online: https://www.bostonherald.com/2021/03/18/20-massachusetts-cities-and-towns-at-high-risk-for-coronavirus-first-increase-in-weeks/ (accessed on 19 December 2021).
- Hanson, M. Pooled COVID Testing in Massachusetts Schools Showing Low Prevalence of Virus among Students, Staff. Mass LIVE, 17 March 2021. Available online: https://www.masslive.com/coronavirus/2021/03/pooled-covid-testing-in-massachusetts-schools-showing-low-prevalence-of-virus-among-students-staff.html (accessed on 19 December 2021).
- Dwinell, J. Charlie Baker Urges all Massachusetts Schools to Jump into Pooled Coronavirus Testing. Boston Herald, 26 February 2021. Available online: https://www.bostonherald.com/2021/02/26/charlie-baker-urges-all-massachusetts-schools-to-jump-into-pooled-coronavirus-testing/ (accessed on 19 December 2021).
- State House News Service. Mass. COVID-19 Case Counts on the Rise Again. Wbur, 27 July 2020. Available online: https://www.wbur.org/news/2020/07/27/massachusetts-coronavirus-cases-positives-up (accessed on 19 December 2021).
- Young, C.A. Baker Expands Hot Spot Testing to 8 More Mass. Communities. Wbur, 27 July 2020. Available online: https://www.wbur.org/news/2020/07/27/massachusetts-charlie-baker-testing-expanded-covid-19-coronavirus (accessed on 19 December 2021).
- Congi, S. Massachusetts Experiencing Rush on COVID-19 Testing before Holidays. WCVB5, 22 December 2020. Available online: https://www.wcvb.com/article/massachusetts-experiencing-rush-on-covid-19-coronavirus-testing-before-holidays/35049752 (accessed on 19 December 2021).
- Rosenfield, M. Long Lines Keep People Waiting for Pre-Christmas COVID Testing. 10 Boston, 23 December 2020. Available online: https://www.nbcboston.com/news/coronavirus/long-lines-keep-people-waiting-for-pre-christmas-covid-testing/2264398/ (accessed on 19 December 2021).
- Klein, A.; Pescaro, M. 190 Mass. Communities, Including Boston, Are at High Risk for COVID-19 Transmission. 10 Boston, 31 December 2020. Available online: https://www.nbcboston.com/news/coronavirus/190-mass-communities-including-boston-are-at-high-risk-for-covid-19-transmission/2269622/ (accessed on 19 December 2021).
- 4358 New COVID-19 Cases, 60 Additional Deaths Reported in Massachusetts. WCVB5, 4 January 2021. Available online: https://www.wcvb.com/article/massachusetts-covid-19-cornonavirus-numbers-daily-update-january-4-2021/35121269 (accessed on 19 December 2021).
- Enos, C. Dozens of COVID-19 Cases Linked to Christmas Eve Gatherings at Woburn Church. Boston Globe, 2 January 2021. Available online: https://www.bostonglobe.com/2021/01/02/metro/dozens-covid-19-cases-linked-christmas-eve-gatherings-woburn-church/ (accessed on 19 December 2021).
- Shi, P.; Keskinocak, P.; Swann, J.L.; Lee, B.Y. The impact of mass gatherings and holiday traveling on the course of an influenza pandemic: A computational model. BMC Public Health 2010, 10, 778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ewing, A.; Lee, E.C.; Viboud, C.; Bansal, S. Contact, travel, and transmission: The impact of winter holidays on influenza dynamics in the United States. J. Infect. Dis. 2017, 215, 732–739. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Huang, J.; Li, C.; Zhao, Y.; Wang, D.; Huang, Z.; Yang, K. The role of seasonality in the spread of COVID-19 pandemic. Environ. Res. 2021, 195, 110874. [Google Scholar] [CrossRef] [PubMed]
- Audi, A.; AlIbrahim, M.; Kaddoura, M.; Hijazi, G.; Yassine, H.M.; Zaraket, H. Seasonality of respiratory viral infections: Will COVID-19 follow suit? Front. Public Health 2020, 8, 576. [Google Scholar] [CrossRef] [PubMed]
- De Simoni, G. Drive-through COVID-19 Testing Site to Open in Medford. 10 Boston, 30 March 2020. Available online: https://www.nbcboston.com/news/coronavirus/drive-thru-covid-19-testing-site-to-open-in-medford-mass/2099463/ (accessed on 19 December 2021).
- Lee, T.B. America’s COVID-19 Testing Has Stalled, and That’s a Big Problem. Ars Technica, 2 April 2020. Available online: https://arstechnica.com/tech-policy/2020/04/americas-covid-19-testing-has-stalled-and-thats-a-big-problem/ (accessed on 19 December 2021).
- Becker, K.M. Baker Closes Mass. Schools, Bans Mid-Size Gatherings, Eating at Restaurants over Coronavirus. 10 Boston, 16 March 2020. Available online: https://www.nbcboston.com/news/local/26-new-coronavirus-cases-in-massachusetts-164-total/2091478/ (accessed on 19 December 2021).
- More than 900 Massachusetts Schools Participating in COVID-19 Pool Testing. WCVB5, 26 February 2021. Available online: https://www.wcvb.com/article/covid-19-pool-testing-underway-at-massachusetts-schools-1614337230/35642430 (accessed on 19 December 2021).
- Krantz, L. Surveillance Pool Testing for COVID-19 Offers New Way to Catch Outbreaks Quickly. Boston Globe, 22 January 2021. Available online: https://www.bostonglobe.com/2021/01/22/nation/strength-numbers-future-covid-19-testing-may-depend-it/ (accessed on 19 December 2021).
- Simon, M.C.; Patton, A.P.; Naumova, E.N.; Levy, J.I.; Kumar, P.; Brugge, D.; Durant, J.L. Combining measurements from mobile monitoring and a reference site to develop models of ambient ultrafine particle number concentration at residences. Environ. Sci. Technol. 2018, 52, 6985–6995. [Google Scholar] [CrossRef]
- Liss, A.; Wu, R.; Chui, K.K.H.; Naumova, E.N. Heat-related hospitalizations in older adults: An amplified effect of the first seasonal heatwave. Sci. Rep. 2017, 7, 39581. [Google Scholar] [CrossRef]
- Hoffman, H. How Day-of-the-Week Effects Impact COVID-19 Data. The Atlantic, 22 February 2021. Available online: https://covidtracking.com/analysis-updates/how-day-of-week-effects-impact-covid-19-data (accessed on 19 December 2021).
- Aliabadi, A.; Sheikhtaheri, A.; Ansari, H. Electronic health record–based disease surveillance systems: A systematic literature review on challenges and solutions. J. Am. Med. Inform. Assoc. 2020, 27, 1977–1986. [Google Scholar] [CrossRef]


| Phase | Start Date | Duration (Days) | Description | Stringency |
|---|---|---|---|---|
| A | 22 January 2020 | 53 | Period before COVID-19 widespread in the United States | 0 |
| B | 15 March 2020 | 64 | Closures of public and private elementary and secondary schools; prohibited gatherings of more than 25 people | 5 |
| C | 18 May 2020 | 45 | Phases I and II reopening | 4 |
| D | 2 July 2020 | 89 | Phase III-Step 1 reopening | 3 |
| E | 29 September 2020 | 70 | Phase III-Step 2 reopening | 2 |
| F | 8 December 2020 | 79 | Return to Phase III-Step 1 | 3 |
| G | 25 February 2021 | 21 | Reentering Phase III-Step 2 reopening | 2 |
| H | 18 March 2021 | 71 | Phase IV reopening | 1 |
| I | 28 May 2021 | 163 | Termination of State of Emergency | 0 |
| Tests | Cases | Deaths | ||||||
|---|---|---|---|---|---|---|---|---|
| Wave | Critical Point | Date | Wave | Critical Point | Date | Wave | Critical Point | Date |
| 1 | Onset | 2 March 2020 | 1 | Onset | 2 March 2020 | 1 | Onset | 2 March 2020 |
| 1 | Peak | 8 May 2020 | 1 | Peak | 20 April 2020 | 1 | Peak | 30 April 2020 |
| 2 | Onset | 4 June 2020 | 2 | Onset 1 | 4 July 2020 | 1 | Resolution | 8 August 2020 |
| 2 | Peak | 25 August 2020 | 2 | Peak 1 | 2 January 2021 | 2 | Onset | 12 September 2020 |
| 3 | Onset | 25 September 2020 | 2 | Onset 2 | 2 March 2021 | 2 | Peak | 15 January 2021 |
| 3 | Peak | 6 December 2020 | 2 | Peak 2 | 1 April 2021 | 2 | Resolution | 7 July 2021 |
| 4 | Onset | 10 March 2021 | 3 | Onset | 23 June 2021 | 3 | Onset | 1 August 2021 |
| 4 | Peak | 4 April 2021 | 3 | Peak | 12 September 2021 | 3 | Peak | 1 October 2021 |
| 5 | Onset | 27 June 2021 | ||||||
| 5 | Peak | 15 September 2021 | ||||||
| Tests | Cases | Deaths | ||||||
|---|---|---|---|---|---|---|---|---|
| Period | Period Type | Start Date | Period | Critical Point | Start Date | Period | Critical Point | Start Date |
| 1 | Acceleration | 2 March 2020 | 1 | Acceleration | 2 March 2020 | 1 | Acceleration | 2 March 2020 |
| 2 | Deceleration | 8 May 2020 | 2 | Deceleration | 20 April 2020 | 2 | Deceleration | 30 April 2020 |
| 3 | Acceleration | 4 June 2020 | 3 | Acceleration | 4 July 2020 | 3 | Steady State | 8 August 2020 |
| 4 | Deceleration | 25 August 2020 | 4 | Deceleration | 2 January 2021 | 4 | Acceleration | 12 September 2020 |
| 5 | Acceleration | 25 September 2020 | 5 | Acceleration | 2 March 2021 | 5 | Deceleration | 15 January 2021 |
| 6 | Deceleration | 6 December 2020 | 6 | Deceleration | 1 April 2021 | 6 | Steady State | 7 July 2021 |
| 7 | Acceleration | 10 March 2021 | 7 | Acceleration | 23 June 2021 | 7 | Acceleration | 1 August 2021 |
| 8 | Deceleration | 4 April 2021 | 8 | Steady State | 12 September 2021 | 8 | Deceleration | 1 October 2021 |
| 9 | Acceleration | 27 June 2021 | ||||||
| 10 | Deceleration | 15 September 2021 | ||||||
| Day-of-Week | Mean [LCI, UCI] | Median [LQR, UQR] | L-Skewness | L-Kurtosis |
|---|---|---|---|---|
| Tests | ||||
| Sunday | 103.28 [83.73, 127.41] | 90.89 [63.90, 145.34] | 0.16 | 0.09 |
| Monday | 239.26 [194.06, 294.98] | 207.89 [146.08, 332.57] | 0.14 | 0.11 |
| Tuesday | 248.50 [201.56, 306.37] | 195.28 [149.10, 339.75] | 0.23 | 0.17 |
| Wednesday | 233.35 [189.27, 287.71] | 199.93 [142.05, 307.45] | 0.19 | 0.17 |
| Thursday | 213.99 [173.56, 263.85] | 183.75 [135.65, 281.46] | 0.18 | 0.17 |
| Friday | 199.09 [161.46, 245.48] | 179.83 [129.81, 268.36] | 0.14 | 0.13 |
| Saturday | 129.26 [104.80, 159.42] | 114.61 [78.54, 173.63] | 0.13 | 0.09 |
| Cases | ||||
| Sunday | 11.69 [9.40, 14.54] | 3.85 [0.56, 17.25] | 0.47 | 0.17 |
| Monday | 17.06 [13.76, 21.15] | 12.69 [3.23, 28.39] | 0.25 | 0.00 |
| Tuesday | 14.78 [11.91, 18.34] | 12.25 [3.20, 19.33] | 0.34 | 0.17 |
| Wednesday | 18.50 [14.93, 22.92] | 15.20 [4.25, 24.07] | 0.35 | 0.18 |
| Thursday | 18.58 [14.99, 23.02] | 14.70 [3.66, 24.23] | 0.36 | 0.19 |
| Friday | 17.77 [14.34, 22.03] | 13.96 [3.66, 23.92] | 0.35 | 0.19 |
| Saturday | 15.45 [12.46, 19.17] | 5.96 [1.18, 22.03] | 0.49 | 0.21 |
| Deaths | ||||
| Sunday | 0.40 [0.27, 0.59] | 0.12 [0.00, 0.47] | 0.57 | 0.32 |
| Monday | 0.30 [0.20, 0.47] | 0.19 [0.06, 0.37] | 0.44 | 0.26 |
| Tuesday | 0.32 [0.21, 0.49] | 0.12 [0.06, 0.37] | 0.53 | 0.32 |
| Wednesday | 0.50 [0.35, 0.72] | 0.28 [0.06, 0.59] | 0.50 | 0.32 |
| Thursday | 0.37 [0.25, 0.55] | 0.25 [0.06, 0.50] | 0.43 | 0.27 |
| Friday | 0.36 [0.24, 0.54] | 0.19 [0.06, 0.43] | 0.46 | 0.25 |
| Saturday | 0.53 [0.37, 0.75] | 0.25 [0.00, 0.56] | 0.64 | 0.47 |
| Phase | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | AIC |
|---|---|---|---|---|---|---|---|
| Tests | |||||||
| Overall | 2.27 [2.11, 2.45] a | 2.33 [2.16, 2.51] a | 2.20 [2.05, 2.37] a | 2.05 [1.90, 2.21] a | 1.94 [1.80, 2.09] a | 1.26 [1.17, 1.35] a | 9188.30 |
| B | 2.26 [2.04, 2.52] a | 2.45 [2.20, 2.72] a | 2.50 [2.25, 2.78] a | 2.41 [2.17, 2.68] a | 2.59 [2.34, 2.88] a | 1.48 [1.34, 1.65] a | 790.47 |
| C | 2.45 [2.01, 2.98] a | 2.73 [2.24, 3.32] a | 2.88 [2.35, 3.53] a | 2.72 [2.22, 3.33] a | 2.51 [2.05, 3.08] a | 1.33 [1.08, 1.63] b | 627.75 |
| D | 2.56 [2.25, 2.91] a | 2.60 [2.28, 2.96] a | 2.45 [2.15, 2.79] a | 2.30 [2.03, 2.62] a | 2.16 [1.90, 2.45] a | 1.29 [1.14, 1.47] a | 1298.50 |
| E | 2.58 [2.12, 3.14] a | 2.63 [2.16, 3.21] a | 2.46 [2.02, 3.00] a | 2.25 [1.84, 2.74] a | 2.17 [1.79, 2.65] a | 1.43 [1.17, 1.74] a | 1107.60 |
| F | 2.32 [1.82, 2.97] a | 2.23 [1.75, 2.83] a | 2.10 [1.65, 2.66] a | 1.79 [1.40, 2.28] a | 1.61 [1.26, 2.06] a | 1.35 [1.05, 1.72] c | 1276.10 |
| G | 2.24 [2.14, 2.35] a | 2.01 [1.92, 2.11] a | 1.91 [1.82, 2.01] a | 1.83 [1.74, 1.92] a | 1.72 [1.63, 1.80] a | 1.19 [1.13, 1.25] a | 223.09 |
| H | 2.27 [2.14, 2.42] a | 2.06 [1.93, 2.19] a | 1.93 [1.82, 2.06] a | 1.79 [1.68, 1.90] a | 1.74 [1.63, 1.85] a | 1.19 [1.12, 1.27] a | 868.16 |
| I | 2.07 [1.84, 2.32] a | 2.27 [2.02, 2.54] a | 2.07 [1.85, 2.33] a | 1.96 [1.75, 2.20] a | 1.74 [1.55, 1.95] a | 1.10 [0.98, 1.23] | 2429.90 |
| Cases | |||||||
| Overall | 2.00 [1.56, 2.57] a | 1.74 [1.36, 2.22] a | 1.94 [1.53, 2.47] a | 1.91 [1.50, 2.43] a | 1.98 [1.56, 2.53] a | 1.32 [1.04, 1.67] c | 6783.20 |
| B | 2.06 [1.81, 2.35] a | 2.24 [1.97, 2.56] a | 2.24 [1.97, 2.56] a | 2.24 [1.97, 2.55] a | 2.25 [1.97, 2.56] a | 1.41 [1.23, 1.61] a | 587.67 |
| C | 2.04 [1.50, 2.79] a | 2.20 [1.62, 3.00] a | 2.18 [1.60, 2.97] a | 2.11 [1.54, 2.90] a | 2.01 [1.46, 2.77] a | 1.13 [0.81, 1.59] | 343.92 |
| D | 1.53 [1.13, 2.07] b | 1.58 [1.16, 2.16] b | 1.87 [1.38, 2.54] a | 1.66 [1.22, 2.26] b | 1.84 [1.35, 2.50] a | 1.21 [0.90, 1.64] | 713.90 |
| E | 0.66 [0.47, 0.92] c | 0.82 [0.58, 1.15] | 0.99 [0.70, 1.39] | 0.92 [0.65, 1.29] | 1.14 [0.81, 1.60] | 1.07 [0.76, 1.50] | 811.69 |
| F | 0.93 [0.89, 0.97] b | 0.85 [0.81, 0.88] a | 1.23 [1.19, 1.28] a | 1.32 [1.27, 1.37] a | 1.00 [0.96, 1.04] | 1.42 [1.36, 1.47] a | 4204.20 |
| G | 0.81 [0.71, 0.92] b | 0.51 [0.44, 0.59] a | 1.17 [1.03, 1.33] c | 1.11 [0.97, 1.27] | 1.14 [1.02, 1.29] c | 1.03 [0.91, 1.15] | 365.18 |
| H | 0.89 [0.65, 1.22] | 0.75 [0.55, 1.03] | 1.37 [1.01, 1.87] c | 1.29 [0.95, 1.75] | 1.30 [0.95, 1.77] | 1.37 [1.01, 1.87] c | 766.20 |
| Deaths | |||||||
| Overall | 0.98 [0.77, 1.27] | 0.92 [0.72, 1.19] | 1.46 [1.15, 1.85] b | 1.28 [1.00, 1.64] c | 1.13 [0.89, 1.45] | 1.24 [0.98, 1.57] | 2356.60 |
| B | 0.44 [0.14, 1.41] | 0.96 [0.32, 2.96] | 1.08 [0.37, 3.15] | 0.76 [0.25, 2.38] | 0.70 [0.24, 2.09] | 1.43 [0.50, 4.06] | 399.09 |
| C | 1.29 [0.74, 2.27] | 0.90 [0.50, 1.63] | 1.50 [0.87, 2.64] | 1.18 [0.66, 2.13] | 1.36 [0.77, 2.43] | 1.17 [0.65, 2.12] | 238.51 |
| D | 1.45 [0.67, 3.19] | 0.87 [0.36, 2.08] | 2.05 [0.97, 4.46] | 3.02 [1.48, 6.36] c | 1.30 [0.59, 2.90] | 2.20 [1.06, 4.68] c | 342.27 |
| E | 0.72 [0.43, 1.18] | 0.39 [0.20, 0.72] b | 1.04 [0.66, 1.66] | 0.88 [0.54, 1.41] | 0.99 [0.62, 1.57] | 0.69 [0.41, 1.13] | 264.52 |
| F | 0.69 [0.49, 0.96] c | 0.84 [0.61, 1.14] | 1.32 [1.00, 1.75] c | 0.77 [0.56, 1.06] | 0.90 [0.66, 1.23] | 1.05 [0.78, 1.42] | 401.37 |
| G | 0.47 [0.18, 1.08] | 0.67 [0.30, 1.45] | 0.81 [0.38, 1.70] | 0.87 [0.42, 1.80] | 0.65 [0.29, 1.39] | 0.99 [0.49, 1.99] | 92.87 |
| H | 2.93 [1.47, 6.37] b | 0.81 [0.30, 2.10] | 2.47 [1.20, 5.49] c | 1.70 [0.81, 3.81] | 2.06 [1.00, 4.56] | 1.68 [0.78, 3.80] | 216.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simpson, R.B.; Lauren, B.N.; Schipper, K.H.; McCann, J.C.; Tarnas, M.C.; Naumova, E.N. Critical Periods, Critical Time Points and Day-of-the-Week Effects in COVID-19 Surveillance Data: An Example in Middlesex County, Massachusetts, USA. Int. J. Environ. Res. Public Health 2022, 19, 1321. https://doi.org/10.3390/ijerph19031321
Simpson RB, Lauren BN, Schipper KH, McCann JC, Tarnas MC, Naumova EN. Critical Periods, Critical Time Points and Day-of-the-Week Effects in COVID-19 Surveillance Data: An Example in Middlesex County, Massachusetts, USA. International Journal of Environmental Research and Public Health. 2022; 19(3):1321. https://doi.org/10.3390/ijerph19031321
Chicago/Turabian StyleSimpson, Ryan B., Brianna N. Lauren, Kees H. Schipper, James C. McCann, Maia C. Tarnas, and Elena N. Naumova. 2022. "Critical Periods, Critical Time Points and Day-of-the-Week Effects in COVID-19 Surveillance Data: An Example in Middlesex County, Massachusetts, USA" International Journal of Environmental Research and Public Health 19, no. 3: 1321. https://doi.org/10.3390/ijerph19031321
APA StyleSimpson, R. B., Lauren, B. N., Schipper, K. H., McCann, J. C., Tarnas, M. C., & Naumova, E. N. (2022). Critical Periods, Critical Time Points and Day-of-the-Week Effects in COVID-19 Surveillance Data: An Example in Middlesex County, Massachusetts, USA. International Journal of Environmental Research and Public Health, 19(3), 1321. https://doi.org/10.3390/ijerph19031321






