Spatial Spillover Effects of Directed Technical Change on Urban Carbon Intensity, Based on 283 Cities in China from 2008 to 2019
Abstract
:1. Introduction
2. Literature Review and Theoretical Hypotheses
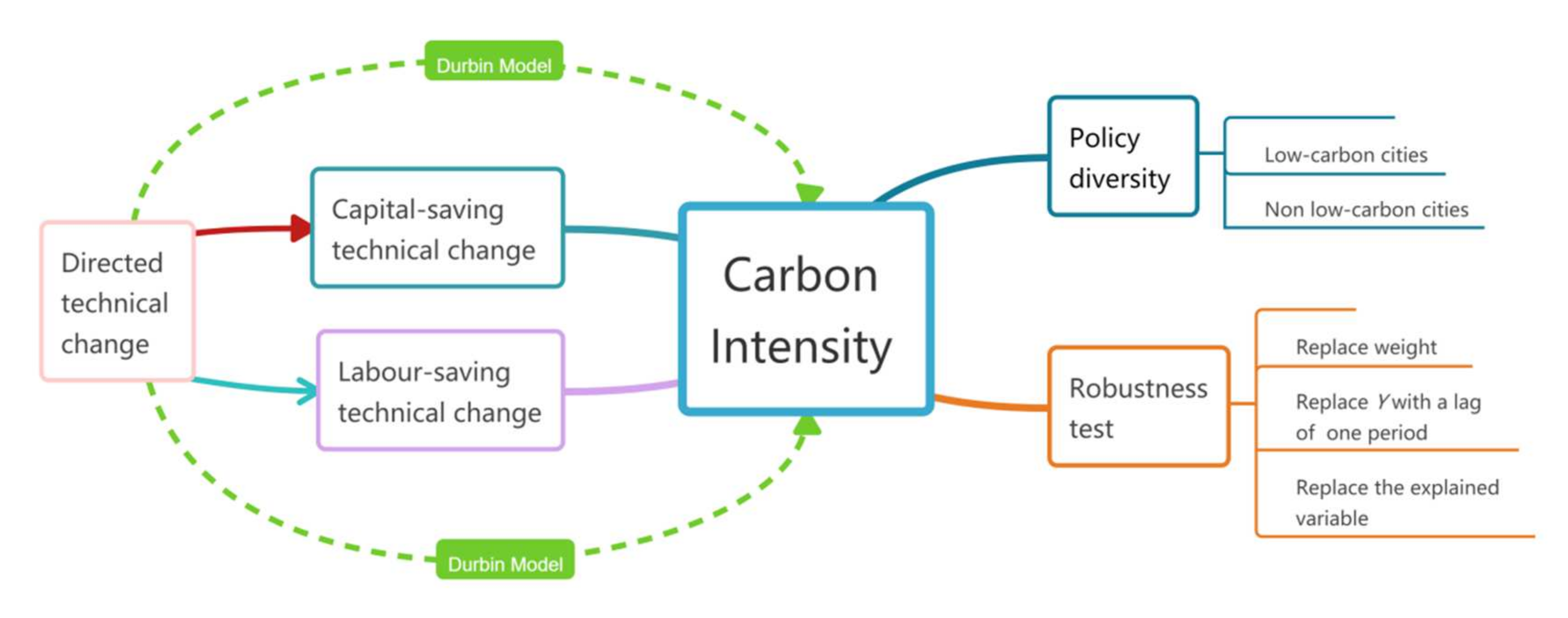
3. Data and Models
3.1. Data
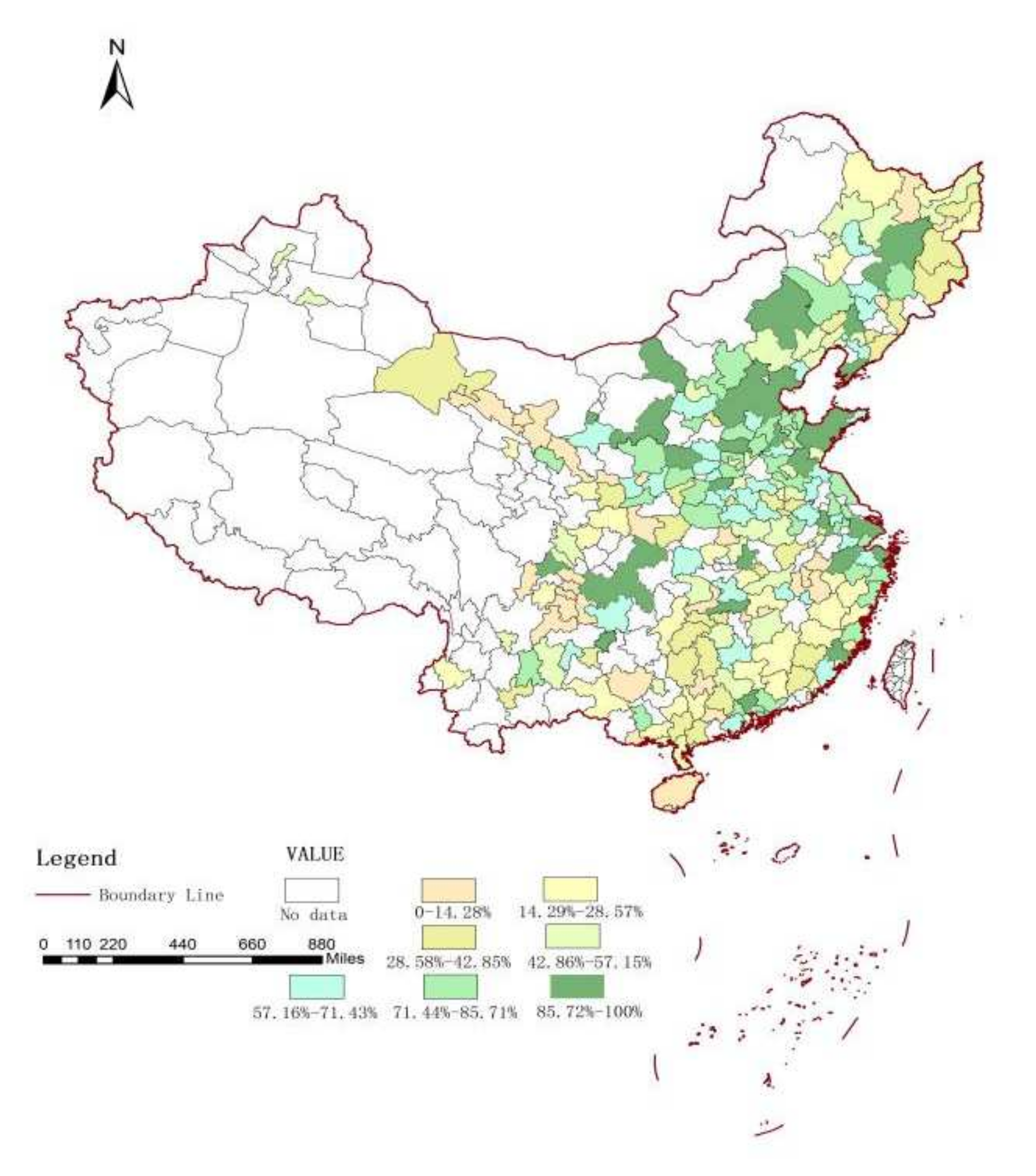
3.1.1. Explained Variable: Carbon Intensity
3.1.2. Core Explanatory Variables: Directed Technical Change
3.1.3. Control Variables
3.2. Models
3.2.1. OLS Regression Model
3.2.2. Spatial Regression Model
3.2.3. Direct and Indirect Effects Regression Model
4. Results Analysis
4.1. OLS Regression Results
4.2. Spatial Regression Results
4.3. Results of Direct and Indirect Effects of Variables
4.4. Robust Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.W.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef] [PubMed]
- Stainforth, D.A.; Calel, R. New priorities for climate science and climate economics in the 2020s. Nat. Commun. 2020, 11, 3864. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-Z.; Li, R.Y.M.; Malik, M.Y.; Murshed, M.; Khan, Z.; Umar, M. Determinants of carbon emission in China: How good is green investment? Sustain. Prod. Consum. 2021, 27, 392–401. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, X. Does financial development have a non-linear impact on energy consumption? Evidence from 30 provinces in China. Energy Econ. 2020, 90, 104845. [Google Scholar] [CrossRef]
- He, Y.; Xu, Y.; Pang, Y.; Tian, H.; Wu, R. A regulatory policy to promote renewable energy consumption in China: Review and future evolutionary path. Renew. Energy 2016, 89, 695–705. [Google Scholar] [CrossRef]
- Yu, J.; Shi, X.; Guo, D.; Yang, L. Economic policy uncertainty (EPU) and firm carbon emissions: Evidence using a China provincial EPU index. Energy Econ. 2021, 94, 105071. [Google Scholar] [CrossRef]
- Chinowsky, P.; Hayles, C.; Schweikert, A.; Strzepek, N.; Strzepek, K.; Schlosser, C.A. Climate change: Comparative impact on developing and developed countries. Eng. Proj. Organ. J. 2011, 1, 67–80. [Google Scholar] [CrossRef] [Green Version]
- Porter, M.E. Competitive Advantage of Nations? The Competitive Advantage of Nations; The Free Press: New York, NY, USA, 1990; pp. 73–93. [Google Scholar]
- Sisco, M.R.; Pianta, S.; Weber, E.U.; Bosetti, V. Global climate marches sharply raise attention to climate change: Analysis of climate search behavior in 46 countries. J. Environ. Psychol. 2021, 75, 101596. [Google Scholar] [CrossRef]
- Antonelli, C.; Feder, C. The new direction of technological change in the global economy. Struct. Chang. Econ. Dyn. 2020, 52, 1–12. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pham, T.A.T.; Tram, H.T.X. Role of information and communication technologies and innovation in driving carbon emissions and economic growth in selected G-20 countries. J. Environ. Manag. 2020, 261, 110162. [Google Scholar] [CrossRef]
- Sajid, M.J.; Niu, H.; Liang, Z.; Xie, J.; Rahman, M.H.U. Final consumer embedded carbon emissions and externalities: A case of Chinese consumers. Environ. Dev. 2021, 39, 100642. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, L.; Zhou, P.; Chang, Y.; Zhou, D.; Pang, M.; Yin, H. Assessing the environmental externalities for biomass- and coal-fired electricity generation in China: A supply chain perspective. J. Environ. Manag. 2019, 246, 758–767. [Google Scholar] [CrossRef] [PubMed]
- Ke, H.; Dai, S.; Yu, H. Spatial effect of innovation efficiency on ecological footprint: City-level empirical evidence from China. Environ. Technol. Innov. 2021, 22, 101536. [Google Scholar] [CrossRef]
- Khanna, N.; Fridley, D.; Hong, L.X. China’s pilot low-carbon city initiative: A comparative assessment of national goals and local plans. Sustain. Cities Soc. 2014, 12, 110–121. [Google Scholar] [CrossRef]
- Mimura, T.; Simayoshi, H.; Suda, T.; Iijima, M.; Mituoka, S. Development of energy saving technology for flue gas carbon dioxide recovery in power plant by chemical absorption method and steam system. Energy Convers. Manag. 1997, 38, S57–S62. [Google Scholar] [CrossRef]
- Adhvaryu, A.; Kala, N.; Nyshadham, A. The light and the heat: Productivity co-benefits of energy-saving technology. Rev. Econ. Stat. 2020, 102, 779–792. [Google Scholar] [CrossRef]
- Almeida, S.T.D.; Borsato, M. Assessing the efficiency of End of Life technology in waste treatment—A bibliometric literature review. Res. Conserv. Recycl. 2019, 140, 189–208. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Shove, E. What is wrong with energy efficiency? Build. Res. Inf. 2018, 46, 779–789. [Google Scholar] [CrossRef]
- Raza, A.; Gholami, R.; Rezaee, R.; Rasouli, V.; Rabiei, M. Significant aspects of carbon capture and storage—A review. Petroleum 2019, 5, 335–340. [Google Scholar] [CrossRef]
- Singh, A.; Mishra, N.; Ali, S.I.; Shukla, N.; Shankar, R. Cloud computing technology: Reducing carbon footprint in beef supply chain. Int. J. Prod. Econ. 2015, 164, 462–471. [Google Scholar] [CrossRef] [Green Version]
- Hicks, J.R.S. The Theory of Wages; Macmillan: London, UK, 1932. [Google Scholar]
- Kennedy, C. Induced bias in innovation and the theory of distribution. Econ. J. 1964, 74, 541–547. [Google Scholar] [CrossRef]
- Samuelson, P.A. Proof that properly anticipated prices fluctuate randomly. Ind. Manag. Rev. 1965, 6, 41–49. [Google Scholar]
- Drandakis, E.M.; Phelps, E.S. A model of induced invention, growth and distribution. Econ. J. 1966, 76, 823–840. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D. Why do new technologies complement skills? Directed technical change and wage inequality. Q. J. Econ. 1998, 113, 1055–1089. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D. Labor and capital: Augmenting technical change. J. Eur. Econ. Assoc. 2003, 1, 199–230. [Google Scholar] [CrossRef] [Green Version]
- Acemoglu, D.; Aghion, P.; Zilibotti, F. Distance to frontier, selection, and economic growth. J. Eur. Econ. Assoc. 2006, 4, 37–74. [Google Scholar] [CrossRef]
- Acemoglu, D. Equilibrium bias of technology. Econometrica 2007, 75, 1371–1409. [Google Scholar] [CrossRef] [Green Version]
- Jones, C.I. The shape of production function and the direction of technical change. Q. J. Econ. 2005, 120, 517–549. [Google Scholar]
- Acemoglu, D. Directed technical change. Rev. Econ. Stud. 2002, 69, 781–809. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.H.; Emer, J.; Sze, V. Eyeriss: A spatial architecture for energy-efficient dataflow for convolutional neural networks. IEEE Micro. 2016, 44, 367–379. [Google Scholar] [CrossRef]
- Huang, J.; Xiang, S.; Wu, P.; Chen, X. How to control China’s energy consumption through technological progress: A spatial heterogeneous investigation. Energy 2022, 238, 121965. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, S.; Yang, Y.; Xie, G.H.; Zhao, W. Spatial disparity of life-cycle greenhouse gas emissions from corn straw-based bioenergy production in China. Appl. Energy 2021, 305, 117854. [Google Scholar] [CrossRef]
- Vega, S.H.; van Leeuwen, E.; van Twillert, N. Uptake of residential energy efficiency measures and renewable energy: Do spatial factors matter? Energy Policy 2021, 160, 112659. [Google Scholar] [CrossRef]
- Yang, L.; Wang, K.-L.; Geng, J.-C. China’s regional ecological energy efficiency and energy saving and pollution abatement potentials: An empirical analysis using epsilon-based measure model. J. Clean. Prod. 2018, 194, 300–308. [Google Scholar] [CrossRef]
- Sun, X. Research on fluctuations and convergency of efficiency in energy conservation and emission reduction in China. Stat. Inf. Forum 2010, 25, 101–107. [Google Scholar] [CrossRef]
- Yao, X.L.; Yu, B. Technical progress, structure change, and carbon dioxide emissions of industry. Sci. Res. Manag. 2012, 33, 35–40. [Google Scholar] [CrossRef]
- Wei, W.X.; Yang, F. Impact of technology advance on carbon dioxide emission in China. Stat. Res. 2010, 27, 36–44. [Google Scholar]
- Färe, R.; Grosskopf, S.; Lovell, C.A.K.; Grifell-Tatjé, E. Biased technical change and the malmquist productivity index. Scand. J. Econ. 1997, 99, 119–127. [Google Scholar] [CrossRef]
- Domazlicky, W. Total factor productivity growth in manufacturing: A regional approach using linear programming. Reg. Sci. Urban Econ. 1999, 29, 105–122. [Google Scholar] [CrossRef]
- Pastor, J.T.; Lovell, C.K.; Aparicio, J. Defining a new graph inefficiency measure for the proportional directional distance function and introducing a new Malmquist productivity index. Eur. J. Oper. Res. 2019, 281, 222–230. [Google Scholar] [CrossRef]
- Kone, A.C.; Buke, T. Factor analysis of projected carbon dioxide emissions according to the ipcc based sustainable emission scenario in turkey. Renew. Energy 2019, 133, 914–918. [Google Scholar] [CrossRef]
- Mulligan, C.; Sala-I-Martin, X. A Labor-Income-Based Measure of the Value of Human Capital: An Application to the States of the United States; NBER Working Papers: Cambridge, MA, USA, 1995. [Google Scholar] [CrossRef]
- Lu, F.; Liu, M.H.; Sun, Y.Y. Agglomeration, TFP and industrial growth. Stud. Sci. Sci. 2018, 36, 1575–1584. [Google Scholar]
- Wang, B.B.; Qi, S.Z. Biased technological progress, factor substitution and China’s industrial energy intensity. Econ. Res. J. 2014, 49, 115–127. [Google Scholar]
- Tu, Z.G.; Chen, L. The direction of technological progress and high-quality economic development: Based on the perspective of TFP and industrial structure upgrading. J. China Univ. Geosci. 2019, 19, 119–135. [Google Scholar]
- Liang, T.; Wang, S.; Lu, C.; Jiang, N.; Long, W.; Zhang, M.; Zhang, R. Environmental impact evaluation of an iron and steel plant in China: Normalized data and direct/indirect contribution. J. Clean. Prod. 2020, 264, 121697. [Google Scholar] [CrossRef]
- Silva, R.; Lbo, R.; Faro, L.E.; Santos, G.; Peixoto, M. Genetic parameters for somatic cell count (scc) and milk production traits of guzerá cows using data normalized by different procedures. Trop. Anim. Health Prod. 2020, 52, 2513–2522. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A. Rethinking the environmental impacts of population, affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar]
- Chen, J.D.; Wang, B.; Huang, S.; Song, M. The influence of increased population density in China on air pollution. Sci. Total Environ. 2020, 735, 139456. [Google Scholar] [CrossRef]
- Acemoglu, D.; Aghion, P.; Bursztyn, L.; Hemous, D. The environment and directed technical change. Am. Econ. Rev. 2012, 102, 131–166. [Google Scholar] [CrossRef] [Green Version]
- Stengos, T.; Fatouros, N. Nuclear Energy, Economic Growth and the Environment: Optimal Policies in a Model with Endogenous Technical Change and Environmental Constraints; University of Guelph: Guelph, ON, Canada, 2020. [Google Scholar]
- Wang, X.; Wang, Y.; Lan, Y. Measuring the bias of technical change of industrial energy and environment productivity in China: A global DEA-Malmquist productivity approach. Environ. Sci. Pollut. Res. 2021, 28, 41896–41911. [Google Scholar] [CrossRef] [PubMed]
- Bao, C.; Chen, X.J.; Liang, G.L. Analysis on the influencing factors of water use efficiency in Henan province based on spatial econometric models. J. Nat. Resour. 2016, 31, 1138–1147. [Google Scholar]
- Anselin, L.; Le, G.J.; Jayet, H. Spatial panel econometrics. In The Econometrics of Panel Data, Fundamentals and Recent Developments in Theory and Practice, 3rd ed.; Matyas, L., Sevestre, P., Eds.; Kluwer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Druska, V.; Horrace, W.C. Generalized moments estimation for spatial panel data: Indonesian rice farming. Am. J. Agric. Econ. 2004, 86, 185–198. [Google Scholar] [CrossRef]
- Baltagi, B.; Song, S.H.; Koh, W. Testing panel data regression models with spatial error correlation. J. Econ. 2003, 117, 123–150. [Google Scholar] [CrossRef]
- Anselin, L.; Hudak, S. Spatial econometrics in practice: A review of software options. Reg. Sci. Urban Econ. 1992, 22, 509–536. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, T.; Wang, Y.; Shi, Z. Research on impacts of population-related factors on carbon emissions in Beijing from 1984 to 2012. Environ. Impact Assess. Rev. 2015, 55, 45–53. [Google Scholar] [CrossRef]
- Bai, C.Q.; Zhou, L.; Xia, M.L.; Feng, C. Analysis of the spatial association network structure of China’s transportation carbon emissions and its driving factors. J. Environ. Manag. 2020, 253, 109765. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef] [Green Version]
- Lesage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gómez-Rubio, V.; Bivand, R.S.; Rue, H. Estimating spatial econometrics models with integrated nested laplace approximation. Mathematics 2021, 9, 2044. [Google Scholar] [CrossRef]
- Anselin, L.; Bera, A.K.; Florax, R.; Yoon, M.J. Simple diagnostic tests for spatial dependence. Reg. Sci. Urban Econ. 1996, 26, 77–104. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Li, Q. Testing AR(1) against MA(1) disturbances in an error component model. J. Econ. 1995, 68, 133–151. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publishers: Boston, MA, USA, 1988. [Google Scholar]
- Zhang, J.F.; Fang, Y. A robust test for spatial errors models. J. Quant. Tech. Econ. 2011, 28, 152–160. [Google Scholar] [CrossRef]

| Variable | Name | Symbol | Data Source |
|---|---|---|---|
| Explained variables | Carbon intensity | lncd | The ratio of urban carbon emissions to GDP; the basic data can be found in the China Urban Statistical Yearbook (2009–2020) and China Urban Environment Yearbook (2009–2020). |
| Core explanatory variables | Directed technological change | lndtc | The capital stock is estimated by the perpetual inventory method based on the year 2000; total employment and real GDP are derived from the China Urban Statistical Yearbook (2009–2020) and China Science and Technology Yearbook (2009–2020). |
| Control variables | Population density (ratio of urban population to urban area) | lnpop | Data from the Statistical Yearbook of Chinese Cities (2009–2020). |
| Average urban night lights | lnnl | NPP-VIIRS NTL (2014–2019) and DMSP-OLS RNTL (2009–2013), and using the method of Chen et al. (2021) to calibrate inconsistent data sources around 2013 [52]. | |
| Foreign direct investment | lnfdi | Data from the Statistical Yearbook of Chinese Cities (2009–2020) | |
| The proportion of tertiary industry to GDP | lnthird | ||
| Total road passenger transport | lntrans | ||
| The number of full-time college teachers | lntechs | ||
| The ratio of pollution control investment to GDP | lnpollution |
| Variable | Symbol | Unit | Observations | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|---|---|
| Carbon intensity | lncd | Tons/RMB 10,000 | 3113 | 0.87 | 2.3901 | 0.49 | 4.23 |
| Directed technological change | lndtc | Data have been normalized | 3113 | 0.65 | 0.7907 | 0.32 | 0.98 |
| Population density (ratio of urban population to urban area) | lnpop | Number of people/hm2 | 3113 | 2.16 | 4.0014 | 1.57 | 3.05 |
| Average urban night lights | lnnl | Candela(cd) | 3113 | 3.70 | 5.0668 | 2.11 | 6.94 |
| Foreign direct investment | lnfdi | RMB 10,000 | 3113 | 2.60 | 1.4762 | 1.70 | 5.08 |
| The proportion of tertiary industry to GDP | lnthird | % | 3113 | 37.8% | 0.1825 | 28.71% | 76.30% |
| Total road passenger transport | lntrans | 10,000 people | 3113 | 3.59 | 2.2003 | 1.04 | 6.68 |
| The number of full-time college teachers | lntechs | 10,000 people | 3113 | 1.61 | 3.2947 | 2.69 | 5.74 |
| The ratio of pollution control investment to GDP | lnpollution | RMB 10,000 | 3113 | 3.98 | 3.0898 | 0.91 | 6.37 |
| Explanatory Variable | Coefficient | t-Value |
|---|---|---|
| lndtc | −0.0162 *** | (−2.83) |
| lnpop | −0.0024 ** | (−2.30) |
| lnnl | 0.0043 *** | (4.37) |
| lnfdi | −0.0624 *** | (−4.92) |
| lnthird | 0.0003 *** | (5.34) |
| lntrans | 0.0048 *** | (4.98) |
| lntechs | −0.0055 | (−0.84) |
| lnpollution | −0.2046 * | (−1.86) |
| Time and Space Are Not Fixed | Time and Space Are Fixed | Time Is Fixed | Space Is Fixed | |
|---|---|---|---|---|
| LM test of spatial lag effect (LMlag) | 41.47 *** (0.000) | 52.48 *** (0.000) | 51.28 ** (0.000) | 47.59 *** (0.000) |
| Robust LM test of spatial lag effect (R-LMlag) | 18.93 *** (0.000) | 46.71 *** (0.000) | 30.38 ** (0.000) | 25.73 *** (0.000) |
| LM test of spatial error effect (LMerr) | 30.65 *** (0.000) | 9.63 *** (0.000) | 38.03 ** (0.000) | 17.92 *** (0.000) |
| Robust LM test for spatial error effects (R-LMerr) | 1.61 (0.107) | 2.30 ** (0.021) | 1.91 * (0.057) | 29.37 *** (0.000) |
| Variable | Coeffcient | Lag Coefficient |
|---|---|---|
| β | θ | |
| Spatial regression coefficient δ | 0.1027 *** (4.91) | − |
| lndtc | −0.0398 *** (−4.50) | −0.0458 *** (−8.28) |
| lnpop | −0.0624 *** (−3.66) | 0.0620 *** (3.53) |
| lnnl | 0.0426 *** (4.37) | 0.3019 *** (6.89) |
| lnfdi | −0.0109 ** (−2.46) | 0.3813 *** (9.37) |
| ln3rd | 0.0167 *** (5.08) | 0.0299 ** (2.31) |
| lntrans | 1.5103 *** (5.34) | 0.0374 *** (2.46) |
| lntechs | −0.0070 (−0.79) | −0.0903 (−1.21) |
| lnpollution | −0.7210 *** (−4.98) | 0.4892 *** (−4.50) |
| Variable | Direct Effect | Indirect Effect | Total Effect |
|---|---|---|---|
| lndtc | −0.0472 *** (−4.69) | −0.0259 ** (−2.08) | −0.0731 *** (−3.99) |
| lnpop | 0.4843 (0.56) | −0.5946 * (1.85) | −0.1103 * (1.90) |
| Lnnl | 0.0305 ** (2.11) | 0.5858 *** (3.99) | 0.6163 *** (5.28) |
| Lnfdi | −0.1671 * (−1.83) | −0.0053 ** (−2.55) | −0.1724 *** (−6.21) |
| Ln3rd | −0.0951 *** (−4.93) | −0.0054 ** (−2.38) | −0.1005 *** (−4.91) |
| lntrans | 0.2376 ** (2.11) | 0.0374 *** (2.46) | 0.2750 *** (3.90) |
| lntechs | 0.0447 (0.16) | 0.0013 (0.70) | 0.0460 (0.99) |
| lnpollution | −0.8181 * (−1.83) | 0.3024 *** (5.13) | −0.5157 *** (4.02) |
| rho | 0.2857 ** (2.51) | ||
| R2 | 0.68 | ||
| likelihood ratio | 1329.0971 | ||
| Low-Carbon Cities | Non-Low-Carbon Cities | |||||
|---|---|---|---|---|---|---|
| Variable | Direct Effect | Indirect Effect | Total Effect | Direct Effect | Indirect Effect | Total Effect |
| lndtc | −0.5346 *** (−2.72) | −0.2616 *** (−3.10) | −0.7962 ** (−2.29) | −0.0436 ** (−2.29) | −0.0074 ** (−2.10) | −0.0510 ** (−1.79) |
| lnpop | −0.3478 ** (−2.13) | −0.1791 * (−1.69) | −0.5269 * (−1.80) | 0.0421 ** (2.41) | 0.0191 * (1.67) | 0.0612 * (1.69) |
| lnnl | 0.1200 *** (3.62) | 0.0132 ** (3.30) | 0.1332 ** (2.06) | 0.0142 * (1.74) | 0.0124 * (1.81) | 0.0266 ** (2.40) |
| lnfdi | −0.1236 ** (−2.53) | −0.0981 ** (−2.07) | −0.2217 ** (−2.03) | −0.0188 *** (−5.75) | −0.0020 *** (−3.96) | −0.0208 *** (−2.85) |
| ln3rd | −0.1028 ** (−2.19) | 0.0145 * (1.82) | 0.0883 * (1.81) | 0.0033 ** (2.23) | 0.0174 * (1.83) | 0.0207 ** (1.74) |
| lntrans | 0.0337 ** (2.06) | 0.0294 * (1.83) | 0.0631 * (1.72) | 0.0013 ** (2.20) | 0.0066 * (1.89) | 0.0079 ** (1.96) |
| lntechs | 0.1394 (1.61) | 0.0110 (0.17) | 0.1504 (0.12) | 0.0411 (1.04) | 0.0007 (0.87) | 0.0418 (0.14) |
| lnpollution | −1.1082 *** (−5.09) | −0.0201 *** (−2.85) | −1.1283 *** (−6.20) | 0.1313 ** (1.96) | −0.0507 ** (−2.12) | 0.0806 ** (2.24) |
| Rho | 0.1793 ** (2.23) | 0.2667 ** (2.50) | ||||
| R2 | 0.76 | 0.69 | ||||
| Likelihood ratio | 1319.8709 | 783.9702 | ||||
| Replacement of Geographic Weights | Dynamic Durbin Model | Replacement of the Explanatory Variable | ||||
|---|---|---|---|---|---|---|
| Variable | Direct Effect | Indirect Effect | Direct Effect | Indirect Effect | Direct Effect | Indirect Effect |
| lndtc | −1.0453 *** (−7.21) | −0.0726 ** (−2.23) | −0.0203 ** (−2.14) | −0.0169 * (−2.75) | −0.0266 *** (−2.48) | −0.0116 ** (−2.48) |
| lnpop | 0.0068 ** (2.42) | 0.0205 * (1.76) | 0.0014 * (1.95) | 0.0167 ** (2.10) | 0.0031 *** (2.83) | 0.0086 *** (4.87) |
| lnnl | 0.0042 *** (2.95) | 0.0076 ** (2.07) | 0.1236 ** (2.47) | 0.0009 ** (2.15) | 0.0051 *** (3.77) | 0.0312 *** (3.18) |
| lnfdi | −0.0136 ** (−2.26) | −0.0199 ** (−2.30) | −0.0410 *** (−4.39) | −0.0209 *** (−6.31) | −0.5134 ** (−2.39) | −0.7758 *** (5.19) |
| ln3rd | 0.0019 ** (1.70) | 0.0025 * (1.92) | 0.0424 ** (2.07) | 0.0086 *** (2.66) | 0.0072 ** (2.23) | 0.0058 ** (1.71) |
| lntrans | 0.0414 *** (3.04) | 0.0015 * (1.95) | 0.0009 * (1.78) | 0.0180 ** (2.05) | 0.0027 * (1.73) | −0.0222 ** (1.88) |
| lntechs | 0.0085 (0.94) | 0.0106 (0.38) | 0.0007 (0.96) | 0.0281 (1.06) | 0.0016 (0.55) | 0.0459 (1.35) |
| lnpollution | −0.0709 *** (−4.39) | 0.0172 *** (2.88) | −0.9781 *** (−4.22) | 0.0338 ** (2.12) | −0.0404 ** (−2.41) | 0.0016 ** (2.40) |
| Rho | 0.2913 *** (2.80) | 0.1433 *** (6.28) | 0.0136 *** (8.50) | |||
| R2 | 0.64 | 0.49 | 0.72 | |||
| Likelihood ratio | 838.7348 | 1092.5382 | 1205.9276 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ke, H. Spatial Spillover Effects of Directed Technical Change on Urban Carbon Intensity, Based on 283 Cities in China from 2008 to 2019. Int. J. Environ. Res. Public Health 2022, 19, 1679. https://doi.org/10.3390/ijerph19031679
Zhang H, Ke H. Spatial Spillover Effects of Directed Technical Change on Urban Carbon Intensity, Based on 283 Cities in China from 2008 to 2019. International Journal of Environmental Research and Public Health. 2022; 19(3):1679. https://doi.org/10.3390/ijerph19031679
Chicago/Turabian StyleZhang, Hui, and Haiqian Ke. 2022. "Spatial Spillover Effects of Directed Technical Change on Urban Carbon Intensity, Based on 283 Cities in China from 2008 to 2019" International Journal of Environmental Research and Public Health 19, no. 3: 1679. https://doi.org/10.3390/ijerph19031679
APA StyleZhang, H., & Ke, H. (2022). Spatial Spillover Effects of Directed Technical Change on Urban Carbon Intensity, Based on 283 Cities in China from 2008 to 2019. International Journal of Environmental Research and Public Health, 19(3), 1679. https://doi.org/10.3390/ijerph19031679





