Multiple COVID-19 Waves and Vaccination Effectiveness in the United States
Abstract
:1. Introduction
2. Methods
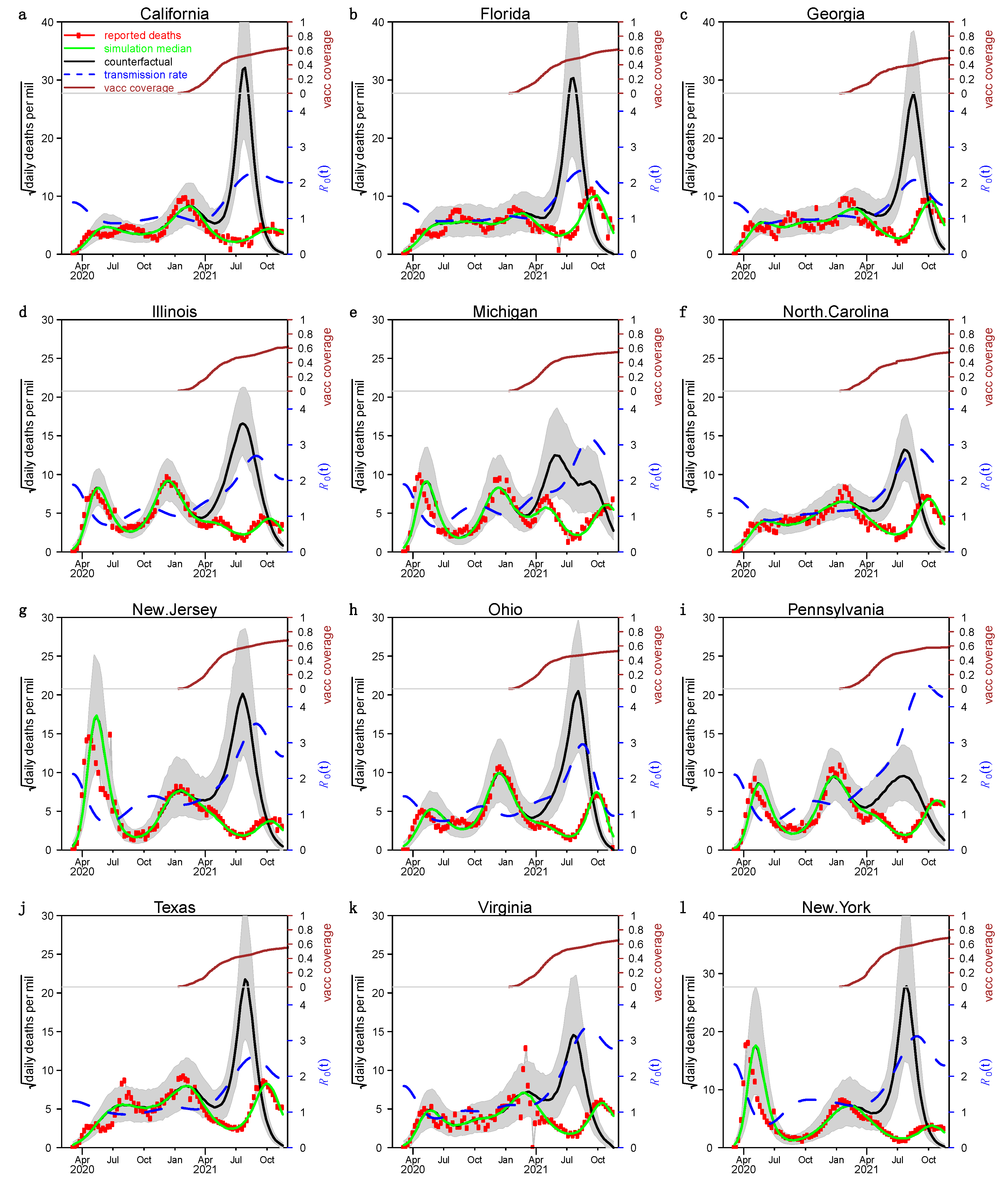
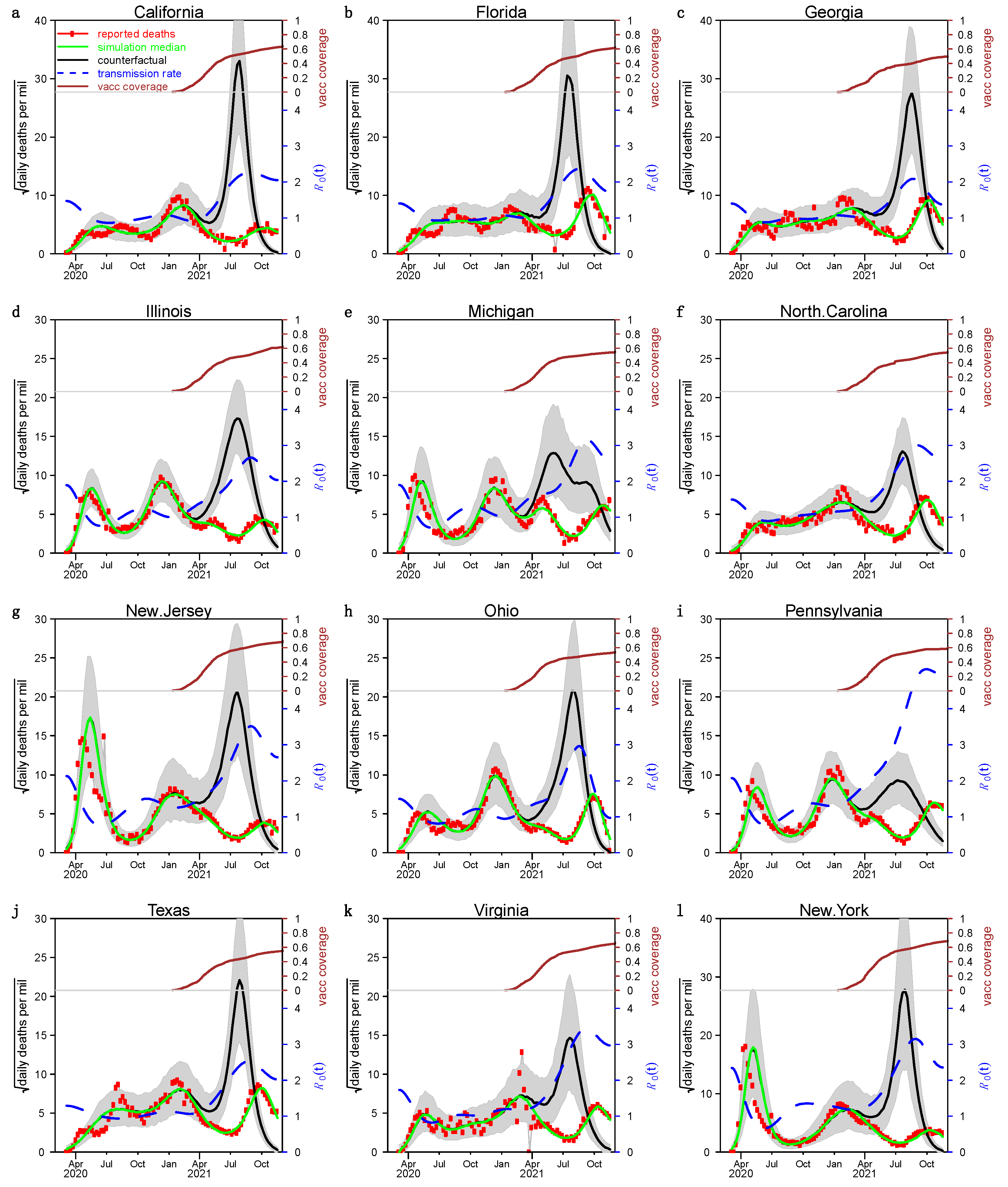
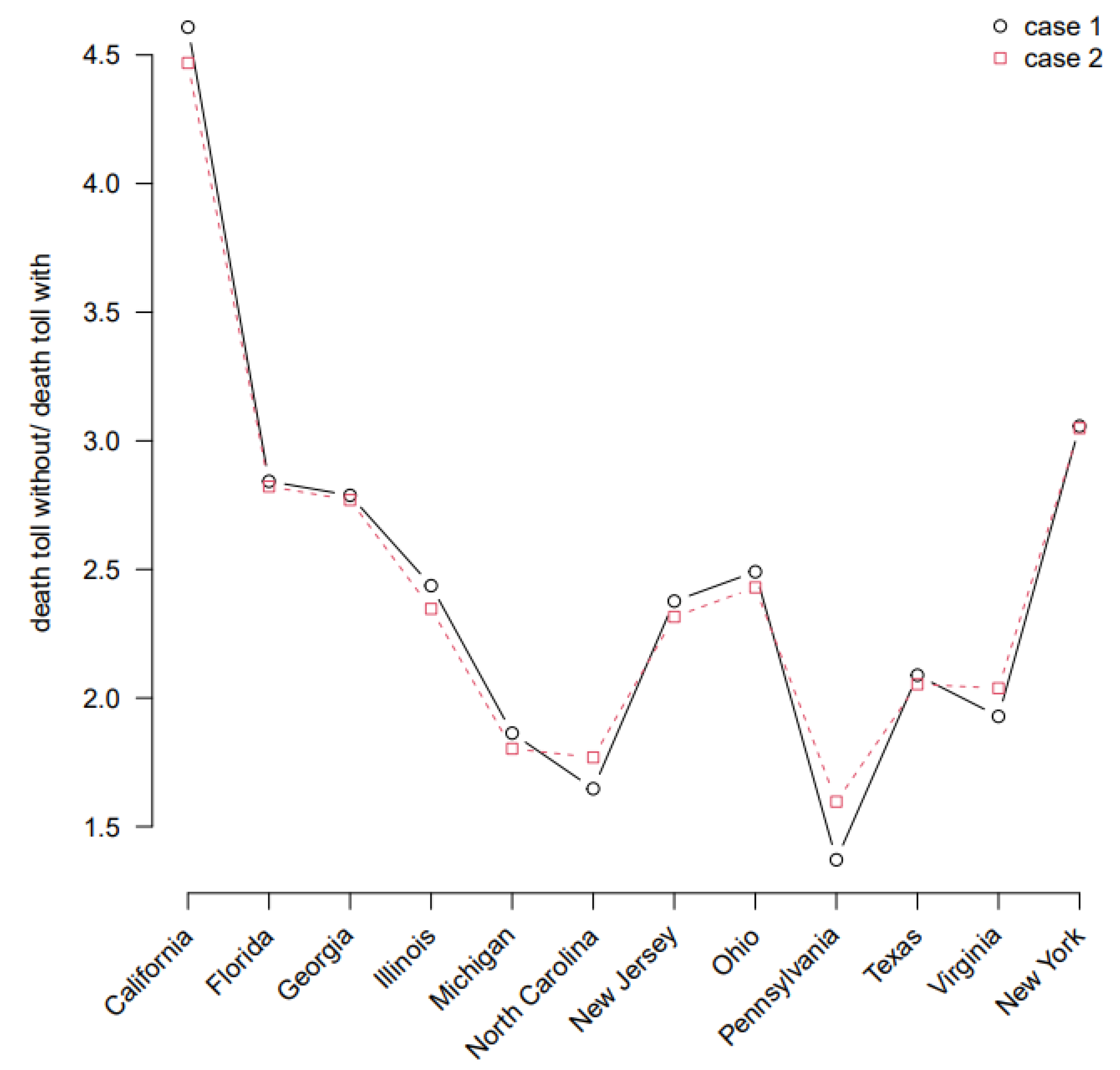
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caroline, K.; Samantha, K.; Jason, S.B. UPDATED: Timeline of the Coronavirus. Available online: https://www.thinkglobalhealth.org/article/updated-timeline-coronavirus (accessed on 4 December 2021).
- WHO. Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/region/amro/country/us (accessed on 24 December 2021).
- Davies, N.G.; Jarvis, C.I.; Edmunds, W.J.; Jewell, N.P.; Diaz-Ordaz, K.; Keogh, R.H. Increased mortality in community-tested cases of SARS-CoV-2 lineage B. 1.1. 7. Nature 2021, 593, 270–274. [Google Scholar]
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.; Russell, T.W.; Tully, D.C.; Washburne, A.D. Estimated transmissibility and impact of SARS-CoV-2 lineage B. 1.1. 7 in England. Science 2021, 372, eabg3055. [Google Scholar] [CrossRef]
- Volz, E.; Mishra, S.; Chand, M.; Barrett, J.C.; Johnson, R.; Geidelberg, L.; Hinsley, W.R.; Laydon, D.J.; Dabrera, G.; O’Toole, Á. Assessing transmissibility of SARS-CoV-2 lineage B. 1.1. 7 in England. Nature 2021, 593, 266–269. [Google Scholar] [CrossRef]
- Adam, D. What scientists know about new, fast-spreading coronavirus variants. Nature 2021, 594, 19–20. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Sarah, A.; Aliza, A.; Anne, B.; Matthew, B.; Weiyi, C.; Julia, C. Coronavirus (COVID-19) Data in the United States. Available online: https://github.com/nytimes/covid-19-data (accessed on 4 December 2021).
- Coronavirus (COVID-19) Vaccinations. Available online: https://ourworldindata.org/covid-vaccinations (accessed on 5 December 2021).
- SARS-CoV-2 Variants in Analyzed Sequences, United States. Available online: https://ourworldindata.org/grapher/covid-variants-area (accessed on 5 December 2021).
- Shu, Y.; McCauley, J. GISAID: Global initiative on sharing all influenza data–from vision to reality. Eurosurveillance 2017, 22, 30494. [Google Scholar] [PubMed] [Green Version]
- Khare, S.; Gurry, C.; Freitas, L.; Schultz, M.B.; Bach, G.; Diallo, A.; Akite, N.; Ho, J.; Lee, R.T.; Yeo, W. GISAID’s Role in Pandemic Response. China CDC Wkly. 2021, 3, 1049. [Google Scholar] [CrossRef]
- Elbe, S.; Buckland-Merrett, G. Data, disease and diplomacy: GISAID’s innovative contribution to global health. Glob. Chall. 2017, 1, 33–46. [Google Scholar]
- Iwasaki, A. What reinfections mean for COVID-19. Lancet Infect. Dis. 2021, 21, 3–5. [Google Scholar] [PubMed]
- CDC COVID-19 Vaccine Breakthrough Case Investigations Team. COVID-19 Vaccine Breakthrough Infections Reported to CDC—United States, 1 January–April 30, 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 792. [Google Scholar]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef]
- Thompson, M.G.; Burgess, J.L.; Naleway, A.L.; Tyner, H.L.; Yoon, S.K.; Meece, J.; Olsho, L.E.; Caban-Martinez, A.J.; Fowlkes, A.; Lutrick, K. Interim estimates of vaccine effectiveness of BNT162b2 and mRNA-1273 COVID-19 vaccines in preventing SARS-CoV-2 infection among health care personnel, first responders, and other essential and frontline workers—Eight US locations, December 2020–March 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 495. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, M.; Rice, M.; Su, Y.; Yang, C. Phased Implementation of COVID-19 Vaccination: Rapid Assessment of Policy Adoption, Reach and Effectiveness to Protect the Most Vulnerable in the US. Int. J. Environ. Res. Public Health 2021, 18, 7665. [Google Scholar] [CrossRef] [PubMed]
- Blaiszik, B.; Graziani, C.; Olds, J.L.; Foster, I. The Delta Variant Had Negligible Impact on COVID-19 Vaccine Effectiveness in the USA. medRxiv 2021. [Google Scholar] [CrossRef]
- Zou, D.; Wang, L.; Xu, P.; Chen, J.; Zhang, W.; Gu, Q. Epidemic model guided machine learning for COVID-19 forecasts in the United States. medRxiv 2020. [Google Scholar] [CrossRef]
- IHME COVID-19 Forecasting Team. Modeling COVID-19 scenarios for the United States. Nat. Med. 2021, 27, 94–105. [Google Scholar] [CrossRef]
- Monod, M.; Blenkinsop, A.; Xi, X.; Hebert, D.; Bershan, S.; Tietze, S.; Baguelin, M.; Bradley, V.C.; Chen, Y.; Coupland, H. Age groups that sustain resurging COVID-19 epidemics in the United States. Science 2021, 371, eabe8372. [Google Scholar]
- Singh, S.; Shaikh, M.; Hauck, K.; Miraldo, M. Impacts of introducing and lifting nonpharmaceutical interventions on COVID-19 daily growth rate and compliance in the United States. Proc. Natl. Acad. Sci. USA 2021, 118, e2021359118. [Google Scholar] [CrossRef]
- Liu, P.; Beeler, P.; Chakrabarty, R.K. COVID-19 progression timeline and effectiveness of response-to-spread interventions across the United States. medRxiv 2020. [Google Scholar] [CrossRef]
- Courtemanche, C.; Garuccio, J.; Le, A.; Pinkston, J.; Yelowitz, A. Strong Social Distancing Measures in The United States Reduced The COVID-19 Growth Rate: Study evaluates the impact of social distancing measures on the growth rate of confirmed COVID-19 cases across the United States. Health Aff. 2020, 39, 1237–1246. [Google Scholar]
- Moghadas, S.M.; Vilches, T.N.; Zhang, K.; Wells, C.R.; Shoukat, A.; Singer, B.H.; Meyers, L.A.; Neuzil, K.M.; Langley, J.M.; Fitzpatrick, M.C.; et al. The Impact of Vaccination on Coronavirus Disease 2019 (COVID-19) Outbreaks in the United States. Clin. Infect. Dis. 2021, 73, 2257–2264. [Google Scholar] [CrossRef]
- Shim, E. Projecting the Impact of SARS-CoV-2 Variants and the Vaccination Program on the Fourth Wave of the COVID-19 Pandemic in South Korea. Int. J. Environ. Res. Public Health 2021, 18, 7578. [Google Scholar] [CrossRef]
- Li, Y.; Ge, L.; Zhou, Y.; Cao, X.; Zheng, J. Toward the Impact of Non-pharmaceutical Interventions and Vaccination on the COVID-19 Pandemic With Time-Dependent SEIR Model. Front. Artif. Intell. 2021, 4, 26. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Anderson, D.; Burnham, K. Model Selection and Multi-Model Inference; Springer: New York, NY, USA, 2004; Volume 63, p. 10. [Google Scholar]
- Song, H.; Fan, G.; Liu, Y.; Wang, X.; He, D. The Second Wave of COVID-19 in South and Southeast Asia and the Effects of Vaccination. Front. Med. (Lausanne) 2021, 8, 773110. [Google Scholar] [CrossRef]
- Song, H.; Fan, G.; Zhao, S.; Li, H.; Huang, Q.; He, D. Forecast of the COVID-19 trend in India: A simple modelling approach. Math. Biosci. Eng. 2021, 18, 9775–9786. [Google Scholar] [CrossRef]
- Rovida, F.; Cassaniti, I.; Percivalle, E.; Sarasini, A.; Paolucci, S.; Klersy, C.; Cutti, S.; Novelli, V.; Marena, C.; Luzzaro, F. Incidence of SARS-CoV-2 infection in health care workers from Northern Italy based on antibody status: Immune protection from secondary infection—A retrospective observational case-controlled study. Int. J. Infect. Dis. 2021, 109, 199–202. [Google Scholar] [CrossRef]
- Lumley, S.F.; O’Donnell, D.; Stoesser, N.E.; Matthews, P.C.; Howarth, A.; Hatch, S.B.; Marsden, B.D.; Cox, S.; James, T.; Warren, F. Antibody status and incidence of SARS-CoV-2 infection in health care workers. N. Engl. J. Med. 2021, 384, 533–540. [Google Scholar] [CrossRef]
- Hall, V.J.; Foulkes, S.; Charlett, A.; Atti, A.; Monk, E.J.; Simmons, R.; Wellington, E.; Cole, M.J.; Saei, A.; Oguti, B. SARS-CoV-2 infection rates of antibody-positive compared with antibody-negative health-care workers in England: A large, multicentre, prospective cohort study (SIREN). Lancet 2021, 397, 1459–1469. [Google Scholar] [CrossRef]
- Hansen, C.H.; Michlmayr, D.; Gubbels, S.M.; Mølbak, K.; Ethelberg, S. Assessment of protection against reinfection with SARS-CoV-2 among 4 million PCR-tested individuals in Denmark in 2020: A population-level observational study. Lancet 2021, 397, 1204–1212. [Google Scholar] [CrossRef]
- Vitale, J.; Mumoli, N.; Clerici, P.; De Paschale, M.; Evangelista, I.; Cei, M.; Mazzone, A. Assessment of SARS-CoV-2 Reinfection 1 Year After Primary Infection in a Population in Lombardy, Italy. JAMA Intern. Med. 2021, 181, 1407–1408. [Google Scholar] [CrossRef]
- Hanrath, A.T.; Payne, B.A.; Duncan, C.J. Prior SARS-CoV-2 infection is associated with protection against symptomatic reinfection. J. Infect. 2021, 82, e29–e30. [Google Scholar] [CrossRef]
- Pilz, S.; Chakeri, A.; Ioannidis, J.P.; Richter, L.; Theiler-Schwetz, V.; Trummer, C.; Krause, R.; Allerberger, F. SARS-CoV-2 re-infection risk in Austria. Eur. J. Clin. Investig. 2021, 51, e13520. [Google Scholar] [CrossRef]
- Gallais, F.; Gantner, P.; Bruel, T.; Velay, A.; Planas, D.; Wendling, M.-J.; Bayer, S.; Solis, M.; Laugel, E.; Reix, N. Evolution of antibody responses up to 13 months after SARS-CoV-2 infection and risk of reinfection. EBioMedicine 2021, 71, 103561. [Google Scholar] [CrossRef]
- Leidi, A.; Koegler, F.; Dumont, R.; Dubos, R.; Zaballa, M.-E.; Piumatti, G.; Coen, M.; Berner, A.; Darbellay Farhoumand, P.; Vetter, P.; et al. Risk of Reinfection After Seroconversion to Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2): A Population-based Propensity-score Matched Cohort Study. Clin. Infect. Dis. 2021, ciab495. [Google Scholar] [CrossRef]
- Kohler, P.; Güsewell, S.; Seneghini, M.; Egger, T.; Leal, O.; Brucher, A.; Lemmenmeier, E.; Möller, J.C.; Rieder, P.; Ruetti, M. Impact of baseline SARS-CoV-2 antibody status on syndromic surveillance and the risk of subsequent COVID-19—A prospective multicenter cohort study. BMC Med. 2021, 19, 270. [Google Scholar] [CrossRef]
- Rovida, F.; Cassaniti, I.; Paolucci, S.; Percivalle, E.; Sarasini, A.; Piralla, A.; Giardina, F.; Sammartino, J.C.; Ferrari, A.; Bergami, F. SARS-CoV-2 vaccine breakthrough infections with the alpha variant are asymptomatic or mildly symptomatic among health care workers. Nat. Commun. 2021, 12, 6032. [Google Scholar] [CrossRef]
- Santacatterina, M.; Sanders, J.W.; Weintraub, W.S. Prevention of COVID-19 with the BNT162b2 and mRNA-1273 Vaccines. N. Engl. J. Med. 2021, 385, 1817–1818. [Google Scholar]
- Fowlkes, A.; Gaglani, M.; Groover, K.; Thiese, M.S.; Tyner, H.; Ellingson, K.; Cohorts, H.-R. Effectiveness of COVID-19 vaccines in preventing SARS-CoV-2 infection among frontline workers before and during B. 1.617. 2 (Delta) variant predominance—Eight US locations, December 2020–August 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1167. [Google Scholar] [CrossRef]
- Naito, T.; Yan, Y.; Tabe, Y.; Seyama, K.; Deshpande, G.A. Real-world evidence for the effectiveness and breakthrough of BNT162b2 mRNA COVID-19 vaccine at a medical center in Japan. Hum. Vaccin. Immunother. 2021, 1–2. [Google Scholar] [CrossRef]
- Edridge, A.W.D.; Kaczorowska, J.; Hoste, A.C.R.; Bakker, M.; Klein, M.; Loens, K.; Jebbink, M.F.; Matser, A.; Kinsella, C.M.; Rueda, P.; et al. Seasonal coronavirus protective immunity is short-lasting. Nat. Med. 2020, 26, 1691–1693. [Google Scholar] [CrossRef]
- Wangari, I.M.; Sewe, S.; Kimathi, G.; Wainaina, M.; Kitetu, V.; Kaluki, W. Mathematical Modelling of COVID-19 Transmission in Kenya: A Model with Reinfection Transmission Mechanism. Comput. Math. Methods Med. 2021, 2021, 5384481. [Google Scholar] [CrossRef]
- Coutinho, R.M.; Marquitti, F.M.D.; Ferreira, L.S.; Borges, M.E.; da Silva, R.L.P.; Canton, O.; Portella, T.P.; Poloni, S.; Franco, C.; Plucinski, M.M.; et al. Model-based estimation of transmissibility and reinfection of SARS-CoV-2 P.1 variant. Commun. Med. 2021, 1, 48. [Google Scholar] [CrossRef]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Marc, G.P.; Moreira, E.D.; Zerbini, C. Safety and efficacy of the BNT162b2 mRNA COVID-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef]
- Chodick, G.; Tene, L.; Rotem, R.S.; Patalon, T.; Gazit, S.; Ben-Tov, A.; Weil, C.; Goldshtein, I.; Twig, G.; Cohen, D.; et al. The Effectiveness of the Two-Dose BNT162b2 Vaccine: Analysis of Real-World Data. Clin. Infect. Dis. 2022, 74, 472–478. [Google Scholar] [CrossRef]
- Mizrahi, B.; Lotan, R.; Kalkstein, N.; Peretz, A.; Perez, G.; Ben-Tov, A.; Chodick, G.; Gazit, S.; Patalon, T. Correlation of SARS-CoV-2-breakthrough infections to time-from-vaccine. Nat. Commun. 2021, 12, 6379. [Google Scholar] [CrossRef]
- Hitchings, M.D.T.; Ranzani, O.T.; Torres, M.S.S.; de Oliveira, S.B.; Almiron, M.; Said, R.; Borg, R.; Schulz, W.L.; de Oliveira, R.D.; da Silva, P.V. Effectiveness of CoronaVac among healthcare workers in the setting of high SARS-CoV-2 Gamma variant transmission in Manaus, Brazil: A test-negative case-control study. Lancet Reg. Health—Am. 2021, 1, 100025. [Google Scholar] [CrossRef]
- Unwin, H.J.T.; Mishra, S.; Bradley, V.C.; Gandy, A.; Mellan, T.A.; Coupland, H.; Ish-Horowicz, J.; Vollmer, M.A.; Whittaker, C.; Filippi, S.L. State-level tracking of COVID-19 in the United States. Nat. Commun. 2020, 11, 6189. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y.; Zhao, S.; He, D. A Simple Model to Estimate the Transmissibility of SARS-CoV-2 Beta, Delta and Omicron Variants in South Africa. 2021. Available online: https://ssrn.com/abstract=3989919 (accessed on 20 December 2021).
- Liu, Y.; Yu, Y.; Zhao, Y.; He, D. Reduction in the Infection Fatality Rate of Omicron (B. 1.1. 529) Variant Compared to Previous Variants in South Africa. Available online: http://dx.doi.org/10.2139/ssrn.4010080 (accessed on 24 December 2021).

| Setting | Percent Reduction in Reinfection | Country | Sample Size | Follow-Up |
|---|---|---|---|---|
| Rovida et al. [33] | 0.74 | Italy | 9610 | 6 months |
| Lumley et al. [34] | 0.89 | United Kingdom | 12,541 | 7.3 months |
| Hall et al. [35] | 0.841 | England | 25,661 | 9.3 months |
| Hansen et al. [36] | 0.805 | Denmark | 525,339 | 10.1 months |
| Vitale et al. [37] | 0.94 | Italy | 15,075 | 9.3 months |
| Hanrath et al. [38] | 1 | England | 11,175 | 8.3 months |
| Pilz et al. [39] | 0.91 | Austria | 8,900,480 | 9.3 months |
| Gallais et al. [40] | 0.96 | France | 1309 | 12 months |
| Leidi et al. [41] | 0.94 | Switzerland | 1496 | 8.2 months |
| Kohler et al. [42] | 0.78 | Switzerland | 2712 | 7.9 months |
| weighted average | 0.9039 |
| Setting | Percent Reduction in Breakthrough Infection | Country | Sample Size | Follow-Up |
|---|---|---|---|---|
| Rovida et al. [43] | 0.86 | Italy | 4066 | 3.7 months |
| Santacatterina et al. [44] | 0.91 | USA | 3975 | 3.9 months |
| Fowlkes et al. [45] | 0.8 | USA | 7112 | 8 months |
| Naito et al. [46] | 0.765 | Japan | 8749 | 6 months |
| weighted average | 0.8159 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Zhao, Y.; Chen, B.; He, D. Multiple COVID-19 Waves and Vaccination Effectiveness in the United States. Int. J. Environ. Res. Public Health 2022, 19, 2282. https://doi.org/10.3390/ijerph19042282
Lin L, Zhao Y, Chen B, He D. Multiple COVID-19 Waves and Vaccination Effectiveness in the United States. International Journal of Environmental Research and Public Health. 2022; 19(4):2282. https://doi.org/10.3390/ijerph19042282
Chicago/Turabian StyleLin, Lixin, Yanji Zhao, Boqiang Chen, and Daihai He. 2022. "Multiple COVID-19 Waves and Vaccination Effectiveness in the United States" International Journal of Environmental Research and Public Health 19, no. 4: 2282. https://doi.org/10.3390/ijerph19042282
APA StyleLin, L., Zhao, Y., Chen, B., & He, D. (2022). Multiple COVID-19 Waves and Vaccination Effectiveness in the United States. International Journal of Environmental Research and Public Health, 19(4), 2282. https://doi.org/10.3390/ijerph19042282







