A Study on the Decay Model of Multi-Block Taxi Travel Demand under the Influence of Major Urban Public Health Events
Abstract
:1. Introduction
1.1. Review of the Literature
1.2. Research Framework
2. Taxi Travel Demand Decay Simulation Based on the DIIM Model
2.1. Block Delineation Based on the k-Means Clustering Method
2.2. Acquisition of Interblock Taxi Travel Demand Table
2.3. Construction of the Taxi Travel Demand Decay Model
2.3.1. IIM Model
2.3.2. DIIM Model
2.4. Determination of Model Parameters
2.4.1. Decay Degree Vector of Travel Demand Intensity
2.4.2. Coefficient Matrix of Travel Demand Decay
2.4.3. Derivative Matrix of Travel Demand Interdependency
2.4.4. Demand Perturbation Vector
3. Case Studies
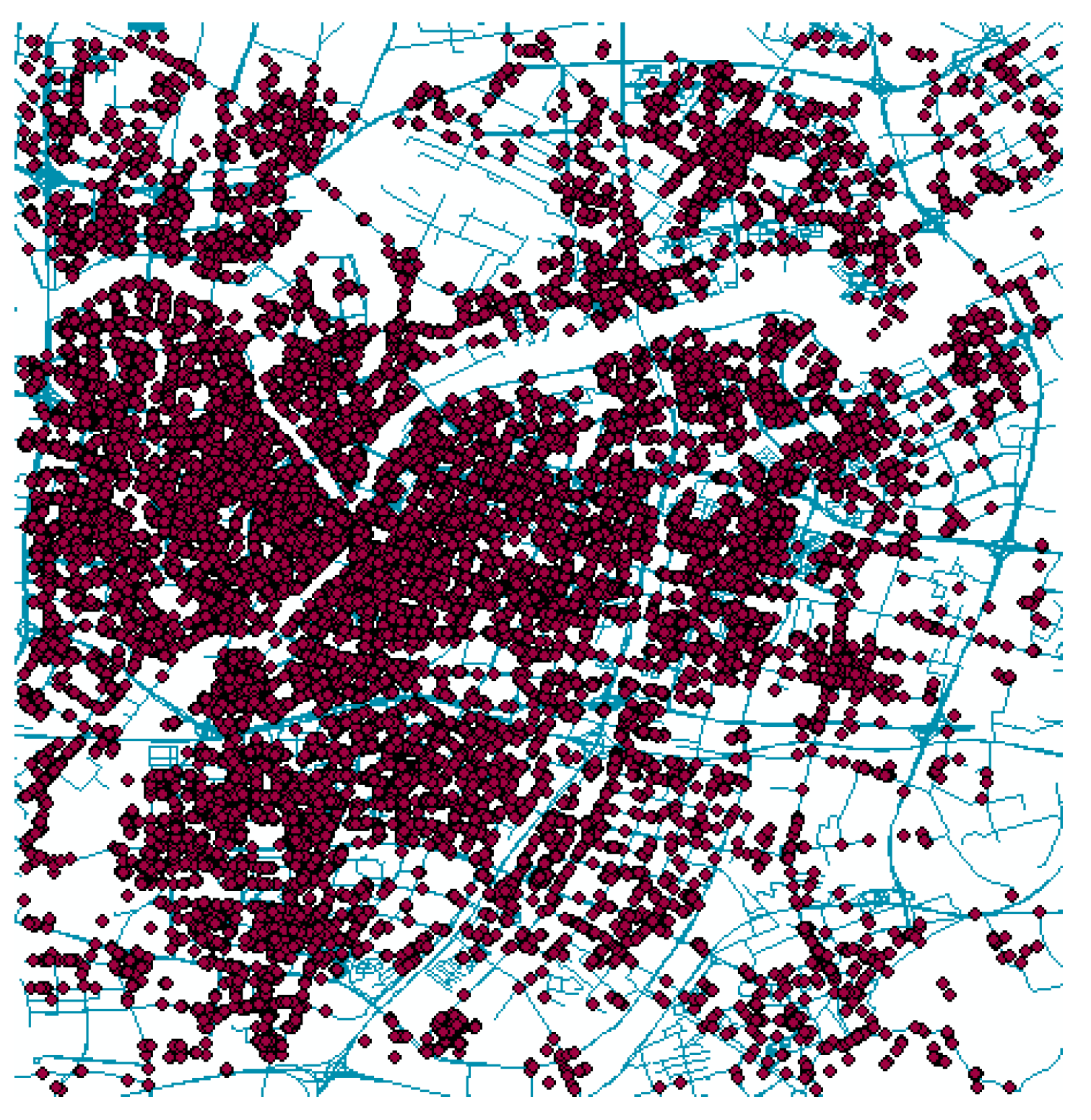
3.1. Overview of the Study Area
3.2. Data Pre-Processing
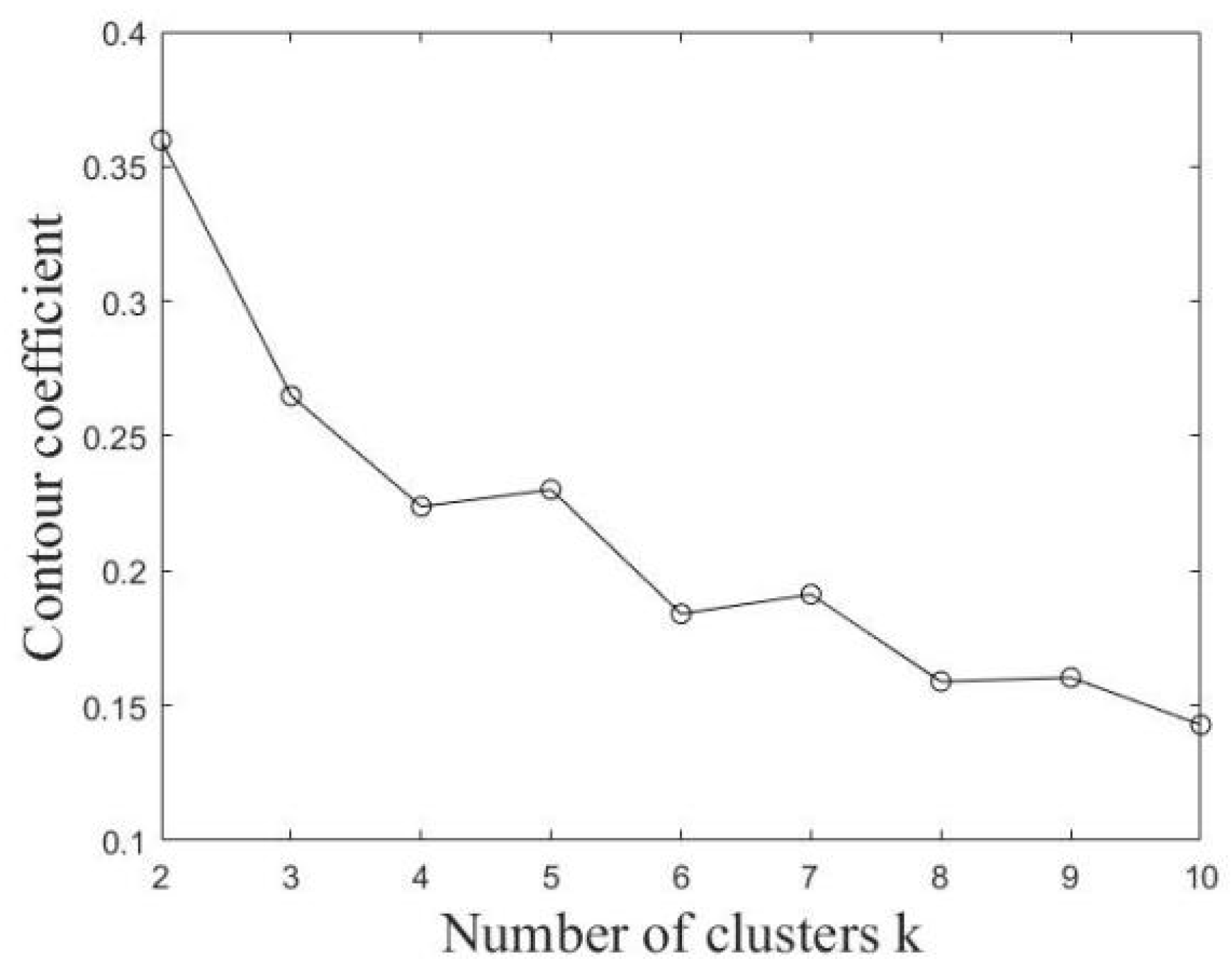
3.3. Block Classification Based on k-Means Clustering
3.4. Travel Demand Table and Other Parameters
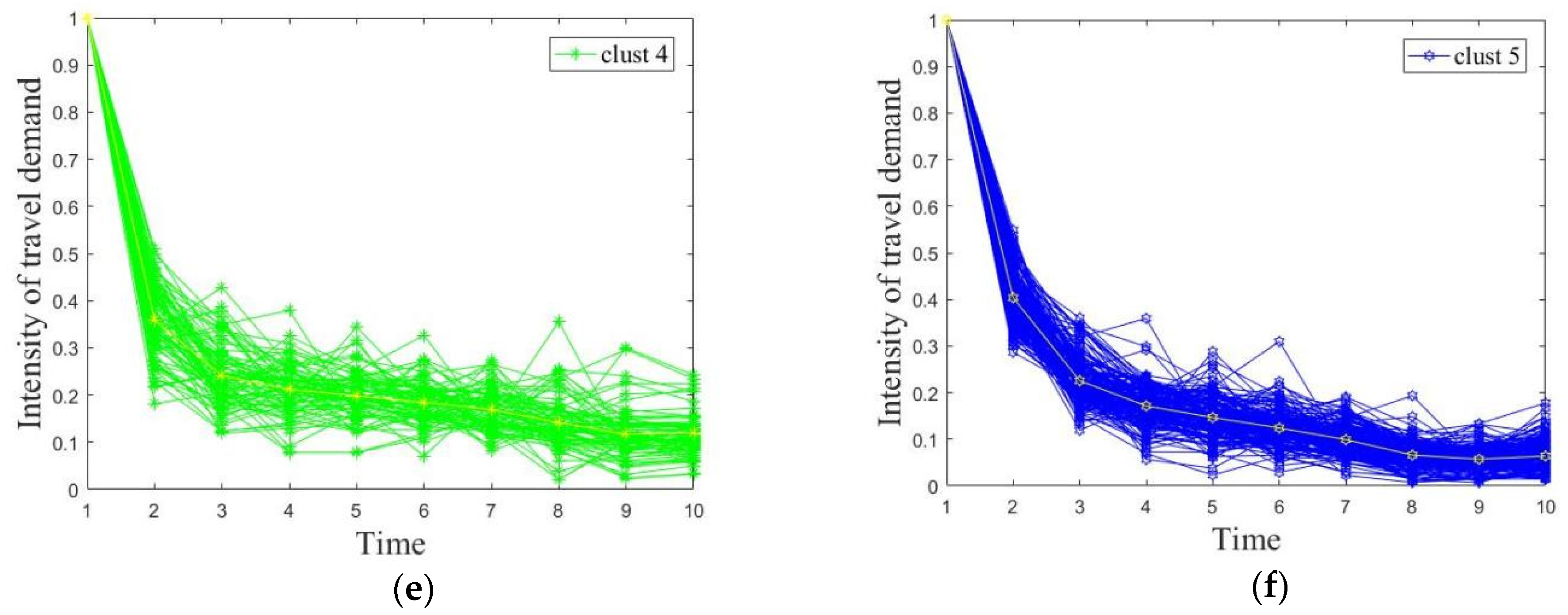
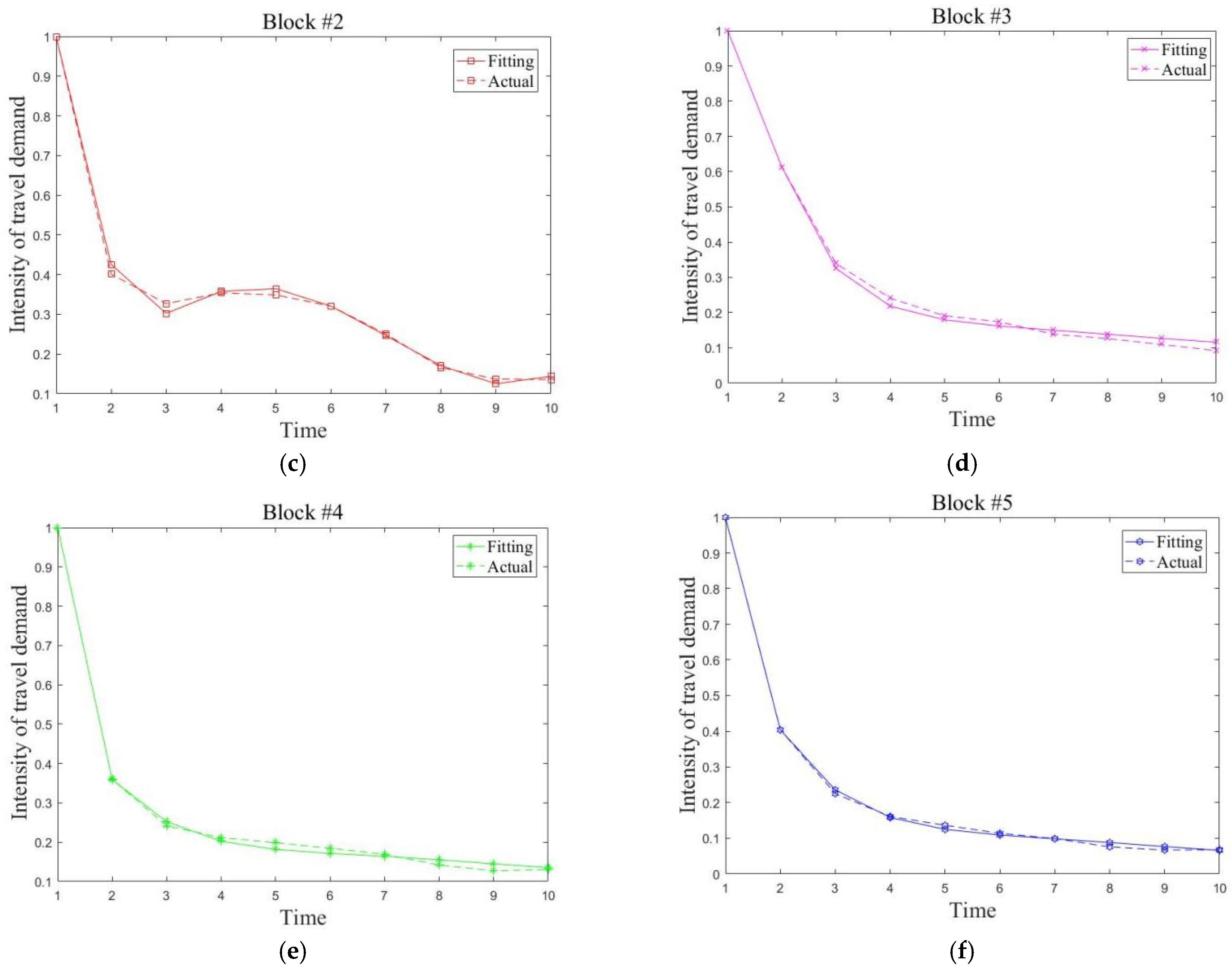
3.5. Analysis of Model Simulation Results
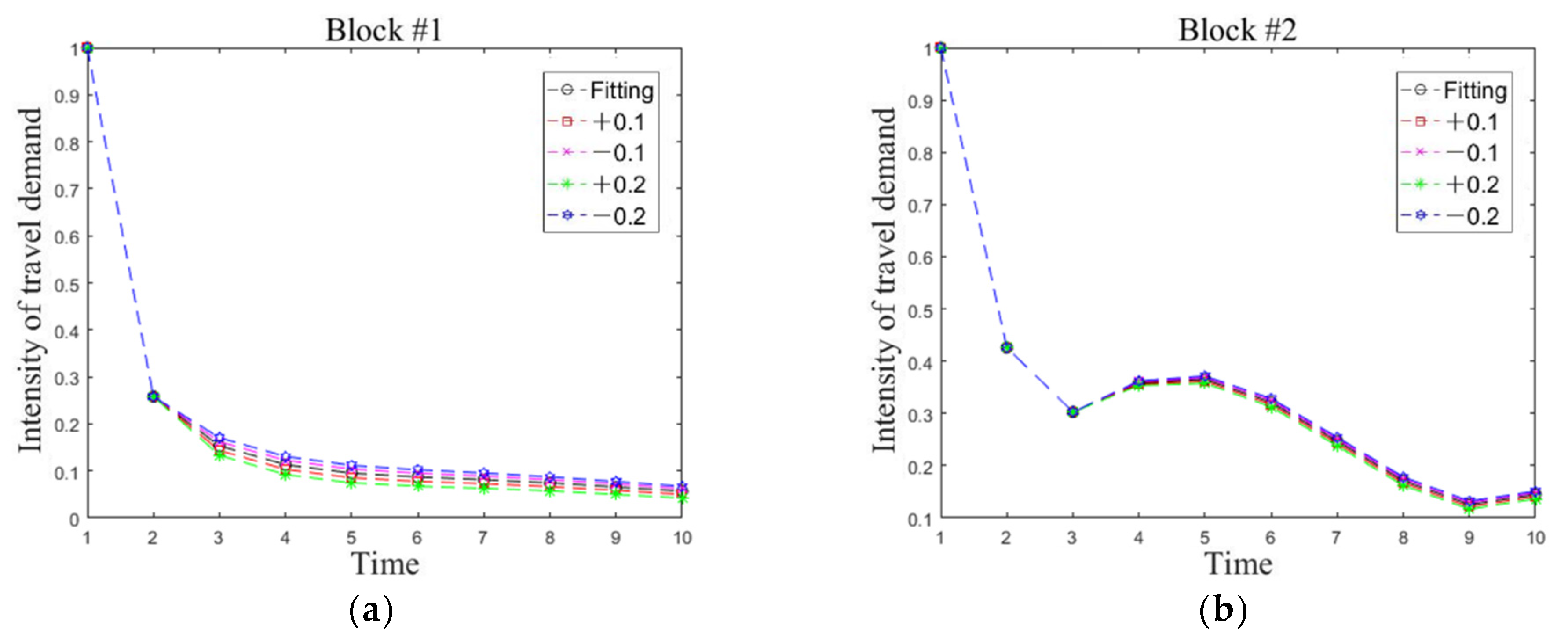
3.6. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dong, W.; Wei, C.; Jian, L.; Ye, J. DeepSD: Supply-demand prediction for online car-hailing services using deep neural networks. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017. [Google Scholar]
- Cui, Y.; Guan, H.; Si, Y.; Qin, Z. Residents’ travel characteristics based on order data of on-line car-hailing: A Case Study of Beijing. Transp. Res. 2018, 4, 20–28. [Google Scholar]
- Zhao, Y.; Zhang, H.; Li, A.; Quan, L. Improving the approaches of traffic demand forecasting in the big data era. Cities 2018, 82, 19–26. [Google Scholar] [CrossRef]
- Ma, Y. Research on Residents’ Behavior of Attractive Areas and Spatio-Temporal Feature Based on Taxi Trajectory Data—A Case of Kunshan City; Nanjing Normal University: Nanjing, China, 2014. [Google Scholar]
- Bao, G.; Liu, X.; Jiang, Y.; Shang, C.; Dong, L.; Tang, S. Research on mining taxi pick-up hotspots area. J. Transp. Eng. 2019, 19, 62–69. [Google Scholar]
- He, Y.; Wang, C. Research on taxi pick-up hotspots based on time and space cluster. Geomat. Spat. Inf. Technol. 2020, 43, 99–102. [Google Scholar]
- Cheng, J.; Liu, J.; Gao, Y. Analyzing the spatio-temporal characteristics of Beijing’s OD trip volume based on time series clustering method. J. Geo-Inf. Sci. 2016, 18, 1227–1239. [Google Scholar]
- Wang, R. Research on Urban Taxi Travel Demand Based on GPS Data; Shandong University: Jinan, China, 2016. [Google Scholar]
- Chen, Z.; Qiao, B.W.; Zhang, J. Identification and spatial interaction of urban functional regions in Beijing based on the characteristics of residents’ traveling. J. Geo-Inf. Sci. 2018, 20, 291–301. [Google Scholar]
- Yang, R. Urban Functional Regions Recognition and Research Based on Data Mining; University of Electronic Science and Technology of China: Chengdu, China, 2019. [Google Scholar]
- Qi, G.; Li, X.; Li, S.; Pan, G. Measuring social functions of city regions from Large-scale taxi behaviors. In Proceedings of the 2011 IEEE International Conference on Pervasive Computing and Communications Workshops, Seattle, WA, USA, 21–25 March 2011. [Google Scholar]
- Pan, G.; Qi, G.; Wu, Z.; Zhang, D.; Li, S. Land-use classification using taxi GPS traces. IEEE Trans. Intell. Transp. Syst. 2013, 14, 113–123. [Google Scholar] [CrossRef]
- Liu, N. Study on the Influence of Rainfall on Traffic Travel Based on Taxi Trajectory Data; Beijing Jiaotong University: Beijing, China, 2017. [Google Scholar]
- Farber, H. Why you can’t find a taxi in the rain and other labor supply lessons from cab drivers. Q. J. Econ. 2015, 130, 1975–2026. [Google Scholar] [CrossRef] [Green Version]
- Chung, E.; Ohtani, O.; Warita, H.; Kuwaharaet, M. Effect of rain on travel demand and traffic accidents. In Proceedings of the 2005 IEEE Conference on Intelligent Transportation Systems, Vienna, Austria, 16 September 2005; pp. 1080–1083. [Google Scholar]
- Kang, C.; Liu, X.; Xu, X.; Qin, K. Impact of weather condition on intra-urban travel behavior: Evidence from taxi trajectory data. J. Geo-Inf. Sci. 2019, 21, 118–127. [Google Scholar]
- Jiang, N.; Li, S.; Cao, S.; Wei, J.; Wang, B.; Qin, N.; Duan, X. Transportation activity patterns of Chinese population during the COVID-19 epidemic. Sch. Energy Environ. Eng. 2020, 33, 1675–1682. [Google Scholar]
- Gao, Y.; Yu, Z.; Qiu, D.; Chu, Q. Analysis and suggestions on changes of online car-hailing during COVID-19. Traffic Transp. 2020, 33, 173–178. [Google Scholar]
- Chang, H.; Tai, Y.; Hsu, J. Context-aware taxi demand hotspots prediction. Int. J. Bus. Intell. Data Min. 2010, 5, 3–18. [Google Scholar] [CrossRef]
- Leonardo, D.O.; James, I.C.; Barry, J.G. Interdependent response of networked systems. J. Infrastruct. Syst. 2007, 13, 185–194. [Google Scholar]
- Leonardo, D.O.; Srivishnu, M.V. Cascading failures in complex infrastructure systems. Struct. Saf. 2009, 31, 157–167. [Google Scholar]
- Leonardo, D.O.; Rojo, J. Reliability Assessment of lifeline systems with radial topology. Comput.-Aided Civ. Infrastruct. Eng. 2011, 26, 111–128. [Google Scholar]
- Brown, T.; Beyeler, W.; Barton, D. Assessing infrastructure inter dependencies: The challenge of risk analysis for complex adaptive systems. Int. J. Crit. Infrastruct. 2004, 1, 108–117. [Google Scholar] [CrossRef]
- Leontief, W.W. Input-output economics. Sci. Am. 1951, 10, 15–21. [Google Scholar] [CrossRef]
- Leontief, W.W. Studies in the Structure of American Economy; Oxford University Press: New York, NY, USA, 1953. [Google Scholar]
- Ghosh, A. Input-output approach to an allocative system. Economic 1958, 25, 58–64. [Google Scholar]
- Tong, L.; Wang, L.; Ding, R.; Liu, L. Study on the dynamic input-output model with coal mine safety. Proced. Eng. 2011, 26, 1997–2002. [Google Scholar]
- Haimes, Y.Y.; Jing, P. Leontief-based model of risk in complex interconnected infrastructures. J. Infrastruct. Syst. 2001, 7, 1–12. [Google Scholar] [CrossRef]
- Haimes, Y.Y.; Horowitz, B.M.; Lambert, J.H.; Santos, J.; Crowther, K.; Lianet, C. Inoperability input-output model for interdependent infrastructure sectors. I: Theory and methodology. J. Infrastruct. Syst. 2005, 11, 67–79. [Google Scholar] [CrossRef]
- Crowther, K.G.; Haimes, Y.Y. Development of the multi-regional inoperability input-output model (MRIIM) for spatial Explicitness in preparedness of interdependent regions. Syst. Eng. 2010, 13, 28–46. [Google Scholar]
- Lian, C.; Haimes, Y.Y. Managing the risk of terrorism to interdependent infrastructure systems through the dynamic inoperability input–output model. Syst. Eng. 2006, 9, 241–258. [Google Scholar] [CrossRef]
- Pant, R.; Barker, K.; Grant, F.H.; Landers, T.L. Interdependent impacts of inoperability at multi-modal transportation container terminals. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 722–737. [Google Scholar] [CrossRef]
- Tan, C.S.; Tan, P.S.; Lee, S.; Pham, M.T. An Inoperability Input-Output Model (IIM) for disruption propagation analysis. In Proceedings of the 2013 IEEE International Conference on Industrial Engineering and Engineering Management, Bangkok, Thailand, 10–13 December 2013; pp. 186–190. [Google Scholar]
- Huang, H.; Wu, J.; Liu, F.; Wang, Y. Measuring accessibility based on improved impedance and attractive functions using taxi trajectory data. Sustainability 2021, 13, 112. [Google Scholar] [CrossRef]
- Zafri, N.M.; Khan, A.; Jamal, S.; Alam, B.M. Impacts of the COVID-19 Pandemic on active travel mode choice in Bangladesh: A study from the perspective of sustainability and new normal situation. Sustainability 2021, 13, 6975. [Google Scholar] [CrossRef]
- Haddawy, P.; Lawpoolsri, S.; Sa-Ngamuang, C.; Yin, M.S.; Cui, L. Effects of COVID-19 government travel restrictions on mobility in a rural border area of Northern Thailand: A mobile phone tracking study. PLoS ONE 2021, 16, e0245842. [Google Scholar] [CrossRef]
- Davis, N.; Raina, G.; Jagannathan, K. A framework for end-to-end deep learning-based anomaly detection in transportation networks—ScienceDirect. Transp. Res. Interdiscip. Perspect. 2020, 5, 100112. [Google Scholar]
- Belhadi, A.; Djenouri, Y.; Srivastava, G.; Djenouri, D.; Cano, A.; Lin, J.C. A Two-Phase Anomaly Detection Model for Secure Intelligent Transportation Ride-Hailing Trajectories. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4496–4506. [Google Scholar] [CrossRef]

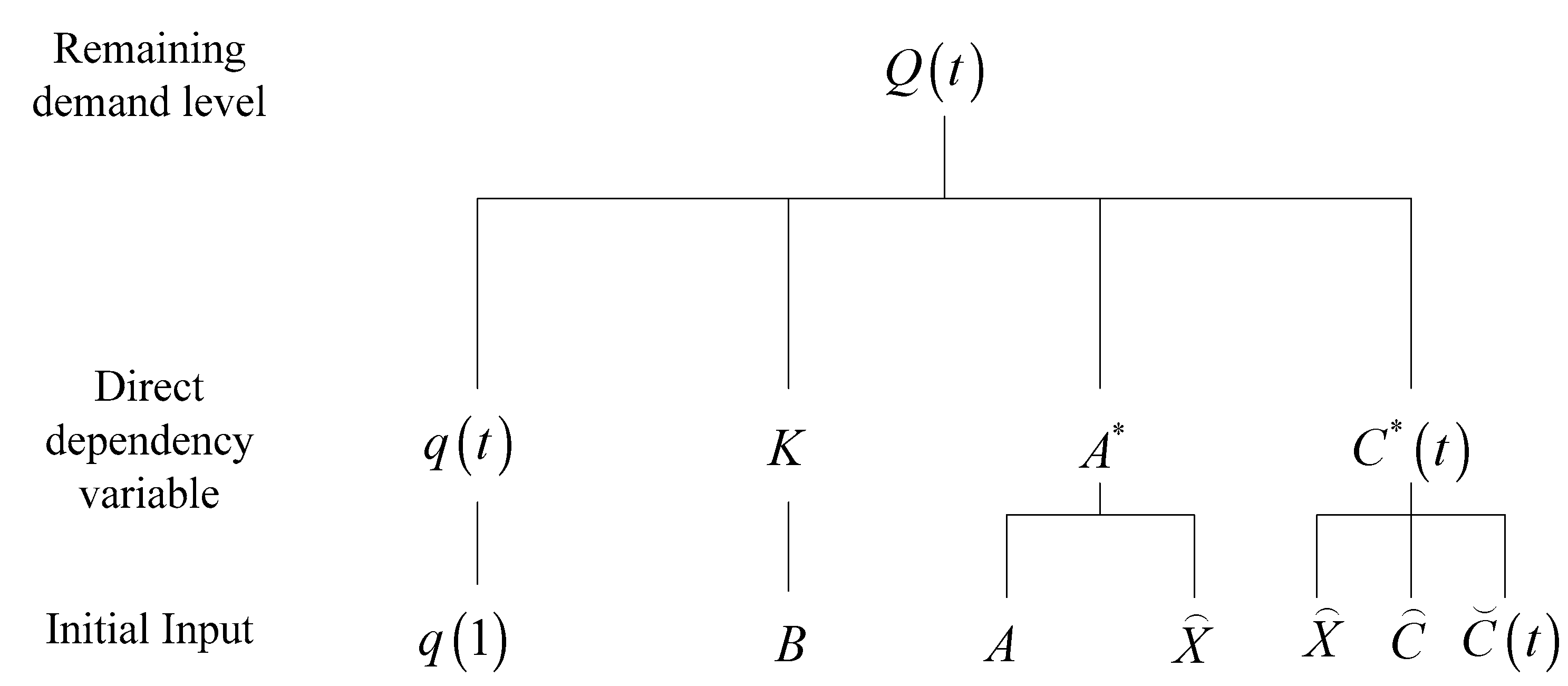






| Blocks | 1 | 2 | … | j | … | n | External Attraction | Total Demand |
|---|---|---|---|---|---|---|---|---|
| 1 | … | … | ||||||
| 2 | … | … | ||||||
| … | … | … | … | … | … | … | … | … |
| … | … | |||||||
| … | … | … | … | … | … | … | … | … |
| … | … | |||||||
| External production | … | … | —— | —— | ||||
| Total demand | … | … | —— | —— |
| Total Time Intervals without Trips | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of grids | 632 | 66 | 58 | 41 | 42 | 31 | 39 | 31 | 38 | 47 | 91 |
| Percentage (%) | 56.6 | 5.9 | 5.2 | 3.7 | 3.8 | 2.8 | 3.5 | 2.8 | 3.4 | 4.2 | 8.2 |
| Average daily taxi trips | 35.13 | 3.43 | 2.25 | 1.59 | 1.07 | 0.67 | 0.48 | 0.25 | 0.16 | 0.07 | 0.00 |
| Different Types of Blocks | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | External Block | Amount of Demand |
|---|---|---|---|---|---|---|---|
| Type 1 | 15,481 | 2360 | 1878 | 4399 | 12,904 | 6175 | 43,196 |
| Type 2 | 2360 | 368 | 439 | 925 | 2429 | 3793 | 10,313 |
| Type 3 | 1878 | 439 | 266 | 659 | 1500 | 1166 | 5907 |
| Type 4 | 4399 | 925 | 659 | 1448 | 3754 | 2363 | 13,547 |
| Type 5 | 12,904 | 2429 | 1500 | 3754 | 11,116 | 5661 | 37,363 |
| Variables | Changing Values | Demand Sensitivity of the Various Types of Blocks (%) | (%) | ||||
|---|---|---|---|---|---|---|---|
| Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | |||
| +0.1 | −7.99 | −1.31 | −2.30 | −2.19 | −3.88 | −3.53 | |
| −0.1 | 7.05 | 1.16 | 2.05 | 1.95 | 3.46 | 3.13 | |
| +0.2 | −17.08 | −2.78 | −4.89 | −4.64 | −8.25 | −7.53 | |
| −0.2 | 13.29 | 2.20 | 3.89 | 3.70 | 6.54 | 5.92 | |
| +0.1 | −0.01 | 0 | −0.01 | 0 | −0.01 | −0.01 | |
| −0.1 | 0.01 | 0 | 0.01 | 0 | 0 | 0 | |
| +0.2 | −0.01 | 0 | −0.02 | −0.01 | −0.01 | −0.01 | |
| −0.2 | 0.01 | 0 | 0.02 | 0.01 | 0.01 | 0.01 | |
| +0.1 | −1.04 | −0.30 | −0.50 | −1.64 | −0.84 | −0.86 | |
| −0.1 | 0.93 | 0.28 | 0.47 | 1.45 | 0.75 | 0.78 | |
| +0.2 | −2.22 | −0.64 | −1.12 | −3.50 | −1.78 | −1.85 | |
| −0.2 | 1.77 | 0.51 | 0.89 | 2.73 | 1.42 | 1.46 | |
| +0.1 | −1.21 | −0.33 | −0.57 | −0.56 | −1.52 | −0.84 | |
| −0.1 | 1.09 | 0.30 | 0.52 | 0.50 | 1.36 | 0.75 | |
| +0.2 | −2.55 | −0.70 | −1.21 | −1.17 | −3.22 | −1.77 | |
| −0.2 | 2.08 | 0.57 | 0.99 | 0.96 | 2.58 | 1.44 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, F.; Huang, Z.; Zheng, P. A Study on the Decay Model of Multi-Block Taxi Travel Demand under the Influence of Major Urban Public Health Events. Int. J. Environ. Res. Public Health 2022, 19, 3631. https://doi.org/10.3390/ijerph19063631
Luo F, Huang Z, Zheng P. A Study on the Decay Model of Multi-Block Taxi Travel Demand under the Influence of Major Urban Public Health Events. International Journal of Environmental Research and Public Health. 2022; 19(6):3631. https://doi.org/10.3390/ijerph19063631
Chicago/Turabian StyleLuo, Feiyi, Zhengfeng Huang, and Pengjun Zheng. 2022. "A Study on the Decay Model of Multi-Block Taxi Travel Demand under the Influence of Major Urban Public Health Events" International Journal of Environmental Research and Public Health 19, no. 6: 3631. https://doi.org/10.3390/ijerph19063631
APA StyleLuo, F., Huang, Z., & Zheng, P. (2022). A Study on the Decay Model of Multi-Block Taxi Travel Demand under the Influence of Major Urban Public Health Events. International Journal of Environmental Research and Public Health, 19(6), 3631. https://doi.org/10.3390/ijerph19063631





