A Hybrid Model for Coronavirus Disease 2019 Forecasting Based on Ensemble Empirical Mode Decomposition and Deep Learning
Abstract
:1. Introduction
2. Materials and Methods
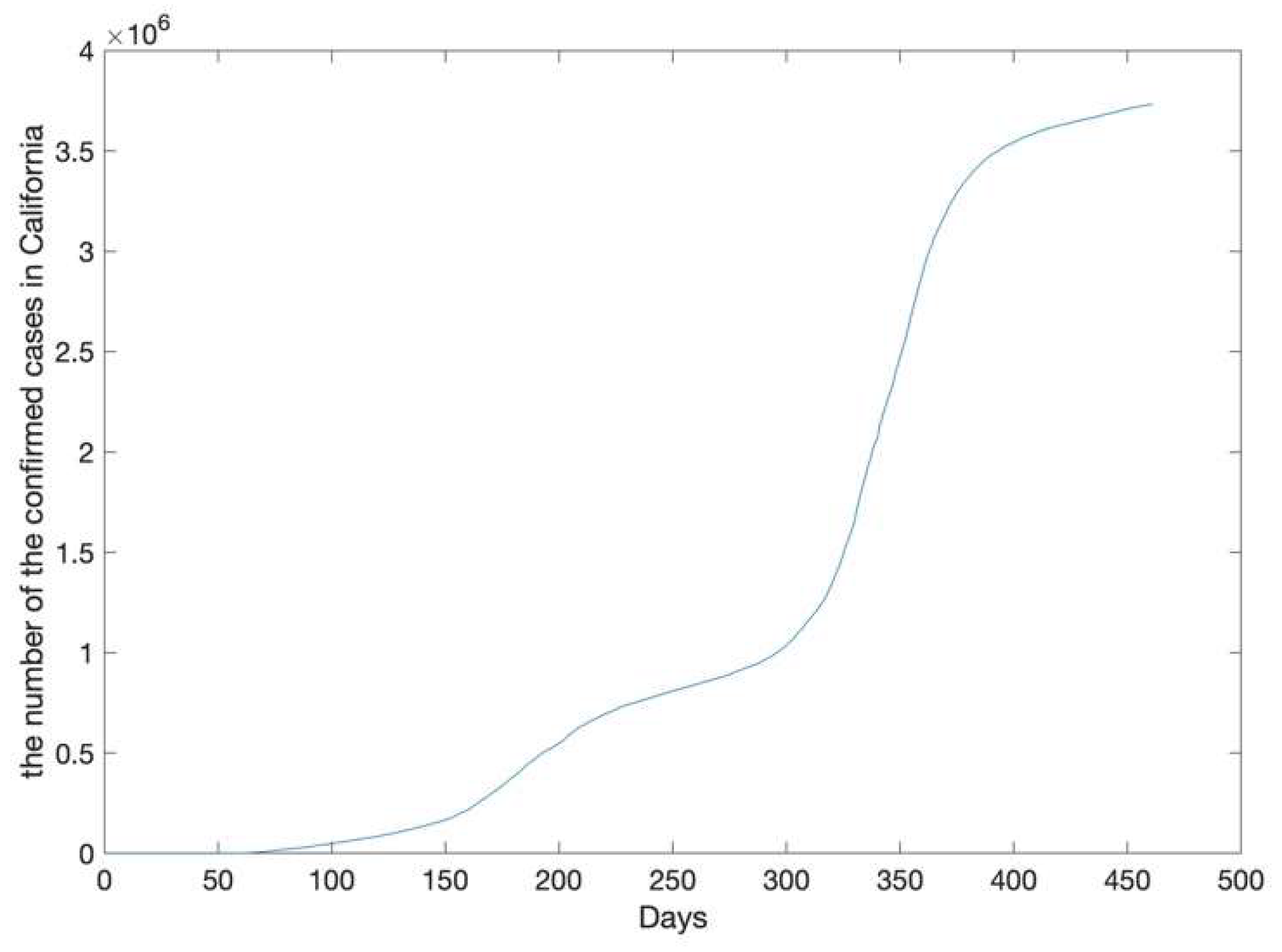
2.1. Study Design and Data
2.2. Study Area
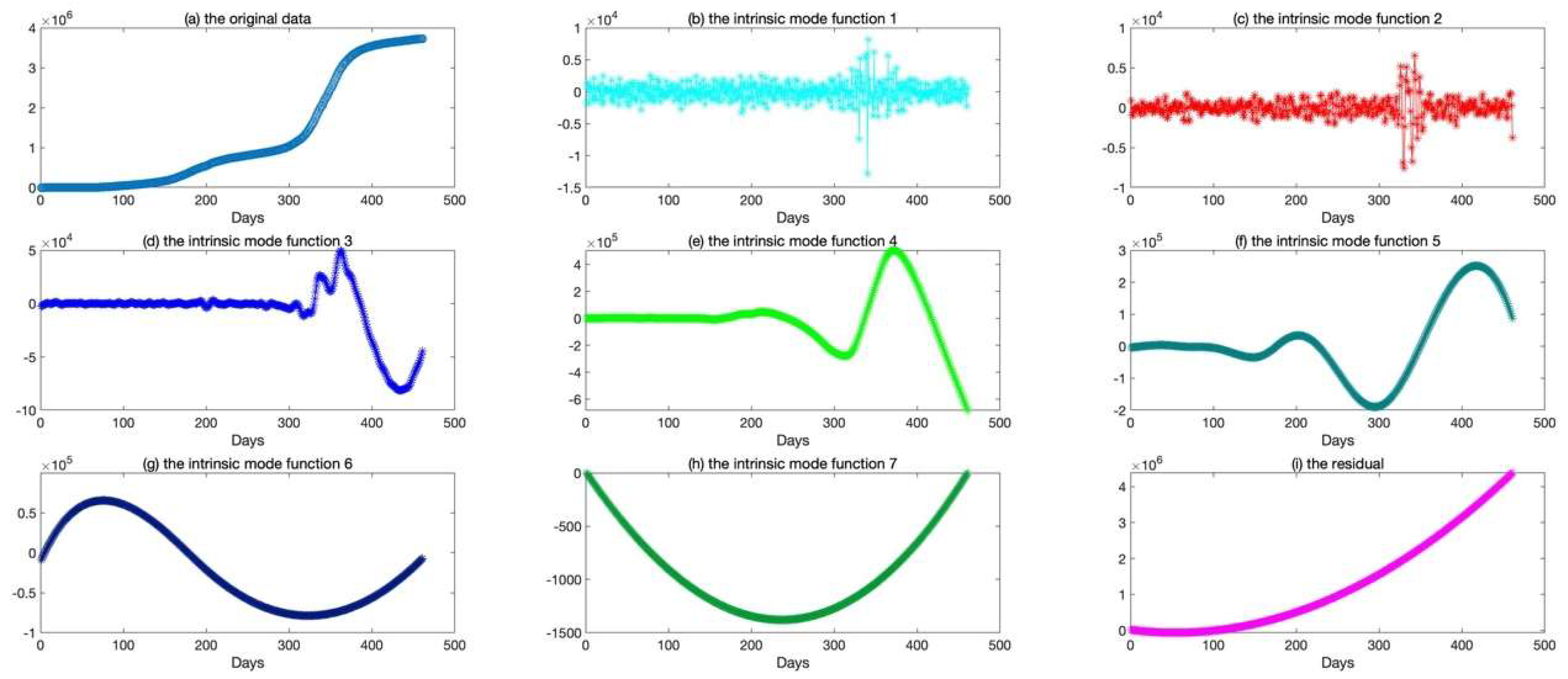
2.3. Empirical Mode Decomposition, EMD
2.4. Ensemble Empirical Mode Decomposition, EEMD
- First, the initial parameters, such as the times of the ensembles and the variance of the added white noise, are set, and white noise is added to the sequence, .
- Second, the local extremum of the sequence, , is extracted.
- Third, the upper envelope, , and the lower envelope, , of the sequence, , are determined.
- Fourth, the mean values of the upper and lower envelope are calculated using the following formula: .
- Fifth, the component is extracted as follows .
- Sixth, if the component, , satisfies the conditions for the establishment of the IMF, the first IMF () is obtained; otherwise, the above steps are repeated until the conditions are met and the first IMF is obtained.
- Seventh, a new sequence is calculated using , and the above steps are repeated until all and the residual sequence are obtained.
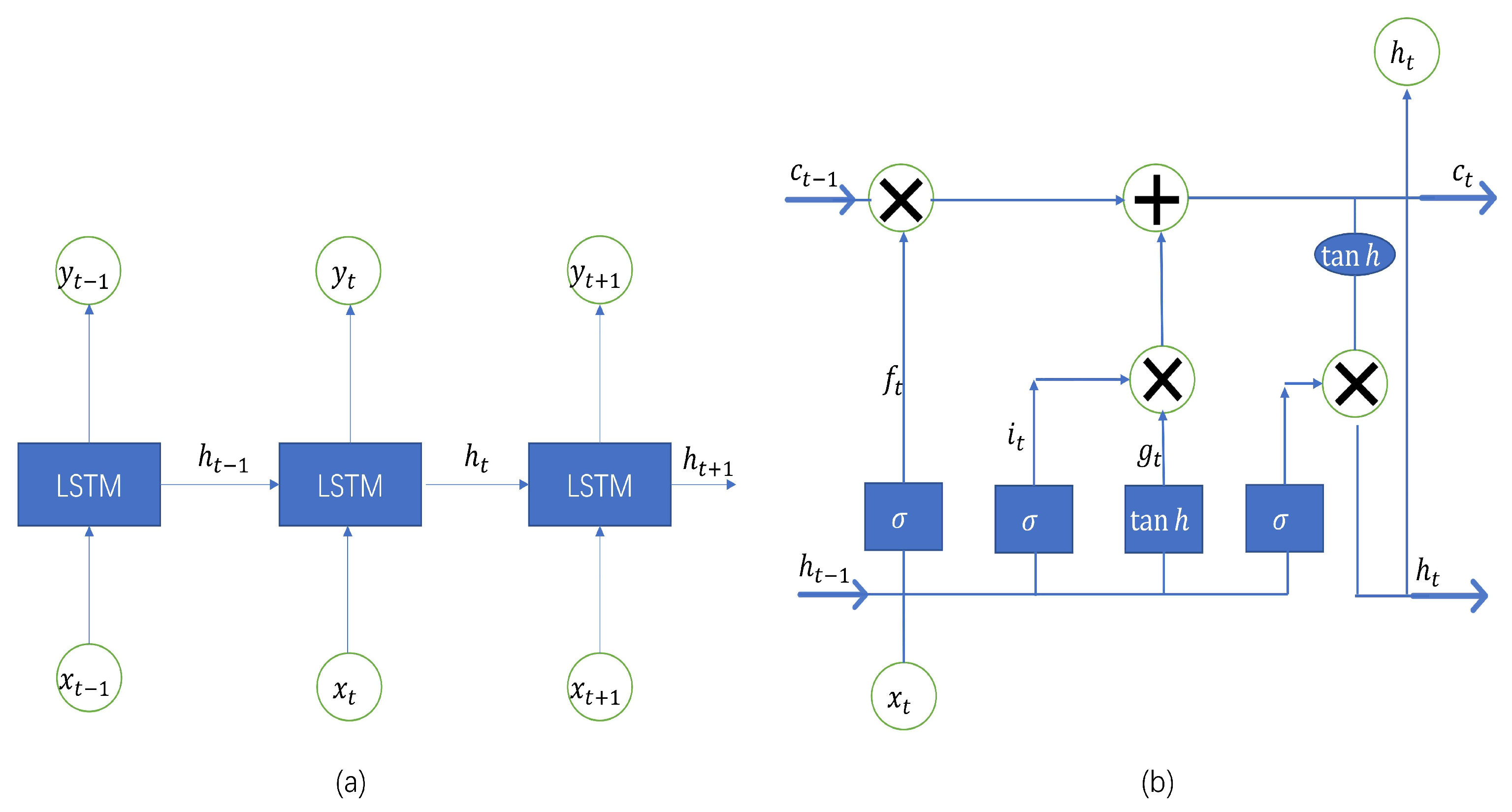
2.5. Long Short-Term Memory, LSTM
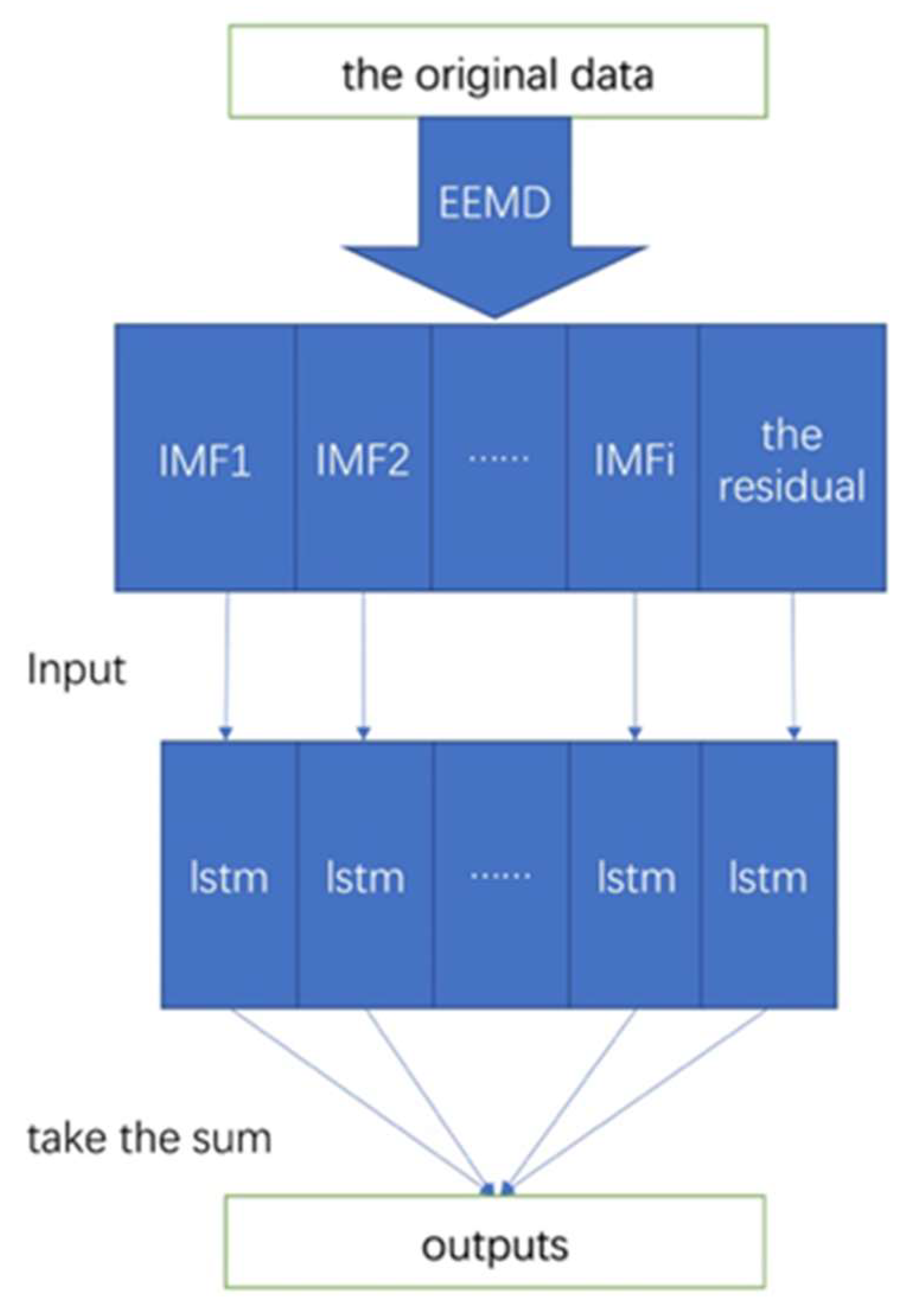
2.6. The Hybrid Model—EEMD-LSTM
2.7. Model Performance Evaluation
3. Results
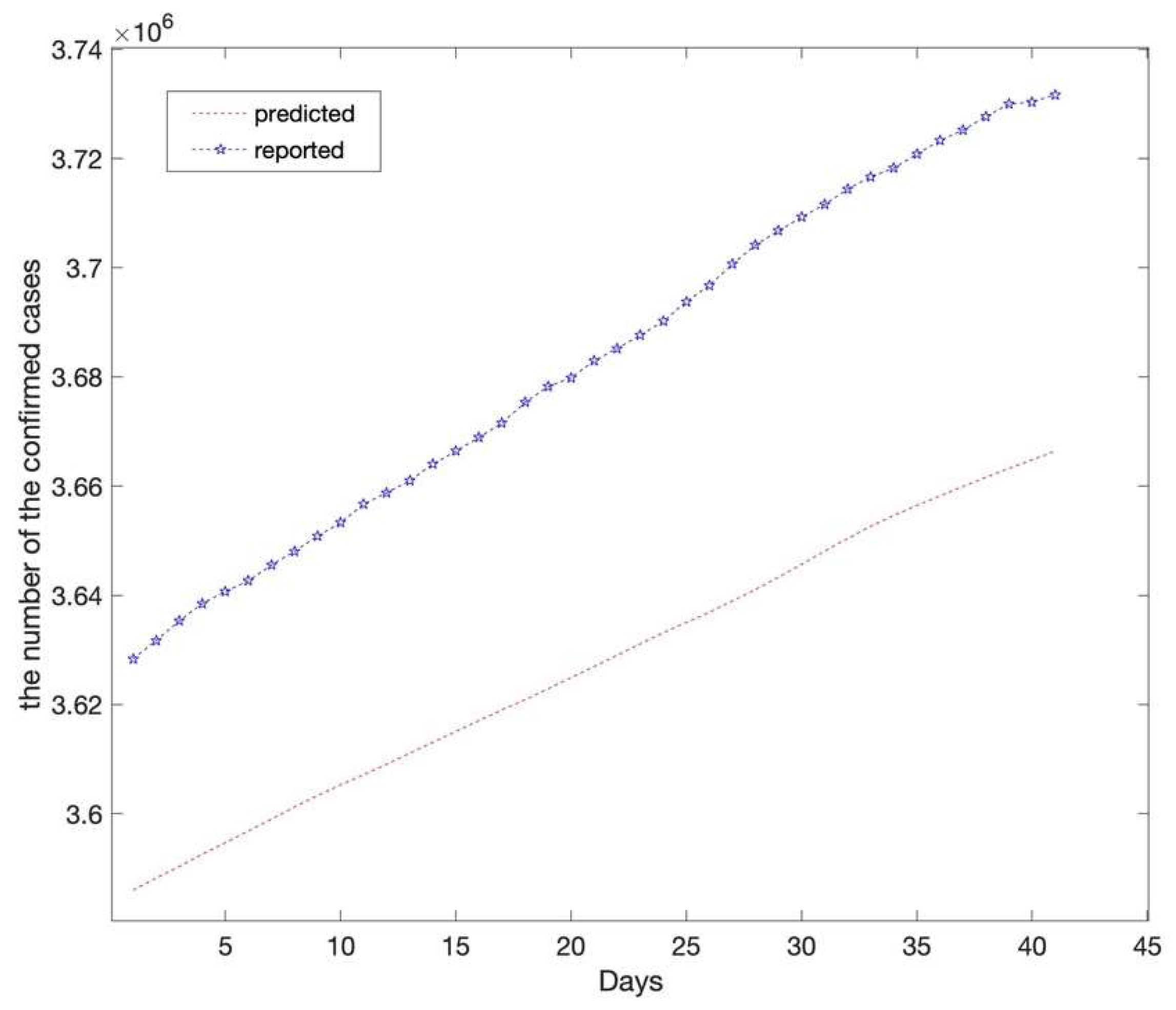
3.1. The Long Short-Term Memory Model
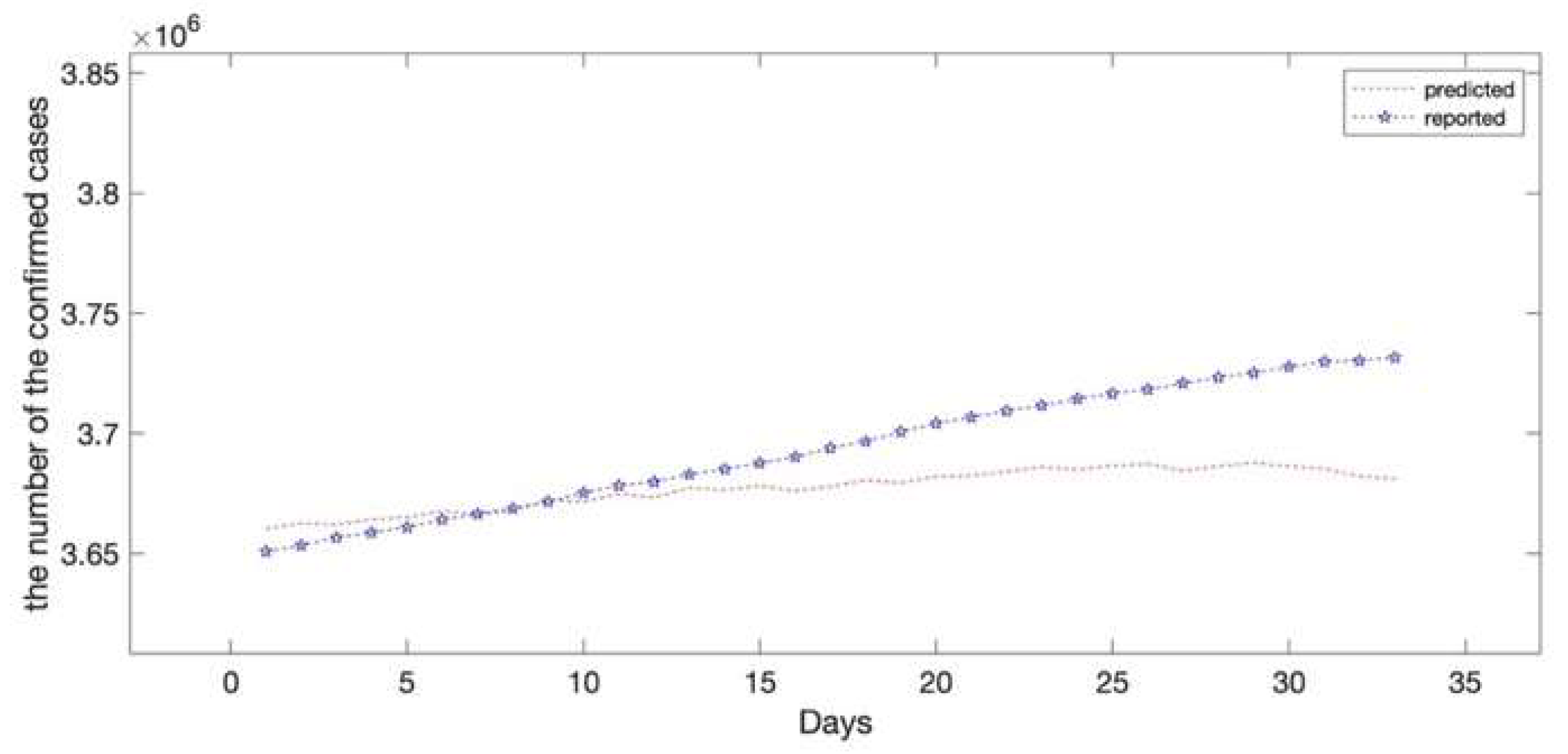
3.2. The Proposed EEMD-LSTM Hybrid Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average |
| EEMD | Ensemble Empirical Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| IMFs | Intrinsic Mode Functions |
| LSTM | Long Short-term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
References
- WHO. Coronavirus Disease (COVID-19) Outbreak. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 24 February 2020).
- Johns Hopkins University. Trace U.S. Pandemic Timelines. 2022. Available online: https://coronavirus.jhu.edu/region/united-states (accessed on 8 April 2022).
- Tang, Z.; Li, X.; Li, H. Prediction of new coronavirus infection based on a modified SEIR model. medRxiv 2020. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Lu, Z.Z.; Du, Z.C.; Zhang, Z.J.; Zhao, Y.; Shen, S.P.; Wang, B.; Hao, Y.T.; Chen, F. Fitting and forecasting the trend of COVID-19 by SEIR(+ CAQ) dynamic model. Zhonghua Liu Xing Bing Xue Za Zhi Zhonghua Liuxingbingxue Zazhi 2020, 41, 470–475. [Google Scholar] [PubMed]
- Zhou, X.; Ma, X.; Hong, N.; Su, L.; Ma, Y.; He, J.; Jiang, H.; Liu, C.; Shan, G.; Zhu, W.; et al. Forecasting the worldwide spread of COVID-19 based on logistic model and SEIR model. medRxiv 2020. [Google Scholar] [CrossRef]
- Roda, W.C.; Varughese, M.B.; Han, D.; Li, M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020, 5, 271–281. [Google Scholar] [CrossRef] [PubMed]
- ArunKumar, K.; Kalaga, D.V.; Kumar, C.M.S.; Chilkoor, G.; Kawaji, M.; Brenza, T.M. Forecasting the dynamics of cumulative COVID-19 cases (confirmed, recovered and deaths) for top-16 countries using statistical machine learning models: Auto-Regressive Integrated Moving Average (ARIMA) and Seasonal Auto-Regressive Integrated Moving Average (SARIMA). Appl. Soft Comput. 2021, 103, 107161. [Google Scholar] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yudistira, N. COVID-19 growth prediction using multivariate long short term memory. arXiv 2020, arXiv:2005.04809. [Google Scholar]
- Kumar, R.L.; Khan, F.; Din, S.; Band, S.S.; Mosavi, A.; Ibeke, E. Recurrent neural network and reinforcement learning model for COVID-19 prediction. Front. Public Health 2021, 9, 744100. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Liu, J.; Li, Y.; Liu, D.; Tong, J.; Li, Z.; Yu, D.; Fan, Y.; Bi, X.; et al. Predicting and analyzing the COVID-19 epidemic in China: Based on SEIRD, LSTM and GWR models. PloS ONE 2020, 15, e0238280. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef] [PubMed]
- Tuli, S.; Tuli, S.; Verma, R.; Tuli, R. Modelling for prediction of the spread and severity of COVID-19 and its association with socioeconomic factors and virus types. medRxiv 2020. [Google Scholar] [CrossRef]
- Rasjid, Z.E.; Setiawan, R.; Effendi, A. A comparison: Prediction of death and infected COVID-19 cases in Indonesia using time series smoothing and LSTM neural network. Procedia Comput. Sci. 2021, 179, 982–988. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Qiang, X.; Aamir, M.; Naeem, M.; Ali, S.; Aslam, A.; Shao, Z. Analysis and forecasting COVID-19 outbreak in Pakistan using decomposition and ensemble model. Comput. Mater. Contin. 2021, 68, 841–856. [Google Scholar] [CrossRef]
- Yang, Q.; Qing, L.; Gao, P.; Zhang, R. Prediction of annual precipitation in the Northern Slope Economic Belt of Tianshan Mountains based on a EEMD-LSTM model. Arid Zone Res. 2021, 38, 1243–1245. [Google Scholar]
- Fang, X.-Q.; Wu, C.-Y.; Yu, S.-H.; Zhang, D.-B.; Ou Yang, Q. Research on Short-Term Forecast Model of Agricultural Product Price Based on EEMD-LSTM. Chin. J. Manag. Sci. 2021, 29, 68–77. [Google Scholar]
- China Data Lab. US COVID-19 Daily Cases with Basemap. 2020. Available online: https://doi.org/10.7910/DVN/HIDLTK (accessed on 14 September 2021).
- World Population Review. 2022. Available online: https://worldpopulationreview.com/states/california-population (accessed on 18 November 2022).
- Zeiler, A.; Faltermeier, R.; Keck, I.R.; Tomé, A.M.; Puntonet, C.G.; Lang, E.W. Empirical mode decomposition-an introduction. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Liang, L.; Song, H.; Kong, Y.; Ma, R.; Hou, Y.; Zhao, J.; Liu, J.; He, N.; Zhang, Y. A method for hand-foot-mouth disease prediction using GeoDetector and LSTM model in Guangxi, China. Sci. Rep. 2019, 9, 17928. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Han, M.; Zhou, Y.; Wang, Y. Lstm recurrent neural networks for influenza trends prediction. In International Symposium on Bioinformatics Research and Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of 2019-nCov and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malki, Z.; Atlam, E.-S.; Ewis, A.; Dagnew, G.; Ghoneim, O.A.; Mohamed, A.A.; Abdel-Daim, M.M.; Gad, I. The COVID-19 pandemic: Prediction study based on machine learning models. Environ. Sci. Pollut. Res. 2021, 28, 40496–40506. [Google Scholar] [CrossRef] [PubMed]

| Lag Days | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|---|---|---|---|---|---|---|---|
| Mean Absolute Percentage Error | 0.030 | 0.018 | 0.033 | 0.031 | 0.047 | 0.025 | 0.029 |
| Mean Absolute Error | 114,048.4453 | 66,214.3438 | 123,150.7422 | 113,253.4453 | 175,371.1406 | 94,208.0391 | 109,076.2812 |
| Root Mean Square Error | 114,269.1406 | 66,306.9688 | 123,698.8281 | 114,207.7812 | 176,172.7344 | 94,910.125 | 110,076.9375 |
| Mean Absolute Percentage Error | Mean Absolute Error | Root Mean Square Error | |
|---|---|---|---|
| LSTM | 0.0151 | 5.58 × 104 | 5.63 × 104 |
| EEMD-LSTM | 0.0051 | 1.90 × 104 | 2.43 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Wan, Y.; Yang, W.; Tan, A.; Jian, J.; Lei, X. A Hybrid Model for Coronavirus Disease 2019 Forecasting Based on Ensemble Empirical Mode Decomposition and Deep Learning. Int. J. Environ. Res. Public Health 2023, 20, 617. https://doi.org/10.3390/ijerph20010617
Liu S, Wan Y, Yang W, Tan A, Jian J, Lei X. A Hybrid Model for Coronavirus Disease 2019 Forecasting Based on Ensemble Empirical Mode Decomposition and Deep Learning. International Journal of Environmental Research and Public Health. 2023; 20(1):617. https://doi.org/10.3390/ijerph20010617
Chicago/Turabian StyleLiu, Shidi, Yiran Wan, Wen Yang, Andi Tan, Jinfeng Jian, and Xun Lei. 2023. "A Hybrid Model for Coronavirus Disease 2019 Forecasting Based on Ensemble Empirical Mode Decomposition and Deep Learning" International Journal of Environmental Research and Public Health 20, no. 1: 617. https://doi.org/10.3390/ijerph20010617
APA StyleLiu, S., Wan, Y., Yang, W., Tan, A., Jian, J., & Lei, X. (2023). A Hybrid Model for Coronavirus Disease 2019 Forecasting Based on Ensemble Empirical Mode Decomposition and Deep Learning. International Journal of Environmental Research and Public Health, 20(1), 617. https://doi.org/10.3390/ijerph20010617





