Numerical Investigation of Very Low Reynolds Cross Orifice Jet for Personalized Ventilation Applications in Aircraft Cabins
Abstract
1. Introduction
2. Methods
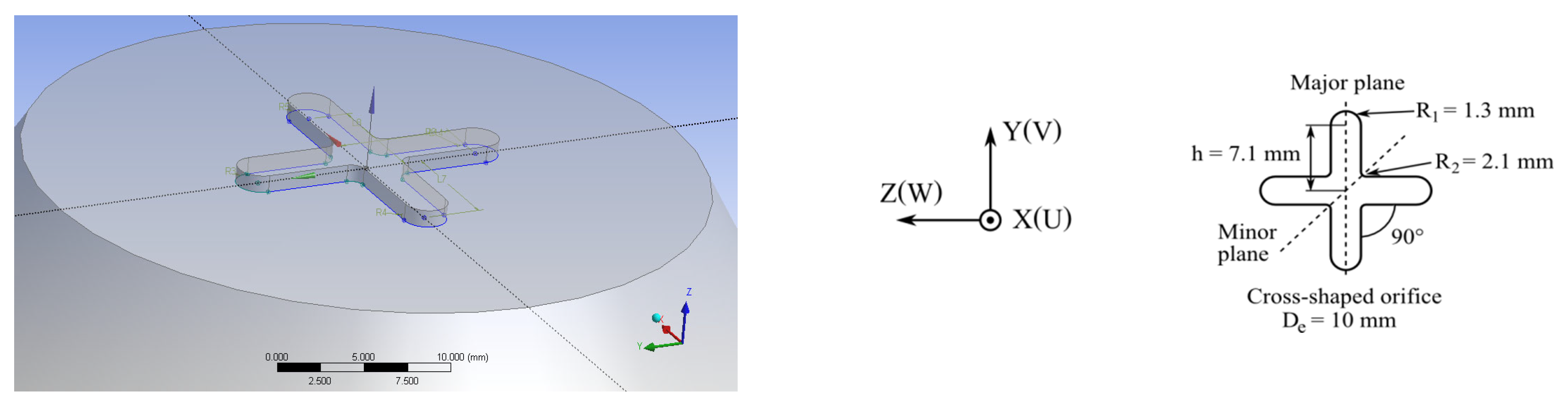
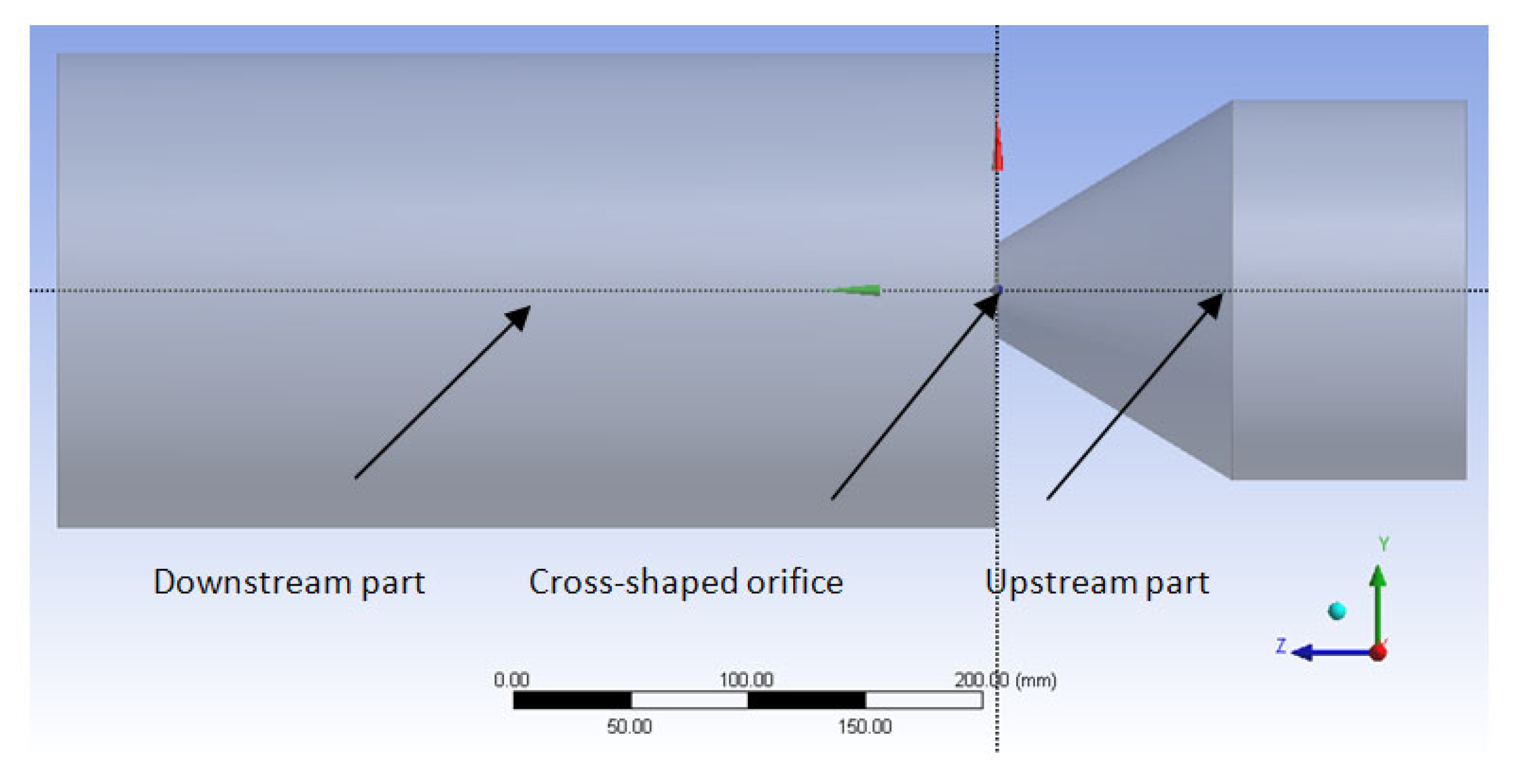
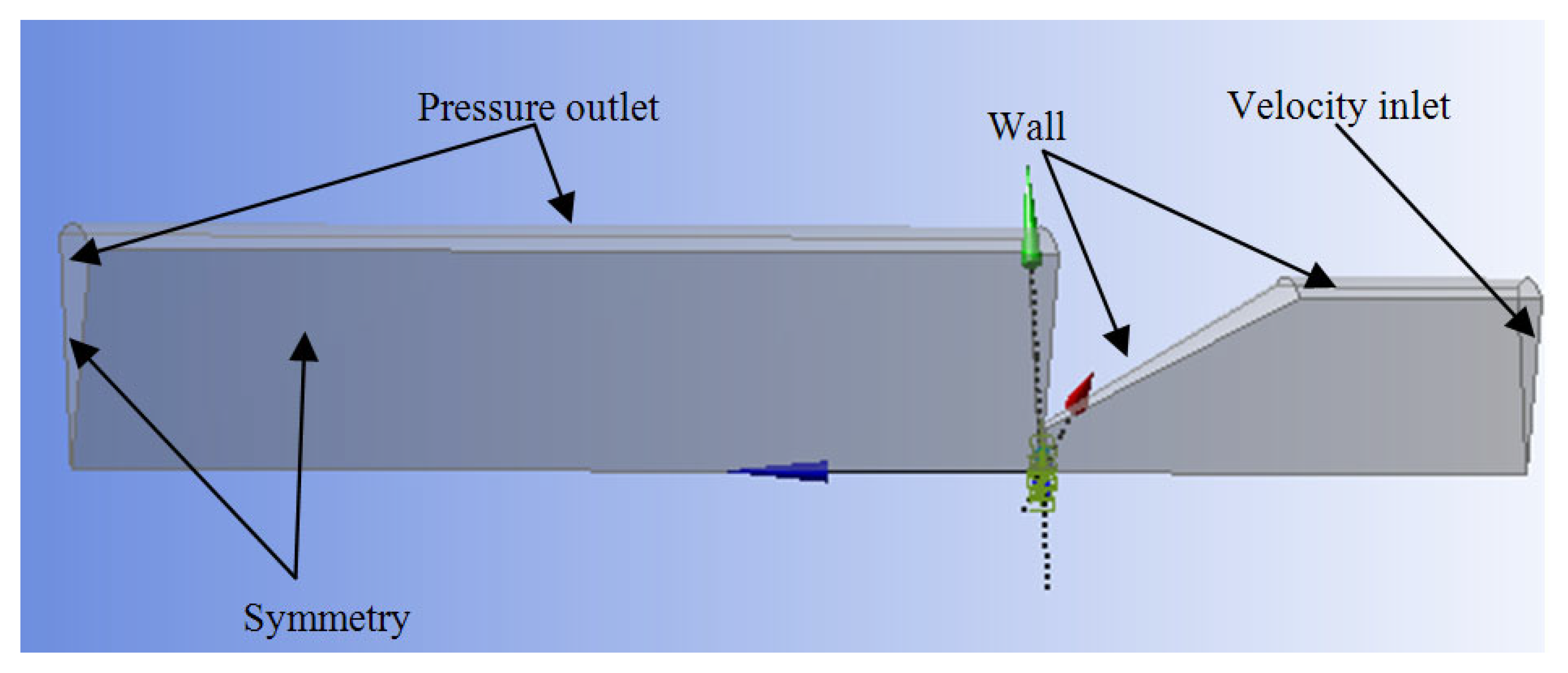
2.1. Numerical Study—Investigated Geometry and Computational Details
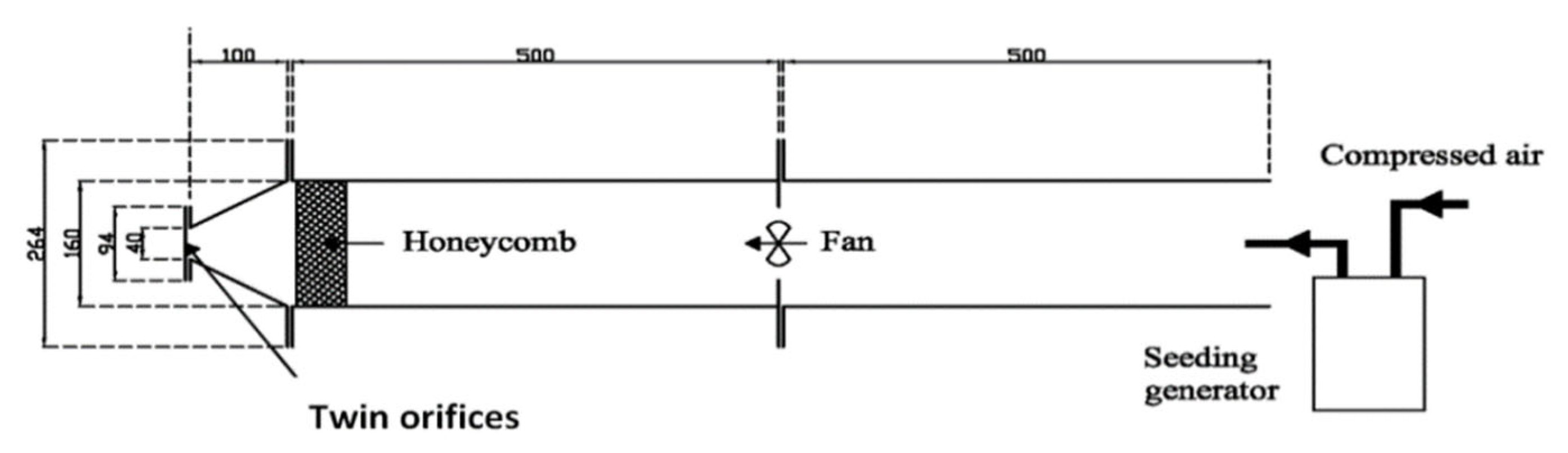
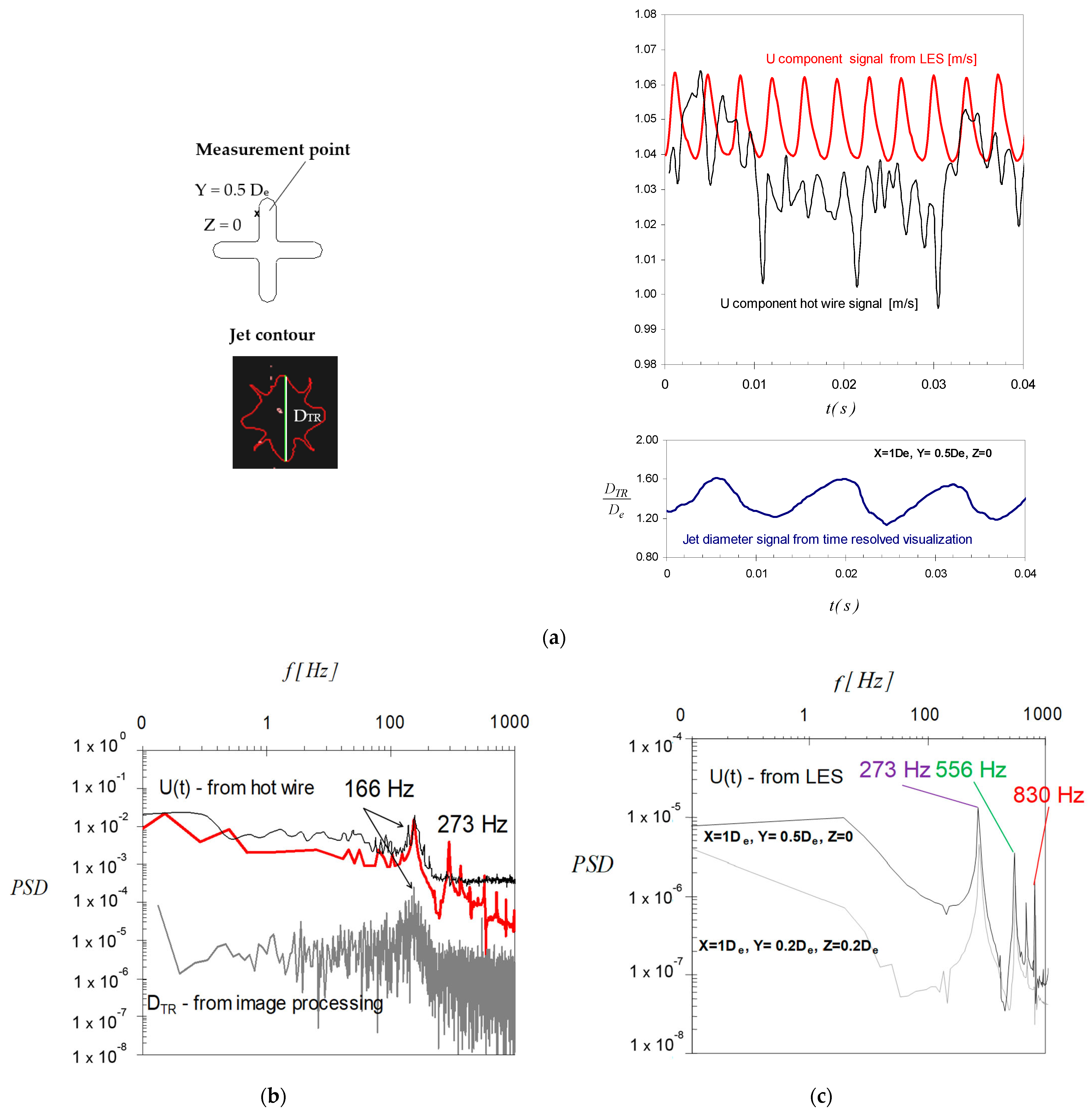
2.2. Experimental Validation of the Numerical Study—Measurement Techniques
3. Results and discussion
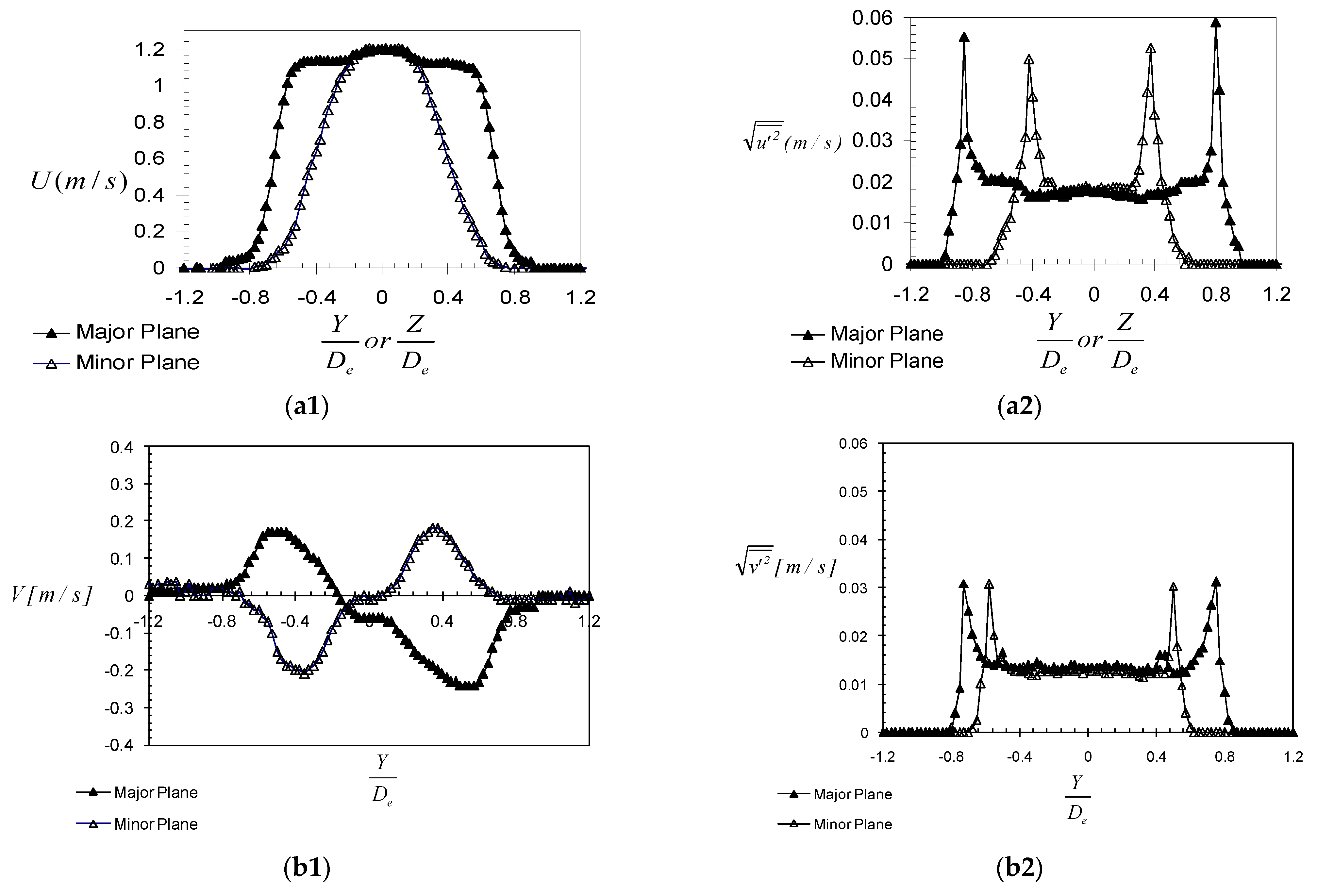
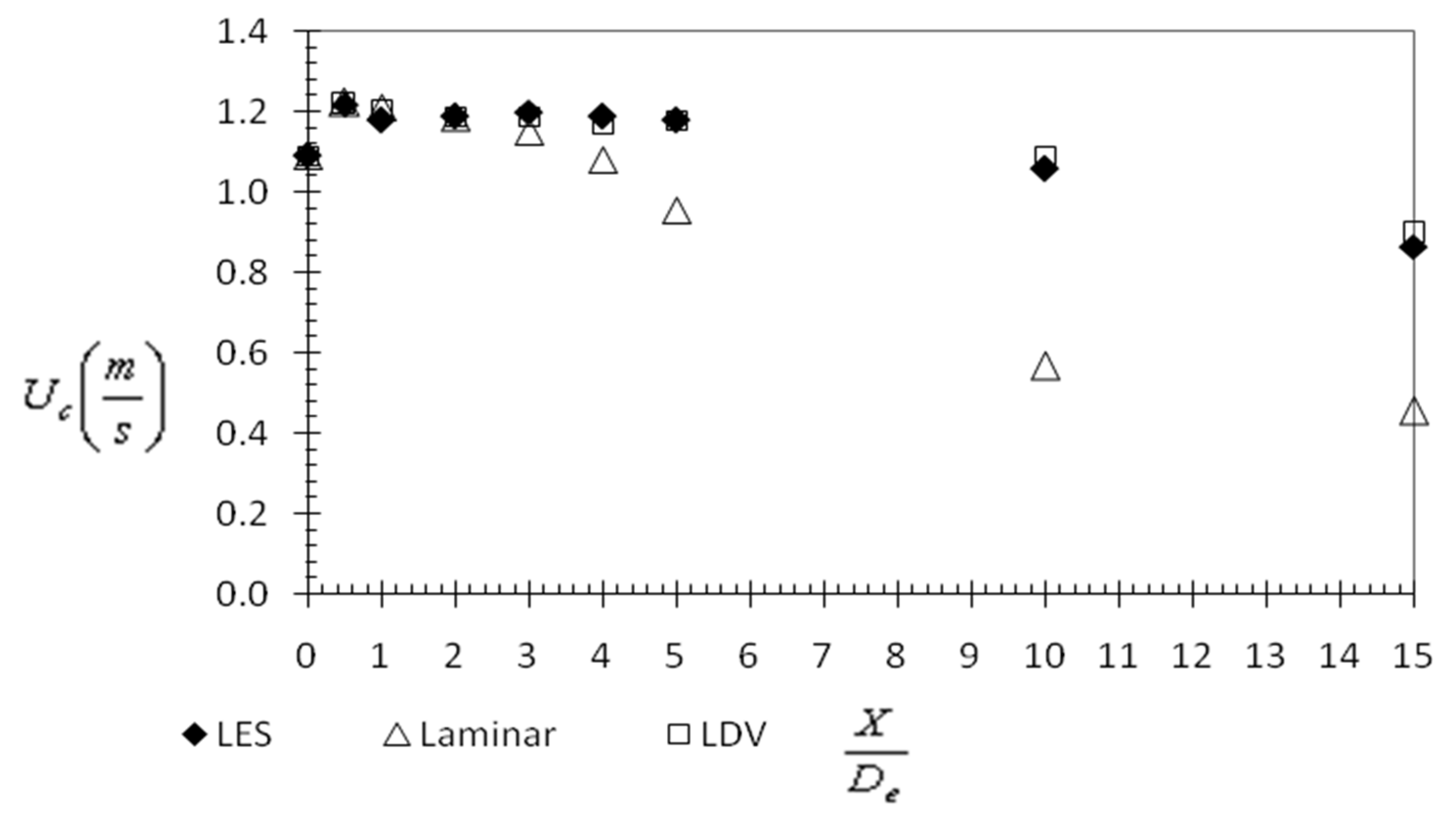
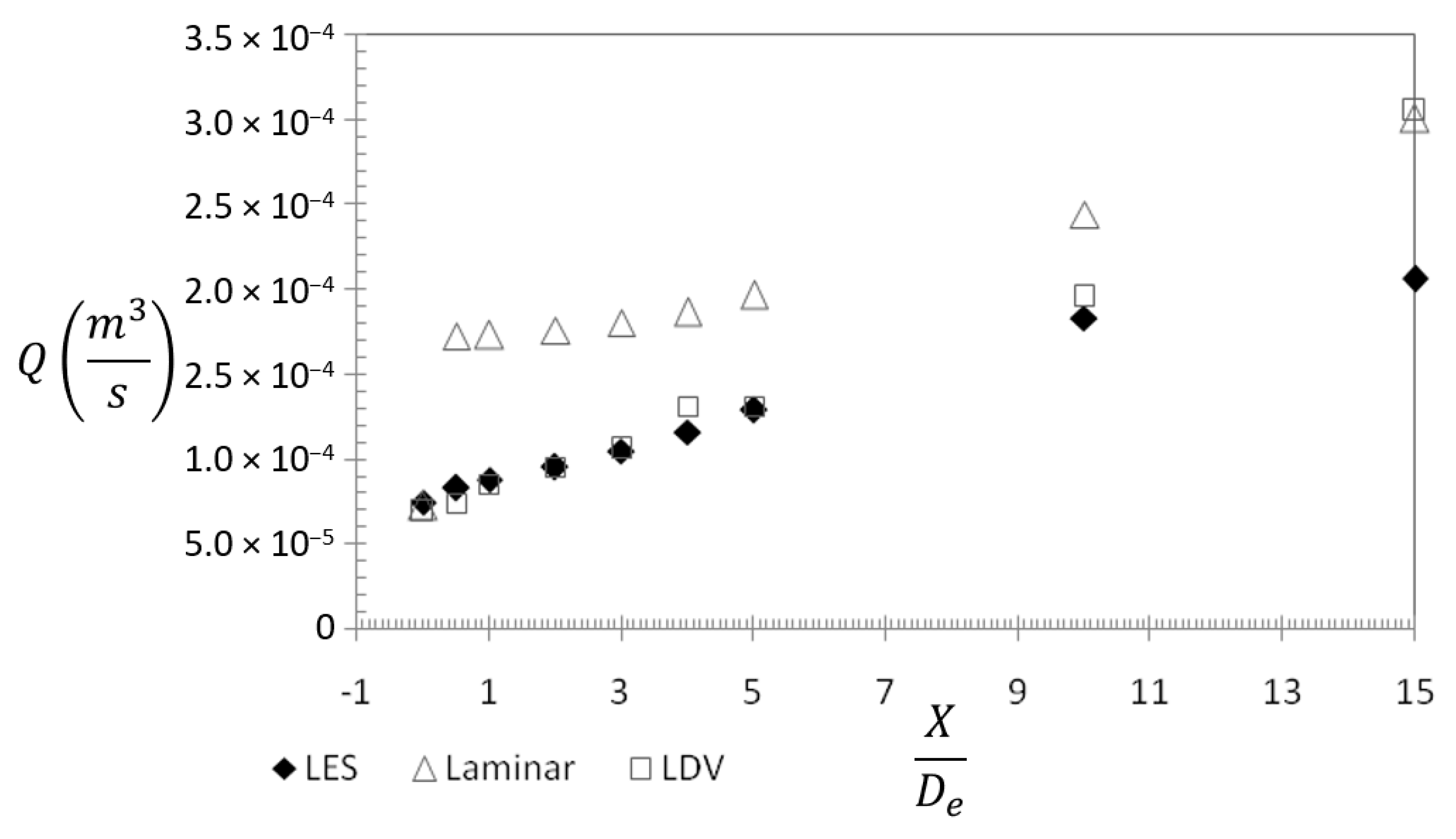
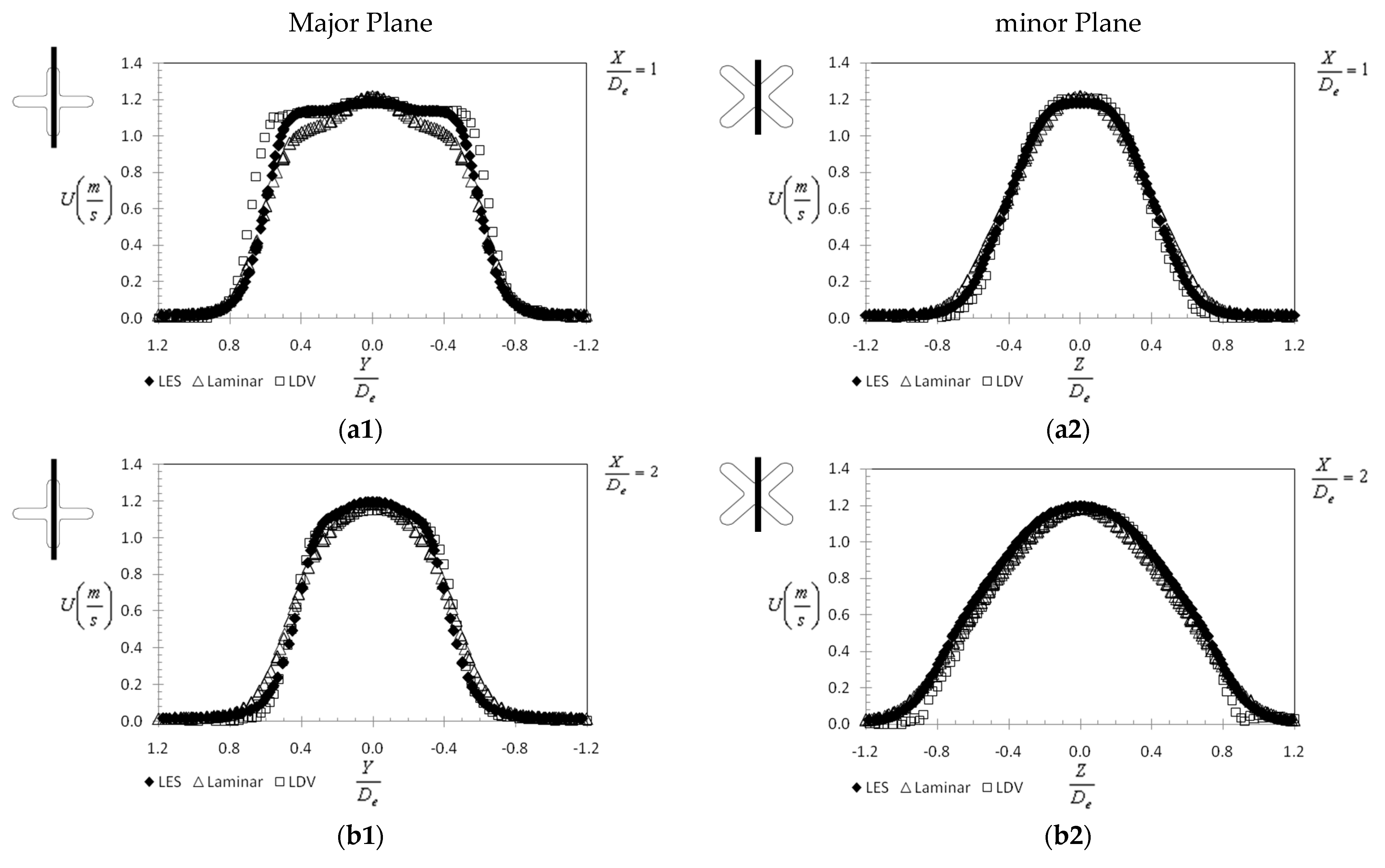
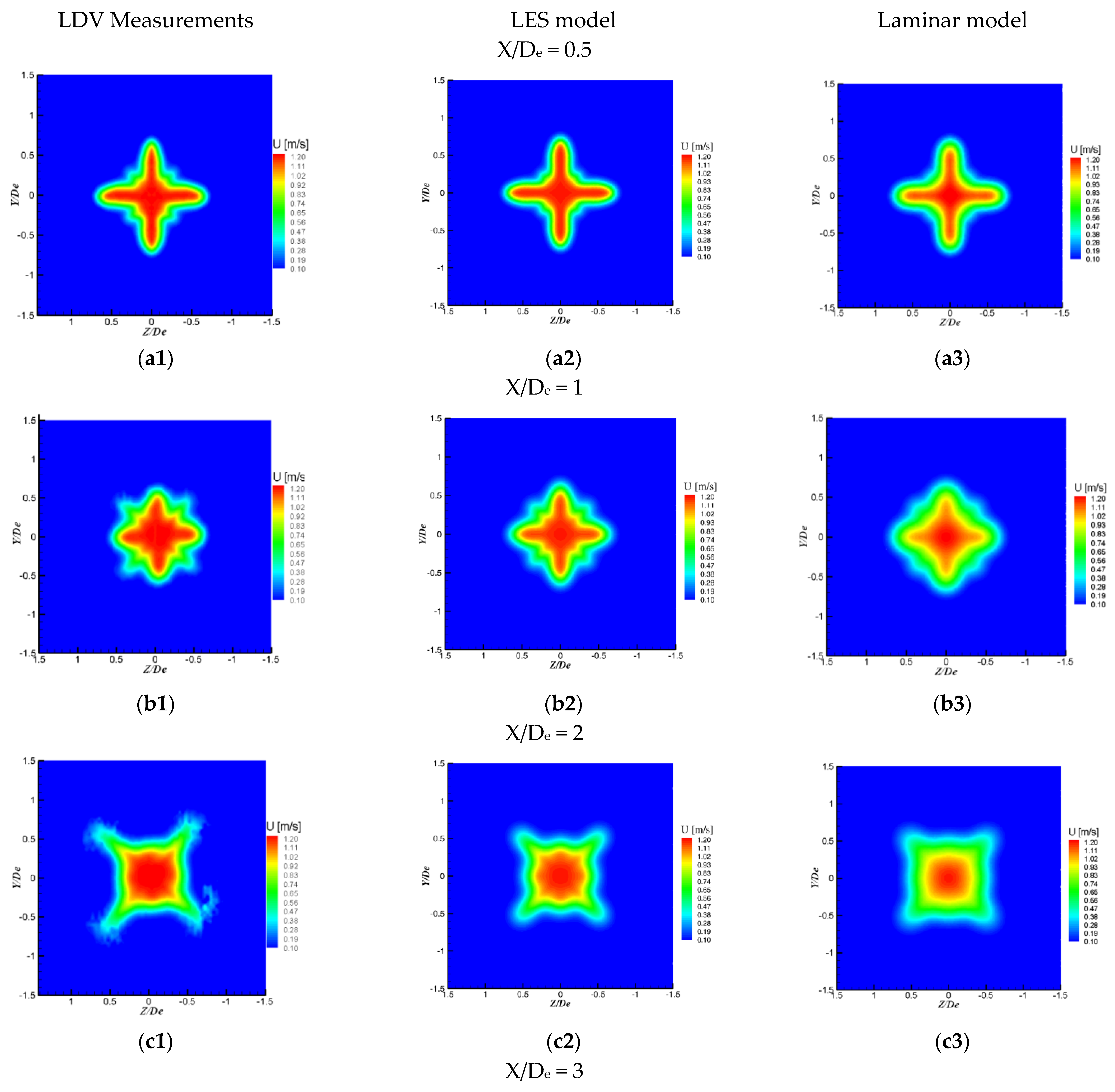
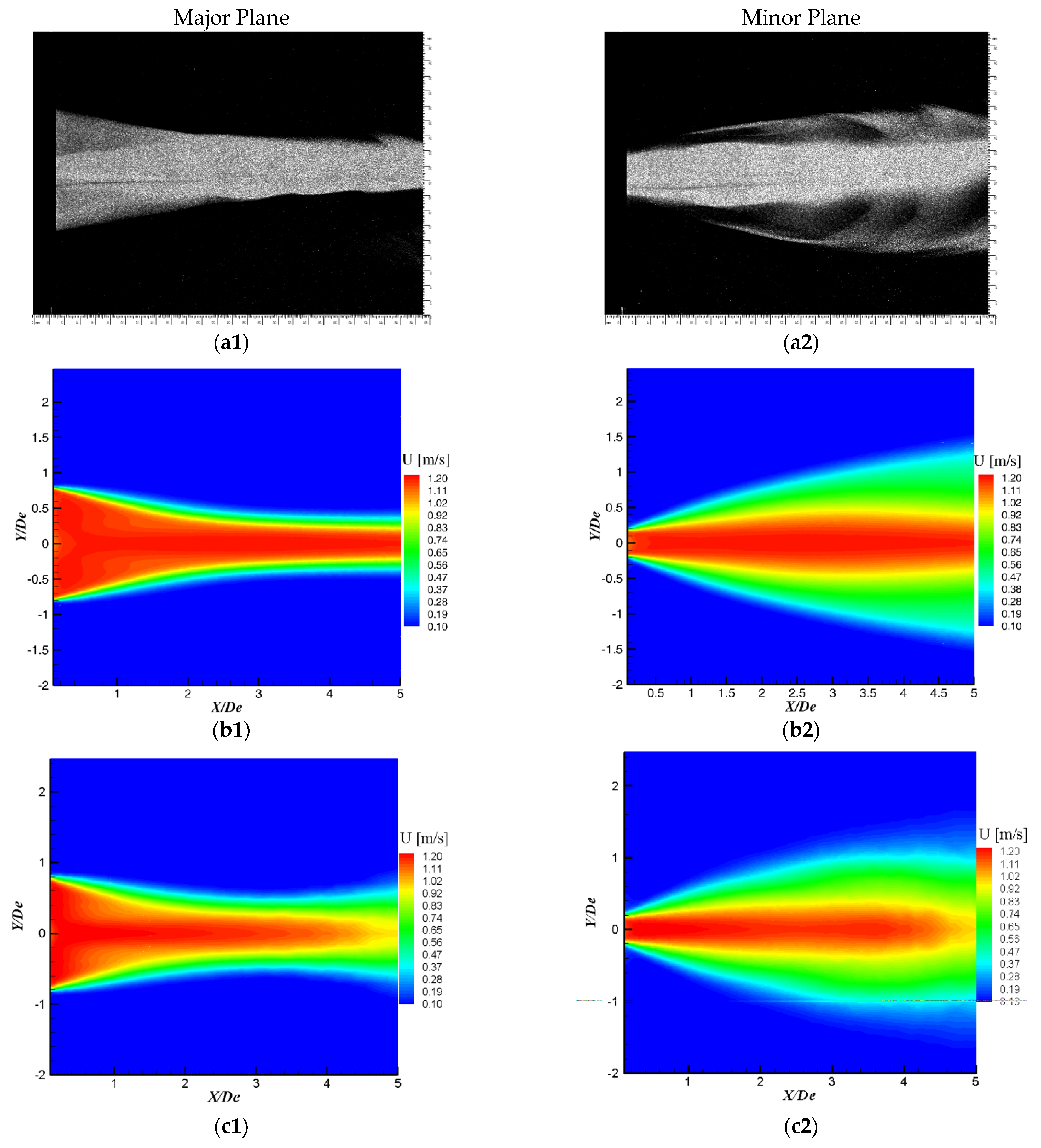
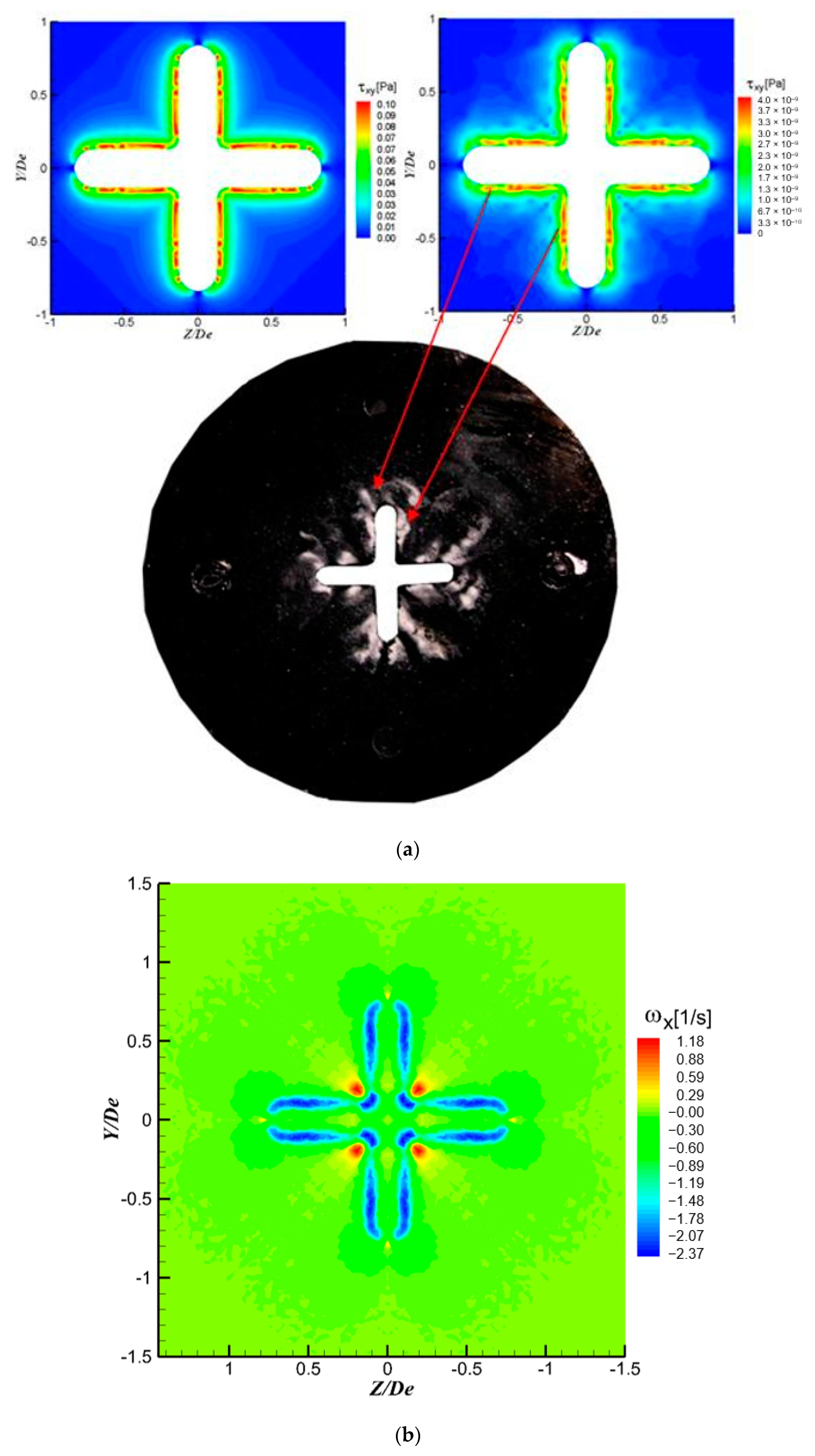
3.1. Global Analysis of the Flow and of the Tested Models
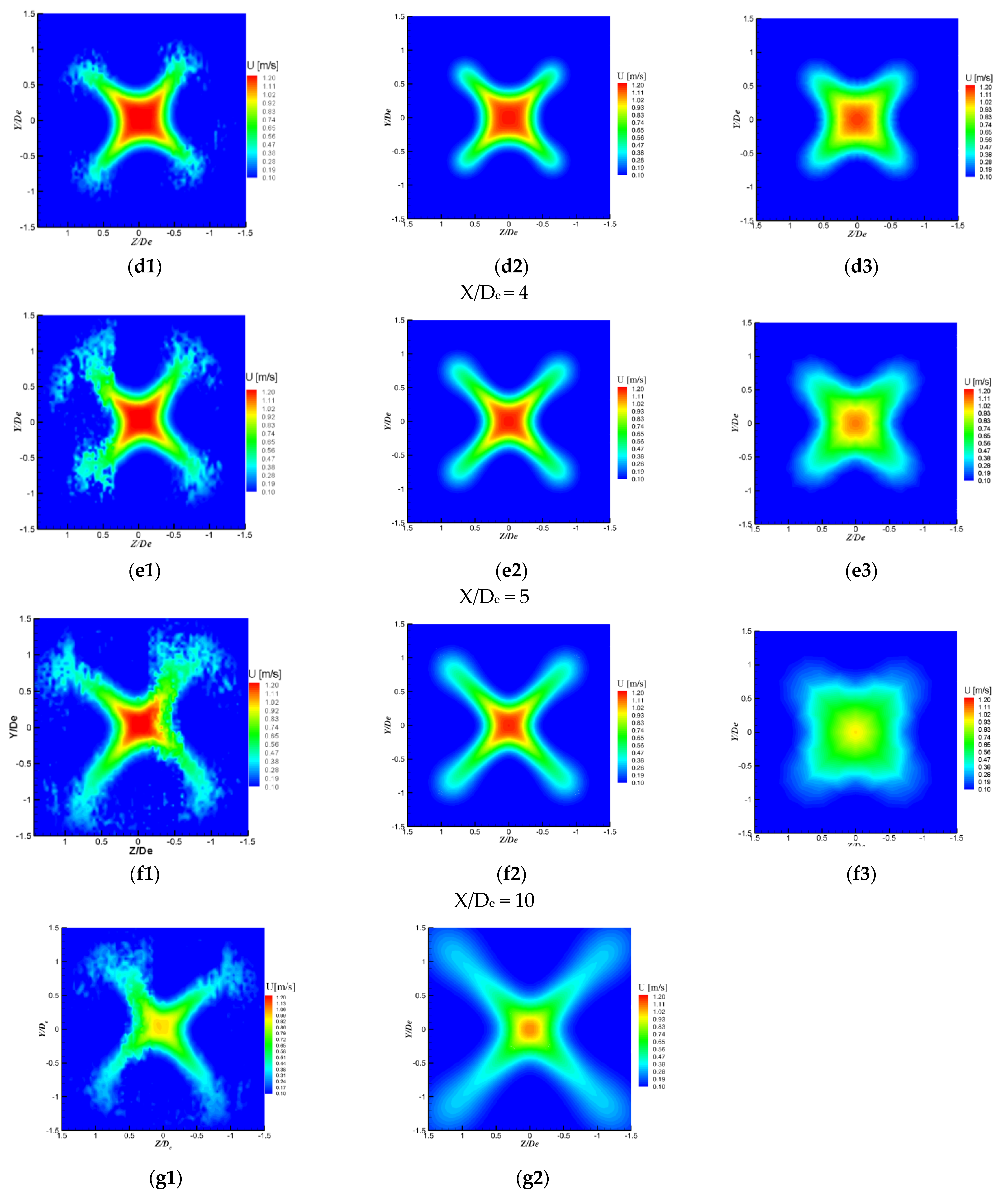
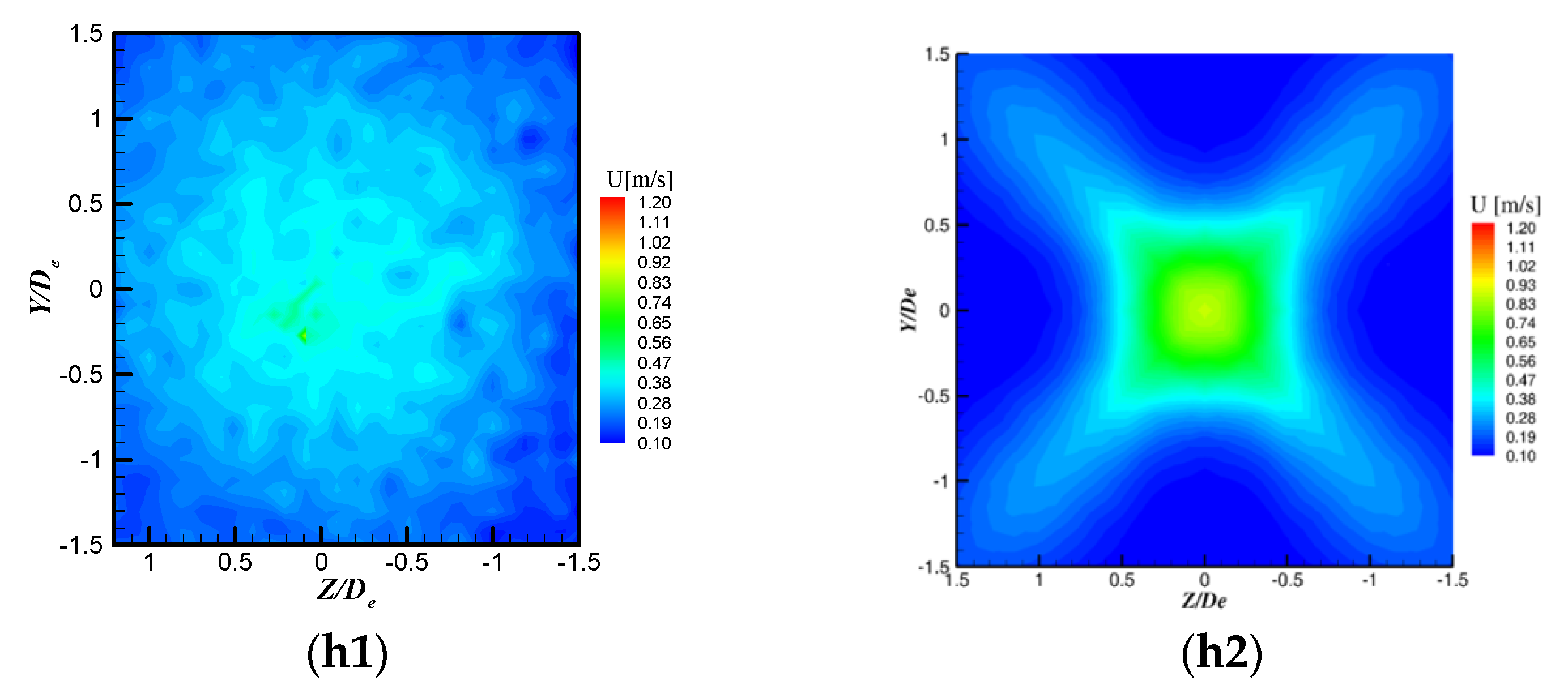
3.2. Discussion of the Flow Dynamics and the LES Model’s Limits in the Studied Case
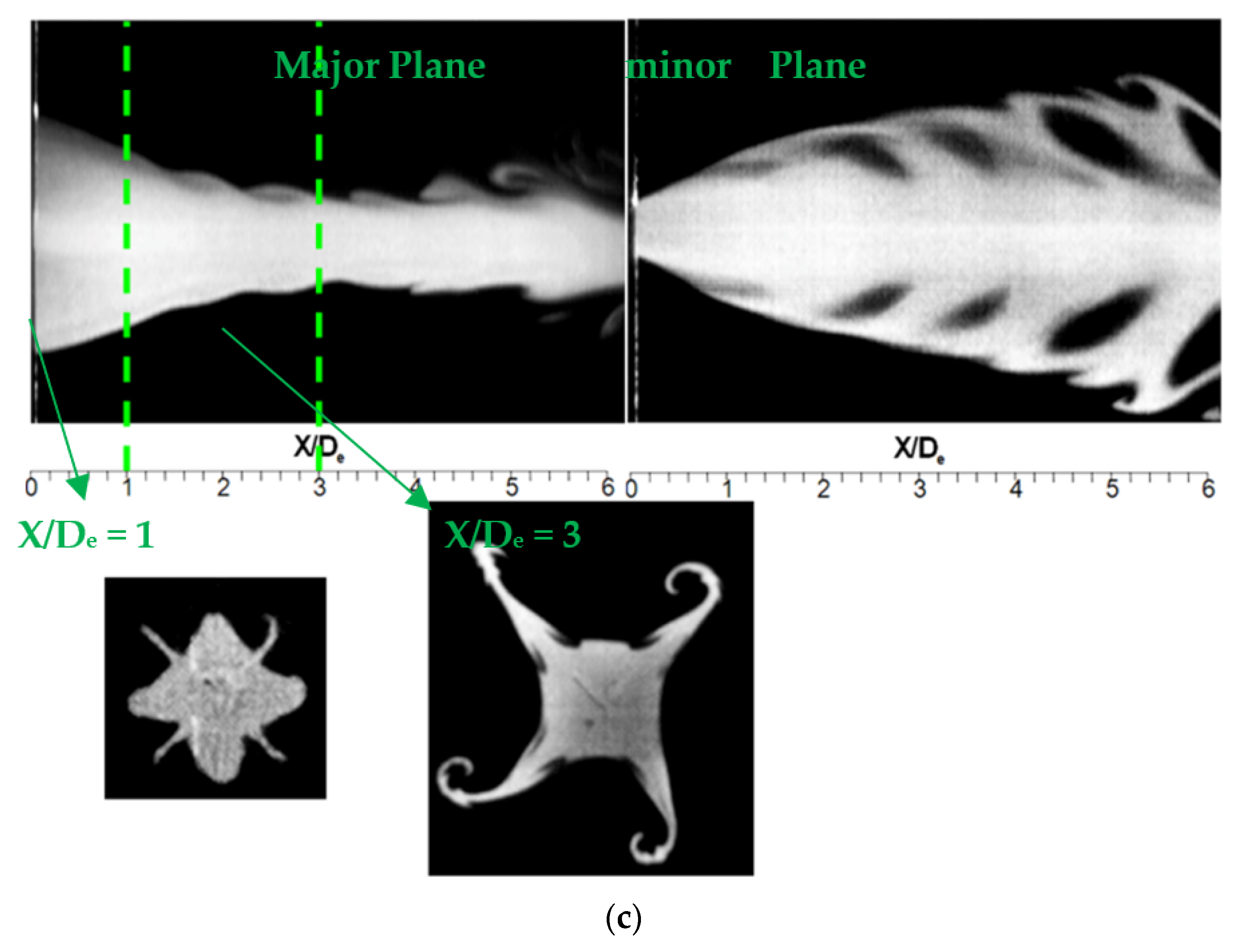
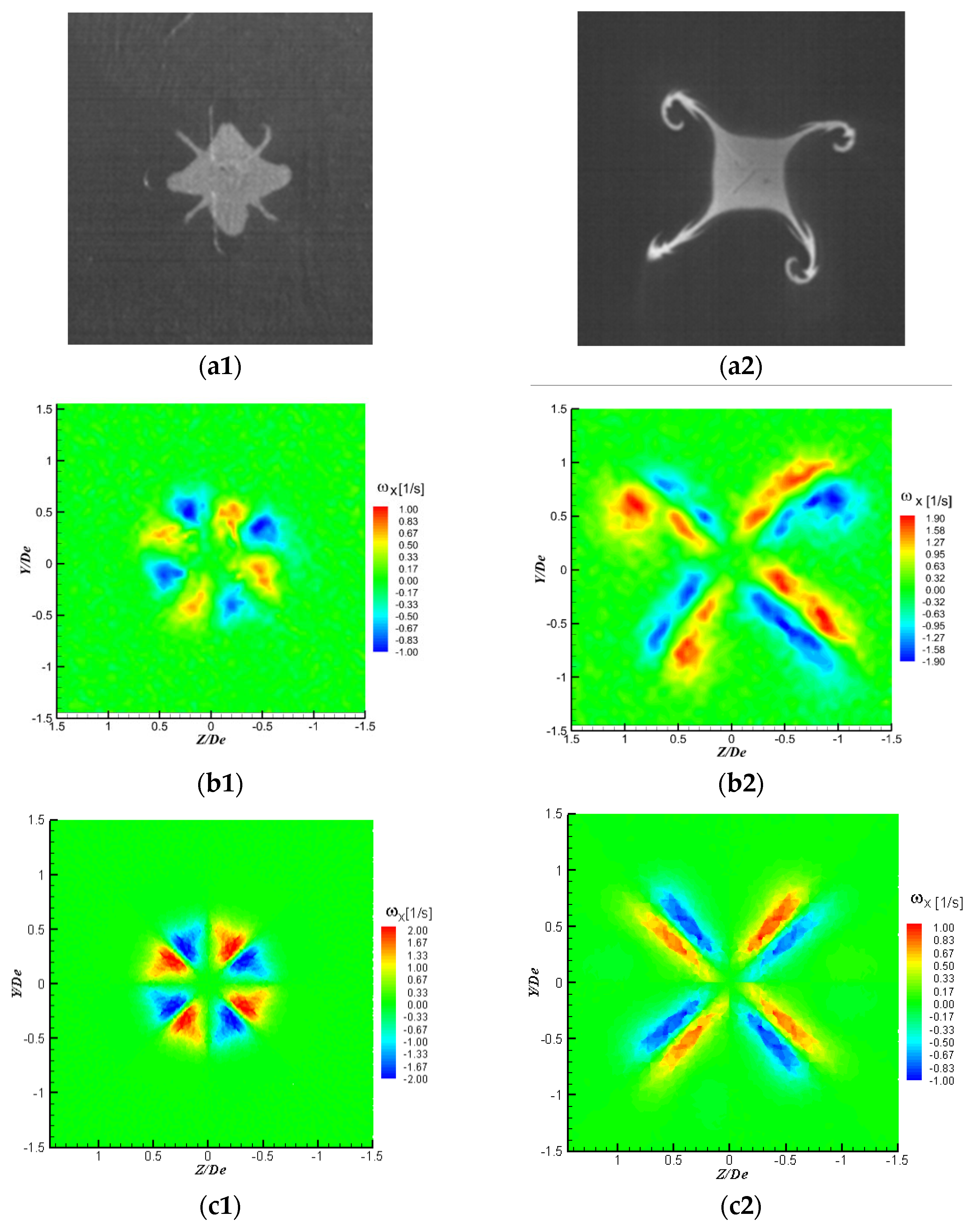
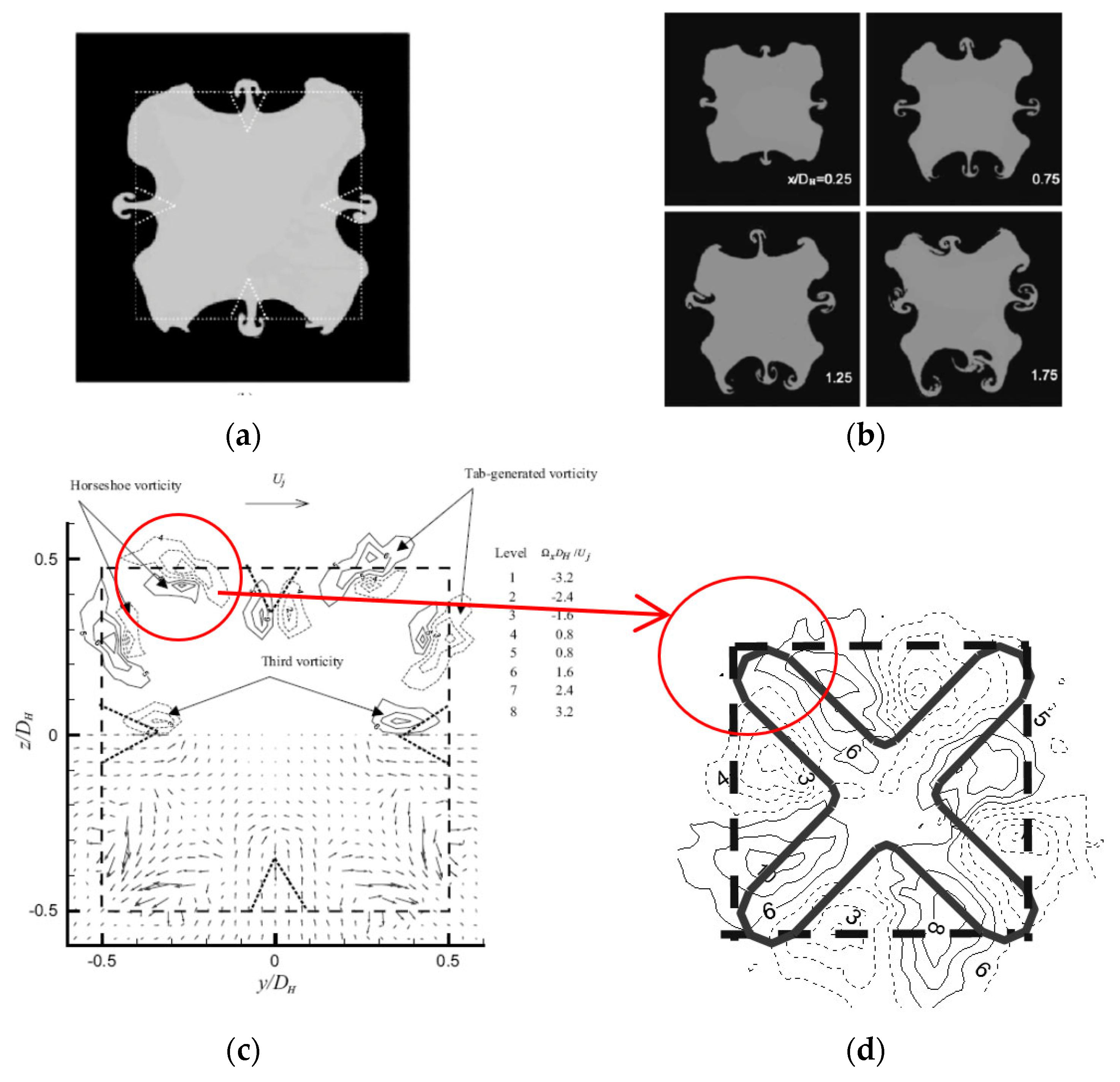
3.3. Discussion of the Vortex Generation Mechanisms in Lobed Orifice Jets
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| De | Equivalent diameter based on the exit area of the elementary orifice (mm) |
| DTR | Jet flow dimension (mm) |
| Q | Flow rate (m3/s) |
| Re | Reynolds number (-) |
| Centerline jet velocity (m/s) | |
| U0mean | Orifice’s mean exit velocity (m/s) |
| U:V,W | Velocity components in X, Y, Z direction (m/s) |
| X, Y, Z | Cartesian coordinates (m) |
| y+ | Non-dimensional wall distance |
| Wall shear stress (Pa) | |
| Streamwise vorticity component (1/s) | |
| Dynamic viscosity (Pa s) |
References
- Leitmeyer, K.; Adlhoch, C. Review Article: Influenza Transmission on Aircraft: A Systematic Literature Review. Epidemiology 2016, 27, 743–751. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Johnson, G.R.; Ristovski, Z.D.; Hargreaves, M.; Mengersen, K.; Corbett, S.; Chao, C.Y.H.; Li, Y.; Katoshevski, D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009, 40, 256–259. [Google Scholar] [CrossRef]
- Stadnytskyi, V.; Anfinrud, P.; Bax, A. Breathing, speaking, coughing or sneezing: What drives transmission of SARS-CoV-2? J. Intern. Med. 2021, 290, 1010–1027. [Google Scholar] [CrossRef] [PubMed]
- Sterling, E.M.; Arundel, A.; Sterling, T.D. Criteria for Human Exposure to Humidity in Occupied Buildings. ASHRAE Trans. 1985, 91, 611–622. [Google Scholar]
- Yang, W.; Elankumaran, S.; Marr, L.C. Relationship between Humidity and Influenza A Viability in Droplets and Implications for Influenza’s Seasonality. PLoS ONE 2012, 7, e46789. [Google Scholar] [CrossRef] [PubMed]
- Metz, J.A.; Finn, A. Influenza and humidity—Why a bit more damp may be good for you! J. Infect. 2015, 71 (Suppl. 1), S54–S58. [Google Scholar] [CrossRef] [PubMed]
- Hinninghofen, H.; Enck, P. Passenger well-being in airplanes. Auton. Neurosci. Basic Clin. 2006, 129, 80–85. [Google Scholar] [CrossRef]
- Liu, W.; Mazumdar, S.; Zhang, Z.; Poussou, S.B.; Liu, J.; Lin, C.-H.; Chen, Q. State-of-the-art methods for studying air distributions in commercial airliner cabins. Build. Environ. 2012, 47, 5–12. [Google Scholar] [CrossRef]
- Breugelmans, J.G.; Zucs, P.; Porten, K.; Broll, S.; Niedrig, M.; Ammon, A.; Krause, G. SARS Transmission and Commercial Aircraft. Emerg. Infect. Dis. 2004, 10, 1502–1503. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Niu, J.; Gao, N. Thermal comfort models: A review and numerical investigation. Build. Environ. 2012, 47, 13–22. [Google Scholar] [CrossRef]
- Veselý, M.; Zeiler, W. Personalized conditioning and its impact on thermal comfort and energy performance—A review. Renew. Sustain. Energy Rev. 2014, 34, 401–408. [Google Scholar] [CrossRef]
- Cao, G.; Awbi, H.; Yao, R.; Fan, Y.; Sirén, K.; Kosonen, R.; Zhang, J. A review of the performance of different ventilation and airflow distribution systems in buildings. Build. Environ. 2014, 73, 171–186. [Google Scholar] [CrossRef]
- ASHRAE. Position Document on Airborne Infectious Diseases. 2020. Available online: https://www.ashrae.org/file%20library/about/position%20documents/airborne-infectious-diseases.pdf (accessed on 28 September 2022).
- Rajaratnam, N. Turbulent Jets; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Pantelic, J.; Sze-To, G.N.; Tham, K.W.; Chao, C.Y.; Khoo, Y.C. Personalized ventilation as a control measure for airborne transmissible disease spread. J. R. Soc. Interface 2009, 6, S715–S726. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Muller, D.; Markwart, M. Numerical study of different air distribution systems for aircraft cabins. In Proceedings of the 11th International Conference on Indoor Air Quality and Climate, Barcelona, Spain, 17–22 August 2008. [Google Scholar]
- Müller, D.; Schmidt, M.; Müller, B. Application of a displacement ventilation system for air distribution in aircraft cabins. In Proceedings of the 3rd International Workshop on Aircraft System Technologies, Hamburg, Germany, 31 March–1 April 2011; pp. 279–288. [Google Scholar]
- Xu, C.; Nielsen, P.V.; Liu, L.; Jensen, R.L.; Gong, G. Impacts of airflow interactions with thermal boundary layer on performance of personalized ventilation. Build. Environ. 2018, 135, 31–41. [Google Scholar] [CrossRef]
- Zhang, T.; Li, P.; Wang, S. A personal air distribution system with air terminals embedded in chair armrests on commercial airplanes. Build. Environ. 2012, 47, 89–99. [Google Scholar] [CrossRef]
- Meslem, A.; Nastase, I.; Allard, F. Passive mixing control for innovative air diffusion terminal devices for buildings. Build. Environ. 2010, 45, 2679–2688. [Google Scholar] [CrossRef]
- Bolashikov, Z.; Melikov, A.; Spilak, M.; Nastase, I.; Meslem, A. Improved inhaled air quality at reduced ventilation rate by control of airflow interaction at the breathing zone with lobed jets. HVACR Res. 2014, 20, 238–250. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A. Vortex Dynamics and mass entrainement in turbulent lobed jets with and without lobe deflection angles. Exp. Fluids 2010, 48, 693–714. [Google Scholar] [CrossRef]
- Melikov, A.K.; Cermak, R.; Majer, M. Personalized ventilation: Evaluation of different air terminal devices. Energy Build. 2002, 34, 829–836. [Google Scholar] [CrossRef]
- Khalifa, E.H.; Janos, M.I.; Dannenhoffer, J.F., III. Experimental investigation of reduced-mixing personal ventilation jets. Build. Environ. 2009, 44, 1551–1558. [Google Scholar] [CrossRef]
- Russo, J.S.; Dang, T.Q.; Khalifa, H.E. Computational analysis of reduced-mixing personal ventilation jets. Build. Environ. 2009, 44, 1559–1567. [Google Scholar] [CrossRef]
- Meslem, A.; El-Hassan, M.; Nastase, I. Analysis of jet entrainment mechanism in the transitional regime by time-resolved PIV. J. Vis. 2010, 14, 41–52. [Google Scholar] [CrossRef]
- Meslem, A.; Nastase, I. Analysis of free or twin-jets for innovative air diffusion terminal units. In Proceedings of the 11th International Conference on Air Distribution in Rooms (Roomvent 2009), Busan, Republic of Korea, 24–27 May 2009. [Google Scholar]
- Meslem, A.; Nastase, I.; Abed-Meraim, K. Experimental investigation of a lobed jet flow mixing performance. J. Eng. Phys. Thermophys. 2007, 81, 106–111. [Google Scholar] [CrossRef]
- Nastase, I. Analyse des Jets Lobés en Vue de Leur Intégration dans les Unités Terminales de Diffusion D’air. Ph.D. Thesis, Université de La Rochelle, La Rochelle, France, 2007. [Google Scholar]
- Nastase, I.; Meslem, A. Passive control of jet flows using lobed nozzle geometries. Mécanique Ind. 2007, 8, 101–109. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A. Vortex dynamics and entrainment mechanisms in low Reynolds orifice jets. J. Vis. 2008, 11, 309–318. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A.; El Hassan, M. Image processing analysis of vortex dynamics of lobed jets from three-dimensional diffusers. Fluid Dyn. Res. 2011, 43, 065502. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A.; Gervais, P. Primary and secondary vortical structures contribution in the entrainement of low Reynolds number jet flows. Exp. Fluids 2008, 44, 1027–1033. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A.; Iordache, V.; Colda, I. Lobed grilles for high mixing ventilation—An experimental analysis in a full scale model room. Build. Environ. 2011, 46, 547–555. [Google Scholar] [CrossRef]
- Kristiawan, M.; Meslem, A.; Nastase, I.; Sobolik, V. Wall shear rates and mass transfer in impinging jets: Comparison of circular convergent and cross-shaped orifice nozzles. Int. J. Heat Mass Transf. 2012, 55, 282–293. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Charters, W.W.S.; Lesslie, D.A. Thermocirculation characteristics of a Trombe wall passive test cell. Sol. Energy 1982, 28, 461–468. [Google Scholar] [CrossRef]
- Fellouah, H.; Ball, C.G.; Pollard, A. Reynolds number effects within the development region of a turbulent round free jet. Int. J. Heat Mass Transf. 2009, 52, 3943–3954. [Google Scholar] [CrossRef]
- Abdel-Rahman, A.A.; Al-Fahed, S.F.; Chakroun, W. The near field characteristics of circular jets at low Reynolds numbers. Mech. Res. Commun. 1996, 23, 313–324. [Google Scholar] [CrossRef]
- Todde, V.; Spazzini, P.G.; Sandberg, M. Experimental analysis of low-Reynolds number free jets. Evolution along the jet centerline and Reynolds number effects. Exp. Fluids 2009, 47, 279–294. [Google Scholar] [CrossRef]
- Matsson, J. An Introduction to ANSYS Fluent 2022; SDC Publications: Mission, KS, USA, 2022. [Google Scholar]
- Jubran, B.A.; Hamdan, M.A.; Tashtoush, B.; Mansour, A.R. An approximate analytical solution for the prediction of transient response of the trombe wall. Int. Commun. Heat Mass Transf. 1993, 20, 567–577. [Google Scholar] [CrossRef]
- Bode, F.; Nastase, I.; Croitoru, C. Mesh dependency study using large eddy simulation of a very low reynolds cross-shaped jet. Math. Model. 2011, 4, 16–23. [Google Scholar]
- Rundström, D.; Moshfegh, B. Large-eddy simulation of an impinging jet in a cross-flow on a heated wall-mounted cube. Int. J. Heat Mass Transf. 2009, 52, 921–931. [Google Scholar] [CrossRef]
- Fluent, Inc. FLUENT, User’s Guide, Software and Documentation V. 6.1.18; Fluent, Inc.: Lebanon, NH, USA, 2003. [Google Scholar]
- Smagorinski, J. General circulation experiments with subgrid models. Rech. Aero 1963, 1, 51–63. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. Dynamic Subgrid-Scale Eddy Viscosity Model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A Proposed Modification of the Germano Subgrid-Scale Closure Model. Phys. Fluids 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Kim, W.-W.; Menon, S. A new dynamic one-equation subgrid-scale model for large eddy simulations. In Proceedings of the AIAA 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, X.; Yao, Z.; Cao, X.; Liu, J.; He, F. Numerical study of the instantaneous flow fields by large eddy simulation and stability analysis in a single aisle cabin model. Build. Environ. 2016, 96, 1–11. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Q. Assessment of Various Turbulence Models for Transitional Flows in an Enclosed Environment (RP-1271). HVACR Res. 2009, 15, 1099–1119. [Google Scholar] [CrossRef]
- Thysen, J.H.; van Hooff, T.; Blocken, B.; van Heijst, G.J.F. CFD simulations of two opposing plane wall jets in a generic empty airplane cabin: Comparison of RANS and LES. Build. Environ. 2021, 205, 108174. [Google Scholar] [CrossRef]
- Shukla, A.K.; Dewan, A. OpenFOAM based LES of slot jet impingement heat transfer at low nozzle to plate spacing using four SGS models. Heat Mass Transf. 2019, 55, 911–931. [Google Scholar] [CrossRef]
- Andersson, B.; Andersson, R.; Håkansson, L.; Mortensen, M.; Sudiyo, R.; Van Wachem, B. Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Adrian, R.J. Laser Velocimetry. In Fluid Mechanics Measurements; Goldstein, R.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 155–240. [Google Scholar]
- Kähler, C.; Sammler, B.; Kompenhans, J. Generation and control of tracer particles for optical flow investigations in air. Exp. Fluids 2002, 33, 736–742. [Google Scholar] [CrossRef]
- Garcia, C.M.; Jackson, P.R.; Garcia, M.H. Confidence Intervals in the Determination of Turbulence Parameters. Exp. Fluids 2006, 40, 514–522. [Google Scholar] [CrossRef]
- Petrie, H.L.; Samimy, M.; Addy, A.L. Laser Doppler velocity biais in separated flows. Exp. Fluids 1988, 6, 80–88. [Google Scholar] [CrossRef]
- Barnett, D.O.; Bentley, H.T. Statistical bias of individual realization laser velocimeters. In Proceedings of the Second International Workshop on Laser Velocimetry, West Lafayette, IN, USA, 27–29 March 1974; pp. 428–444. [Google Scholar]
- Tummers, M.J.; Jacobse, J.; Voorbrood, S.G.J. Turbulent flow in the near field of a round impinging jet. Int. J. Heat Mass Transf. 2011, 54, 4939–4948. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data. Analysis and Measurement Procedures, 2nd ed.; Wiley-Interscience Publication: Hoboken, NJ, USA, 1986; p. 566. [Google Scholar]
- Butier, A. Vélocimétrie Laser Pour la Mécanique des Fluids; Hermes Science Publication: London, UK, 2017; ISBN 978-2-7462-4748-2. [Google Scholar]
- Zaman, K.B.M.Q. Axis switching and spreading of an asymmetric jet: The role of coherent structure dynamics. J. Fluid Mech. 1996, 316, 1–27. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q. Spreading characteristics and thrust of jets from asymmetric nozzles. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit (AIAA), Reno, NV, USA, 15–18 January 1996. Paper No 96-0200. [Google Scholar]
- Zaman, K.B.M.Q. Spreading characteristics of compressible jets from nozzles of various geometries. J. Fluid Mech. 1999, 383, 197–228. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q.; Reeder, M.F.; Samimy, M. Control of axisymmetric jet using vortex generators. Phys. Fluids 1994, 6, 778–793. [Google Scholar] [CrossRef]
- Elrod, H.G. Computations charts and theory for circular and rectangular jets. ASHVE Trans. 1954, 60, 1514. [Google Scholar]
- Tuve, G.L. Air velocities in ventilating jets, ASHVE Research Report No. 1476. ASHVE Trans. 1953, 58, 261–283. [Google Scholar]
- Fanger, P.O.; Melikov, A.K.; Hanzawa, H.; Ring, J. Air turbulence and sensation of draught. Energy Build. 1988, 12, 21–39. [Google Scholar] [CrossRef]
- Mi, J.; Nathan, G.J.; Nobes, D.S. Mixing characteristics of axisymmetric free jets from a contoured nozzle an orifice plate and a pipe. J. Fluids Eng. 2001, 123, 878–883. [Google Scholar] [CrossRef]
- Wang, X.K.; Chua, L.P.; Yu, S.C.M. On the near field of a square jet with vortex generating tabs. Fluid Dyn. Res. 2003, 32, 99–117. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q. Streamwise vorticity generation and mixing enhancement in free jets by delta tabs. In Proceedings of the 3rd Shear Flow Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Yuan, Y. Jet Fluid Mixing Control Through Manipulation of Inviscid Flow Structures. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2000. [Google Scholar]
- Yu, H.D.; Girimaji, S.S. Near-field turbulent simulations of rectangular jets using lattice Boltzmann method. Phys. Fluids 2005, 17, 125106. [Google Scholar] [CrossRef]
- Nastase, I.; Meslem, A.; Bowmans, T. Vortical structures analysis in jet flows using a classical 2D-PIV system and time resolved visualization image processing. J. Flow Vis. Image Process. 2008, 15, 275–300. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bode, F.I.; Nastase, I. Numerical Investigation of Very Low Reynolds Cross Orifice Jet for Personalized Ventilation Applications in Aircraft Cabins. Int. J. Environ. Res. Public Health 2023, 20, 740. https://doi.org/10.3390/ijerph20010740
Bode FI, Nastase I. Numerical Investigation of Very Low Reynolds Cross Orifice Jet for Personalized Ventilation Applications in Aircraft Cabins. International Journal of Environmental Research and Public Health. 2023; 20(1):740. https://doi.org/10.3390/ijerph20010740
Chicago/Turabian StyleBode, Florin Ioan, and Ilinca Nastase. 2023. "Numerical Investigation of Very Low Reynolds Cross Orifice Jet for Personalized Ventilation Applications in Aircraft Cabins" International Journal of Environmental Research and Public Health 20, no. 1: 740. https://doi.org/10.3390/ijerph20010740
APA StyleBode, F. I., & Nastase, I. (2023). Numerical Investigation of Very Low Reynolds Cross Orifice Jet for Personalized Ventilation Applications in Aircraft Cabins. International Journal of Environmental Research and Public Health, 20(1), 740. https://doi.org/10.3390/ijerph20010740






