Exploration of the Relationships between Men’s Healthy Life Expectancy in Japan and Regional Variables by Integrating Statistical Learning Methods
Abstract
:1. Introduction
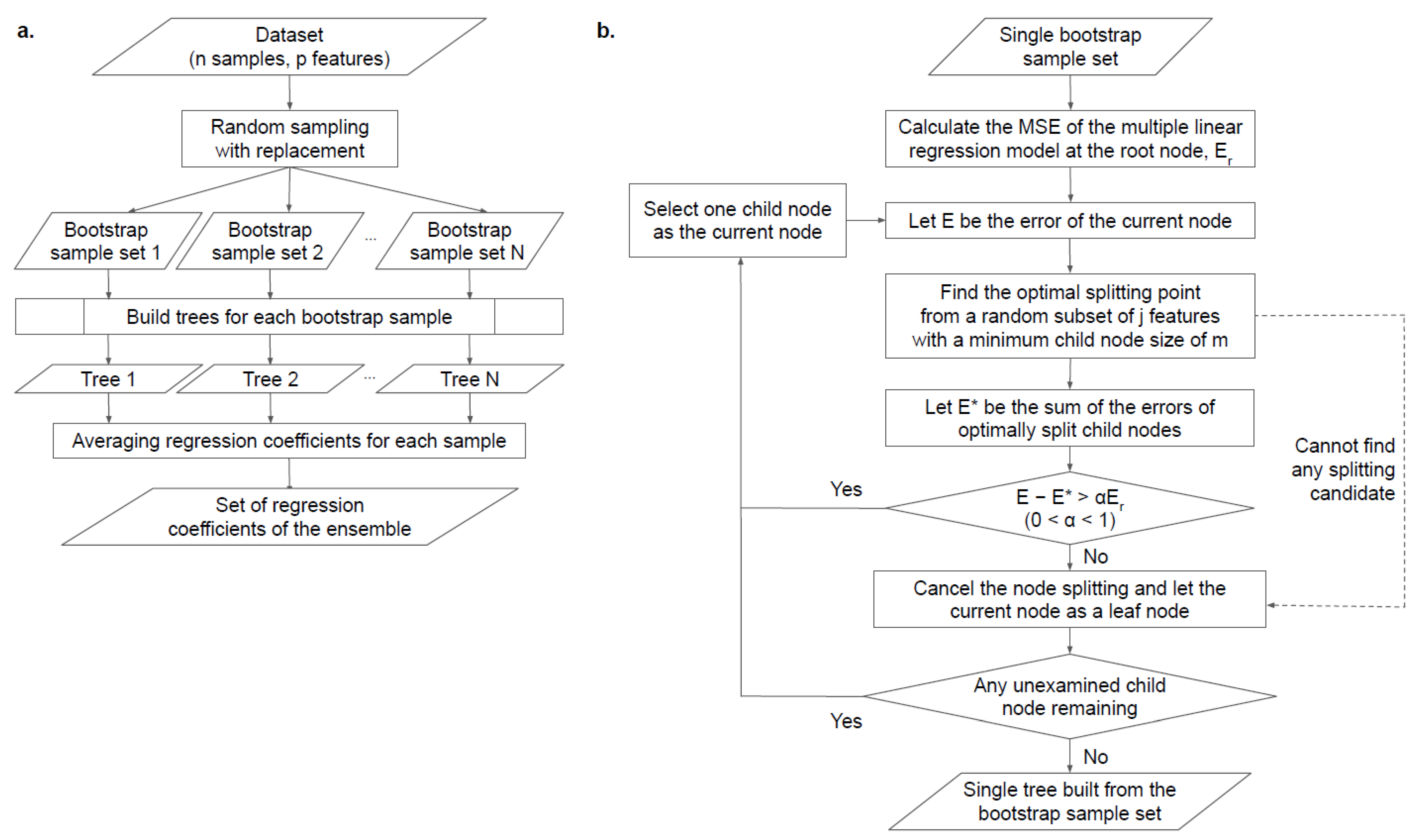
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Robine, J.M.; Romieu, I.; Cambois, E. Health expectancy indicators. Bull. World Health Organ. 1999, 77, 181–185. [Google Scholar] [PubMed]
- Mathers, C.D.; Sadana, R.; Salomon, J.A.; Murray, C.J.; Lopez, A.D. Healthy life expectancy in 191 countries, 1999. Lancet 2001, 357, 1685–1691. [Google Scholar] [CrossRef] [PubMed]
- Pamuk, E.R.; Wagener, D.K.; Molla, M.T. Achieving national health objectives: The impact on life expectancy and on healthy life expectancy. Am. J. Public Health 2004, 94, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, S.; Kawado, M.; Seko, R.; Murakami, Y.; Hayashi, M.; Kato, M.; Noda, T.; Ojima, T.; Nagai, M.; Tsuji, I. Trends in disability-free life expectancy in Japan, 1995–2004. J. Epidemiol. 2010, 20, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, I. Epidemiologic Research on Healthy Life Expectancy and Proposal for Its Extension: A Revised English Version of Japanese in the Journal of the Japan Medical Association 2019;148(9):1781-4. JMA J. 2020, 3, 149–153. [Google Scholar] [PubMed]
- Tsuji, I. Current status and issues concerning Health Japan 21 (second term). Nutr. Rev. 2020, 78, 14–17. [Google Scholar] [CrossRef]
- Fukuda, Y.; Nakamura, K.; Takano, T. Municipal health expectancy in Japan: Decreased healthy longevity of older people in socioeconomically disadvantaged areas. BMC Public Health 2005, 5, 65. [Google Scholar] [CrossRef]
- Naito, Y.; Goto, E.; Lin, H.-R.; Hara, K.; Sasaki, N.; Imanaka, Y. Factors related to active life expectancy across secondary medical areas. J. Jpn. Soc. Healthc. Adm. 2020, 57, 2–10. [Google Scholar]
- Schober, P.; Vetter, T.R. Linear Regression in Medical Research. Anesth. Analg. 2021, 132, 108–109. [Google Scholar] [CrossRef]
- Slinker, B.K.; Glantz, S.A. Multiple linear regression: Accounting for multiple simultaneous determinants of a continuous dependent variable. Circulation 2008, 117, 1732–1737. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Liu, S.; Tsoka, S.; Papageorgiou, L.G. Mathematical Programming for Piecewise Linear Regression Analysis. Expert Syst. Appl. 2016, 44, 156–167. [Google Scholar] [CrossRef]
- Yang, L.; Liu, S.; Tsoka, S.; Papageorgiou, L.G. A regression tree approach using mathematical programming. Expert Syst. Appl. 2017, 78, 347–357. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; Adams, N., Sterling, L., Eds.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Wang, Y.; Witten, I.H. Induction of model trees for predicting continuous classes. In Proceedings of the Poster Papers of the 9th European Conference on Machine Learning, Prague, Czech Republic, 23–25 April 1997; pp. 128–137. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Suzuki, J. Statistical Learning with Math and Python; Springer: Singapore, 2021; pp. 171–198. [Google Scholar]
- Hashimoto, S.; Kawado, M. The Page of Healthy Life Expectancy. Available online: http://toukei.umin.jp/kenkoujyumyou/ (accessed on 27 May 2023).
- e-Stat Portal Site of Official Statistics of Japan. Available online: https://www.e-stat.go.jp/ (accessed on 27 May 2023).
- The Cabinet Office of Japan. “Mieruka” (Visualization) Database of Economic, Financial and Living Indicators. Available online: https://www5.cao.go.jp/keizai-shimon/kaigi/special/reform/mieruka/db_top/index.html (accessed on 27 May 2023).
- The Ministry of Health, Labour and Welfare of Japan. Survey Results on the Long-Term Care Prevention Projects and the Comprehensive Projects for Long-Term Care Prevention and Daily Life Support (Regional Supporting Projects), Fiscal Year 2015 (Heisei 27). Available online: https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000141576.html (accessed on 27 May 2023).
- Ninchisho (Dementia) Supporter Caravan. Available online: https://www.caravanmate.com/ (accessed on 27 May 2023).

| Variable | Unit/Calculation | Abbreviation |
|---|---|---|
| Proportion of graduates with tertiary education or higher | % | TE |
| Proportion of elderly (aged ≥ 65) single-person households, men | % | ES |
| Unemployment rate | % | UE |
| Proportion of workers aged 65 and over | % | EW |
| Proportion of primary industry workers | % | PW |
| Proportion of primary and secondary industry workers | % | IW |
| Proportion of car-only commuters | % | CM |
| Taxable income | yen, per taxpayer, ln-transformed | TI |
| Financial strength index | basic financial revenue divided by basic financial need | FI |
| Municipal tobacco tax collection | thousand yen, per thousand people aged ≥ 15, ln-transformed | TB |
| Number of dementia supporters | per thousand people aged ≥ 65, ln-transformed | DS |
| Number of participants in community-based salons for preventive care | per thousand people aged ≥ 65 | CS |
| Total population | person | TP |
| Proportion of inhabitable areas | % | IA |
| Population density in inhabitable areas | person, per hectare | PD |
| Proportion of population without flush toilet | % | NT |
| Variable | Loading for PC1 | Variable | Loading for PC1 |
|---|---|---|---|
| TE | 0.84 | FI | 0.63 |
| ES | 0.59 | TB | −0.056 |
| UE | −0.18 | DS | −0.21 |
| EW | −0.59 | CS | −0.24 |
| PW | −0.78 | TP | 0.38 |
| IW | −0.75 | IA | 0.66 |
| CM | −0.87 | PD | 0.81 |
| TI | 0.85 | NT | −0.65 |
| Std. β | Std. Error | p-Value | 95% CI | ||
|---|---|---|---|---|---|
| const. | 0 | 0.027 | 1 | −0.053 | 0.053 |
| TE | 0.6056 | 0.071 | <0.001 | 0.465 | 0.746 |
| ES | −0.2048 | 0.058 | <0.001 | −0.319 | −0.091 |
| UE | −0.1508 | 0.036 | <0.001 | −0.222 | −0.079 |
| EW | −0.0328 | 0.04 | 0.413 | −0.111 | 0.046 |
| PW | −0.0384 | 0.046 | 0.405 | −0.129 | 0.052 |
| IW | 0.1705 | 0.052 | 0.001 | 0.069 | 0.272 |
| CM | −0.0849 | 0.06 | 0.16 | −0.203 | 0.034 |
| TI [ln] | 0.0847 | 0.068 | 0.214 | −0.049 | 0.218 |
| FI | 0.0378 | 0.049 | 0.444 | −0.059 | 0.135 |
| TB [ln] | −0.099 | 0.038 | 0.01 | −0.174 | −0.024 |
| DS [ln] | 0.0524 | 0.029 | 0.075 | −0.005 | 0.11 |
| CS | 0.0379 | 0.028 | 0.177 | −0.017 | 0.093 |
| TP | −0.0451 | 0.03 | 0.133 | −0.104 | 0.014 |
| IA | −0.1311 | 0.04 | 0.001 | −0.209 | −0.053 |
| PD | −0.0426 | 0.073 | 0.561 | −0.187 | 0.101 |
| NT | −0.0517 | 0.036 | 0.148 | −0.122 | 0.018 |
| Std. β | Std. Error | p-Value | 95% CI | ||
|---|---|---|---|---|---|
| const. | 0.1277 | 0.092 | 0.163 | −0.052 | 0.308 |
| TE | 0.5585 | 0.079 | <0.001 | 0.403 | 0.714 |
| ES | −0.1852 | 0.06 | 0.002 | −0.303 | −0.067 |
| UE | −0.2924 | 0.046 | <0.001 | −0.383 | −0.201 |
| EW | −0.1223 | 0.049 | 0.013 | −0.218 | −0.026 |
| PW | −0.0272 | 0.071 | 0.701 | −0.166 | 0.112 |
| IW | 0.1242 | 0.058 | 0.034 | 0.009 | 0.239 |
| CM | −0.0817 | 0.068 | 0.227 | −0.214 | 0.051 |
| TI [ln] | −0.0853 | 0.126 | 0.497 | −0.332 | 0.161 |
| FI | 0.0271 | 0.053 | 0.61 | −0.077 | 0.132 |
| TB [ln] | −0.13 | 0.041 | 0.002 | −0.21 | −0.05 |
| DS [ln] | 0.0398 | 0.029 | 0.172 | −0.017 | 0.097 |
| CS | −0.0409 | 0.039 | 0.3 | −0.118 | 0.036 |
| TP | −0.0358 | 0.033 | 0.279 | −0.101 | 0.029 |
| IA | −0.1255 | 0.042 | 0.003 | −0.208 | −0.043 |
| PD | 0.2084 | 0.2 | 0.299 | −0.185 | 0.602 |
| NT | 0.0001 | 0.044 | 0.998 | −0.087 | 0.087 |
| const. × trpz (PC1; −4, −0.5, 0.5, 4) | −0.3502 | 0.433 | 0.418 | −1.2 | 0.5 |
| TE × linz (PC1; −1.5, 0.5) | 0.2429 | 0.166 | 0.144 | −0.083 | 0.569 |
| UE × trpz (PC1; −3, −2, 1, 3) | −0.3759 | 0.081 | <0.001 | −0.534 | −0.218 |
| EW × linz (PC1; −3, 0.5) | 0.2551 | 0.107 | 0.018 | 0.044 | 0.466 |
| PW × lins (PC1; 0, 4) | 1.0704 | 0.69 | 0.121 | −0.285 | 2.426 |
| IW × linz (PC1; −3, 1.5) | 0.3829 | 0.138 | 0.006 | 0.111 | 0.655 |
| CM × trpz (PC1; −4, −2.5, −1, 1) | −0.2627 | 0.157 | 0.094 | −0.571 | 0.045 |
| TI [ln] × trpz (PC1; −2.5, −1, 1, 2.5) | −0.4119 | 0.138 | 0.003 | −0.683 | −0.141 |
| TB [ln] × lins (PC1; −3, 2) | 0.0501 | 0.108 | 0.642 | −0.162 | 0.262 |
| DS [ln] × linz (PC1; −2, 2.5) | 0.1449 | 0.079 | 0.068 | −0.011 | 0.301 |
| CS × linz (PC1; −3.5, −0.5) | 0.202 | 0.072 | 0.005 | 0.061 | 0.343 |
| CS × lins (PC1; 2.5, 4) | 0.0884 | 0.154 | 0.567 | −0.215 | 0.392 |
| TP × lins (PC1; −3.5, 0) | 0.7658 | 0.521 | 0.142 | −0.258 | 1.789 |
| PD × linz (PC1; −4.5, −2) | 1.3946 | 0.564 | 0.014 | 0.286 | 2.503 |
| PD × linz (PC1; −2, 2.5) | 0.3306 | 0.344 | 0.337 | −0.346 | 1.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, F.; Nakamura, K. Exploration of the Relationships between Men’s Healthy Life Expectancy in Japan and Regional Variables by Integrating Statistical Learning Methods. Int. J. Environ. Res. Public Health 2023, 20, 6782. https://doi.org/10.3390/ijerph20186782
Sato F, Nakamura K. Exploration of the Relationships between Men’s Healthy Life Expectancy in Japan and Regional Variables by Integrating Statistical Learning Methods. International Journal of Environmental Research and Public Health. 2023; 20(18):6782. https://doi.org/10.3390/ijerph20186782
Chicago/Turabian StyleSato, Fumiya, and Keiko Nakamura. 2023. "Exploration of the Relationships between Men’s Healthy Life Expectancy in Japan and Regional Variables by Integrating Statistical Learning Methods" International Journal of Environmental Research and Public Health 20, no. 18: 6782. https://doi.org/10.3390/ijerph20186782
APA StyleSato, F., & Nakamura, K. (2023). Exploration of the Relationships between Men’s Healthy Life Expectancy in Japan and Regional Variables by Integrating Statistical Learning Methods. International Journal of Environmental Research and Public Health, 20(18), 6782. https://doi.org/10.3390/ijerph20186782






