Spatial Association Network Evolution and Variance Decomposition of Economic Sustainability Development Efficiency in China
Abstract
:1. Introduction
2. Literature Review
2.1. Defining Sustainable Economic Development
2.2. Factors Influencing Sustainable Economic Development
2.3. Economic Sustainable Development Efficiency (ESDE)
2.4. Spatial Variation and Social Network Analysis
3. Methods and Data
3.1. Index System and Data Sources
3.2. Super-EBM Model of Unexpected Output
3.2.1. Super-EBM Model
3.2.2. EBM-Malmquist Model
3.3. Modified Gravity Model
3.4. Social Network Analysis
4. Result Analysis
4.1. The Economic Sustainable Development Efficiency (ESDE)
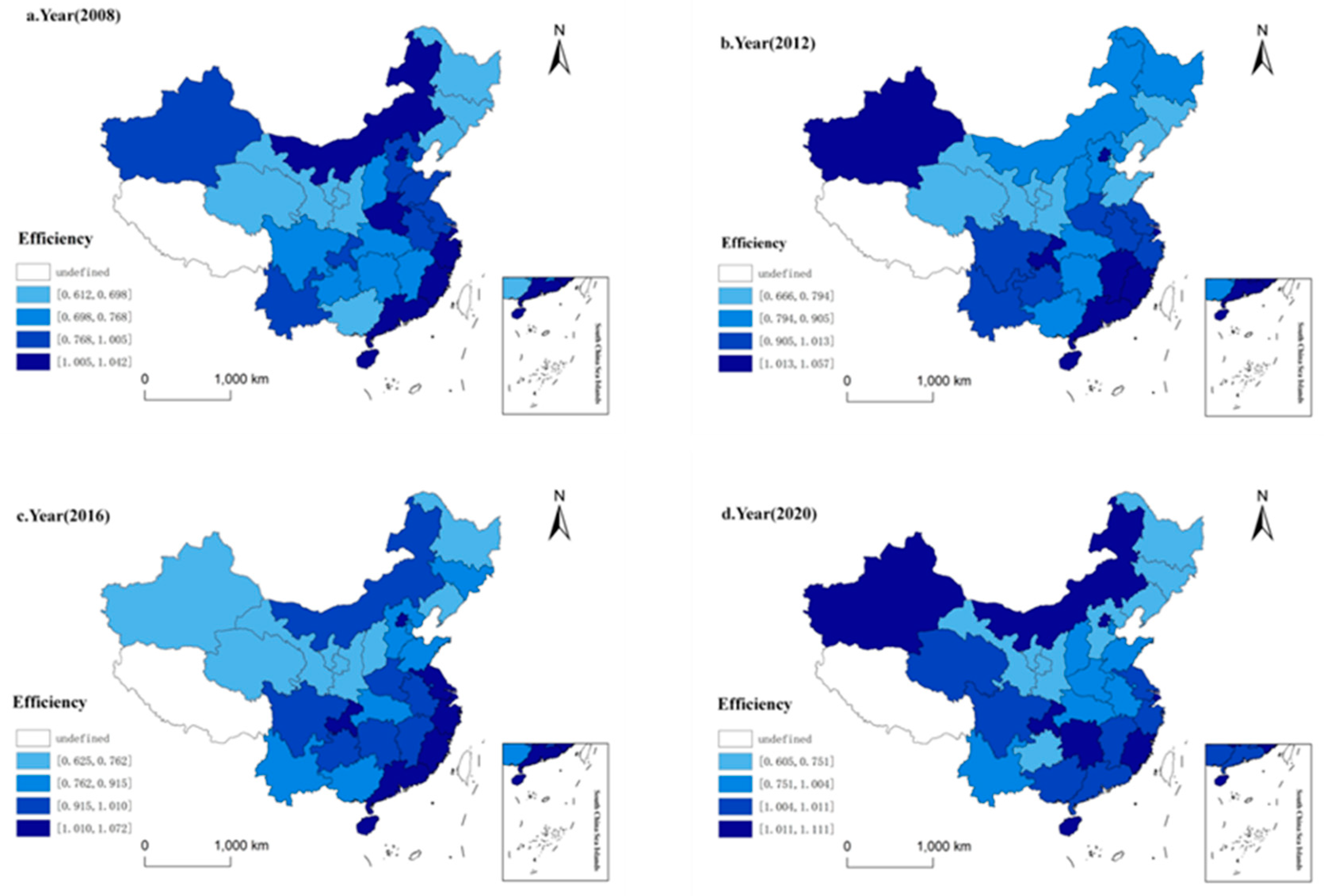
4.1.1. Analysis of Overall Efficiency
4.1.2. Analysis of Malmquist Index
4.2. Analysis of Regional Differences and Dynamic Evolution
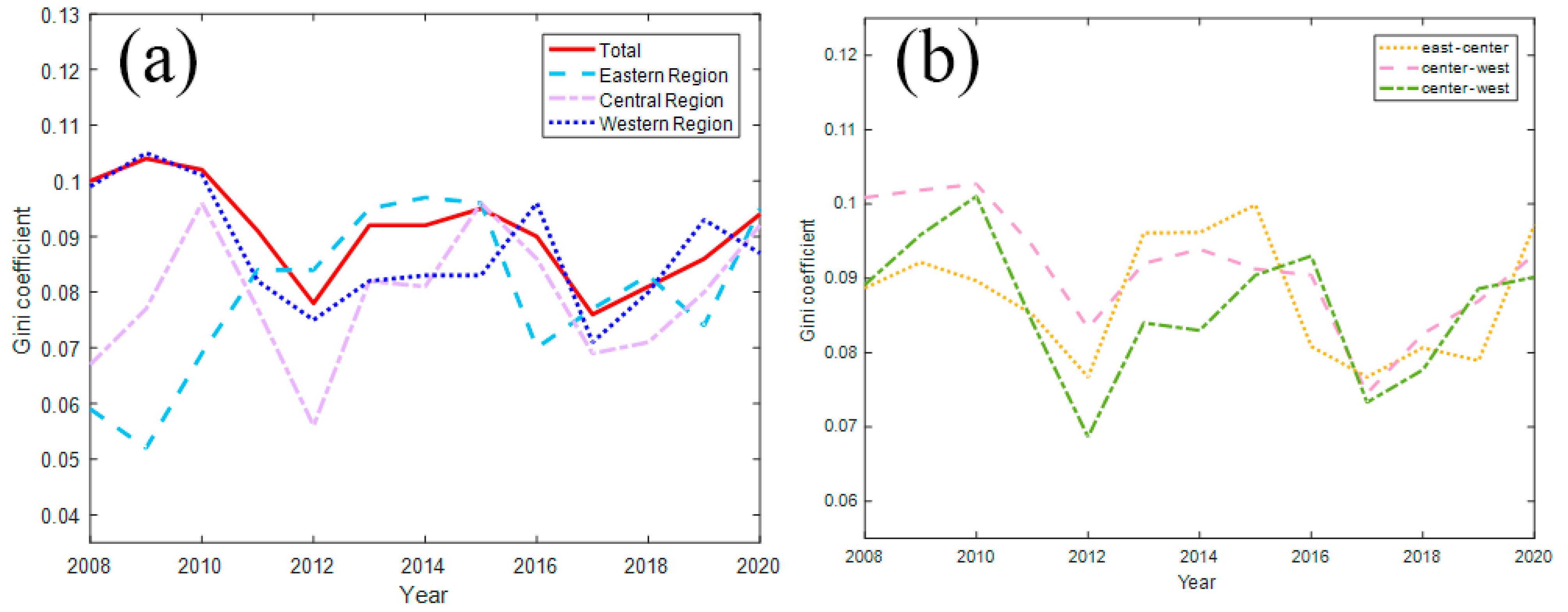
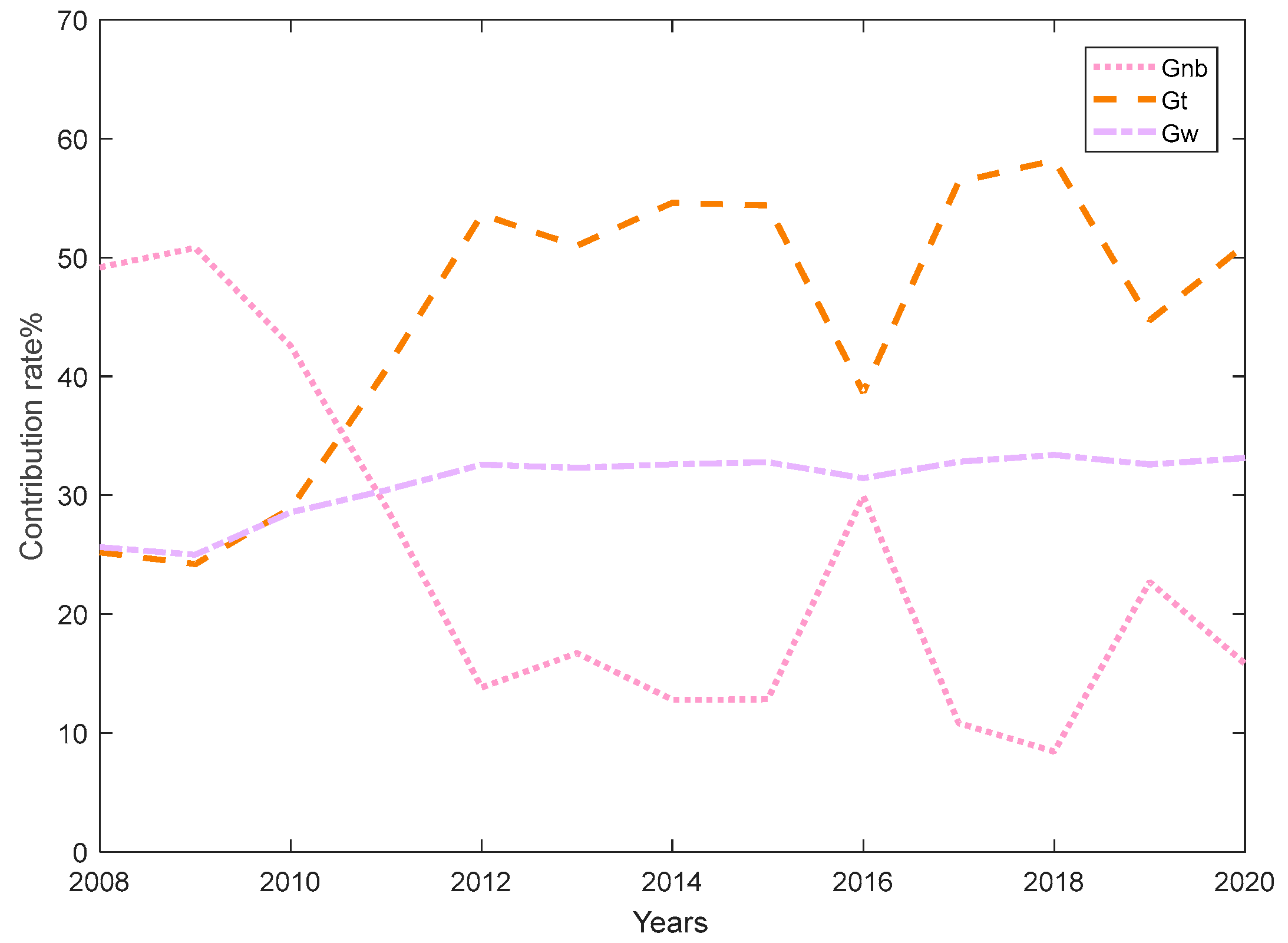
4.2.1. Estimation and Decomposition of Regional Differences in ESDE
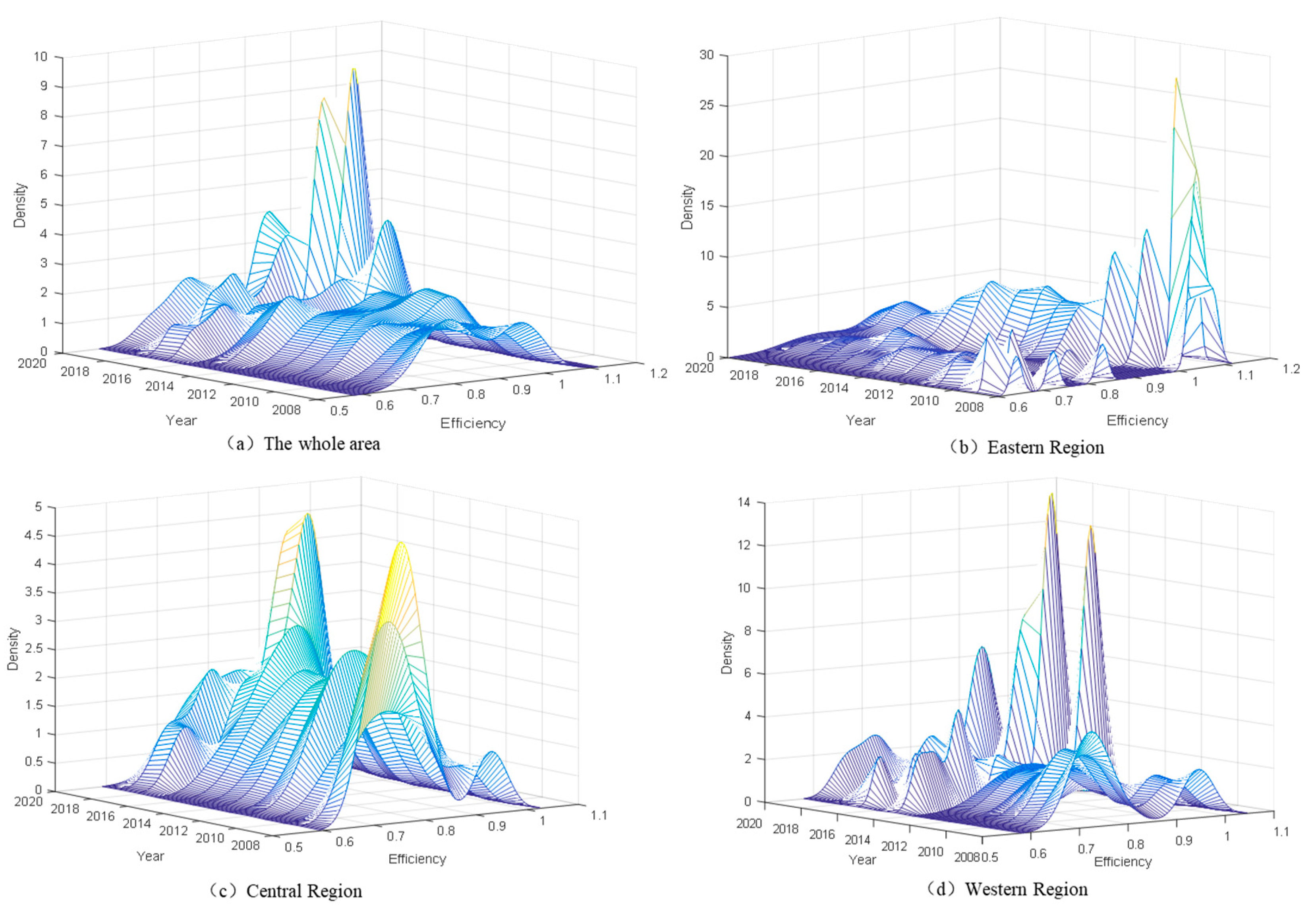
4.2.2. Dynamic Evolution of ESDE Regional Variation Distribution Based on 3D Kernel Density
4.3. Analysis of Spatial Network Characteristics
4.3.1. Overall Network Characteristics Analysis
4.3.2. Individual Network Characteristics Analysis
5. Conclusions and Recommendation
5.1. Conclusions
- (1)
- China’s overall ESDE is on an upward trend. The ESDE in the eastern regions of Beijing, Shanghai, Jiangsu, Zhejiang and Guangdong are leading at high levels, while the ESDE in the central regions of Liaoning, Jilin and Heilongjiang are lagging behind. The western regions are mostly at a medium level of ESDE, the eastern regions are in the leading position, and the central and western regions are keeping up with the East, while ESDE in the Northeast is lagging behind.
- (2)
- The overall regional differences in China’s ESDE have fluctuated and have tended to widen in recent years. On a national level, the ESDE exhibits a “gradient effect” and weak polarization. The ESDE in the eastern region does not appear to be polarized; however, there is a tendency for the differences to widen, and the ESDE in the central region is evidently disparate and fluctuates, while the ESDE in the western region appears to have a gradient effect with multi-polarization in some years.
- (3)
- The regional ESDE has shown significant spatial unevenness, with Beijing-Tianjin, the Yangtze River Delta and Guangzhou as the core of the circle structure. The role of the central and western provinces in the spatial network is weak, showing an apparent pattern of geographical differentiation with high density in the east and low density in the west, and the spatial interaction and spillover effects are also weak. Furthermore, the ESDE’s inter-provincial transmission and spillover costs are decreasing, the interaction paths are moving towards a more reasonable and coordinated direction, and the stability of the network is improving. Overall, the network structure of ESDE is stable and continues to progress in a positive direction, though there is still considerable improvement potential.
- (4)
- Beijing, Tianjin and the Yangtze River Delta have higher spillover relationships than beneficiary relationships in the correlation network, resulting in significant spillover effects on other regions; the node out-degrees of the northeast, northwest, southwest and central regions are less than the node in-degrees, as the spillover relationships in the above regions are lower than the beneficiary relationships; the regions receive more spillover effects from other regions in the correlation network and show significant beneficiary effects.
5.2. Recommendation
- (1)
- The spillover relationship is low in central and western China, and their spillover effects need to be strengthened. The western region has greater advantages in terms of promoting clean energy compared to the eastern region; the rapid development of clean energy could significantly contribute to sustainable development. Moreover, it would be beneficial to strengthen capital and technology investment in the central and western regions, focus on clean energy development policies, and use clean energy development to enhance sustainable economic spatial spillover relations, thus supporting sustainable economic development.
- (2)
- For economically less developed regions, the level of investment in environmental protection has to be enhanced while maintaining economic growth. These regions thus will need the support and supervision of government and national policies. Meanwhile, it would be beneficial to enhance the leading role of Beijing, Tianjin and the Yangtze River Delta in ESDE to strengthen the sustainable economic development of nearby regions.
- (3)
- Strengthen the effectiveness of the policy impact of market regulation and government macro-control, accelerate the spatial movement of economic factor resources and improve the inter-provincial economic connections for sustainable development. Reduce channels for inter-regional spillover and redundant interactions to enhance the network structure of ESDE, lower the cost of ESDE transmission and spillover between provinces, enhance the hierarchy and stability of spatially connected networks, and comprehensively enhance China’s sustainable economic development.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, I.; Zakari, A.; Dagar, V.; Singh, S. World energy trilemma and transformative energy developments as determinants of economic growth amid environmental sustainability. Energy Econ. 2022, 108, 105884. [Google Scholar]
- Hake, J.-F.; Fischer, W.; Venghaus, S.; Weckenbrock, C. The German Energiewende–history and status quo. Energy 2015, 92, 532–546. [Google Scholar]
- Jaiswal, K.K.; Chowdhury, C.R.; Yadav, D.; Verma, R.; Dutta, S.; Jaiswal, K.S.; SelvaKumar, K.K. Renewable and sustainable clean energy development and impact on social, economic, and environmental health. Energy Nexus 2022, 7, 100118. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q.; Fang, C.; Zhou, C. The relationship between economic growth, energy consumption, and CO2 emissions: Empirical evidence from China. Sci. Total Environ. 2016, 542, 360–371. [Google Scholar]
- Alola, A.A.; Bekun, F.V.; Sarkodie, S.A. Dynamic impact of trade policy, economic growth, fertility rate, renewable and non-renewable energy consumption on ecological footprint in Europe. Sci. Total Environ. 2019, 685, 702–709. [Google Scholar] [CrossRef]
- Qiao, Z.; Meng, X.; Wu, L. Forecasting carbon dioxide emissions in APEC member countries by a new cumulative grey model. Ecol. Indic. 2021, 125, 107593. [Google Scholar]
- Venghaus, S.; Dieken, S. From a few security indices to the FEW Security Index: Consistency in global food, energy and water security assessment. Sustain. Prod. Consum. 2019, 20, 342–355. [Google Scholar]
- Prasetyo, P.E.; Kistanti, N.R. Human capital, institutional economics and entrepreneurship as a driver for quality & sustainable economic growth. Entrep. Sustain. Issues 2020, 7, 2575. [Google Scholar]
- Hoang, T.C.; Black, M.C.; Knuteson, S.L.; Roberts, A.P. Environmental pollution, management, and sustainable development: Strategies for Vietnam and other developing countries. Environ. Manag. 2019, 63, 433–436. [Google Scholar]
- Pan, S.; Li, B.; Nie, H. Research on the Path of China’s Sustainable Economic Development from the Perspective of Energy Constraints. Inq. Into Econ. Issues 2020, 2, 158–169. [Google Scholar]
- Zhang, J.; Zhang, N.; Bai, S. Assessing the carbon emission changing for sustainability and high-quality economic development. Environ. Technol. Innov. 2021, 22, 101464. [Google Scholar] [CrossRef]
- Liu, H.; Wang, D.; Shang, J. From the Perspective of Green Low-Carbon Technological Progress:Can Green Credit Help Promote Sustainable Economic Development? Jilin Univ. J. Soc. Sci. Ed. 2020, 60, 96–105+237. [Google Scholar] [CrossRef]
- D’Adamo, I.; Gastaldi, M.; Morone, P. Economic sustainable development goals: Assessments and perspectives in Europe. J. Clean. Prod. 2022, 354, 131730. [Google Scholar]
- Atkinson, G. Sustainable Development and Policy: A Brief Review of the Literature & Current Practice Final Report to the Government Economic Service Group on Sustainable Development. 2009. Available online: https://www.semanticscholar.org/paper/SUSTAINABLE-DEVELOPMENT-AND-POLICY-%3A-A-BRIEF-REVIEW-Atkinson/3ed85af99f97a36022e6dd60934c06e798a54d85 (accessed on 2 February 2023).
- Stivers, R.L. The Sustainable Society: Ethics and Economic Growth; Westminister Press: Louisville, KY, USA, 1976. [Google Scholar]
- Commission, B. United Nations World Commission on Environment and Development. Our Common Future; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Pezzey, J.C. Economic Analysis of Sustainable Growth and Sustainable Development; World Bank: Washington, DC, USA, 1992. [Google Scholar]
- Dailami, M.; Dhareshwar, A.; Kaufmann, D.; Kishor, N.; Lopez, R.; Thomas, V.; Wang, Y. The Quality of Growth; World Bank Publications: Herndon, VA, USA, 2000. [Google Scholar]
- Barro, R.J. Quantity and Quality of Economic Growth; Banco Central de Chile: Santiago, Chile, 2002. [Google Scholar]
- Brock, W.A.; Taylor, M.S. Economic growth and the environment: A review of theory and empirics. Handb. Econ. Growth 2005, 1, 1749–1821. [Google Scholar]
- Illge, L.; Schwarze, R. A matter of opinion—How ecological and neoclassical environmental economists and think about sustainability and economics. Ecol. Econ. 2009, 68, 594–604. [Google Scholar] [CrossRef]
- Bartelmus, P. Use and usefulness of sustainability economics. Ecol. Econ. 2010, 69, 2053–2055. [Google Scholar]
- Wang, Q.; Huang, R. The impact of COVID-19 pandemic on sustainable development goals—A survey. Environ. Res. 2021, 202, 111637. [Google Scholar]
- Khan, I.; Hou, F.; Zakari, A.; Irfan, M.; Ahmad, M. Links among energy intensity, non-linear financial development, and environmental sustainability: New evidence from Asia Pacific Economic Cooperation countries. J. Clean. Prod. 2022, 330, 129747. [Google Scholar]
- Bai, X.; Wang, K.-T.; Tran, T.K.; Sadiq, M.; Trung, L.M.; Khudoykulov, K. Measuring China’s green economic recovery and energy environment sustainability: Econometric analysis of sustainable development goals. Econ. Anal. Policy 2022, 75, 768–779. [Google Scholar]
- Dabbous, A.; Tarhini, A. Does sharing economy promote sustainable economic development and energy efficiency? Evidence from OECD countries. J. Innov. Knowl. 2021, 6, 58–68. [Google Scholar] [CrossRef]
- Hosan, S.; Karmaker, S.C.; Rahman, M.M.; Chapman, A.J.; Saha, B.B. Dynamic links among the demographic dividend, digitalization, energy intensity and sustainable economic growth: Empirical evidence from emerging economies. J. Clean. Prod. 2022, 330, 129858. [Google Scholar]
- Winans, K.; Dlott, F.; Harris, E.; Dlott, J. Sustainable value mapping and analysis methodology: Enabling stakeholder participation to develop localized indicators mapped to broader sustainable development goals. J. Clean. Prod. 2021, 291, 125797. [Google Scholar]
- Qu, J.; Wang, B.; Liu, X. A modified super-efficiency network data envelopment analysis: Assessing regional sustainability performance in China. Socio-Econ. Plan. Sci. 2022, 82, 101262. [Google Scholar] [CrossRef]
- Tao, X.; Wang, P.; Zhu, B. Provincial green economic efficiency of China: A non-separable input–output SBM approach. Appl. Energy 2016, 171, 58–66. [Google Scholar] [CrossRef]
- Zhao, P.-j.; Zeng, L.-e.; Lu, H.-y.; Zhou, Y.; Hu, H.-y.; Wei, X.-Y. Green economic efficiency and its influencing factors in China from 2008 to 2017: Based on the super-SBM model with undesirable outputs and spatial Dubin model. Sci. Total Environ. 2020, 741, 140026. [Google Scholar]
- Wen, X.; Yao, S.; Sauer, J. Evaluation of sustainable development considering natural conditions: A parametric slacks-based measure of efficiency approach. J. Clean. Prod. 2022, 340, 130788. [Google Scholar]
- Swain, R.B.; Ranganathan, S. Modeling interlinkages between sustainable development goals using network analysis. World Dev. 2021, 138, 105136. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, X. Analysis of energy consumption structure on CO2 emission and economic sustainable growth. Energy Rep. 2022, 8, 1667–1679. [Google Scholar]
- Ren, Y.; Fang, C.; Li, G. Spatiotemporal characteristics and influential factors of eco-efficiency in Chinese prefecture-level cities: A spatial panel econometric analysis. J. Clean. Prod. 2020, 260, 120787. [Google Scholar]
- Tone, K.; Tsutsui, M. An epsilon-based measure of efficiency in DEA–a third pole of technical efficiency. Eur. J. Oper. Res. 2010, 207, 1554–1563. [Google Scholar]
- Che, L.; Bai, Y.; Zhou, L.; Wang, F.; Ji, X.; Qiao, F. Spatial pattern and spillover effects of green development efficiency in China. Sci. Geogr. Sin. 2018, 38, 1788–1798. [Google Scholar]
- Zhao, L.; Cao, N.; Han, Z.; Gao, X. Spatial correlation network and influencing factors of green economic efficiency in China. Resour. Sci. 2021, 43, 1933–1946. [Google Scholar]
- Ren, J.; Ma, Y. Research progress and prospects of green development from the perspective of geography. J. Geogr. Cartogr. 2020, 3, 65–83. [Google Scholar]
- Chen, M.; Liu, W.; Wang, S.; Liu, Y. Spatial pattern and temporal trend of urban ecological efficiency in the Yangtze River Economic Belt. Res. Sci. 2020, 42, 1087–1098. [Google Scholar]
- Zhang, H.; Geng, Z.; Yin, R.; Zhang, W. Regional differences and convergence tendency of green development competitiveness in China. J. Clean. Prod. 2020, 254, 119922. [Google Scholar]
- Wang, Z.; Wang, X.; Liang, L. Green economic efficiency in the Yangtze River Delta: Spatiotemporal evolution and influencing factors. Ecosyst. Health Sustain. 2019, 5, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Tong, Y.; Zou, W. The evolution and a temporal-spatial difference analysis of green development in China. Sustain. Cities Soc. 2018, 41, 52–61. [Google Scholar] [CrossRef]
- Liu, H.; Jia, W. Spatial network correlation and convergence test of regional economic growth in China. Sci. Geogr. Sin. 2019, 39, 726–733. [Google Scholar]
- Liu, S.; Xiao, Q. An empirical analysis on spatial correlation investigation of industrial carbon emissions using SNA-ICE model. Energy 2021, 224, 120183. [Google Scholar]
- Zhang, R.; Tai, H.; Cheng, K.; Zhu, Y.; Hou, J. Carbon emission efficiency network formation mechanism and spatial correlation complexity analysis: Taking the Yangtze River Economic Belt as an example. Sci. Total Environ. 2022, 841, 156719. [Google Scholar]
- Shen, W.; Liang, H.; Dong, L.; Ren, J.; Wang, G. Synergistic CO2 reduction effects in Chinese urban agglomerations: Perspectives from social network analysis. Sci. Total Environ. 2021, 798, 149352. [Google Scholar]
- Ding, L.; Wu, M.; Jiao, Z.; Nie, Y. The positive role of trade openness in industrial green total factor productivity—Provincial evidence from China. Environ. Sci. Pollut. Res. 2022, 29, 6538–6551. [Google Scholar]
- Andersen, P.; Petersen, N.C. A procedure for ranking efficient units in data envelopment analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Tone, K. A strange case of the cost and allocative efficiencies in DEA. J. Oper. Res. Soc. 2002, 53, 1225–1231. [Google Scholar]
- Wang, K.; Liu, Y.; Shi, L.; Liu, L.; Meng, X.; Yang, B. Yangtze River Economic Zone spatial and temporal disparities in industrial green water resource efficiency and influencing factors based on two-step analysis of EBM-Tobit Model. Resour. Sci. 2017, 39, 1522–1534. [Google Scholar]
- Malmquist, S. Index numbers and indifference surfaces. Trab. de Estadística 1953, 4, 209–242. [Google Scholar]
- Yun-jun, Z.; Yun, T. An Analysis of the Evolution of and Difference in Tourism Efficiency of Key Tourism Cities in China—Based on the Super-Efficiency EBM Model. J. Southwest Univ. 2021, 43, 109–119. [Google Scholar]
- Huang, R.; Li, X. The Mechanism and Path for Digital Technology to Improve the Efficiency of China’s Tourism Industry. Contemp. Econ. Res. 2021, 2, 75–84. [Google Scholar]
- Wei, L. Influence of Urban Agglomeration Economic Cooperation on Regional Coordinated Development: Based on Comparison Between Beijing-Tianjin-Hebei and Shanghai-Jiangsu-Zhejiang. Sci. Geogr. Sin. 2018, 38, 575–579. [Google Scholar]
- Liu, H.; Jia, W. Convergence test and coordinated development of China’s regional economic growth under different spatial network correlations. Nankai Econ. Stud. 2019, 3, 104–124. [Google Scholar]
- Zhang, D.; Lu, Y. Study on the Spatial Correlation and Explanation of Carbon Emission in China—Based on Social Network Analysis. Soft Sci. 2017, 31, 15–18. [Google Scholar]
- Scott, J. Social Network Analysis; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2017. [Google Scholar]


| Variables | The First Level | The Second Level | Unit | Weight |
|---|---|---|---|---|
| Input indicators | Capital | The stock of fixed asset investment | CNY 100 million | |
| Environmental Governance | Local fiscal expenditure on environmental protection | CNY 100 million | 0.4091 | |
| Complete investment in industrial pollution control | CNY ten thousand | 0.5909 | ||
| Social Security | Local fiscal social security and employment expenditures | CNY 100 million | 0.3048 | |
| local medical expenditure | CNY 100 million | 0.3660 | ||
| Local fiscal education expenditure | CNY 100 million | 0.3292 | ||
| Technology | Intramural expenditure on R&D | CNY ten thousand | 0.5608 | |
| Local fiscal science and technology expenditure | CNY 100 million | 0.4392 | ||
| Resources | Total water supply | million tons | 0.4456 | |
| Urban Green Area | million hectares | 0.3093 | ||
| Energy consumption | 10,000 tce | 0.2451 | ||
| Labor | Number of employees | ten thousand | ||
| Output indicators | Expected Output | GDP | CNY 100 million | |
| Undesired Output | COD | Tons | ||
| SO2 | Tons |
| Region | ESDE | Region | ESDE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2008 | 2012 | 2016 | 2020 | Average | 2008 | 2012 | 2016 | 2020 | Average | ||
| Beijing | 1.0342 | 1.0559 | 1.0706 | 1.1101 | 1.0673 | Hunan | 0.7466 | 0.8969 | 1.0019 | 1.0183 | 0.9459 |
| Tianjin | 0.7585 | 0.6663 | 0.8032 | 0.8278 | 0.7342 | Guangdong | 1.0108 | 1.0147 | 1.022 | 1.0044 | 1.0134 |
| Hebei | 0.8444 | 0.8359 | 0.8047 | 0.6948 | 0.8153 | Guangxi | 0.6972 | 0.8851 | 0.7918 | 1.0065 | 0.8180 |
| Shanxi | 0.7653 | 0.8179 | 0.7092 | 0.7622 | 0.7825 | Hainan | 1.0407 | 1.0488 | 1.0499 | 1.0969 | 1.0600 |
| Inner Mongolia | 1.0074 | 0.8178 | 1.0090 | 1.0106 | 0.9547 | Chongqing | 0.7700 | 1.0143 | 1.0413 | 1.0155 | 0.9700 |
| Liaoning | 0.6946 | 0.696 | 0.7044 | 0.6049 | 0.6743 | Sichuan | 0.6997 | 0.9131 | 0.9215 | 1.0038 | 0.9050 |
| Jilin | 0.6548 | 0.7925 | 0.7883 | 0.7428 | 0.7355 | Guizhou | 0.7070 | 1.003 | 1.0055 | 0.7474 | 0.8895 |
| Heilongjiang | 0.6768 | 0.7971 | 0.6414 | 0.6142 | 0.6575 | Yunnan | 1.0038 | 1.009 | 0.9103 | 0.8195 | 0.9879 |
| Shanghai | 1.0165 | 1.0213 | 1.0176 | 1.0333 | 1.0233 | Shaanxi | 0.6122 | 0.7609 | 0.7556 | 0.7479 | 0.7264 |
| Jiangsu | 1.0045 | 1.0052 | 1.0152 | 1.0104 | 1.0111 | Gansu | 0.6780 | 0.742 | 0.6808 | 0.6944 | 0.7121 |
| Zhejiang | 1.0113 | 1.0035 | 1.0104 | 1.0066 | 1.0061 | Qinghai | 0.6516 | 0.7447 | 0.7371 | 1.0053 | 0.7753 |
| Anhui | 0.8191 | 1.0022 | 0.9188 | 1.0005 | 0.9533 | Ningxia | 0.6502 | 0.7141 | 0.6255 | 0.6554 | 0.6587 |
| Fujian | 1.0065 | 1.0169 | 1.0178 | 1.0243 | 1.0189 | Xinjiang | 1.0032 | 1.0160 | 0.6988 | 1.0368 | 0.9860 |
| Jiangxi | 0.7618 | 1.0241 | 1.0082 | 1.0070 | 0.9576 | Eastern region | 0.9474 | 0.9161 | 0.9363 | 0.9256 | 0.9294 |
| Shandong | 1.0000 | 0.7129 | 0.7831 | 0.7682 | 0.7992 | Central region | 0.7700 | 0.9028 | 0.8659 | 0.8649 | 0.8559 |
| Henan | 1.0048 | 1.0025 | 1.0047 | 1.0036 | 0.9708 | Western region | 0.7709 | 0.8746 | 0.8343 | 0.8857 | 0.8530 |
| Hubei | 0.7307 | 0.8894 | 0.8544 | 0.7704 | 0.8438 | The whole area | 0.8354 | 0.8973 | 0.8801 | 0.8948 | 0.8818 |
| Region | 2009 | 2012 | 2016 | 2020 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MI | EC | TC | MI | EC | TC | MI | EC | TC | MI | EC | TC | |
| Beijing | 1.0168 | 0.9989 | 1.0179 | 0.7158 | 0.9829 | 0.7283 | 1.0849 | 1.0151 | 1.0688 | 0.9948 | 0.9951 | 0.9997 |
| Tianjin | 0.9506 | 0.9612 | 0.9890 | 0.9452 | 0.9938 | 0.9510 | 1.2822 | 1.3115 | 0.9777 | 0.9098 | 0.9681 | 0.9398 |
| Hebei | 0.9704 | 1.1847 | 0.8191 | 0.9540 | 0.8349 | 1.1426 | 1.1507 | 1.1069 | 1.0396 | 0.8469 | 0.9515 | 0.8900 |
| Shanxi | 0.8627 | 0.9300 | 0.9276 | 0.9617 | 0.8171 | 1.1769 | 1.1124 | 0.9146 | 1.2163 | 0.8484 | 0.9660 | 0.8782 |
| Inner Mongolia | 0.7404 | 1.0001 | 0.7403 | 0.9989 | 1.0451 | 0.9558 | 1.1429 | 1.0033 | 1.1391 | 0.9906 | 0.9800 | 1.0109 |
| Liaoning | 0.9342 | 0.9935 | 0.9404 | 0.9879 | 1.0904 | 0.9061 | 1.1237 | 1.0112 | 1.1113 | 0.8059 | 0.8559 | 0.9415 |
| Jilin | 0.8959 | 0.9769 | 0.9171 | 0.9852 | 1.0821 | 0.9105 | 1.2162 | 1.1659 | 1.0432 | 0.9354 | 0.9810 | 0.9535 |
| Heilongjiang | 0.8799 | 0.9460 | 0.9301 | 1.0004 | 1.2143 | 0.8238 | 1.1256 | 1.0827 | 1.0396 | 0.9198 | 0.9539 | 0.9643 |
| Shanghai | 0.9994 | 1.0009 | 0.9985 | 0.9702 | 0.9967 | 0.9734 | 1.0879 | 0.9961 | 1.0921 | 1.0053 | 1.0028 | 1.0024 |
| Jiangsu | 0.9701 | 0.9994 | 0.9706 | 0.9063 | 0.9993 | 0.9070 | 1.1017 | 0.9999 | 1.1018 | 1.0054 | 0.9984 | 1.0070 |
| Zhejiang | 0.8935 | 0.9889 | 0.9035 | 0.9484 | 0.9976 | 0.9507 | 1.1537 | 1.0089 | 1.1435 | 1.0031 | 0.9981 | 1.0050 |
| Anhui | 0.9698 | 1.0277 | 0.9436 | 0.9835 | 0.9994 | 0.9841 | 1.0768 | 1.0308 | 1.0446 | 0.8201 | 0.9978 | 0.8219 |
| Fujian | 0.9893 | 1.0029 | 0.9865 | 0.8685 | 0.9986 | 0.8698 | 1.1171 | 0.9986 | 1.1187 | 0.9937 | 0.9984 | 0.9953 |
| Jiangxi | 0.9747 | 1.0244 | 0.9514 | 1.2541 | 1.0074 | 1.2449 | 1.0590 | 0.9989 | 1.0602 | 1.0030 | 1.0013 | 1.0017 |
| Shandong | 0.9681 | 1.0006 | 0.9675 | 0.9480 | 0.9991 | 0.9489 | 1.1467 | 1.0990 | 1.0434 | 0.8338 | 0.8723 | 0.9559 |
| Henan | 0.8351 | 0.9991 | 0.8359 | 0.9926 | 1.1497 | 0.8633 | 1.1351 | 1.0000 | 1.1351 | 0.9952 | 0.9944 | 1.0009 |
| Hubei | 0.9597 | 1.0192 | 0.9416 | 0.9841 | 1.0309 | 0.9546 | 1.0885 | 0.9791 | 1.1117 | 0.8095 | 0.8365 | 0.9677 |
| Hunan | 0.9500 | 1.0198 | 0.9315 | 0.9681 | 0.9524 | 1.0165 | 1.1034 | 1.0004 | 1.1030 | 1.0066 | 1.0087 | 0.9979 |
| Guangdong | 0.9941 | 0.9995 | 0.9946 | 0.8557 | 0.9955 | 0.8596 | 1.2144 | 1.0014 | 1.2126 | 0.9991 | 0.9932 | 1.0059 |
| Guangxi | 0.8808 | 1.0121 | 0.8702 | 0.9767 | 1.0317 | 0.9467 | 1.0630 | 0.9590 | 1.1085 | 0.9426 | 1.3057 | 0.7219 |
| Hainan | 0.8639 | 0.9981 | 0.8655 | 0.9668 | 0.9939 | 0.9727 | 0.9014 | 0.9860 | 0.9142 | 1.0789 | 1.0234 | 1.0542 |
| Chongqing | 0.9505 | 1.0154 | 0.9360 | 1.0091 | 1.0056 | 1.0035 | 1.3225 | 1.0238 | 1.2918 | 0.9810 | 0.9721 | 1.0091 |
| Sichuan | 0.9688 | 1.0182 | 0.9515 | 1.0360 | 1.1242 | 0.9215 | 1.1117 | 0.9206 | 1.2076 | 0.8367 | 0.9961 | 0.8400 |
| Guizhou | 0.9561 | 1.0129 | 0.9439 | 1.0529 | 1.2159 | 0.8660 | 1.3104 | 0.9892 | 1.3247 | 0.8646 | 0.9377 | 0.9220 |
| Yunnan | 0.9678 | 1.0023 | 0.9656 | 1.0068 | 0.9994 | 1.0073 | 1.0901 | 0.9076 | 1.2010 | 0.6957 | 0.8080 | 0.8611 |
| Shaanxi | 0.9358 | 0.9803 | 0.9546 | 1.0684 | 1.0977 | 0.9734 | 1.0999 | 1.0150 | 1.0837 | 0.8681 | 0.9692 | 0.8957 |
| Gansu | 0.9510 | 1.0184 | 0.9338 | 0.9882 | 1.0256 | 0.9635 | 1.1099 | 0.9703 | 1.1439 | 0.8753 | 0.9447 | 0.9266 |
| Qinghai | 0.8365 | 0.9283 | 0.9011 | 0.9722 | 1.0790 | 0.9010 | 1.1087 | 0.9820 | 1.1290 | 1.1512 | 1.1797 | 0.9758 |
| Ningxia | 0.9395 | 0.9946 | 0.9446 | 0.9890 | 1.0082 | 0.9809 | 1.0093 | 0.9346 | 1.0799 | 1.0458 | 1.1291 | 0.9262 |
| Xinjiang | 0.6847 | 0.9990 | 0.6854 | 0.7248 | 1.0022 | 0.7233 | 1.0198 | 0.6977 | 1.4617 | 1.0036 | 1.0312 | 0.9733 |
| The whole area | 0.9300 | 1.0032 | 0.9283 | 0.9650 | 1.0141 | 0.9583 | 1.1297 | 1.0425 | 1.0874 | 0.9247 | 0.9619 | 0.9609 |
| Eastern region | 0.9591 | 1.0117 | 0.9503 | 0.9152 | 0.9893 | 0.9282 | 1.1240 | 1.0486 | 1.0749 | 0.9524 | 0.9689 | 0.9815 |
| Central region | 0.9111 | 0.9890 | 0.9211 | 1.0231 | 1.0430 | 0.9940 | 1.1162 | 1.0246 | 1.0929 | 0.9045 | 0.9616 | 0.9412 |
| Western region | 0.8920 | 0.9983 | 0.8934 | 0.9839 | 1.0577 | 0.9312 | 1.1262 | 0.9457 | 1.1973 | 0.9323 | 1.0230 | 0.9148 |
| Year | Contribution Rate (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| East | Center | West | East–Center | Center–West | Center–West | |||||
| 2008 | 0.1000 | 0.0590 | 0.0670 | 0.0990 | 0.0887 | 0.1009 | 0.0891 | 49.1700 | 25.2000 | 25.6300 |
| 2009 | 0.1040 | 0.0520 | 0.0770 | 0.1050 | 0.0922 | 0.1019 | 0.0959 | 50.8080 | 24.2030 | 24.9890 |
| 2010 | 0.1020 | 0.0690 | 0.0960 | 0.1010 | 0.0897 | 0.1027 | 0.1010 | 42.5430 | 28.8930 | 28.5630 |
| 2011 | 0.0910 | 0.0840 | 0.0770 | 0.0820 | 0.0852 | 0.0944 | 0.0841 | 29.0200 | 40.5560 | 30.4240 |
| 2012 | 0.0780 | 0.0840 | 0.0560 | 0.0750 | 0.0767 | 0.0833 | 0.0687 | 13.8190 | 53.6090 | 32.5720 |
| 2013 | 0.0920 | 0.0950 | 0.0820 | 0.0820 | 0.0961 | 0.0920 | 0.0840 | 16.7100 | 50.9820 | 32.3070 |
| 2014 | 0.0920 | 0.0970 | 0.0810 | 0.0830 | 0.0962 | 0.0939 | 0.0830 | 12.7920 | 54.6110 | 32.5970 |
| 2015 | 0.0950 | 0.0960 | 0.0960 | 0.0830 | 0.0999 | 0.0913 | 0.0904 | 12.8360 | 54.3850 | 32.7790 |
| 2016 | 0.0900 | 0.0700 | 0.0860 | 0.0960 | 0.0808 | 0.0904 | 0.0930 | 29.9030 | 38.6650 | 31.4310 |
| 2017 | 0.0760 | 0.0770 | 0.0690 | 0.0710 | 0.0767 | 0.0745 | 0.0733 | 10.8240 | 56.3640 | 32.8130 |
| 2018 | 0.0810 | 0.0830 | 0.0710 | 0.0800 | 0.0807 | 0.0825 | 0.0777 | 8.4360 | 58.1750 | 33.3890 |
| 2019 | 0.0860 | 0.0740 | 0.0800 | 0.0930 | 0.0789 | 0.0870 | 0.0886 | 22.6990 | 44.7110 | 32.5900 |
| 2020 | 0.0940 | 0.0950 | 0.0920 | 0.0870 | 0.0972 | 0.0932 | 0.0902 | 15.8240 | 51.0470 | 33.1290 |
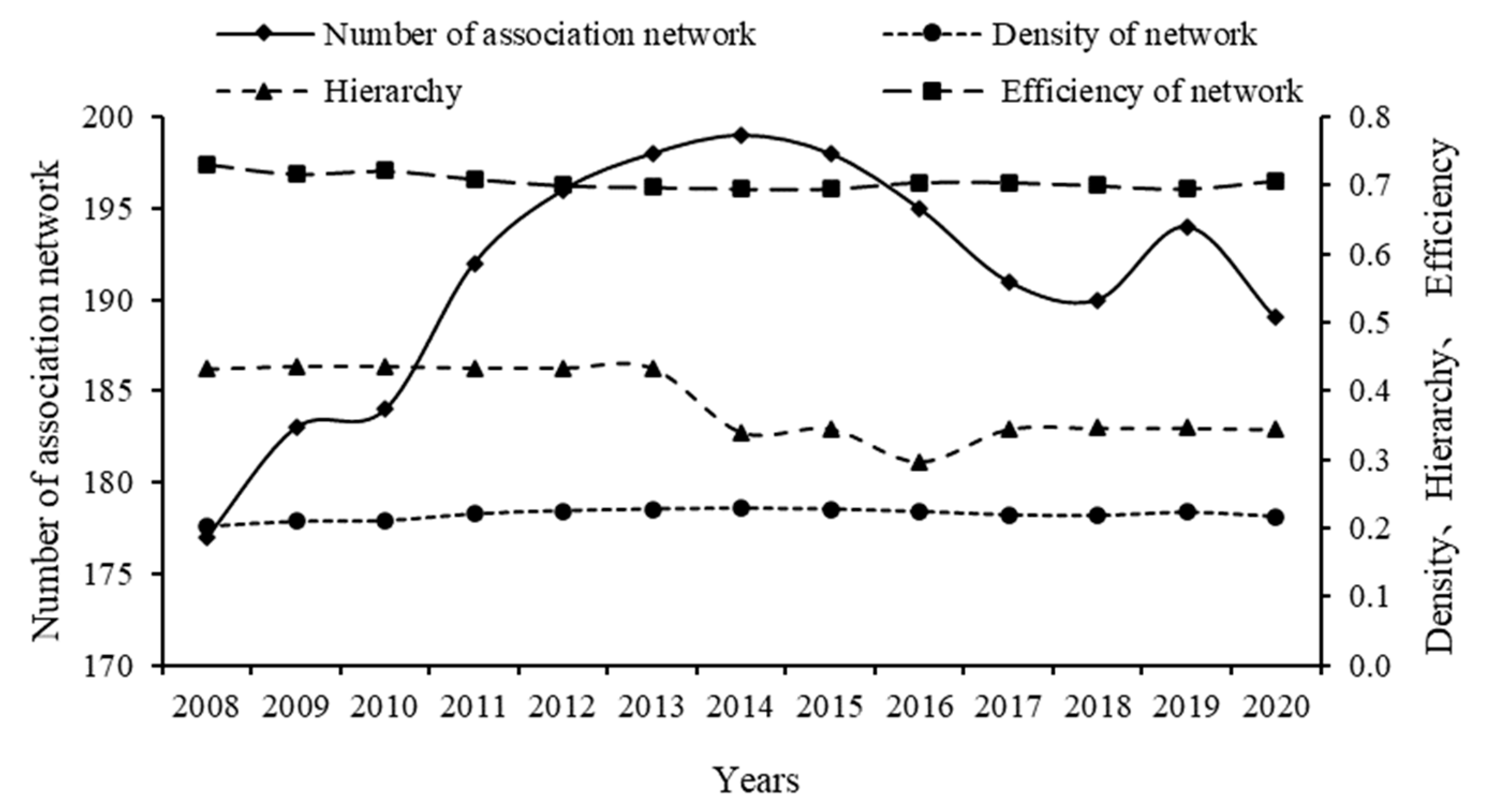
| Year | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of association networks | 177 | 183 | 184 | 192 | 196 | 198 | 199 | 198 | 195 | 191 | 190 | 194 | 189 |
| Density of network | 0.2034 | 0.2103 | 0.2115 | 0.2207 | 0.2253 | 0.2276 | 0.2287 | 0.2276 | 0.2241 | 0.2195 | 0.2184 | 0.223 | 0.2172 |
| Hierarchy | 0.432 | 0.4361 | 0.4361 | 0.4337 | 0.4337 | 0.4337 | 0.3404 | 0.3452 | 0.2974 | 0.3444 | 0.346 | 0.346 | 0.3444 |
| Efficiency of network | 0.7315 | 0.7167 | 0.7217 | 0.7094 | 0.6995 | 0.697 | 0.6946 | 0.6946 | 0.7044 | 0.7044 | 0.6995 | 0.6946 | 0.7069 |
| Region | Year 2008 | Year 2012 | Year 2016 | Year 2020 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In- Degree | Out- Degree | Number of Association Network | In- Degree | Out- Degree | Number of Association Network | In- Degree | Out- Degree | Number of Association Network | In- Degree | Out- Degree | Number of Association Network | |
| Beijing | 6 | 24 | 30 | 6 | 24 | 30 | 6 | 23 | 29 | 6 | 24 | 30 |
| Tianjin | 5 | 15 | 20 | 5 | 16 | 21 | 5 | 12 | 17 | 3 | 10 | 13 |
| Hebei | 4 | 3 | 7 | 5 | 4 | 9 | 5 | 4 | 9 | 5 | 5 | 10 |
| Shanxi | 5 | 2 | 7 | 5 | 3 | 8 | 6 | 5 | 11 | 5 | 2 | 7 |
| Inner Mongolia | 3 | 1 | 4 | 6 | 1 | 7 | 5 | 2 | 7 | 5 | 1 | 6 |
| Liaoning | 5 | 2 | 7 | 6 | 2 | 8 | 4 | 2 | 6 | 5 | 1 | 6 |
| Jilin | 6 | 1 | 7 | 6 | 1 | 7 | 6 | 0 | 6 | 5 | 0 | 5 |
| Heilongjiang | 6 | 1 | 7 | 7 | 1 | 8 | 7 | 0 | 7 | 7 | 0 | 7 |
| Shanghai | 7 | 27 | 34 | 8 | 27 | 35 | 7 | 27 | 34 | 7 | 27 | 34 |
| Jiangsu | 5 | 22 | 27 | 5 | 25 | 30 | 5 | 27 | 32 | 6 | 26 | 32 |
| Zhejiang | 4 | 20 | 24 | 4 | 19 | 23 | 4 | 18 | 22 | 4 | 19 | 23 |
| Anhui | 3 | 6 | 9 | 3 | 6 | 9 | 3 | 6 | 9 | 3 | 4 | 7 |
| Fujian | 7 | 1 | 8 | 9 | 6 | 15 | 7 | 6 | 13 | 8 | 10 | 18 |
| Jiangxi | 6 | 5 | 11 | 7 | 6 | 13 | 7 | 6 | 13 | 7 | 6 | 13 |
| Shandong | 7 | 11 | 18 | 6 | 9 | 15 | 7 | 9 | 16 | 5 | 9 | 14 |
| Henan | 6 | 5 | 11 | 6 | 9 | 15 | 6 | 8 | 14 | 6 | 6 | 12 |
| Hubei | 5 | 4 | 9 | 6 | 5 | 11 | 8 | 5 | 13 | 7 | 5 | 12 |
| Hunan | 5 | 2 | 7 | 7 | 3 | 10 | 7 | 3 | 10 | 7 | 2 | 9 |
| Guangdong | 10 | 14 | 24 | 10 | 11 | 21 | 11 | 10 | 21 | 10 | 10 | 20 |
| Guangxi | 5 | 1 | 6 | 6 | 2 | 8 | 7 | 4 | 11 | 7 | 3 | 10 |
| Hainan | 5 | 1 | 6 | 6 | 1 | 7 | 7 | 1 | 8 | 6 | 1 | 7 |
| Chongqing | 7 | 2 | 9 | 8 | 3 | 11 | 8 | 5 | 13 | 8 | 6 | 14 |
| Sichuan | 8 | 2 | 10 | 8 | 2 | 10 | 6 | 2 | 8 | 8 | 2 | 10 |
| Guizhou | 6 | 2 | 8 | 8 | 4 | 12 | 8 | 2 | 10 | 7 | 2 | 9 |
| Yunnan | 5 | 1 | 6 | 8 | 2 | 10 | 7 | 2 | 9 | 7 | 2 | 9 |
| Shaanxi | 7 | 0 | 7 | 7 | 1 | 8 | 6 | 1 | 7 | 5 | 1 | 6 |
| Gansu | 7 | 2 | 9 | 8 | 3 | 11 | 10 | 4 | 14 | 9 | 5 | 14 |
| Qinghai | 8 | 0 | 8 | 8 | 0 | 8 | 7 | 1 | 8 | 8 | 0 | 8 |
| Ningxia | 8 | 0 | 8 | 6 | 0 | 6 | 7 | 0 | 7 | 6 | 0 | 6 |
| Xinjiang | 6 | 0 | 6 | 6 | 0 | 6 | 6 | 0 | 6 | 7 | 0 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Cao, Y. Spatial Association Network Evolution and Variance Decomposition of Economic Sustainability Development Efficiency in China. Int. J. Environ. Res. Public Health 2023, 20, 2966. https://doi.org/10.3390/ijerph20042966
Fang X, Cao Y. Spatial Association Network Evolution and Variance Decomposition of Economic Sustainability Development Efficiency in China. International Journal of Environmental Research and Public Health. 2023; 20(4):2966. https://doi.org/10.3390/ijerph20042966
Chicago/Turabian StyleFang, Xin, and Yun Cao. 2023. "Spatial Association Network Evolution and Variance Decomposition of Economic Sustainability Development Efficiency in China" International Journal of Environmental Research and Public Health 20, no. 4: 2966. https://doi.org/10.3390/ijerph20042966





